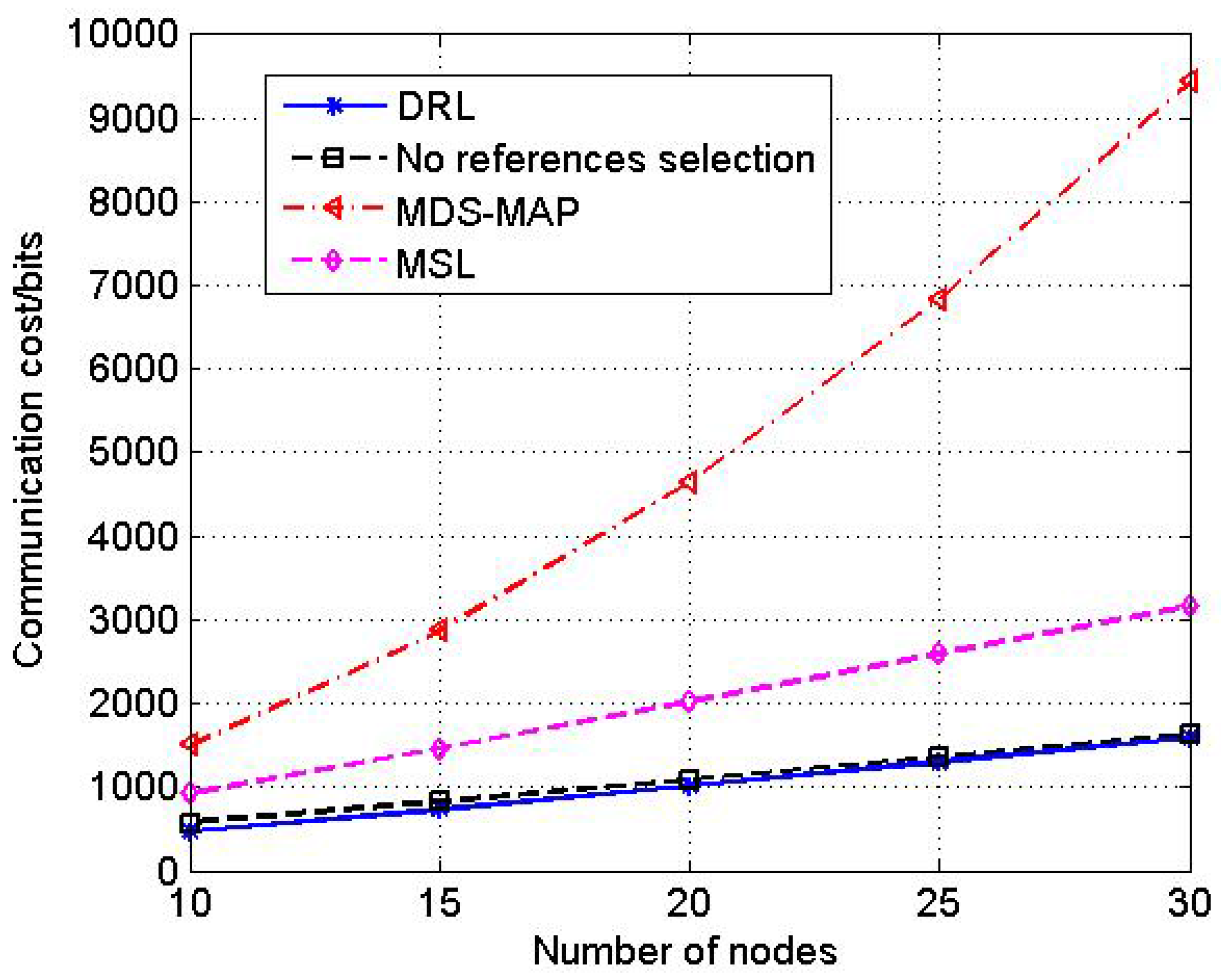
DRL is a range-based localization algorithm. It can be used in static or relatively static UANs. The proposed DRL algorithm includes two schemes. (1) a Double Rate Scheme is proposed for multi-hop UANs which separates the localization process into two procedures by changing the bit duration . Each procedure uses different transmission modes including the high rate transmission mode (HM) and the low rate transmission mode (LM) to make the range measurement in the multi-hop UANs more accurate while maintaining the data transmission rate; (2) An optimal selection scheme of reference nodes is proposed to accomplish the localization procedure with only one anchor and reduce the influence of anchor and references’ topology on the localization performance to increase the localization accuracy as well.
3.1. The Double Rate Scheme
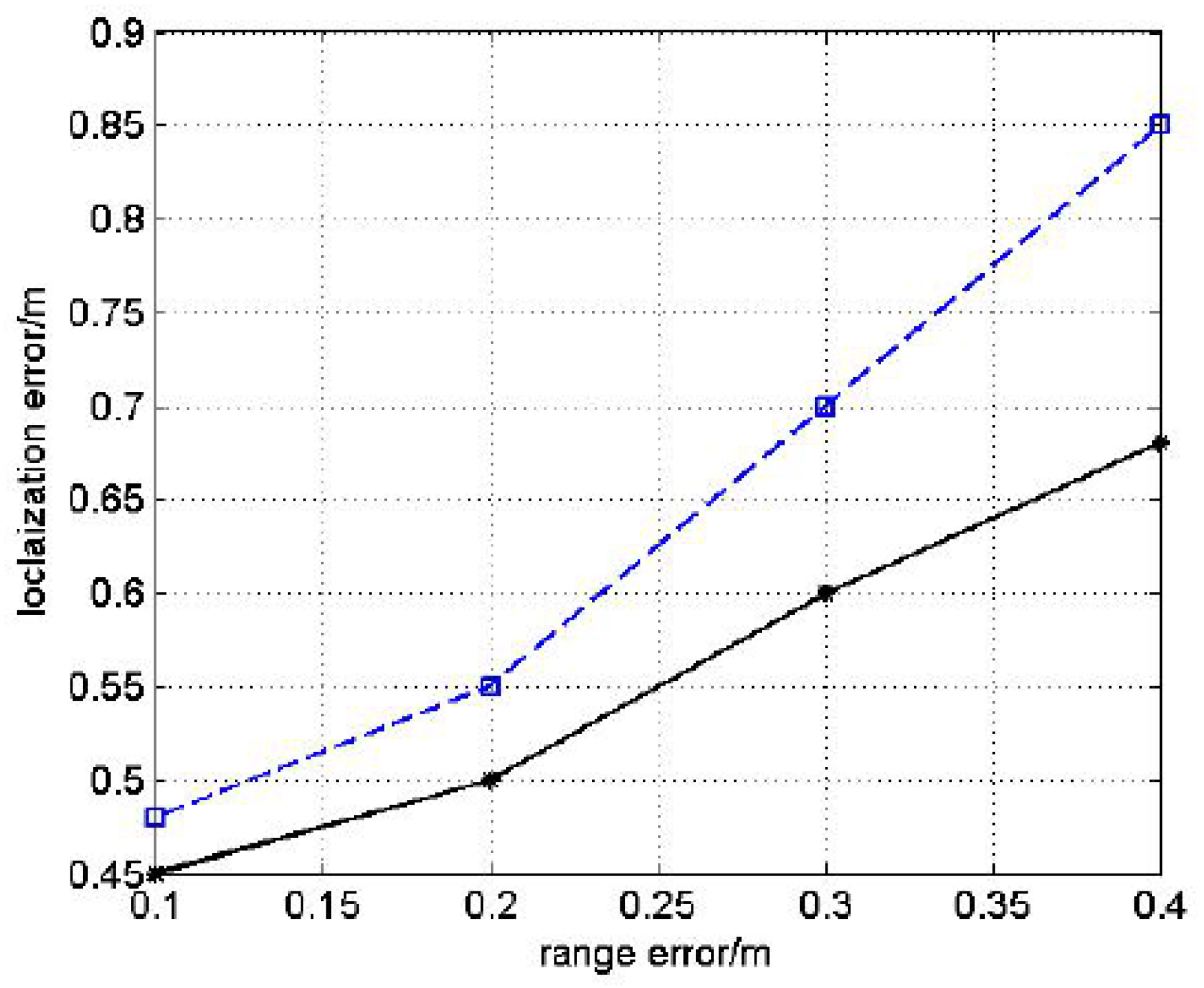
Recently, most of the localization algorithms have a good performance only for one-hop UANs. However, one-hop UANs have a limitation on the detection range and other networks’ applications. In this paper, we mainly focus on the multi-hop networks which can increase the network’s scale, but introduce a challenge in terms of ranging accuracy which will ultimately have an effect on the localization performance.
In this section, we propose a Double Rate Scheme by analyzing the relationship between bit duration and transmission range in an underwater environment. In this scheme, we separate the localization process into two procedures and each procedure uses a different transmission mode to increase the ranging accuracy in multi-hop UANs while maintaining the data transmission rate.
3.1.1. The Relationship between Code-Width and Transmission Range
The sonar equation is shown in Equation (
1).
is the Source Level which is connected with the nodes’ property;
is the Transmission Loss;
is the Noise Level;
and should be selected according to the environment;
is the Signal to Noise Ratio;
All of the parameters above are measured by .
is the signal power;
is the noise power;
is the unilateral power spectral density of Gaussian white noise;
B is the bandwidth of signal; for binary data,
is the bit duration of signal. means the transmission time duration of one bit data.
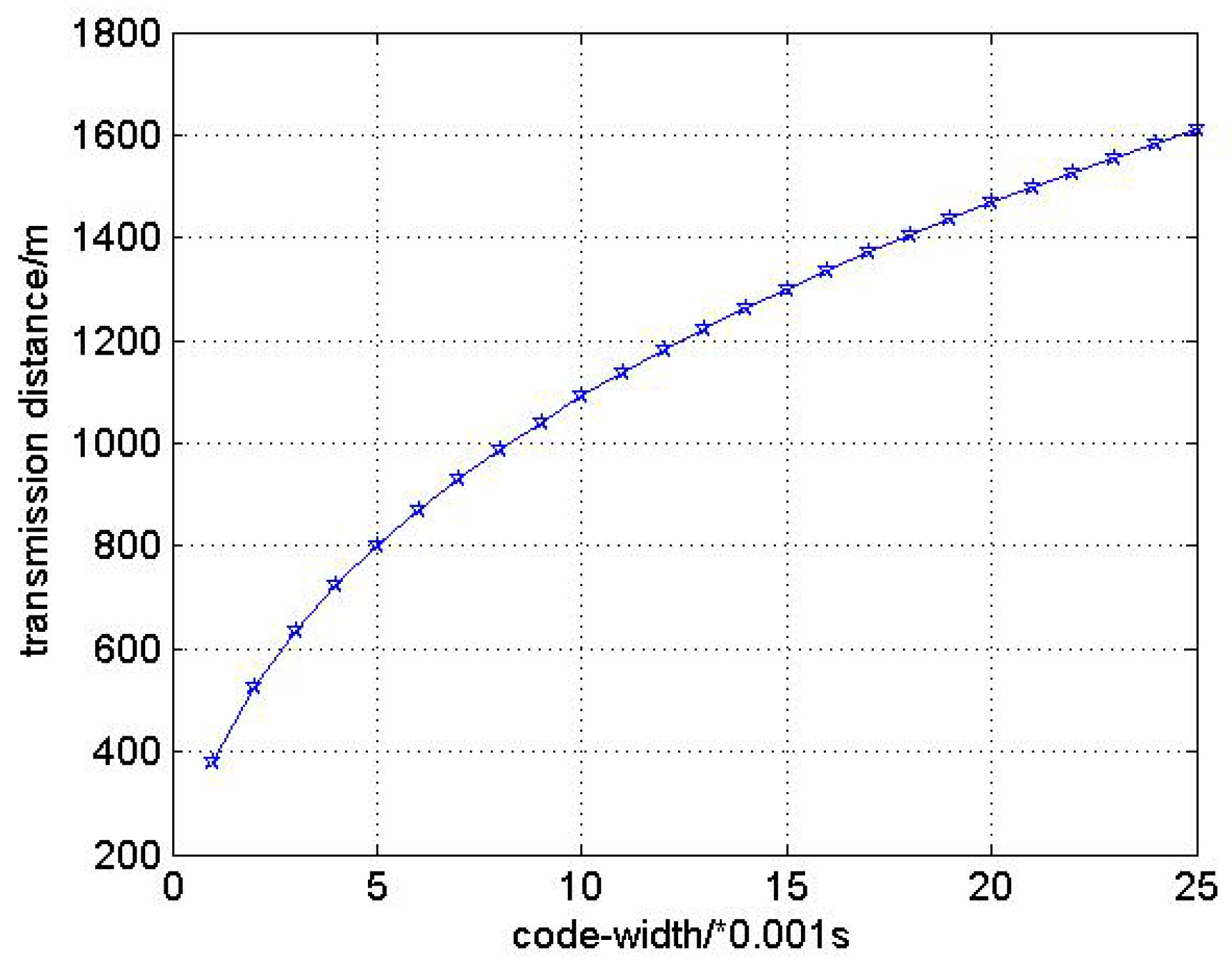
From Equations (1)–(3), we can see that if of transmitted signal is increased N times, the bandwidth B will reduce to and will be increased by . While, if we keep , and be unchangeable, the will be ultimately increased by .
is the is the coefficient of sound absorption. . f is the frequency of transmission signal. r is the transmission distance.
From Equation (
4) we can see that the increase of bit duration
will finally enlarge the transmission distance
r which will make the ranging signal cover a larger scope and improve the distance measurement accuracy in multi-hop networks.
3.1.2. The Double Rate Scheme in DRL Algorithm
Based on the relationship between and the transmission range, in this paper, we propose a Double Rate Scheme that separates the localization process into ranging procedure and localization procedure. Each of them uses different transmission mode by choosing proper .
The two transmission modes are defined as low-rate transmission mode (LM) and high-rate transmission mode (HM), which are used in the ranging and localization procedure respectively.
- (1)
Low-rate Mode(LM): The signal of the low-rate mode has a large code-width which could transmit a great distance based on Equation (
3). Hence, the LM signal can be used in the ranging procedure by choosing an appropriate code-width so that the signal could transmit across the network to increase the ranging accuracy in multi-hop networks.
- (2)
High-rate Mode(HM): In contrast, the signal of the high-rate mode has a small code-width which could only transmit a one hop distance. However, signal of HM could be used in the localization procedure to transmit a mass of data at a high rate.
According to the analysis above, the proposed Double Rate Scheme could improve the ranging accuracy in multi-hop networks as well as maintaining the data transmission rate.
3.2. The Optimal Selection Scheme of Reference Nodes for One Anchor UANs
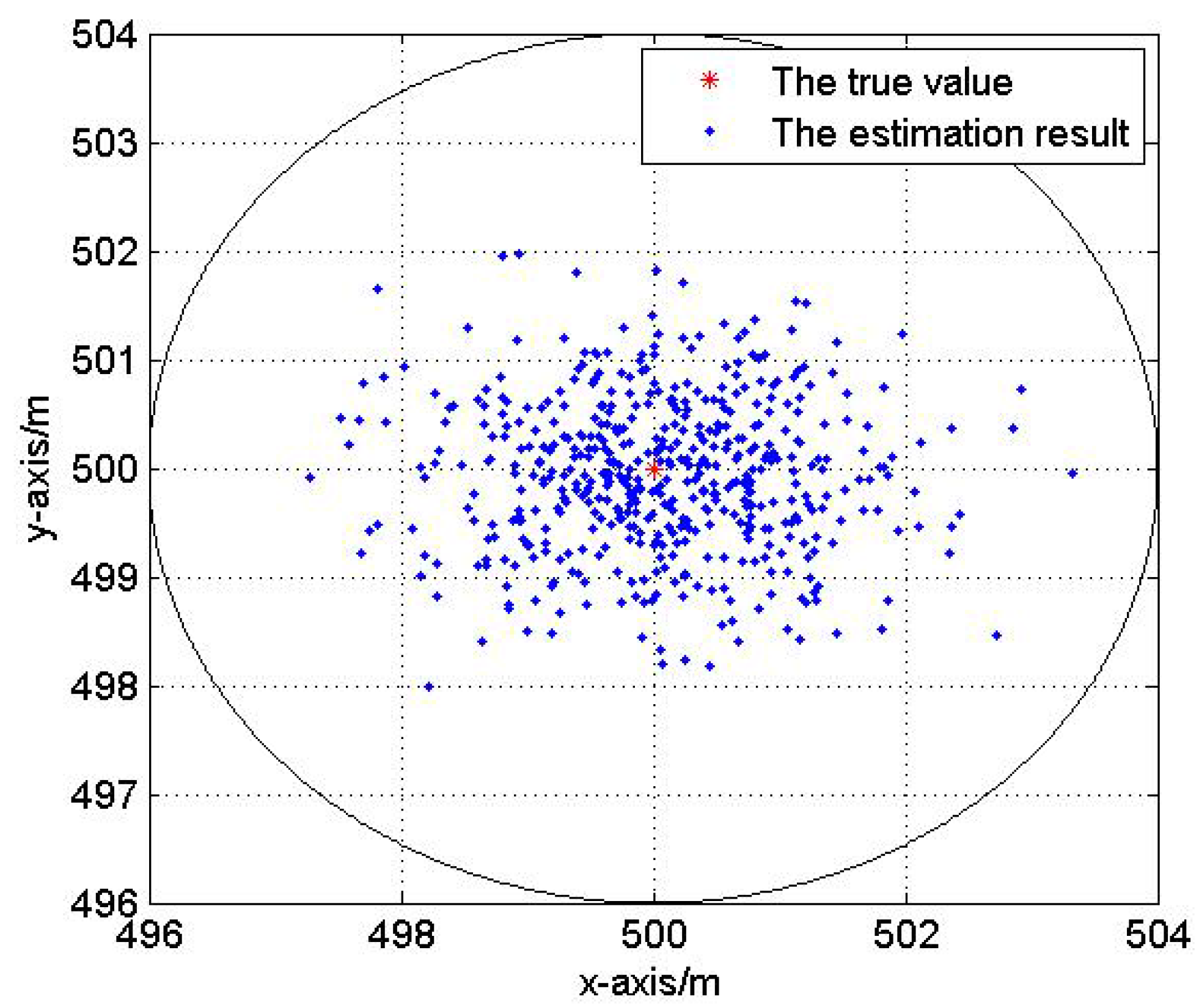
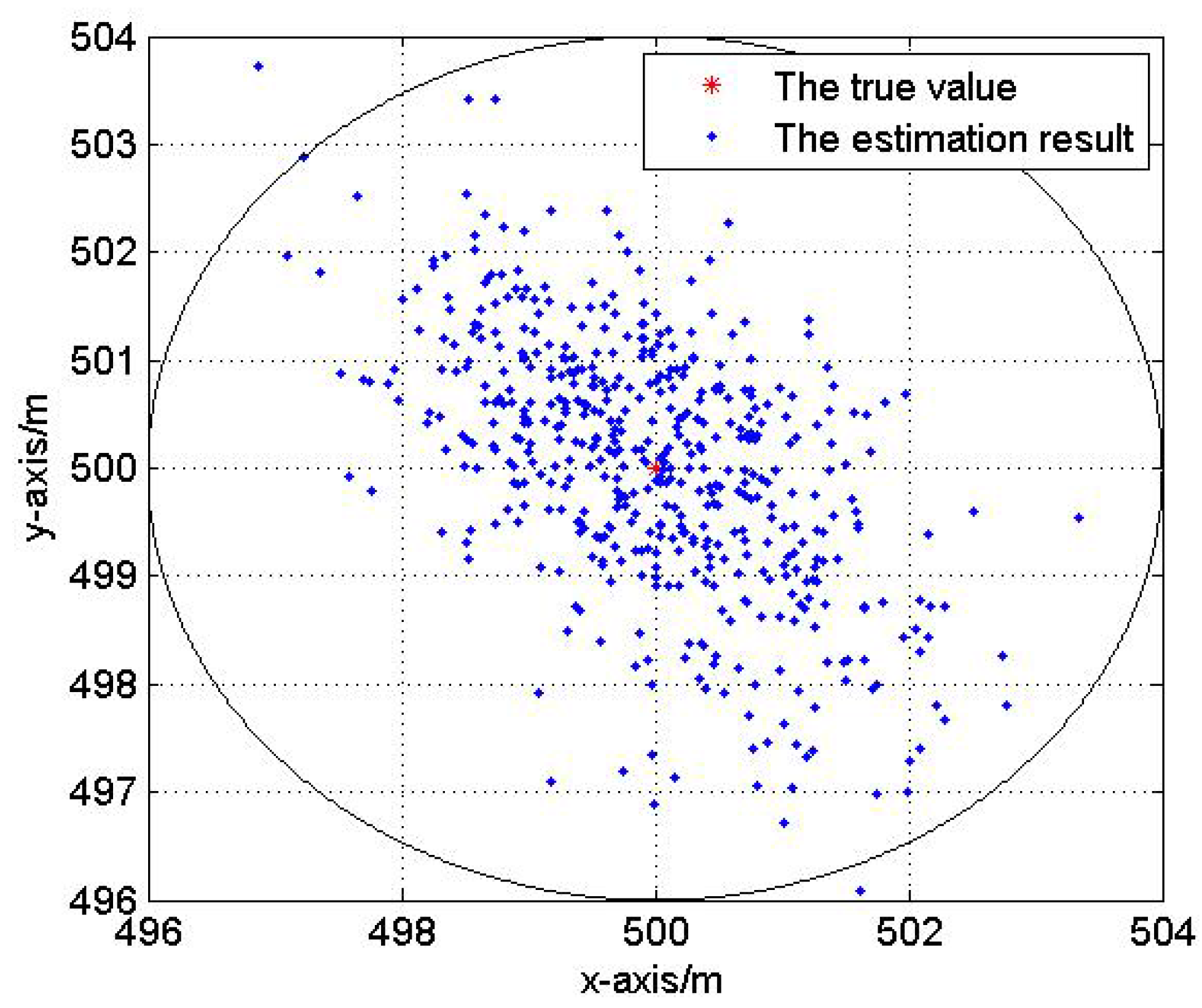
The proposed DRL algorithm only needs one anchor to accomplish the localization procedure with high accuracy. The only anchor selects two unknown nodes in UANs as references to help. However, different references’ selection has different localization performance. Hence, in this section, we propose an Optimal Selection Scheme of reference nodes to reduce the influence of references’ topology on localization accuracy.
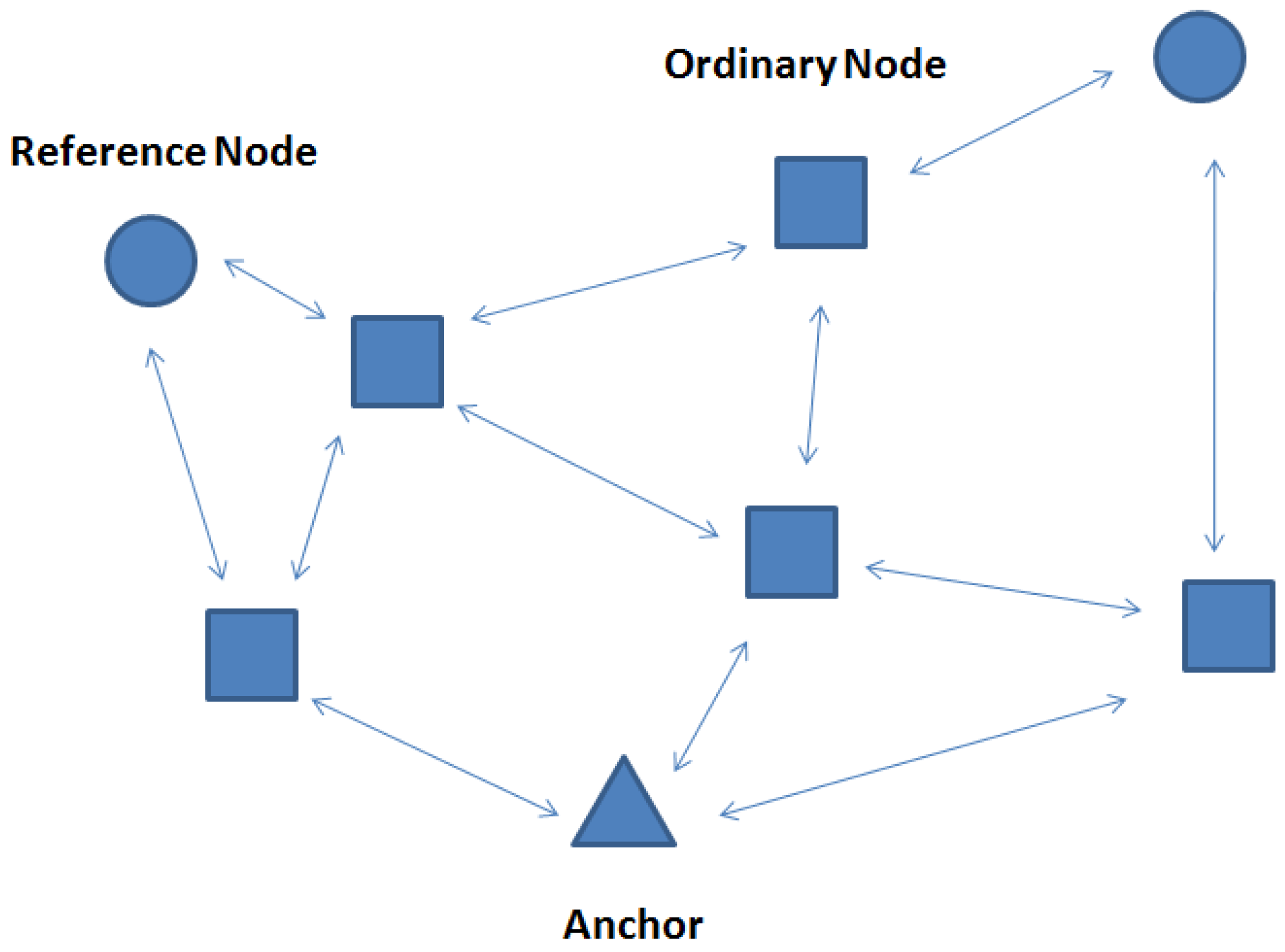
Assume that P sensor nodes are randomly distributed in a region including one anchor and P-1 unknown nodes. Two reference nodes and are selected by from all unknown nodes and the rest of them are ordinary nodes , , . The distance between ordinary node and , , are expressed by , and respectively.
is the additive measurement noise error.
The least square (LS) estimation of Equation (
5) is
The resulting estimation function (6) is a non-linear form. By expensing and subtracting the Equation (
6), we get
Then we linearize (6) into Equation (
7) and derive the solution as in Equation (
8).
According to the analysis above, we can also get the estimated location error of node i .
Hence, the estimated location error
E for the whole network with
M nodes is shown as Equation (
9).
Then we can find the optimum reference nodes
,
from
E to get the minimum location error. Transform Equation (
8) into an optimization problem.
, and should not be in a line. Thus, the proposed algorithm should not work in a linear network structure.
The optimization problem (11) can be solved using interior point methods. According to the objective function, we find the optimal references selection and in the constraint area that makes the localization error to be minimum.
DRL can be extended to the 3-dimensional networks by selecting three reference nodes.
3.3. The Implementation of DRL Algorithm
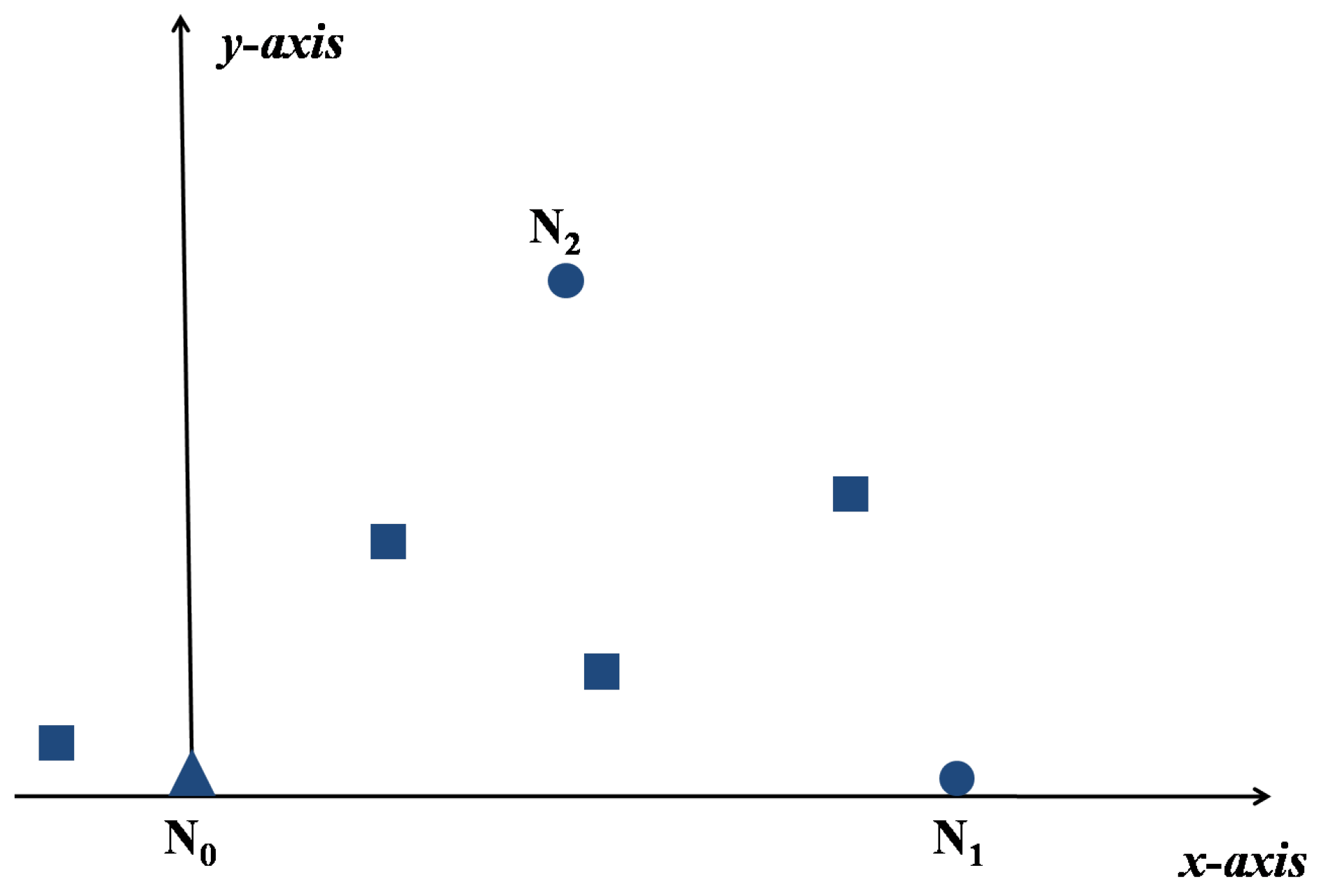
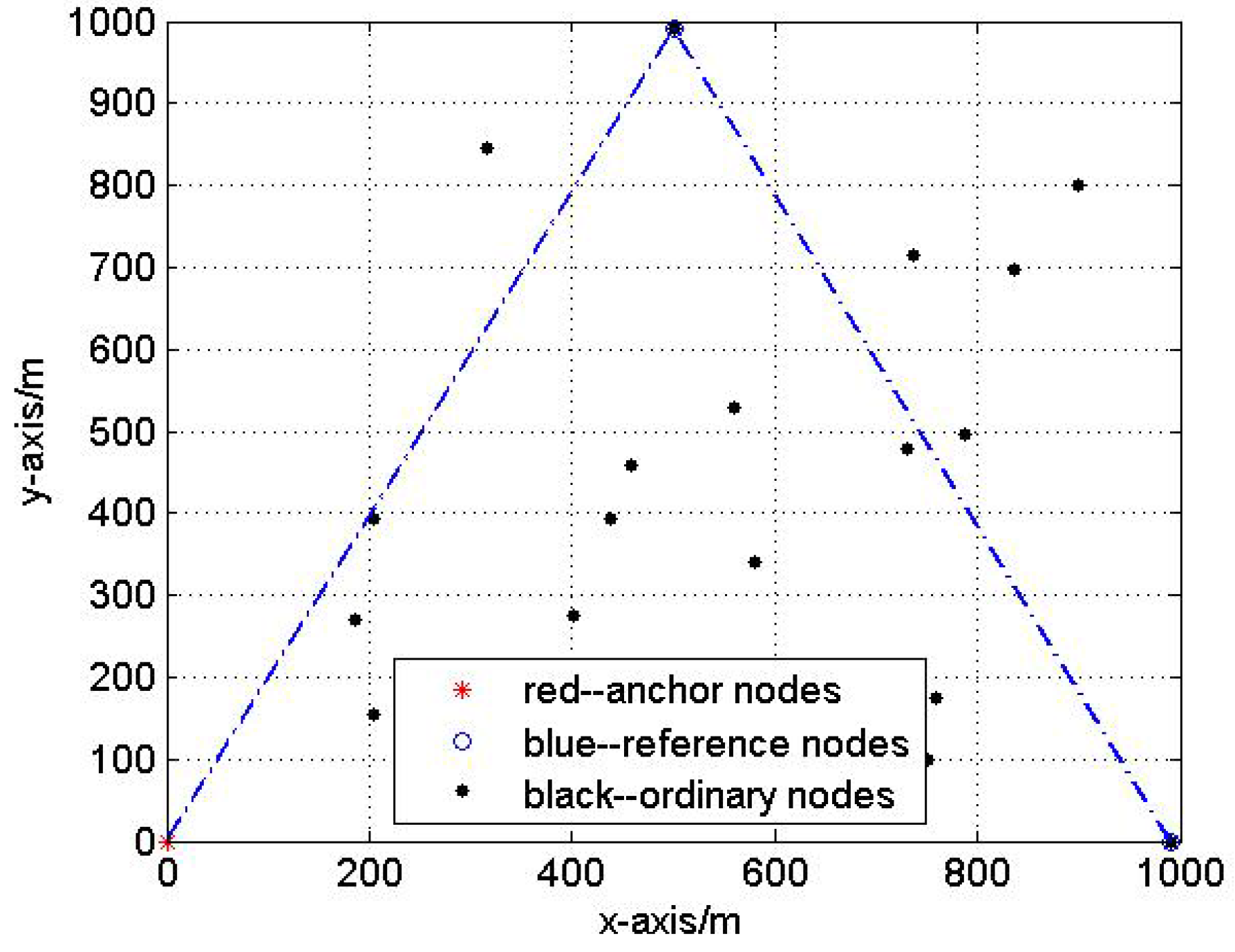
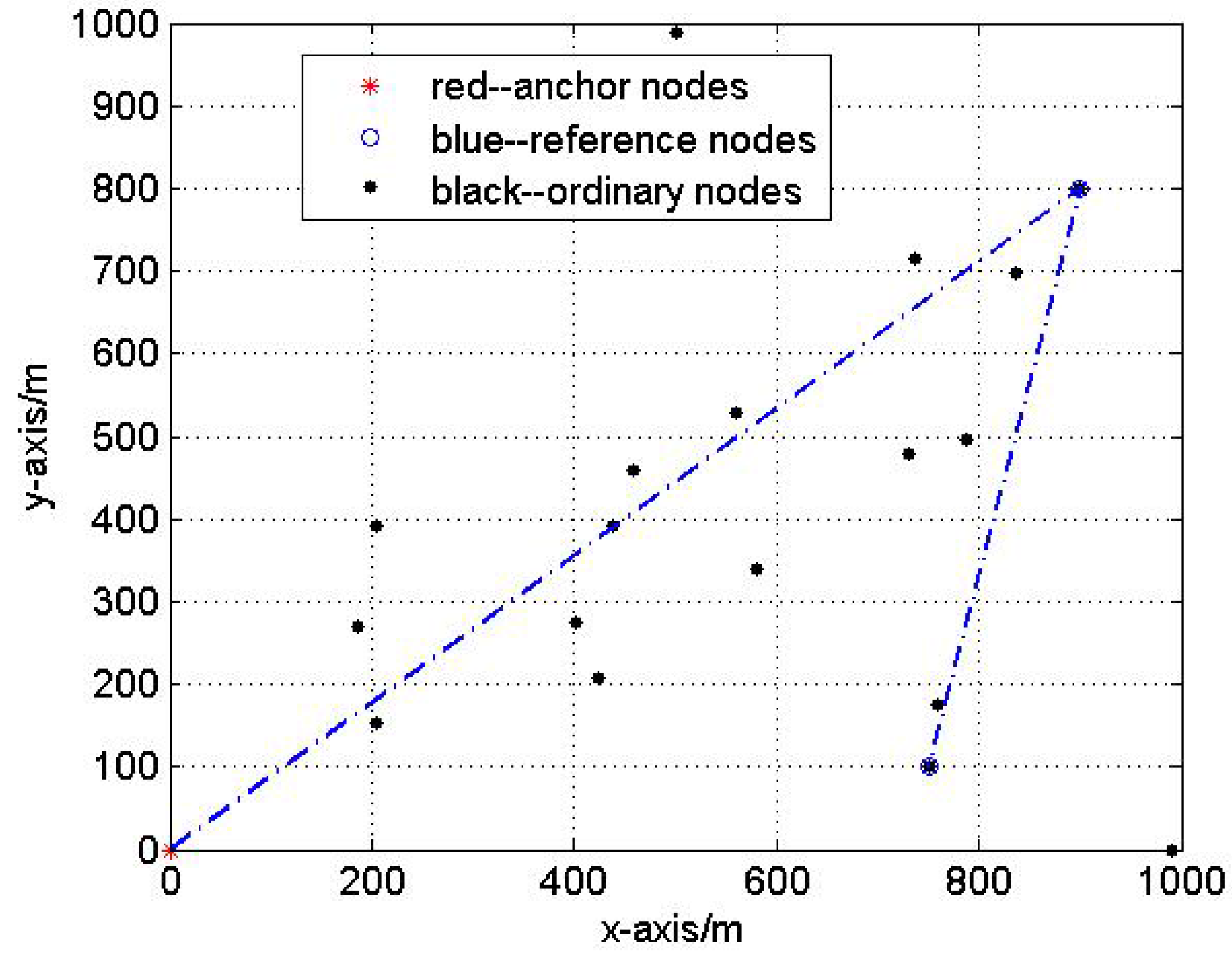
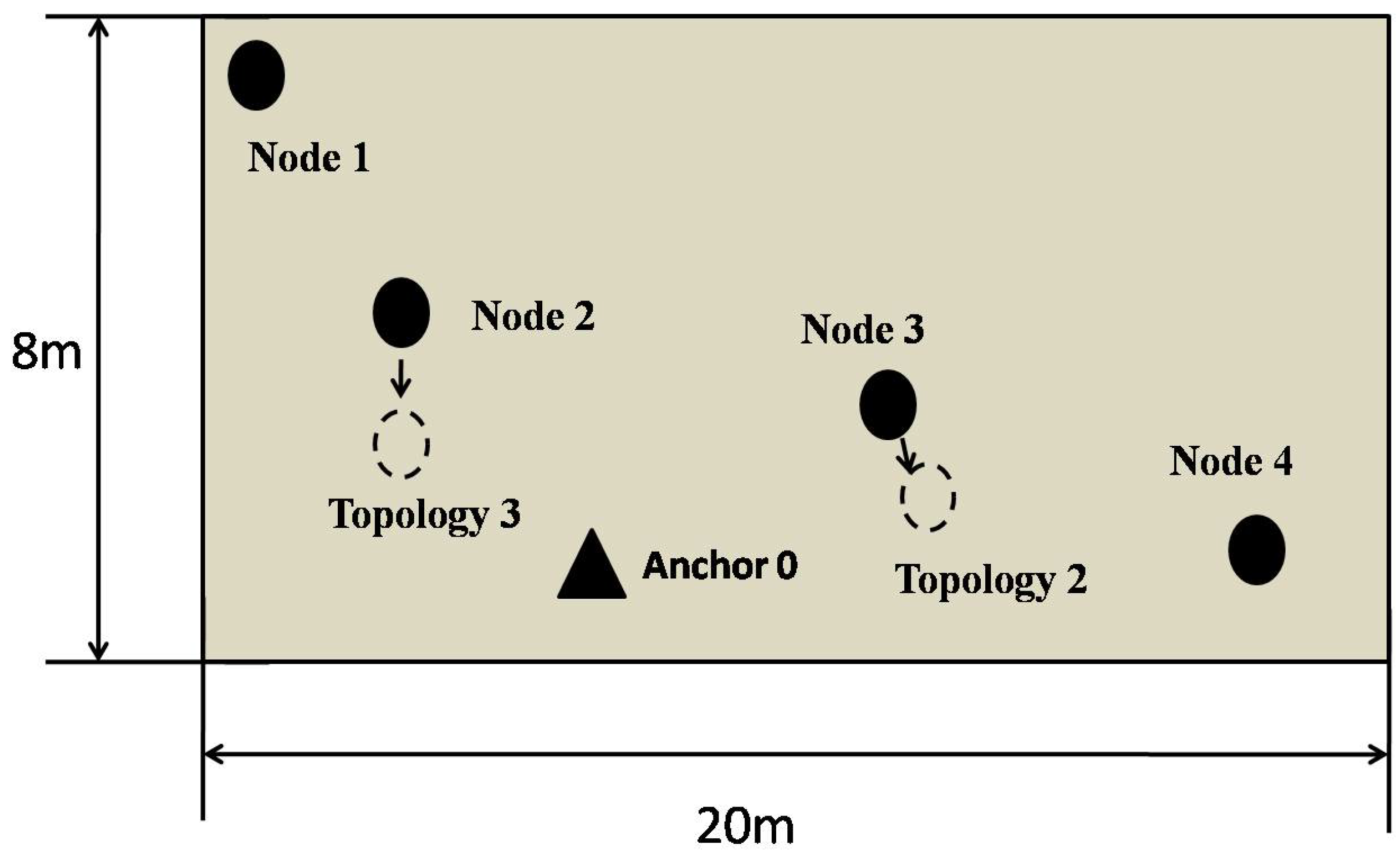
We also assume that the underwater network contains one anchor , 2 reference nodes and selected by the anchor, ordinary nodes. Set be the origin of coordinate, .
Based on the scope of underwater network and nodes’ power, we choose an appropriate code-width for the Double Rate Scheme.
The network uses TDMA (Time Division Multiple Address) protocol and TOA (Time of Arrival) ranging method [
17,
18] to reduce the transmission interference in UANs.
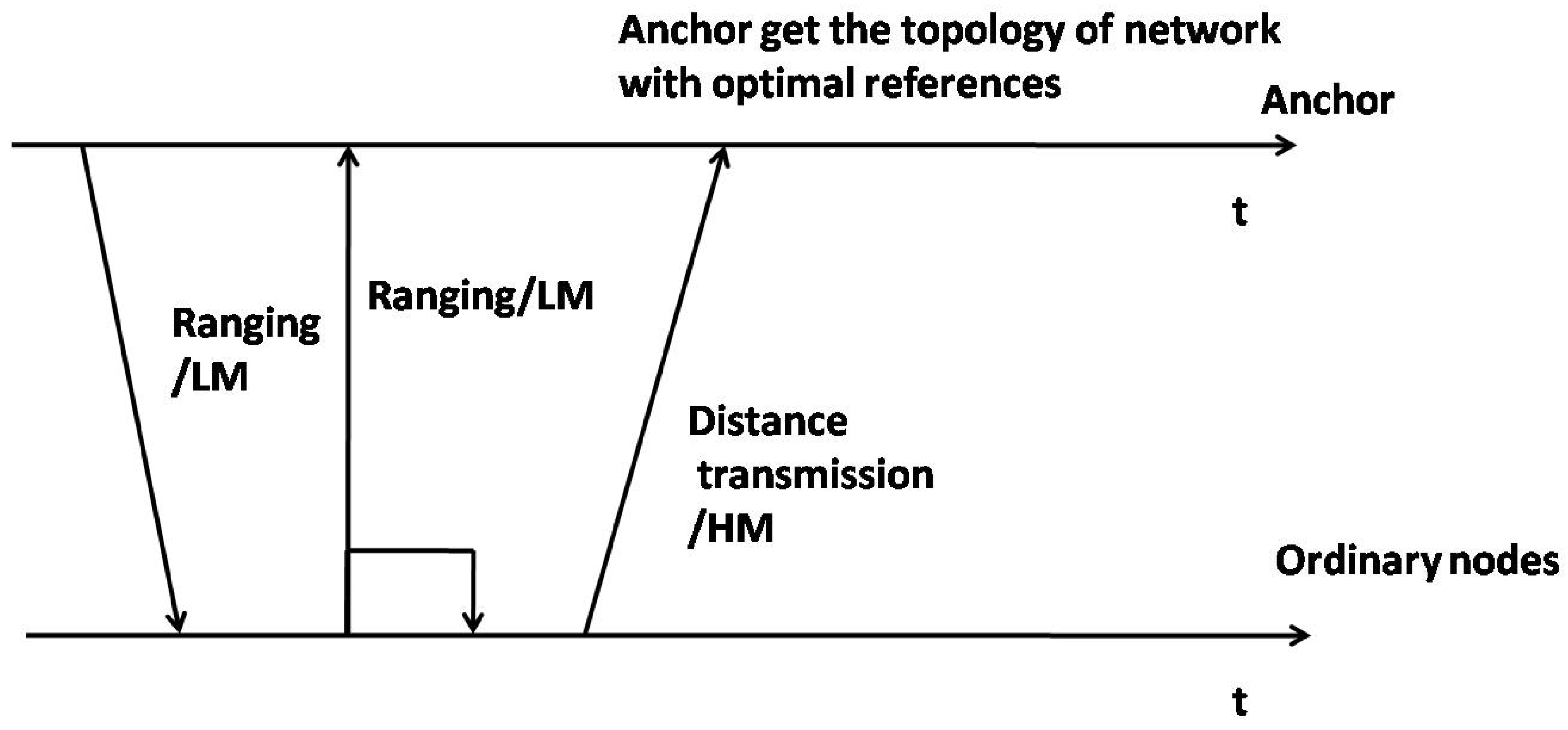
Step 1: The anchor broadcasts “hello” to the other nodes with the sending time stamp by LM mode.
Step 2: Same as Step 1, other nodes broadcast time stamp information by LM mode to the whole network.
Step 3: Every node can make some distance between itself and the other nodes, then send the ranging information to the anchor by HM mode.
Step 4: The anchor
selects the optimal reference nodes
and
according to Equation (
10) with the ranging information in Step 3. Then by setting
be the
x-axis,
in the first quadrant, we can get the relative coordinate system as shown in
Figure 2.
Step 5:
gets the location information of each node and the topology of whole network according to Equation (
8). Then the localization procedure ends.
The localization process is shown in
Figure 3.
If the scope of UANs is out of the range of the LM transmission mode, the localization procedure should be accomplished by different clusters which are divided by the transmission range of LM mode. The boundary nodes which have obtained their positions will be the anchor in new cluster and the localization procedure will end when all the unknown nodes have been localized.