A Low-Complexity DOA and Polarization Method of Polarization-Sensitive Array
Abstract
:1. Introduction
2. Problem Formulation
2.1. Quaternions
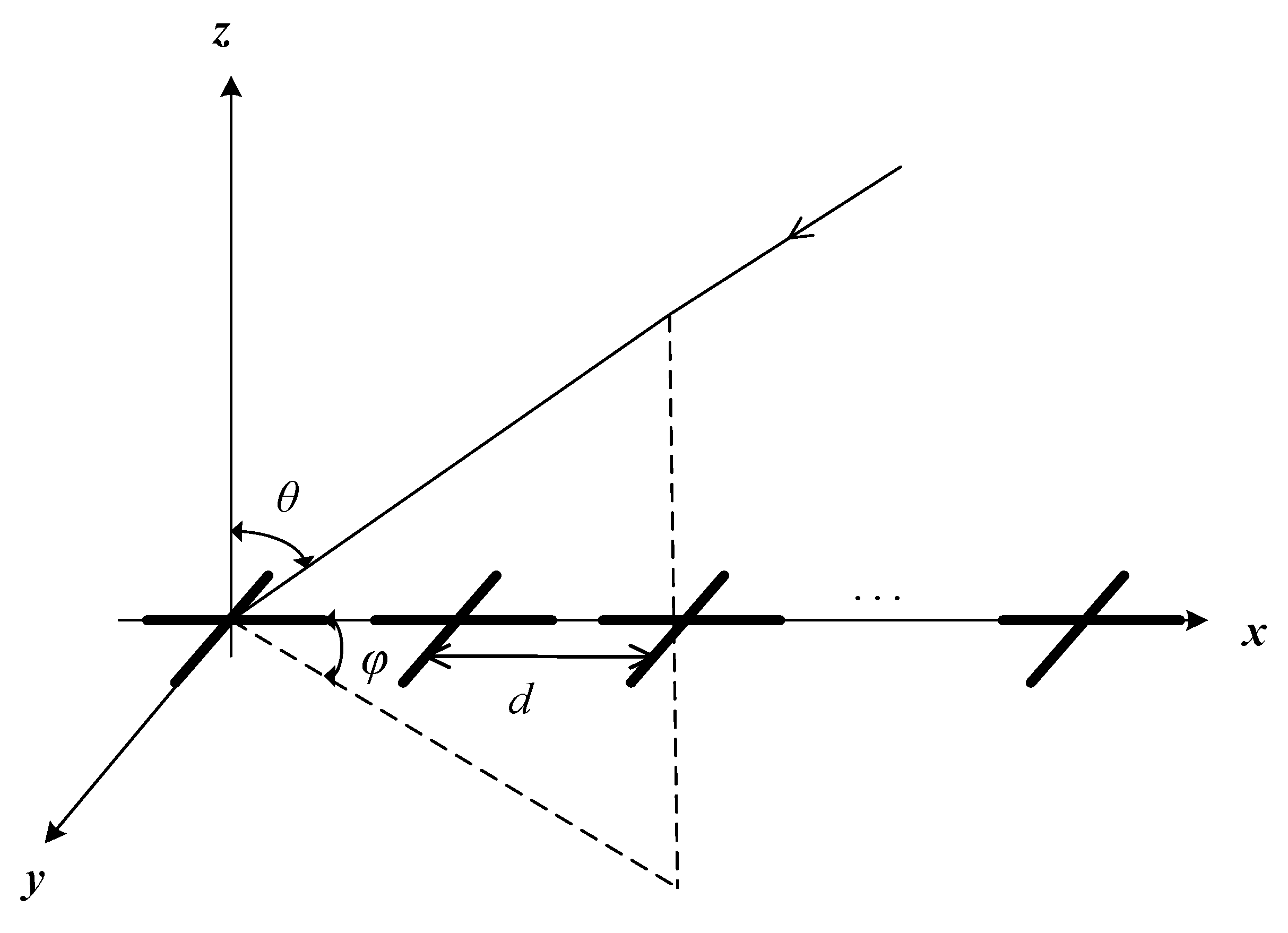
2.2. Array Configuration and Mathematical Model
- (1)
- The K incoherent arriving signals are narrow band and circular signals, which means .
- (2)
- The entries of are white Gaussian noise and uncorrelated with each other. Noise from different sensors are independent, which means .
3. Proposed Algorithm
3.1. Half-Quaternions Model
3.2. DOA Estimation
3.3. Polarization Parameter Estimation
3.4. Oblique Projection Operators
| Algorithm 1 Steps in the Proposed Method |
| Input: |
| 1. obtain according to Equation (11) |
| DOA Estimation: |
| 2. Calculate the covariance matrix via Equation (8) |
| 3. Divide into and according to Equation (19) |
| 4. Calculate according to Equation (23) |
| 5. Calculate the roots of which lie on the unit circle |
| 6. The estimates of DOA () are obtained from Equation (25) |
| Polarization Parameter Estimation: |
| 7. Calculate the covariance matrix and the noise subspace via Equation (26) |
| 8. Calculate and according to Equation (28) |
| 9. Obtain the generalized eigenvectors corresponding to the smallest eigenvalue from Equation (32) |
| 10. Estimate Polarization Parameters ( and ) via Equation (32) |
| Oblique Projecting Filter |
| 11. Find out the target signal and the interferences through Equation (33) |
| 12. Compute the oblique projection operators via Equation (34) |
| 13. Filter out interfering signals using Equation (35) |
4. Computational Complexity
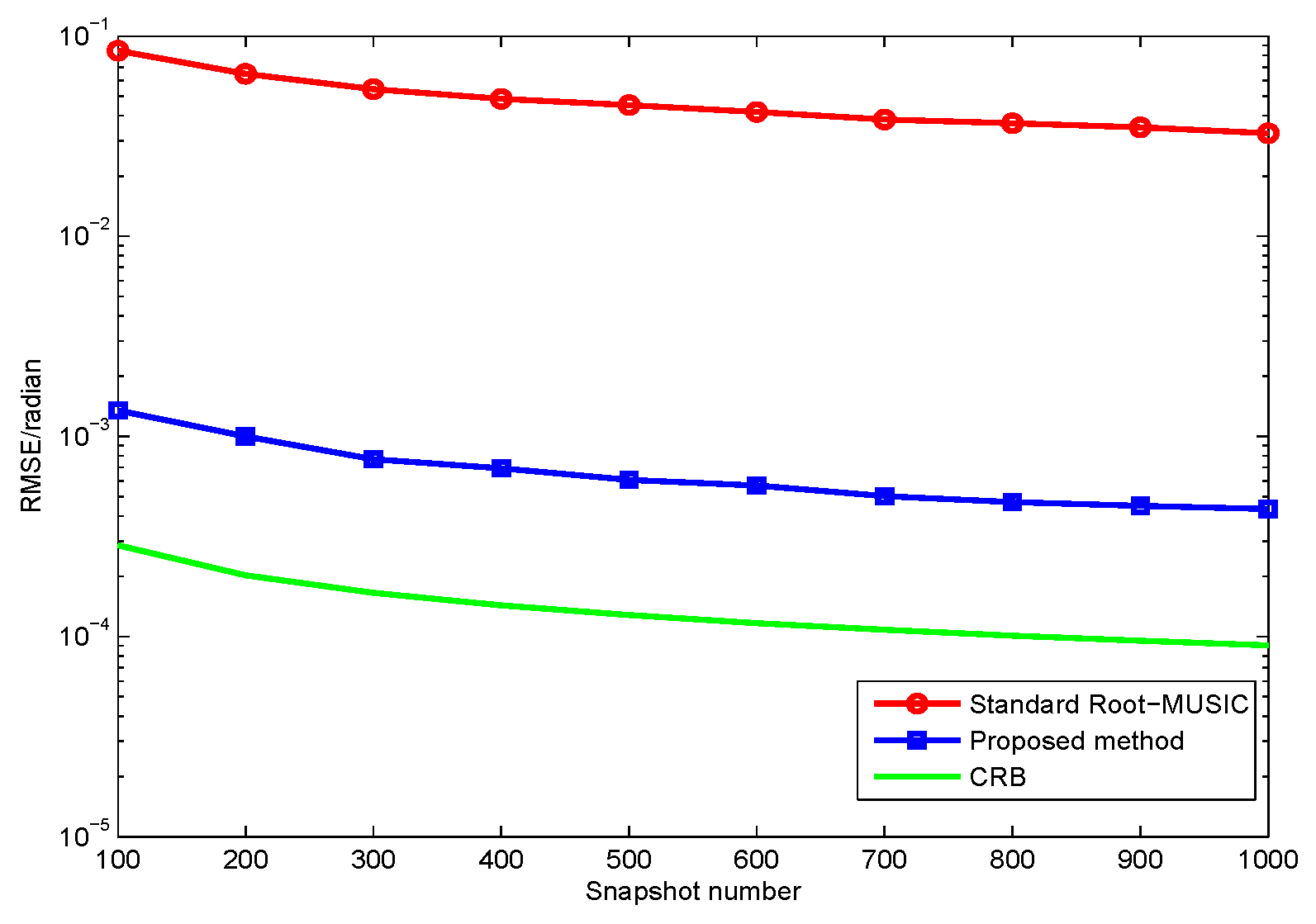
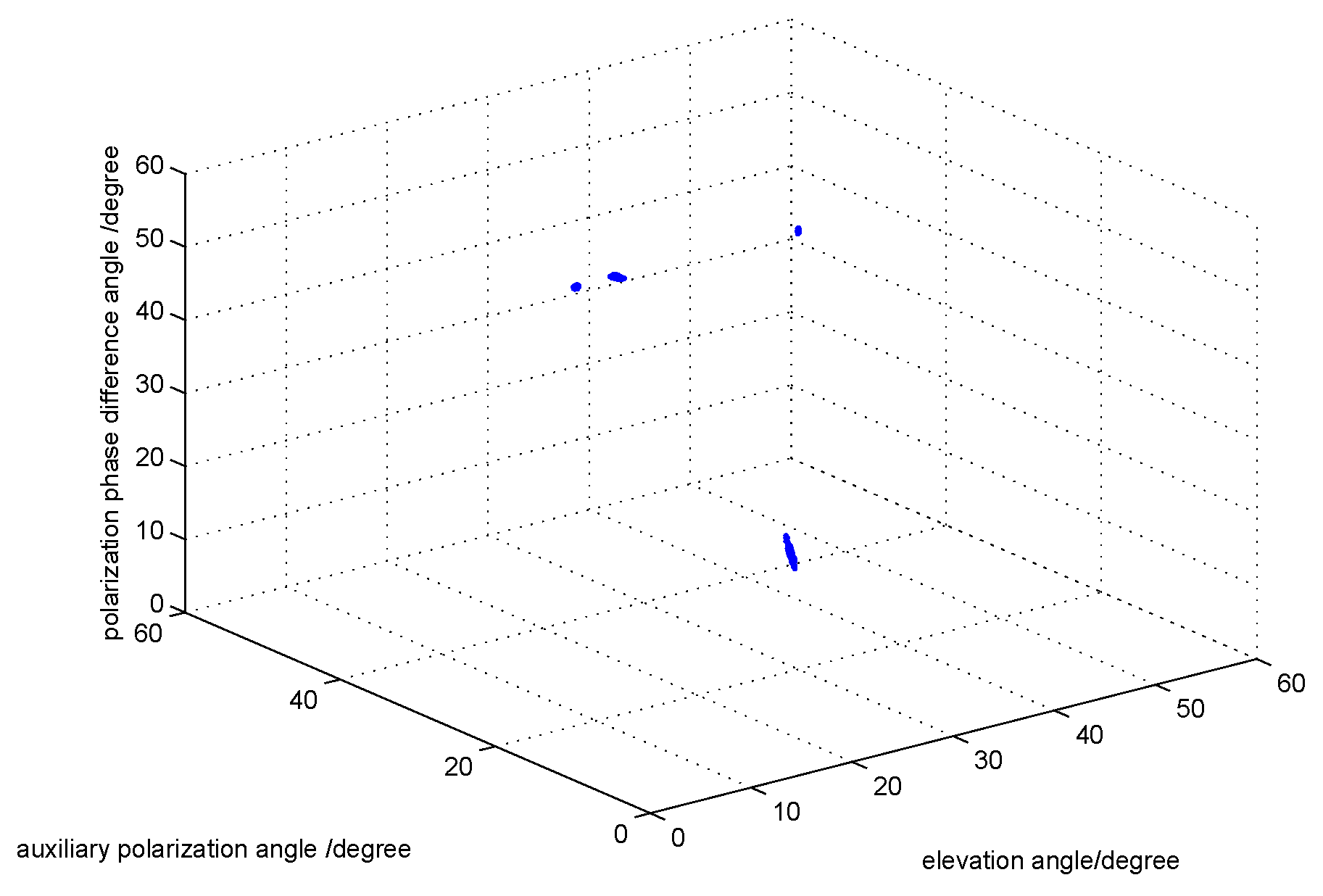
5. Simulation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wan, L.T.; Han, G.J.; Han, G.J. PD Source Diagnosis and Localization in Industrial High-Voltage Insulation System via Multimodal Joint Sparse Representation. IEEE Trans. Ind. Electron. 2016, 63, 2506–2516. [Google Scholar] [CrossRef]
- Gu, C.; He, J.; Li, H.; Zhu, X. Target localization using MIMO electromagnetic. Signal Process. 2013, 93, 2103–2107. [Google Scholar] [CrossRef]
- Zheng, G.; Wu, B. Polarisation smoothing for coherent source direction finding with multiple-input and multiple-output electromagnetic vector sensor array. IET Signal Process. 2016, 10, 873–879. [Google Scholar] [CrossRef]
- Gu, Y.; Goodman, N.A. Information-theoretic compressive sensing kernel optimization and Bayesian Cramér-Rao bound for time delay estimation. IEEE Trans. Signal Process. 2017, in press. [Google Scholar] [CrossRef]
- Gu, Y.; Leshem, A. Robust Adaptive Beamforming Based on Interference Covariance Matrix Reconstruction and Steering Vector Estimation. IEEE Trans. Signal Process. 2012, 60, 3881–3885. [Google Scholar]
- Gu, Y.; Goodman, N.A.; Hong, S.; Li, Y. Robust adaptive beamforming based on interference covariance matrix sparse reconstruction. Signal Process. 2014, 96, 375–381. [Google Scholar] [CrossRef]
- Si, W.; Zhao, P.; Qu, Z. Two-Dimensional DOA and Polarization Estimation for a Mixture of Uncorrelated and Coherent Sources with Sparsely-Distributed Vector Sensor Array. Sensors 2016, 16, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Goossens, R.; Rogier, H. A Hybrid UCA-RARE/Root-MUSIC Approach for 2-D Direction of Arrival Estimation in Uniform Circular Arrays in the Presence of Mutual Coupling. IEEE Trans. Antenna Propag. 2007, 55, 841–849. [Google Scholar] [CrossRef]
- Shen, Q.; Zhang, Y.; Amin, M.G. Generalized coprime array configurations for direction-of-arrival estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar]
- Sun, F.; Gao, B.; Chen, L.; Lan, P. A Low-Complexity ESPRIT-Based DOA Estimation Method for Co-Prime Linear Arrays. Sensors 2016, 16, 1367. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Zhou, C.; Gu, Y.; Goodman, N.A.; Qu, F. Source Estimation Using Coprime Array: A Sparse Reconstruction Perspective. IEEE Sens. J. 2017, 17, 755–765. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, Y.; Wan, L.; Tian, Z. Beamforming of Joint Polarization-Space Matched Filtering for Conformal Array. Sci. World J. 2013, 2013, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.T.; Li, L.; Zoltowski, M.D. Root-MUSIC-based direction-finding and polarization estimation using diversely polarized possibly collocated antennas. IEEE Antenna Wirel. Propag. Lett. 2004, 3, 129–132. [Google Scholar] [CrossRef]
- Rahamim, D.; Tabrikian, J.; Shavit, R. Source localization using vector sensor array in a multipath environment. IEEE Trans. Signal Process. 2004, 52, 3096–3103. [Google Scholar] [CrossRef]
- Hajian, M.; Nikookar, H.; Der Zwan, F. Branch correlation measurements and analysis in an indoor Rayleigh fading channel for polarization diversity using a dual polarized patch antenna. IEEE Microw. Wirel. Compon. Lett. 2005, 15, 555–557. [Google Scholar] [CrossRef]
- Cheng, Q.; Hua, Y. Performance analysis of the MUSIC and Pencil-MUSIC algorithms for diversely polarized array. IEEE Trans. Signal Process. 1996, 32, 284–299. [Google Scholar]
- Zoltowski, M.D.; Wong, K.T. ESPRIT-based 2-D direction finding with a sparse uniform array of electromagnetic vector sensors. IEEE Trans. Signal Process. 2000, 48, 2195–2204. [Google Scholar] [CrossRef]
- Li, J.; Compton, R.T. Angle and polarization esrimation using ESPRIT with a polarization sensitive array. IEEE Trans. Antenna Propag. 1991, 39, 1376–1383. [Google Scholar] [CrossRef]
- Silverstein, S.D.; Zoltowski, M.D. The mathematical basis for element and fourier beamspace MUSIC and root-MUSIC algorithms. Digit. Signal Process. 1991, 1, 161–175. [Google Scholar] [CrossRef]
- Schutte, H.D.; Wenzel, J. Hypercomplex numbers in digital signal processing. In Proceedings of the IEEE International Symposium on Circuits and Systems, New Orleans, LA, USA, 1–3 May 1990; pp. 1557–1560. [Google Scholar]
- Miron, S.; Bihan, N.L.; Mars, J.I. Quaternion-MUSIC for vector-sensor array processing. IEEE Trans. Signal Process. 2006, 54, 1218–1229. [Google Scholar] [CrossRef]
- Yuan, X. Estimating the DOA and the Polarization of a Polynomial-Phase Signal Using a Single Polarized Vector-Sensor. IEEE Trans. Signal Process. 2012, 60, 1270–1282. [Google Scholar] [CrossRef]
- Weiss, A.J.; Friedlander, B. Maximum Likelihood Signal Estimation for Polarization Sensitive Arrays. IEEE Trans. Antennas Propag. 1993, 41, 918–925. [Google Scholar] [CrossRef]
- Lee, H.; Stovall, R. Maximum Likelihood Methods for Determining the Direction of Arrival for a Single Electromagnetic Source with Unknown Polarization. IEEE Trans. Signal Process. 1994, 43, 474–479. [Google Scholar] [CrossRef]
- He, J.; Jiang, S.; Wang, J. Polarization difference smoothing for direction finding of coherent signals. IEEE Trans. Aerosp. Electron. Syst.. 2010, 46, 469–480. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Z. Polarimetric angular smoothing algorithm for an electromagnetic vector-sensor array. IET Radar Sona. Navig. 2007, 1, 230–240. [Google Scholar] [CrossRef]
- Behrens, R.T.; Scharf, L.L. Signal Processing Applications of Oblique Projection Operators. IEEE Trans. Signal Process. 1994, 42, 1413–1424. [Google Scholar] [CrossRef]
- Yuan, X.; Wong, K.T.; Xu, Z. Various compositions to form a triad of collocated dipoles/loops, for direction finding and polarization esitmation. IEEE Sens. J. 2012, 12, 1763–1771. [Google Scholar] [CrossRef]
- Häge, M.; Oispuu, M. DOA and polarization accuracy study for an imperfect dual-polarized antenna array. In Proceedings of the 19th European Signal Processing Conference, Barcelona, Spain, 29 August–2 September 2011; pp. 599–603. [Google Scholar]




| Methods | Covariance Matrix | Peak Search |
|---|---|---|
| Proposed | without | |
| MUSIC |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, W.; Diao, M.; Gao, L.; Liu, L. A Low-Complexity DOA and Polarization Method of Polarization-Sensitive Array. Sensors 2017, 17, 1170. https://doi.org/10.3390/s17051170
Dong W, Diao M, Gao L, Liu L. A Low-Complexity DOA and Polarization Method of Polarization-Sensitive Array. Sensors. 2017; 17(5):1170. https://doi.org/10.3390/s17051170
Chicago/Turabian StyleDong, Wen, Ming Diao, Lipeng Gao, and Lutao Liu. 2017. "A Low-Complexity DOA and Polarization Method of Polarization-Sensitive Array" Sensors 17, no. 5: 1170. https://doi.org/10.3390/s17051170
APA StyleDong, W., Diao, M., Gao, L., & Liu, L. (2017). A Low-Complexity DOA and Polarization Method of Polarization-Sensitive Array. Sensors, 17(5), 1170. https://doi.org/10.3390/s17051170





