A Two-Axis Goniometric Sensor for Tracking Finger Motion
Abstract
:1. Introduction
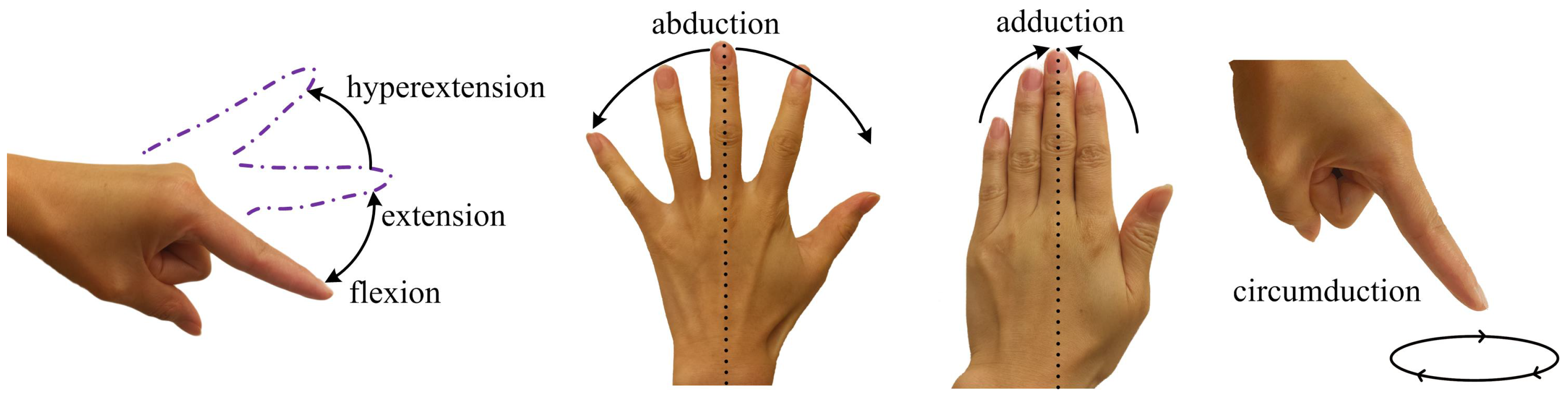
2. Hand Skeleton Model
3. Sensor Design
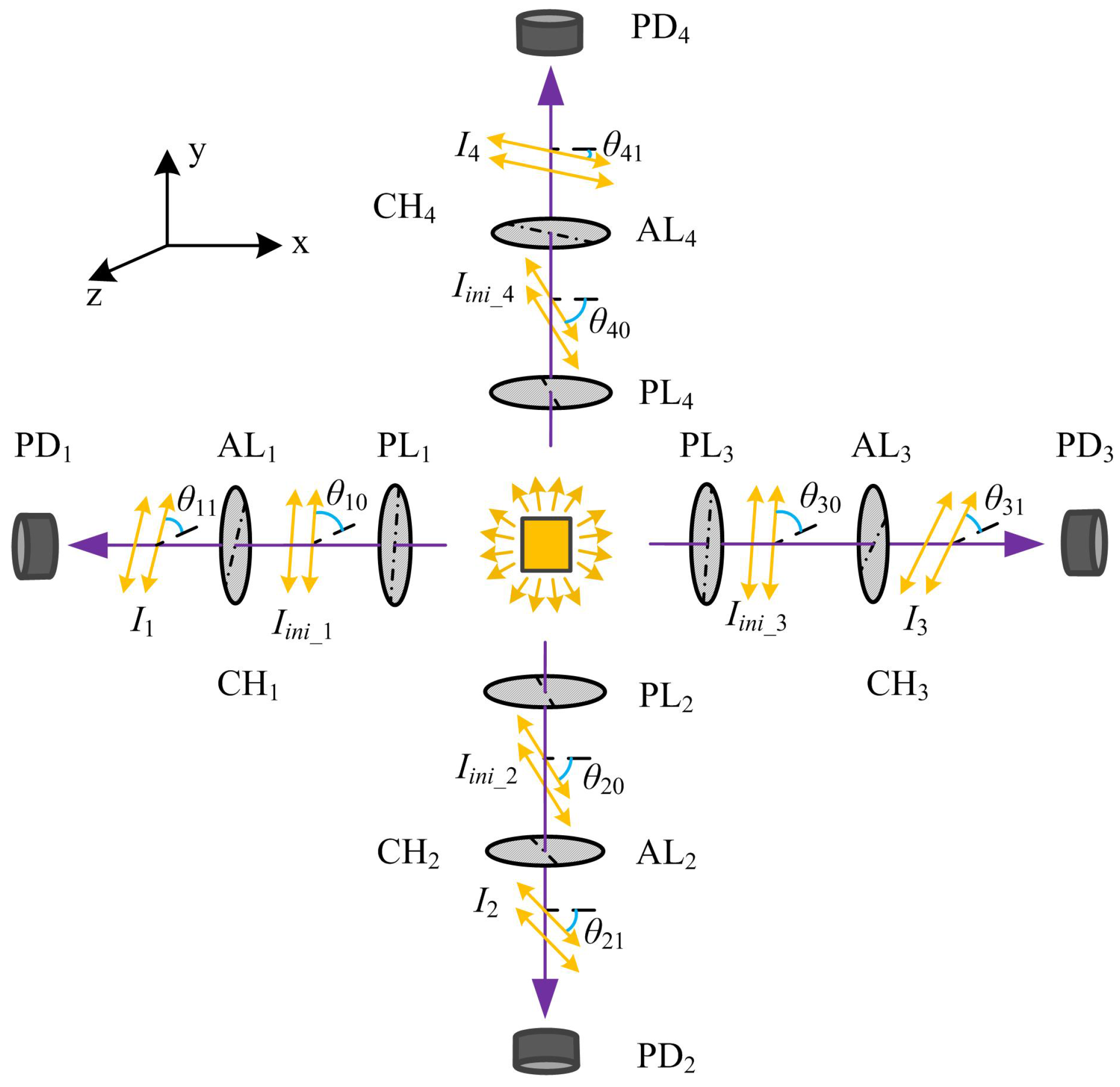
3.1. Principle of Operation
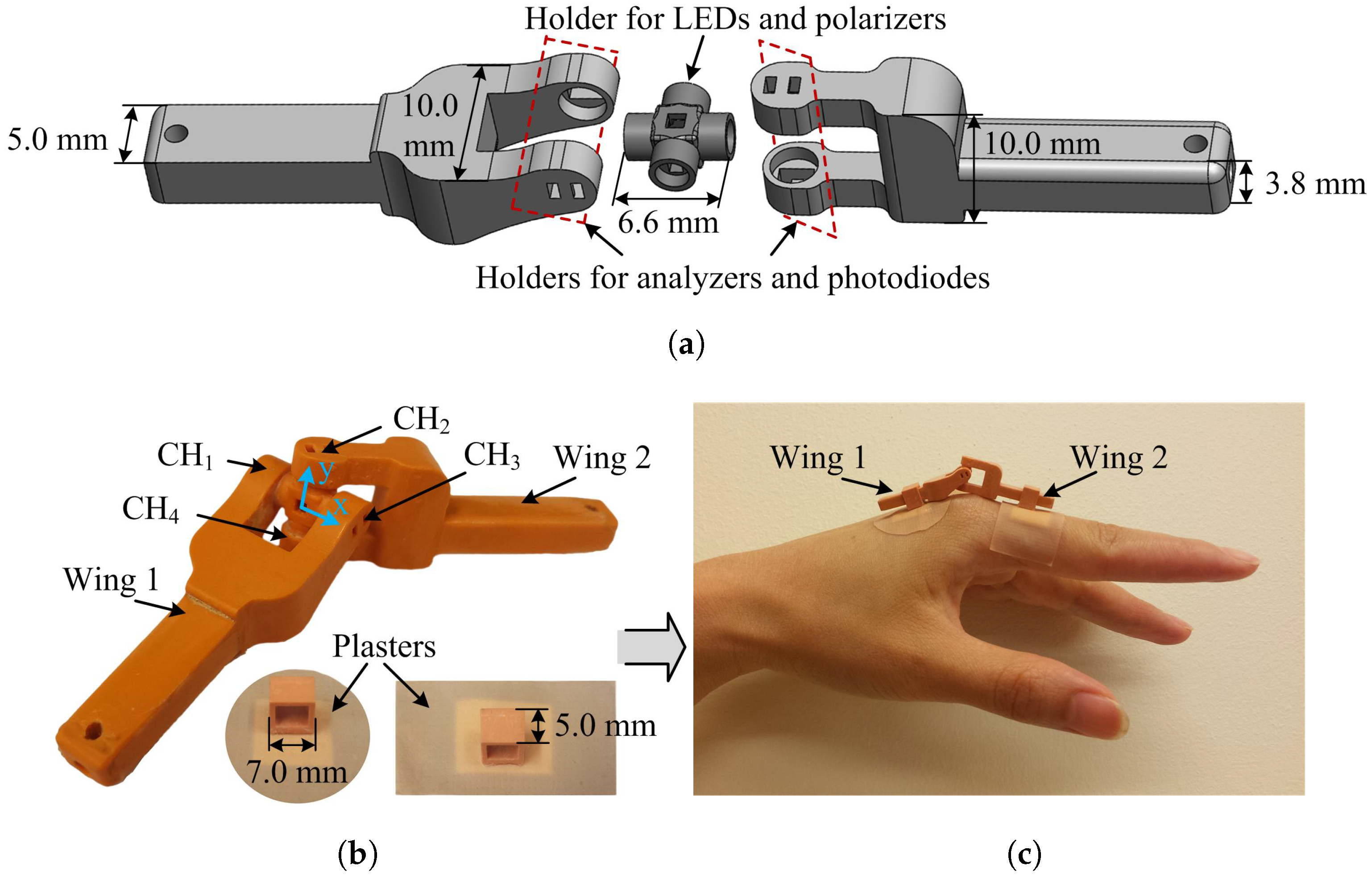
3.2. Sensor Manufacture
4. Methods
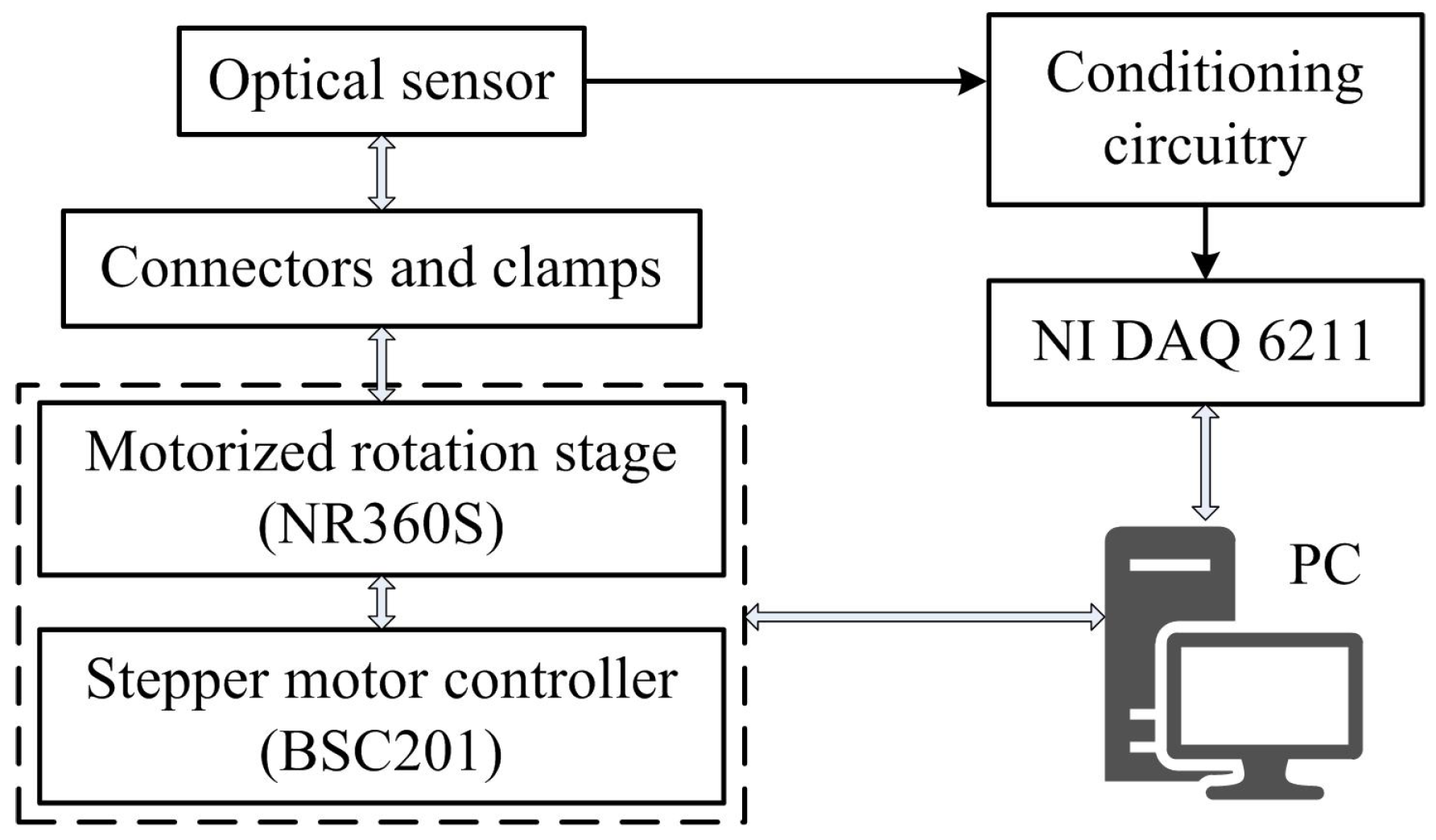
4.1. Measurement Apparatus
4.2. Data Fusion Approach
5. Sensor Characteristics
6. Sensor Performance Validation
6.1. Random Angle Testing
6.2. Finger Motion Detection
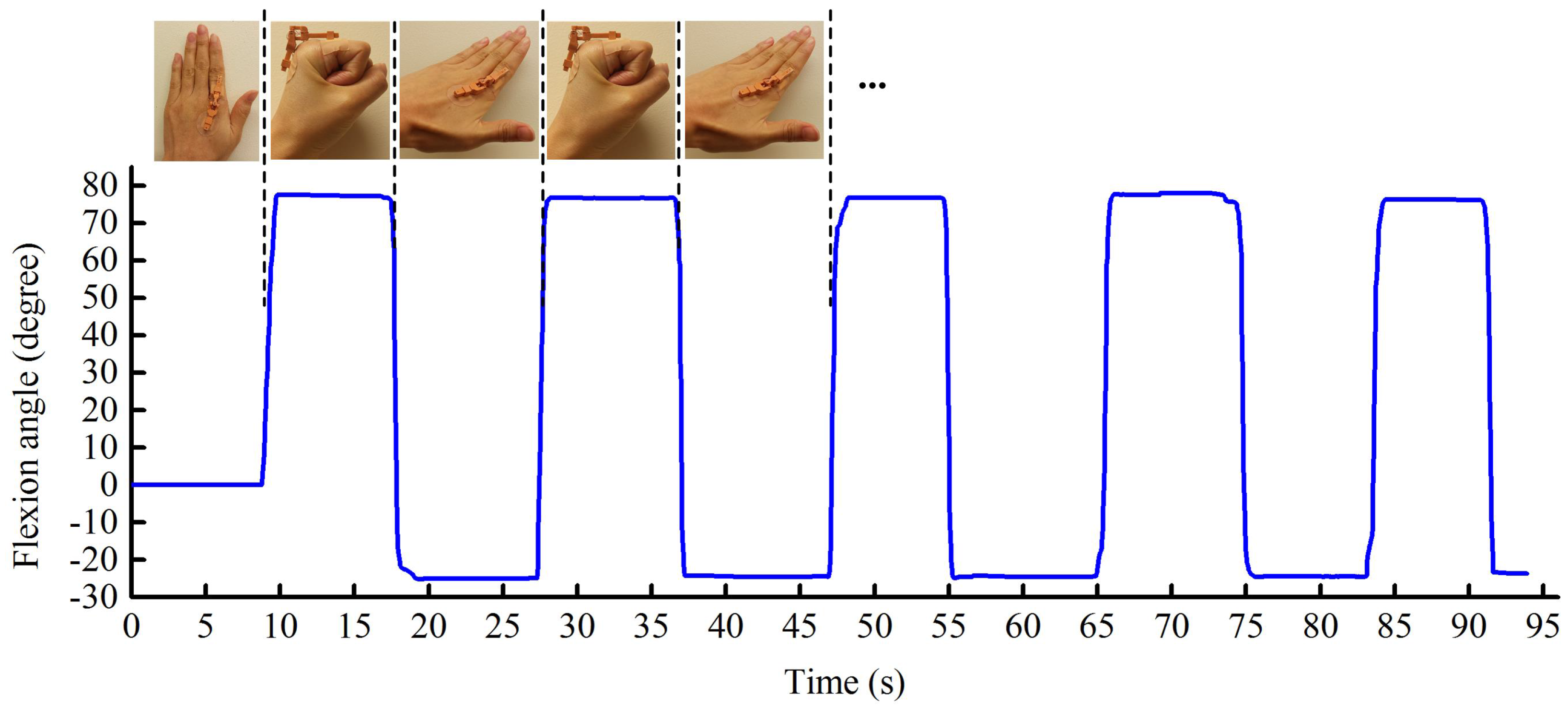
6.2.1. Finger Flexion and Extension
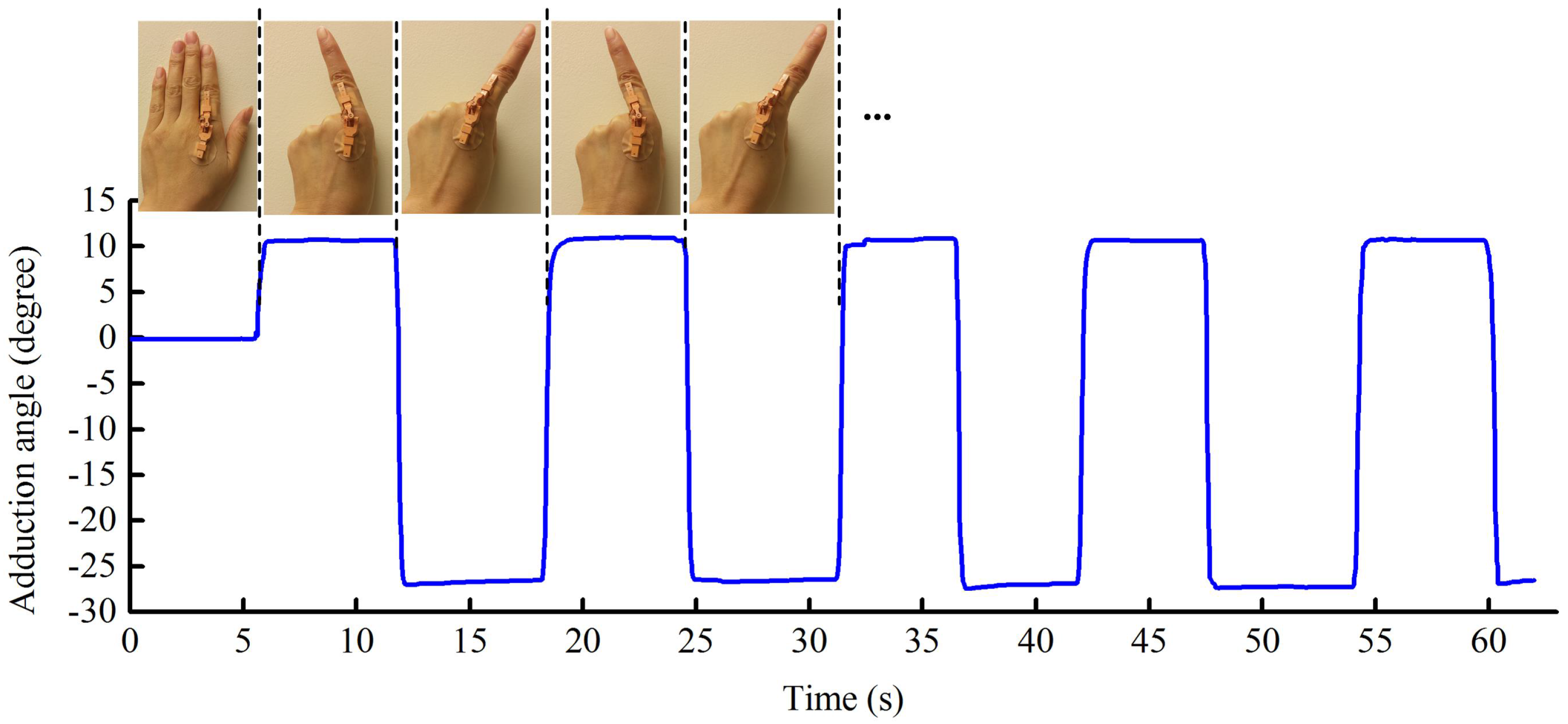
6.2.2. Finger Abduction and Adduction
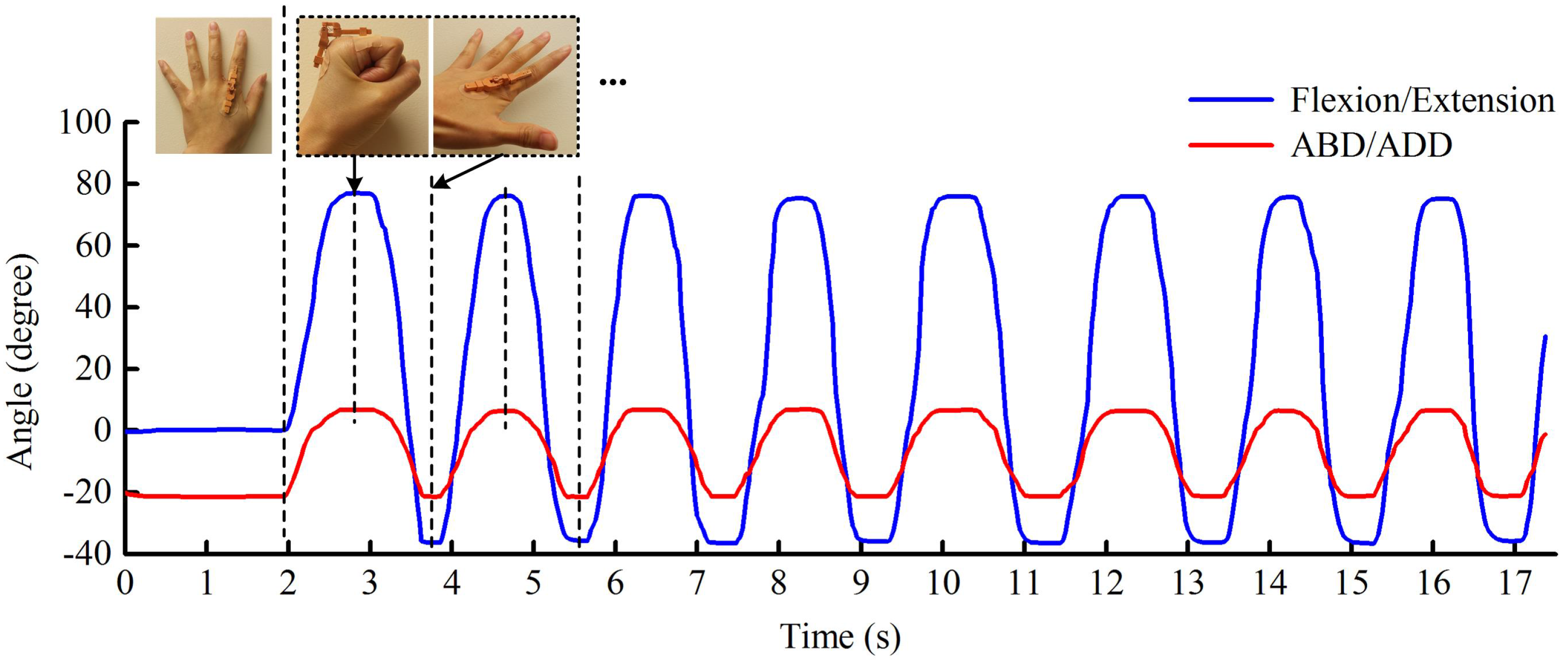
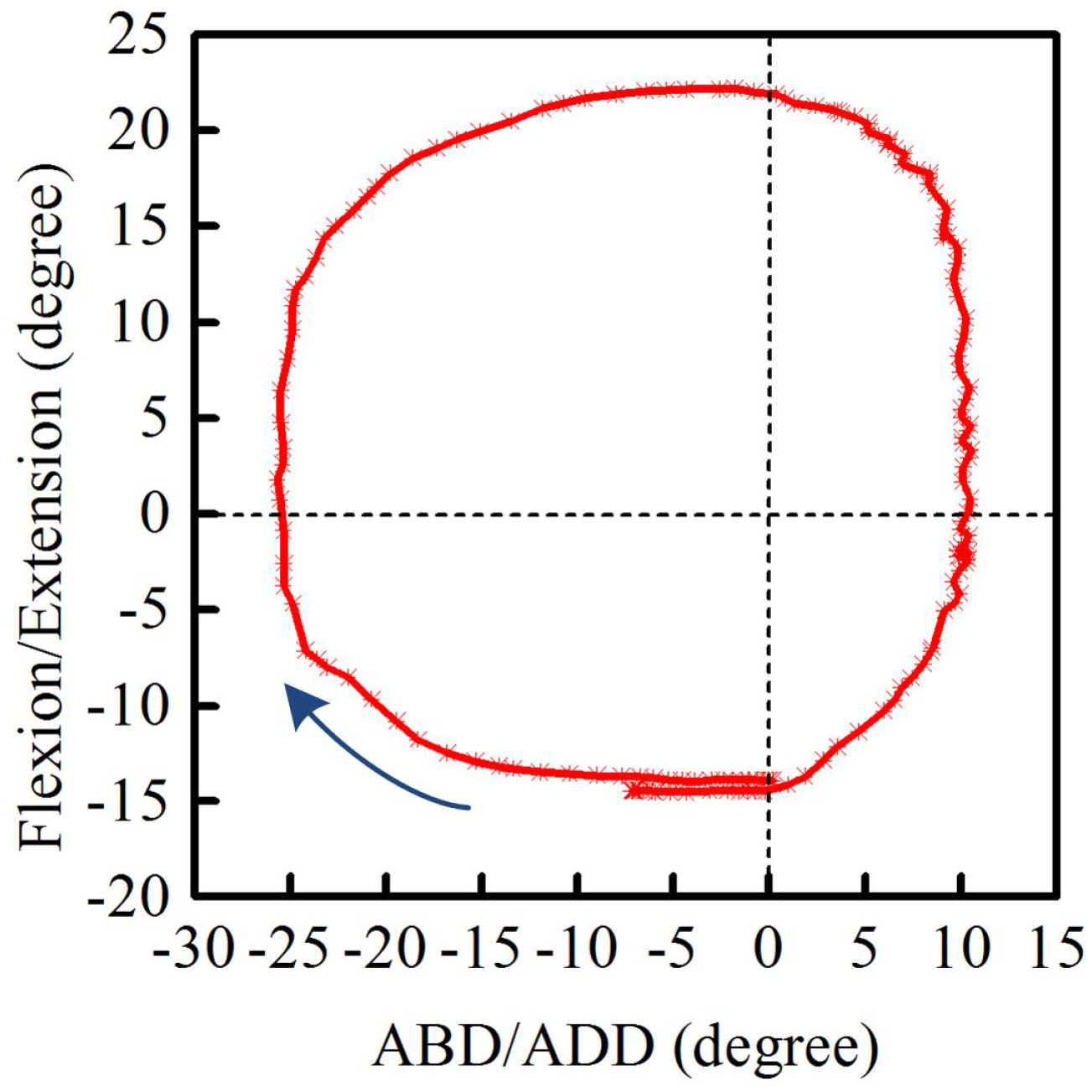
6.2.3. Finger Flexion/Extension and Abduction/Adduction
6.2.4. Finger Circumduction
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Henley, C.N. Motion of the Fingers, Thumb, and Wrist—Language of Hand and Arm Surgery Series. Available online: http://noelhenley.com/532/motion-of-the-fingers-thumb-and-wrist-language-of-hand-and-arm-surgery-series/ (accessed on 3 February 2017).
- Saladin, K.S. Support and Movement. In Human Anatomy, 2nd ed.; Wheatley, C.H., Queck, K.A., Eds.; Michelle Watnick: New York, NY, USA, 2008; pp. 243–245. [Google Scholar]
- Dutton, M. Orthopaedic Examination, Evaluation, and Intervention. Available online: http://highered.mheducation.com/sites/0071474013/student_view0/chapter8/goniometry.html (accessed on 3 February 2017).
- Macionis, V. Reliability of the standard goniometry and diagrammatic recording of finger joint angles: A comparative study with healthy subjects and non-professional raters. BMC Musculoskelet. Disord. 2013, 14, 17. [Google Scholar] [CrossRef] [PubMed]
- Yamada, T.; Hayamizu, Y.; Yamamoto, Y.; Yomogida, Y.; Izadi-Najafabadi, A.; Futaba, D.N.; Hata, K. A stretchable carbon nanotube strain sensor for human-motion detection. Nat. Nanotechnol. 2011, 6, 296–301. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhao, S.; Zeng, X.; Huang, W.; Gong, Z.; Zhang, G.; Sun, R.; Wong, C.P. Highly Stretchable and Sensitive Strain Sensor Based on Facilely Prepared Three-Dimensional Graphene Foam Composite. ACS Appl. Mater. Interfaces 2016, 8, 18954–18961. [Google Scholar] [CrossRef] [PubMed]
- Chossat, J.B.; Tao, Y.; Duchaine, V.; Park, Y.L. Wearable soft artificial skin for hand motion detection with embedded microfluidic strain sensing. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2568–2573. [Google Scholar]
- Yoon, S.G.; Koo, H.J.; Chang, S.T. Highly Stretchable and Transparent Microfluidic Strain Sensors for Monitoring Human Body Motions. ACS Appl. Mater. Interfaces 2015, 7, 27562–27570. [Google Scholar] [CrossRef] [PubMed]
- Fahn, C.S.; Sun, H. Development of a fingertip glove equipped with magnetic tracking sensors. Sensors 2010, 10, 1119–1140. [Google Scholar] [CrossRef] [PubMed]
- Nishiyama, M.; Watanabe, K. Wearable sensing glove with embedded hetero-core fiber-optic nerves for unconstrained hand motion capture. IEEE Trans. Instrum. Meas. 2009, 58, 3995–4000. [Google Scholar] [CrossRef]
- Da Silva, A.F.; Goncalves, A.F.; Mendes, P.M.; Correia, J.H. FBG sensing glove for monitoring hand posture. IEEE Sens. J. 2011, 11, 2442–2448. [Google Scholar] [CrossRef]
- Perez-Ramirez, C.A.; Almanza-Ojeda, D.L.; Guerrero-Tavares, J.N.; Mendoza-Galindo, F.J.; Estudillo-Ayala, J.M.; Ibarra-Manzano, M.A. An Architecture for Measuring Joint Angles Using a Long Period Fiber Grating-Based Sensor. Sensors 2014, 14, 24483–24501. [Google Scholar] [CrossRef] [PubMed]
- Moreira, A.H.; Queirós, S.; Fonseca, J.; Rodrigues, P.L.; Rodrigues, N.F.; Vilaça, J.L. Real-time hand tracking for rehabilitation and character animation. In Proceedings of the 2014 IEEE 3rd International Conference on the Serious Games and Applications for Health (SeGAH), Rio de Janeiro, Brazil, 14–16 May 2014; pp. 1–8. [Google Scholar]
- Choi, Y.; Yoo, K.; Kang, S.J.; Seo, B.; Kim, S.K. Development of a low-cost wearable sensing glove with multiple inertial sensors and a light and fast orientation estimation algorithm. J. Supercomput. 2016. [Google Scholar] [CrossRef]
- Saggio, G.; Riillo, F.; Sbernini, L.; Quitadamo, L.R. Resistive flex sensors: A survey. Smart Mater. Struct. 2015, 25, 013001. [Google Scholar] [CrossRef]
- Flexpoint Sensor Systems Inc. Available online: http://www.flexpoint.com/ (accessed on 3 February 2017).
- Wang, L.; Meydan, T.; Williams, P.; Kutrowski, T. A proposed optical-based sensor for assessment of hand movement. In Proceedings of the 2015 IEEE Sensors, Busan, Korea, 1–4 November 2015; pp. 1–4. [Google Scholar]
- Wang, L.; Meydan, T.; Williams, P. Design and Evaluation of a 3-D Printed Optical Sensor for Monitoring Finger Flexion. IEEE Sens. J. 2017, 17, 1937–1944. [Google Scholar] [CrossRef]
- Chen, K.Y.; Lyons, K.; White, S.; Patel, S. uTrack: 3D input using two magnetic sensors. In Proceedings of the 26th Annual ACM Symposium on User Interface Software and Technology, New York, NY, USA, 8–11 October 2013; pp. 237–244. [Google Scholar]
- Bilro, L.; Oliveira, J.G.; Pinto, J.L.; Nogueira, R.N. A reliable low-cost wireless and wearable gait monitoring system based on a plastic optical fibre sensor. Meas. Sci. Technol. 2011, 22, 045801. [Google Scholar] [CrossRef]
- Babchenko, A.; Maryles, J. A sensing element based on 3D imperfected polymer optical fibre. J. Opt. A Pure Appl. Opt. 2006, 9, 1–5. [Google Scholar] [CrossRef]
- Williams, N.W.; Penrose, J.M.T.; Caddy, C.M.; Barnes, E.; Hose, D.R.; Harley, P. A goniometric glove for clinical hand assessment construction, calibration and validation. J. Hand Surg. (Br. Eur. Vol.) 2000, 25, 200–207. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Chen, I.M.; Yeo, S.H.; Lim, C.K. Development of finger-motion capturing device based on optical linear encoder. J. Rehabil. Res. Dev. 2011, 48, 69–82. [Google Scholar] [CrossRef] [PubMed]
- Gentner, R.; Classen, J. Development and evaluation of a low-cost sensor glove for assessment of human finger movements in neurophysiological settings. J. Neurosci. Methods 2009, 178, 138–147. [Google Scholar] [CrossRef] [PubMed]
- Oess, N.P.; Wanek, J.; Curt, A. Design and evaluation of a low-cost instrumented glove for hand function assessment. J. Neuroeng. Rehabil. 2012, 9, 2. [Google Scholar] [CrossRef] [PubMed]
- Simone, L.K.; Sundarrajan, N.; Luo, X.; Jia, Y.; Kamper, D.G. A low cost instrumented glove for extended monitoring and functional hand assessment. J. Neurosci. Methods 2007, 160, 335–348. [Google Scholar] [CrossRef] [PubMed]
- Saggio, G. A novel array of flex sensors for a goniometric glove. Sens. Actuators A Phys. 2014, 205, 119–125. [Google Scholar] [CrossRef]
- Bowman, D.A.; Wingrave, C.A.; Campbell, J.M.; Ly, V.Q. Using Pinch Gloves (TM) for both Natural and Abstract Interaction Techniques in Virtual Environments; Departmental Technical Report in the Department of Computer Science, Virginia Polytechnic Institute and State University: Blacksburg, VA, USA.
- Dipietro, L.; Sabatini, A.M.; Dario, P. A survey of glove-based systems and their applications. IEEE Trans. Syst. Man Cybern. C (Appl. Rev.) 2008, 38, 461–482. [Google Scholar] [CrossRef]
- CyberGlove Systems LLC. Available online: http://www.cyberglovesystems.com/ (accessed on 3 February 2017).
- Humanware. Available online: http://www.hmw.it/en/humanglove.html (accessed on 3 February 2017).
- 5DT. Available online: http://www.5dt.com/data-gloves/ (accessed on 3 February 2017).
- Borghetti, M.; Sardini, E.; Serpelloni, M. Sensorized glove for measuring hand finger flexion for rehabilitation purposes. IEEE Trans. Instrum. Meas. 2013, 62, 3308–3314. [Google Scholar] [CrossRef]
- Ju, Z.; Liu, H. Human hand motion analysis with multisensory information. IEEE/ASME Trans. Mechatron. 2014, 19, 456–466. [Google Scholar] [CrossRef]
- Lee, J.; Kunii, T.L. Model-based analysis of hand posture. IEEE Comput. Graph. Appl. 1995, 15, 77–86. [Google Scholar]
- Kortier, H.G.; Sluiter, V.I.; Roetenberg, D.; Veltink, P.H. Assessment of hand kinematics using inertial and magnetic sensors. J. Neuroeng. Rehabil. 2014, 11, 70. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Huang, T.S. Hand modeling, analysis and recognition. IEEE Signal Process. Mag. 2001, 18, 51–60. [Google Scholar]
- Palastanga, N.; Soames, R. Introduction and The upper limb. In Anatomy and Human Movement: Structure and Function, 6th ed.; Demetriou-Swanwick, R., Davies, S., Eds.; Elsevier Churchill Livingstone: London, UK, 2012. [Google Scholar]
- Degeorges, R.; Parasie, J.; Mitton, D.; Imbert, N.; Goubier, J.N.; Lavaste, F. Three-dimensional rotations of human three-joint fingers: An optoelectronic measurement. Preliminary results. Surg. Radiol. Anat. 2005, 27, 43–50. [Google Scholar] [CrossRef] [PubMed]
- EnvisionTEC. Available online: https://envisiontec.com/ (accessed on 31 March 2017).
- Farnell element14. Available online: http://uk.farnell.com/ (accessed on 3 February 2017).
- Edmund Optics Ltd. Available online: http://www.edmundoptics.co.uk/ (accessed on 3 February 2017).
- Thorlabs, Inc. Available online: https://www.thorlabs.com/ (accessed on 3 February 2017).
- Park, Y.; Lee, J.; Bae, J. Development of a Wearable Sensing Glove for Measuring the Motion of Fingers Using Linear Potentiometers and Flexible Wires. IEEE Trans. Ind. Inf. 2015, 11, 198–206. [Google Scholar] [CrossRef]
- Oess, N.P.; Wanek, J.; van Hedel, H.J. Enhancement of bend sensor properties as applied in a glove for use in neurorehabilitation settings. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Buenos Aires, Argentina, 31 August–4 September 2010; pp. 5903–5906. [Google Scholar]
- ImageJ. Available online: https://imagej.nih.gov/ij/ (accessed on 17 March 2017).
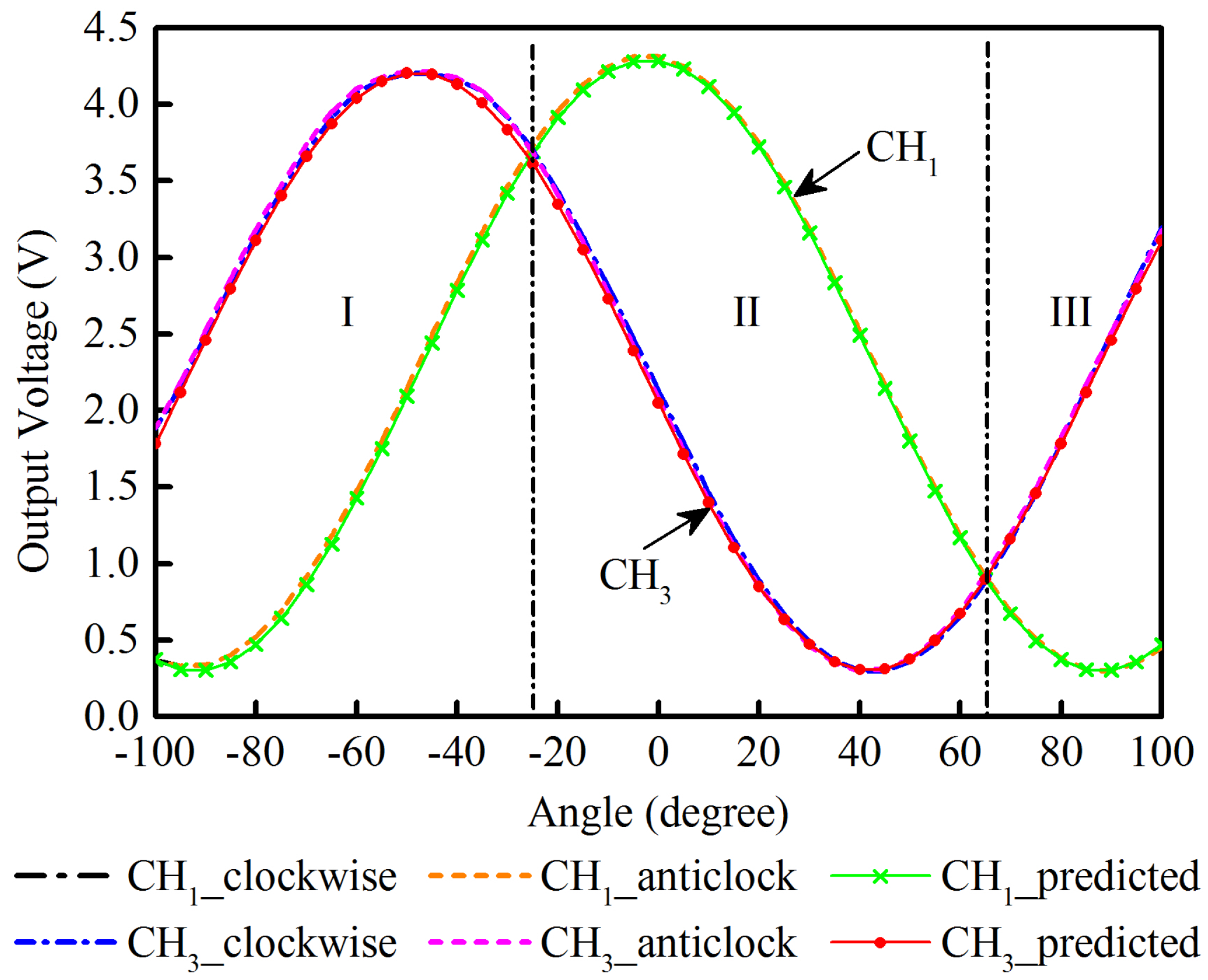
| Channels | Deviations from the Predicted Voltages | Hysteresis | RSD | |
|---|---|---|---|---|
| Rotations about the x-axis | CH | ±2.4% | 1.6% | 0.4% |
| CH | ±2.1% | 1.4% | 0.6% | |
| Rotations about the y-axis | CH | ±2.5% | 2.0% | 0.6% |
| CH | ±2.3% | 1.9% | 0.4% | |
| overall | ±2.3% | 1.7% | 0.5% | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Meydan, T.; Williams, P.I. A Two-Axis Goniometric Sensor for Tracking Finger Motion. Sensors 2017, 17, 770. https://doi.org/10.3390/s17040770
Wang L, Meydan T, Williams PI. A Two-Axis Goniometric Sensor for Tracking Finger Motion. Sensors. 2017; 17(4):770. https://doi.org/10.3390/s17040770
Chicago/Turabian StyleWang, Lefan, Turgut Meydan, and Paul Ieuan Williams. 2017. "A Two-Axis Goniometric Sensor for Tracking Finger Motion" Sensors 17, no. 4: 770. https://doi.org/10.3390/s17040770
APA StyleWang, L., Meydan, T., & Williams, P. I. (2017). A Two-Axis Goniometric Sensor for Tracking Finger Motion. Sensors, 17(4), 770. https://doi.org/10.3390/s17040770






