Non-Destructive Evaluation of the Leaf Nitrogen Concentration by In-Field Visible/Near-Infrared Spectroscopy in Pear Orchards
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plant Material and Treatments
2.2. Spectra Collection
2.3. Modelling Methods
2.4. Data Pre-Treatment
2.5. Leaf Nitrogen Concentration and Yield Estimation
3. Results
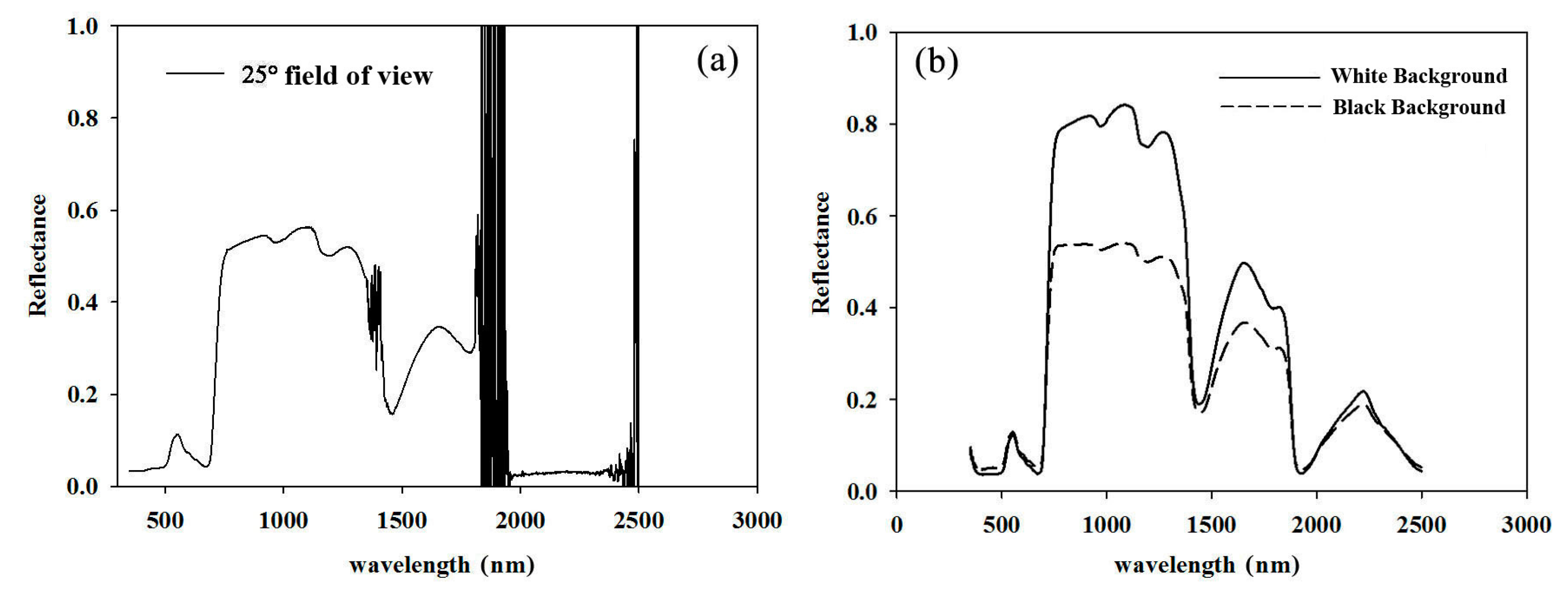
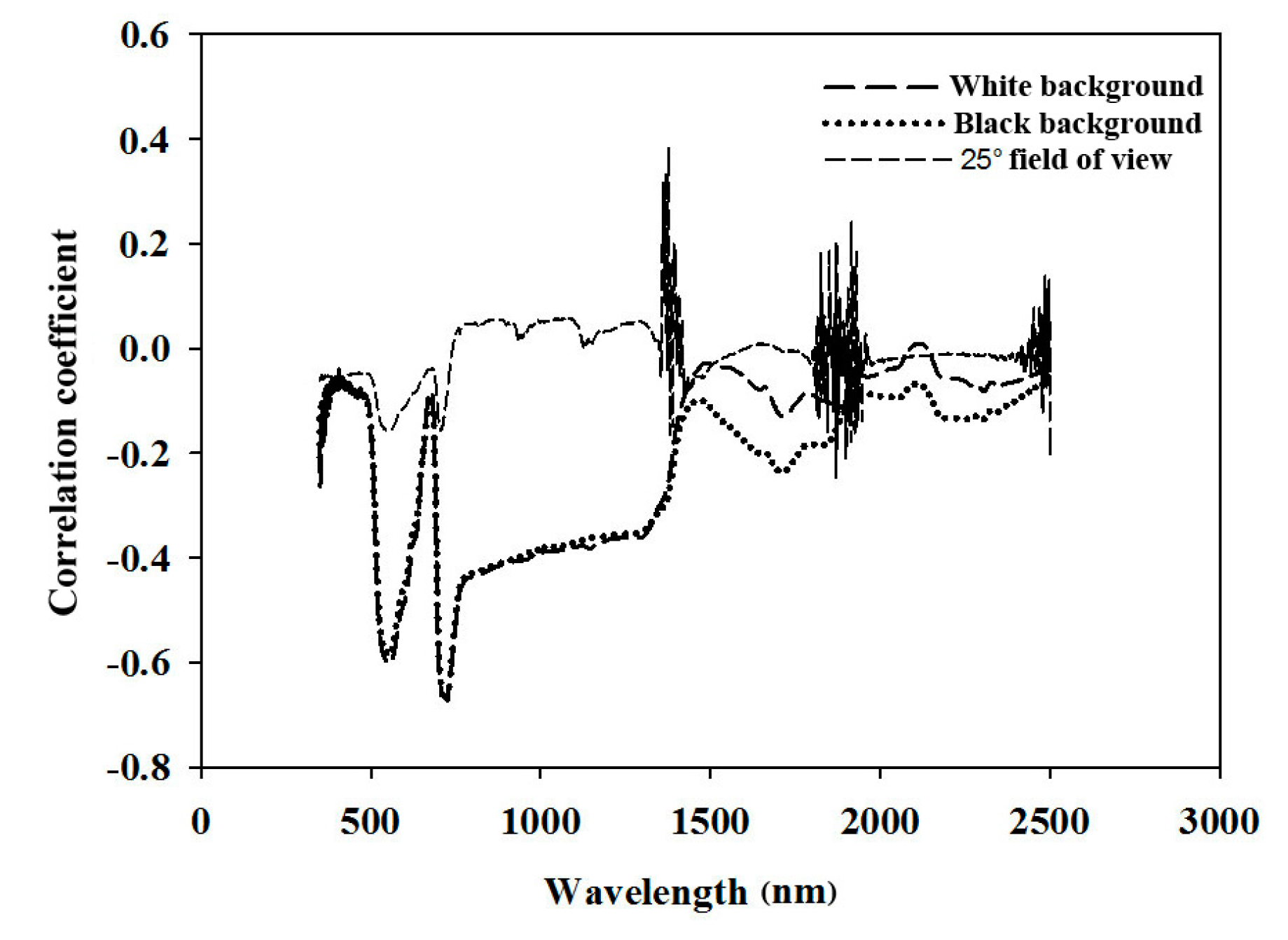
3.1. Establishment of the Non-Destructive Measurement
3.2. Performances of Four Chemometrics
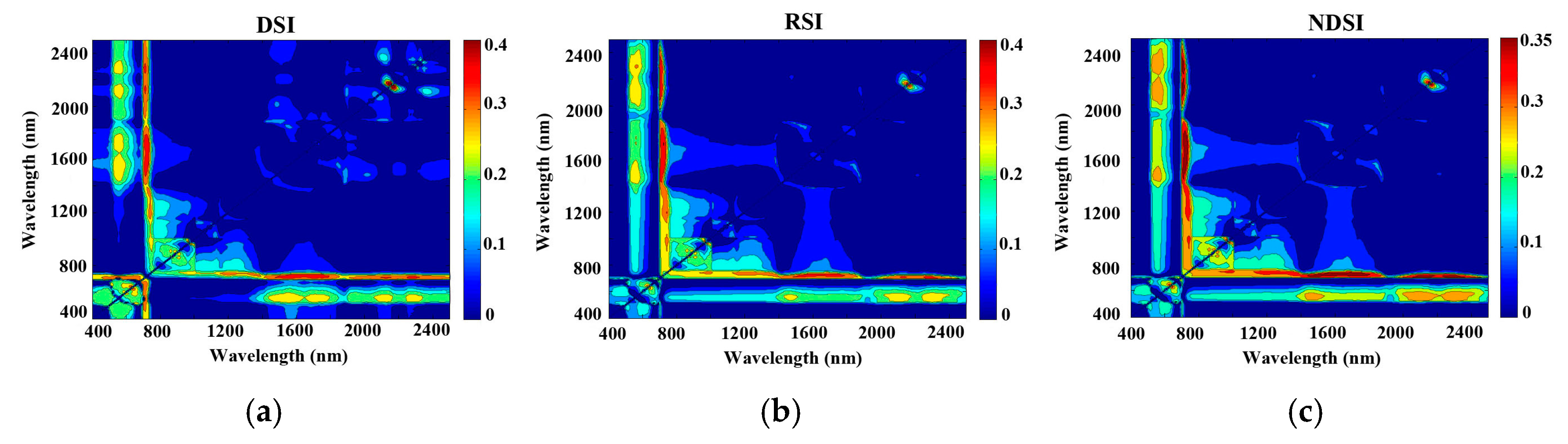
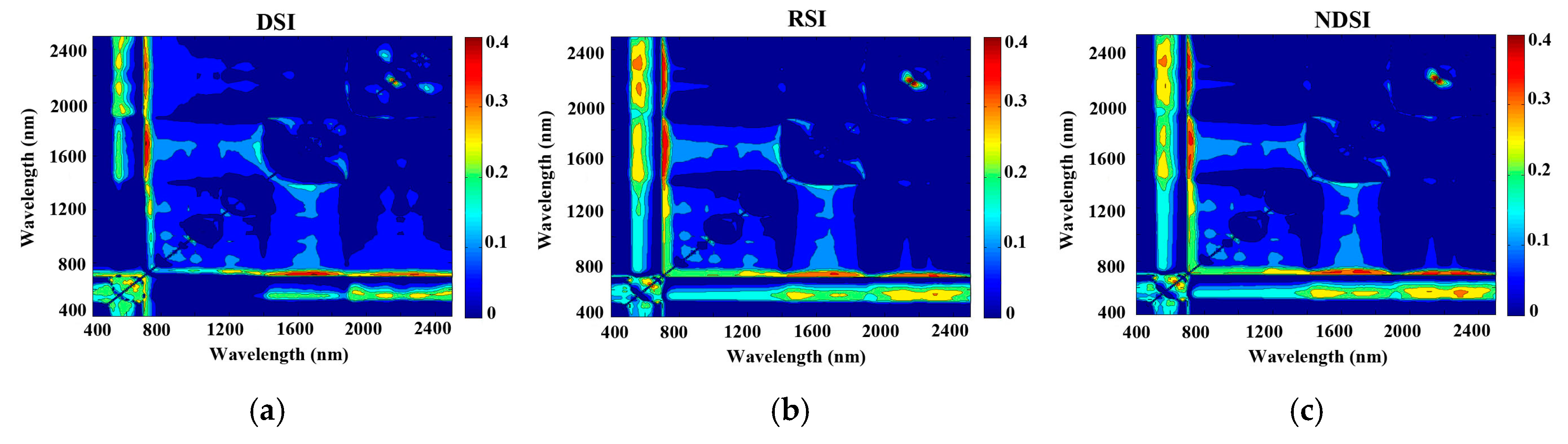
3.3. Modelling the Three Vegetation Indices
3.4. Two-Year Nitrogen Status as Dependent on the N Treatment
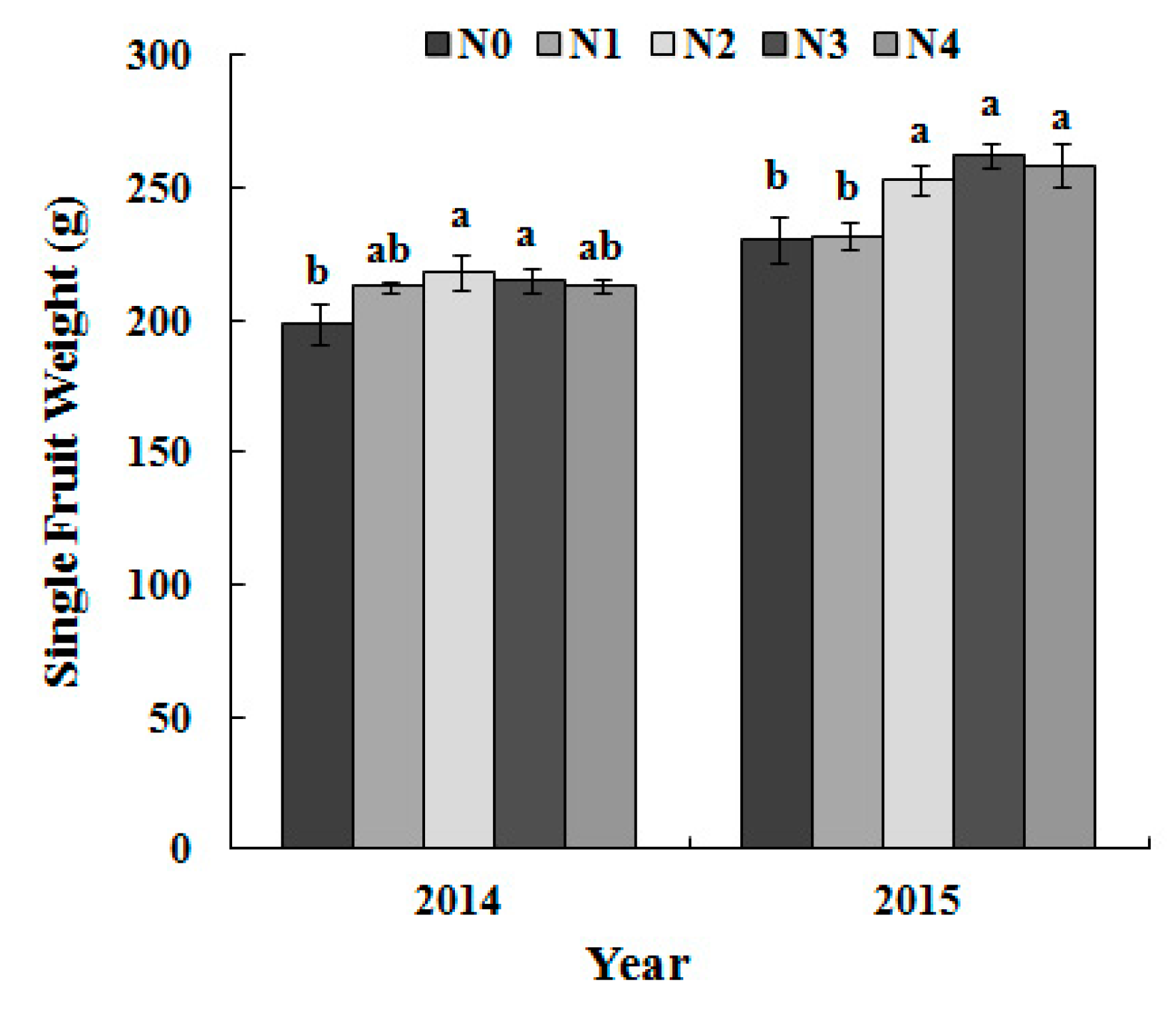
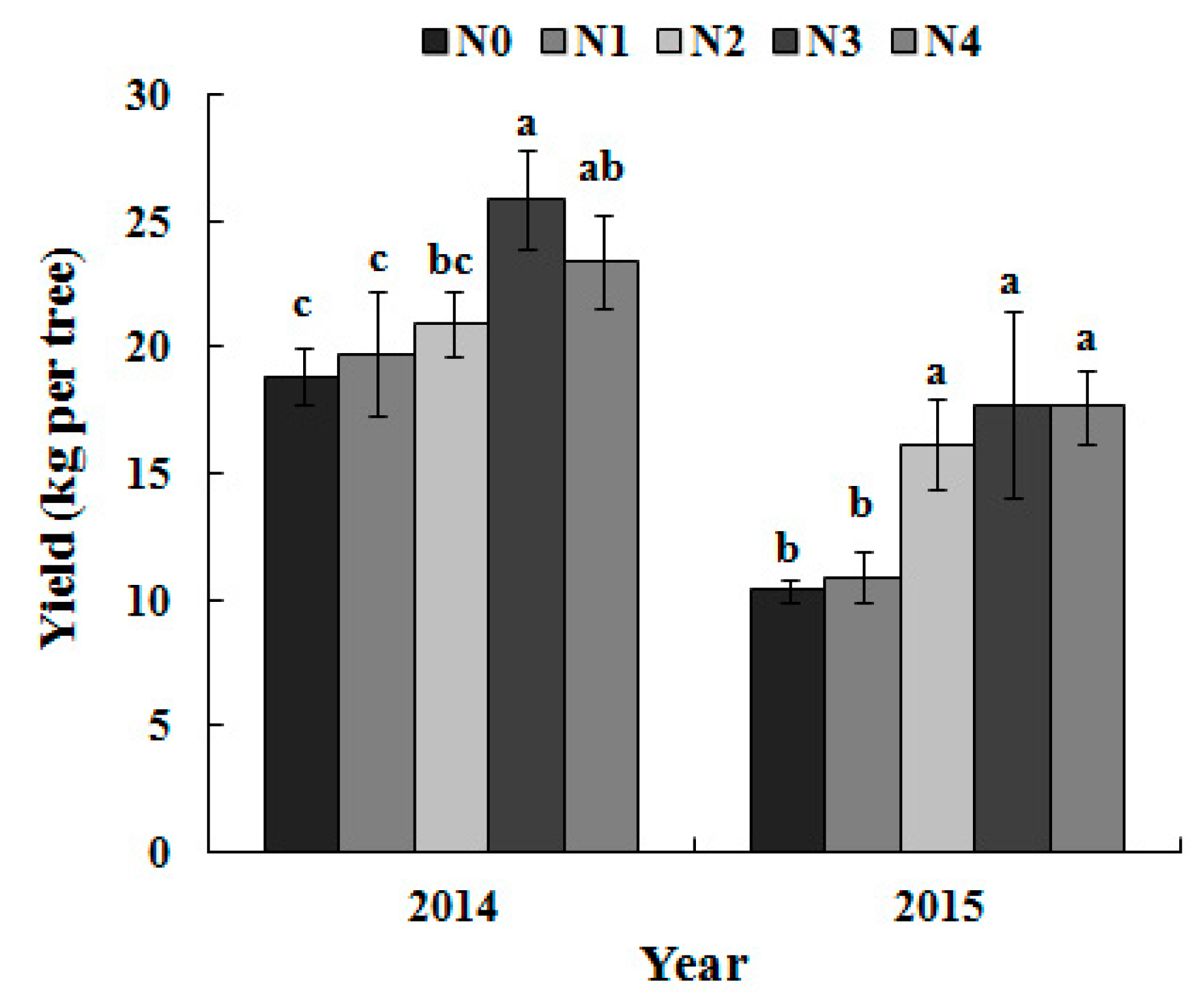
3.5. Single-Fruit Weight and Yield per Tree as Dependent on the N Treatment
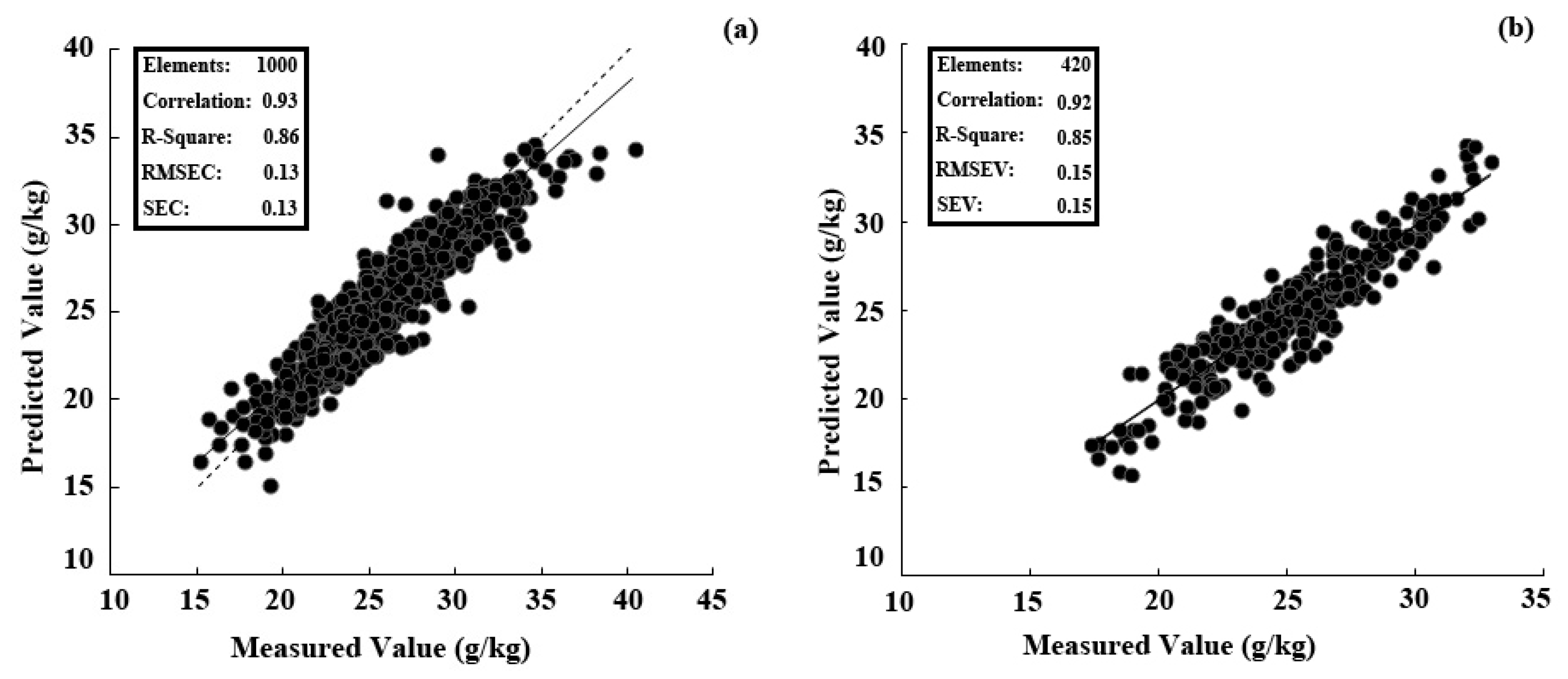
3.6. Performance of the Best PLSR Model Tested with Samples Collected in Two Years
3.7. Relationship Between the Leaf Nitrogen Concentration and Yield
4. Discussion
4.1. In-Field Spectral Measurement of Pear Leaves
4.2. Comparison of Modelling Methods
4.3. Threshold of Leaf N Concentration and Right Diagnostic Time
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brunetto, G.; Melo, G.W.B.D.; Toselli, M.; Quartieri, M.; Tagliavini, M. The role of mineral nutrition on yields and fruit quality in grapevine, pear and apple. Rev. Bras. Frutic. 2015, 37, 1089–1104. [Google Scholar] [CrossRef]
- Sugar, D.; Righetti, T.L.; Sanchez, E.E.; Khemira, H. Management of nitrogen and calcium in pear trees for enhancement of fruit resistance to postharvest decay. HortTechnology 1992, 2, 382–387. [Google Scholar]
- Tagliavini, M.; Scudellari, D.; Marangoni, B.; Toselli, M. Nitrogen fertilization management in orchards to reconcile productivity and environmental aspects. Nutr. Cycl. Agroecosys. 1995, 43, 93–102. [Google Scholar]
- El-Jendoubi, H.; Abadía, J.; Abadía, A. Assessment of nutrient removal in bearing peach trees (Prunus persica L. Batsch) based on whole tree analysis. Plant Soil 2013, 369, 421–437. [Google Scholar] [CrossRef]
- Quartieri, M.; Millard, P.; Tagliavini, M. Storage and remobilization of nitrogen by pear (Pyrus communis L.) trees as affected by timing of N supply. Eur. J. Agron. 2002, 17, 105–110. [Google Scholar] [CrossRef]
- Luo, C.; Xue, L.; Liu, M. Nondestructive measurement of sugar content in navel orange based on Vis-NIR spectroscopy. In Computer and Computing Technologies in Agriculture IV; Springer: Berlin/Heidelberg Germany, 2010; pp. 467–473. [Google Scholar]
- Bo, S.; Jonsson, A.; Börjesson, T. Use of near infrared reflectance spectroscopy to predict nitrogen uptake by winter wheat within fields with high variability in organic matter. Plant Soil 2005, 269, 251–258. [Google Scholar]
- Shi, J.Y.; Zou, X.B.; Zhao, J.W.; Wang, K.L.; Chen, Z.W.; Huang, X.W. Nondestructive diagnostics of nitrogen deficiency by cucumber leaf chlorophyll distribution map based on near infrared hyperspectral imaging. Sci. Hortic. 2012, 138, 190–197. [Google Scholar]
- Ulissi, V.; Antonucci, F.; Benincasa, P. Nitrogen content estimation in tomato leaves by VIS-NIR non-destructive spectroscopy. Sensors 2011, 11, 6411–6424. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Jin, Z.L.; Naeem, M.S. Applying Near-Infrared Spectroscopy and Chemometrics to Determine Total Amino Acids in Herbicide-Stressed Oilseed Rape Leave. Food Bioprocess Tech. 2011, 4, 1314–1321. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, H.; Shen, C.; Chen, Q.; Dong, C.; Xu, Y. Determination of Nitrogen Concentration in Fresh Pear Leaves by Visible/Near-Infrared Reflectance Spectroscopy. Agron. J. 2014, 106, 1867–1872. [Google Scholar]
- Yoder, B.J.; Pettigrew-Crosby, R.E. Predicting nitrogen and chlorophyll content and concentrations from reflectance spectra (400–2500 nm) at leaf and canopy scales. Remote Sens. Environ. 1995, 53, 199–211. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, Y.; Feng, W.; Yao, X.; Cao, W. Monitoring leaf nitrogen in wheat using canopy reflectance spectra. Can. J. Plant Sci. 2006, 86, 1037–1046. [Google Scholar] [CrossRef]
- Potůčková, M.; Červená, L.; Kupková, L.; Lhotáková, Z.; Lukeš, P.; Hanuš, J. Comparison of reflectance measurements acquired with a contact probe and an integration sphere: Implications for the spectral properties of vegetation at a leaf level. Sensors 2016, 16, 1801. [Google Scholar] [CrossRef] [PubMed]
- Menesattia, P.; Antonuccia, F.; Pallottinoa, F. Estimation of plant nutritional status by Vis–NIR spectrophotometric analysis on orange leaves [Citrus sinensis (L) Osbeck cv Tarocco]. Biosyst. Eng. 2010, 105, 448–454. [Google Scholar] [CrossRef]
- Martens, B.H.; Naes, K.H.T. Chapter Multivariate Calibration by Data Compression. In Near-Infrared Technology in the Agricultural and Food Industries, 2nd ed.; American Association of Cereal Chemists, Inc.: St. Pual, MN, USA, 2010; pp. 57–87. [Google Scholar]
- Wold, S.; Sjostrom, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemome Intell. Lab. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Atzberger, C.; Guerif, M.; Baret, F.; Werner, W. Comparative analysis of three chemometric techniques for the spectroradiometric assessment of canopy chlorophyll content in winter wheat. Comput. Electron. Agric. 2010, 73, 165–173. [Google Scholar] [CrossRef]
- Broge, N.H.; Mortensen, J.V. Deriving green crop area index and canopy chlorophyll density of winter wheat from spectral reflectance data. Remote Sens. Environ. 2002, 81, 45–57. [Google Scholar] [CrossRef]
- Rondeaux, G. Vegetation monitoring by remote sensing: A review of biophysical indices. Photo Interpret. 1995, 3, 197–216. [Google Scholar]
- Jago, R.A.; Cutler, M.E.J.; Curran, P.J. Estimating canopy chlorophyll concentration from field and airborne spectra. Remote Sens. Environ. 1999, 68, 217–224. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Atzberger, C.; Skidmore, A.K.; Abkar, A.A. Leaf area index derivation from hyperspectral vegetation indices and the red edge position. Int. J. Remote Sens. 2009, 30, 6199–6218. [Google Scholar] [CrossRef]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Xue, L.; Cao, W.; Luo, W.; Dai, T.; Zhu, Y. Monitoring leaf nitrogen status in rice with canopy spectral reflectance. Agron. J. 2004, 196, 135–142. [Google Scholar] [CrossRef]
- Feng, W.; Yao, X.; Zhu, Y.; Tian, Y.; Cao, W. Monitoring leaf nitrogen status with hyperspectral reflectance in wheat. Eur. J. Agron. 2008, 28, 394–404. [Google Scholar] [CrossRef]
- Lamb, D.W.; Steyn-ross, M.; Schaare, P.; Hanna, M.M.; Silvester, W.; Steyn-Ross, A. Estimating leaf nitrogen concentration in ryegrass (Lolium spp.) pasture using the chlorophyll red-edge: The oretical modelling and experimental observations. Int. J. Remote Sens. 2002, 23, 3619–3648. [Google Scholar]
- Serrano, L. Remote sensing of biomass and yield of winter wheat under different nitrogen supplies. Crop Sci. 2000, 40, 723–731. [Google Scholar] [CrossRef]
- Weber, V.S.; Araus, J.L.; Cairns, J.E.; Sanchez, C.; Melchinger, A.E.; Orsini, E. Prediction of grain yield using reflectance spectra of canopy and leaves in maize plants grown under different water regimes. Field Crops Res. 2012, 128, 82–90. [Google Scholar] [CrossRef]
- Sepulcre-Cantó, G.; Zarco-Tejada, P.J.; Jiménez-Muñoz, J.C.; Sobrino, J.A.; Soriano, M.A.; Fereres, E. Monitoring yield and fruit quality parameters in open-canopy tree crops under water stress. Implications for aster. Remote Sens. Environ. 2007, 107, 455–470. [Google Scholar] [CrossRef]
- Ye, X.; Sakai, K.; Sasao, A.; Asada, S. Potential of airborne hyperspectral imagery to estimate fruit yield in citrus. Chemometr. Intell. Lab. 2008, 90, 132–144. [Google Scholar] [CrossRef]
- Lu, R.K. Soil Chemical Analysis Methods in Agriculture; China Agricultural Sciences and Technical Press: Beijing, China, 2000. (In Chinese) [Google Scholar]
- Olsen, S.R. Estimation of Available Phosphorus in Soils by Extraction with Sodium Bicarbonate; Miscellaneous Paper Institute for Agricultural Research Samaru: Washington, DC, USA, 1954. [Google Scholar]
- Sommers, L.E. Chemical analysis of ecological materials. J. Environ. Qual. 1977, 41, 494–495. [Google Scholar] [CrossRef]
- Tagliavini, M.; Quartieri, M.; Millard, P. Remobilised nitrogen and root uptake of nitrate for leaf growth, flowers and developing fruits of pear (P. communis) trees. Plant Soil 1997, 195, 137–142. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, X.; Ouyang, A. Nondestructive measurement of soluble solid content of navel orange fruit by visible-NIR spectrometric technique with PLSR and PCA-BPNN. LWT Food Sci. Technol. 2010, 43, 602–607. [Google Scholar] [CrossRef]
- Yao, X.; Zhu, Y.; Tian, Y.C.; Feng, W.; Cao, W.X. Exploring hyperspectral bands and estimation indices for leaf nitrogen accumulation in wheat. Int. J. Appl. Earth. Obs. 2010, 12, 89–100. [Google Scholar] [CrossRef]
- Saeys, W.; Mouazen, A.M.; Ramon, H. Potential for onsite and online analysis of pig manure using visible and near infrared reflectance spectroscopy. Biosyst. Eng. 2005, 91, 393–402. [Google Scholar] [CrossRef]
- Gomez, A.H.; He, Y.; Pereira, A.G. Non-destructive measurement of acidity, soluble solids and firmness of Satsuma mandarin using Vis/NIR-spectroscopy techniques. J. Food Eng. 2006, 77, 313–319. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Rotbart, N.; Schmilovitch, Z.; Cohen, Y.; Alchanatis, V.; Erel, R.; Ignat, T.; Shenderey, C.; Dag, A.; Yermiyahu, U. Estimating olive leaf nitrogen concentration using visible and near-infrared spectral reflectance. Biosyst. Eng. 2013, 114, 426–434. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Barankova, B.; Lazar, D.; Naus, J. Analysis of the effect of chloroplast arrangement on optical properties of green tobacco leaves. Remote Sens. Environ. 2016, 174, 181–196. [Google Scholar] [CrossRef]
- Serbin, S.P.; Dillaway, D.N.; Kruger, E.L.; Townsend, P.A. Leaf optical properties reflect variation in photosynthetic metabolism and its sensitivity to temperature. J. Exp. Bot. 2012, 63, 489–502. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.T.; Lee, B.W. Assessment of rice leaf growth and nitrogen status by hyperspectral canopy reflectance and partial least square regression. Eur. J. Agron. 2006, 24, 349–356. [Google Scholar] [CrossRef]
- Gobron, N. Theoretical limits to the estimation of the leaf area index on the basis of visible and near-infrared remote sensing data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1438–1445. [Google Scholar] [CrossRef]
- Blackburn, G.A. Relationships between Spectral Reflectance and Pigment Concentrations in Stacks of Deciduous Broadleaves. Remote Sens. Environ. 1999, 70, 224–237. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Jiang, Z.; Wang, C.; Yang, C. Modeling and prediction of CO2 exchange response to environment for small sample size in cucumber. Comput. Electron. Agric. 2014, 108, 39–45. [Google Scholar] [CrossRef]
- Sanchez, E.E.; Righetti, T.L.; Sugar, D.; Lombard, P.B. Recycling of nitrogen in field-grown ‘Comice’ pears. J. Hort. Sci. 1991, 66, 541–546. [Google Scholar]
- Graeff, S.; Claupein, W. Quantifying nitrogen status of corn (Zea mays L.) in the field by reflectance measurements. Eur. J. Agron. 2003, 19, 611–618. [Google Scholar] [CrossRef]



| Dataset | Samples Collected in May | Samples Collected in June | ||||||
|---|---|---|---|---|---|---|---|---|
| Sample No. | Min. | Max. | Mean | Sample No. | Min. | Max. | Mean | |
| (g/kg) | (g/kg) | |||||||
| Total | 340 | 18.7 | 35.2 | 25.4 ± 3.0 | 370 | 20.3 | 30.9 | 24.7 ± 1.9 |
| Calibration | 290 | 20.5 | 35.2 | 27.4 ± 2.7 | 310 | 20.3 | 30.9 | 24.8 ± 2.0 |
| Validation | 50 | 18.7 | 30.2 | 23.4 ± 2.4 | 60 | 21.4 | 28.2 | 24.5 ± 1.7 |
| Method † | Black Background | White Background | ||||||
|---|---|---|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | |||||
| R2 | RMSEC | R2 | RMSEV | R2 | RMSEC | R2 | RMSEV | |
| PCR | 0.42 | 0.23 | 0.41 | 0.24 | 0.42 | 0.25 | 0.40 | 0.26 |
| SMLR | 0.78 | 0.14 | 0.75 | 0.19 | 0.77 | 0.14 | 0.73 | 0.20 |
| PLSR | 0.86 | 0.12 | 0.81 | 0.13 | 0.82 | 0.13 | 0.78 | 0.15 |
| BPNN | 0.89 | 0.23 | 0.67 | 0.17 | 0.88 | 0.24 | 0.61 | 0.18 |
| Vegetation Index †† | Black Background | White Background | ||
|---|---|---|---|---|
| R2 | Wavelength of Max R2 | R2 | Wavelength of Max R2 | |
| DSI | 0.46 | 2170 nm, 2150 nm | 0.41 | 1690 nm, 710 nm |
| RSI | 0.40 | 1710 nm, 720 nm | 0.44 | 2170 nm, 2150 nm |
| NDSI | 0.39 | 1690 nm, 730 nm | 0.44 | 2150 nm, 2170 nm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Shen, C.; Liu, N.; Jin, X.; Fan, X.; Dong, C.; Xu, Y. Non-Destructive Evaluation of the Leaf Nitrogen Concentration by In-Field Visible/Near-Infrared Spectroscopy in Pear Orchards. Sensors 2017, 17, 538. https://doi.org/10.3390/s17030538
Wang J, Shen C, Liu N, Jin X, Fan X, Dong C, Xu Y. Non-Destructive Evaluation of the Leaf Nitrogen Concentration by In-Field Visible/Near-Infrared Spectroscopy in Pear Orchards. Sensors. 2017; 17(3):538. https://doi.org/10.3390/s17030538
Chicago/Turabian StyleWang, Jie, Changwei Shen, Na Liu, Xin Jin, Xueshan Fan, Caixia Dong, and Yangchun Xu. 2017. "Non-Destructive Evaluation of the Leaf Nitrogen Concentration by In-Field Visible/Near-Infrared Spectroscopy in Pear Orchards" Sensors 17, no. 3: 538. https://doi.org/10.3390/s17030538
APA StyleWang, J., Shen, C., Liu, N., Jin, X., Fan, X., Dong, C., & Xu, Y. (2017). Non-Destructive Evaluation of the Leaf Nitrogen Concentration by In-Field Visible/Near-Infrared Spectroscopy in Pear Orchards. Sensors, 17(3), 538. https://doi.org/10.3390/s17030538





