1. Introduction
With the increasing demand for 3-dimensional (3D) geospatial information in various fields such as civil engineering and construction [
1,
2], environmental monitoring [
3,
4], and disaster management [
5,
6], a number of devices and algorithms for the 3D reconstruction have been developed and utilized. In general, all 3D mapping techniques can be classified into range-based techniques using a 3D laser scanner, also called Light Detecting and Ranging (LiDAR), and image-based 3D reconstruction techniques based on the principles of computer vision and photogrammetry [
7,
8]. By using those techniques, the 3D information (X, Y, Z) of observed objects is represented by a point cloud. The 3D laser scanner directly measures the 3D coordinates of objects with extremely high accuracy and resolution, but is financially prohibitive. Alternatively, image-based 3D reconstruction methods have been developed and applied to reducing the cost of acquiring point clouds [
9,
10]. Using corresponding features in overlapped images, the 3D coordinates of objects are calculated. However, the image-based 3D reconstruction technique has much noise and low accuracy and is highly affected by the captured space. If there is no feature in the captured space or the space is too dark or bright, the 3D reconstruction cannot be performed and many noisy points occur. In this regard, the 3D laser scanner is utilized by the engineers who require geospatial data of high resolution and accuracy [
11,
12].
According to the scanning geometry, laser scanners can be classified into terrestrial laser scanners and mobile laser scanners. Terrestrial laser scanners spherically scan the surrounding space using two freely rotating axes in a fixed position and generate more accurate, precise, and dense information than mobile laser scanners [
13]. With their high performance, terrestrial laser scanners has been widely applied to the fields requiring highly accurate and dense 3D information like construction sites [
14,
15]. On the other hand, mobile laser scanners mounted on a moving vehicle rapidly rotate or oscillate horizontally at a certain fixed vertical angle. In general, mobile laser scanners with high scan rates are designed to be mounted on different vehicles such as automobiles and drones. As the platform where the mobile laser scanner is mounted moves, a point cloud is generated with respect to the trajectory of the platform. The trajectory information can be obtained from a navigation sensor like a Global Navigation Satellite System (GNSS)/Inertial Navigation System (INS) and the point cloud is formed based on the geometric relationship between the navigation sensor and the laser scanner [
13,
16]. Moreover, by integrating the mobile laser scanner with a camera, color information can be added to the generated point cloud.
A system combining multiple sensors with a navigation sensor on a moving vehicle is called a Mobile Mapping System (MMS). In the early 1990s, MMSs combining a code-only GNSS, stereo digital cameras, and supplementary dead-reckoning sensors were developed and utilized in applications based on the image-based 3D reconstruction technique [
17,
18]. As the accuracy of laser measurement and navigation sensors has improved, mobile laser scanners have become one of the main components of any MMS. In particular, as near real-time and periodical 3D mapping is required for the autonomous driving systems, the laser-based measurement MMS has been developed and widely utilized to generate the high-quality 3D geospatial information about urban environments [
19,
20,
21,
22].
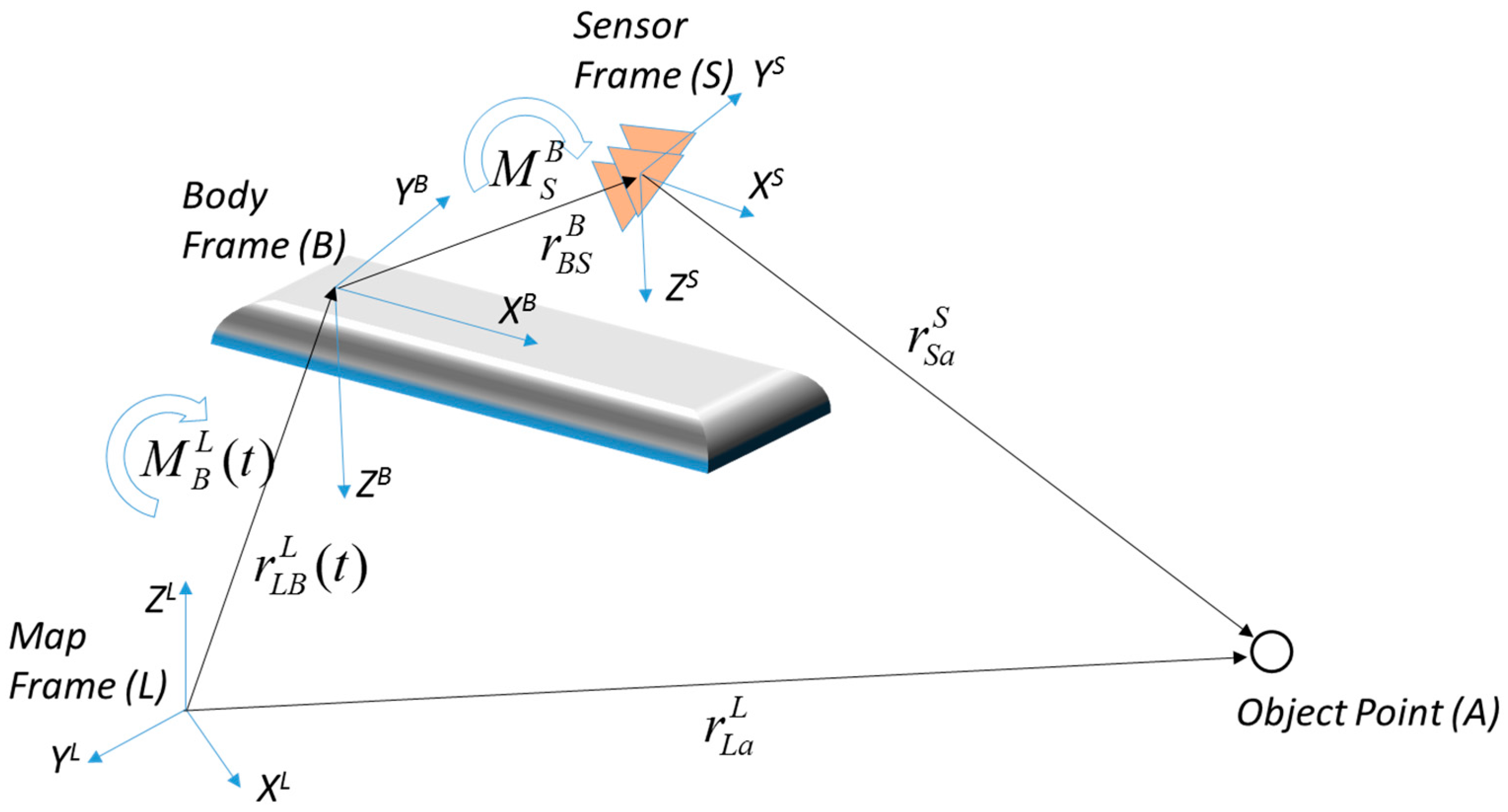
To integrate the datasets captured by each sensor mounted on the MMS into the unified single coordinate system, the calibration, which is the process to estimate the orientation (boresight) and position (lever-arm) parameters, is required with the reference datasets [
16,
23,
24]. When the boresight and lever-arm parameters defining the geometric relationship between each sensing data and GNSS/INS data are determined, georeferenced data can be generated. However, even after precise calibration, the boresight and lever-arm parameters of an MMS can be shaken and the errors that deteriorate the accuracy of the georeferenced data might accumulate. Accordingly, for the stable operation of multiple sensors, precise calibration must be conducted periodically.
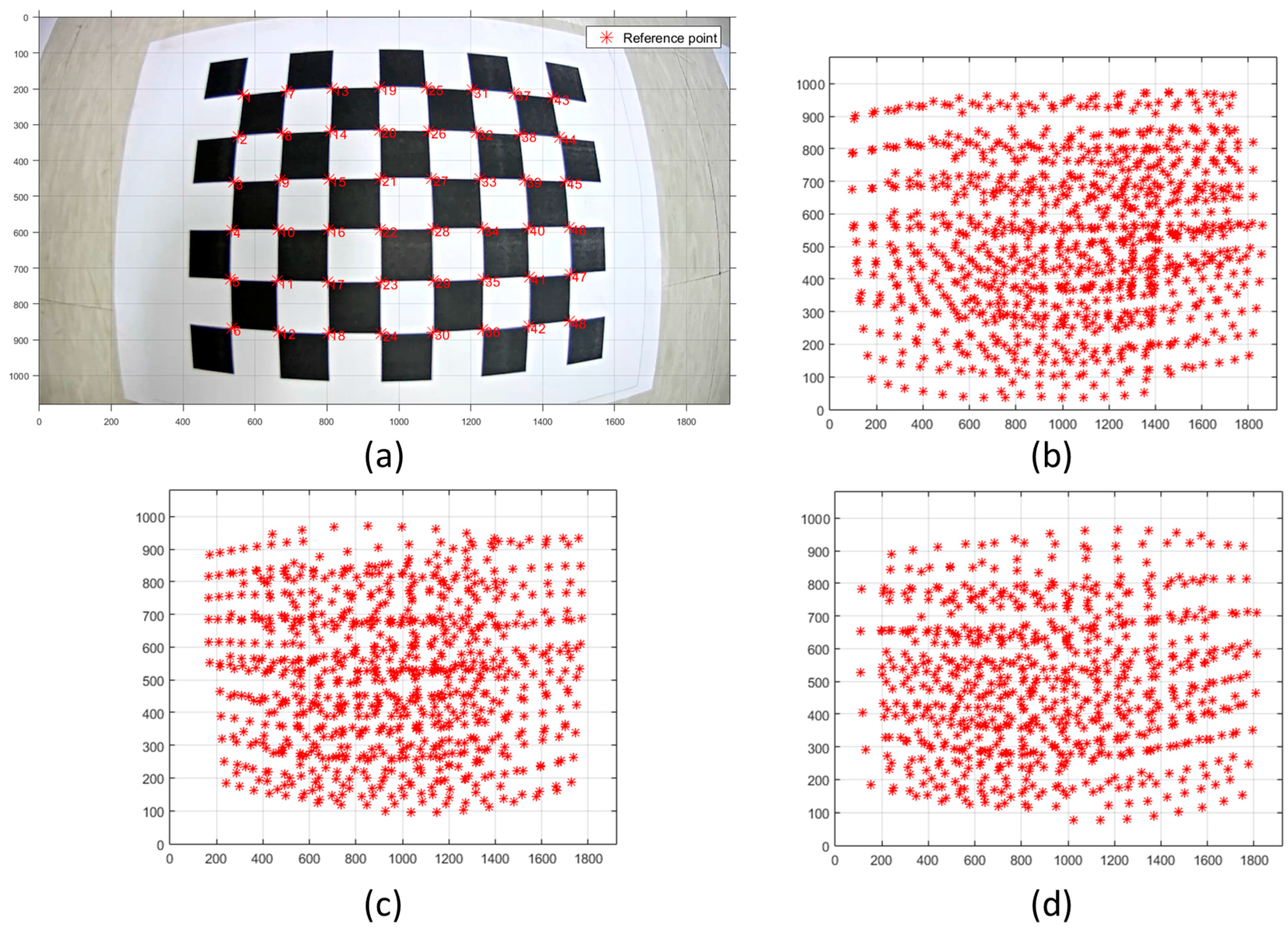
In general, the calibration process is performed based on the observation models and constraints to define the geometric relationship between the observed object in real world and in the sensing data. For example, in the case of camera calibration, a calibration model is generally designed based on a collinearity equation with the Exterior Orientation Parameters (EOPs) and Interior Orientation Parameters (IOPs) [
25,
26]. To configure the constraints for the camera calibration, a checkerboard which has repetitive black and white (BW) patterns and whose spacing is accurately known is generally utilized [
27,
28]. For example, computer vision libraries such as OpenCV [
29] and Matlab Toolbox [
30] provide camera calibration tools based on the checkerboard approach. With the calibrated parameters, the correction of lens distortion, which is presented in a fisheye lens or wide angle lens camera image, and geometric analysis such as visual odometry can be performed [
31]. Furthermore, ground control features of which ground coordinates are known can be used as geometric constraints. For example, since the checkerboard-based calibration method is difficult to apply to an airborne system due to the long distance between the sensor and ground, Chiang et al. [
32] used ground control points to calibrate the time-offset of the camera shutter and to estimate the trajectory of the camera mounted on an airborne vehicle.
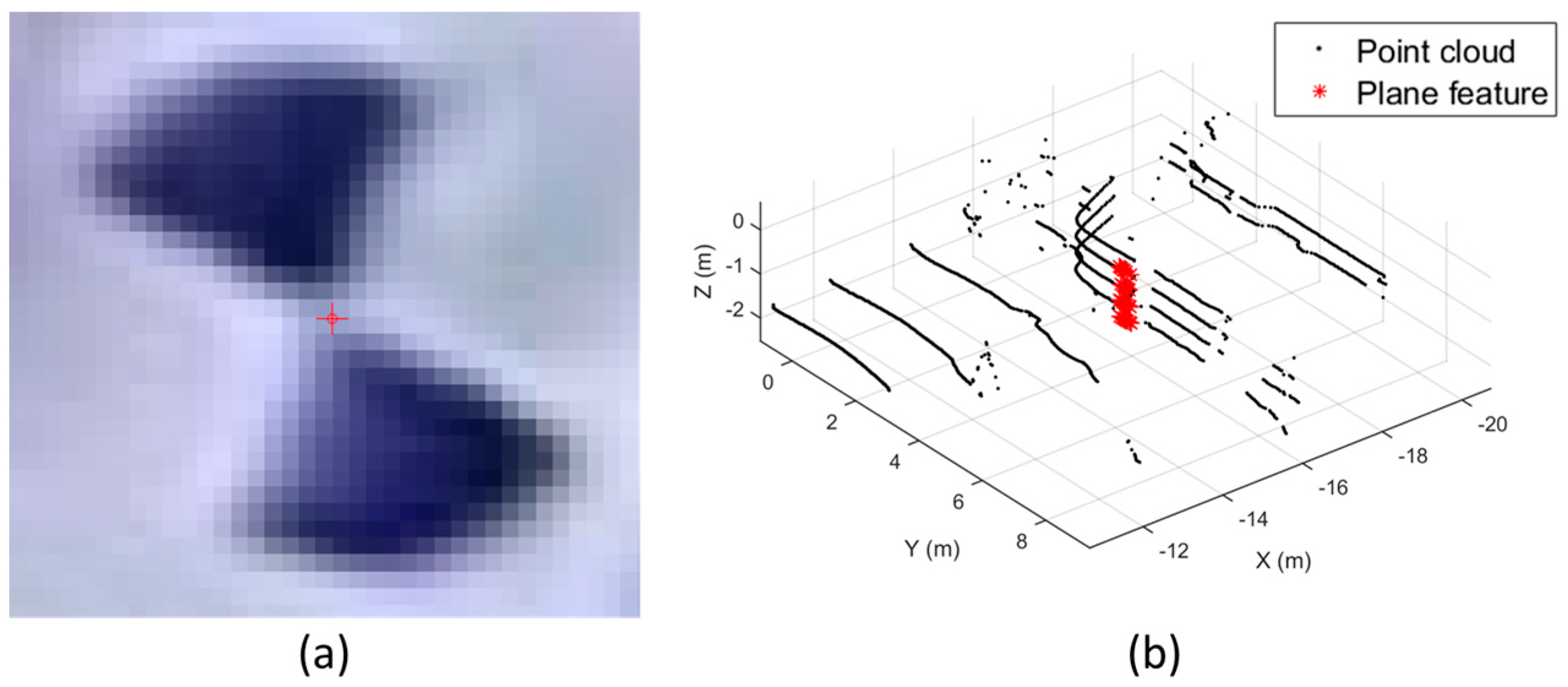
While point-based calibration techniques using a checkerboard or ground control points can be a practical solution for the calibration of camera systems, it is difficult to extract accurate corner or edge points from the sparse point clouds generated by the mobile laser scanner due to its low accuracy and resolution. Alternatively, the line, plane, and cylindrical features, which can be defined by mathematical equations, have been widely applied for the calibration of laser scanners [
33,
34,
35]. For example, the plane features can be precisely extracted from a sparse point cloud using a RANdom SAmple Consensus (RANSAC) algorithm even if there exist noisy points in the point cloud [
36]. With the orthogonality constraints of multiple planes installed in the laser scanning view, the boresight parameters can be estimated with least-squares adjustment [
37,
38,
39,
40]. Furthermore, based on the least-squares adjustment, the boresight and lever-arm parameters of the MMS can be stochastically calculated using the plane features as geometric constraints. Filin [
41] applied the least-squares adjustment with the plane features to calibrate an airborne laser scanning system. Glennie [
42] performed the boresight calibration of a mobile laser scanner with the plane features captured in a kinematic mode.
Obviously, the precision of the calibrated parameters is directly affected by the accuracy and geometry of the ground control features, and the construction of the accurate and dense ground control features for the calibration is important. To collect the ground control features, a total station or a laser tracker, which is the laser-based equipment to achieve the 3D coordinate of a point target with a sub-millimeter accuracy, are generally utilized [
43,
44,
45]. Even though the observation accuracy of the total station is significantly high, the point positioning techniques are labor-intensive and it is difficult for general users to achieve a number of accurate control point coordinates. Moreover, since different types of features are required for the calibration of each sensor on the MMS, it is difficult to make a common ground control dataset.
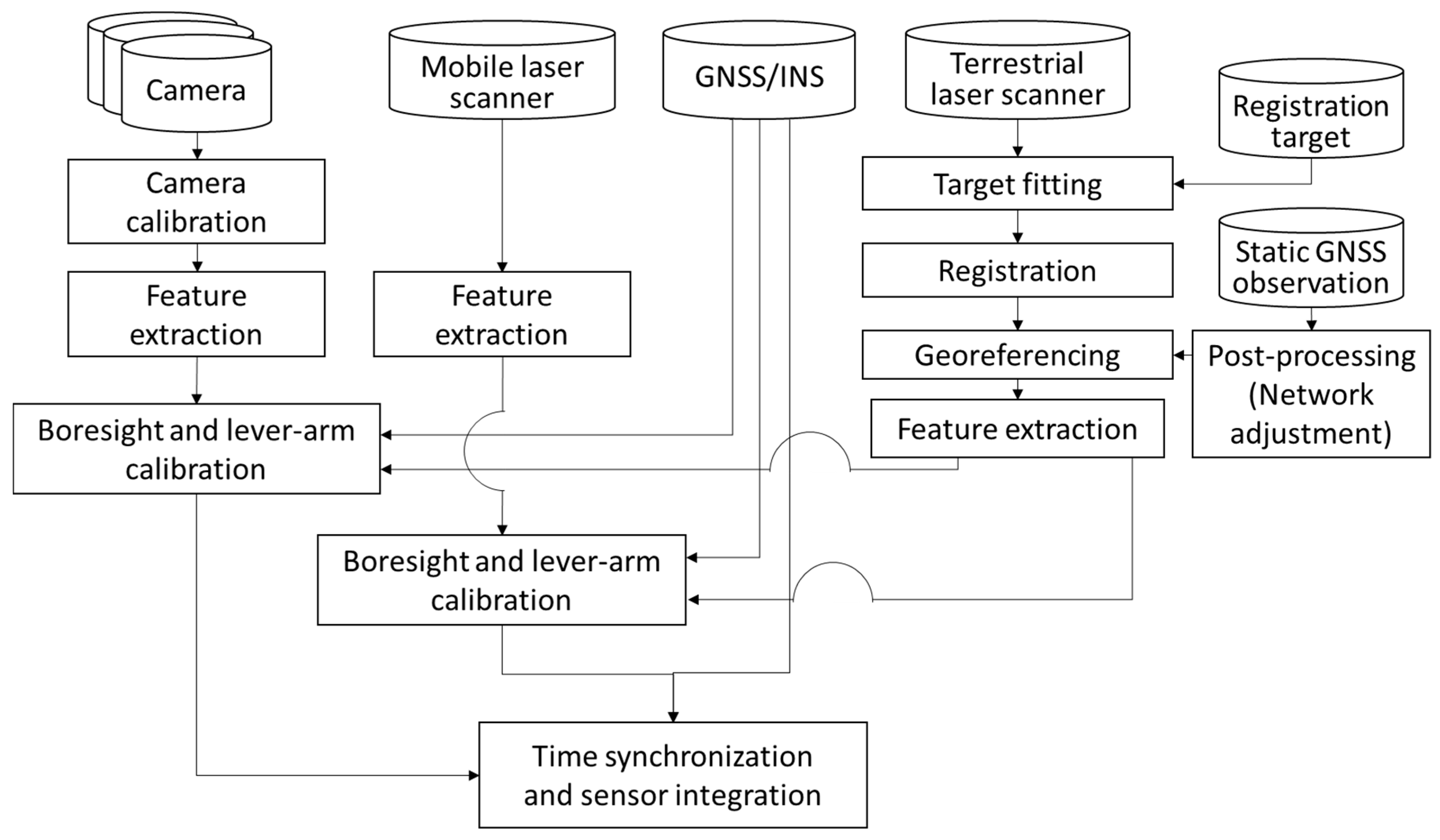
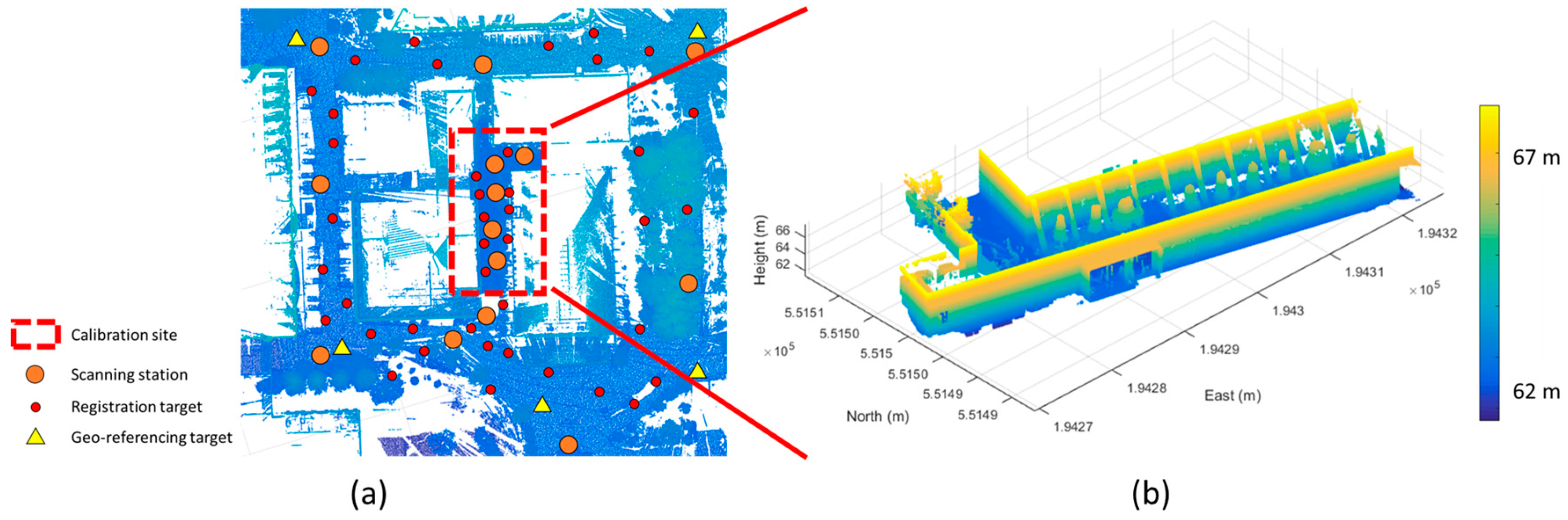
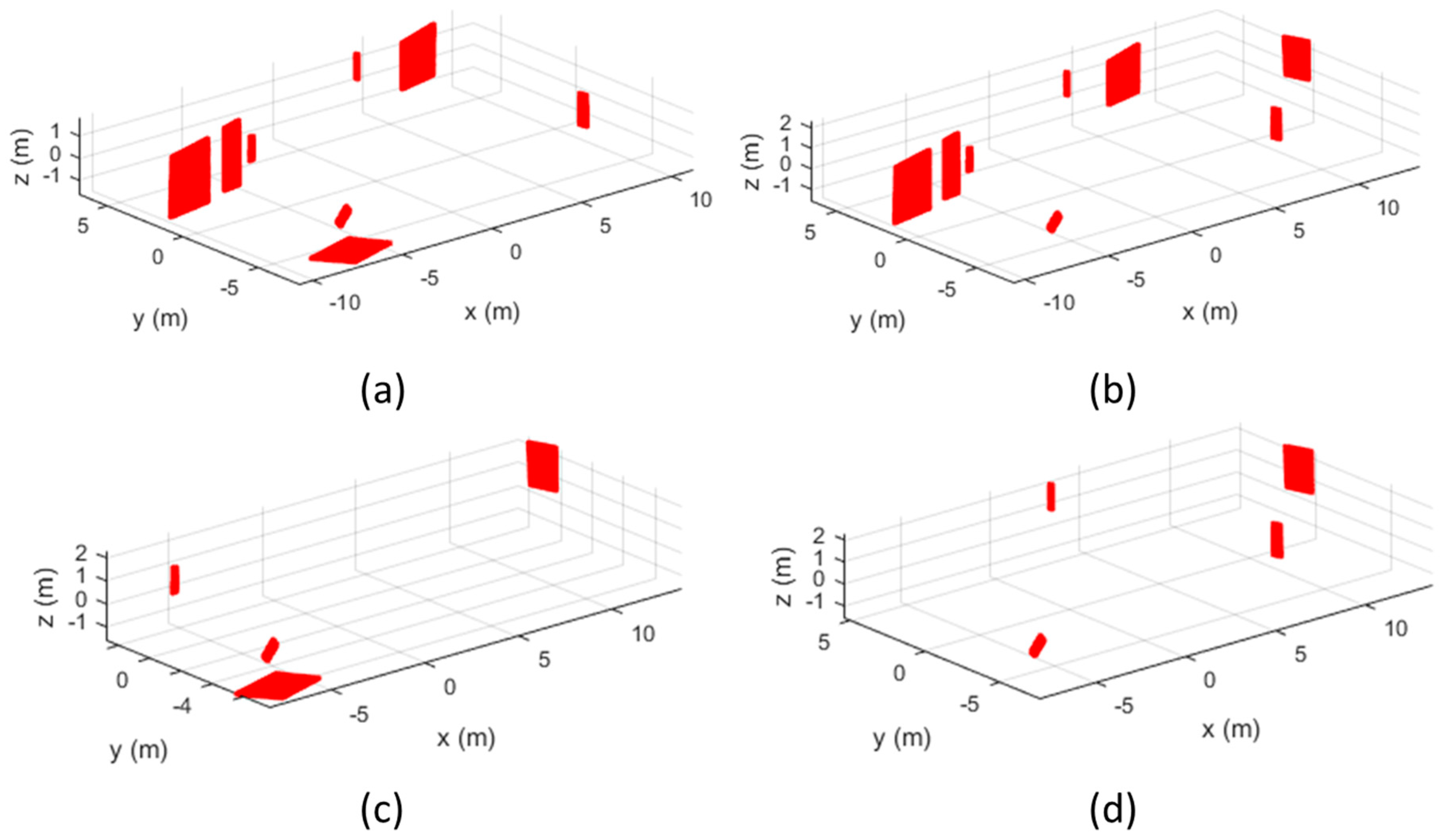
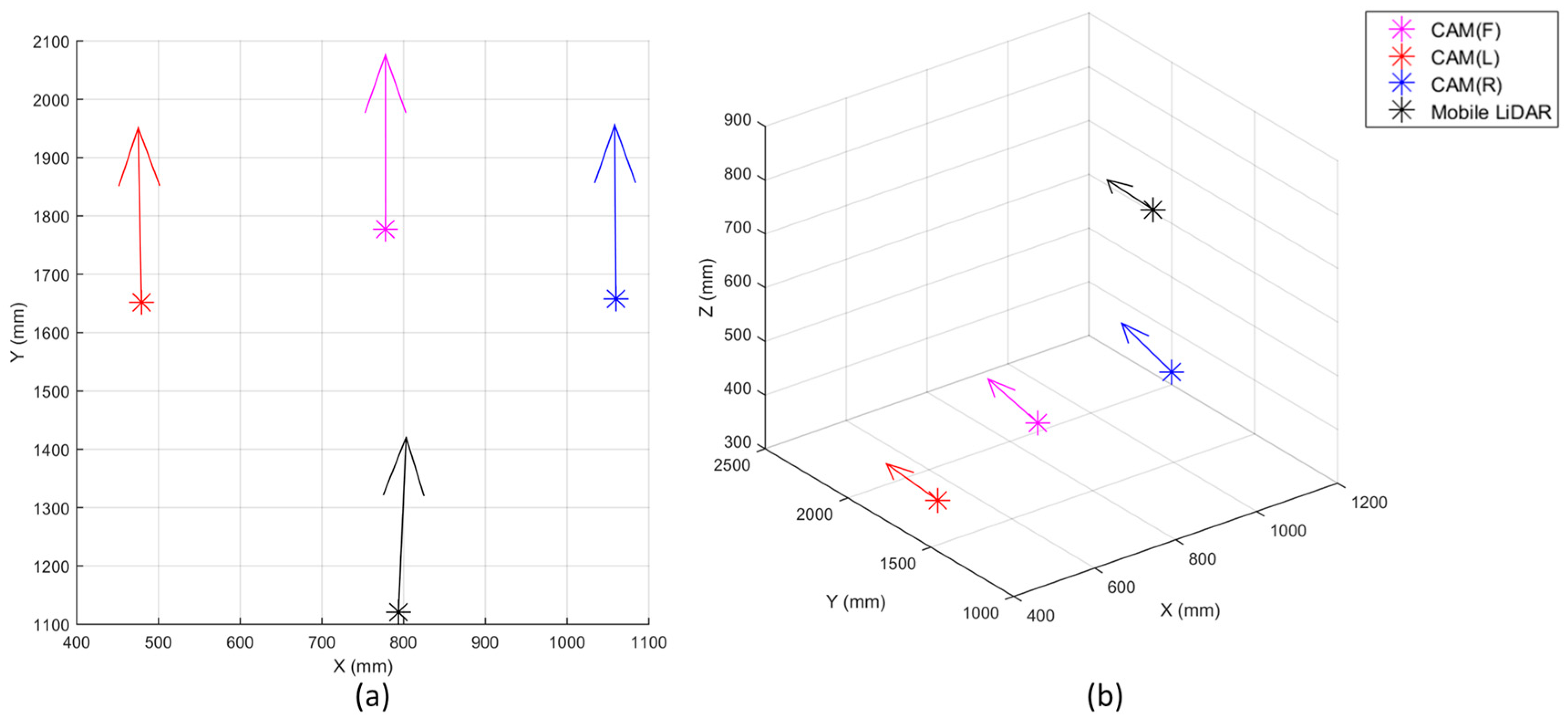
In this paper, we have devised a method for utilizing the terrestrial laser scanner to simultaneously calibrate the camera and mobile laser scanner mounted on the MMS. On our MMS, devised for conducting the calibration experiment, three network video cameras, one mobile laser scanner, and one GNSS/INS were mounted. The devised MMS calibration process can be largely divided into two steps. As the first step for constructing the dataset of the ground control features, the terrestrial laser scanning data needs to be accurately georeferenced. In the second step point and plane features were extracted from the georeferenced terrestrial laser scanning data and matched with the features extracted from the mobile laser scanning data and the captured images. Before applying the boresight and lever-arm calibration of the devised MMS, the camera calibration to estimate the camera IOPs was conducted separately using the checkerboard approach. The calibration parameters of each sensor and their precisions were calculated based on the least-squares adjustment.
5. Discussion and Future Work
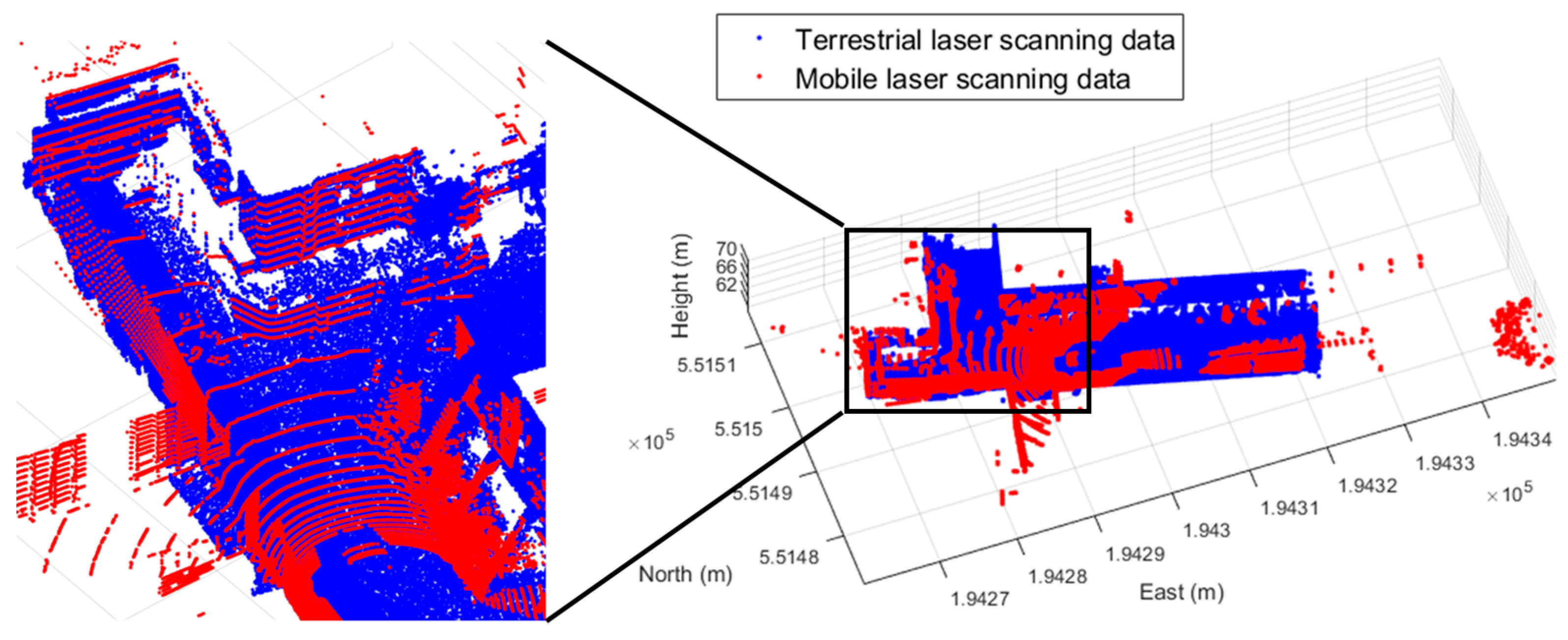
In this paper, the MMS combining the GNSS/INS, cameras and mobile laser scanner was developed and the boresight and lever-arm calibration of the MMS was conducted. The calibration approach based on the least squares adjustment using point features and plane features has been widely applied and continuously analyzed in existing researches for sensor calibration. However, for the adjustment, it is difficult to collect proper reference data for the calibration. In this regard, the utilization of the terrestrial laser scanner could be an alternative solution to efficiently achieve a reference dataset. Comparing with the total station and laser finder, which are generally used for collecting accurate positioning data, the terrestrial laser scanner could obtain a dense and precise point cloud and reference features for the MMS calibration.
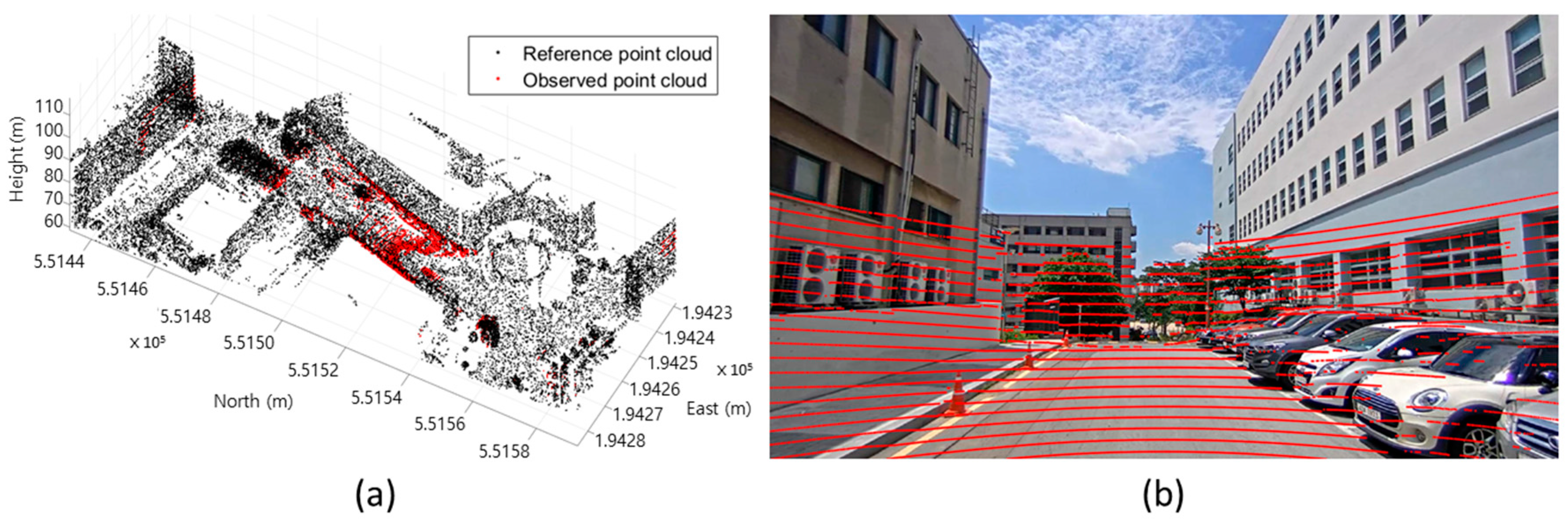
Through the calibration parameters and GNSS/INS observation, the multi-sensor integration was conducted successfully and the point clouds observed by the mobile laser scanner were georeferenced into the absolute coordinate system or accurately projected onto the time-synchronized image (
Figure 16).
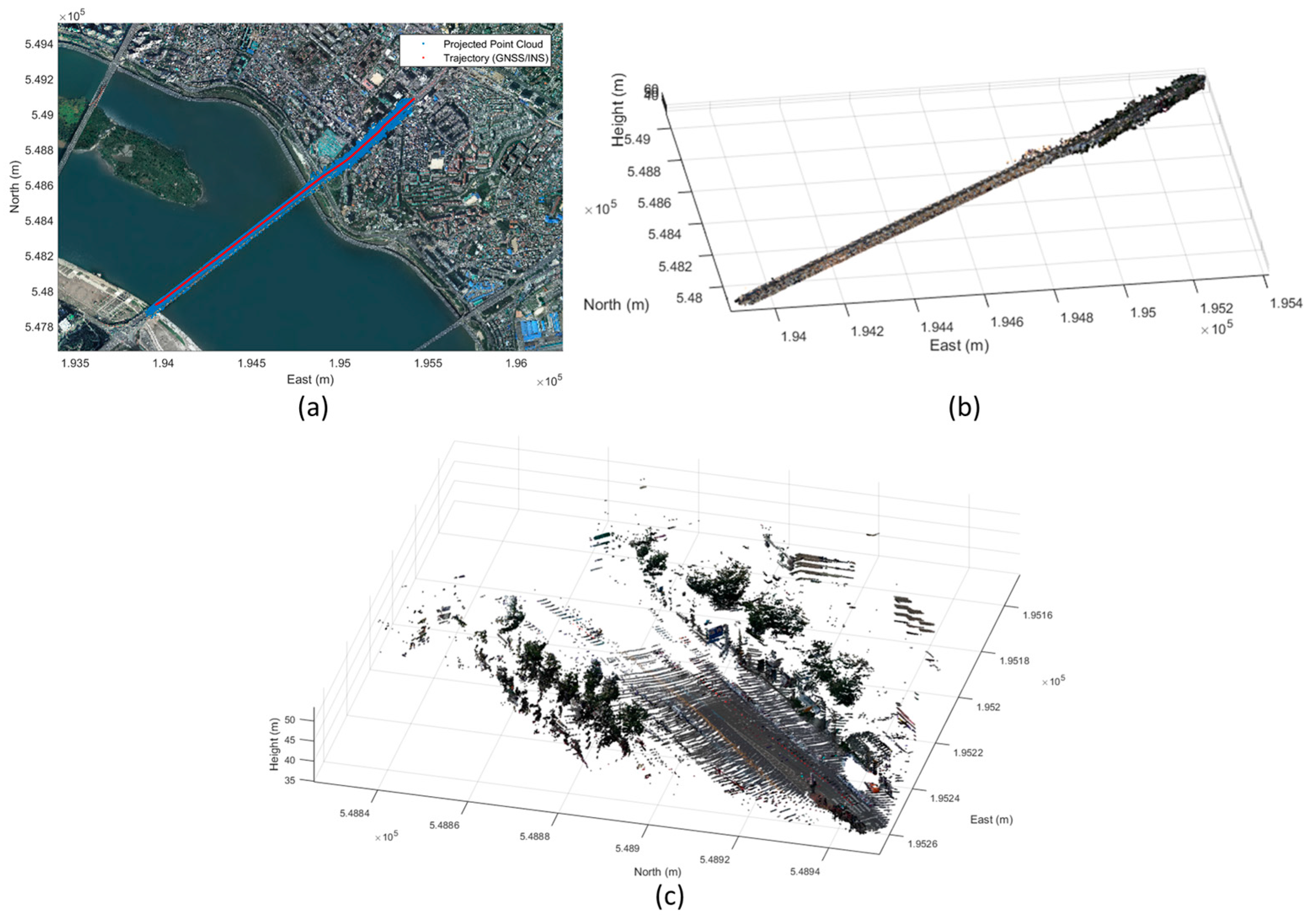
The dataset continuously collected from the moving platform can be represented by two information formats: (1) the point cloud representing the 3D shape and color information of the observed objects (
Figure 17); and (2) the 3D positional information of the objects extracted from the continuous images (
Figure 18).
As shown in
Figure 17, the point cloud observed from the MMS were directly georeferenced and could represent the 3D shapes of objects. However, the point cloud generated from the MMS was too sparse to extract the accurate road facility information. In particular, when objects were far from the MMS, the vertical point density of the generated point cloud became lower. For this reason, our research team alternatively designed the scheme of the road facility mapping based on image processing techniques. Moreover, as shown in
Figure 18, the road facilities can be extracted from images and have absolute 3D coordinates. Our research team expects that the collected information of road facilities can be used as the basic data for the operation of autonomous cars. However, since the urban blockage of GNSS signals due to high and dense buildings significantly causes locational biases in the point cloud observed by the designed MMS, a proper Simultaneous Localization and Mapping (SLAM) technique to improve the stability and accuracy of observation should be developed and applied.