Dual MIMU Pedestrian Navigation by Inequality Constraint Kalman Filtering
Abstract
:1. Introduction
2. Principle and Theory
2.1. Discrete Kalman Filter
2.2. Inequality Kalman Filter
3. Methods
3.1. Generalized Likelihood Ratio Test (GLRT)
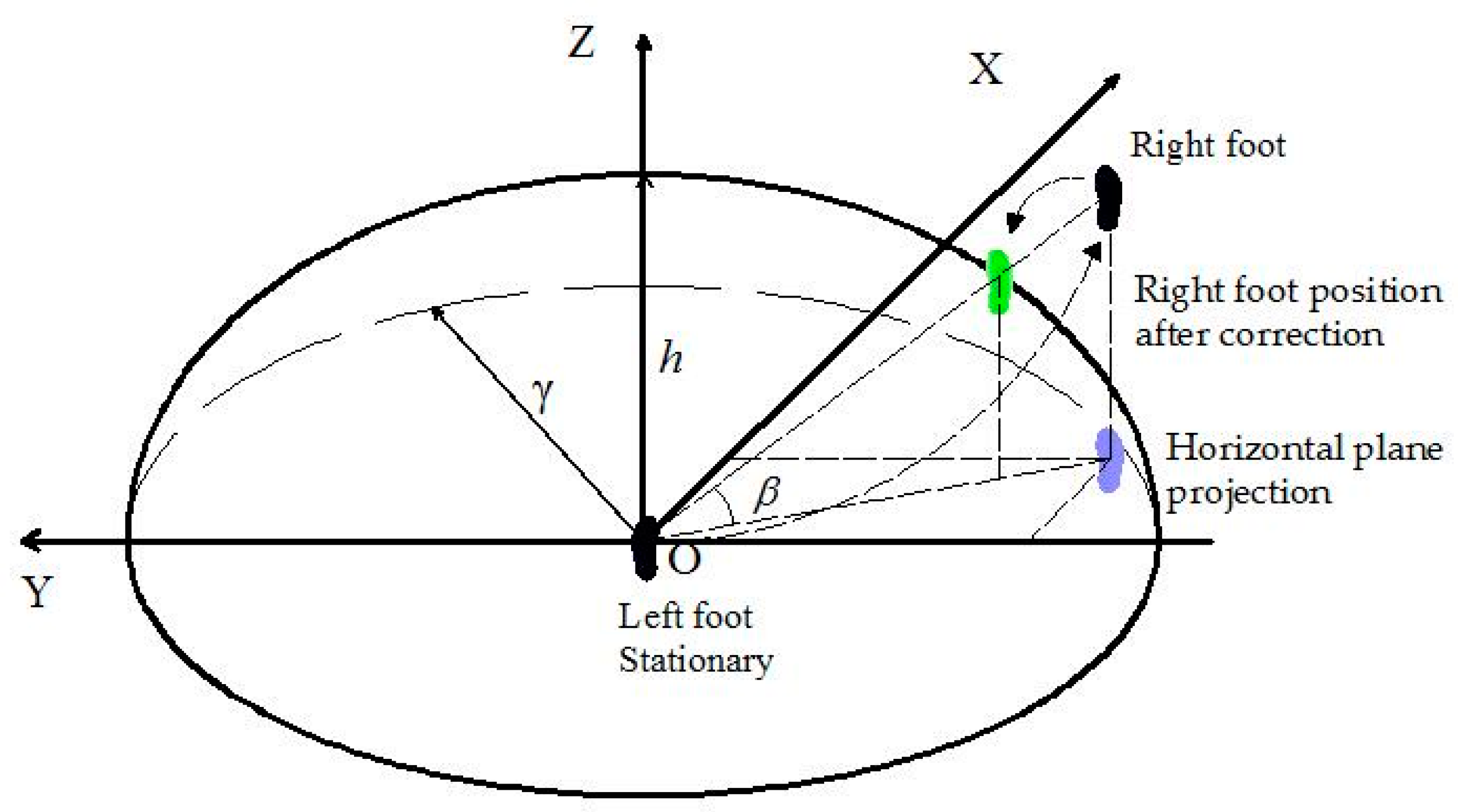
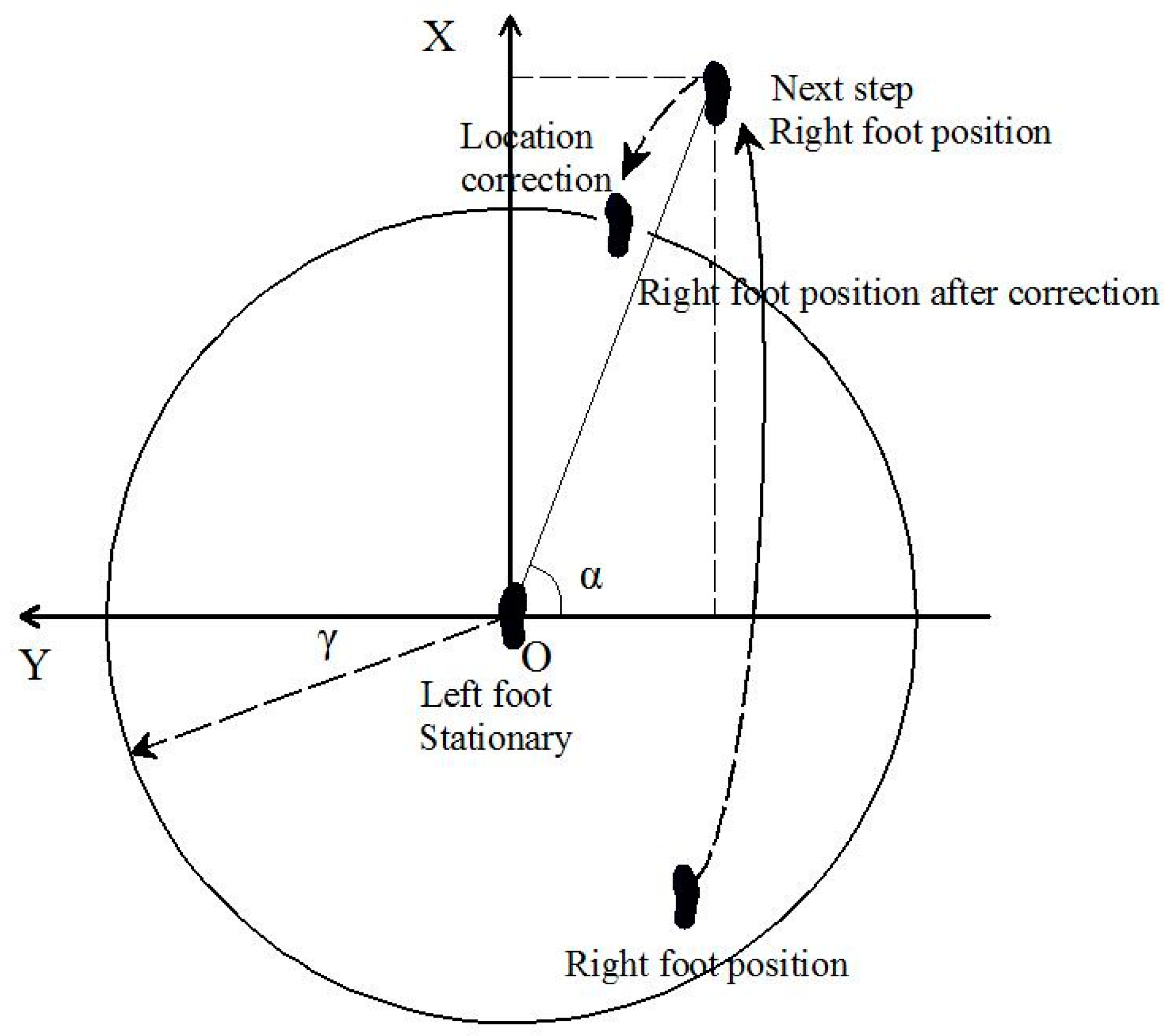
3.2. The Ellipsoidal Constraint Method
4. Experiment
- (1)
- In a complex 2D environment: some closed trajectory containing a straight line path and turning eight times (turning angle: 90°).
- (2)
- In a complex 3D environment: a six-story staircase, and parts of corridors in the Sheng-Hua building at the Central South University. The walk strats at the first floor and ends at the sixth floor.
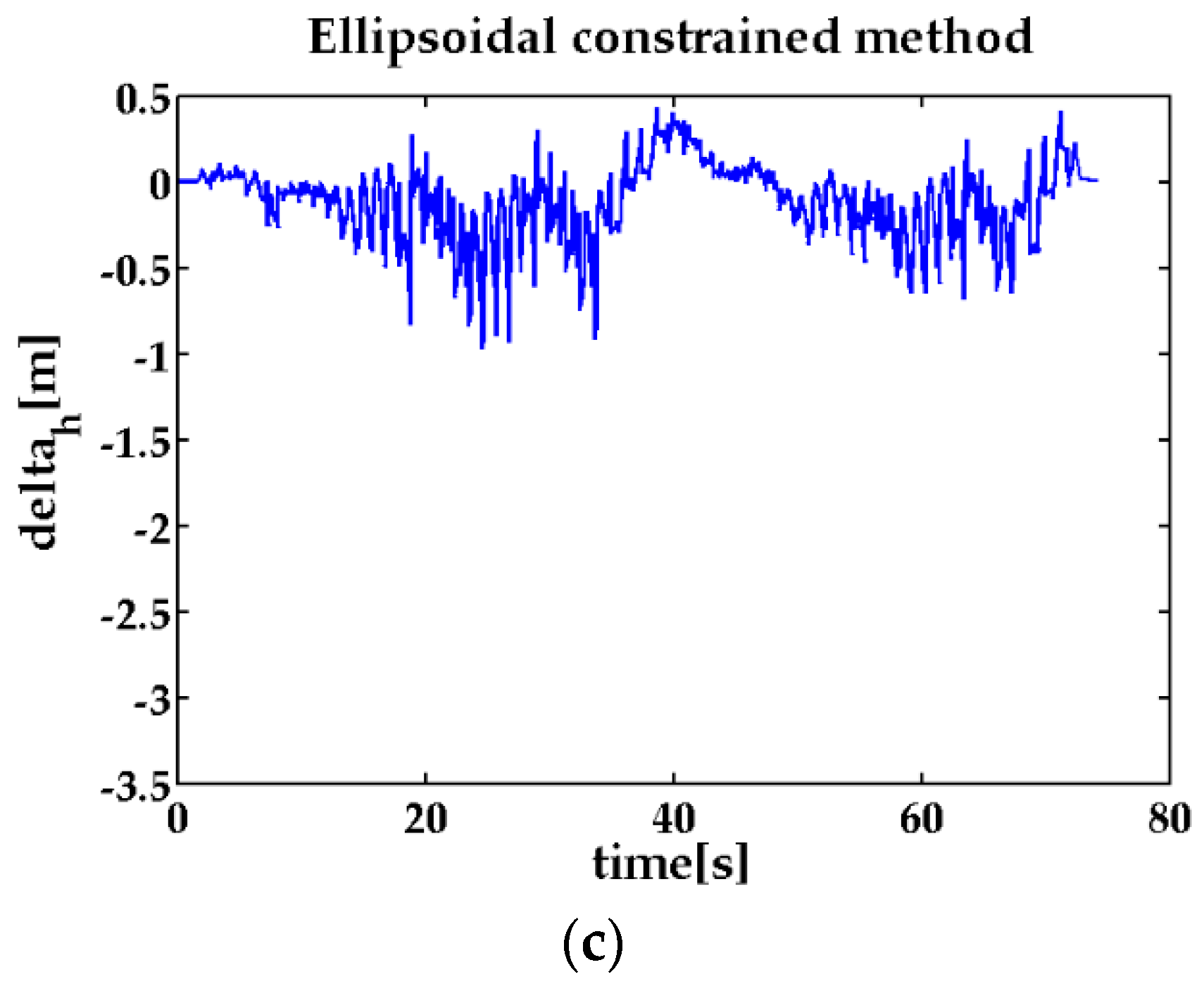
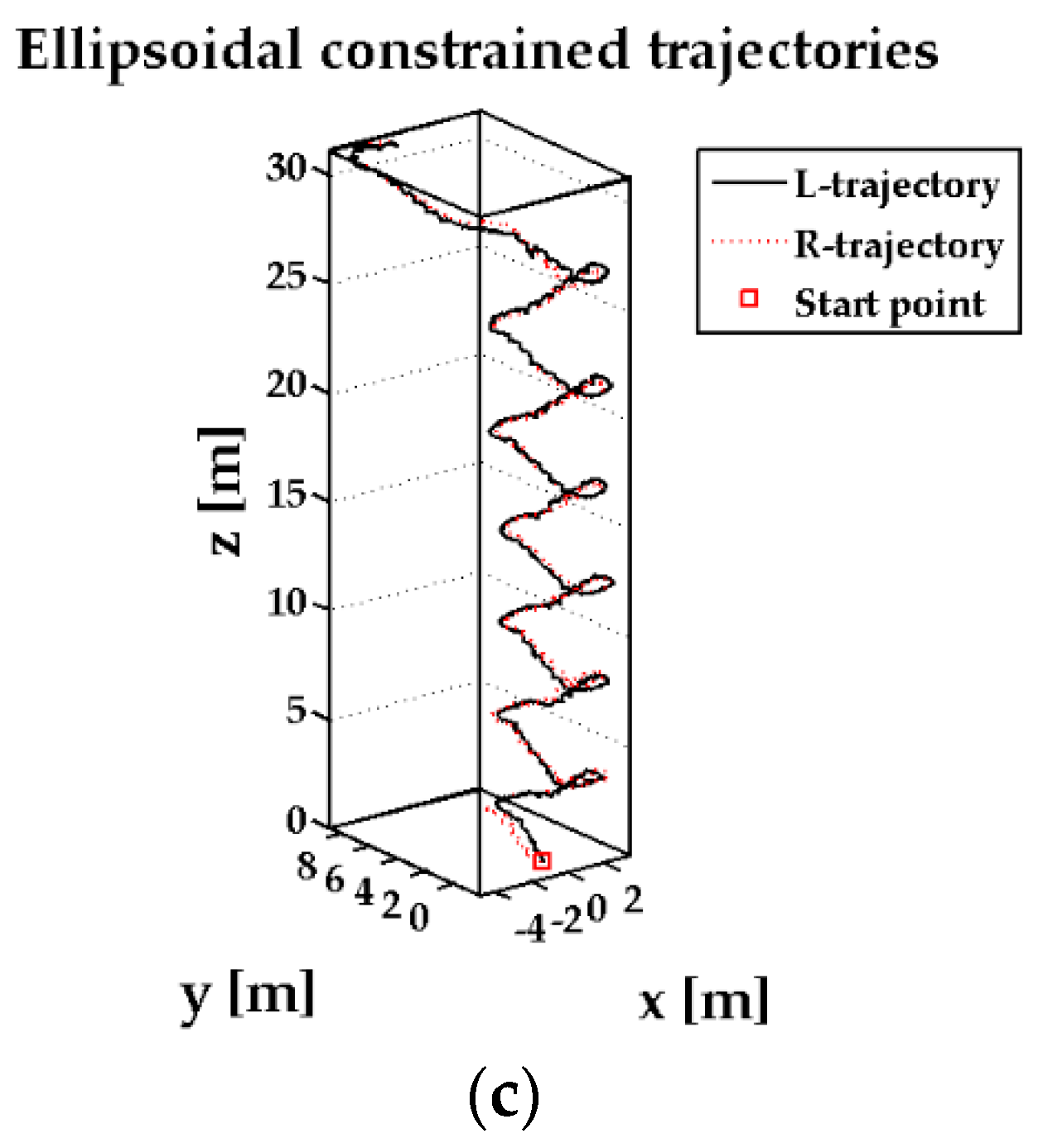
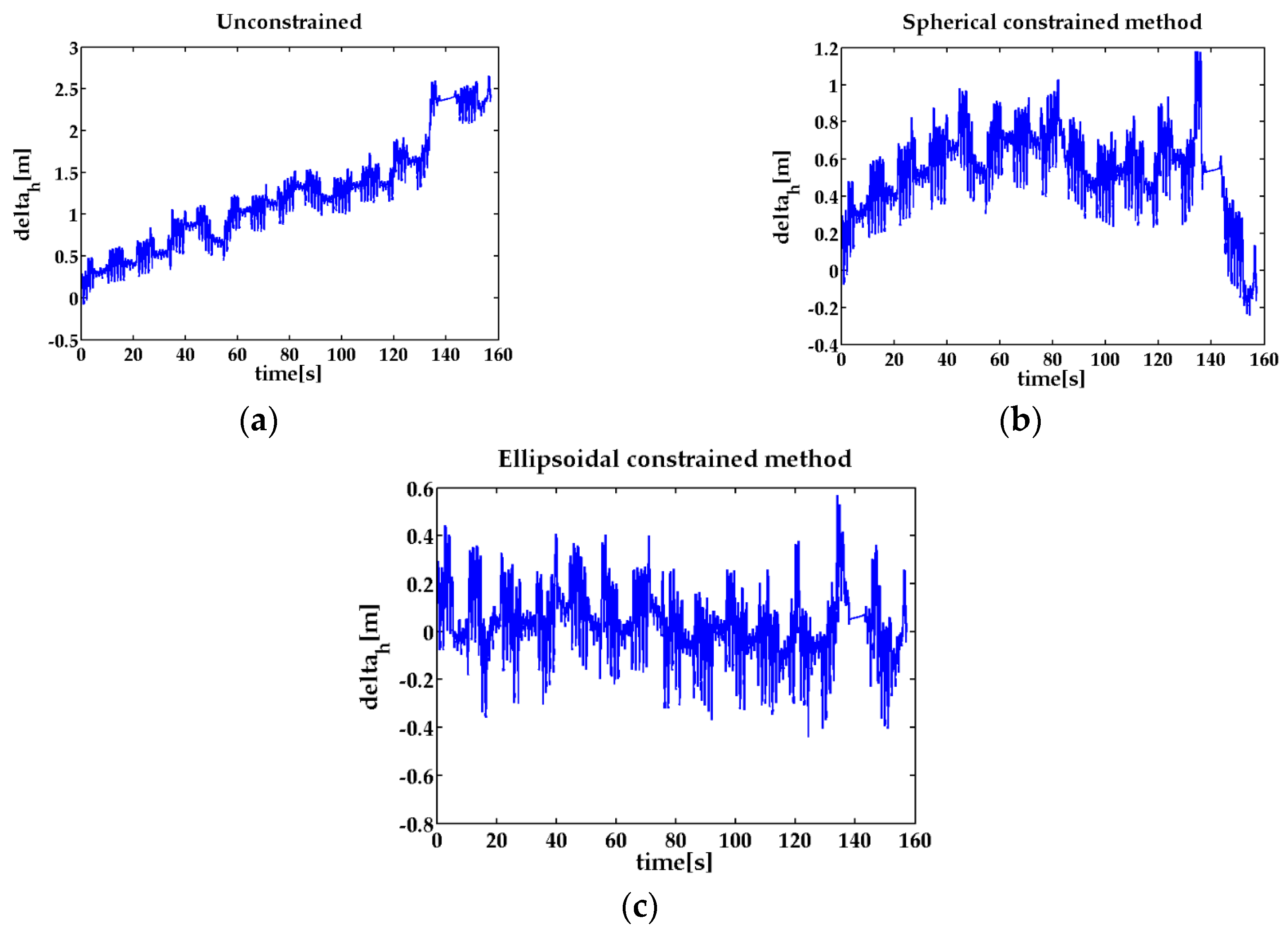
5. Results
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Akeila, E.; Salcic, Z.; Swain, A. Reducing Low-Cost INS Error Accumulation in Distance Estimation Using Self-Resetting. IEEE Instrum. Meas. 2014, 63, 177–184. [Google Scholar] [CrossRef]
- Zhou, X.C.; Chen, J.X.; Dong, Y.; Lu, X.R.; Cui, J.W.; Zheng, B.Y. Pedestrian navigation with foot-mounted inertial sensors in wearable body area networks. In Proceedings of the 2014 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA), Angkor Wat, Cambodia, 9–12 December 2014; pp. 1–4.
- Ashkar, R.; Romanovas, M.; Goridko, V.; Schwaab, M.; Traechtler, M.; Manoli, Y. A low-cost shoe-mounted Inertial Navigation System with magnetic disturbance compensation. In Proceedings of the 2013 International Conference on Indoor Positioning and Indoor Navigation, Montbéliard, France, 28–31 October 2013; pp. 1–10.
- Jimenez, A.R.; Seco, F.; Prieto, J.C.; Guevara, J. Indoor pedestrian navigation using an INS/EKF framework for yaw drift reduction and a foot-mounted IMU. In Proceedings of the 2010 7th Workshop on Positioning Navigation and Communication, Dresden, Germany, 11–12 March 2010; pp. 135–143.
- Skog, I.; Handel, P.; Nilsson, J.O.; Rantakokko, J. Zero-Velocity Detection—An Algorithm Evaluation. IEEE Trans. Biomed. Eng. 2010, 57, 2657–2666. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, J.O.; Skog, I.; Handel, P.; Hari, K.V.S. Foot-mounted INS for everybody an open-source embedded implementation. In Proceedings of the 2012 IEEE/ION Position Location and Navigation Symposium (PLANS), Myrtle Beach, SC, USA, 23–26 April 2012; pp. 140–145.
- Nilsson, J.O.; Skog, I.; Händel, P. A note on the limitations of ZUPTs and the implications on sensor error modeling. In Proceedings of the 2012 International Conference on Indoor Positioning and Indoor Navigation, Sydney, Australia, 13–15 November 2012; pp. 1–4.
- Skog, I.; Nilsson, J.O.; Zachariah, D.; Händel, P. Fusing the information from two navigation systems using an upper bound on their maximum spatial separation. In Proceedings of the 2012 International Conference on Indoor Positioning and Indoor Navigation, Sydney, Australia, 13–15 November 2012; pp. 14–30.
- Prateek, G.V.; Girisha, R.; Hari, K.V.S.; Händel, P. Data Fusion of Dual Foot-Mounted INS to Reduce the systematic Heading Drift. In Proceedings of the 2013 International Conference on Intelligent Systems, Vallabh Vidyanagar, India, 1–2 March 2013; pp. 208–213.
- Mbalawata, I.S.; Särkkä, S.; Haario, H. Parameter estimation in stochastic differential equations with Markov chain Monte Carlo and non-linear Kalman filtering. Comp. Stat. 2013, 28, 1195–1223. [Google Scholar] [CrossRef]
- Choukroun, D.; Bar-Itzhack, I.Y.; Oshman, Y. Novel quaternion Kalman filter. IEEE Trans. Aerosp. Electron. Syst. 2013, 42, 174–190. [Google Scholar] [CrossRef]
- Tully, S.; Kantor, G.; Choset, H. Inequality constrained Kalman filtering for the localization and registration of a surgical robot. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 5147–5152.
- Jonghoek, K.; Taeil, S.; Ryu, J. Inequality constrained Kalman filter for Bearing-Only Target Motion Analysis. In Proceedings of the 2015 15th International Conference on Control, Automation and Systems, Busan, Korea, 13–16 October 2015; pp. 1607–1611.
- Dan, S.; Dan, S. Kalman Filter Constraint Tuning for Turbofan Engine Health Estimation. Eur. J. Control 2006, 12, 331–343. [Google Scholar]
- Gupta, N.; Hauser, R. Kalman Filtering with Equality and Inequality State Constraints; Oxford University Computing Laboratory Numerical Analysis Group: Oxford, UK, 2007; pp. 1–26. [Google Scholar]
- Simon, B.D. Kalman filtering with state constraints: A survey of linear and nonlinear algorithms. IET Control Theory Appl. 2010, 4, 1303–1318. [Google Scholar] [CrossRef]
- Skog, I.; Nilsson, J.O.; Handel, P. Evaluation of zero-velocity detectors for foot-mounted inertial navigation systems. In Proceedings of the 2010 International Conference on Indoor Positioning and Indoor Navigation, Zurich, Switzerland, 15–17 September 2010; pp. 1–6.
- Gao, Z.Y.; Li, D.S.; Wang, Y.Z. Combining ZUPT with hybrid particle filter for vehicle MEMS-INS. Electr. Mach. Control 2010, 14, 31–35. [Google Scholar]
- Wang, Z.; Zhao, H.; Qiu, S.; Gao, Q. Stance phase detection for ZUPT-aided foot-mounted pedestrian navigation system. IEEE/ASME Trans. Mech. 2015, 1, 3170–3180. [Google Scholar] [CrossRef]
- Brand, T.J.; Phillips, R.E. Foot-to-Foot Range Measurement as an Aid to Personal Navigation. In Proceedings of the 59th Annual Meeting of The Institute of Navigation and CIGTF 22nd Guidance Test Symposium, Albuquerque, NM, USA, 23–25 June 2003; pp. 113–121.
- Girisha, R.; Prateek, G.V.; Hari, K.V.S.; Händel, P. Fusing the navigation information of dual foot-mounted zero-velocity-update-aided inertial navigation systems. In Proceedings of the 2014 International Conference on Signal Processing and Communications, Gold Coast, Australia, 22–25 July 2014; pp. 1–6.




| Sensors | Accelerometer | Gyroscope | ||
|---|---|---|---|---|
| Typ | Max | Typ | Max | |
| Standard full range | 50 | - | 450 | - |
| Bias repeatability (1 year) | 0.03 | 0.05 | 0.2 | 0.5 |
| In-run bias stability | 40 | - | 10 | - |
| Noise density | 80 | 150 | 0.01 | 0.015 |
| Non-linearity | 0.03% FS | 5% FS | 0.01% FS | - |
| Method | (L/R) 2D RMSE (m) | (L/R) 3D RMSE (m) | Remarks |
|---|---|---|---|
| Unconstraint | 1.2640/0.9493 | 1.5473/1.2293 | Time: 73 s Distance: 61.6 m Error rate(%): 0.93 |
| Spherical constraint | 0.6533/0.6194 | 0.8732/0.8482 | |
| Ellipsoidal constraint | 0.5709/0.5953 | 0.6977/0.7174 |
| Method | Left-3D RMSE (m) | Right-3D RMSE (m) | Remarks |
|---|---|---|---|
| Unconstraint | 1.6712 | 0.8249 | Time: 157 s Height: 31.75 m Error rate(%): 1.71 |
| Spherical constraint | 0.7676 | 0.7874 | |
| Ellipsoidal constraint | 0.6537 | 0.5414 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Wang, Y.; Wu, Y. Dual MIMU Pedestrian Navigation by Inequality Constraint Kalman Filtering. Sensors 2017, 17, 427. https://doi.org/10.3390/s17020427
Shi W, Wang Y, Wu Y. Dual MIMU Pedestrian Navigation by Inequality Constraint Kalman Filtering. Sensors. 2017; 17(2):427. https://doi.org/10.3390/s17020427
Chicago/Turabian StyleShi, Wei, Yang Wang, and Yuanxin Wu. 2017. "Dual MIMU Pedestrian Navigation by Inequality Constraint Kalman Filtering" Sensors 17, no. 2: 427. https://doi.org/10.3390/s17020427
APA StyleShi, W., Wang, Y., & Wu, Y. (2017). Dual MIMU Pedestrian Navigation by Inequality Constraint Kalman Filtering. Sensors, 17(2), 427. https://doi.org/10.3390/s17020427






