A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals
Abstract
:1. Introduction
- (1)
- We propose a novel and simple learning framework, which works directly on raw temporal signals. A comparison with traditional methods that require extra feature extraction is shown in Figure 1.
- (2)
- This algorithm itself has strong domain adaptation capacity, and the performance can be easily improved by a simple domain adaptation method named AdaBN.
- (3)
- This algorithm performs well under noisy environment conditions, when working directly on raw noisy signals with no pre-denoising methods.
- (4)
- We try to explore the inner mechanism of WDCNN model in mechanical feature learning and classification by visualizing the feature maps learned by WDCNN.
2. A Brief Introduction to CNN
2.1. Convolutional Layer
2.2. Activation Layer
2.3. Pooling Layer
2.4. Batch Normalization
3. Proposed WDCNN Intelligent Diagnosis Method
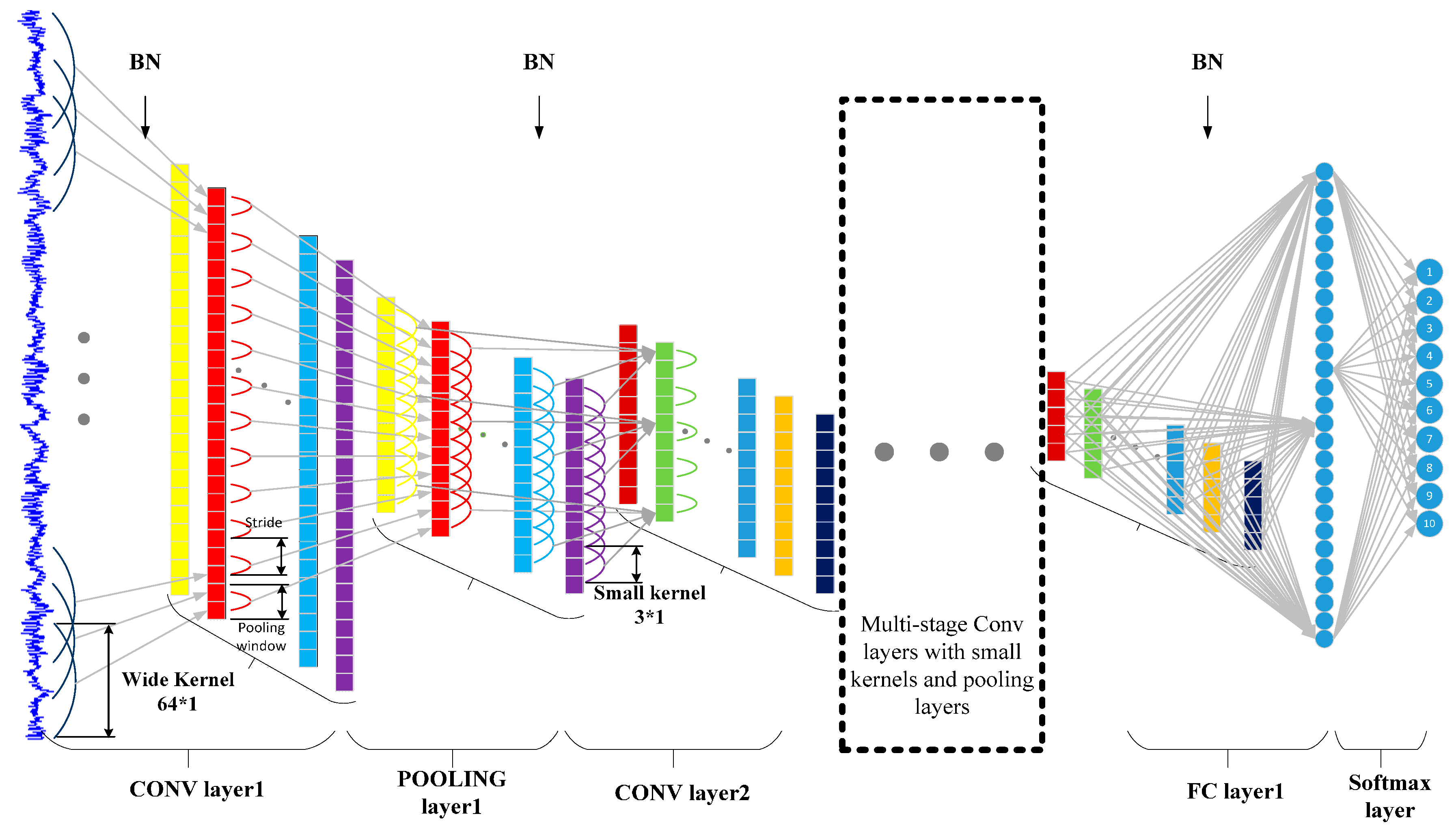
3.1. Architecture of the Proposed WDCNN Model
3.2. Training of the WDCNN
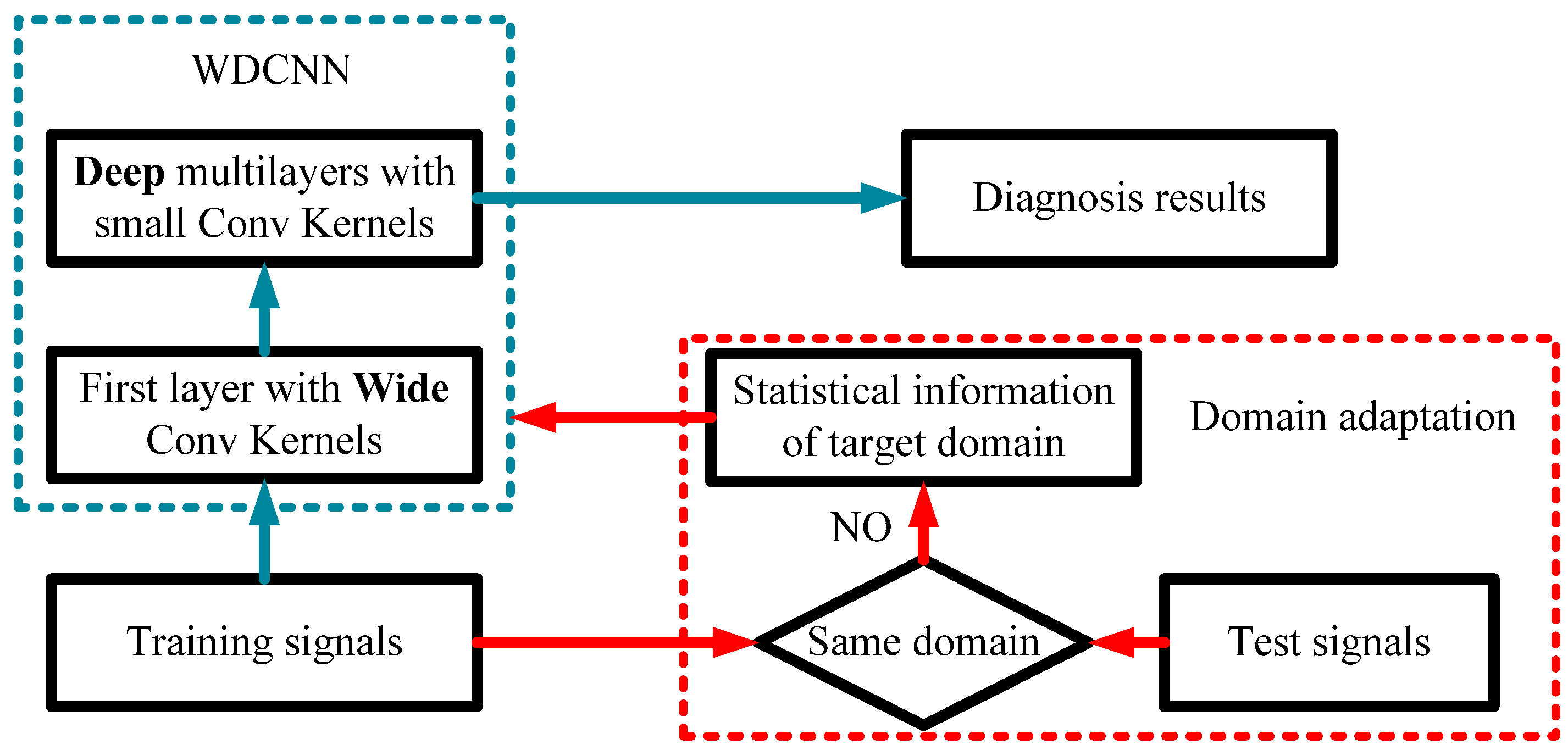
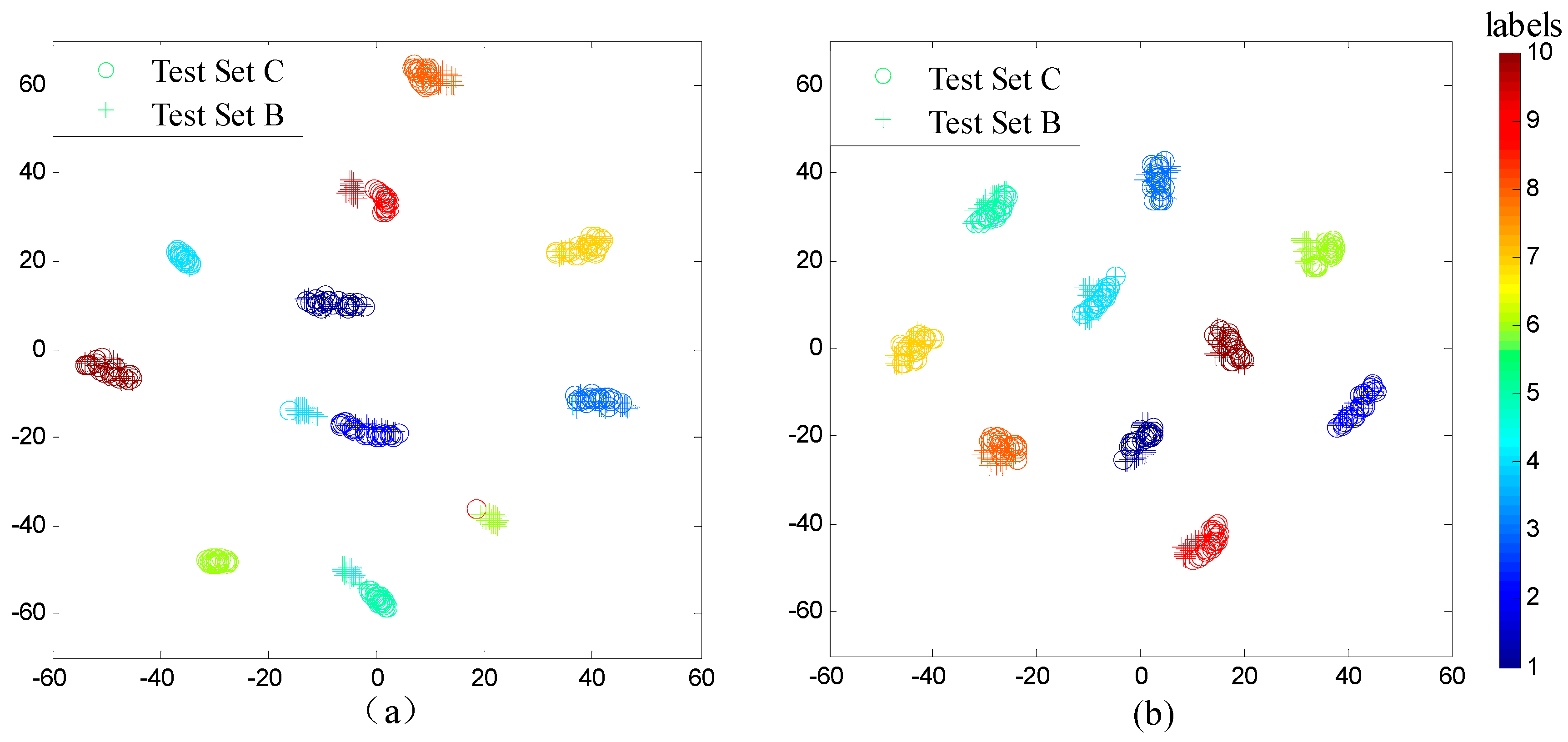
3.3. Domain Adaptation Framework for WDCNN
| Algorithm 1 AdaBN for WDCNN | |
| Input: | Input of neuron i in BN layers of WDCNN for unlabeled target signal p, ,where The trained scale and shift parameters and for neuron i using the labeled source signals. |
| output: | Adjusted structure of WDCNN |
| For | Each neuron i and each signal p in target domain Calculate the mean and variance of all the samples in target domain: Calculate the BN output by: |
| End for | |
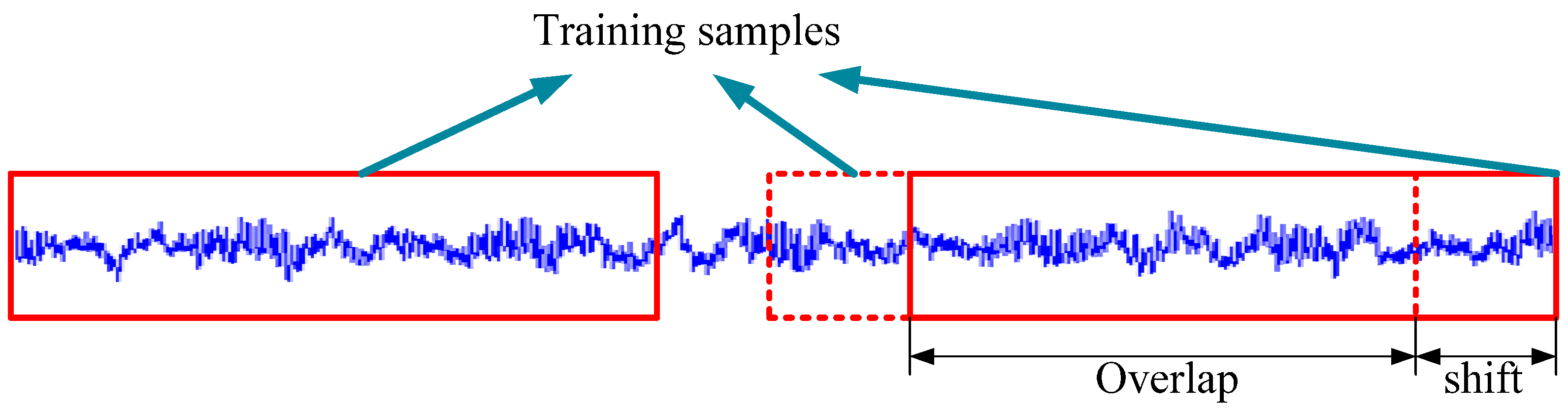
3.4. Data Augumentation
4. Validation of the Proposed WDCNN Model
4.1. Data Description
4.2. Experimental Setup
4.2.1. Baseline System
4.2.2. Parameters of the Proposed CNN
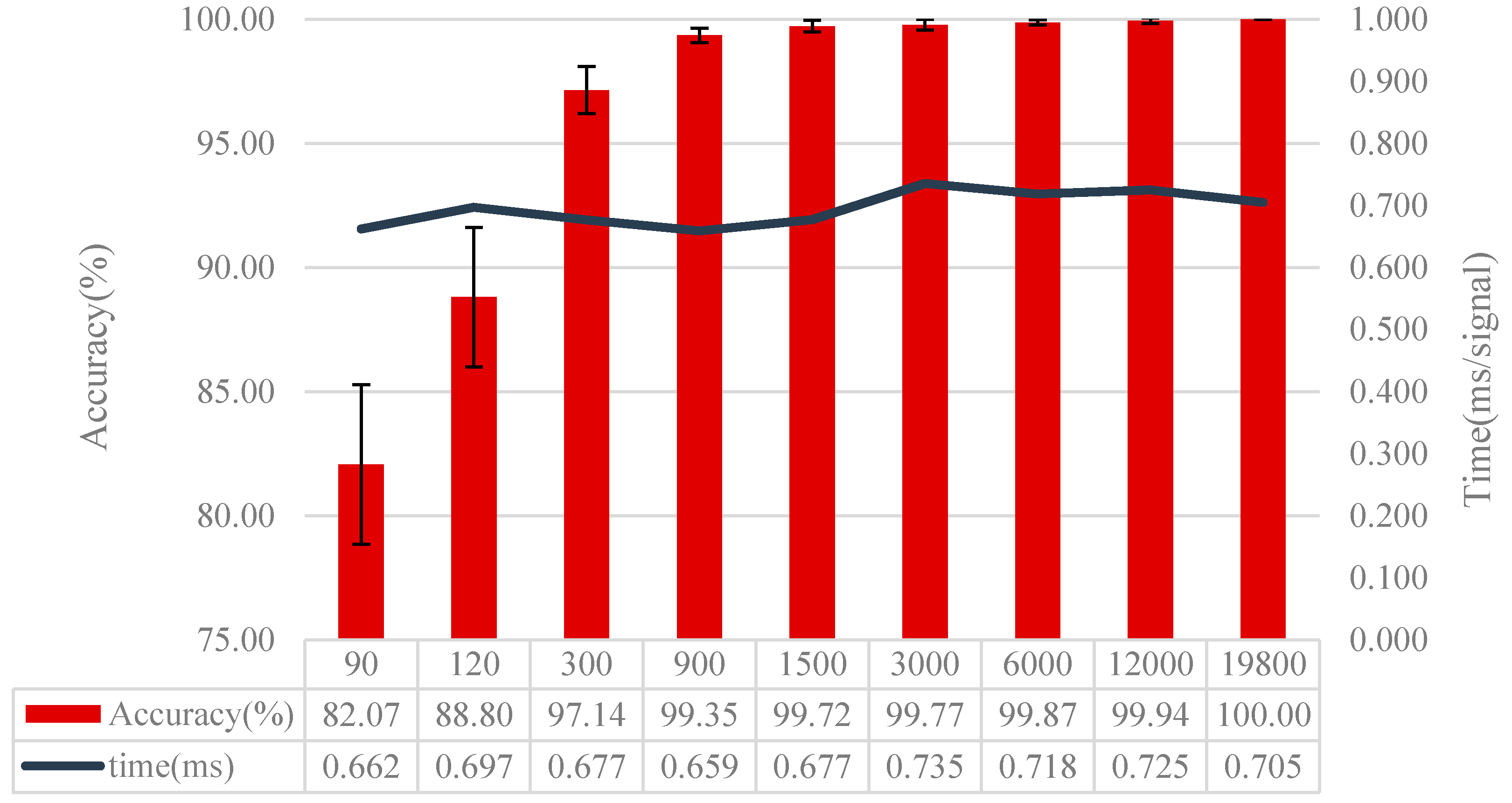
4.3. Effect of the Data Number for Training
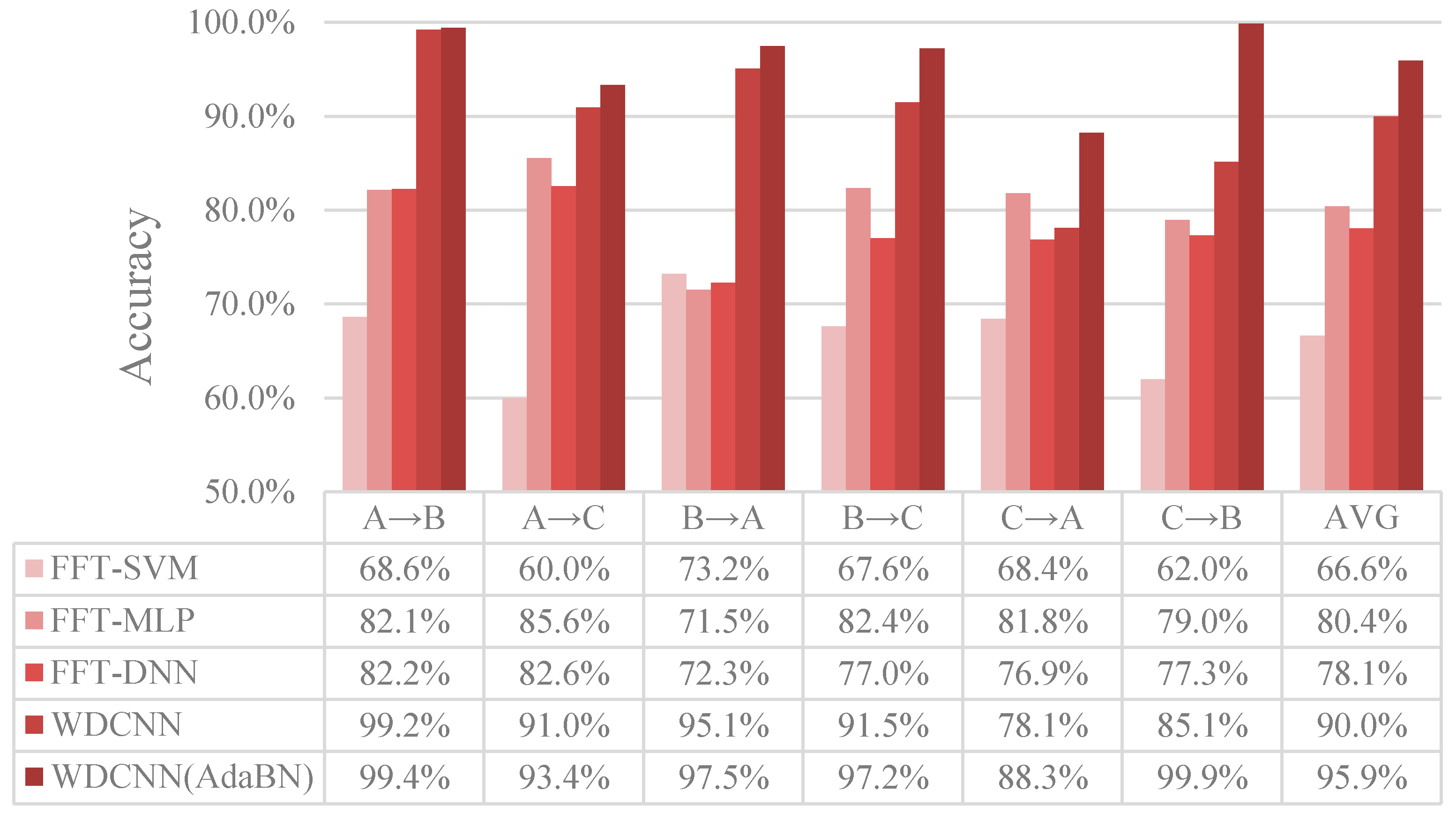
4.4. Performance under Different Working Environment
4.4.1. Case Study I: Performance across Different Load Domains
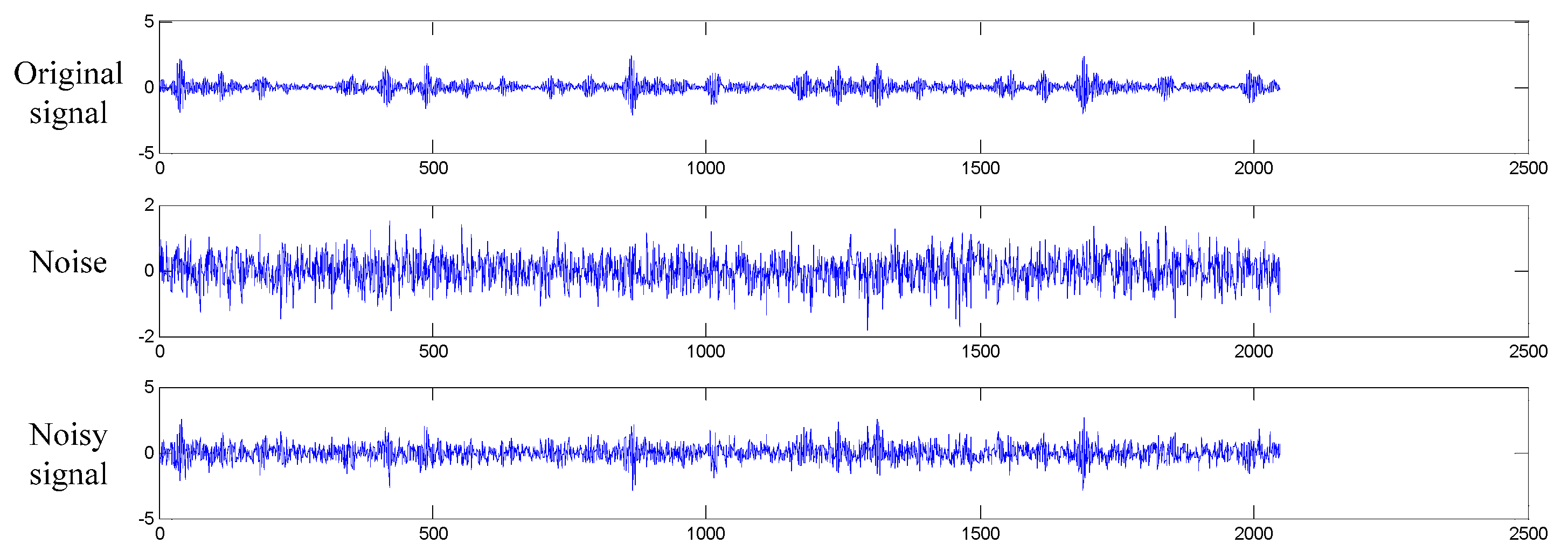
4.4.2. Case Study II: Performance under Noise Environment
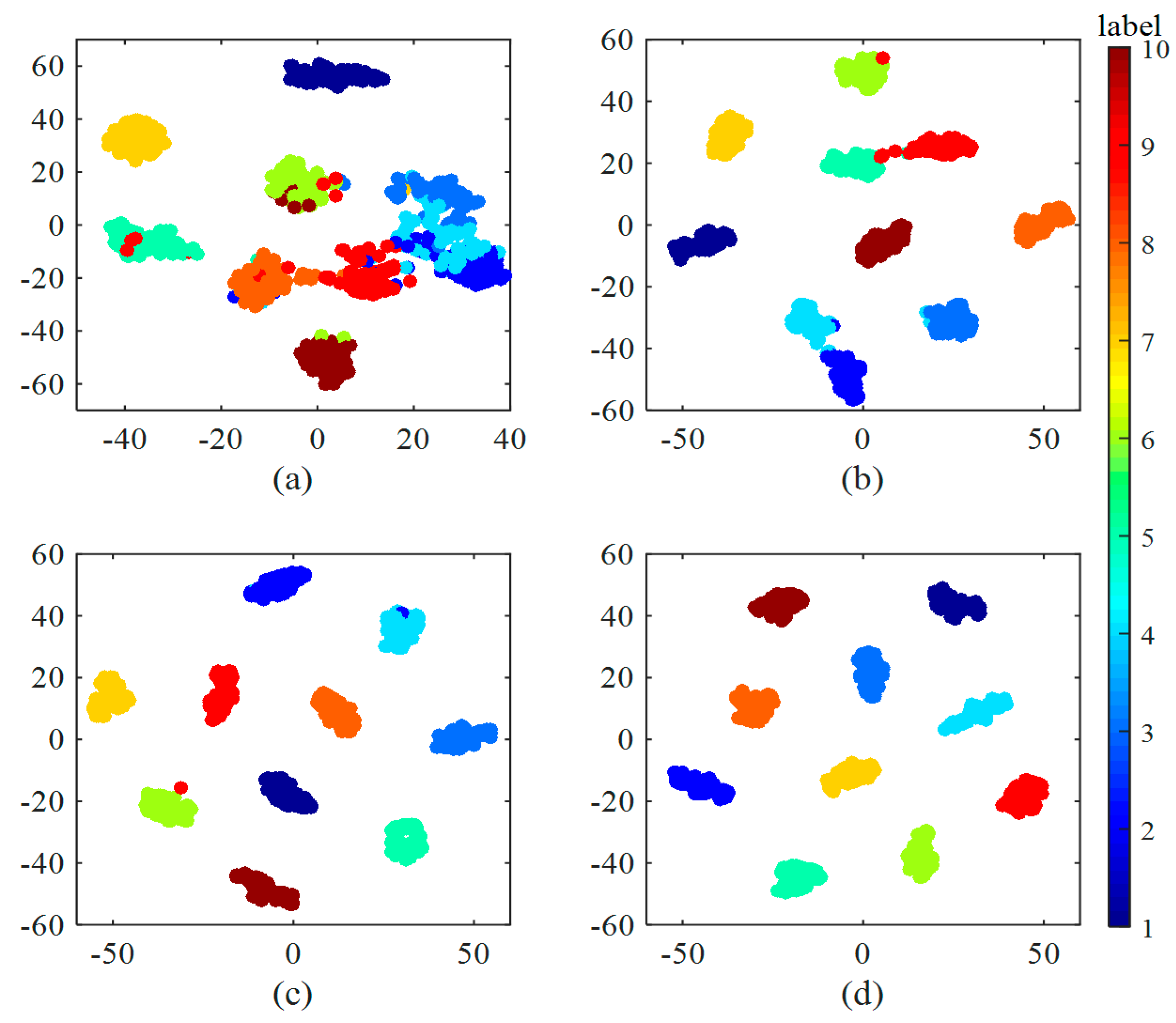
4.5. Networks Visualizations
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| WDCNN | Deep Convolutional Neural Networks with Wide First-layer Kernels |
| AdaBN | Adaptive Batch Normalization |
| DNN | Deep Neural Network |
| SVM | Support Vector Machine |
| MLP | Multi-Layer Perceptron |
| ReLU | Rectified Linear Unit |
| BN | Batch Normalization |
| FFT | Fast Fourier Transformation |
| t-SNE | T-distributed Stochastic Neighbor Embedding |
| SNR | Signal-to-Noise Ratio |
References
- Jayaswal, P.; Verma, S.N.; Wadhwani, A.K. Development of EBP-Artificial neural network expert system for rolling element bearing fault diagnosis. J. Vib. Control 2011, 17, 1131–1148. [Google Scholar] [CrossRef]
- Yiakopoulos, C.T.; Gryllias, K.C.; Antoniadis, I.A. Rolling element bearing fault detection in industrial environments based on a K-means clustering approach. Expert Syst. Appl. 2011, 38, 2888–2911. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement 2016, 77, 80–94. [Google Scholar] [CrossRef]
- Prieto, M.D.; Cirrincione, G.; Espinosa, A.G.; Ortega, J.A.; Henao, H. Bearing fault detection by a novel condition-monitoring scheme based on statistical-time features and neural networks. IEEE Trans. Ind. Electron. 2013, 60, 3398–3407. [Google Scholar] [CrossRef]
- Li, K.; Chen, P.; Wang, S. An intelligent diagnosis method for rotating machinery using least squares mapping and a fuzzy neural network. Sensors 2012, 12, 5919–5939. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zheng, Y.; Zhao, Z.; Wang, J. Bearing fault diagnosis based on statistical locally linear embedding. Sensors 2015, 15, 16225–16247. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Park, C.G. Double Fault Detection of Cone-Shaped Redundant IMUs Using Wavelet Transformation and EPSA. Sensors 2014, 14, 3428–3444. [Google Scholar] [CrossRef] [PubMed]
- Rai, V.K.; Mohanty, A.R. Bearing fault diagnosis using FFT of intrinsic mode functions in Hilbert–Huang transform. Mech. Syst. Signal Process. 2007, 21, 2607–2615. [Google Scholar] [CrossRef]
- Misra, M.; Yue, H.H.; Qin, S.J.; Ling, C. Multivariate process monitoring and fault diagnosis by multi-scale PCA. Comput. Chem. Eng. 2002, 26, 1281–1293. [Google Scholar] [CrossRef]
- Widodo, A.; Yang, B.S. Application of nonlinear feature extraction and support vector machines for fault diagnosis of induction motors. Expert Syst. Appl. 2007, 33, 241–250. [Google Scholar] [CrossRef]
- Pandya, D.H.; Upadhyay, S.H.; Harsha, S.P. Fault diagnosis of rolling element bearing with intrinsic mode function of acoustic emission data using APF-KNN. Expert Syst. Appl. 2013, 40, 4137–4145. [Google Scholar] [CrossRef]
- Hajnayeb, A.; Ghasemloonia, A.; Khadem, S.E.; Moradi, M.H. Application and comparison of an ANN-based feature selection method and the genetic algorithm in gearbox fault diagnosis. Expert Syst. Appl. 2011, 38, 10205–10209. [Google Scholar] [CrossRef]
- Li, B.; Chow, M.Y.; Tipsuwan, Y.; Hung, J.C. Neural-network-based motor rolling bearing fault diagnosis. IEEE Trans. Ind. Electron. 2000, 47, 1060–1069. [Google Scholar] [CrossRef]
- Santos, P.; Villa, L.F.; Reñones, A.; Bustillo, A.; Maudes, J. An SVM-based solution for fault detection in wind turbines. Sensors 2015, 15, 5627–5648. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Hu, X.; Yang, F. Support vector machine with genetic algorithm for machinery fault diagnosis of high voltage circuit breaker. Measurement 2011, 44, 1018–1027. [Google Scholar] [CrossRef]
- Konar, P.; Chattopadhyay, P. Bearing fault detection of induction motor using wavelet and Support Vector Machines (SVMs). Appl. Soft Comput. 2011, 11, 4203–4211. [Google Scholar] [CrossRef]
- Amar, M.; Gondal, I.; Wilson, C. Vibration spectrum imaging: A novel bearing fault classification approach. IEEE Trans. Ind. Electron. 2015, 62, 494–502. [Google Scholar] [CrossRef]
- Saravanan, N.; Ramachandran, K.I. Incipient gear box fault diagnosis using discrete wavelet transform (DWT) for feature extraction and classification using artificial neural network (ANN). Expert Syst. Appl. 2010, 37, 4168–4181. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2012; pp. 1097–1105. [Google Scholar]
- Abdel-Hamid, O.; Mohamed, A.R.; Jiang, H.; Penn, G. Applying convolutional neural networks concepts to hybrid NN-HMM model for speech recognition. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 4277–4280.
- Kim, Y. Convolutional neural networks for sentence classification. arXiv 2014. [Google Scholar]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; van de Walle, R.; van Hoecke, S. Convolutional Neural Network Based Fault Detection for Rotating Machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Guo, X.; Chen, L.; Shen, C. Hierarchical adaptive deep convolution neural network and its application to bearing fault diagnosis. Measurement 2016, 93, 490–502. [Google Scholar] [CrossRef]
- Ince, T.; Kiranyaz, S.; Eren, L.; Askar, M.; Gabbouj, M. Real-time motor fault detection by 1D convolutional neural networks. IEEE Trans. Ind. Electron. 2016, 63, 7067–7075. [Google Scholar] [CrossRef]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C. Rolling Element Bearings Fault Intelligent Diagnosis Based on Convolutional Neural Networks Using Raw Sensing Signal. In Advances in Intelligent Information Hiding and Multimedia Signal Processing: Proceeding of the Twelfth International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Kaohsiung, Taiwan, 21–23 November 2016; Volume 2, pp. 77–84; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An Intelligent Fault Diagnosis Method Using Unsupervised Feature Learning Towards Mechanical Big Data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014. [Google Scholar]
- Li, Y.; Wang, N.; Shi, J.; Liu, J.; Hou, X. Revisiting Batch Normalization for Practical Domain Adaptation. arXiv 2016. [Google Scholar]
- Cui, X.; Goel, V.; Kingsbury, B. Data augmentation for deep convolutional neural network acoustic modeling. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 4545–4549.
- Lou, X.; Loparo, K.A. Bearing fault diagnosis based on wavelet transform and fuzzy inference. Mech. Syst. Signal Process. 2004, 18, 1077–1095. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- TensorFlow. Available online: www.tensorflow.org (accessed on 21 February 2017).
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014. [Google Scholar]
- Villa, L.F.; Reñones, A.; Perán, J.R.; de Miguel, L.J. Angular resampling for vibration analysis in wind turbines under non-linear speed fluctuation. Mech. Syst. Signal Process. 2011, 25, 2157–2168. [Google Scholar] [CrossRef]
- Santos, P.; Maudes, J.; Bustillo, A. Identifying maximum imbalance in datasets for fault diagnosis of gearboxes. J. Intell. Manuf. 2015. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]




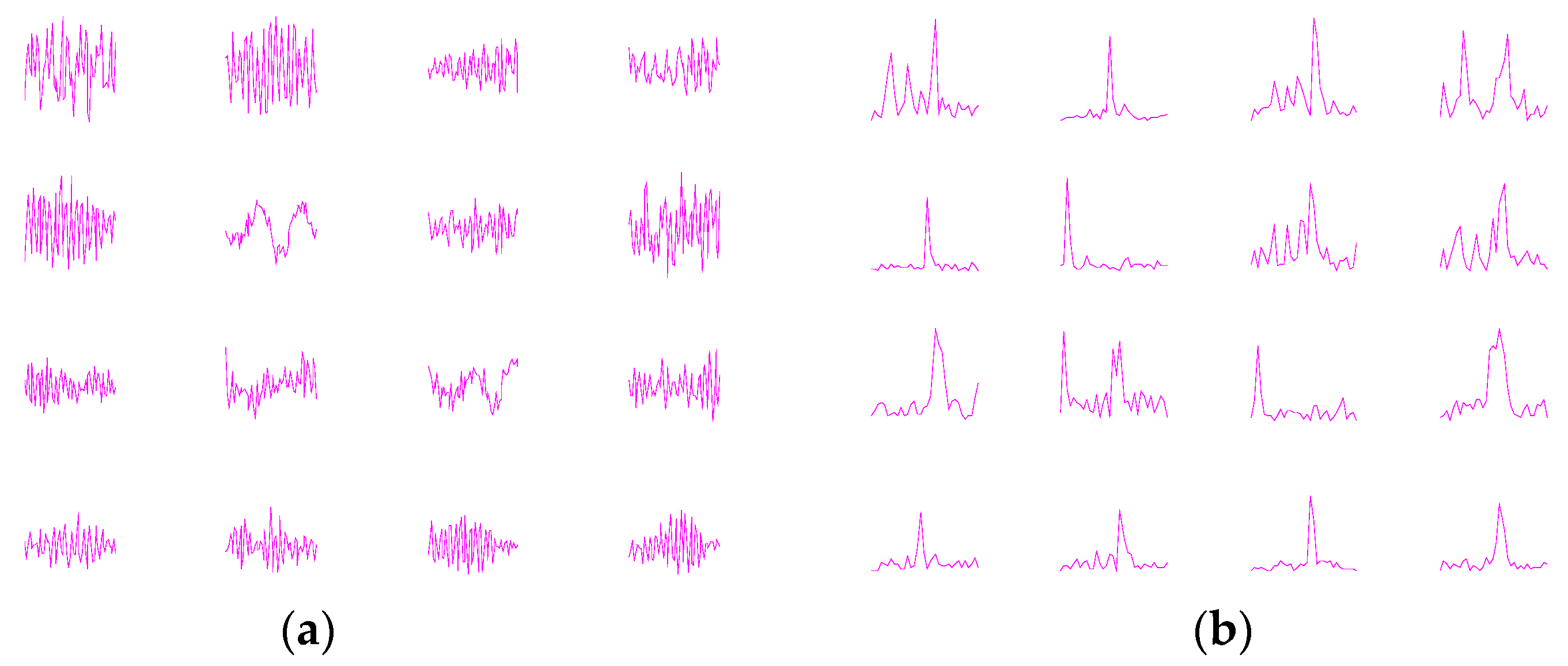

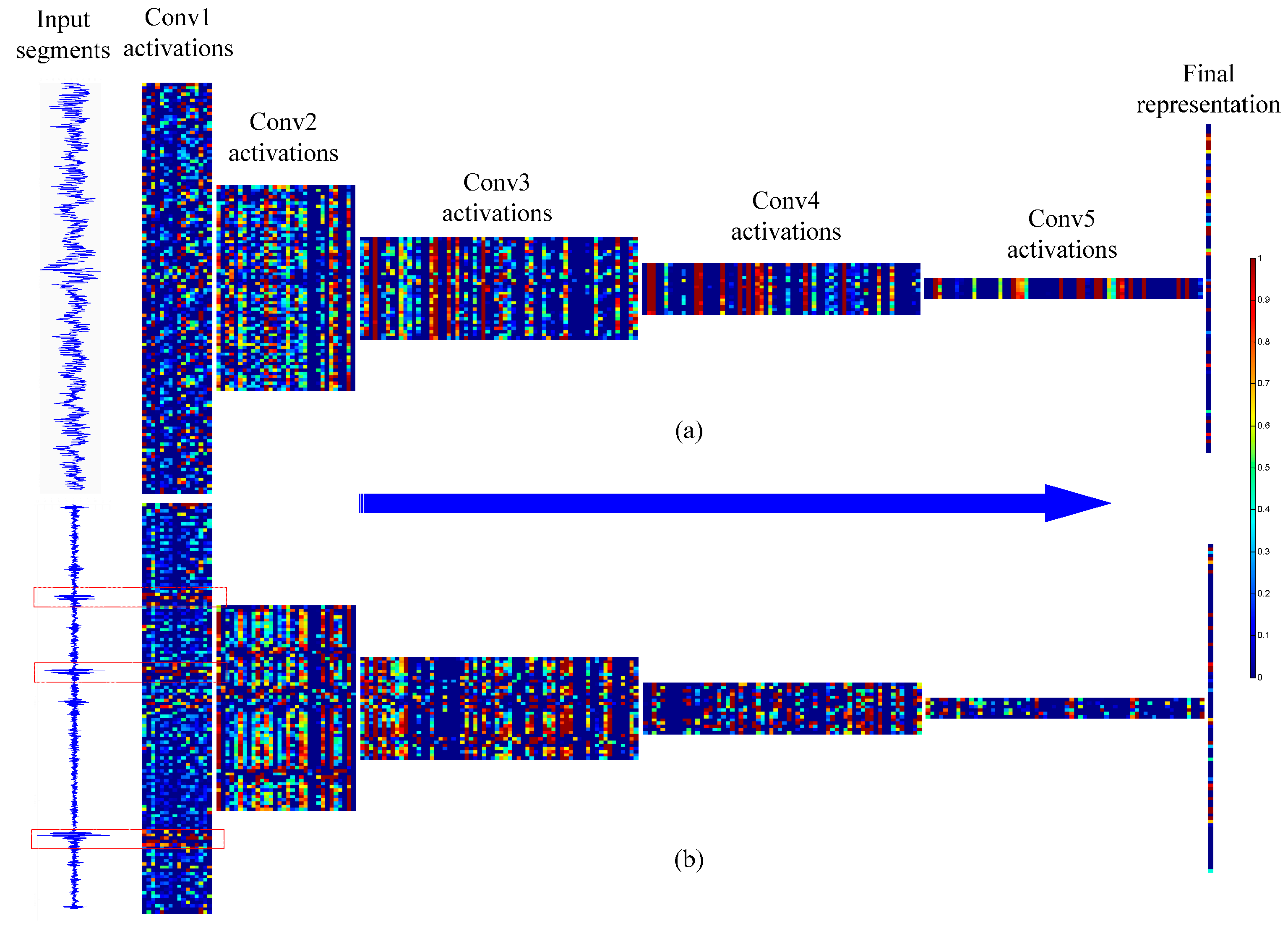
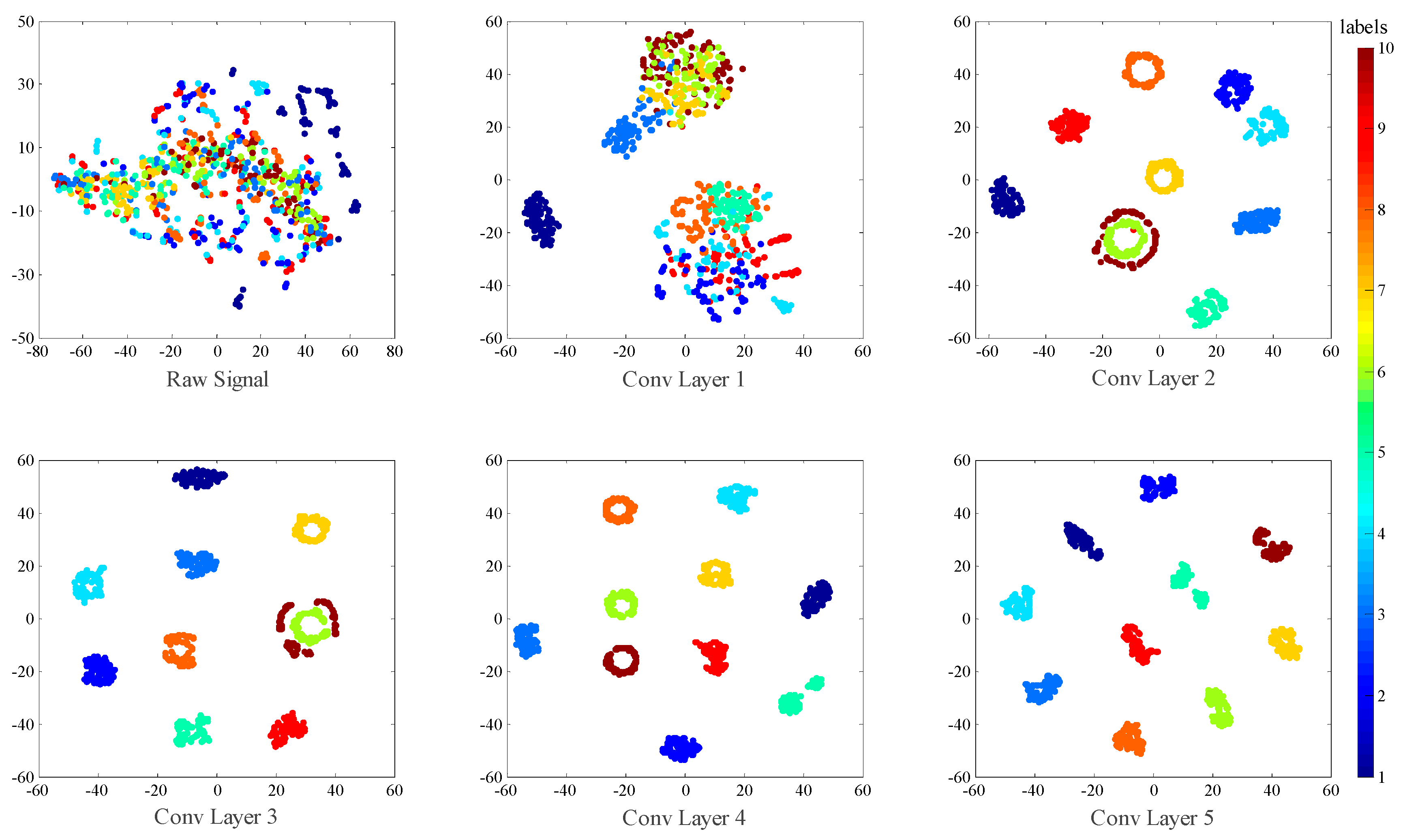
| Fault Location | None | Ball | Inner Race | Outer Race | Load | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Category Labels | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| Fault diameter (inch) | 0 | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 | ||
| Dataset A no. | Train | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 1 |
| Test | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | ||
| Dataset B no. | Train | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 2 |
| test | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | ||
| Dataset C no. | train | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 660 | 3 |
| test | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | ||
| Dataset D no. | Train | 1980 | 1980 | 1980 | 1980 | 1980 | 1980 | 1980 | 1980 | 1980 | 1980 | 1,2,3 |
| Test | 75 | 75 | 75 | 75 | 75 | 75 | 75 | 75 | 75 | 75 | ||
| No. | Layer Type | Kernel Size/Stride | Kernel Number | Output Size (Width × Depth) | Padding |
|---|---|---|---|---|---|
| 1 | Convolution1 | 64 × 1/16 × 1 | 16 | 128 × 16 | Yes |
| 2 | Pooling1 | 2 × 1/2 × 1 | 16 | 64 × 16 | No |
| 3 | Convolution2 | 3 × 1/1 × 1 | 32 | 64 × 32 | Yes |
| 4 | Pooling2 | 2 × 1/2 × 1 | 32 | 32 × 32 | No |
| 5 | Convolution3 | 3 × 1/1 × 1 | 64 | 32 × 64 | Yes |
| 6 | Pooling3 | 2 × 1/2 × 1 | 64 | 16 × 64 | No |
| 7 | Convolution4 | 3 × 1/1 × 1 | 64 | 16 × 64 | Yes |
| 8 | Pooling4 | 2 × 1/2 × 1 | 64 | 8 × 64 | No |
| 9 | Convolution5 | 3 × 1/1 × 1 | 64 | 6 × 64 | No |
| 10 | Pooling5 | 2 × 1/2 × 1 | 64 | 3 × 64 | No |
| 11 | Fully-connected | 100 | 1 | 100 × 1 | |
| 12 | Softmax | 10 | 1 | 10 |
| Scenario Settings for Domain Adaptation | |||
|---|---|---|---|
| Domain types | Source domain | Target domain | |
| Description | labeled signals under one single load | unlabeled signals under another load | |
| Domain details | Training set A | Test set B | Test set C |
| Training set B | Test set C | Test set A | |
| Training set C | Test set A | Test set B | |
| Target | Diagnose unlabeled vibration signals in target domain | ||
| Kernel Size | SNR (dB) | |||||||
|---|---|---|---|---|---|---|---|---|
| −4 | −2 | 0 | 2 | 4 | 6 | 8 | 10 | |
| 16 | 27.14% | 40.89% | 55.37% | 72.03% | 85.71% | 94.58% | 98.41% | 99.35% |
| 24 | 35.32% | 52.72% | 70.15% | 84.75% | 94.37% | 98.50% | 99.64% | 99.82% |
| 32 | 42.00% | 57.66% | 72.76% | 86.53% | 95.47% | 98.40% | 99.52% | 99.69% |
| 40 | 46.84% | 63.03% | 77.55% | 90.20% | 97.07% | 99.21% | 99.71% | 99.82% |
| 48 | 50.15% | 66.16% | 80.21% | 92.08% | 97.69% | 99.35% | 99.73% | 99.87% |
| 56 | 51.67% | 66.83% | 80.85% | 92.32% | 97.84% | 99.21% | 99.73% | 99.79% |
| 64 | 51.75% | 67.15% | 82.03% | 93.06% | 98.07% | 99.29% | 99.79% | 99.81% |
| 72 | 53.69% | 68.53% | 82.23% | 92.93% | 97.91% | 99.35% | 99.71% | 99.82% |
| 80 | 56.07% | 69.39% | 84.24% | 94.84% | 98.69% | 99.44% | 99.83% | 99.85% |
| 88 | 56.05% | 71.62% | 85.33% | 95.04% | 98.46% | 99.37% | 99.74% | 99.83% |
| 96 | 64.29% | 78.80% | 89.91% | 96.97% | 99.03% | 99.62% | 99.81% | 99.85% |
| 104 | 62.91% | 79.21% | 90.36% | 97.52% | 99.23% | 99.77% | 99.81% | 99.84% |
| 112 | 66.95% | 80.81% | 90.51% | 97.01% | 98.88% | 99.54% | 99.83% | 99.81% |
| 120 | 61.84% | 77.60% | 90.47% | 97.40% | 99.08% | 99.67% | 99.81% | 99.87% |
| 128 | 60.88% | 77.49% | 89.79% | 97.28% | 99.13% | 99.59% | 99.83% | 99.83% |
| Max | 66.95% | 80.81% | 90.51% | 97.52% | 99.23% | 99.77% | 99.83% | 99.87% |
| Kernel Size | SNR (dB) | |||||||
|---|---|---|---|---|---|---|---|---|
| −4 | −2 | 0 | 2 | 4 | 6 | 8 | 10 | |
| 16 | 81.84% | 90.38% | 95.66% | 98.45% | 99.01% | 99.54% | 99.75% | 99.77% |
| 24 | 87.24% | 93.99% | 97.34% | 99.03% | 99.61% | 99.81% | 99.87% | 99.89% |
| 32 | 89.81% | 95.16% | 97.93% | 99.29% | 99.55% | 99.76% | 99.77% | 99.86% |
| 40 | 90.96% | 95.99% | 98.32% | 99.33% | 99.59% | 99.75% | 99.83% | 99.89% |
| 48 | 91.69% | 96.29% | 98.33% | 99.39% | 99.67% | 99.80% | 99.81% | 99.88% |
| 56 | 92.65% | 96.59% | 98.61% | 99.47% | 99.70% | 99.77% | 99.86% | 99.87% |
| 64 | 92.56% | 96.79% | 98.77% | 99.49% | 99.67% | 99.83% | 99.87% | 99.93% |
| 72 | 92.36% | 96.39% | 98.51% | 99.35% | 99.61% | 99.76% | 99.79% | 99.84% |
| 80 | 92.31% | 96.70% | 98.67% | 99.40% | 99.62% | 99.76% | 99.87% | 99.86% |
| 88 | 92.61% | 97.02% | 98.77% | 99.45% | 99.63% | 99.75% | 99.81% | 99.83% |
| 96 | 92.65% | 97.04% | 98.77% | 99.57% | 99.67% | 99.80% | 99.83% | 99.84% |
| 104 | 92.45% | 96.57% | 98.63% | 99.51% | 99.67% | 99.79% | 99.81% | 99.91% |
| 112 | 91.70% | 96.31% | 98.68% | 99.43% | 99.67% | 99.79% | 99.89% | 99.91% |
| 120 | 92.11% | 96.46% | 98.75% | 99.47% | 99.66% | 99.77% | 99.83% | 99.89% |
| 128 | 91.92% | 96.53% | 98.67% | 99.38% | 99.63% | 99.73% | 99.82% | 99.87% |
| Max | 92.65% | 97.04% | 98.77% | 99.57% | 99.70% | 99.83% | 99.89% | 99.93% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals. Sensors 2017, 17, 425. https://doi.org/10.3390/s17020425
Zhang W, Peng G, Li C, Chen Y, Zhang Z. A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals. Sensors. 2017; 17(2):425. https://doi.org/10.3390/s17020425
Chicago/Turabian StyleZhang, Wei, Gaoliang Peng, Chuanhao Li, Yuanhang Chen, and Zhujun Zhang. 2017. "A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals" Sensors 17, no. 2: 425. https://doi.org/10.3390/s17020425
APA StyleZhang, W., Peng, G., Li, C., Chen, Y., & Zhang, Z. (2017). A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals. Sensors, 17(2), 425. https://doi.org/10.3390/s17020425





