Dynamic Fluid in a Porous Transducer-Based Angular Accelerometer
Abstract
:1. Introduction
2. Structure and Principle of LCAA
3. Theoretical Model of the Dynamic Fluid in LCAA
3.1. Fluid Transients
3.2. Wave Speed
3.3. Dynamic Permeability Model of the Porous Transducer
4. Experiments
4.1. Porous Transducer
4.1.1. Fabrication and Permeability Measurement
4.1.2. Experiments on the Streaming Potential
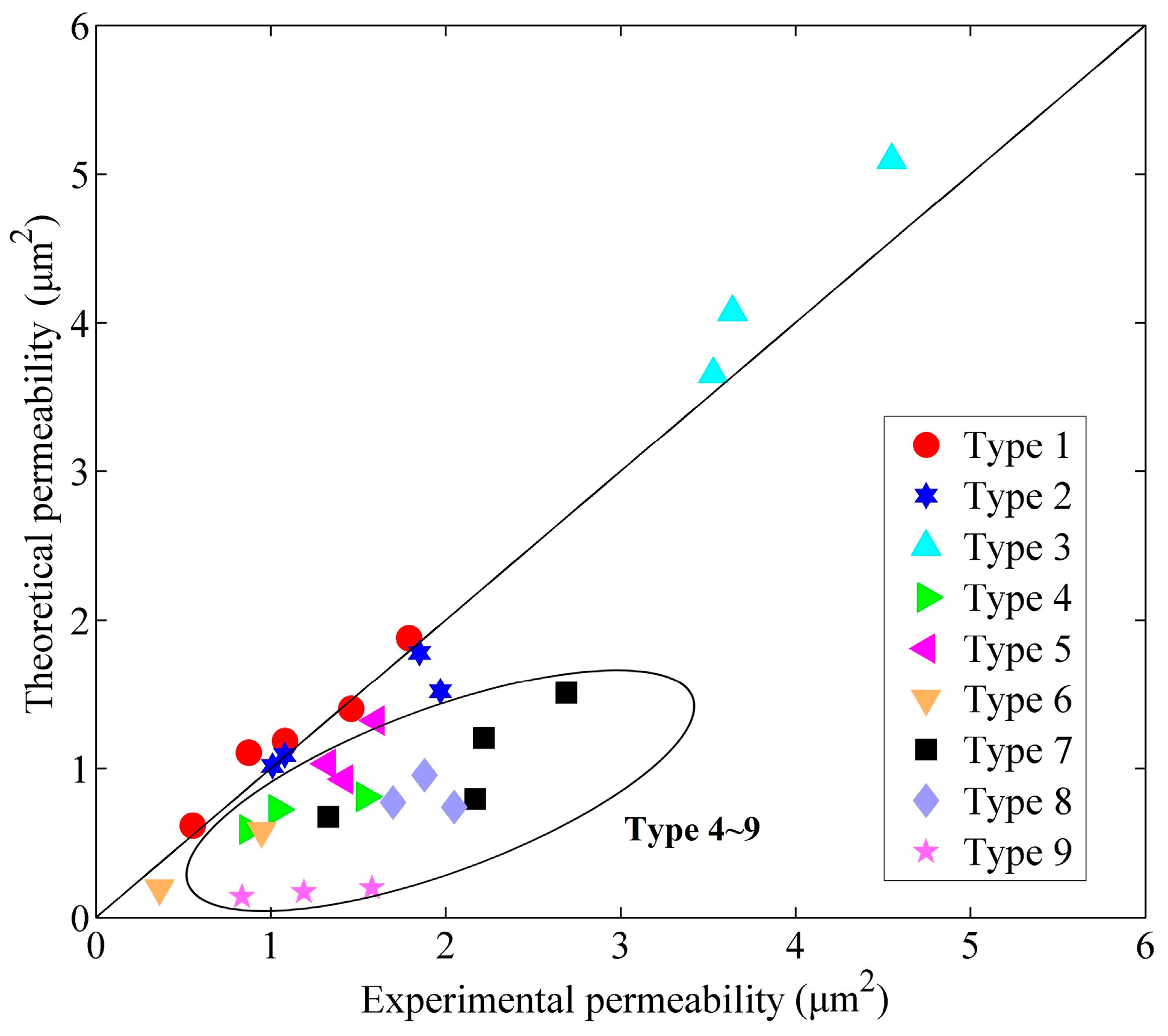
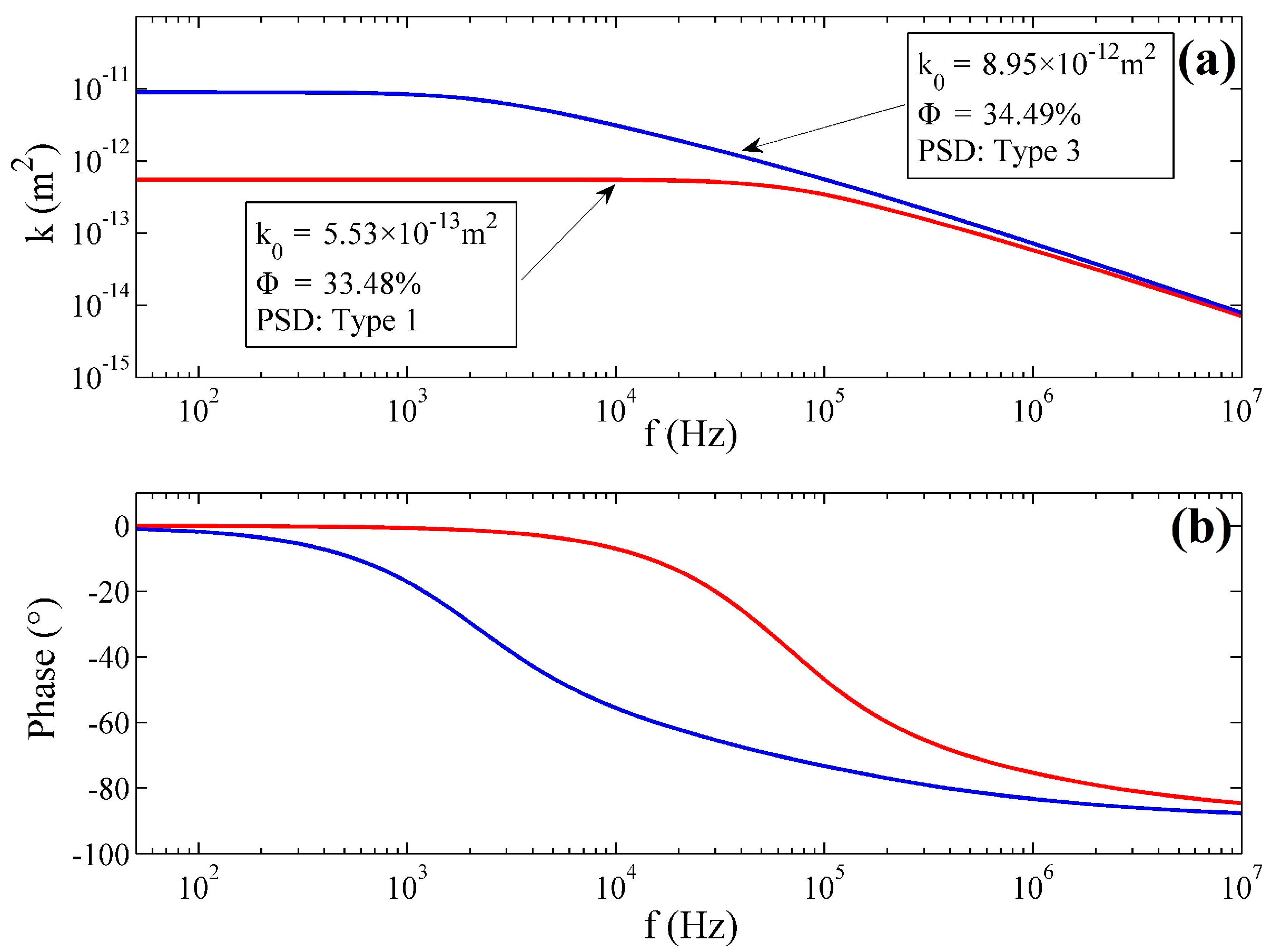
4.1.3. Simulation of the Dynamic Permeability Model
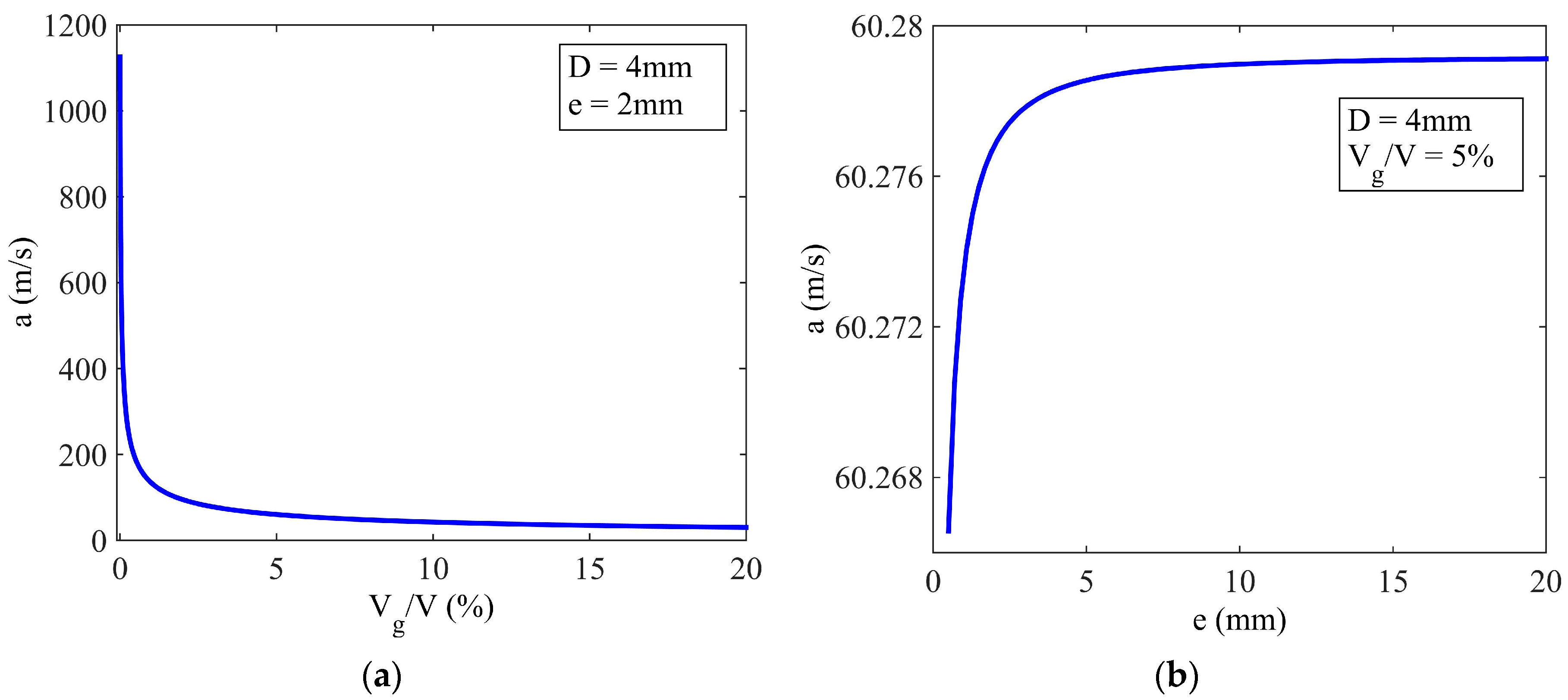
4.2. Simulation of the Wave Speed
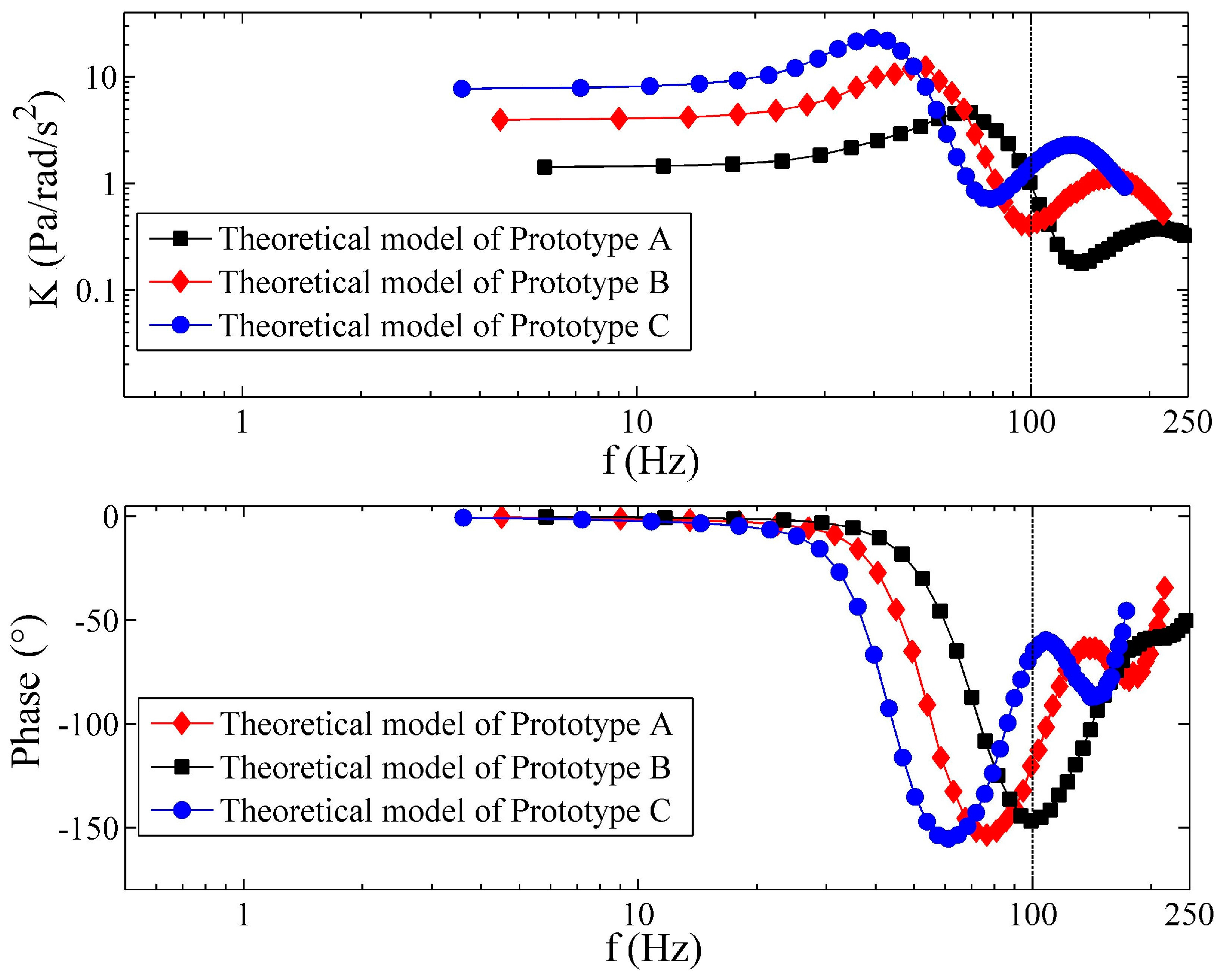
4.3. Simulation of the Frequency Response of the Fluidic System
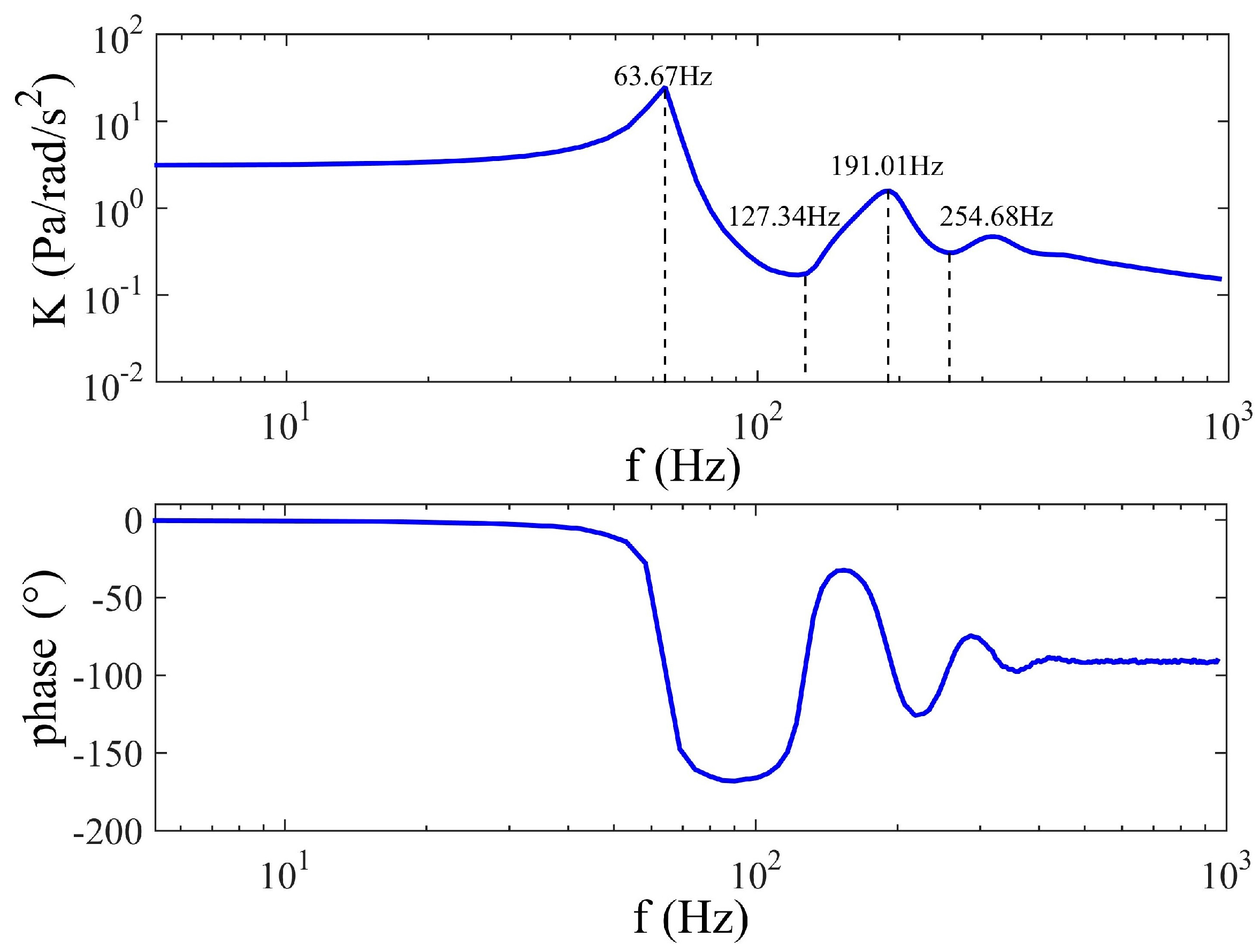
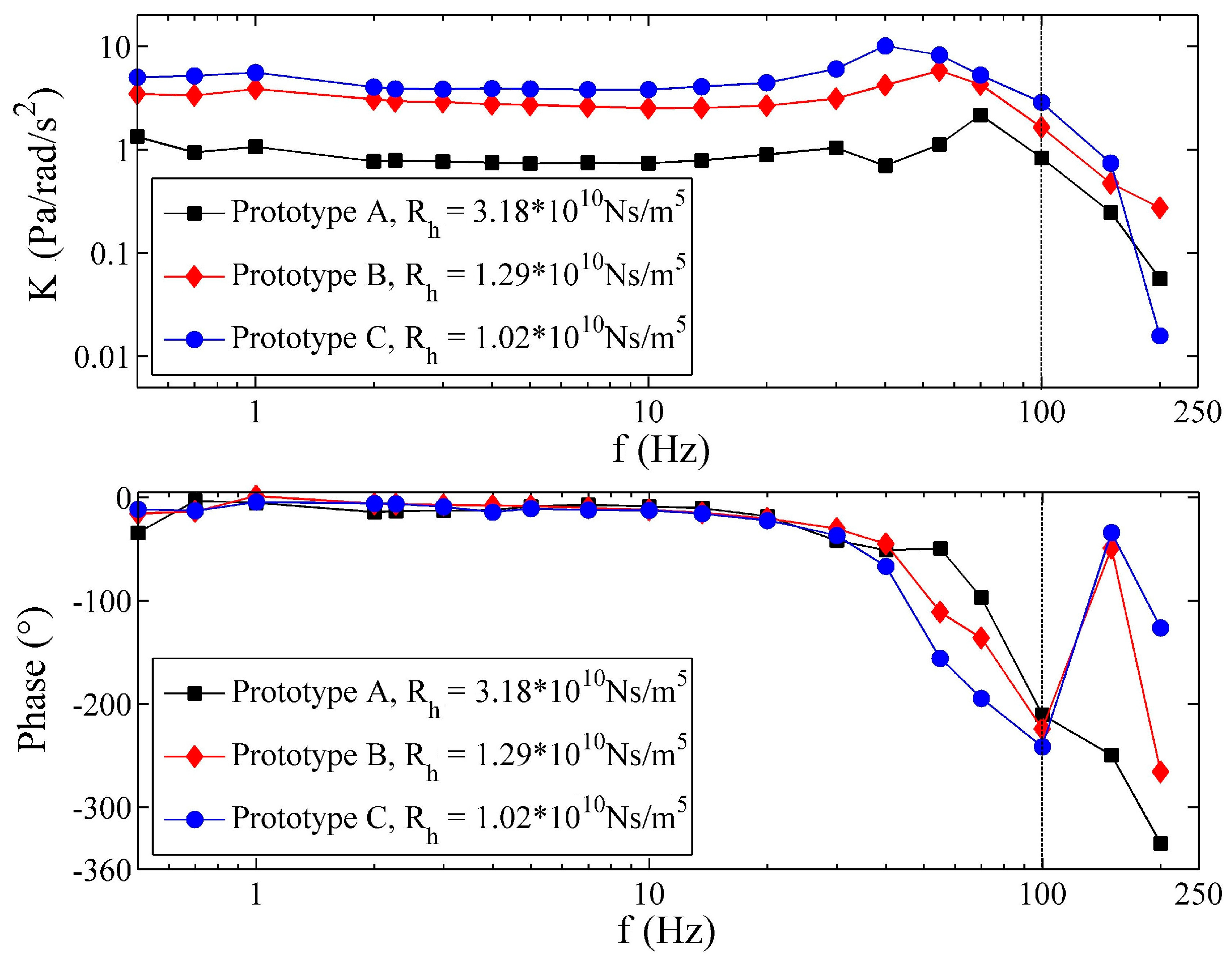
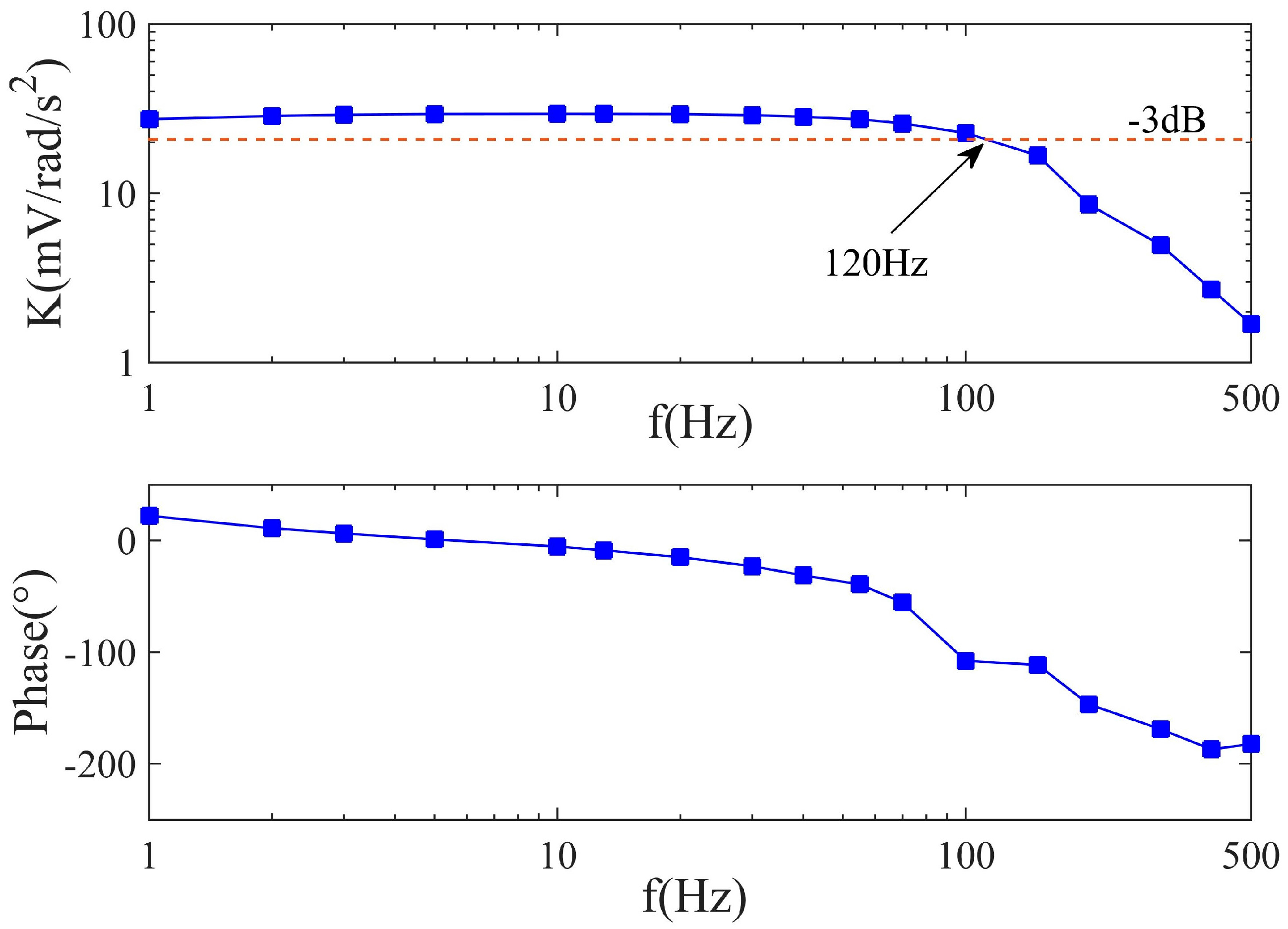
4.4. Experiments of the Frequency Response of the Fluidic System
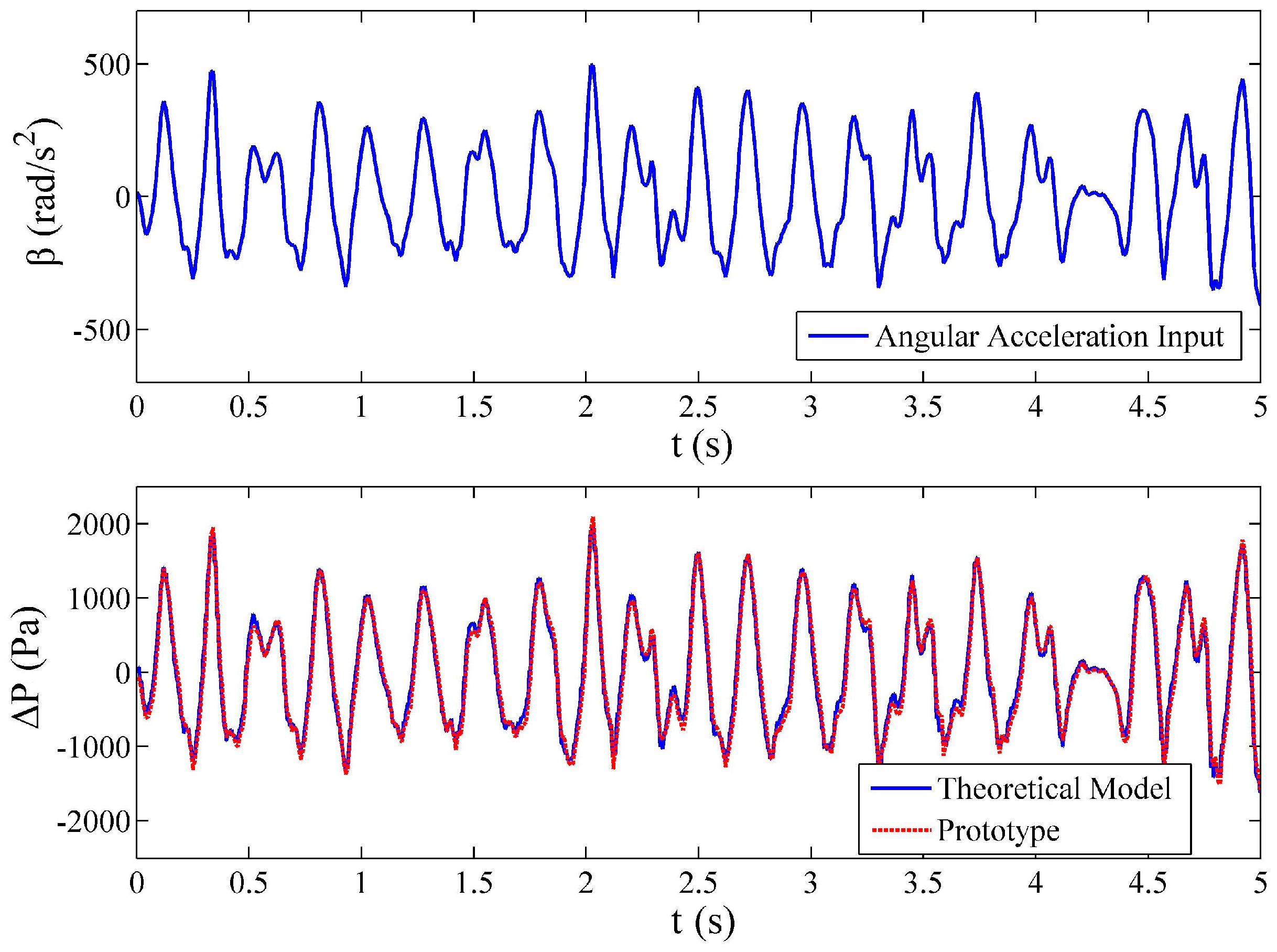
4.5. Experiment of the Transient Response of the Fluidic System
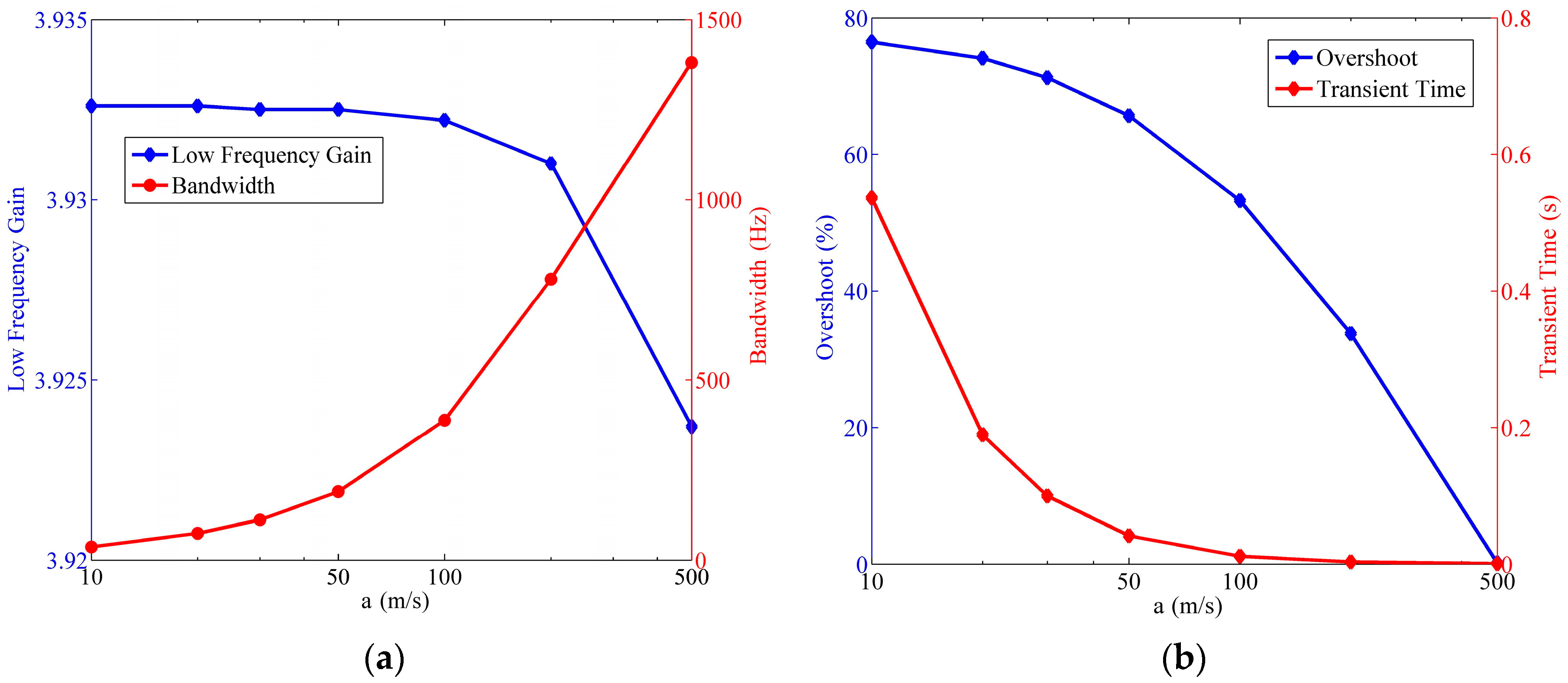
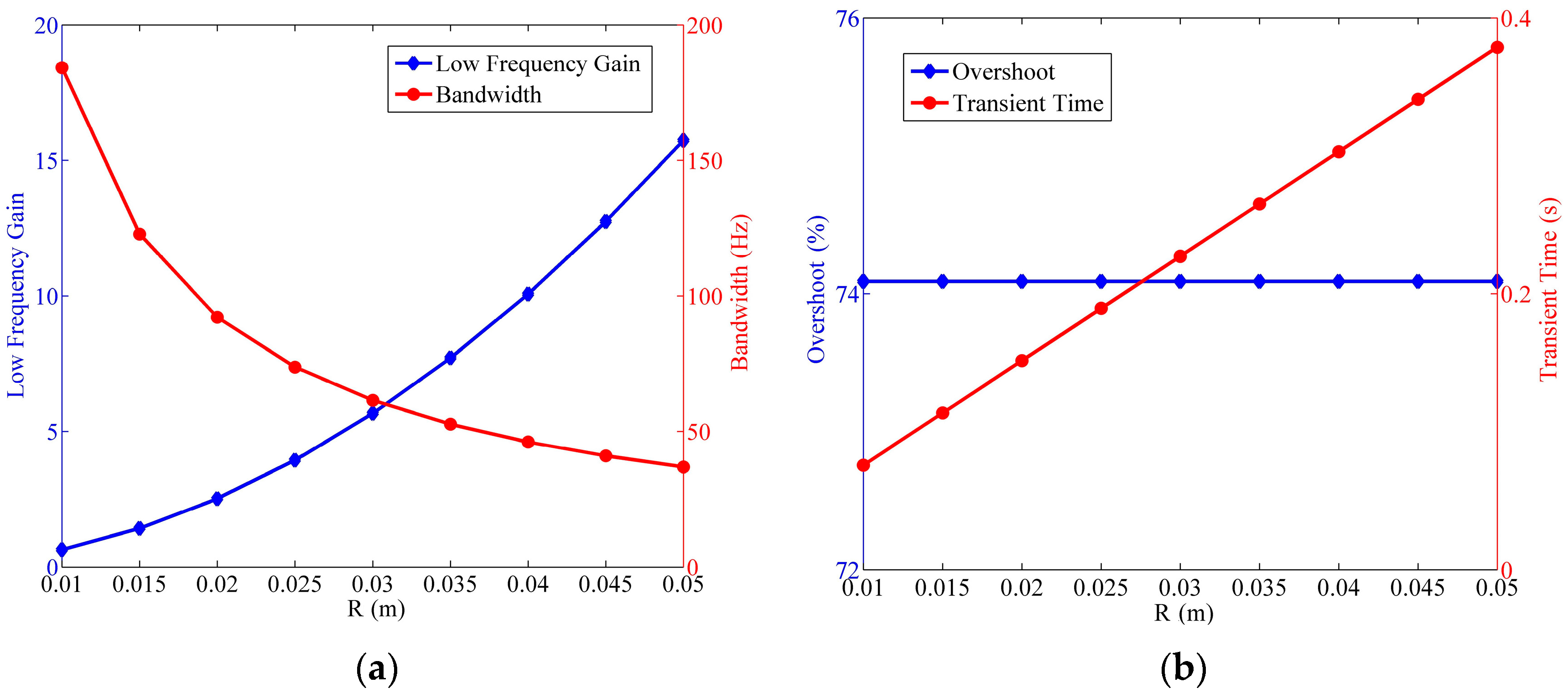
4.6. Influence of Structural Parameters
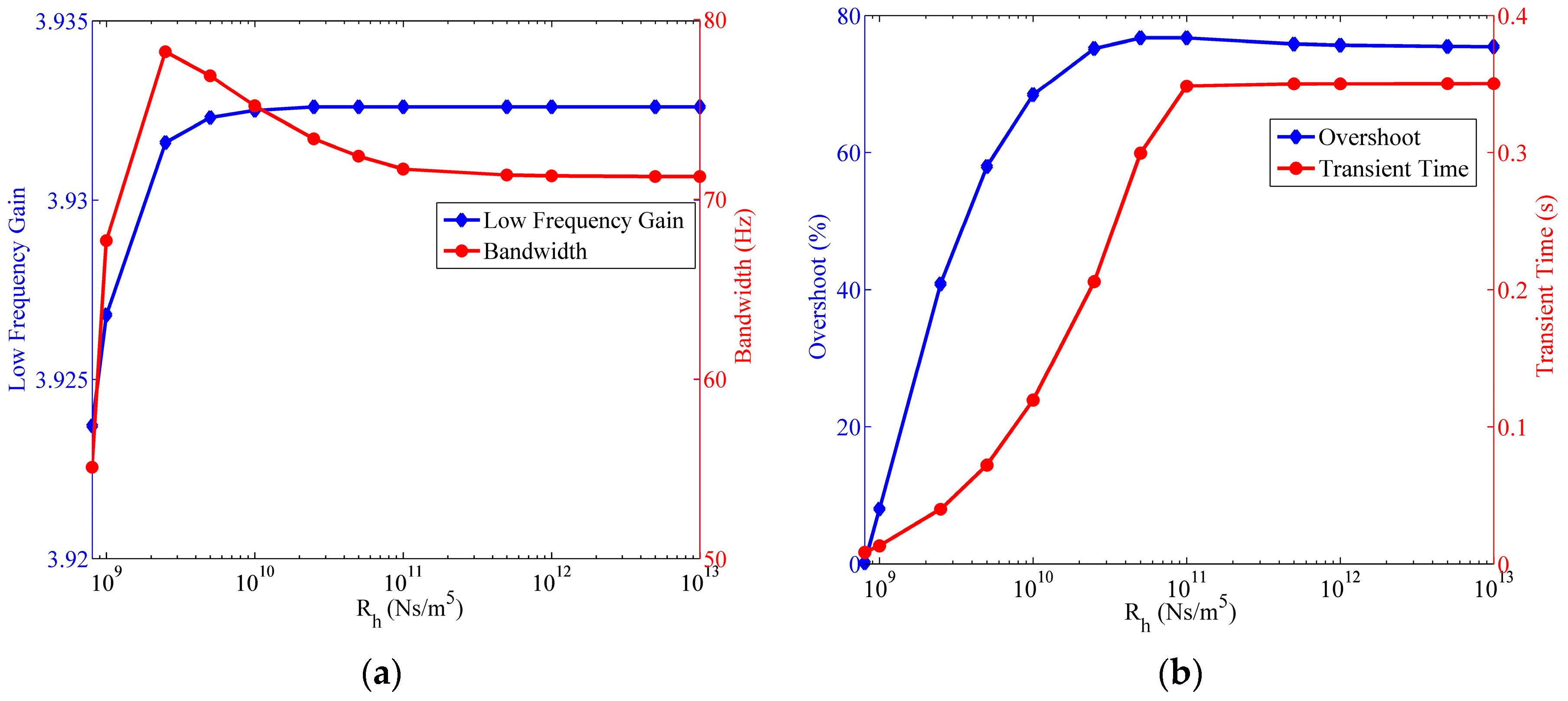
- Low frequency gain: the system gain at low frequency, which has an effect on the magnitude of the output signal of the system. Small low frequency gain would lead to the low signal-noise ratio of the sensor.
- Bode magnitude −3-dB bandwidth: the standard bandwidth of the system, which influences the operating frequency range of the sensor.
- Step response overshoot: relative height of the peak in step response, which mainly depends on the damping of the system.
- Step response transient time: transient time of the system changing into the 2% range of the new stable state in the step response.
4.6.1. Influence of Hydrodynamic Resistance
4.6.2. Influence of the Wave Speed
4.6.3. Influence of the Radius of the Circular Tube
4.6.4. Influence of the Cross-Section Radius
4.7. Performance of the LCAA
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wu, X.S.; Chen, W.Y. Review on angular accelerometer development. J. Chin. Inert. Technol. 2007, 15, 458–463. [Google Scholar]
- Ovaska, S.J.; Valiviita, S. Angular acceleration measurement: A review. IEEE Trans. Instrum. Meas. 1998, 47, 1211–1217. [Google Scholar] [CrossRef]
- Moody, M.V.; Paik, H.J.; Canavan, E.R. Principle and performance of a superconducting angular accelerometer. Rev. Sci. Instrum. 2003, 1310–1318. [Google Scholar] [CrossRef]
- Zhou, G.G.; Lin, M.B. A study on floated-fly-wheel angular accelerometer. J. Shanghai Jiaotong Univ. 1995, 74, 135–141. [Google Scholar]
- Gola, A.; Chiesa, E.; Lasalandra, E.; Pasolini, F.; Tronconi, M.; Ungaretti, T.; Baschirotto, A. Interface for MEMS-based rotational accelerometer for HDD applications with 2.5 rad/s2 resolution and digital output. IEEE Sens. J. 2003, 3, 383–392. [Google Scholar] [CrossRef]
- Lin, J.M.; Lin, C.H. A novel wireless thermal convection type angular accelerometer with xenon gas filled in hemispherical chamber of floating and non-floating structures. J. Comput. 2013, 8, 2389–2397. [Google Scholar] [CrossRef]
- Alrowais, H.; Getz, P.; Kim, M.G.; Su, J.J. Bio-inspired fluidic thermal angular accelerometer. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems, Shanghai, China, 24–28 January 2016.
- Zhao, H.; Feng, H. A novel angular acceleration sensor based on the electromagnetic induction principle and investigation of its calibration tests. Sensors 2013, 13, 10370–10385. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Agafonov, V.; Yu, H.Y. Molecular electric transducers as motion sensors: A review. Sensors 2013, 13, 4581–4597. [Google Scholar] [CrossRef] [PubMed]
- Zaitsev, D.; Agafonov, V.; Egorov, E.; Antonov, A.; Shabalina, A. Molecular electronic angular motion transducer broad band self-noise. Sensors 2015, 15, 29378–29392. [Google Scholar] [CrossRef] [PubMed]
- Krishtop, V.G.; Agafonov, V.M.; Bugaev, A.S. Technological principles of motion parameter transducers based on mass and charge transport in electrochemical microsystem. Russ. J. Electrochem. 2012, 48, 746–755. [Google Scholar] [CrossRef]
- Neeshpapa, A.; Antonov, A.; Agafonov, V. A low-noise dc seismic accelerometer based on a combination of MET/MEMS sensors. Sensors 2015, 15, 365–381. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, V.A.; Safonov, M.V. Dynamic characteristic of an electrochemical cell with gauze electrodes in convective diffusion conditions. Russ. J. Electrochem. 2004, 40, 518–520. [Google Scholar] [CrossRef]
- Leugoud, R.; Kharlamov, A. Second generation of a rotational electrochemical seismometer using magnetohydrodynamic technology. J. Seismol. 2012, 16, 587–593. [Google Scholar] [CrossRef]
- Wolfaardt, H.J. Theory of the Microfluidic Channel Angular Accelerometer for Inertial Measurement Applications; Master of Engineering; University of Pretoria: Pretoria, South Africa, 2005. [Google Scholar]
- Cheng, S.Y.; Wang, M.L.; Li, X.; Xiao, M.F.; Fu, M.Y.; Zheng, X. Transfer function of fluidic system in liquid-circular angular accelerometer. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference, Taipei, Taiwan, 23–26 May 2016.
- Cheng, S.Y.; Fu, M.Y.; Wang, M.L.; Li, X.; Xiao, M.F.; Wang, T.L. Modeling for Fluid Transients in Liquid-Circular Angular Accelerometer. IEEE Sens. J. 2017, 17, 267–273. [Google Scholar] [CrossRef]
- Wu, X.R.; Zhou, M.; Sun, R.K.; Ma, G.S.; Hong, F. An introduction to the research and application of a new type angular accelerometer. J. Nav. Aeronaut. Eng. Inst. 2003, 18, 631–635. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014; pp. 39–52. [Google Scholar]
- Wylie, E.B.; Streeter, V.L. Fluid Transients; McGraw-Hill International Book Co.: New York, NY, USA, 1978. [Google Scholar]
- Delgado, A.V.; Gonalez-Caballero, F.; Hunter, R.J.; Koopal, L.K.; Lyklema, J. Measurement and interpretation of electrokinetic phenomena. Pure Appl. Chem. 2005, 77, 1753–1805. [Google Scholar] [CrossRef]
- Alkafeef, S.F.; Alajmi, A.F. Streaming potentials and conductivities of reservoir rock cores in aqueous and non-aqueous liquids. Colloids Surf. A Physiochem. Eng. Asp. 2006, 289, 141–148. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. 1937, 15, 150–167. [Google Scholar] [CrossRef]
- MacDonald, M.J.; Chu, C.F.; Guilloit, P.P.; Ng, K.M. A generalized Blake-Kozeny equation for multisized spherical particles. AIChE J. 1991, 37, 1583–1588. [Google Scholar] [CrossRef]
- Norris, A.N. Low-frequency dispersion and attenuation in partially saturated rocks. J. Acoust. Soc. Am. 1993, 94, 359–370. [Google Scholar] [CrossRef]
- Wang, J.; Hu, H.S.; Guan, W.; Li, H. Electrokinetic experimental study on saturated rock samples: Zeta potential and surface conductance. Geophys. J. Int. 2015, 201, 869–877. [Google Scholar] [CrossRef]
- Glover, P.W.J.; Déry, N. Streaming potential coupling coefficient of quartz glass bead packs: Dependence on grain diameter, pore size, and pore throat radius. Geophysics 2010, 75, F225–F241. [Google Scholar] [CrossRef]
- Perrier, F.; Froidefond, T. Electrical conductivity and streaming potential coefficient in a moderately alkaline lava series. Earth Planet. Sci. Lett. 2003, 210, 351–363. [Google Scholar] [CrossRef]
- Jouniaux, L.; Pozzi, J.P. Permeability dependence of streaming potential in rocks for various fluid conductivities. Geophys. Res. Lett. 1995, 22, 485–488. [Google Scholar] [CrossRef]
- Johnson, D.L.; Koplik, J. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. J. Fluid Mech. 1987, 176, 379–402. [Google Scholar] [CrossRef]
- Byon, C.; Kim, S.J. The effect of the particle size distribution and packing structure on the permeability of sintered porous wicks. Int. J. Heat Mass Transfer. 2013, 61, 499–504. [Google Scholar] [CrossRef]
- Panda, M.N.; Lake, L.W. Estimation of single-phase permeability from parameters of particle-size distribution. Am. Assoc. Pet. Geol. Bull. 1994, 78, 1028–1039. [Google Scholar]
- Sauter Mean Diameter. Available online: https://en.wikipedia.org/wiki/Sauter_mean_diameter (access on 2 February 2017).
- ASM Series Angular Accelerometer. Available online: http://jewellinstruments.com/wp-content/uploads/2016/06/Jewell_SC_Data-Sheet-ASM-Series-Angular-Accelerometer_Jul_15-REV.C.pdf (accessed on 1 December 2016).
- Lide, D.R. CRC Hand Book of Chemistry and Physics, 80th ed.; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Smits, J.G.; Choi, W.S.; Ballato, A. Resonance and antiresonance of symmetric and asymmetric cantilevered piezoelectric flexors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1997, 44, 250–258. [Google Scholar] [CrossRef] [PubMed]
- Ural, S.O.; Tuncdemir, S.; Zhuang, Y.; Uchino, K. Development of a high power piezoelectric characterization system and its application for resonance/antiresonance mode characterization. Jpn. J. Appl. Phys. 2009, 48, 056509. [Google Scholar] [CrossRef]








| Type | Mixture Proportion | d(0.1) (μm) | d(0.5) (μm) | d(0.9) (μm) | (μm) |
|---|---|---|---|---|---|
| 1 | - | 23.94 | 34.39 | 49.53 | 33.08 |
| 2 | - | 36.99 | 52.62 | 74.69 | 50.68 |
| 3 | - | 56.99 | 80.15 | 112.32 | 77.35 |
| 4 | Type 1:Type 2 = 1:1 | 30.83 | 45.61 | 67.44 | 43.57 |
| 5 | Type 1:Type 2 = 1:3 | 34.92 | 50.14 | 71.78 | 48.19 |
| 6 | Type 1:Type 2 = 3:1 | 25.59 | 38.68 | 59.03 | 36.85 |
| 7 | Type 1:Type 3 = 1:1 | 33.11 | 57.91 | 99.38 | 52.82 |
| 8 | Type 1:Type 3 = 1:3 | 36.15 | 71.31 | 123.20 | 60.43 |
| 9 | Type 1:Type 3 = 3:1 | 22.56 | 40.50 | 79.64 | 37.21 |
| Material | Young’s Modulus (GPa) | Poisson Ratio | Density (kg/m3) | Bulk Modulus (GPa) | Viscosity (mPa·s) |
|---|---|---|---|---|---|
| Glass | 46 | 0.24 | 2500 | - | - |
| ABS Plastic | 1.7 | 0.33 | 1050 k | - | - |
| Water | - | - | 998 | 2.19 | 1.01 |
| Prototype | R (mm) | r (mm) |
|---|---|---|
| A | 15 | 4 |
| B | 25 | 4 |
| C | 35 | 4 |
| Prototype | Kth (Pa/rad/s2) | Kex (Pa/rad/s2) | Loss Factor (Kth/Kex) |
|---|---|---|---|
| A | 1.41 | 1.16 | 1.22 |
| B | 3.93 | 3.56 | 1.10 |
| C | 7.70 | 5.97 | 1.29 |
| Average | - | - | 1.20 |
| Index | Value |
|---|---|
| Bandwidth | 0.5~120 Hz |
| Measurement Range | −25,000°/s2~+25,000°/s2 |
| Scale Factor | 0.5 mVs2/° |
| Dead Band | 1°/s2 |
| Relative Error | 1% |
| Power Supply | ±15 V |
| Temperature Range | −40~+60 °C |
| External Size | Φ75 mm × 41 mm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, S.; Fu, M.; Wang, M.; Ming, L.; Fu, H.; Wang, T. Dynamic Fluid in a Porous Transducer-Based Angular Accelerometer. Sensors 2017, 17, 416. https://doi.org/10.3390/s17020416
Cheng S, Fu M, Wang M, Ming L, Fu H, Wang T. Dynamic Fluid in a Porous Transducer-Based Angular Accelerometer. Sensors. 2017; 17(2):416. https://doi.org/10.3390/s17020416
Chicago/Turabian StyleCheng, Siyuan, Mengyin Fu, Meiling Wang, Li Ming, Huijin Fu, and Tonglei Wang. 2017. "Dynamic Fluid in a Porous Transducer-Based Angular Accelerometer" Sensors 17, no. 2: 416. https://doi.org/10.3390/s17020416
APA StyleCheng, S., Fu, M., Wang, M., Ming, L., Fu, H., & Wang, T. (2017). Dynamic Fluid in a Porous Transducer-Based Angular Accelerometer. Sensors, 17(2), 416. https://doi.org/10.3390/s17020416






