Figure 1.
Strain measurement with strain gauge: (a) strain gauge locates at the crack; and (b) strain gauge locates at some distance away from the crack.
Figure 1.
Strain measurement with strain gauge: (a) strain gauge locates at the crack; and (b) strain gauge locates at some distance away from the crack.
Figure 2.
Area sensing with long-gauge sensors.
Figure 2.
Area sensing with long-gauge sensors.
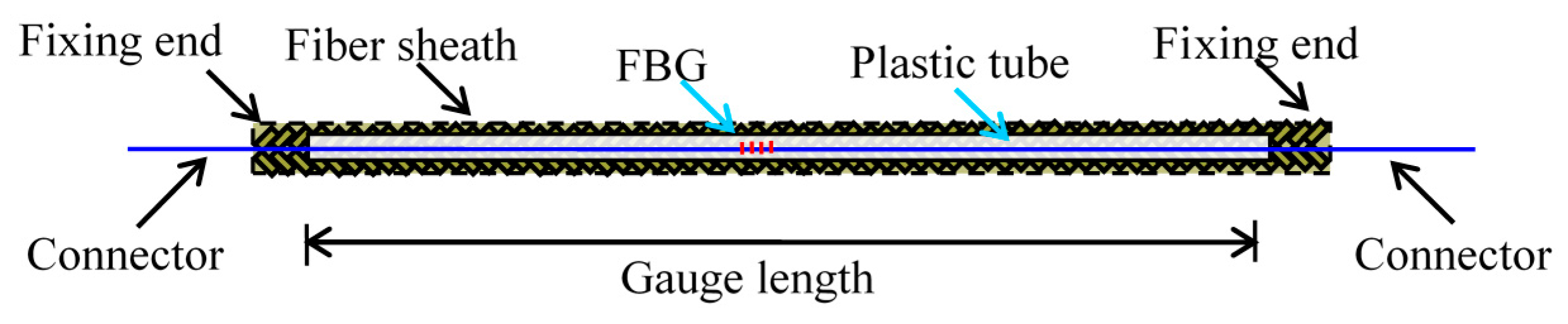
Figure 3.
Packaged long-gauge Fiber Bragg Grating (FBG) sensor.
Figure 3.
Packaged long-gauge Fiber Bragg Grating (FBG) sensor.
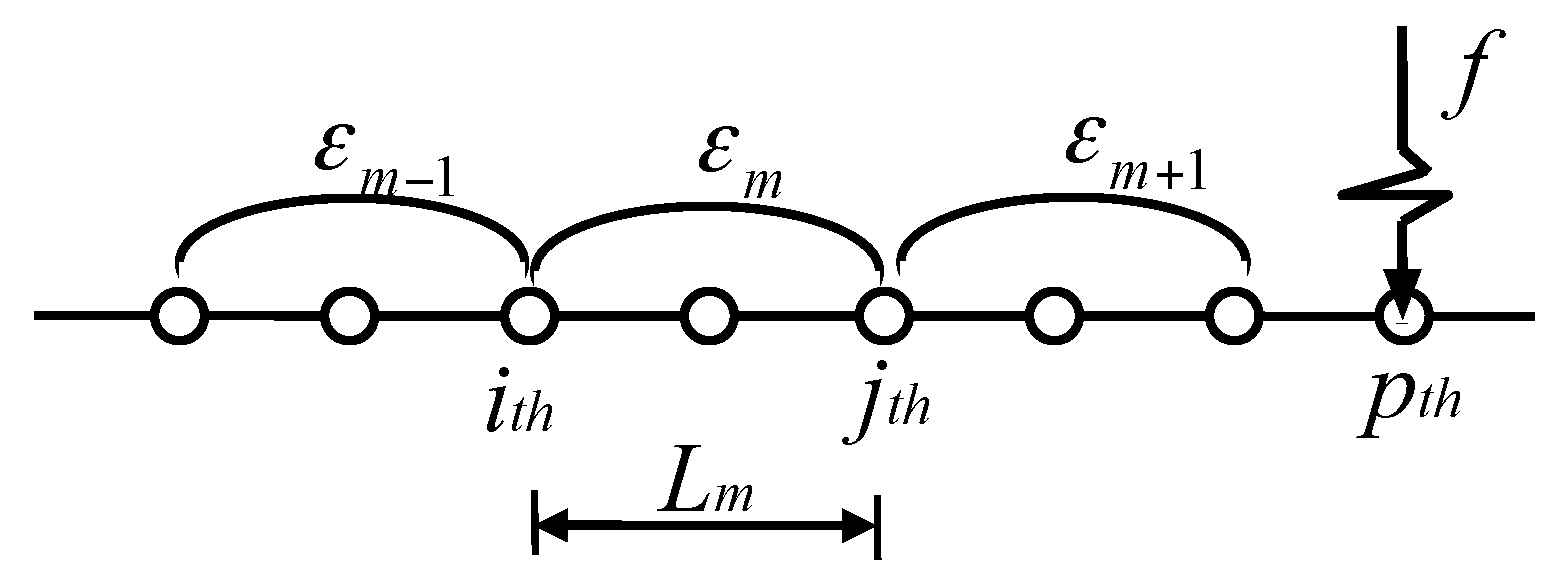
Figure 4.
Macro-strain measurements for beam structure.
Figure 4.
Macro-strain measurements for beam structure.
Figure 5.
Strain distribution along the cross section with sensors installed at: (a) different sides of the neutral axis; and (b) the same side of the neutral axis.
Figure 5.
Strain distribution along the cross section with sensors installed at: (a) different sides of the neutral axis; and (b) the same side of the neutral axis.
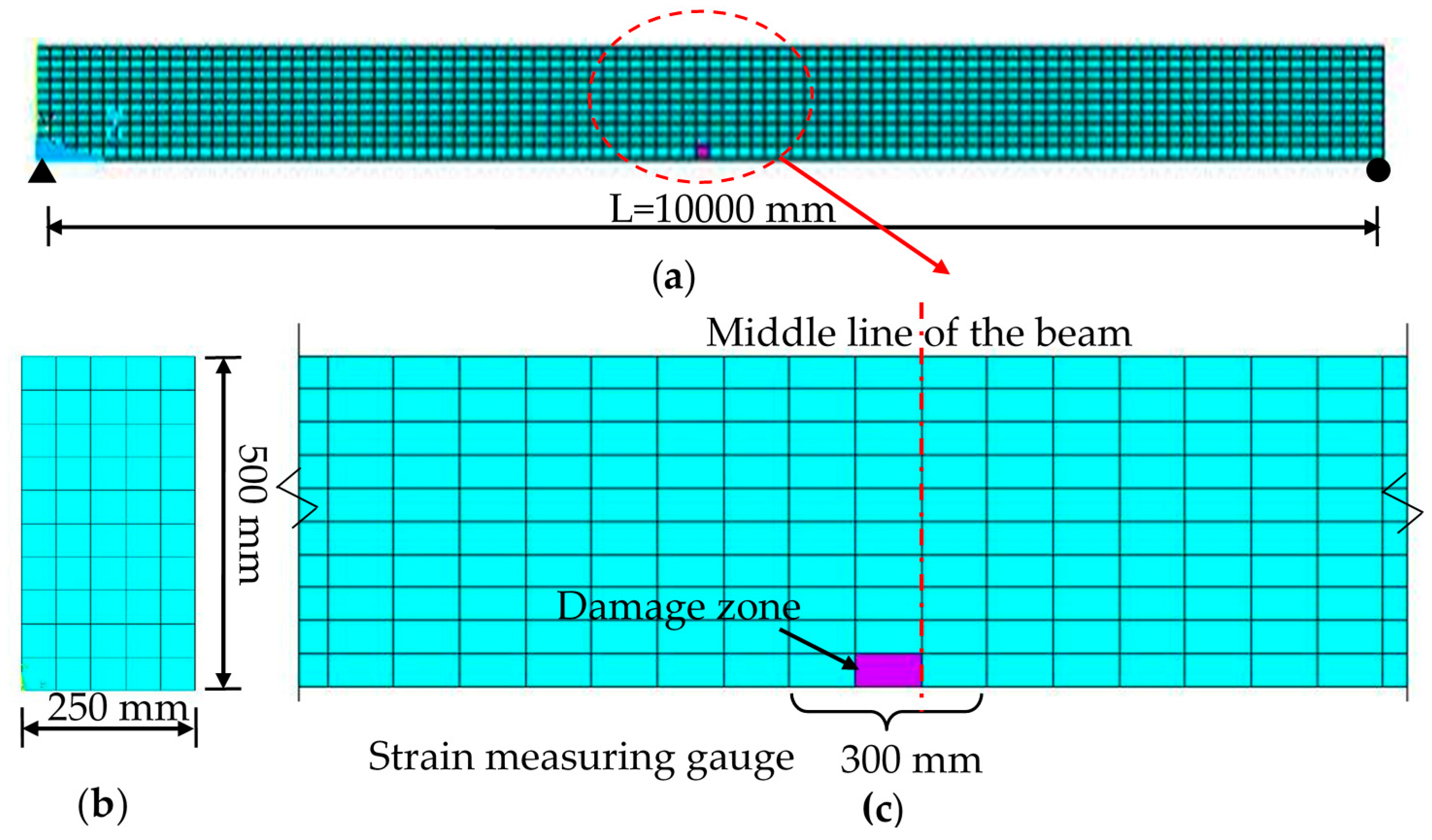
Figure 6.
Finite Element (FE) beam model: (a) beam; (b) cross section; and (c) damaged zone and monitored zone.
Figure 6.
Finite Element (FE) beam model: (a) beam; (b) cross section; and (c) damaged zone and monitored zone.
Figure 7.
Damage sensitivity with different spatial sensor installations: (a) sensor installation; and (b) relative change of neutral axis position coefficient (NAPC).
Figure 7.
Damage sensitivity with different spatial sensor installations: (a) sensor installation; and (b) relative change of neutral axis position coefficient (NAPC).
Figure 8.
Typical strain results at Case I: (a) the whole time history; and (b) local part focused.
Figure 8.
Typical strain results at Case I: (a) the whole time history; and (b) local part focused.
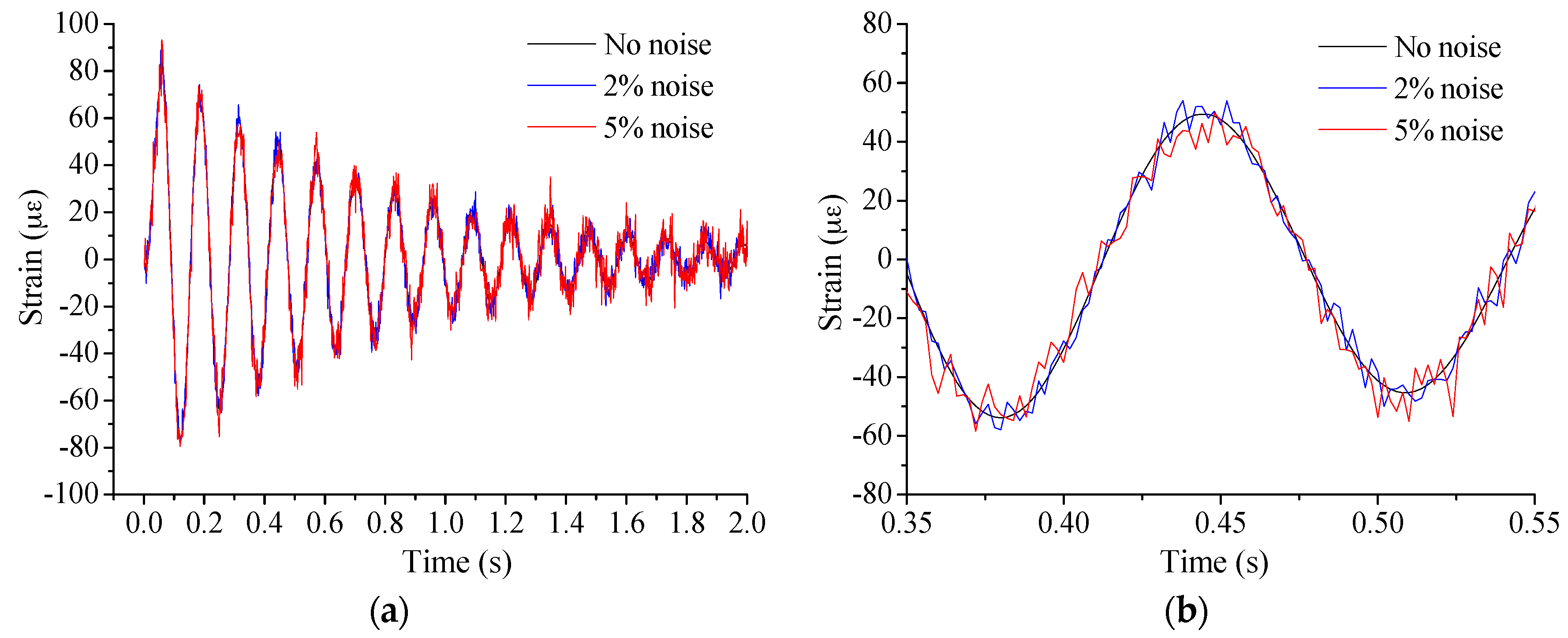
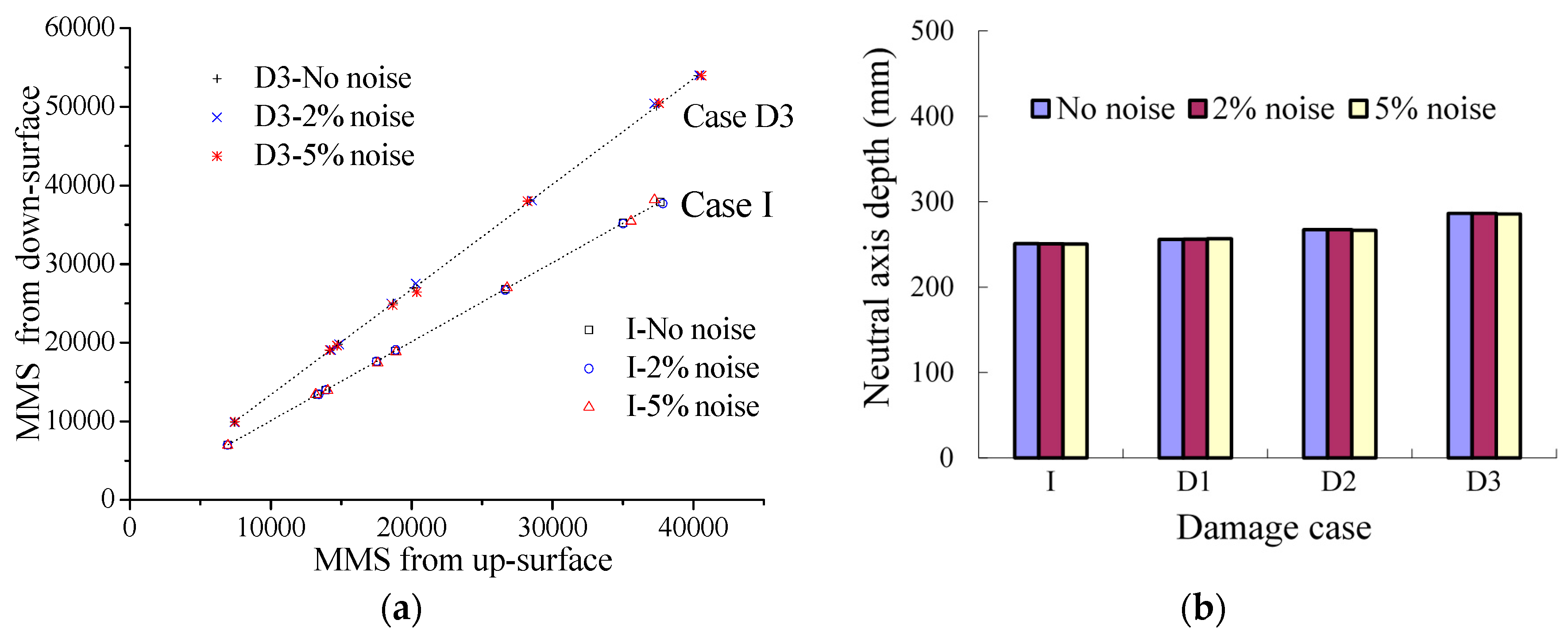
Figure 9.
Performance of the proposed method under noise: (a) NAPC; and (b) neutral axis depth.
Figure 9.
Performance of the proposed method under noise: (a) NAPC; and (b) neutral axis depth.
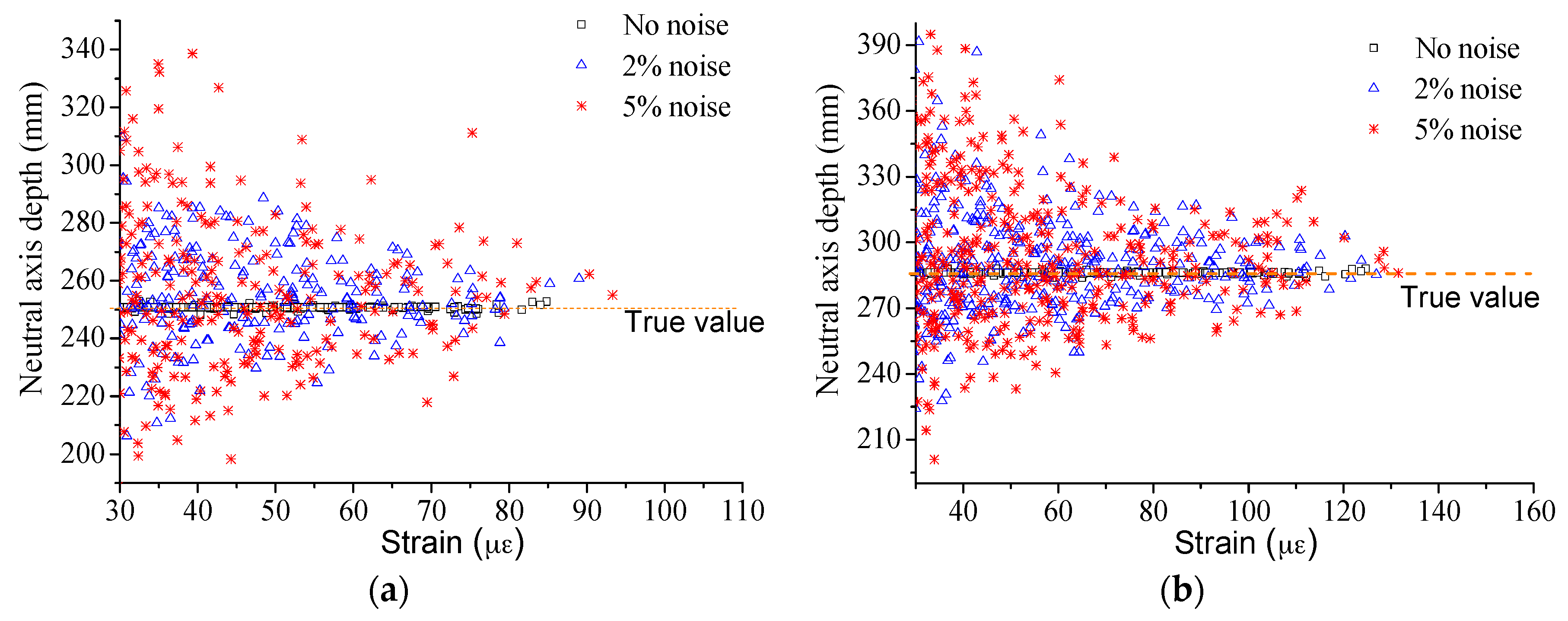
Figure 10.
Performance of the traditional method under noise at Case: (a) I; and (b) D3.
Figure 10.
Performance of the traditional method under noise at Case: (a) I; and (b) D3.
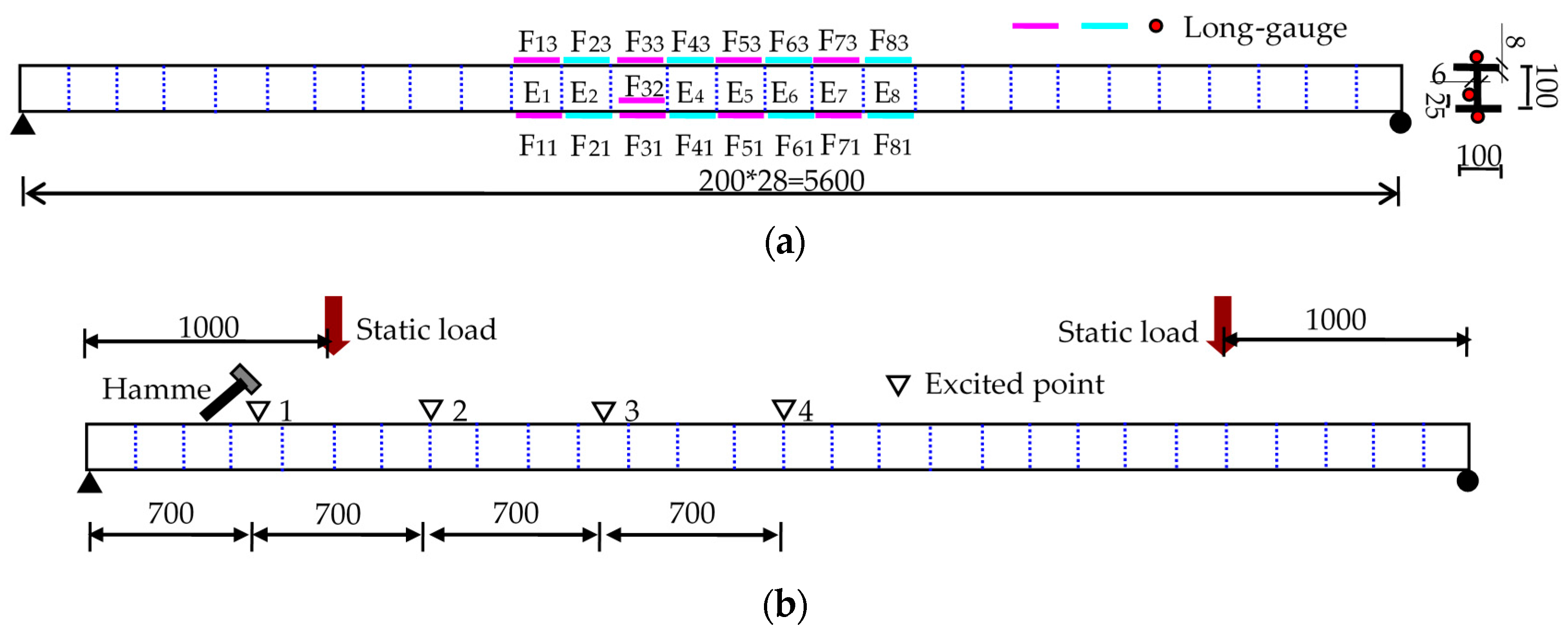
Figure 11.
Experimental description for the steel beam tests (Unit: mm): (a) sensor installation at steel beam; and (b) loading position.
Figure 11.
Experimental description for the steel beam tests (Unit: mm): (a) sensor installation at steel beam; and (b) loading position.
Figure 12.
The steel beam experiment field: (a) dynamic test and data logger; and (b) damage simulation.
Figure 12.
The steel beam experiment field: (a) dynamic test and data logger; and (b) damage simulation.
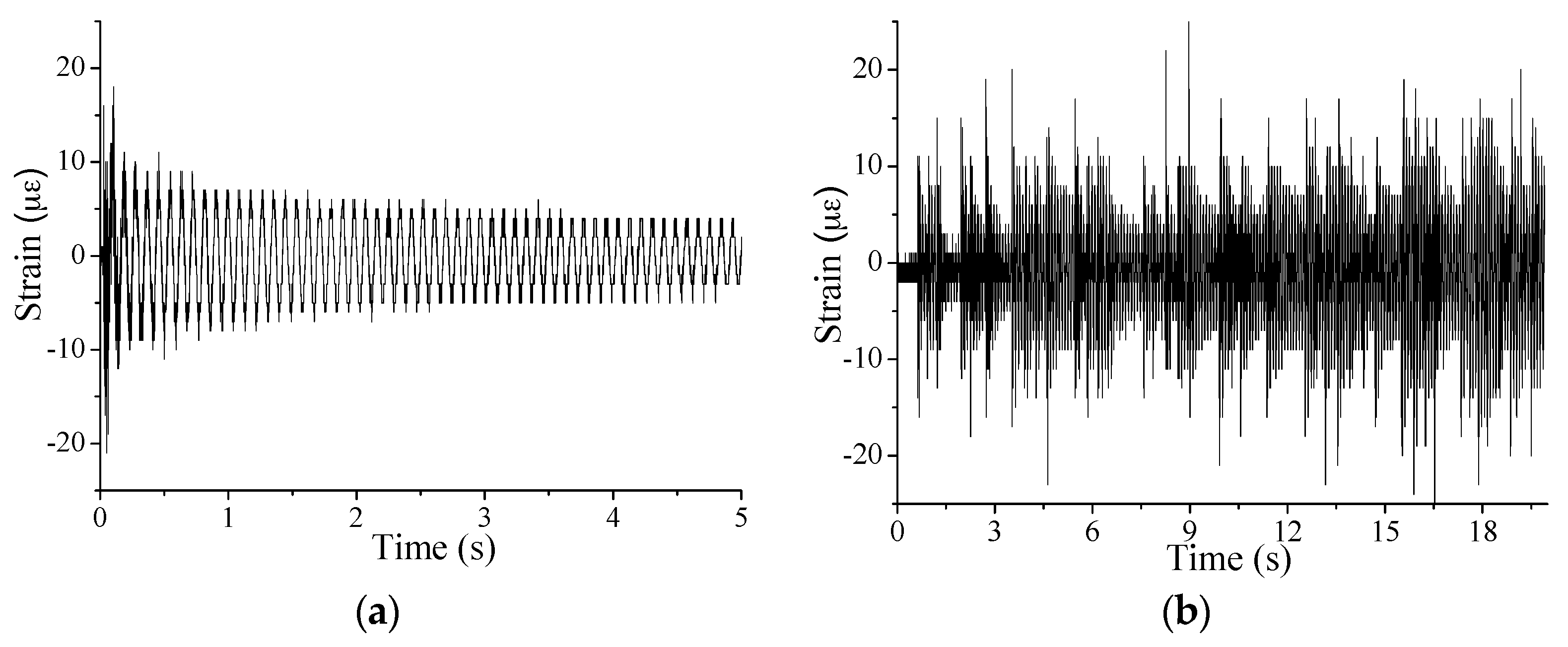
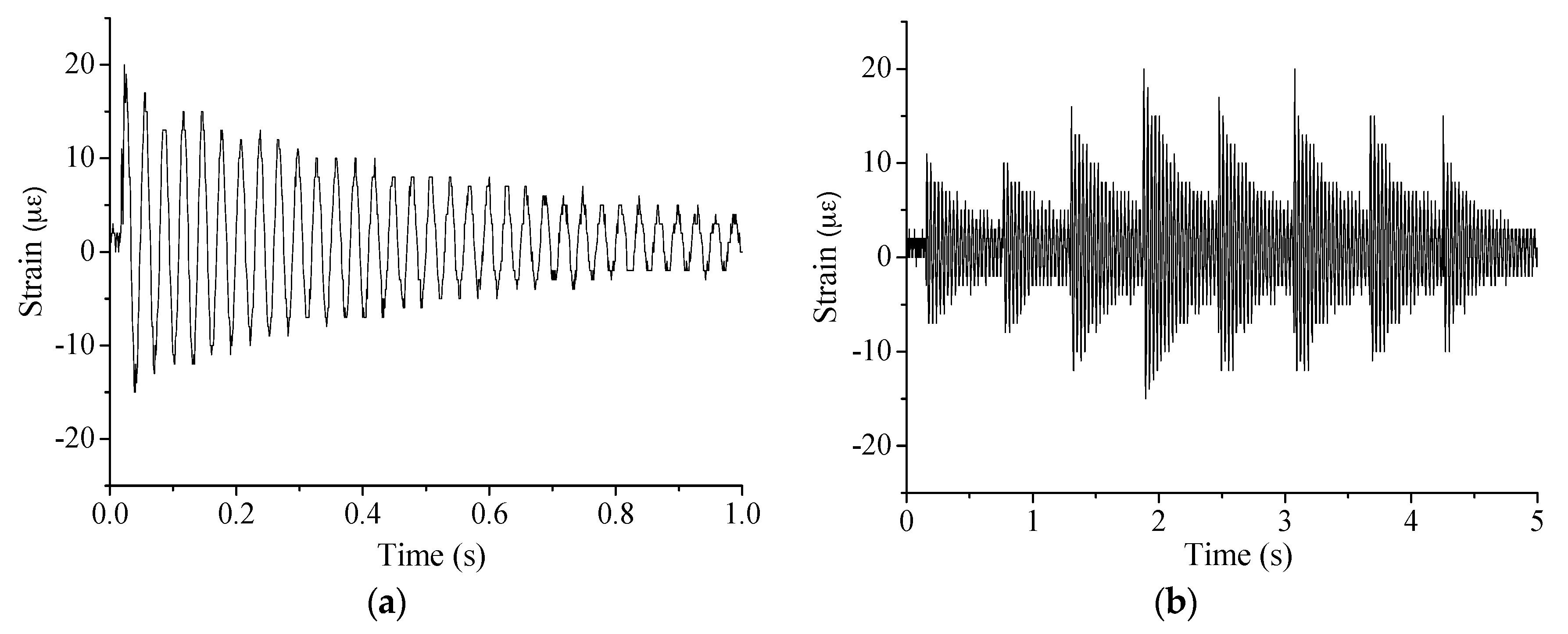
Figure 13.
Typical macro-strain results for the steel beam test under: (a) single-point excitation; and (b) random excitation.
Figure 13.
Typical macro-strain results for the steel beam test under: (a) single-point excitation; and (b) random excitation.
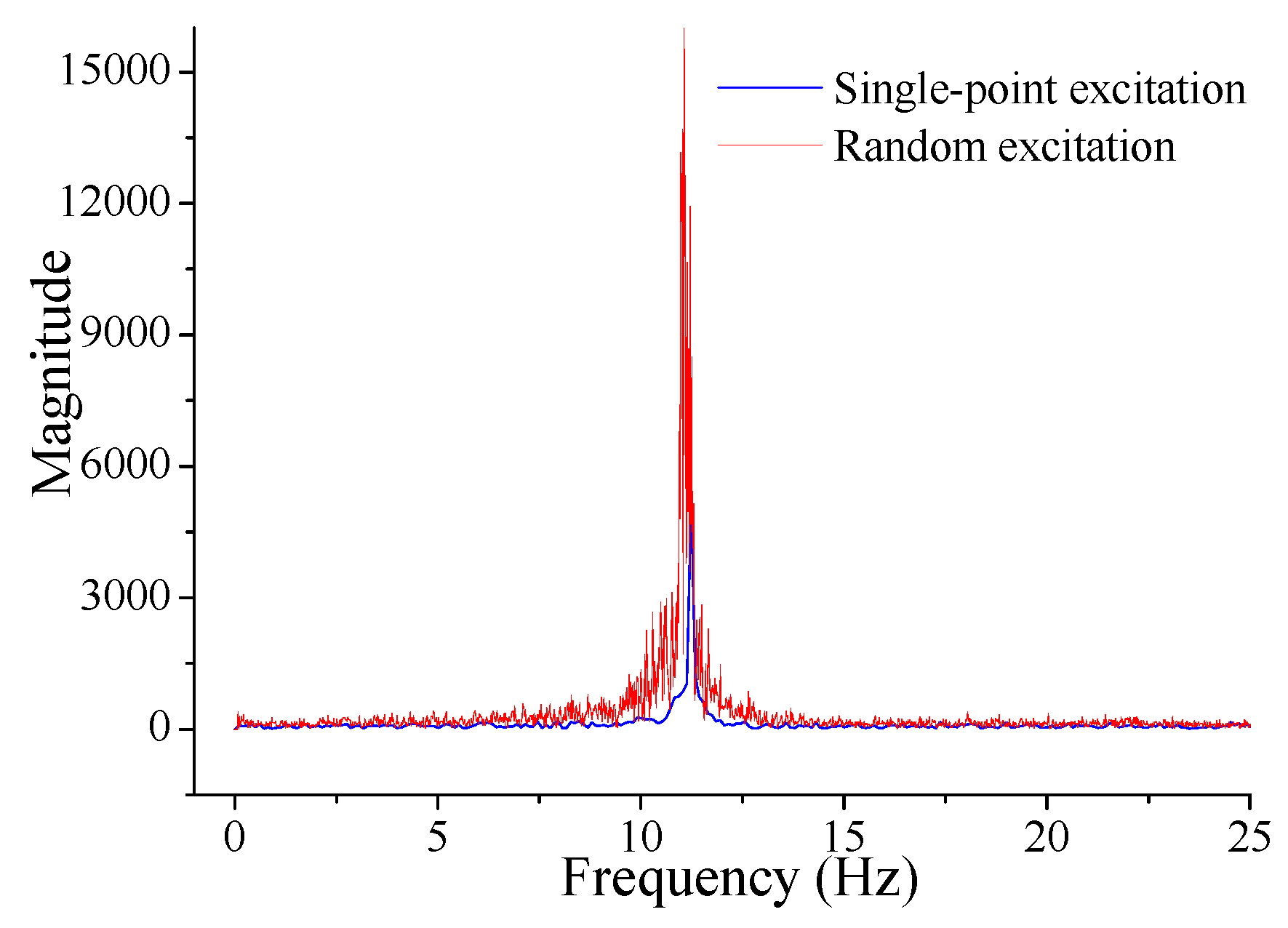
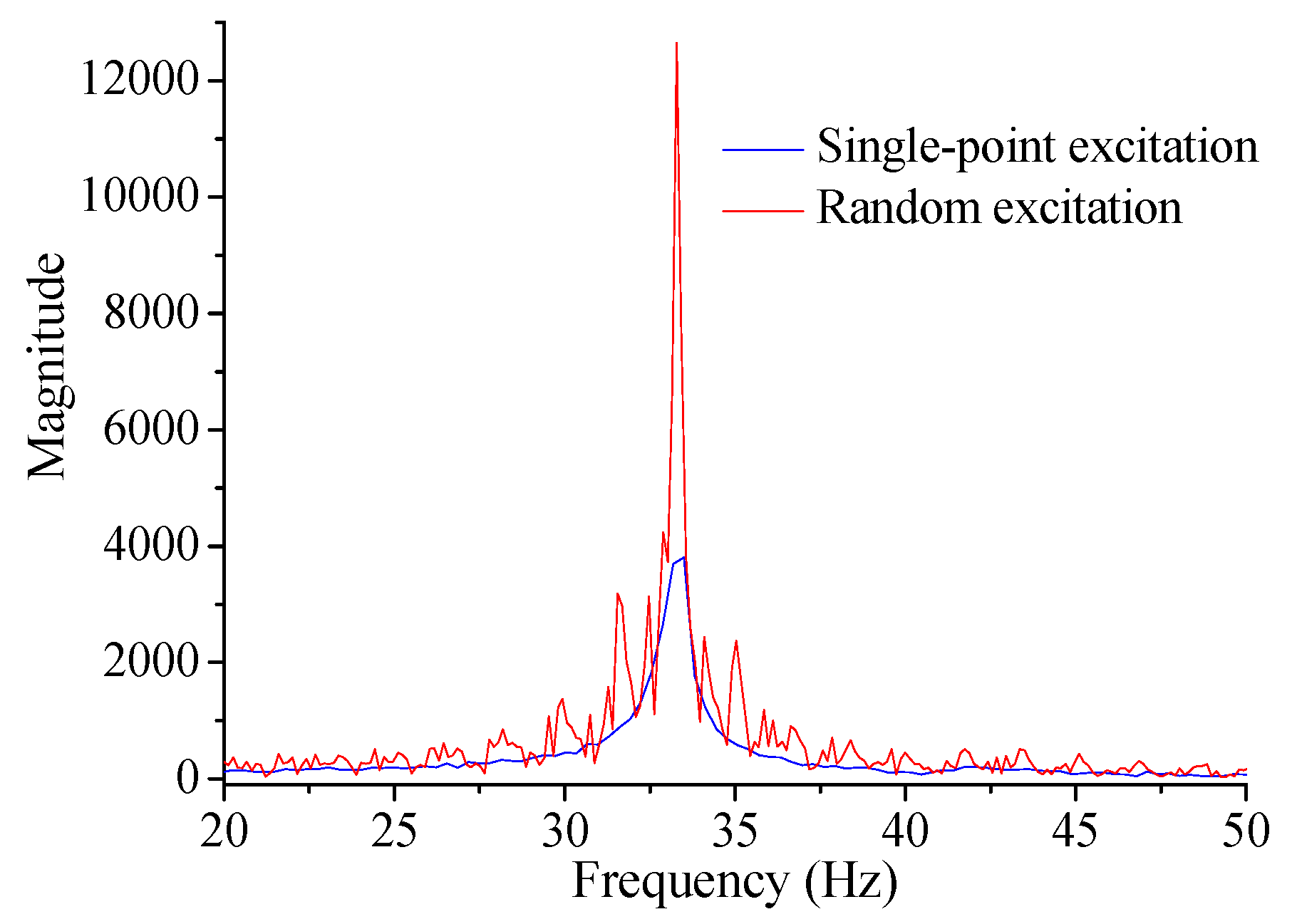
Figure 14.
Typical results of macro-strain based frequency spectrum for the steel beam test.
Figure 14.
Typical results of macro-strain based frequency spectrum for the steel beam test.
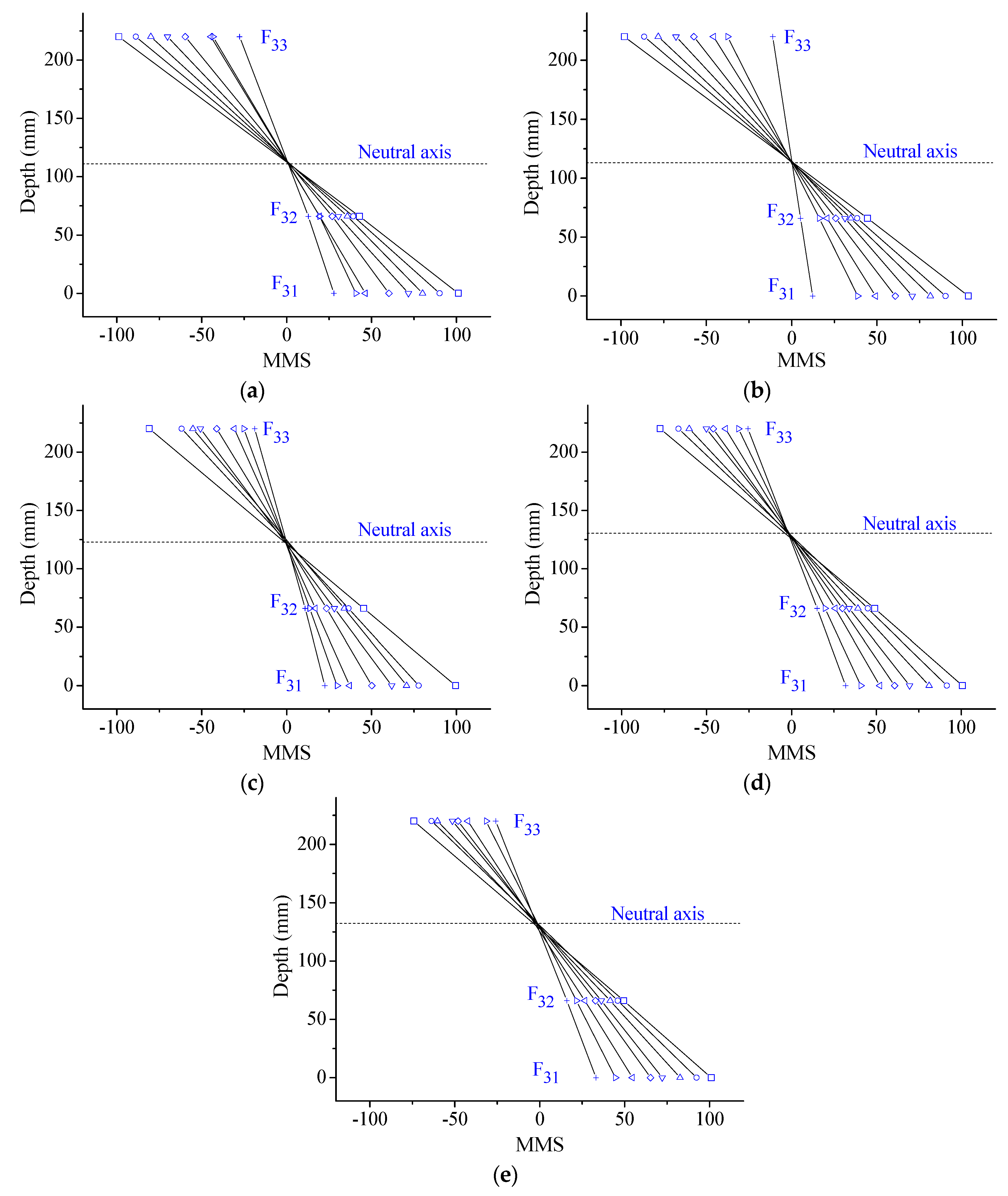
Figure 15.
Modal macro-strain (MMS) distribution along the depth of the element E3 of the steel beam at Case: (a) I; and (b) D8.
Figure 15.
Modal macro-strain (MMS) distribution along the depth of the element E3 of the steel beam at Case: (a) I; and (b) D8.
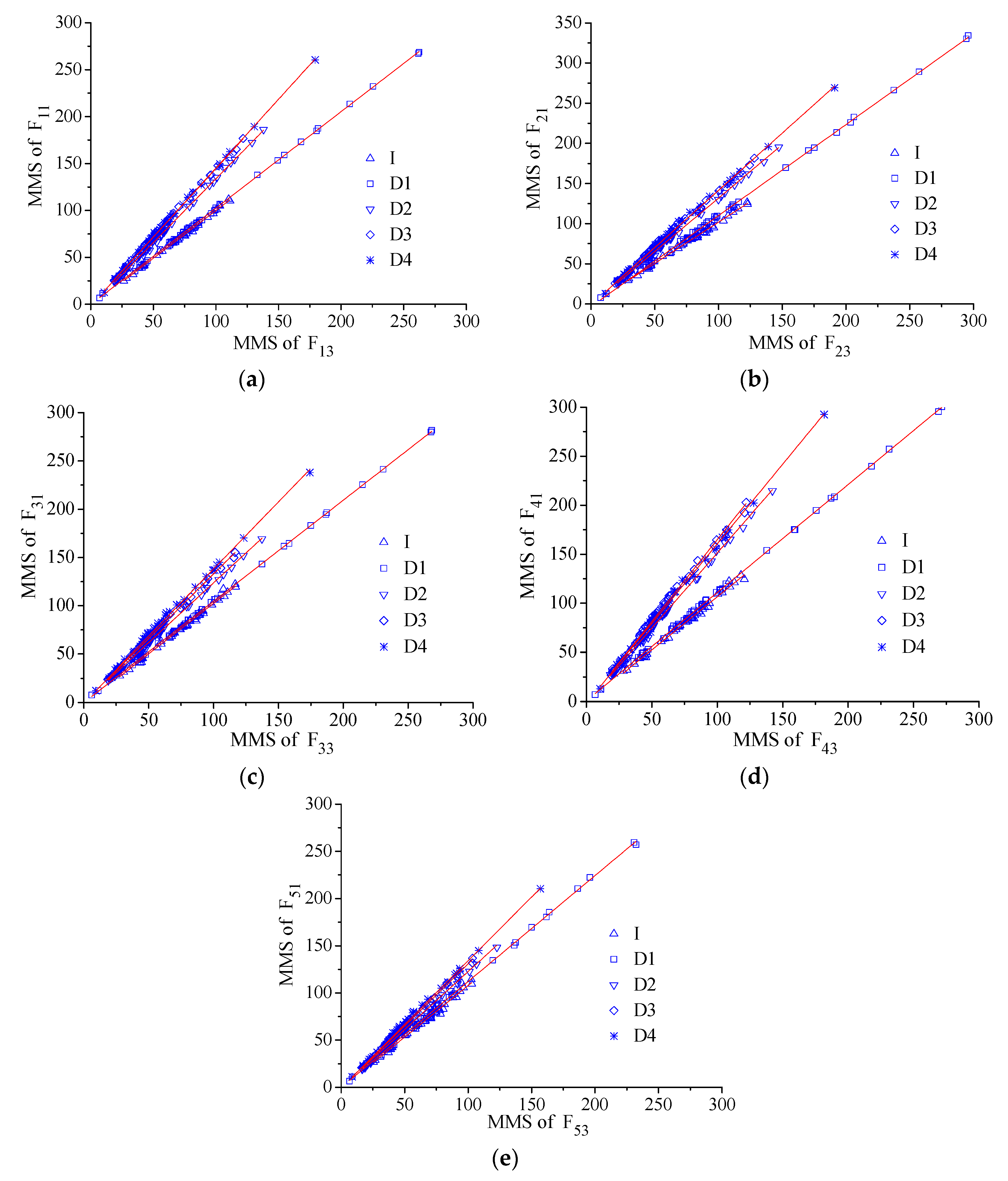
Figure 16.
NAPC extracting of the steel beam from dynamic tests for: (a) E1; and (b) E3.
Figure 16.
NAPC extracting of the steel beam from dynamic tests for: (a) E1; and (b) E3.
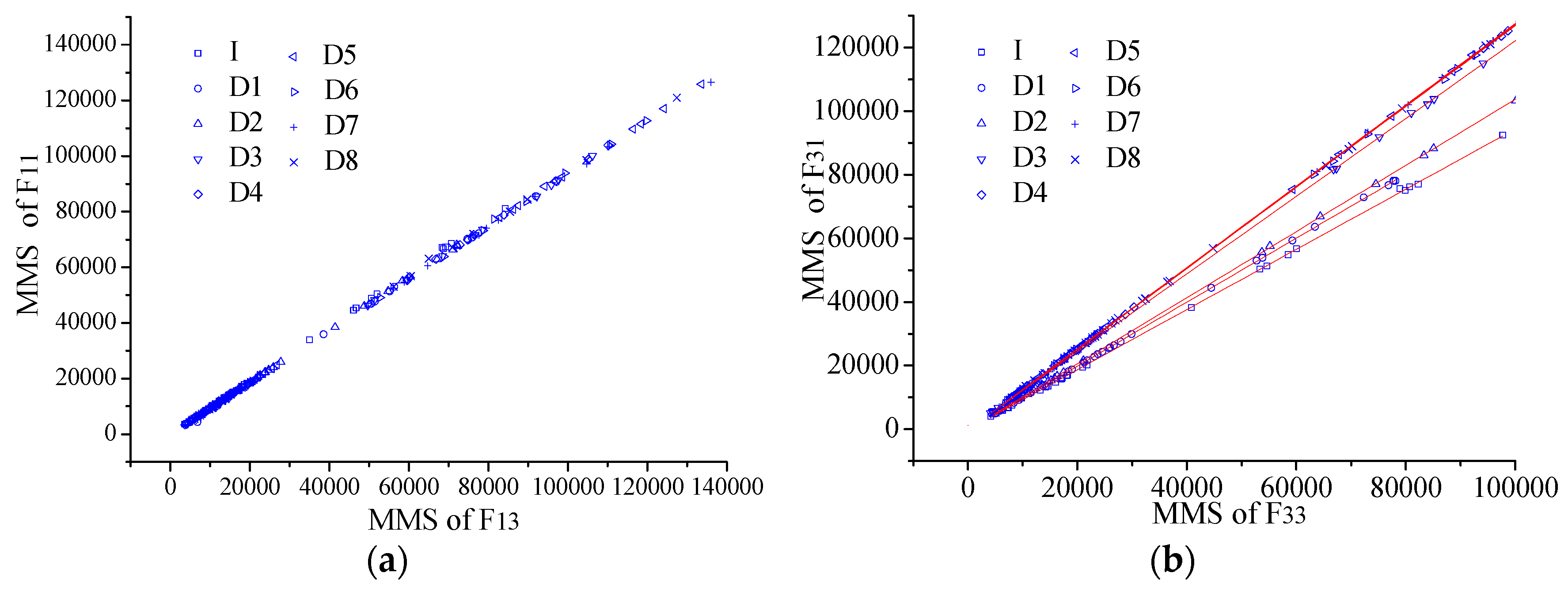
Figure 17.
NAPC results of the steel beam: (a) absolute value; and (b) relative change.
Figure 17.
NAPC results of the steel beam: (a) absolute value; and (b) relative change.
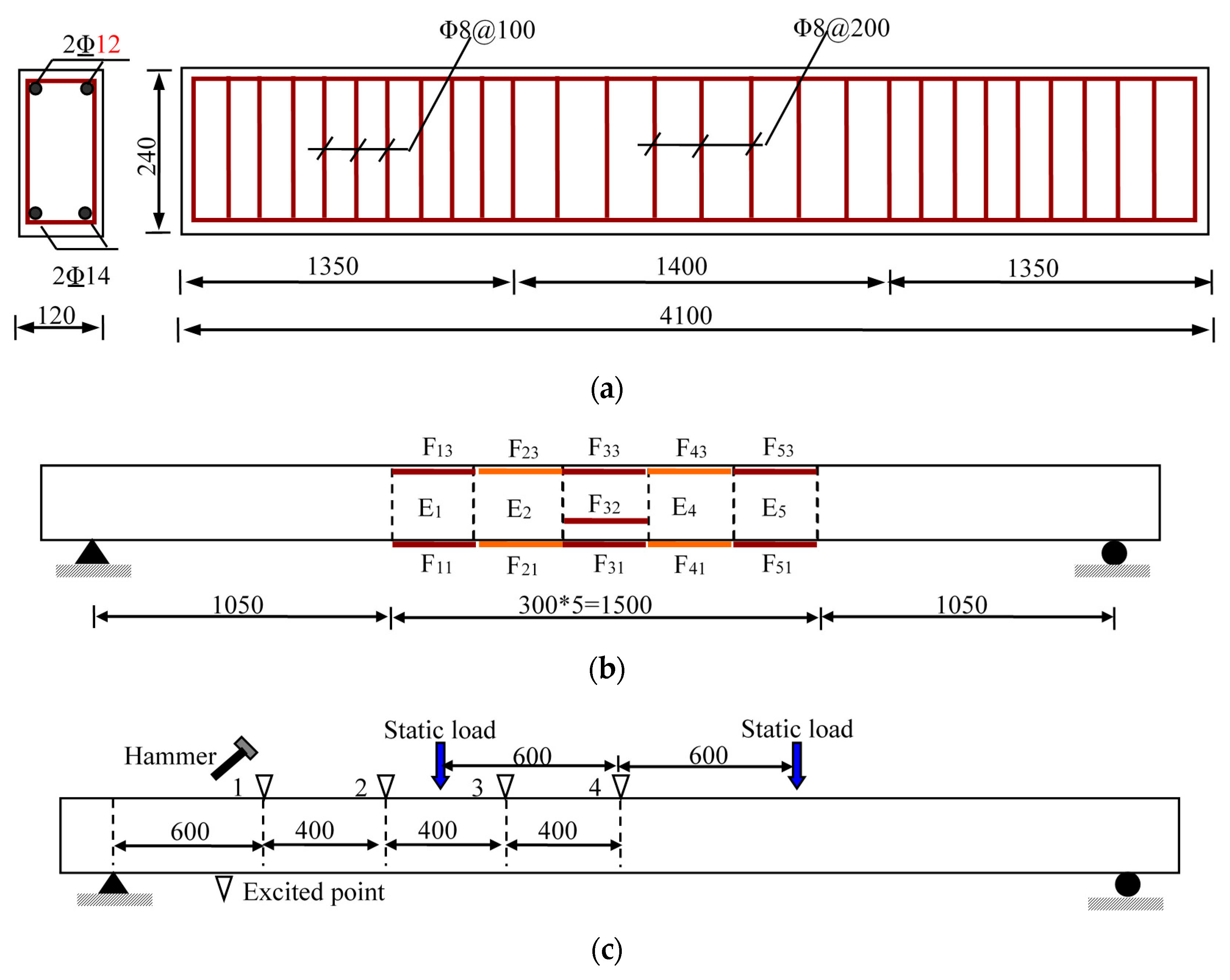
Figure 18.
Experiment setup (Unit: mm): (a) reinforced concrete (RC) beam; (b) long-gauge FBG sensor distribution; and (c) loading positions.
Figure 18.
Experiment setup (Unit: mm): (a) reinforced concrete (RC) beam; (b) long-gauge FBG sensor distribution; and (c) loading positions.
Figure 19.
Experiment field: (a) beam specimen, loader and data logger; and (b) long-gauge FBG sensors.
Figure 19.
Experiment field: (a) beam specimen, loader and data logger; and (b) long-gauge FBG sensors.
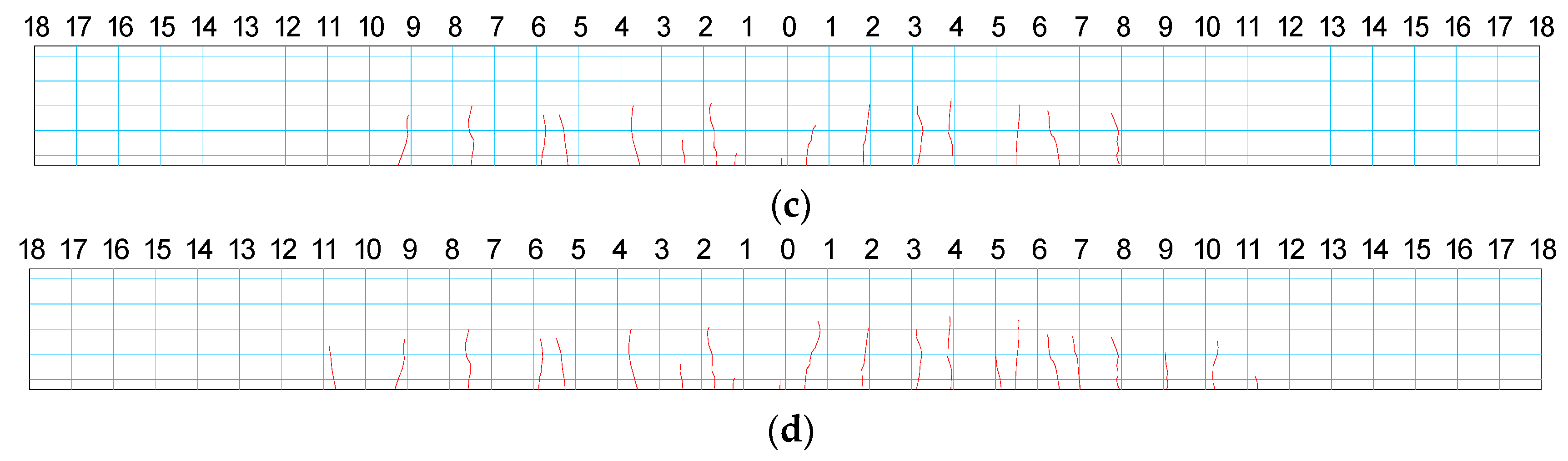
Figure 20.
Concrete crack distribution at Case: (a) D1; (b) D2; (c) D3; and (d) D4.
Figure 20.
Concrete crack distribution at Case: (a) D1; (b) D2; (c) D3; and (d) D4.
Figure 21.
Typical macro-strain results under: (a) single-point excitation; and (b) random excitation.
Figure 21.
Typical macro-strain results under: (a) single-point excitation; and (b) random excitation.
Figure 22.
Typical results of macro-strain based frequency spectrum.
Figure 22.
Typical results of macro-strain based frequency spectrum.
Figure 23.
MMS distribution along the depth of the element E3 at Case: (a) I; (b) D1; (c) D2; (d) D3; and (e) D4.
Figure 23.
MMS distribution along the depth of the element E3 at Case: (a) I; (b) D1; (c) D2; (d) D3; and (e) D4.
Figure 24.
NAPC extracting from dynamic tests for: (a) E1; (b) E2; (c) E3; (d) E4; and (e) E5.
Figure 24.
NAPC extracting from dynamic tests for: (a) E1; (b) E2; (c) E3; (d) E4; and (e) E5.
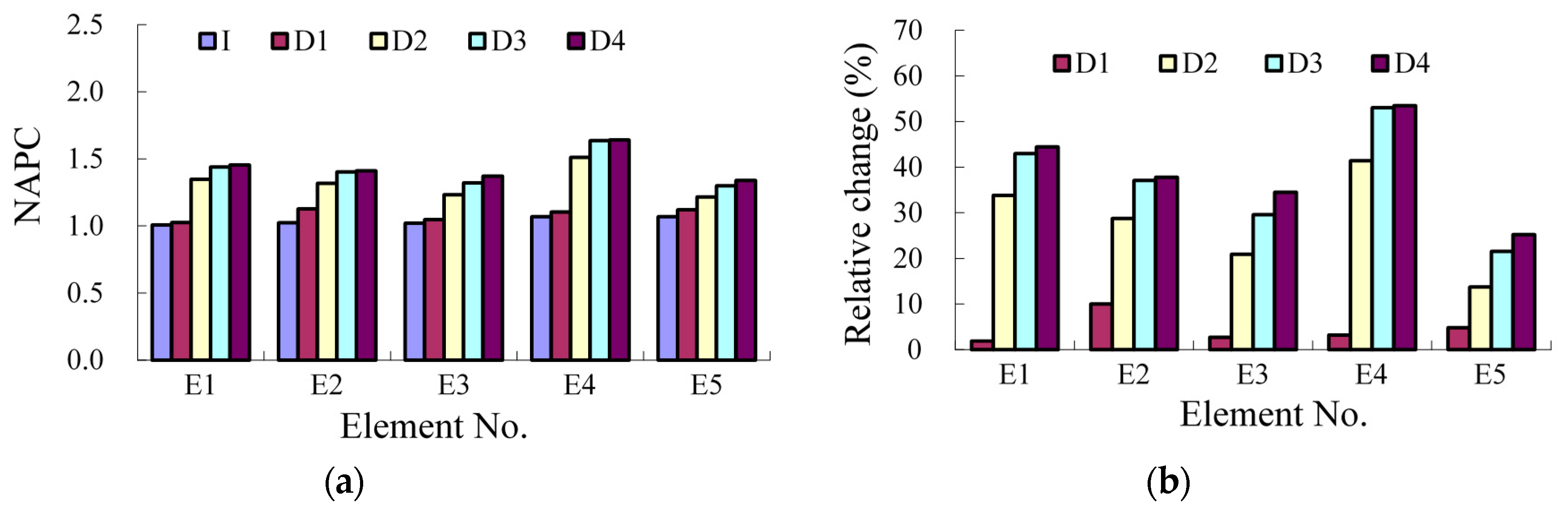
Figure 25.
Results of NAPC: (a) absolute value; and (b) relative change.
Figure 25.
Results of NAPC: (a) absolute value; and (b) relative change.
Figure 26.
Results of neutral axis depth: (a) absolute value; and (b) relative change.
Figure 26.
Results of neutral axis depth: (a) absolute value; and (b) relative change.
Table 1.
The damage case for FE models.
Table 1.
The damage case for FE models.
| Damage Case | I | D1 | D2 | D3 |
|---|
| Stiffness loss (%) | 0 | 30 | 70 | 100 |
Table 2.
The results of neutral axis position coefficient (NAPC).
Table 2.
The results of neutral axis position coefficient (NAPC).
| Damage Case | I | D1 | D2 | D3 |
|---|
| Modal analysis | 1.007 | 1.047 | 1.144 | 1.334 |
| Static analysis | 1.000 | 1.042 | 1.141 | 1.330 |
| Relative deviation (%) | 0.7 | 0.5 | 0.3 | 0.3 |
Table 3.
Comparison results of damage sensitivity (%).
Table 3.
Comparison results of damage sensitivity (%).
| Damage Case | Resonant Frequency (Bending Mode) | Neutral Axis Depth | NAPC | Strain Mode [16] | Curvature Mode [17] |
|---|
| First | Second | Third | Fourth | Fifth |
|---|
| D1 | −0.1 | 0.0 | −0.1 | 0.0 | 0.0 | 1.9 | 4.0 | 4.2 | 2.3 |
| D2 | −0.3 | 0.0 | −0.3 | 0.0 | −0.1 | 6.3 | 13.6 | 15.3 | 8.5 |
| D3 | −0.8 | 0.0 | −0.8 | 0.0 | −0.4 | 13.9 | 32.5 | 39.2 | 22.2 |
Table 4.
Damage cases for the steel beam test.
Table 4.
Damage cases for the steel beam test.
| Damage Case | I | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 |
|---|
| Damage quantity of E3 (%) | 0 | 3 | 5 | 15 | 18 | 18 | 18 | 18 | 18 |
| Damage quantity of E7 (%) | 0 | 0 | 0 | 0 | 0 | 3 | 5 | 15 | 18 |
Table 5.
The results of neutral axis depth with modal analysis (mm).
Table 5.
The results of neutral axis depth with modal analysis (mm).
| Damage Case | I | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 |
|---|
| E1 | 50.0 | 50.2 | 50.2 | 50.2 | 50.3 | 50.3 | 50.1 | 50.4 | 50.3 |
| E2 | 49.5 | 49.7 | 50.0 | 49.8 | 49.8 | 49.7 | 49.6 | 49.9 | 49.8 |
| E3 | 49.9 | 51.5 | 52.3 | 56.3 | 57.4 | 57.4 | 57.3 | 57.4 | 57.4 |
| E4 | 50.0 | 50.2 | 50.3 | 50.3 | 50.7 | 50.8 | 50.5 | 50.8 | 50.7 |
| E5 | 49.7 | 49.8 | 49.8 | 49.7 | 49.8 | 49.8 | 49.8 | 49.8 | 49.8 |
| E6 | 50.1 | 50.3 | 50.5 | 50.3 | 50.4 | 50.2 | 50.2 | 50.5 | 50.3 |
| E7 | 49.7 | 49.8 | 49.7 | 49.7 | 49.8 | 51.5 | 52.1 | 56.6 | 57.4 |
| E8 | 50.6 | 50.8 | 50.7 | 50.8 | 50.9 | 50.8 | 50.9 | 51.5 | 51.5 |
Table 6.
The relative difference compared with static tests (%).
Table 6.
The relative difference compared with static tests (%).
| Damage Case | I | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 |
|---|
| E1 | 0.6 | 0.5 | −0.2 | 0.8 | 0.5 | 1.0 | −1.1 | −0.6 | −0.3 |
| E2 | −0.4 | 0.1 | 0.2 | 0.7 | 0.0 | 0.4 | −1.2 | −0.7 | −0.2 |
| E3 | 0.5 | 0.5 | −0.1 | 1.8 | 1.2 | 1.7 | −0.2 | 0.3 | 0.8 |
| E4 | −0.7 | 0.1 | 0.1 | 0.7 | 0.1 | 0.7 | −1.4 | −0.2 | −0.1 |
| E5 | 1.0 | 1.5 | 1.0 | 2.2 | 1.7 | 2.6 | 0.6 | 0.5 | 1.2 |
| E6 | 0.3 | 1.0 | 1.1 | 1.7 | 1.4 | 1.5 | −0.3 | 0.8 | 0.9 |
| E7 | 0.3 | 1.0 | 0.0 | 1.0 | 0.5 | 1.7 | −0.5 | 0.4 | 0.5 |
| E8 | 1.0 | 1.8 | 1.2 | 2.2 | 1.8 | 2.4 | 0.8 | 1.8 | 1.7 |
Table 7.
The results of NAPC.
Table 7.
The results of NAPC.
| Damage Case | I | D1 | D2 | D3 | D4 |
|---|
| E1 | 1.007 | 1.026 | 1.347 | 1.439 | 1.454 |
| E2 | 1.023 | 1.126 | 1.318 | 1.403 | 1.410 |
| E3 | 1.020 | 1.048 | 1.233 | 1.321 | 1.371 |
| E4 | 1.068 | 1.103 | 1.511 | 1.635 | 1.640 |
| E5 | 1.069 | 1.121 | 1.216 | 1.300 | 1.339 |
Table 8.
The vertical distance between the two sensors (mm).
Table 8.
The vertical distance between the two sensors (mm).
| Element Number | E1 | E2 | E3 | E4 | E5 |
| Distance | 223 | 216 | 220 | 214 | 222 |
Table 9.
The results of neutral axis depth with the proposed method (mm).
Table 9.
The results of neutral axis depth with the proposed method (mm).
| Damage Case | I | D1 | D2 | D3 | D4 |
|---|
| E1 | 112 | 113 | 128 | 132 | 132 |
| E2 | 109 | 114 | 123 | 126 | 126 |
| E3 | 111 | 113 | 121 | 125 | 127 |
| E4 | 111 | 112 | 129 | 133 | 133 |
| E5 | 115 | 117 | 122 | 125 | 127 |
Table 10.
The results of neutral axis depth with the static method (mm).
Table 10.
The results of neutral axis depth with the static method (mm).
| Damage Case | I | D1 | D2 | D3 | D4 |
|---|
| E1 | 111 | 150 | 155 | 156 | 166 |
| E2 | 110 | 145 | 149 | 149 | 161 |
| E3 | 112 | 149 | 152 | 153 | 166 |
| E4 | 112 | 149 | 153 | 153 | 161 |
| E5 | 115 | 149 | 152 | 153 | 160 |
Table 11.
The comparison results with the static method (%).
Table 11.
The comparison results with the static method (%).
| Damage Case | I | D1 | D2 | D3 | D4 |
|---|
| E1 | 1.2 | −24.8 | −17.6 | −15.6 | −20.5 |
| E2 | −1.1 | −21.0 | −17.7 | −15.6 | −21.3 |
| E3 | −0.7 | −24.5 | −20.3 | −18.3 | −23.2 |
| E4 | −2.2 | −24.5 | −16.0 | −13.3 | −17.4 |
| E5 | 1.0 | −21.1 | −20.1 | −18.2 | −20.8 |