Toward Improving Electrocardiogram (ECG) Biometric Verification using Mobile Sensors: A Two-Stage Classifier Approach
Abstract
:1. Introduction
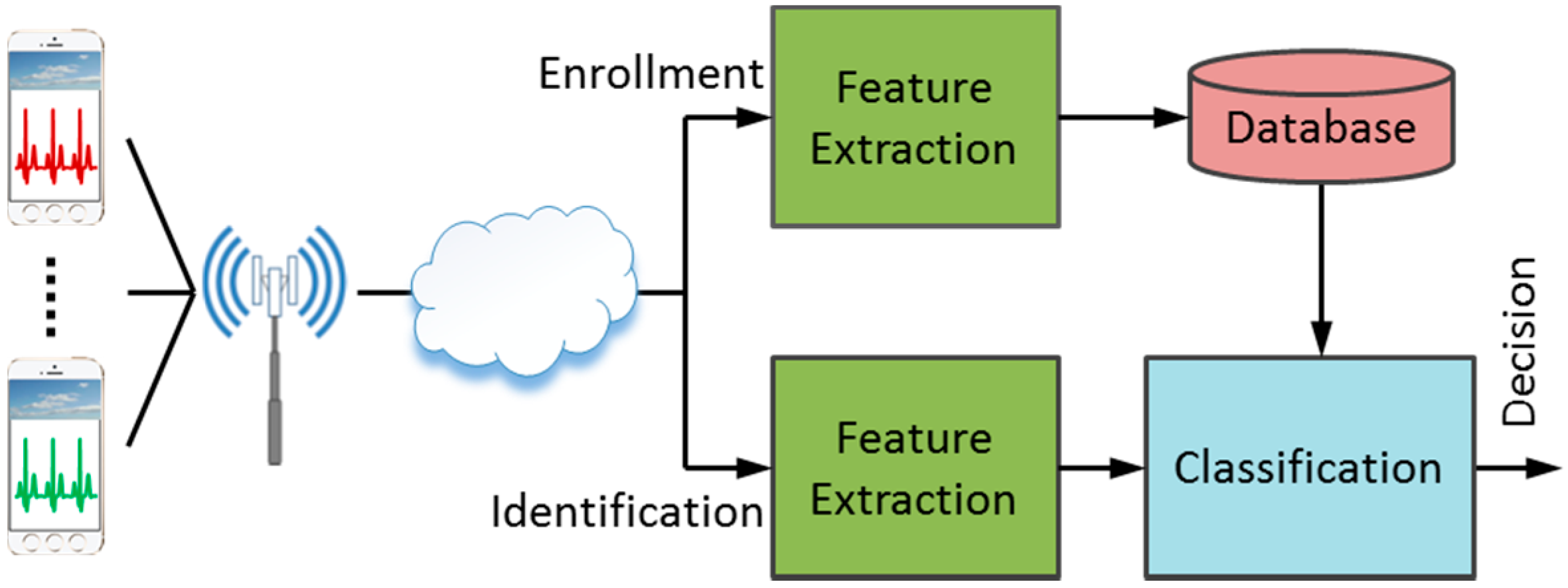
2. System Framework
3. Data Sources
4. Methodology
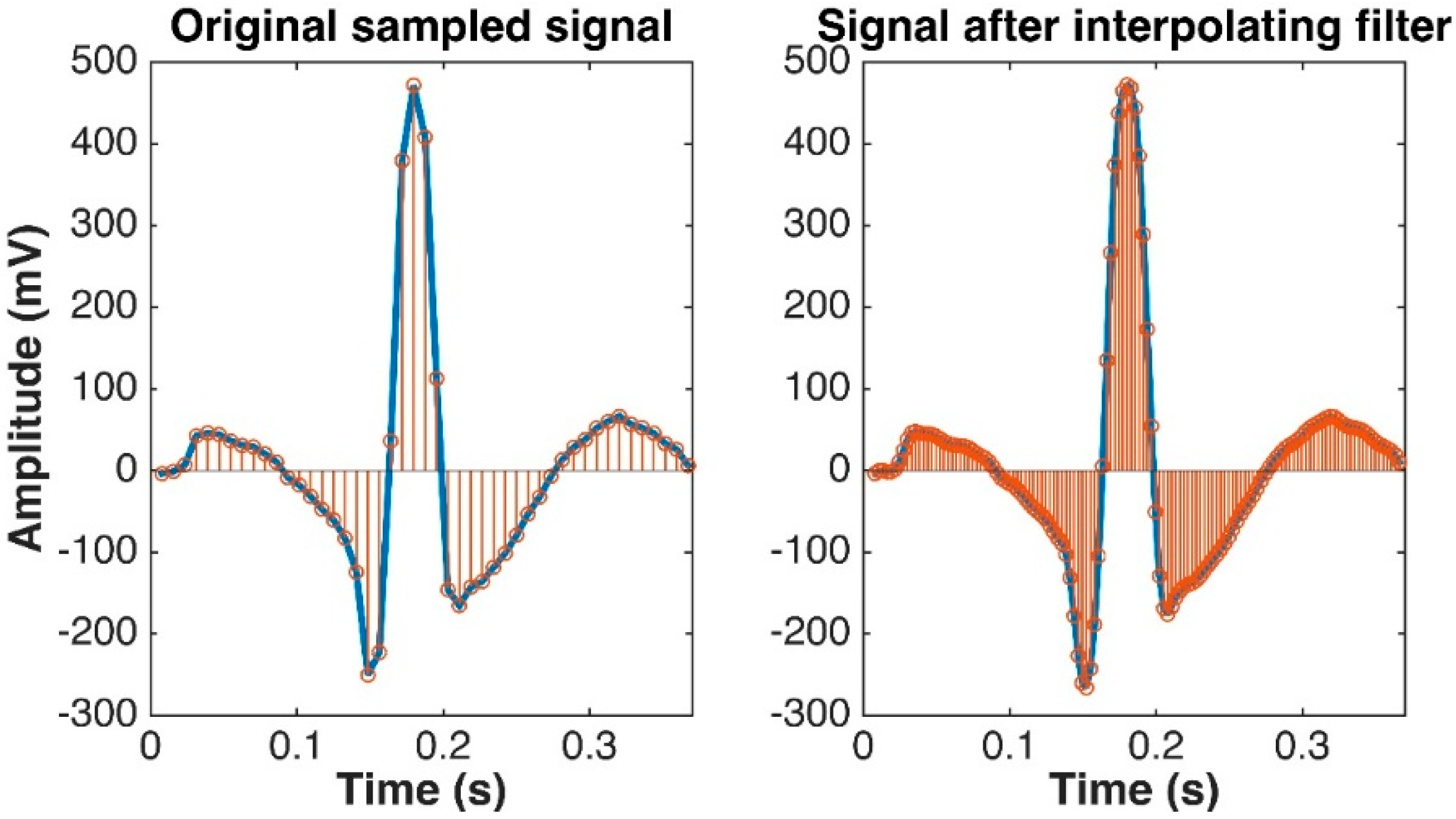
4.1. Data Pre-Processing
4.2. R-Peak Detection
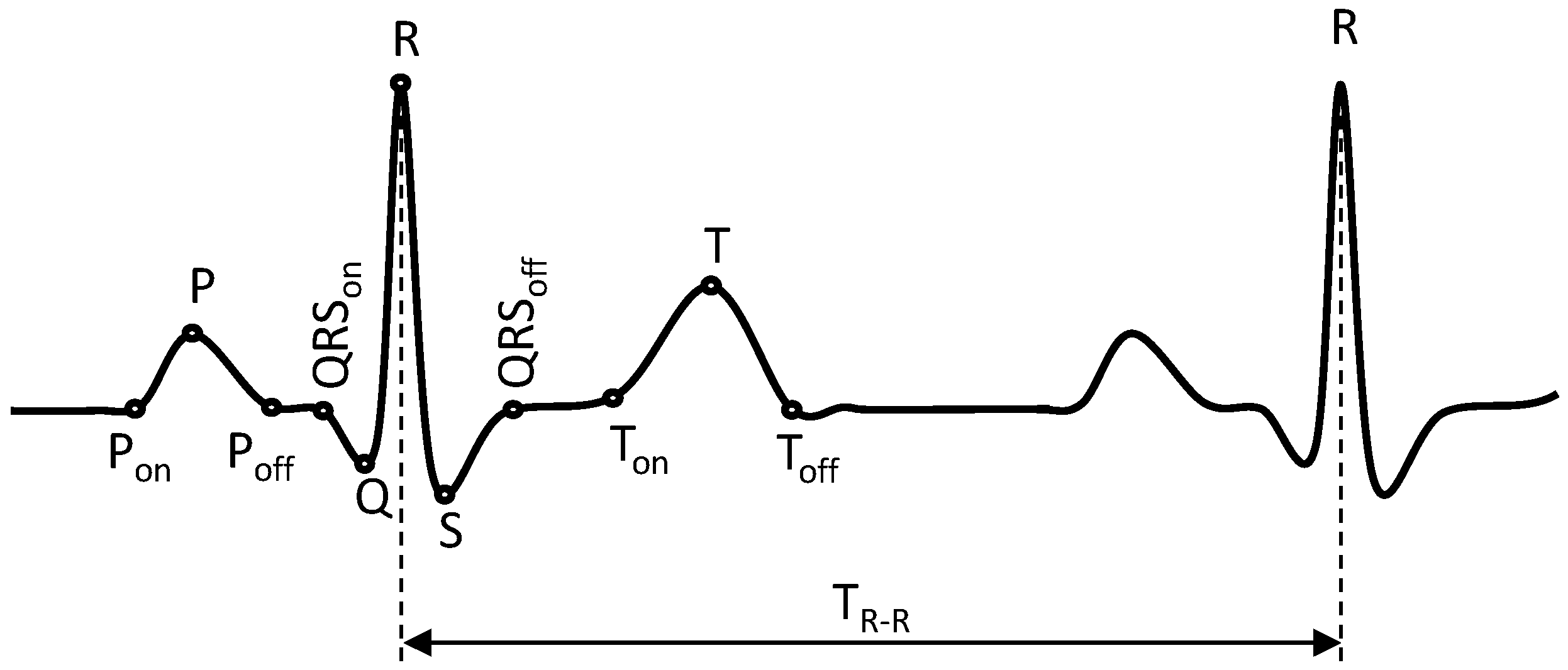
4.3. P-QRS-T Complex Delineation
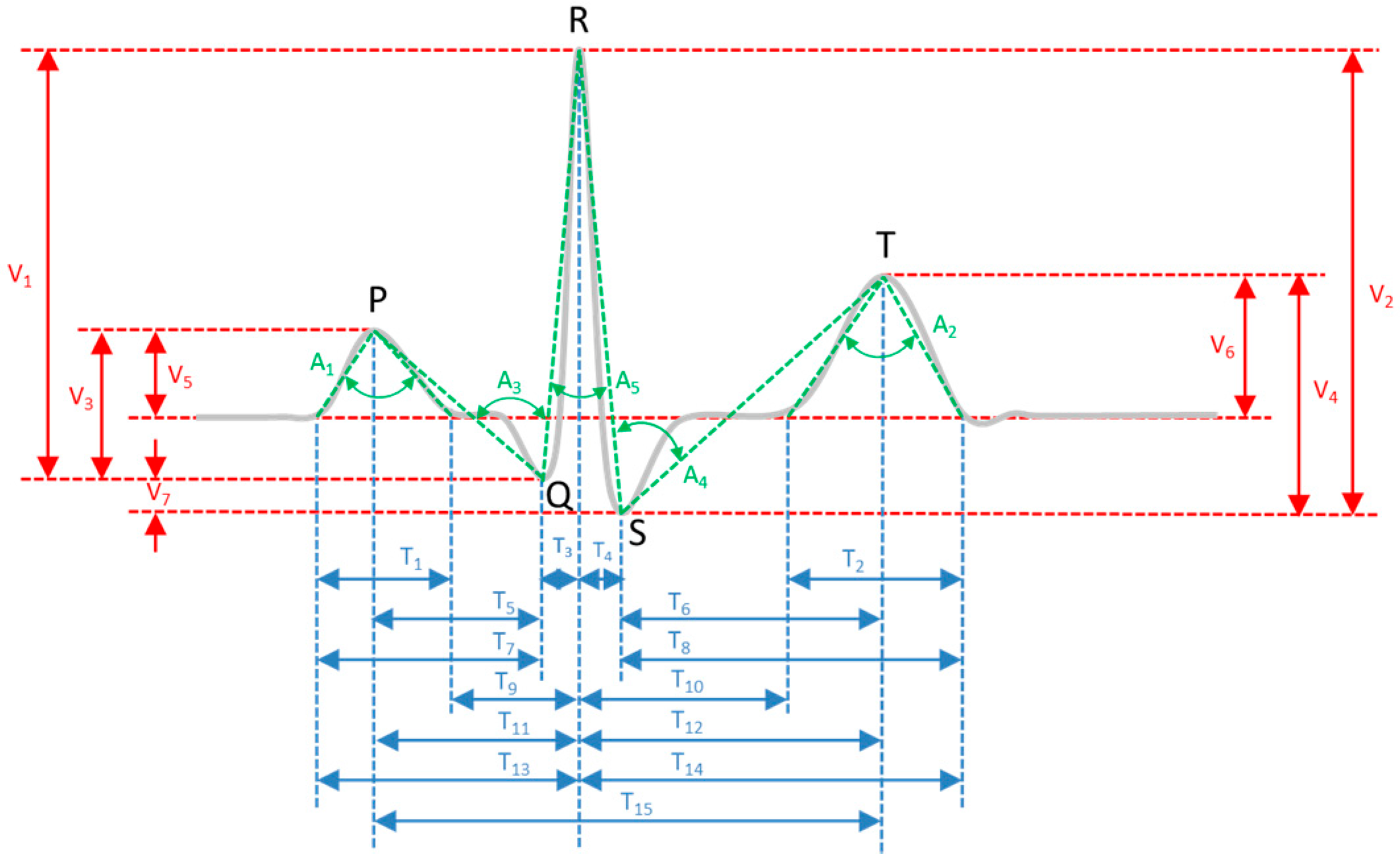
4.4. Fiducial Feature Extraction
4.5. Non-Fiducial Feature Extraction
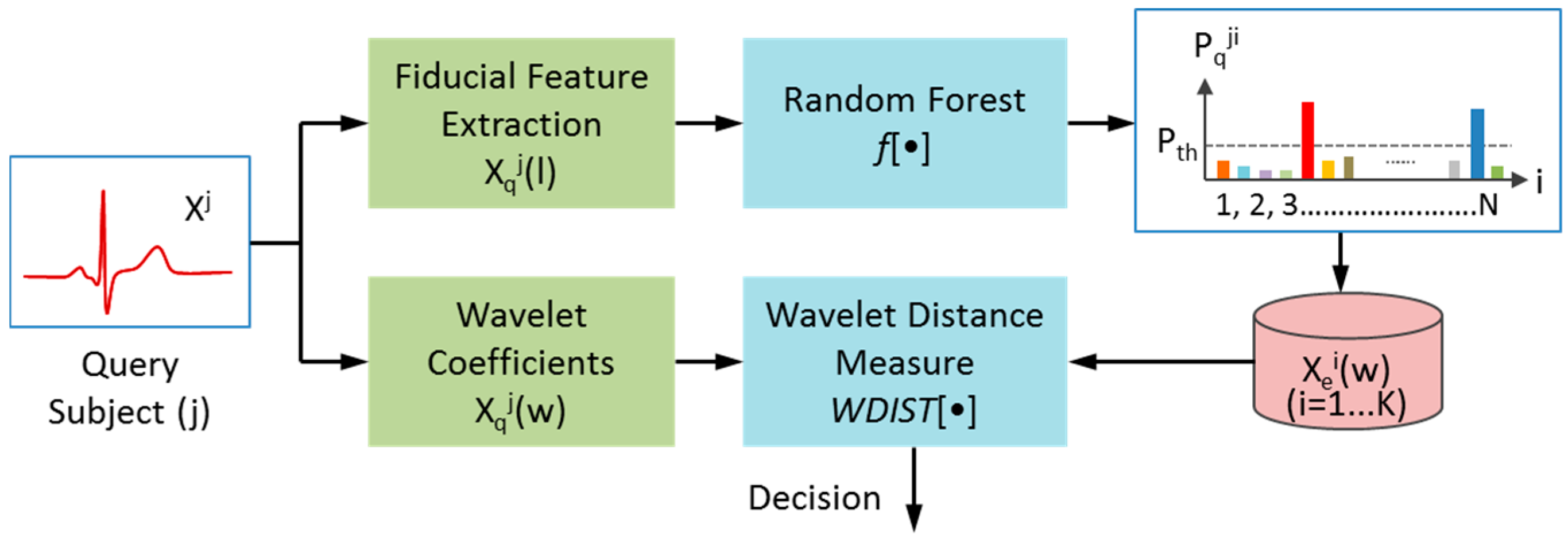
4.6. Two-Stage Subject Verification System
5. Results and Discussion
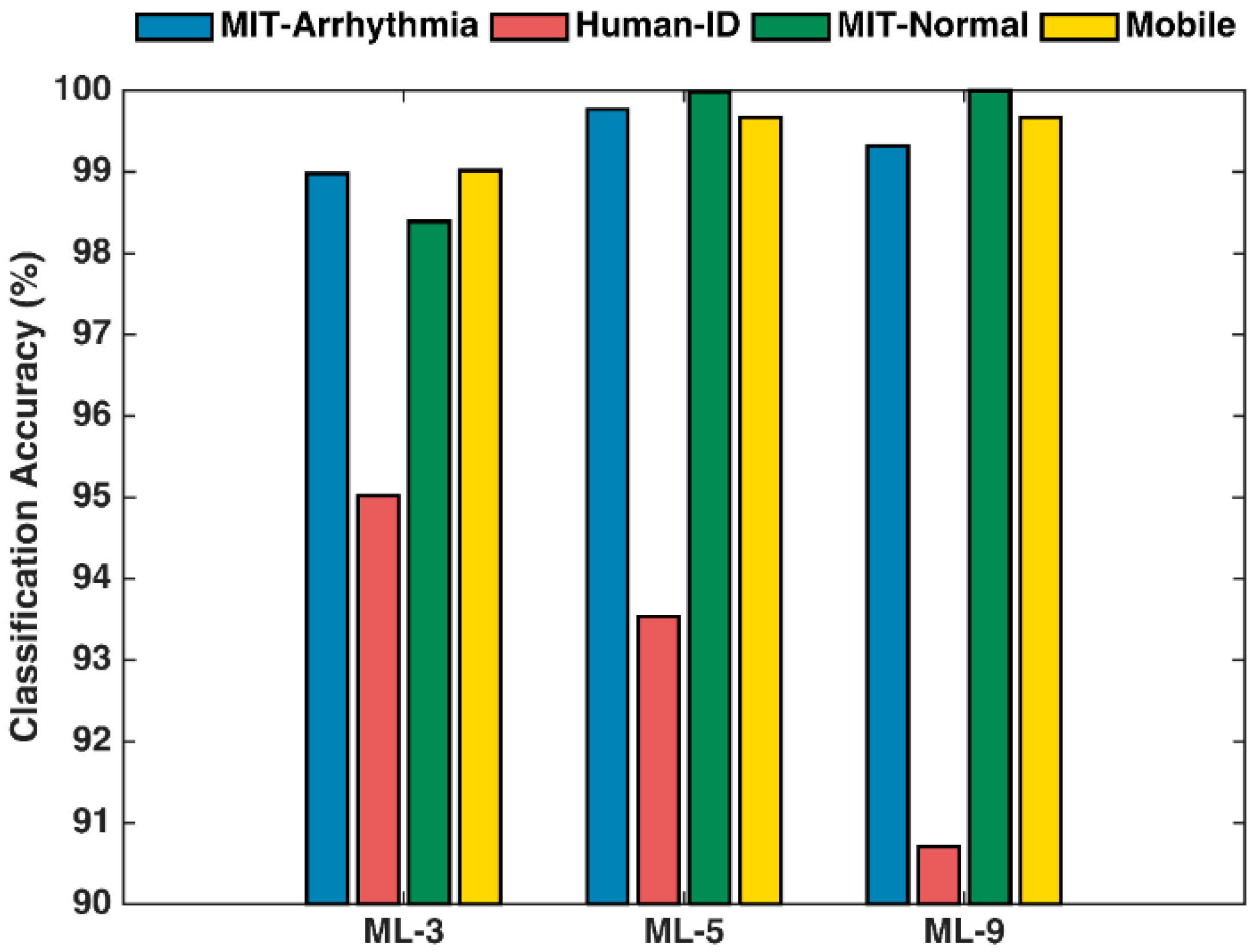
5.1. Single Random Forest Classifier
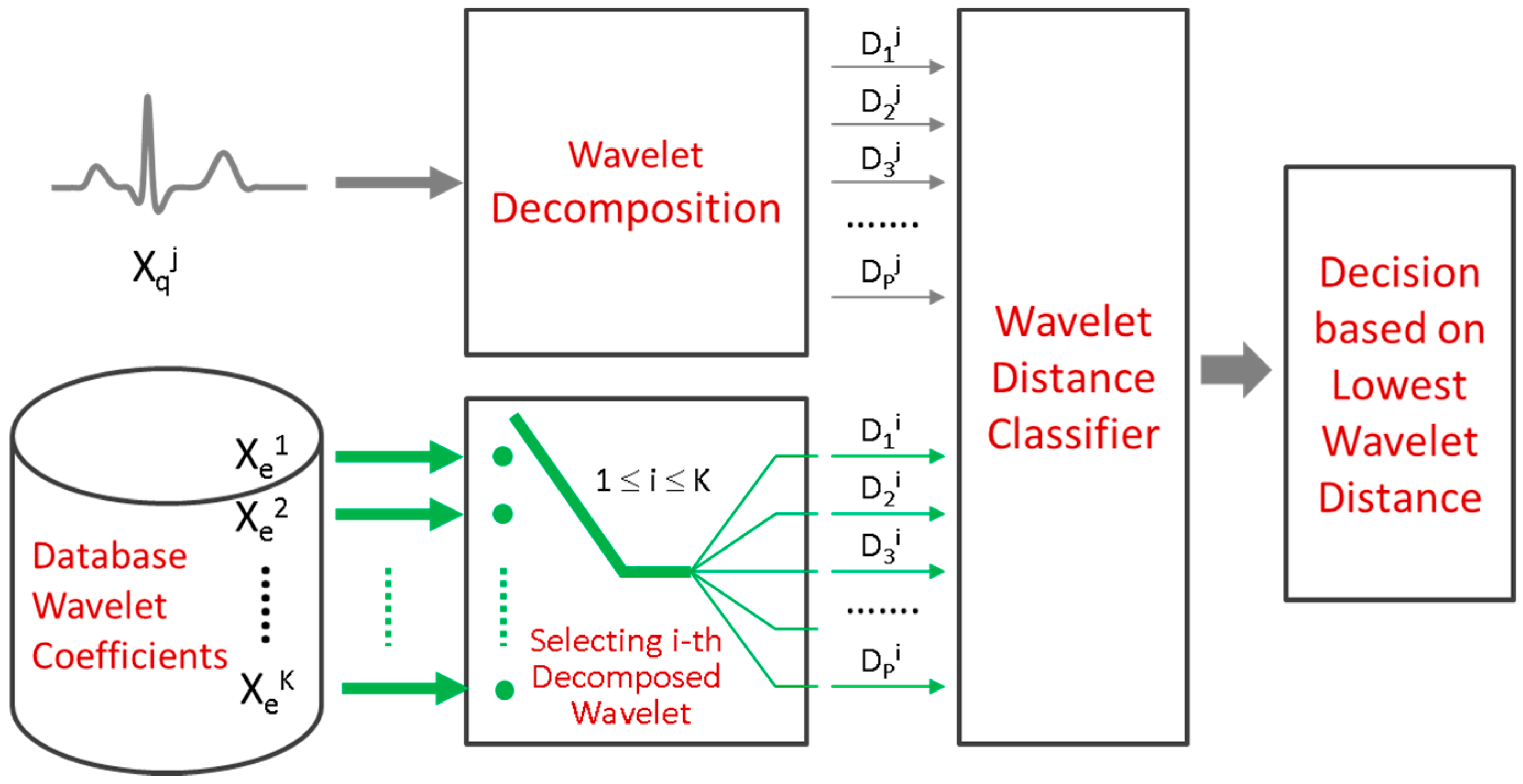
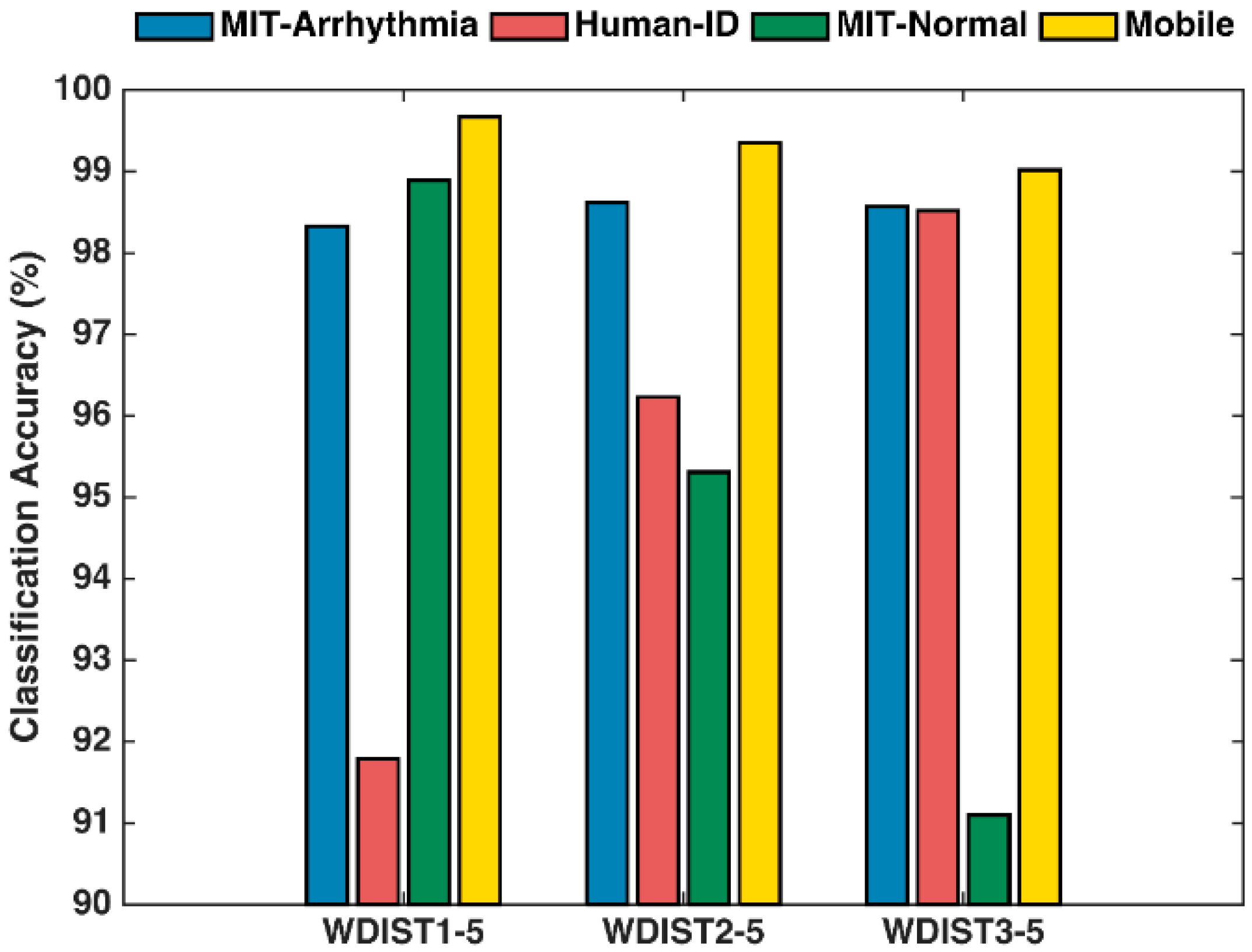
5.2. Single Wavelet Distance Classifier
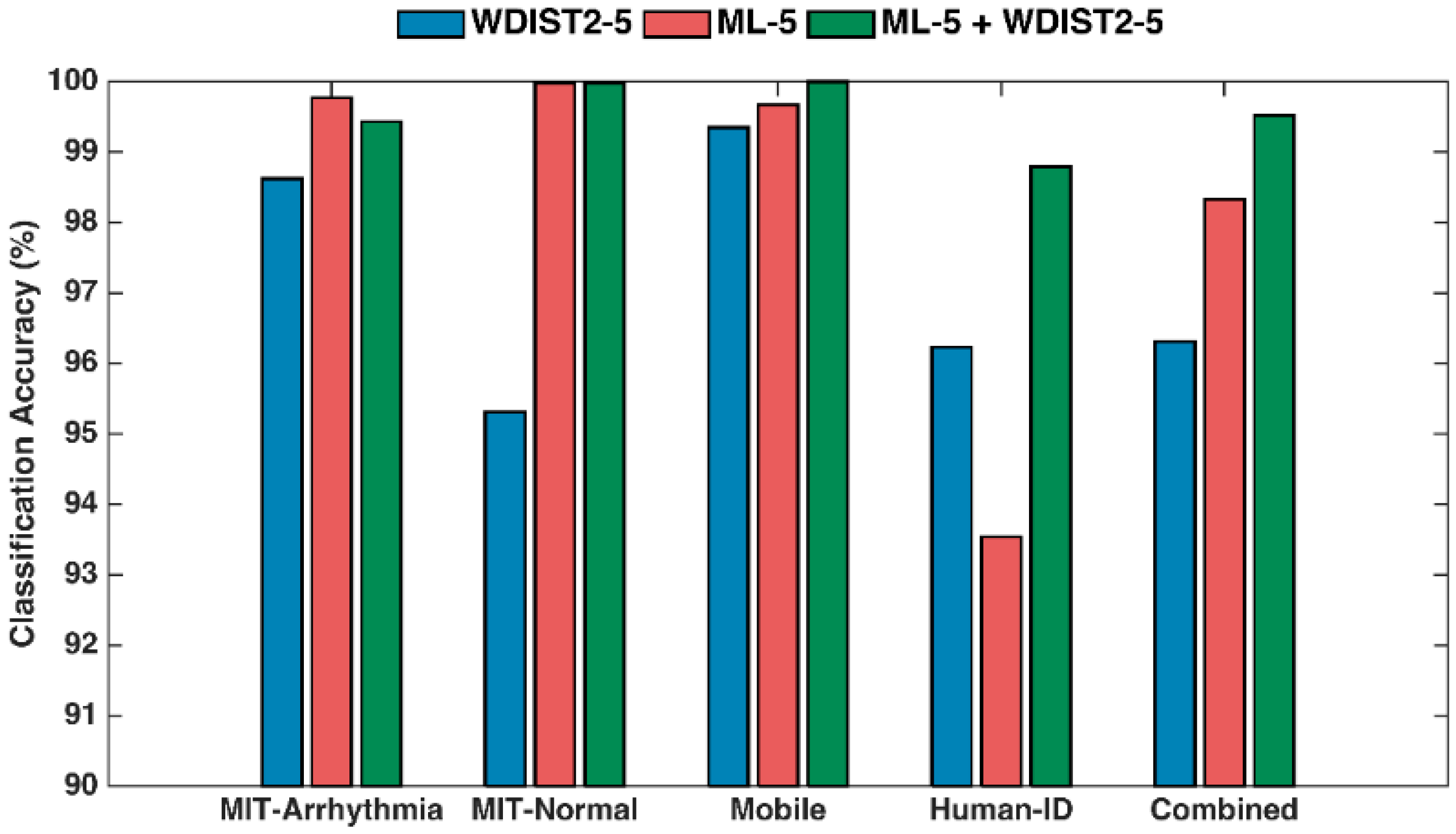
5.3. Two-Stage Classifier
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Patel, S.; Park, H.; Bonato, P.; Chan, L.; Rodgers, M. A review of wearable sensors and systems with application in rehabilitation. J. Neuroeng. Rehabil. 2012, 9, 21. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Wang, Q.; Ren, K.; Lou, W. Privacy-Preserving Public Auditing for Data Storage Security in Cloud Computing. In Proceedings of the INFOCOM, San Diego, CA, USA, 15–19 March 2010; pp. 1–9.
- Boulos, M.N.K.; Wheeler, S.; Tavares, C.; Jones, R. How smartphones are changing the face of mobile and participatory healthcare: An overview, with example from eCAALYX. Biomed. Eng. Online 2011, 10, 24. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Bolle, R.; Pankanti, S. (Eds.) Biometrics: Personal Identification in Networked Society; Springer Science & Business Media: New York, NY, USA, 2006; Volume 479.
- Israel, S.A.; Irvine, J.M.; Cheng, A.; Wiederhold, M.D.; Wiederhold, B.K. ECG to identify individuals. Pattern Recogn. 2005, 38, 133–142. [Google Scholar] [CrossRef]
- Shen, T.W.; Tompkins, W.J.; Hu, Y.H. One-lead ECG for identity verification. In Proceedings of the Second Joint Conference 24th Annual International Conference of the Engineering in Medicine and Biology Society, Annual Fall Meeting of the Biomedical Engineering Society, Houston, TX, USA, 23–26 October 2002; Volume 1, pp. 62–63.
- Biel, L.; Pettersson, O.; Philipson, L.; Wide, P. ECG analysis: A new approach in human identification. IEEE Trans. Instrum. Meas. 2001, 50, 808–812. [Google Scholar] [CrossRef]
- Irvine, J.M.; Wiederhold, B.K.; Gavshon, L.W.; Israel, S.A.; McGehee, S.B.; Meyer, R.; Wiederhold, M.D. Heart rate variability: A new biometric for human identification. In Proceedings of the International Conference on Artificial Intelligence (IC-AI’01), Las Vegas, NV, USA, 25–28 June 2001; 2001; pp. 1106–1111. [Google Scholar]
- Kyoso, M.; Uchiyama, A. Development of an ECG identification system. In Proceedings of the 23rd Annual International Conference of Engineering in Medicine and Biology Society, Istanbul, Turkey, 25–28 October 2001; Volume 4, pp. 3721–3723.
- Chan, A.D.; Hamdy, M.M.; Badre, A.; Badee, V. Wavelet distance measure for person identification using electrocardiograms. IEEE Trans. Instrum. Meas. 2008, 57, 248–253. [Google Scholar] [CrossRef]
- Shen, T.W.D.; Tompkins, W.J.; Hu, Y.H. Implementation of a one-lead ECG human identification system on a normal population. J. Eng. Comput. Innov. 2010, 2, 12–21. [Google Scholar]
- Wübbeler, G.; Stavridis, M.; Kreiseler, D.; Bousseljot, R.D.; Elster, C. Verification of humans using the electrocardiogram. Pattern Recogn. Lett. 2007, 28, 1172–1175. [Google Scholar] [CrossRef]
- Agrafioti, F.; Hatzinakos, D. Fusion of ECG sources for human identification. In Proceedings of the 2008 ISCCSP 2008 3rd International Symposium on Communications, Control and Signal Processing, St. Julian’s, Malta, 12–14 March 2008; pp. 1542–1547.
- Singh, Y.N.; Gupta, P. Biometrics method for human identification using electrocardiogram. In Proceedings of the International Conference on Biometrics, Alghero, Italy, 2–5 June 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1270–1279. [Google Scholar]
- Agrafioti, F.; Hatzinakos, D. ECG based recognition using second order statistics. In Proceedings of the CNSR 2008 6th Annual Communication Networks and Services Research Conference, Halifax, NS, Canada, 5–8 May 2008; pp. 82–87.
- Irvine, J.M.; Israel, S.A. A sequential procedure for individual identity verification using ECG. EURASIP J. Adv. Signal Process. 2009, 1, 1–13. [Google Scholar] [CrossRef]
- Ince, T.; Kiranyaz, S.; Gabbouj, M. A generic and robust system for automated patient-specific classification of ECG signals. IEEE Trans. Biomed. Eng. 2009, 56, 1415–1426. [Google Scholar] [CrossRef] [PubMed]
- Martis, R.J.; Acharya, U.R.; Min, L.C. ECG beat classification using PCA, LDA, ICA and discrete wavelet transform. Biomed. Signal Process. Control 2013, 8, 437–448. [Google Scholar] [CrossRef]
- Lin, C.H. Frequency-domain features for ECG beat discrimination using grey relational analysis-based classifier. Comput. Math. Appl. 2008, 55, 680–690. [Google Scholar] [CrossRef]
- Daamouche, A.; Hamami, L.; Alajlan, N.; Melgani, F. A wavelet optimization approach for ECG signal classification. Biomed. Signal Process. Control 2012, 7, 342–349. [Google Scholar] [CrossRef]
- Saini, I.; Singh, D.; Khosla, A. QRS detection using K-Nearest Neighbor algorithm (KNN) and evaluation on standard ECG databases. J. Adv. Res. 2013, 4, 331–344. [Google Scholar] [CrossRef] [PubMed]
- Christov, I.; Gómez-Herrero, G.; Krasteva, V.; Jekova, I.; Gotchev, A.; Egiazarian, K. Comparative study of morphological and time-frequency ECG descriptors for heartbeat classification. Med. Eng. Phys. 2006, 28, 876–887. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Yai, J. A neural network to identify human subjects with electrocardiogram signals. In Proceedings of the World Congress on Engineering and Computer Science, San Francisco, CA, USA, 22–24 October 2008.
- Li, M.; Narayanan, S. Robust ECG biometric by fusing temporal and cepstral information. In Proceedings of the 2010 20th International Conference on Pattern Recognition (ICPR), Istanbul, Turkey, 23–26 August 2010; pp. 1326–1329.
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. Physiobank, physiotoolkit, and physionet components of a new research resource for complex physiologic signals. Circulation 2000, 101, 215–220. [Google Scholar] [CrossRef]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH arrhythmia database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Martínez, J.P.; Almeida, R.; Olmos, S.; Rocha, A.P.; Laguna, P. A wavelet-based ECG delineator: Evaluation on standard databases. IEEE Trans. Biomed. Eng. 2004, 51, 570–581. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.H.; Palreddy, S.; Tompkins, W.J. A patient-adaptable ECG beat classifier using a mixture of experts approach. IEEE Trans. Biomed. Eng. 1997, 44, 891–900. [Google Scholar] [PubMed]
- Maglaveras, N.; Stamkopoulos, T.; Diamantaras, K.; Pappas, C.; Strintzis, M. ECG pattern recognition and classification using non-linear transformations and neural networks: A review. Int. J. Med. Inform. 1998, 52, 191–208. [Google Scholar] [CrossRef]
- Prasad, G.K.; Sahambi, J.S. Classification of ECG arrhythmias using multi-resolution analysis and neural networks. In Proceedings of the TENCON 2003 Conference on Convergent Technologies for the Asia-Pacific Region, Bangalore, India, 15–17 October 2003; Volume 1, pp. 227–231.
- De Chazal, P.; O’Dwyer, M.; Reilly, R.B. Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans. Biomed. Eng. 2004, 51, 1196–1206. [Google Scholar] [CrossRef] [PubMed]
- Salahuddin, L.; Kim, D. Detection of acute stress by heart rate variability (HRV) using a prototype mobile ECG sensor. In Proceedings of the International Conference on Hybrid Information Technology, Cheju Island, Korea, 9–11 November 2006; pp. 453–459.
- Wang, Y.; Plataniotis, K.; Hatzinakos, D. Integrating Analytic and Appearance Attributes for Human Identification from ECG signals. In Proceedings of the IEEE Biometrics Symposium 2006, Baltimore, MD, USA, 19–21 September 2006.
- Odinaka, I.; Lai, P.H.; Kaplan, A.D.; O’Sullivan, J.A.; Sirevaag, E.J.; Rohrbaugh, J.W. ECG biometric recognition: A comparative analysis. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1812–1824. [Google Scholar] [CrossRef]
- Kailanto, H.; Hyvarinen, E.; Hyttinen, J. Mobile ECG measurement and analysis system using mobile phone as the base station. In Proceedings of the 2008 Second International Conference on Pervasive Computing Technologies for Healthcare, Tampere, Finland, 30 January–1 February 2008; pp. 12–14.
- Ottenbacher, J.; Kirst, M.; Jatoba, L.; Huflejt, M.; Grossmann, U.; Stork, W. Reliable motion artifact detection for ECG monitoring systems with dry electrodes. In Proceedings of the 2008 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–24 August 2008; pp. 1695–1698.
- Szczepański, A.; Saeed, K. A mobile device system for early warning of ECG anomalies. Sensors 2014, 14, 11031–11044. [Google Scholar] [CrossRef] [PubMed]
- Sufi, F.; Khalil, I.; Habib, I. Polynomial distance measurement for ECG based biometric authentication. Secur. Commun. Netw. 2010, 3, 303–319. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, X.; Liu, X.; Dong, J. A framework for ECG morphology features recognition. In Proceedings of the 2010 IEEE 23rd International Symposium on Computer-Based Medical Systems (CBMS), Perth, Australia, 12–15 October 2010; pp. 85–91.
- Chernenko, S. ECG Processing-R-Peaks Detection, Librow TM. 2012. Available online: www.librow.com (accessed on 14 January 2016).
- Pan, J.; Tompkins, W.J. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 3, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Vandenberk, B.; Vandael, E.; Robyns, T.; Vandenberghe, J.; Garweg, C.; Foulon, V.; Willems, R. Which QT Correction Formulae to Use for QT Monitoring? J. Am. Heart Assoc. 2016, 5, e003264. [Google Scholar] [CrossRef] [PubMed]
- Nyquist, H. Certain topics in telegraph transmission theory. Proc. IEEE 2002, 90, 280–305. [Google Scholar] [CrossRef]
- Fatemian, S.Z.; Hatzinakos, D. A new ECG feature extractor for biometric recognition. In Proceedings of the 16th International Conference on Digital Signal Processing, Santorini, Greece, 5–7 July 2009; pp. 1–6.
- Zokaee, S.; Faez, K. Human Identification Based on Electrocardiogram and Palmprint. Int. J. Electr. Comput. Eng. 2012, 2, 261–266. [Google Scholar]
- Sasikala, P.; Wahidabanu, R.S.D. Identification of individuals using electrocardiogram. Int. J. Comput. Sci. Netw. Secur. 2010, 10, 147–153. [Google Scholar]
- Zeng, F.; Tseng, K.K.; Huang, H.N.; Tu, S.Y.; Pan, J.S. A new statistical-based algorithm for ECG identification. In Proceedings of the Eighth International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP), Piraeus-Athens, Greece, 18–20 July 2012; pp. 301–304.




| Data Sources | Subject Type | Subject Quantity | Number of Recordings | Sampling Rate |
|---|---|---|---|---|
| Mobile Phone | Healthy | 30 | Single | 400 Hz |
| PhysioNet Human-ID | Age between 13 and 75 | 89 | 2–20 times over 6 months | 500 Hz |
| MIT-BIH | Arrhythmia | 47 | Single | 360 Hz |
| MIT-BIH | Normal sinus rhythm | 18 | Single | 128 Hz |
| Mix of above | Mix of above | 184 | Mix of above | 360 Hz |
| Method | Fiducial Points | Temporal | Amplitude | Angle |
|---|---|---|---|---|
| ML-9 | P, Q, R, S, T, Pon, Poff, Ton, Toff | T1 to T15 | V1, V2, V3, V4, V5, V6, V7 | A1 to A6 |
| ML-5 | P, Q, R, S, T | T3 to T6, T11, T12, T15 | V1, V2, V3, V4, V7 | A3 to A5 |
| ML-3 | Q, R, S | T3, T4 | V1, V2, V7 | A5 |
| Decomposition Level (p = 1 … 5) | Frequency Bandwidth Fp (Hz) | Number of Wavelet Coefficients |
|---|---|---|
| D1 | 90 to 180 | 144 |
| D2 | 45 to 90 | 72 |
| D3 | 22.5 to 45 | 36 |
| D4 | 11.25 to 22.5 | 18 |
| D5 | 6.75 to 11.25 | 9 |
| A5 | 0–6.75 | 9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, R.; Perkowski, M. Toward Improving Electrocardiogram (ECG) Biometric Verification using Mobile Sensors: A Two-Stage Classifier Approach. Sensors 2017, 17, 410. https://doi.org/10.3390/s17020410
Tan R, Perkowski M. Toward Improving Electrocardiogram (ECG) Biometric Verification using Mobile Sensors: A Two-Stage Classifier Approach. Sensors. 2017; 17(2):410. https://doi.org/10.3390/s17020410
Chicago/Turabian StyleTan, Robin, and Marek Perkowski. 2017. "Toward Improving Electrocardiogram (ECG) Biometric Verification using Mobile Sensors: A Two-Stage Classifier Approach" Sensors 17, no. 2: 410. https://doi.org/10.3390/s17020410
APA StyleTan, R., & Perkowski, M. (2017). Toward Improving Electrocardiogram (ECG) Biometric Verification using Mobile Sensors: A Two-Stage Classifier Approach. Sensors, 17(2), 410. https://doi.org/10.3390/s17020410






