Quasi-Static Calibration Method of a High-g Accelerometer
Abstract
:1. Introduction
2. Principle of Quasi-Static Calibration
2.1. Principle of Quasi-Static Calibration of High-g Accelerometer
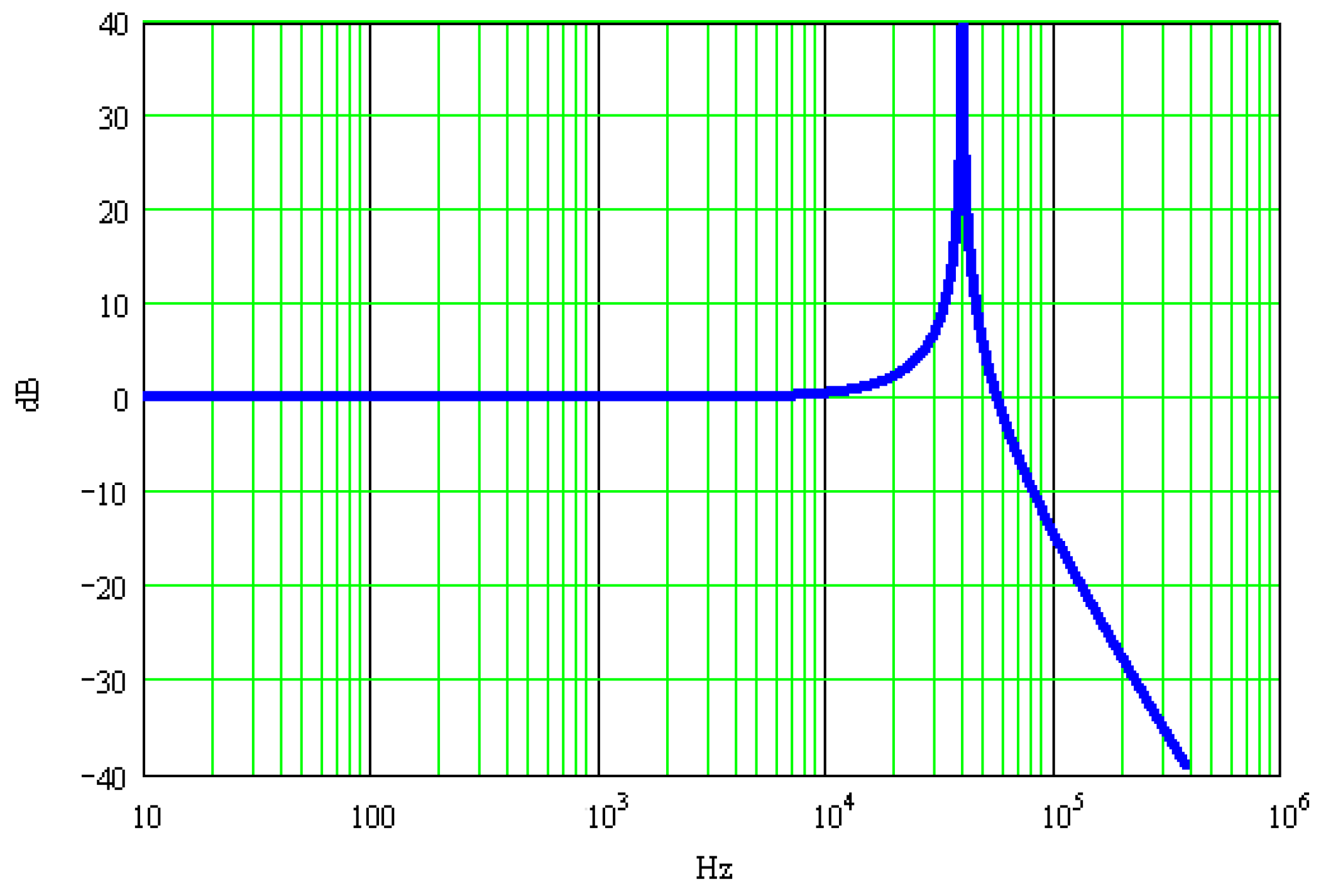
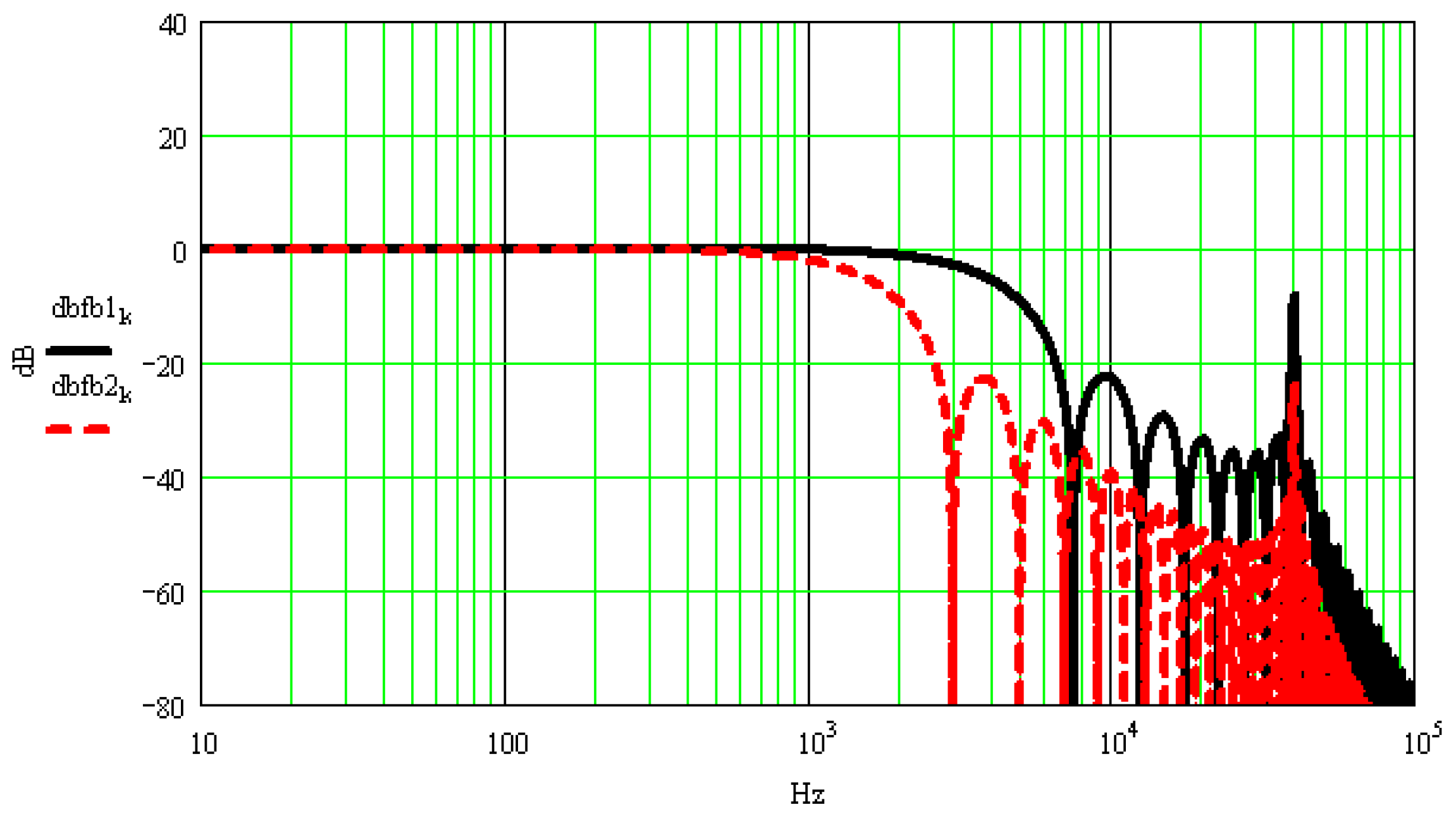
2.2. Minimum Pulse Width of Excitation Signal Required for Quasi-Static Calibration
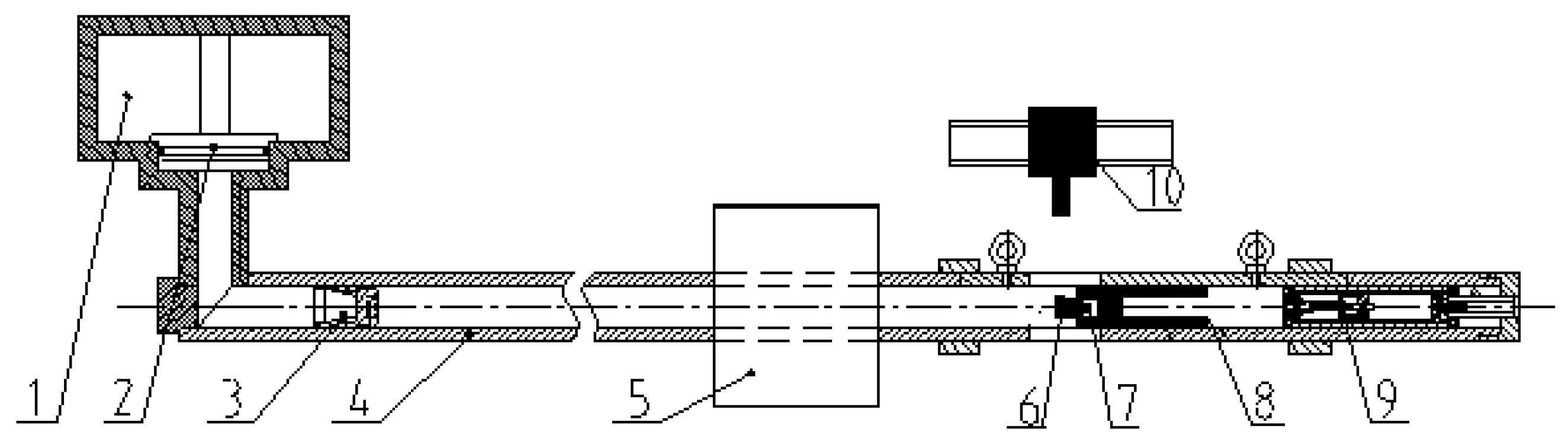
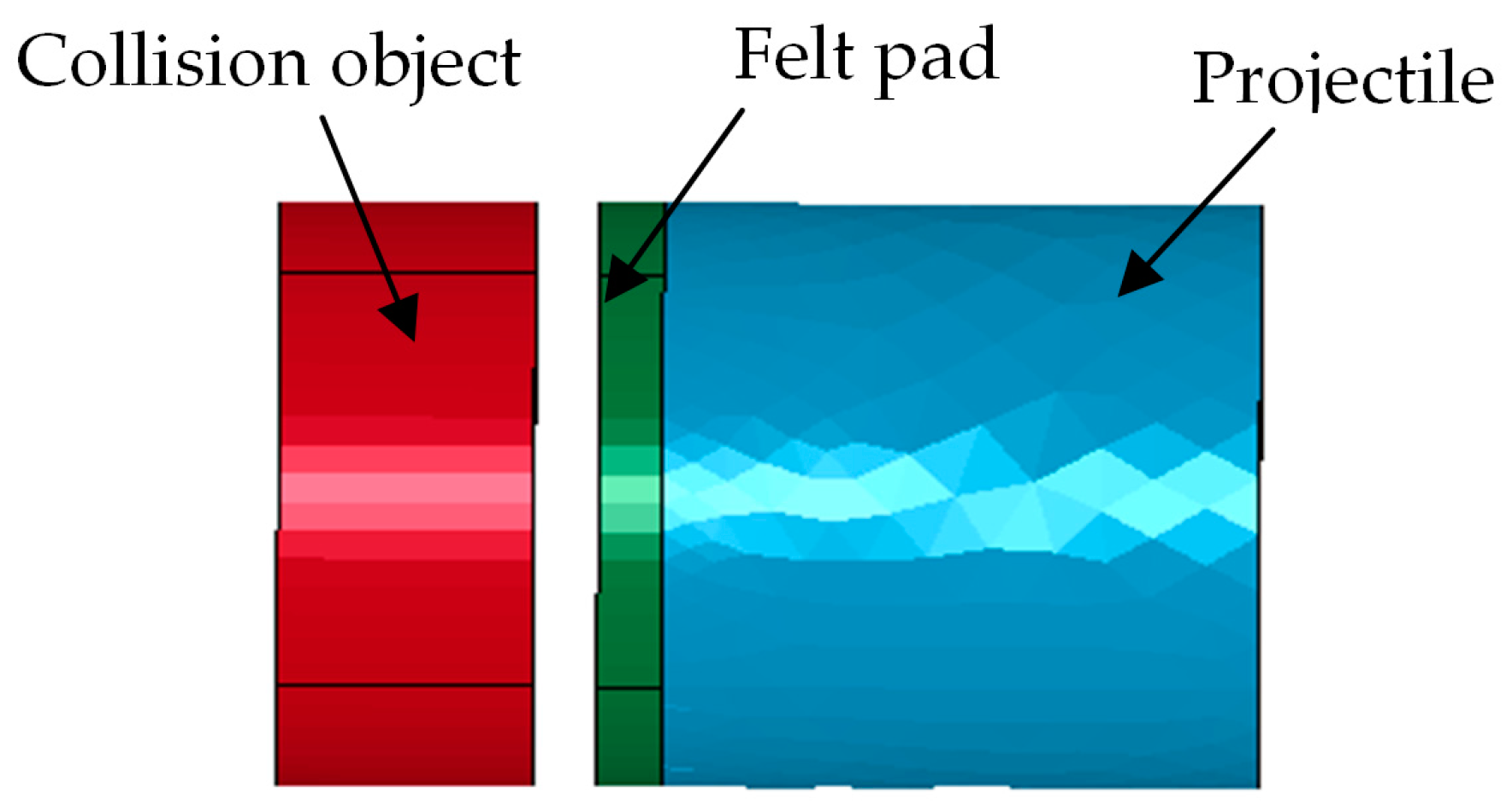
3. The Quasi-Static Calibration Testing System
4. Factors Influencing Excitation Pulse Width
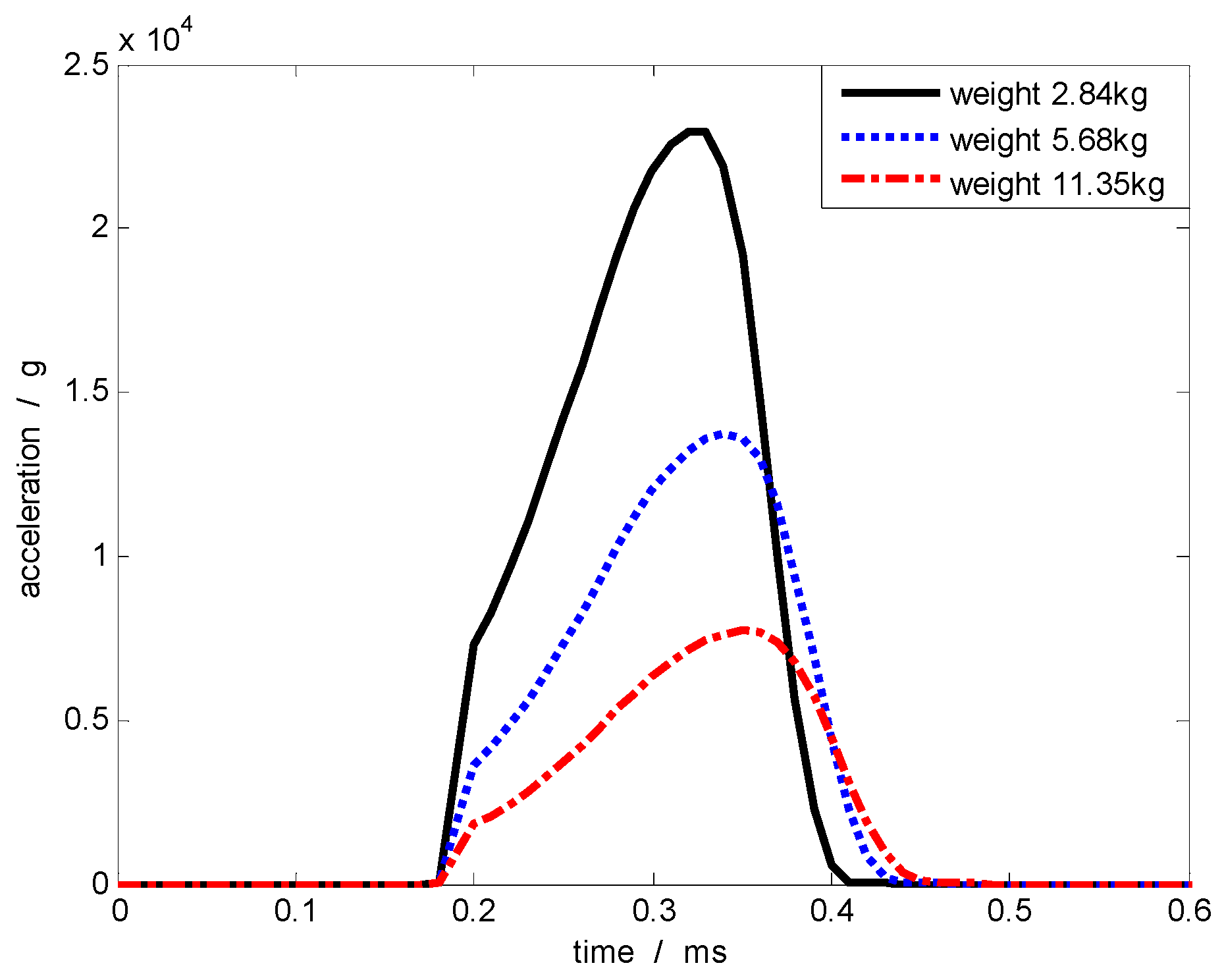
4.1. Influence of the Collision Object’s Mass on Excitation Pulse
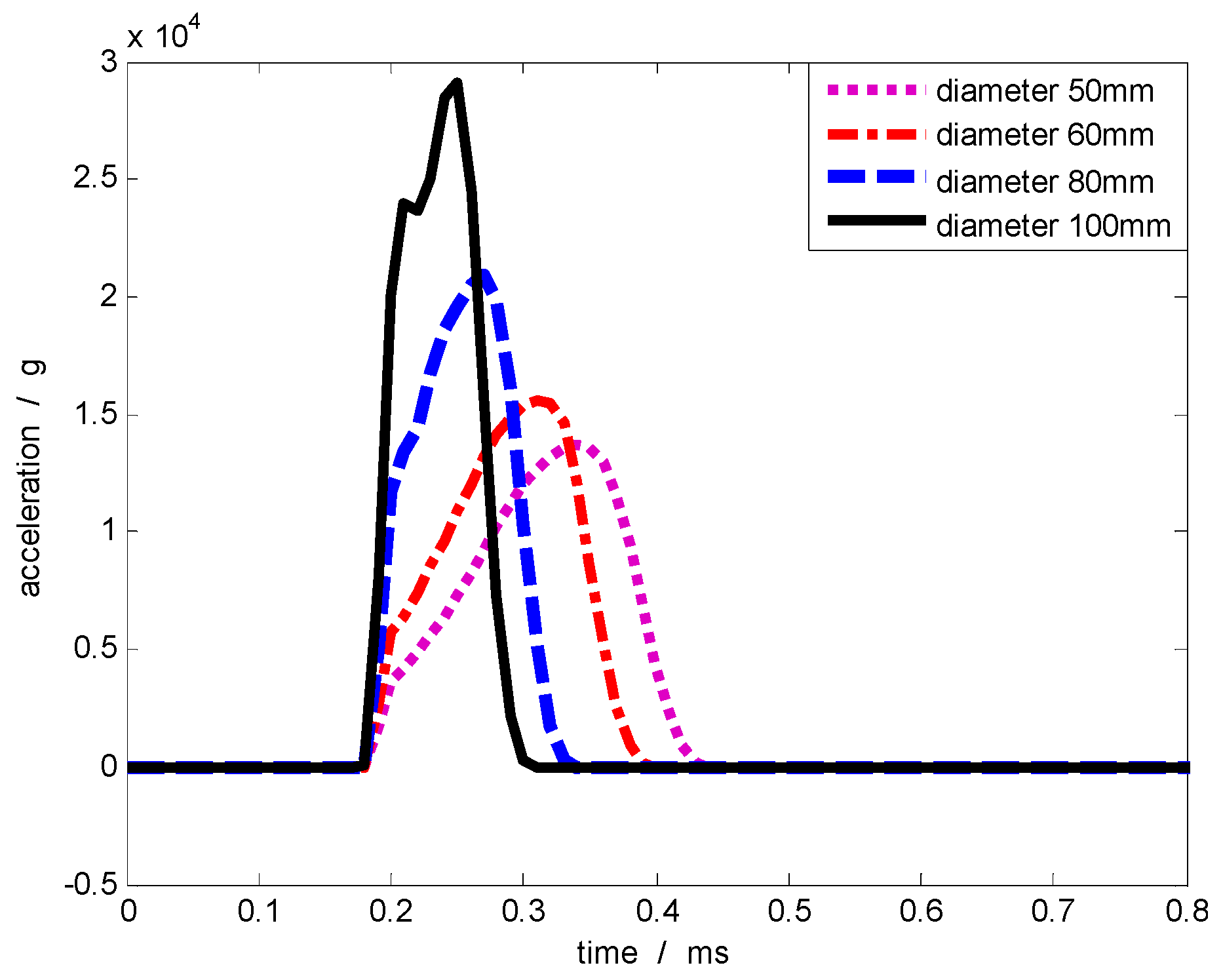
4.2. Influence of Collision Contact Area on Excitation Pulse
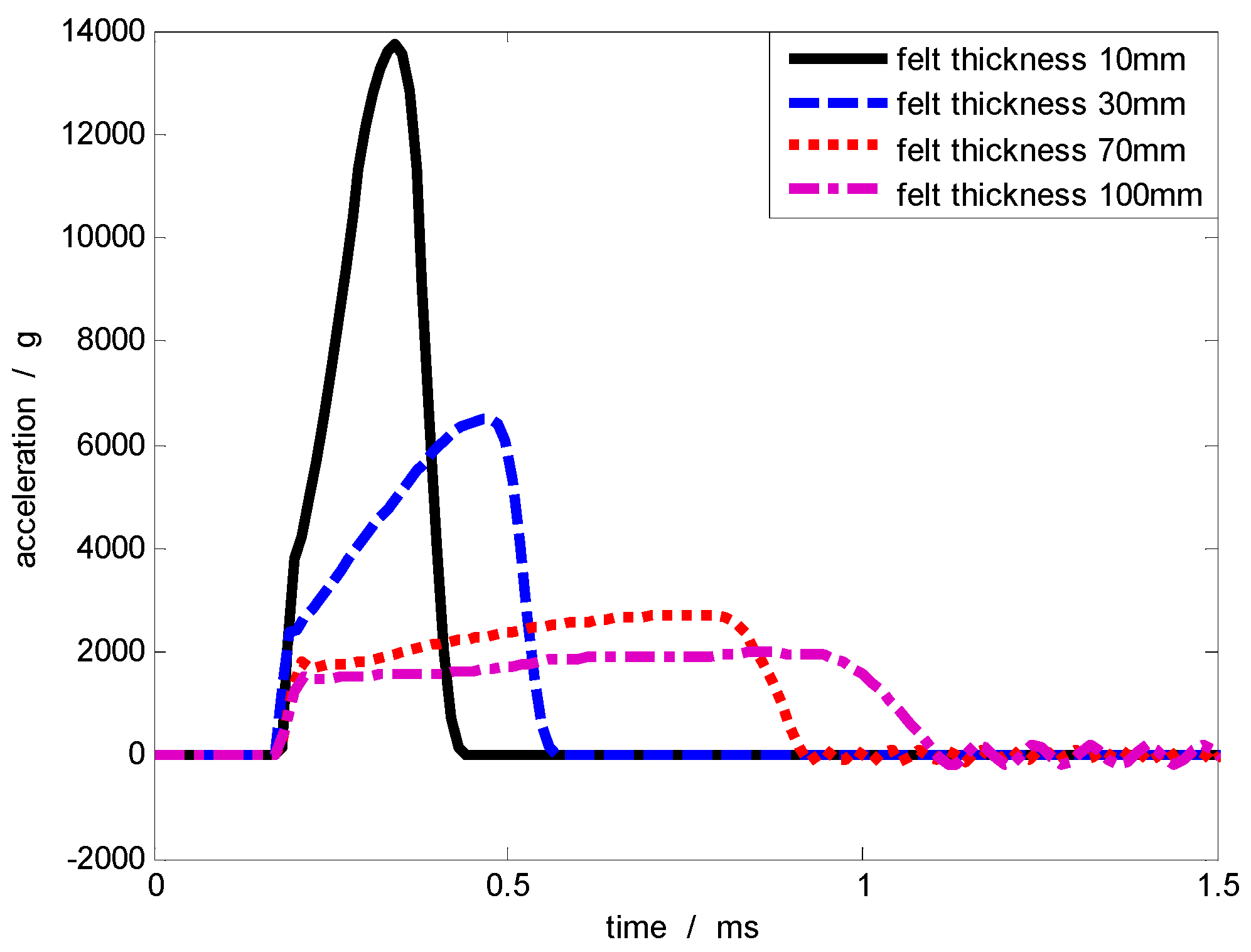
4.3. Influence of Felt Pad Thickness on Excitation Pulse
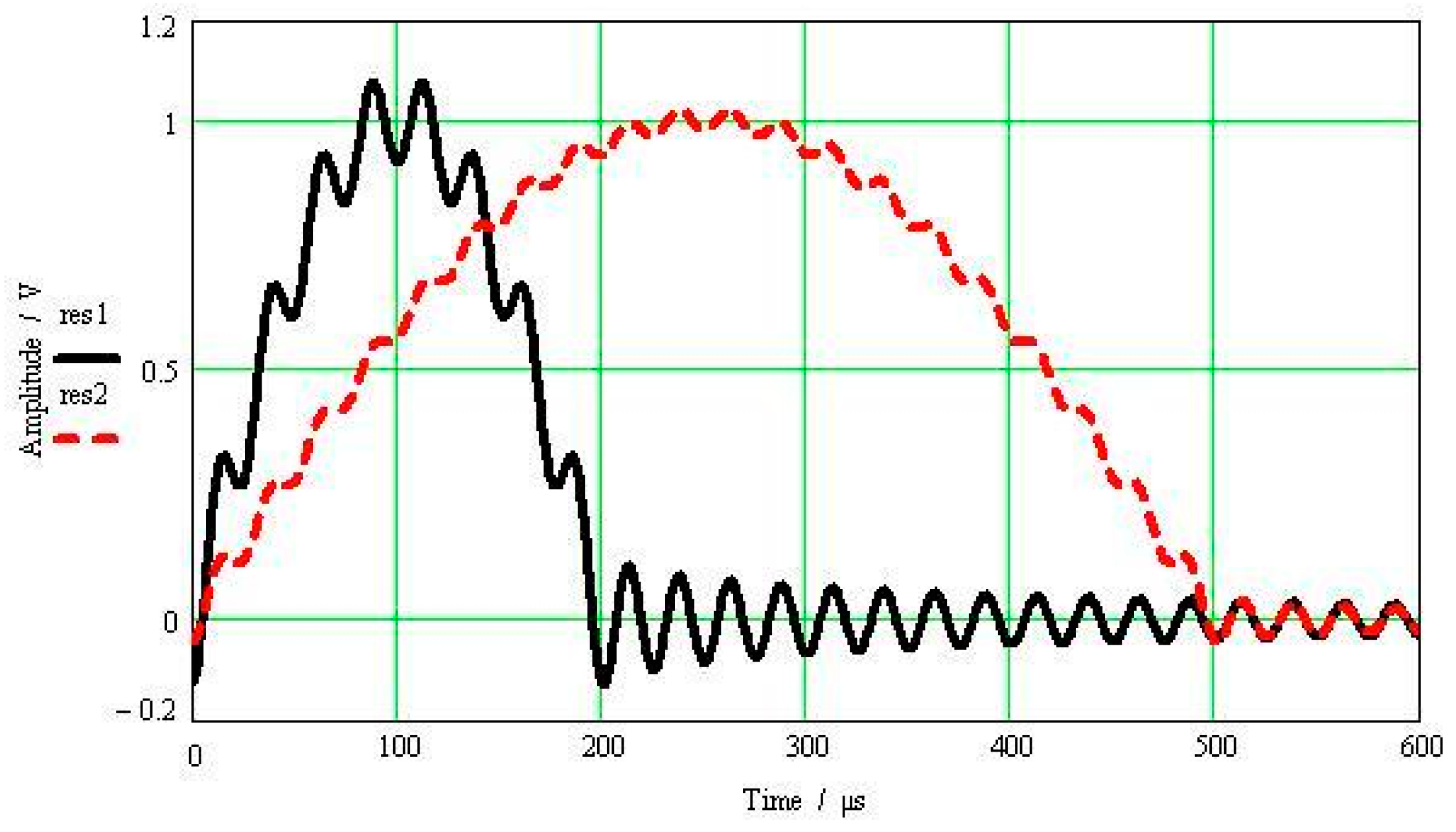
5. Quasi-Static Calibration Test
6. Conclusions
- (1)
- A second-order mathematical model is used to describe the response characteristics of the high-g accelerometer, and deduces the relationship between and among the minimum pulse width of the excitation signals, resonant frequency, and calibration error of the calibrated accelerometer. With this method, the impact sensitivity of the calibrated accelerometer is gained within a certain error range. Increasing the width of the excitation pulse reduces amplitude changes of the response signal caused by resonant frequency, and effectively lowered the calibration error of impact sensitivity.
- (2)
- The finite element method is applied to simulate the dynamic collision process. As indicated by our results, acceleration signals with a pulse width less than 1000 μs are obtained by changing the collision contact area and the number of layers of the felt pad; acceleration signals with an amplitude of 103–105 g are gained by changing the mass of the collision object and the projectile velocity.
- (3)
- We conduct a quasi-static calibration test of a piezoelectric-type high-g accelerometer and apply the least squares method to obtain the impact sensitivity of the accelerometer from the calibration data. When the calibration error is 3%, the quasi-static calibration of high-g accelerometers with resonant frequency above 20 kHz is realized. Thus, high-g accelerometers calibrated using this method can satisfy the demands of engineering tests.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Togami, T.C.; Brown, F.A.; Forrestal, M.J. Performance evaluation of accelerometers to 200,000 G. J. Appl. Mech. 1998, 65, 266–268. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Togami, T.C.; Baker, W.E. Performance evaluation of accelerometers used for penetration experiments. Exp. Mech. 2003, 43, 90–96. [Google Scholar] [CrossRef]
- Paul, M.B.; James, D.C.; Bruce, L.K. Investigation on the response of segmented concrete targets to projectile impacts. Int. J. Impact Eng. 2009, 36, 926–939. [Google Scholar]
- Zhang, W.D.; Chen, L.J.; Xiong, J.J. Ultra-high g deceleration-time measurement for the penetration in to steel target. Int. J. Impact Eng. 2007, 34, 436–447. [Google Scholar] [CrossRef]
- Fan, J.B.; Wang, Y.; Zu, J. Triaxial acceleration measurement for oblique penetration into concrete target. IEEE Trans. Instrum. Meas. 2010, 11, 2907–2913. [Google Scholar] [CrossRef]
- Von Martens, H.J.; Taubner, A.; Wolfgang, W. Traceability of vibration and shock measurements by laser interferometry. Measurement 2000, 28, 3–20. [Google Scholar] [CrossRef]
- Link, A.; Von Martens, H.J. Calibration of accelerometers by shock excitation and laser interferometry. Shock Vib. 2000, 7, 101–112. [Google Scholar] [CrossRef]
- Wang, S.Y.; Cao, C.Z.; Fei, P.D. High-g accelerometer dynamic calibration by a laser differential Doppler technique. Rev. Sci. Instrum. 1996, 67, 2022–2025. [Google Scholar] [CrossRef]
- Ueda, K.; Umeda, A. Improvement of novel NRLM method for accelerometer characterization to the range 102 ms−2. Sens. Actuators A 1996, 54, 517–522. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 16063-13: Methods for the Calibration of Vibration and Shock Transducers, Part 13: Primary Shock Calibration Using Laser Interferometry; ISO: Geneva, Switzerland, 2001. [Google Scholar]
- Huang, Y.C.; Chen, J.K.; Hao, H.C. The set up of primary calibration system for shock acceleration in NML. Measurement 2012, 45, 2383–2387. [Google Scholar] [CrossRef]
- Nozato, H.; Usuda, T.; Oota, A. Calibration of vibration pick-ups with laser interferometry: Part IV. Development of a shock acceleration exciter and calibration system. Meas. Sci. Technol. 2010, 21, 1–10. [Google Scholar] [CrossRef]
- Yu, M.; Hu, H.B.; Zuo, A.B. Establishment of new generation national primary standard device for shock acceleration calibration. J. Vib. Shock 2013, 32, 124–129. (In Chinese) [Google Scholar]
- Wang, Y.; Fan, J.B.; Xu, P. Shock calibration of the high-g triaxial accelerometer. In Proceedings of the 25th IEEE International Conference Instrumentation and Measurement Technology, Victoria, BC, Canada, 12–15 May 2008.
- Brucke, M.; Siegmund, G.; Ehrmann, C. Measurement uncertainty of high-shock calibration systems. In Proceedings of the 20th IMEKO World Congress, Busan, Korea, 9–14 September 2012.
- Nozato, H.; Oota, A.; Shigami, T. The methods for the calibration of vibration pick-ups by laser interferometry: Part V. Uncertainty evaluation on the ratio of transducer’s peakout put value to peak input acceleration in shock calibration. Meas. Sci. Technol. 2011, 22, 1–9. [Google Scholar] [CrossRef]
- Zhang, Y.; Zu, J.; Zhang, H.Y. Dynamic calibration method of high-pressure transducer basedon quasi-d function excitation source. Measurement 2012, 45, 1981–1988. [Google Scholar] [CrossRef]
- Xu, P.; Zu, J.; Fan, J.B. A novel air gun and its application in anti-high g shock ability of memory measurement equipment. In Proceeding of the 7th international conference on Shock & Impact Loads on Structure, Beijing, China, 17–19 October 2007.


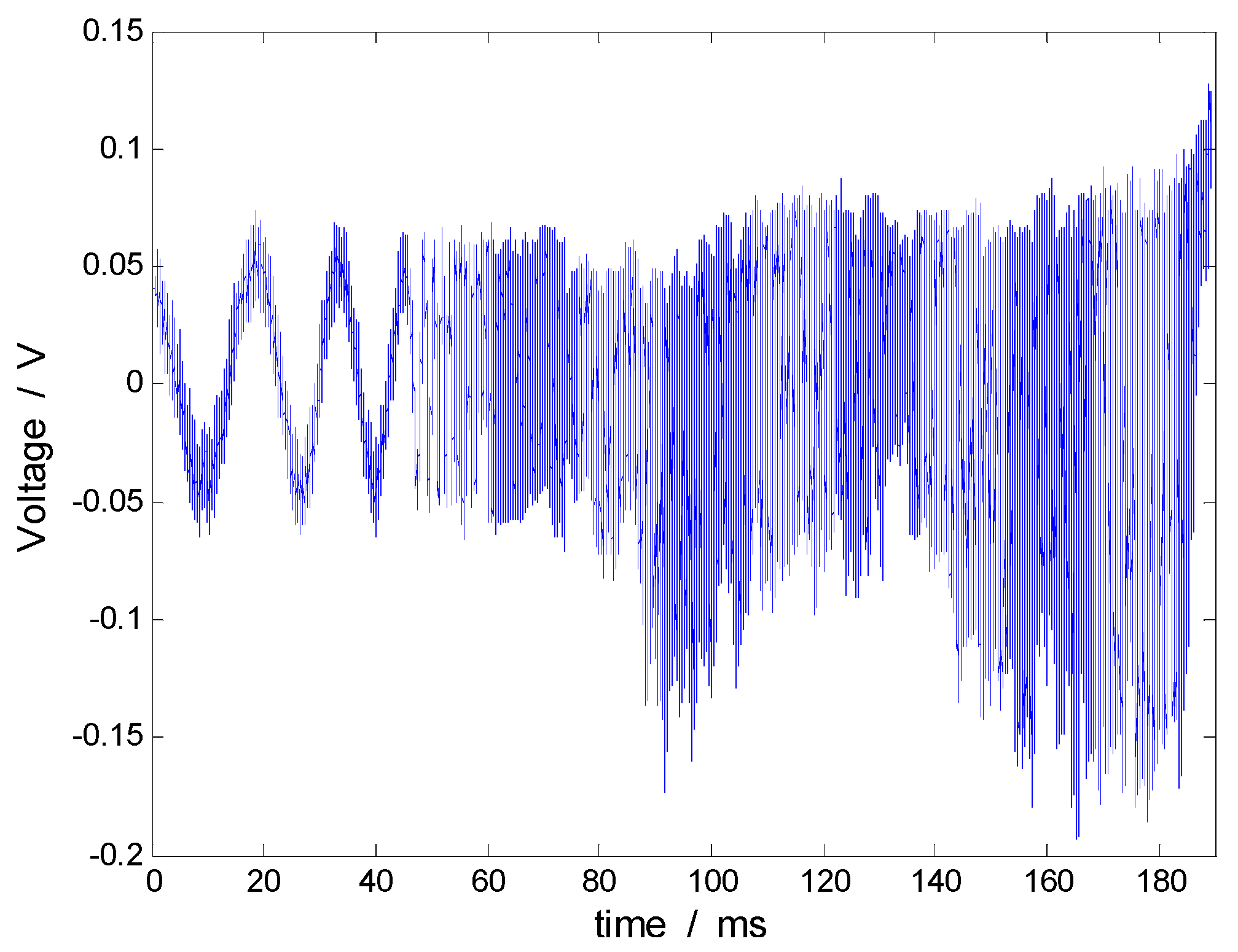
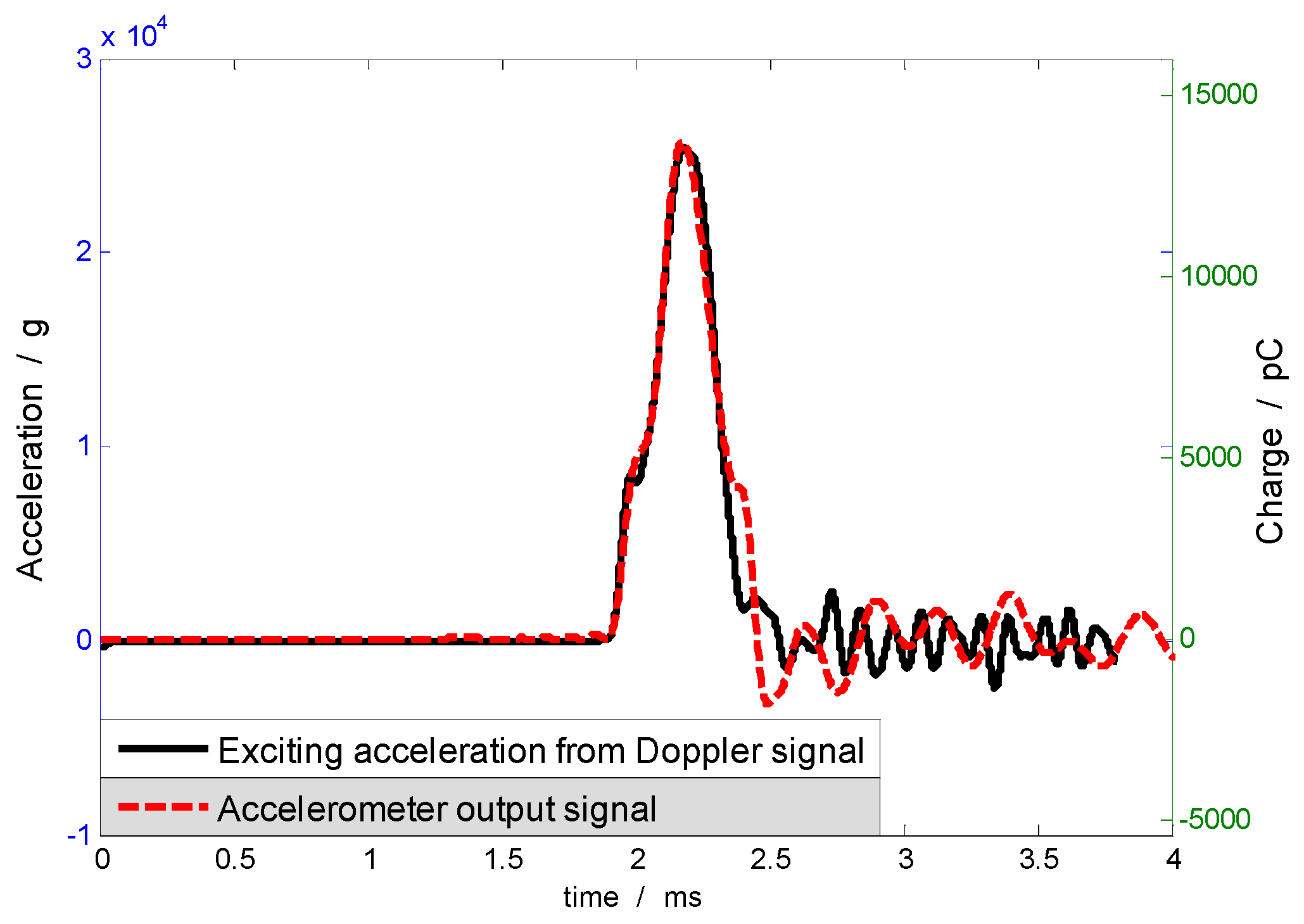
| Frequency | 10 | 20 | 30 | 40 | 50 | 60 | |
|---|---|---|---|---|---|---|---|
| Pulse width τ (μs) | 5050 | 2525 | 1683 | 1263 | 1010 | 842 | |
| 1717 | 858 | 572 | 429 | 343 | 286 | ||
| 1050 | 525 | 350 | 263 | 210 | 175 | ||
| Collision Surface Diameter (mm) | Collision Object Mass (kg) | Acceleration Amplitude (g) | Acceleration Pulse Width (µs) | Speed (m/s) |
|---|---|---|---|---|
| 100 | 11.35 | 15,859 | 140 | 12.19 |
| 5.68 | 29,061 | 120 | 20.83 | |
| 2.84 | 49,087 | 110 | 32.21 | |
| 50 | 11.35 | 7714 | 270 | 9.94 |
| 5.68 | 13,730 | 260 | 17.22 | |
| 2.84 | 22,970 | 230 | 48.68 |
| Contact Surface Diameter (mm) | Acceleration Amplitude (g) | Acceleration Pulse Width (µs) | Speed (m/s) |
|---|---|---|---|
| 50 | 13,730 | 260 | 17.22 |
| 60 | 15,480 | 220 | 19.60 |
| 70 | 18,280 | 190 | 19.86 |
| 80 | 20,950 | 160 | 19.50 |
| 90 | 24,500 | 140 | 20.00 |
| 100 | 29,061 | 120 | 20.83 |
| Felt Pad Thickness (mm) | Acceleration Amplitude (g) | Acceleration Pulse Width (µs) | Speed (m/s) |
|---|---|---|---|
| 10 | 13,730 | 260 | 17.22 |
| 30 | 6482 | 420 | 16.47 |
| 50 | 5832 | 725 | 15.43 |
| 70 | 2721 | 735 | 15.61 |
| 90 | 2249 | 865 | 15.20 |
| 100 | 1930 | 952 | 14.92 |
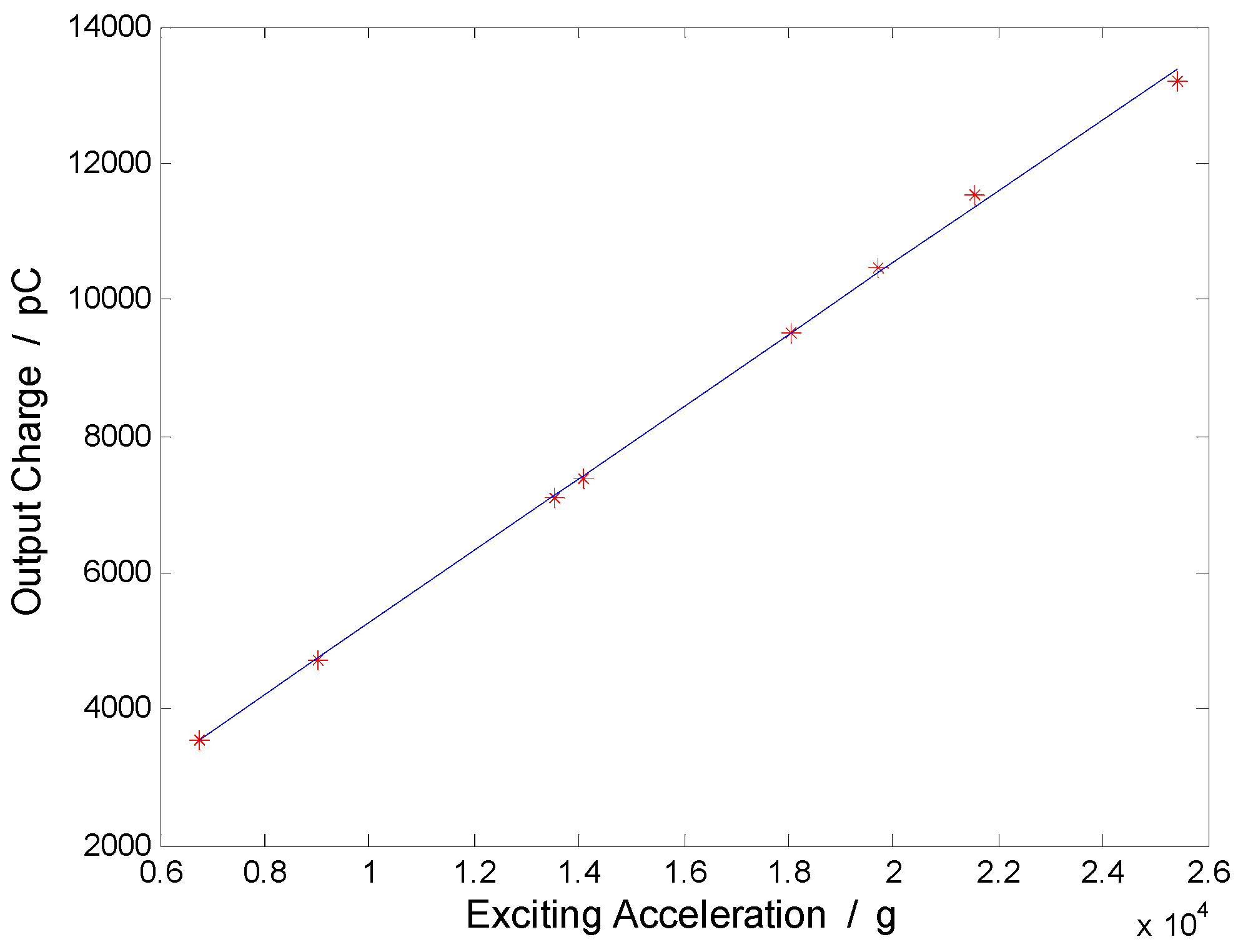
| Test Number | Excitation Acceleration Peak Value (g) | Pulse Width (μs) | Output Charge Peak Value (pC) | Impact Sensitivity (pC/g) | Response Error ε (%) |
|---|---|---|---|---|---|
| 1 | 6775 | 843 | 3529 | 0.521 | 2.07 |
| 2 | 9032 | 673 | 4724 | 0.523 | 1.53 |
| 3 | 13,550 | 599 | 7100 | 0.524 | 1.22 |
| 4 | 14,110 | 531 | 7379 | 0.523 | 1.40 |
| 5 | 18,060 | 523 | 9518 | 0.527 | 0.58 |
| 6 | 19,730 | 446 | 10,477 | 0.531 | 0.20 |
| 7 | 21,530 | 433 | 11,519 | 0.535 | 0.66 |
| 8 | 25,410 | 418 | 13,213 | 0.520 | 1.85 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Fan, J.; Zu, J.; Xu, P. Quasi-Static Calibration Method of a High-g Accelerometer. Sensors 2017, 17, 409. https://doi.org/10.3390/s17020409
Wang Y, Fan J, Zu J, Xu P. Quasi-Static Calibration Method of a High-g Accelerometer. Sensors. 2017; 17(2):409. https://doi.org/10.3390/s17020409
Chicago/Turabian StyleWang, Yan, Jinbiao Fan, Jing Zu, and Peng Xu. 2017. "Quasi-Static Calibration Method of a High-g Accelerometer" Sensors 17, no. 2: 409. https://doi.org/10.3390/s17020409
APA StyleWang, Y., Fan, J., Zu, J., & Xu, P. (2017). Quasi-Static Calibration Method of a High-g Accelerometer. Sensors, 17(2), 409. https://doi.org/10.3390/s17020409





