Formal Uncertainty and Dispersion of Single and Double Difference Models for GNSS-Based Attitude Determination
Abstract
:1. Introduction
2. Theoretical Analysis
2.1. Comparison between SD and DD under Non-Common Clock Scheme
2.2. Comparison between Non-Common Clock SD and Common Clock SD without UPD
2.3. Common Clock SD with UPD Estimated and Constrained
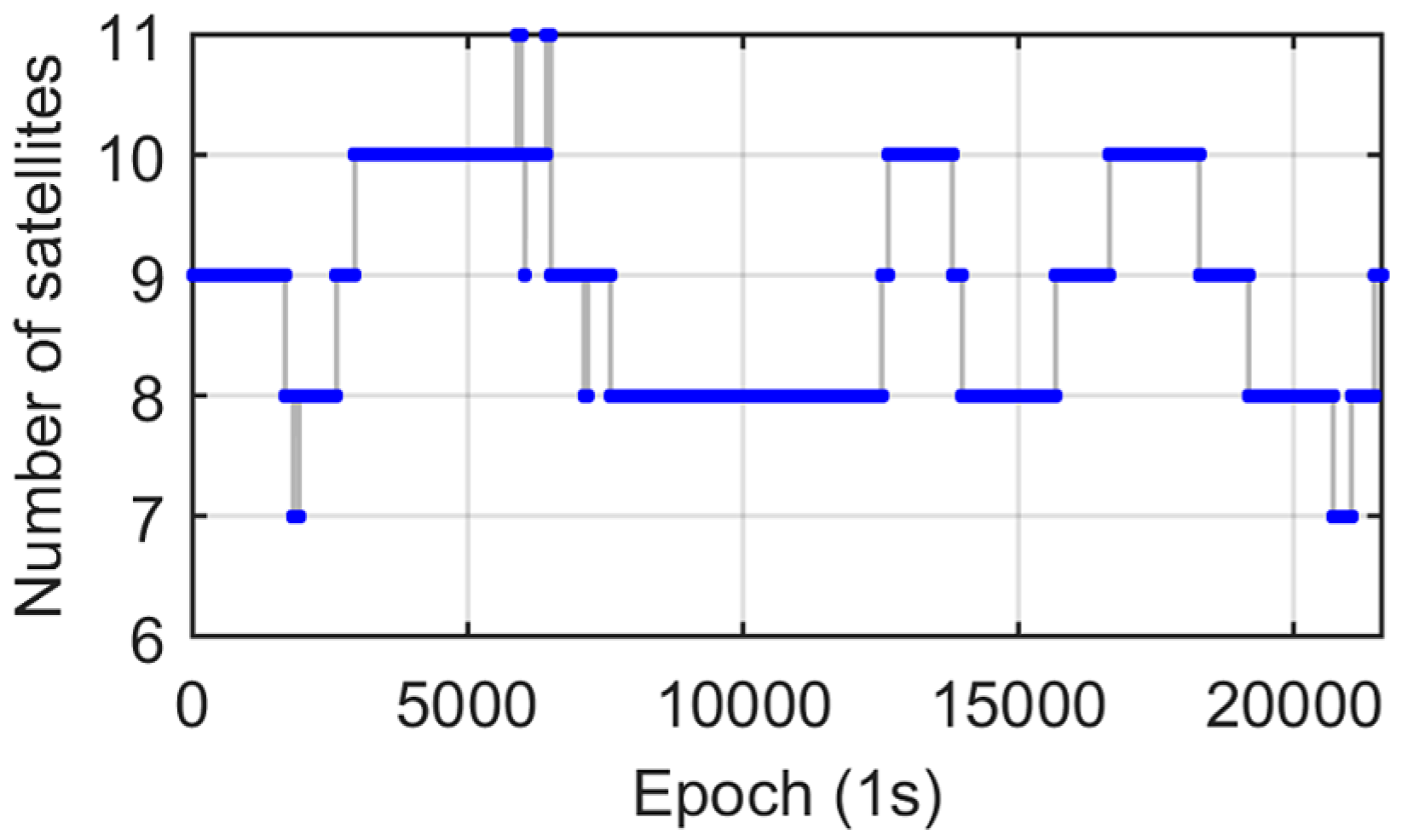
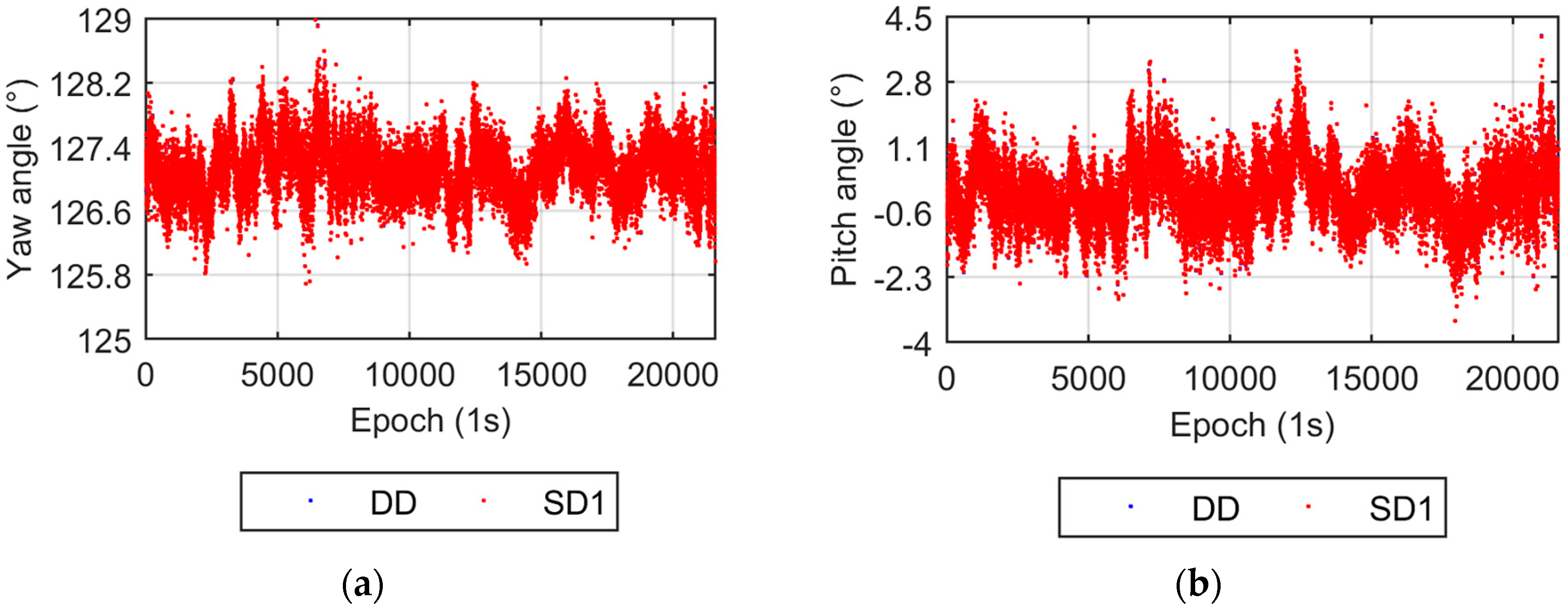
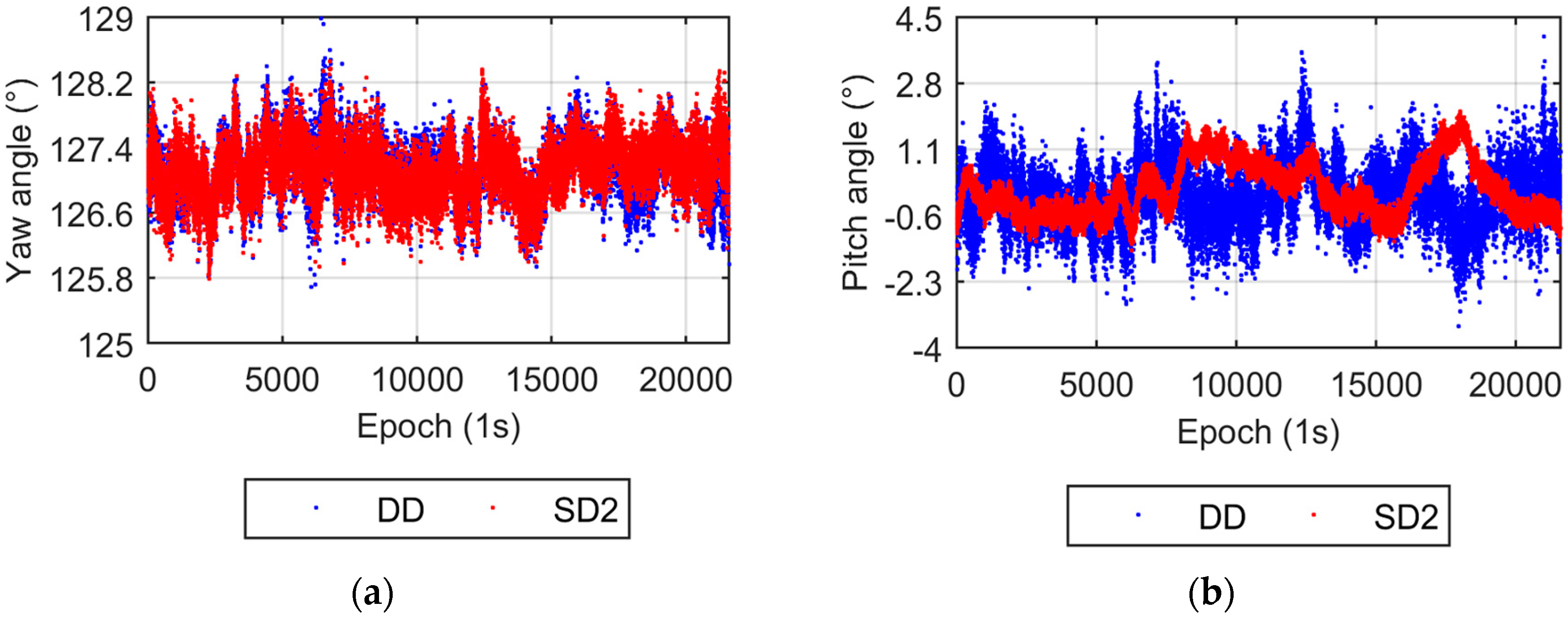
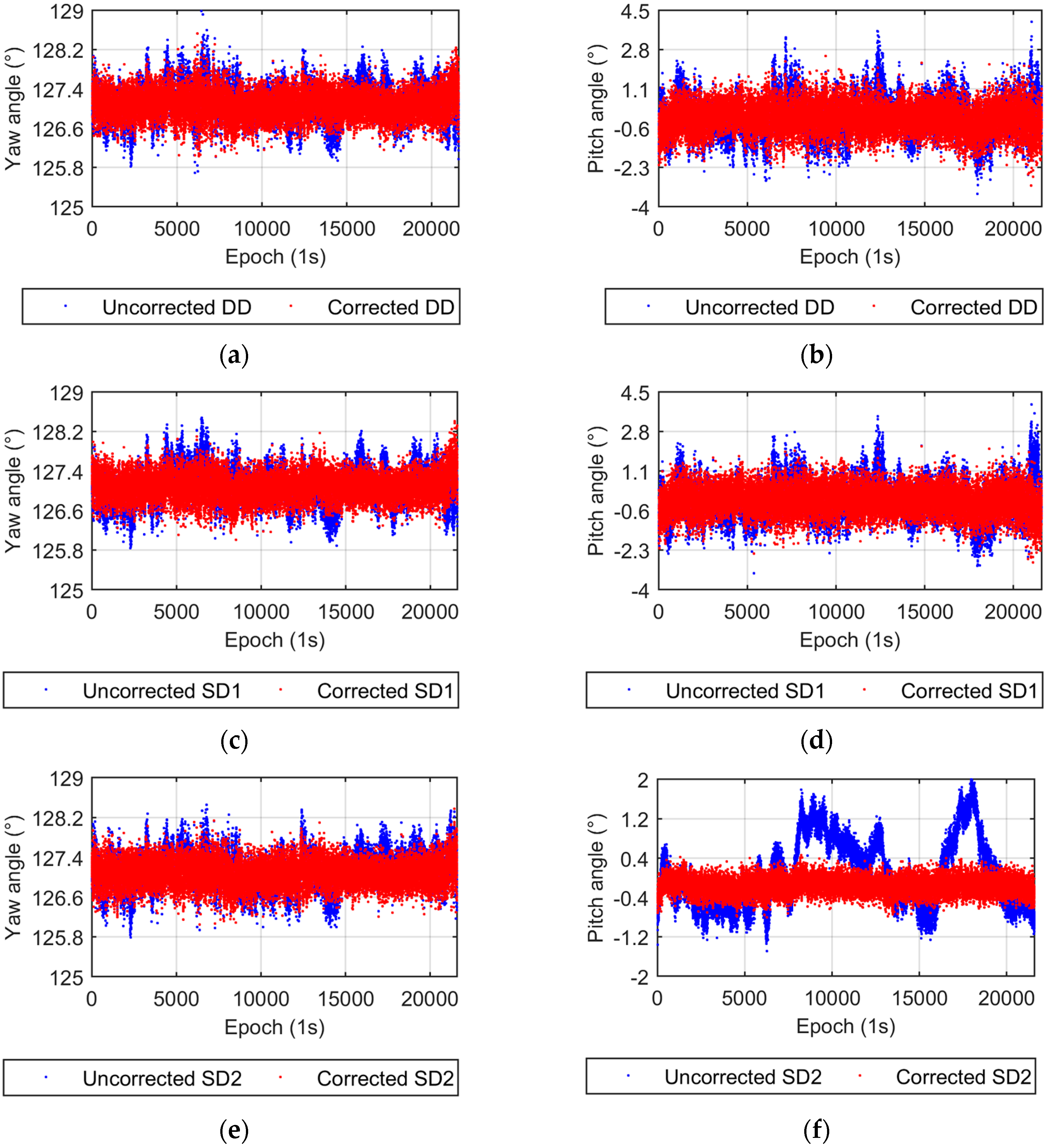
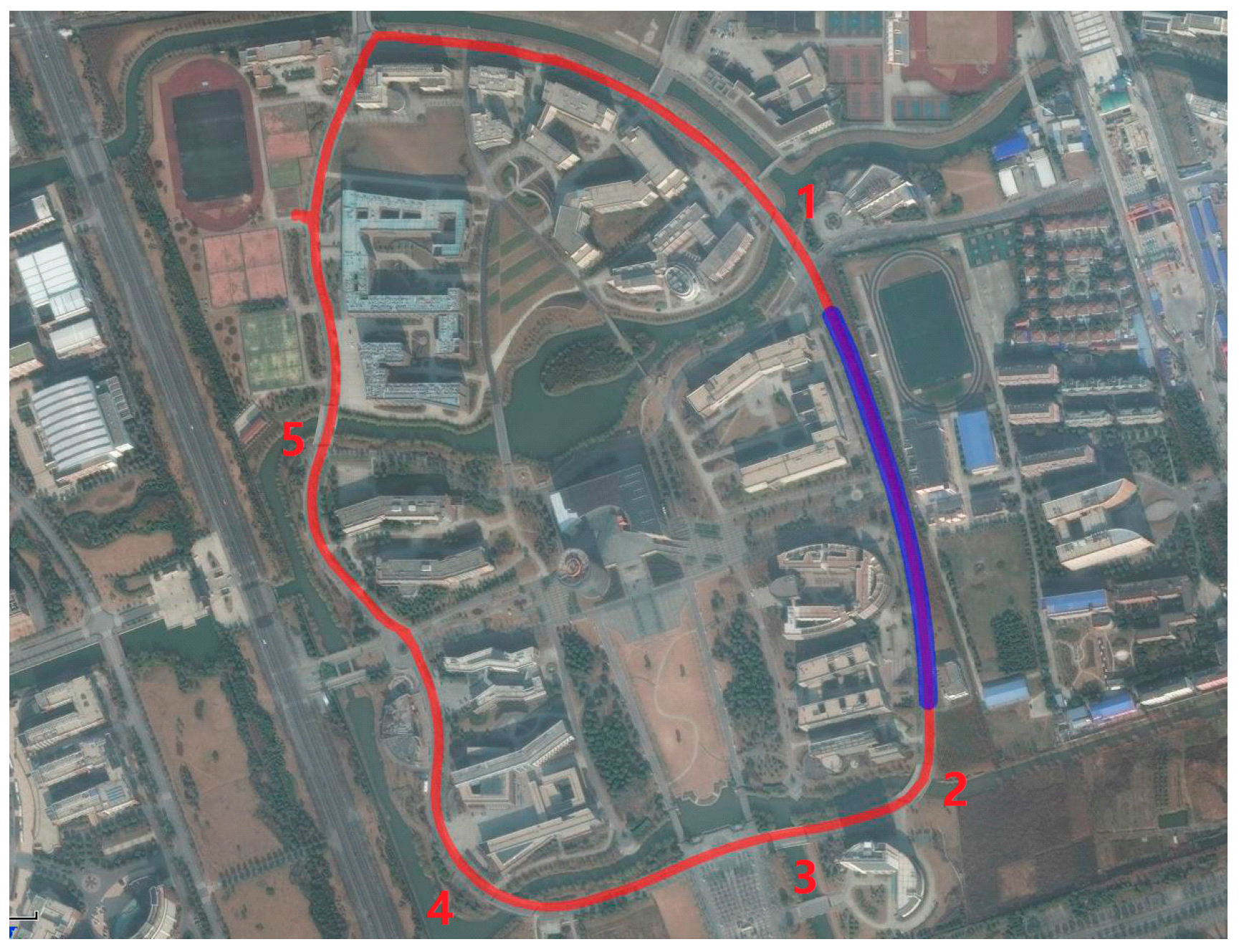
3. Experiments
3.1. Static Roof Test
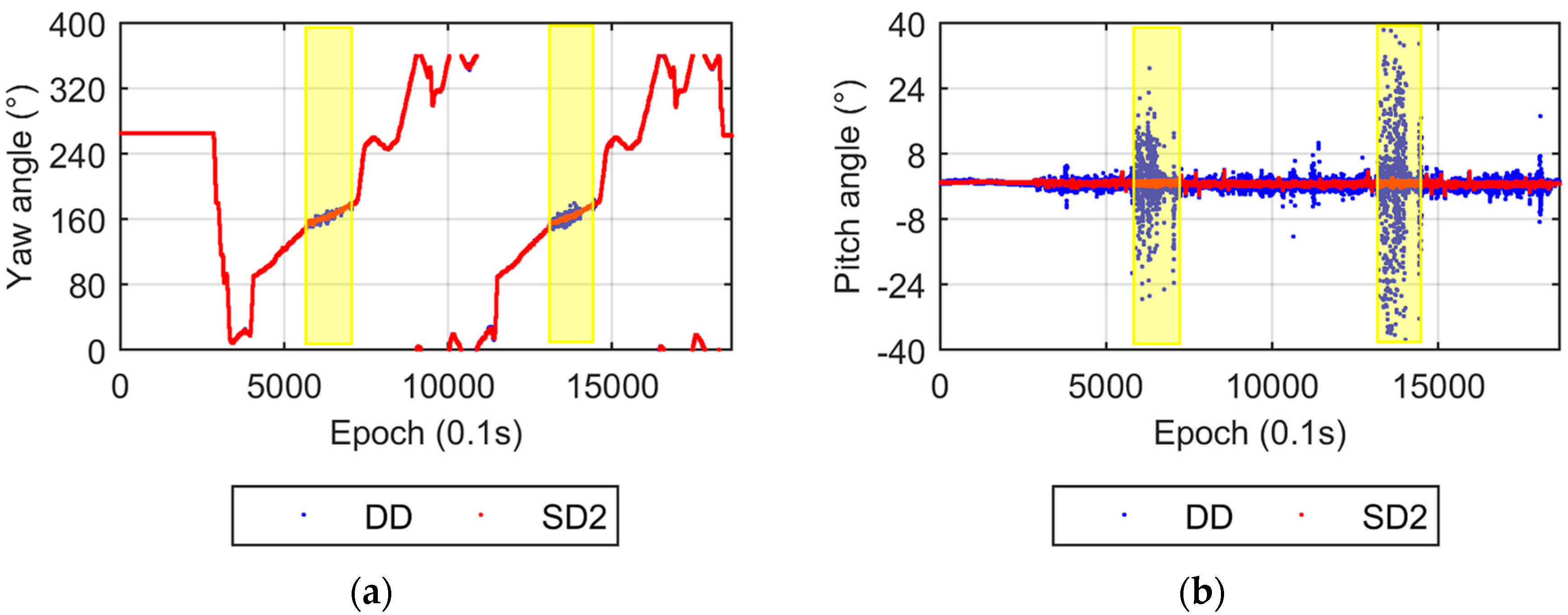
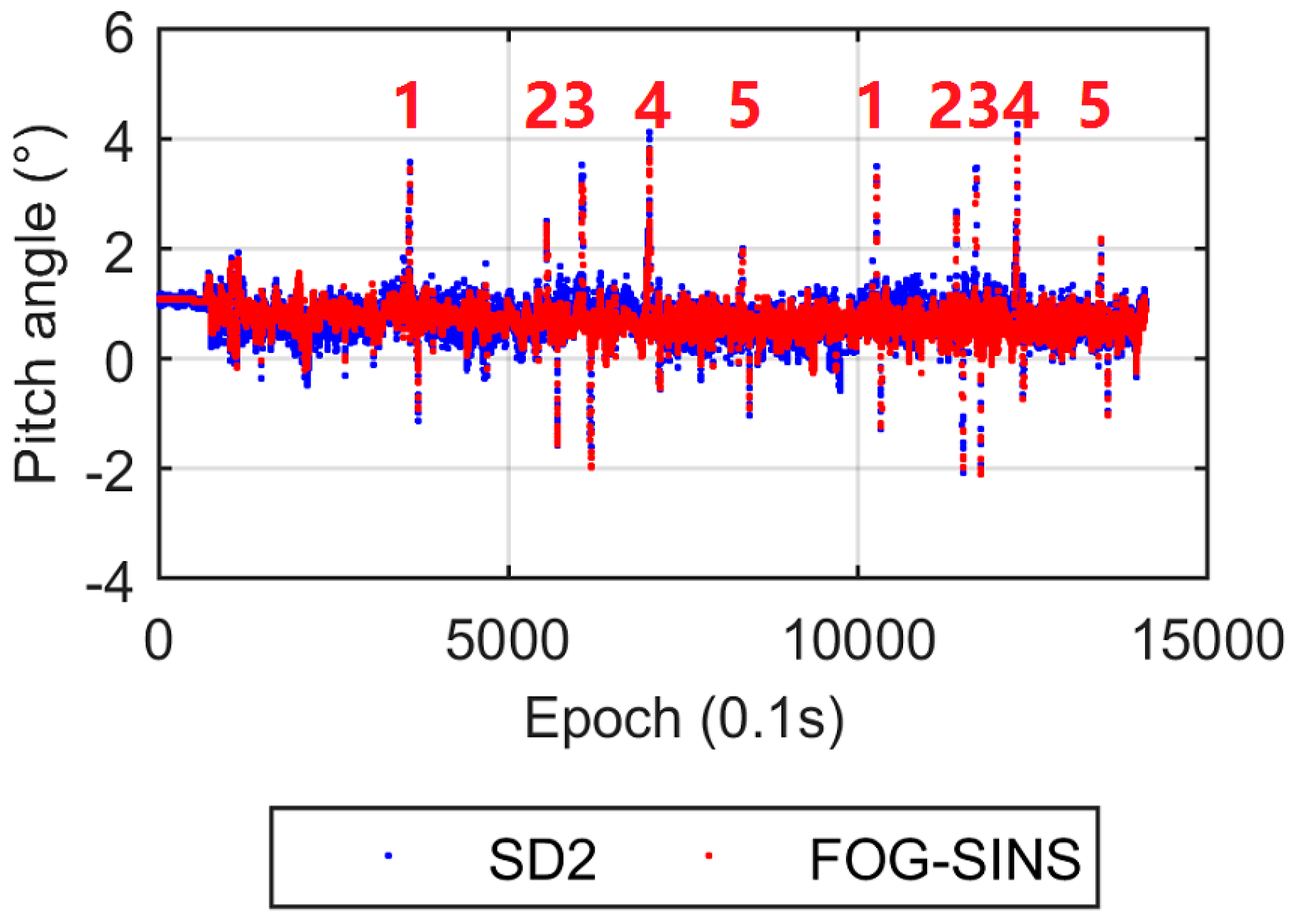
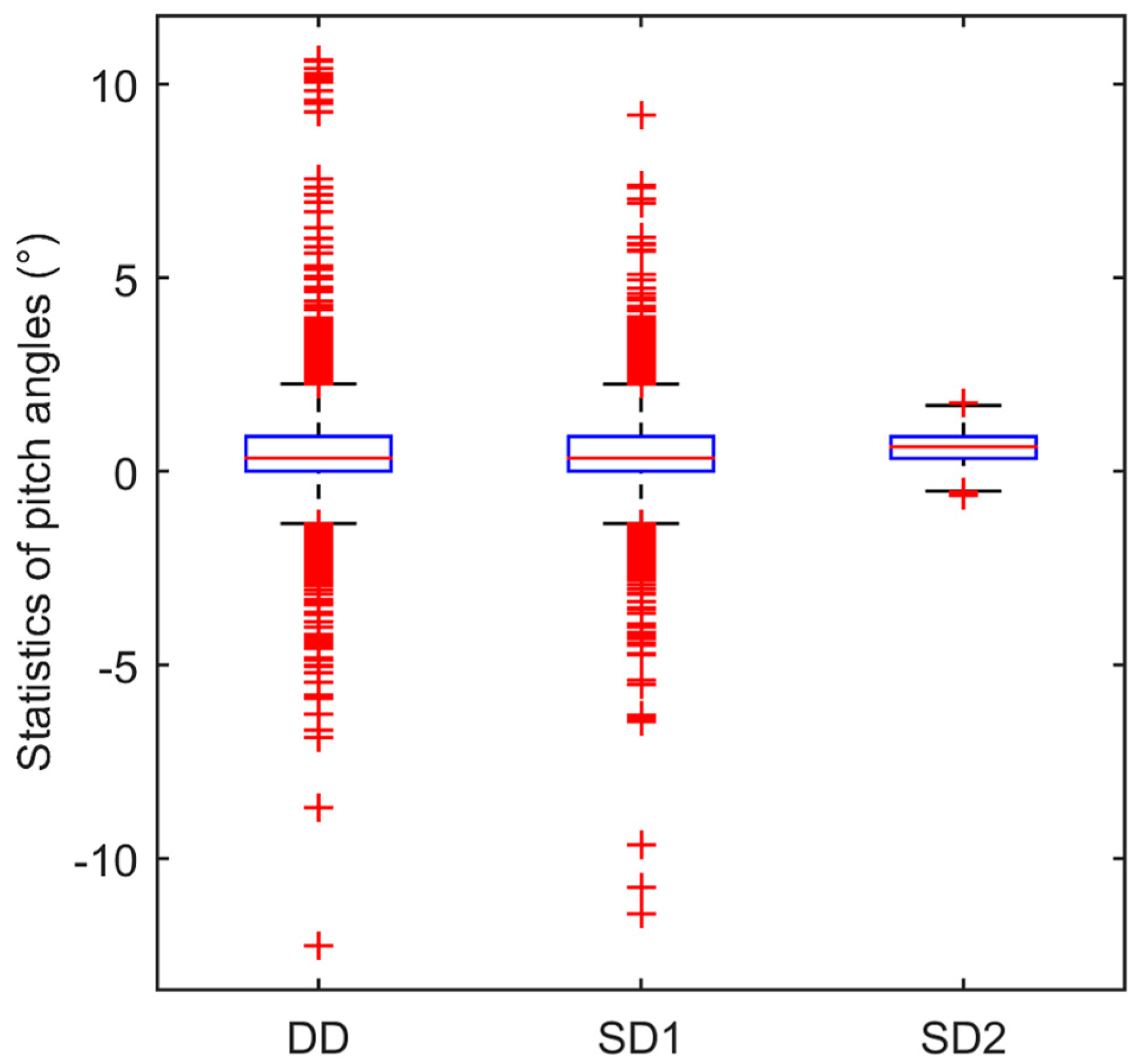
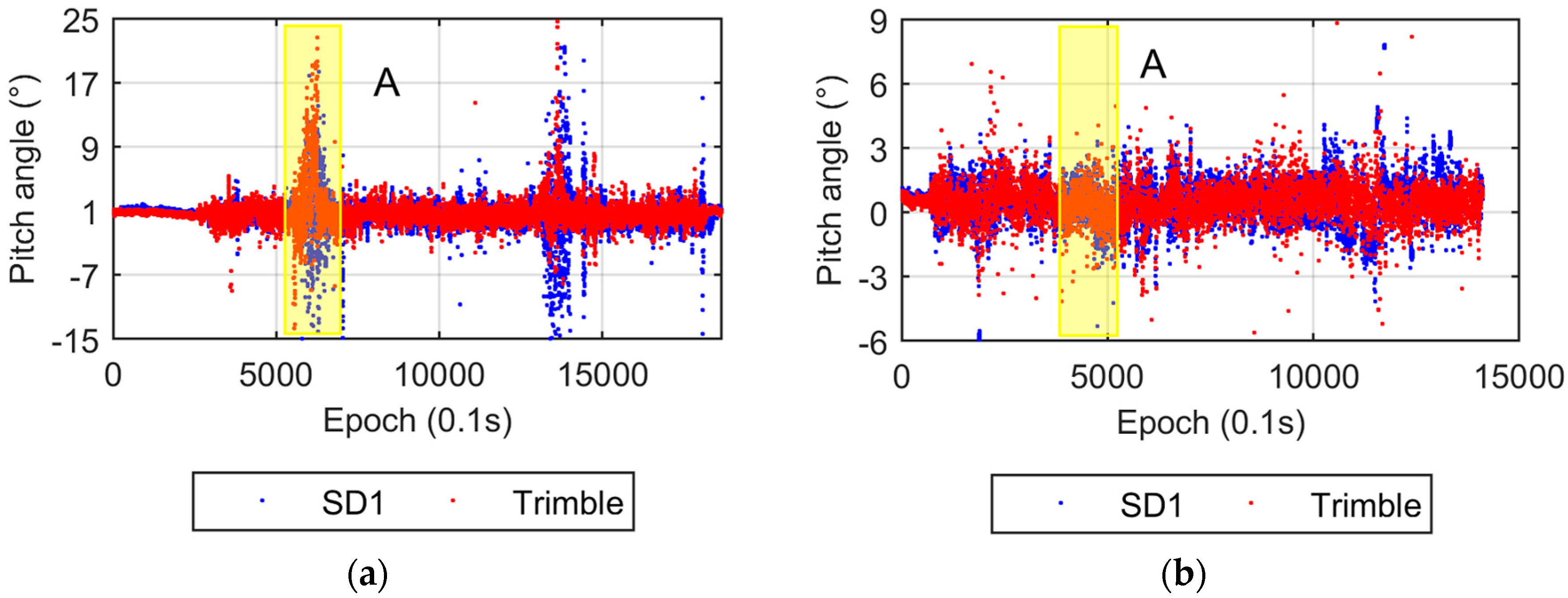
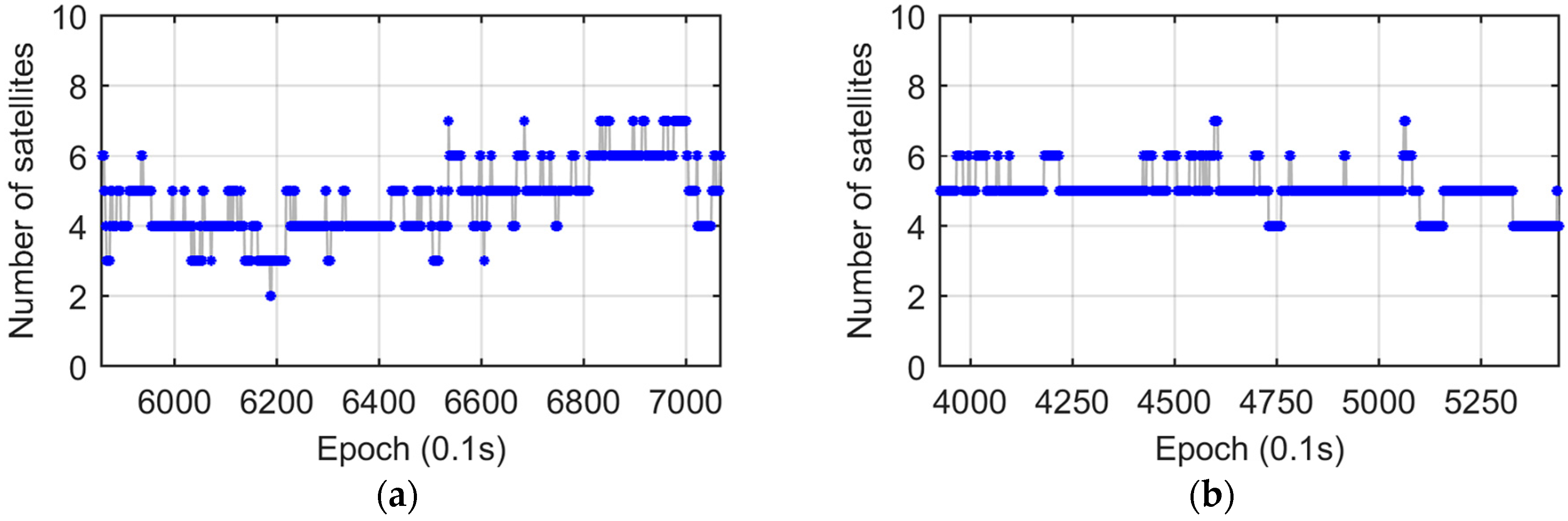
3.2. Vehicle Test
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Axelrad, P.; Ward, L. On-orbit GPS based attitude and antenna baseline estimation. In Proceedings of the ION-NTM, San Diego, CA, USA, 24–26 January 1994; pp. 441–450.
- Park, C.; Kim, I.; Jee, G.I.; Lee, J.G. An error analysis of GPS compass. In Proceedings of the 36th SICE Annual Conference, Tokushima, Japan, 29–31 July 1997.
- Kim, D.; Langley, R.B. GPS ambiguity resolution and validation: Methodologies, trends and issues. In Presented at the Seventh GNSS Workshop—International Symposium on GPS/GNSS, Seoul, Korea, 30 November–2 December 2000.
- Dai, L.; Hu, G.R.; Ling, K.V.; Nagarajan, N. Real-time Attitude Determination for Microsatellite by Lambda Method Combined with Kalman Filtering. In Proceedings of the 22nd AIAA International Communications Satellite Systems Conference and Exhibit 2004 (ICSSC), Monterey, CA, USA, 9–12 May 2004.
- Giorgi, G.; Buist, P.J. Single-epoch, single-frequency, standalone full attitude determination: Experimental results. In Presented at the Fourth ESA Workshop on Satellite Navigation User Equipment Technologies, NAVITEC08, ESA-ESTEC, Noordwijk, The Netherlands, 10–12 December 2008.
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuh, H. Tightly coupled integration of multi-GNSS PPP and MEMS inertial measurement unit data. GPS Solut. 2016. [Google Scholar] [CrossRef]
- Rabbou, M.A.; El-Rabbany, A. Tightly coupled integration of GPS precise point positioning and MEMS-based inertial systems. GPS Solut. 2015, 19, 601–609. [Google Scholar] [CrossRef]
- Sabatini, R.; Rodríguez, L.; Kaharkar, A.; Bartel, C.; Shaid, T. Carrier-phase GNSS attitude determination and control system for unmanned aerial vehicle applications. J. Aeronaut. Aerosp. Eng. 2013, 2, 297–322. [Google Scholar]
- Teunissen, P.J.G.; Giorgi, G.; Buist, P.J. Testing of a new single-frequency GNSS carrier phase attitude determination method: Land, ship and aircraft experiments. GPS Solut. 2011, 15, 15–28. [Google Scholar] [CrossRef]
- Giorgi, G.; Teunissen, P.J.G.; Gourlay, T.P. Instantaneous global navigation satellite system (GNSS)-based attitude determination for maritime applications. IEEE J. Ocean. Eng. 2012, 37, 348–362. [Google Scholar] [CrossRef]
- Buist, P.J.; Teunissen, P.J.G.; Verhagen, S.; Giorgi, G. A vectorial bootstrapping approach for integrated GNSS-based relative positioning and attitude determination of spacecraft. Acta Astron. 2011, 68, 1113–1125. [Google Scholar] [CrossRef]
- Hatch, R. Instantaneous ambiguity resolution. In Proceedings of the KIS’90, Banff, AB, Canada, 10–13 September 1990; pp. 299–308.
- Teunissen, P.J.G. A new method for fast carrier phase ambiguity estimation. In Proceedings of the IEEE PLANS’94, Las Vegas, NV, USA, 11–15 April 1994; pp. 562–573.
- Park, C.; Kim, I.; Lee, J.G.; Lee, G.I. Efficient technique to fix GPS carrier phase integer ambiguity on-the-fly. IEE Proc. Radar Sonar Navig. 1997, 144, 148–155. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Chang, X.W.; Yang, X.; Zhou, T. Mlambda: A modified lambda method for integer least-squares estimation. J. Geod. 2005, 79, 552–565. [Google Scholar] [CrossRef]
- Park, C.; Teunissen, P.J.G. A baseline constrained LAMBDA method for an integer ambiguity resolution of GNSS attitude determination systems. J. Inst. Control Robot. Syst. 2008, 14, 587–594. [Google Scholar]
- Wang, B.; Miao, L.; Wang, S.; Shen, J. A constrained lambda method for GPS attitude determination. GPS Solut. 2009, 13, 97–107. [Google Scholar] [CrossRef]
- Giorgi, G.; Teunissen, P.J.G. Carrier phase GNSS attitude determination with the multivariate constrained lambda method. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 6–13 March 2010.
- Chen, W.T.; Qin, H.L.; Zhang, Y.Z.; Jin, T. Accuracy assessment of single and double difference models for the single epoch GPS compass. Adv. Space Res. 2012, 49, 725–738. [Google Scholar] [CrossRef]
- Dong, D.N.; Chen, W.; Cai, M.M.; Zhou, F.; Wang, M.H.; Yu, C.; Zheng, Z.Q.; Wang, Y.F. Multi-antenna synchronized global navigation satellite system receiver and its advantages in high-precision positioning applications. Front. Earth Sci. 2016, 10, 772–783. [Google Scholar] [CrossRef]
- Ge, M.R.; Gendt, G.; Rothacher, M.; Shi, C.H.; Liu, J.S. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, K.; Roberts, C.; Murata, M. On-the-fly GPS-based attitude determination using single- and double-differenced carrier phase measurements. GPS Solut. 2004, 8, 93–102. [Google Scholar] [CrossRef]
- Park, K.; Crassidis, J.L. A Robust GPS receiver self survey algorithm. Navigation 2006, 53, 259–268. [Google Scholar] [CrossRef]
- Wang, Y.Q. GPS/GLONASS Attitude Determination Research under Long Endurance and High Dynamic Conditions. Ph.D. Thesis, Shanghai Jiaotong University, Shanghai, China, 2008. [Google Scholar]
- Teunissen, P.J.G. GPS double difference statistics: With and without using satellite geometry. J. Geod. 1997, 71, 138–148. [Google Scholar] [CrossRef]
- Blewitt, G. Carrier phase ambiguity resolution for the global positioning system applied to geodetic baselines up to 2000 km. J. Geophys. Res. 1989, 94, 10187–10203. [Google Scholar] [CrossRef]
- Dong, D.N.; Wang, M.H.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.Q.; Cai, M.M.; Cheng, Y.N.; Lv, J.Y. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map. J. Geod. 2016, 90, 255–262. [Google Scholar] [CrossRef]
- Cai, M.M.; Chen, W.; Dong, D.N.; Song, L.; Wang, M.H.; Wang, Z.R.; Zhou, F.; Zheng, Z.Q.; Yu, C. Reduction of Kinematic Short Baseline Multipath Effects Based on Multipath Hemispherical Map. Sensors 2016, 16, 1677. [Google Scholar] [CrossRef] [PubMed]
- McGill, R.; Tukey, J.W.; Larsen, W.A. Variations of Boxplots. Am. Stat. 1978, 32, 12–16. [Google Scholar]
- Wang, Y.Q.; Zhan, X.Q.; Zhang, Y.H. Improved ambiguity function method based on analytical resolution for GPS attitude determination. Meas. Sci. Technol. 2007, 18, 2985–2990. [Google Scholar] [CrossRef]




| FU | Std | Mean | |||||||
|---|---|---|---|---|---|---|---|---|---|
| DD | SD1 | SD2 | DD | SD1 | SD2 | DD | SD1 | SD2 | |
| BE (mm) | 2.279 | 2.279 | 2.206 | 2.350 | 2.350 | 2.315 | 316.832 | 316.832 | 316.823 |
| BN (mm) | 2.642 | 2.642 | 2.506 | 2.404 | 2.404 | 2.423 | −239.761 | −239.761 | −239.826 |
| BU (mm) | 5.742 | 5.737 | 1.882 | 5.639 | 5.635 | 4.725 | −0.730 | −0.729 | 0.556 |
| Std | Mean | |||||
|---|---|---|---|---|---|---|
| DD | SD1 | SD2 | DD | SD1 | SD2 | |
| BE (mm) | 1.696 | 1.696 | 1.672 | 317.176 | 317.176 | 317.188 |
| BN (mm) | 1.916 | 1.916 | 1.841 | −239.648 | −239.648 | −239.612 |
| BU (mm) | 4.145 | 4.140 | 1.109 | −1.236 | −1.235 | −1.122 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Yu, C.; Dong, D.; Cai, M.; Zhou, F.; Wang, Z.; Zhang, L.; Zheng, Z. Formal Uncertainty and Dispersion of Single and Double Difference Models for GNSS-Based Attitude Determination. Sensors 2017, 17, 408. https://doi.org/10.3390/s17020408
Chen W, Yu C, Dong D, Cai M, Zhou F, Wang Z, Zhang L, Zheng Z. Formal Uncertainty and Dispersion of Single and Double Difference Models for GNSS-Based Attitude Determination. Sensors. 2017; 17(2):408. https://doi.org/10.3390/s17020408
Chicago/Turabian StyleChen, Wen, Chao Yu, Danan Dong, Miaomiao Cai, Feng Zhou, Zhiren Wang, Lei Zhang, and Zhengqi Zheng. 2017. "Formal Uncertainty and Dispersion of Single and Double Difference Models for GNSS-Based Attitude Determination" Sensors 17, no. 2: 408. https://doi.org/10.3390/s17020408
APA StyleChen, W., Yu, C., Dong, D., Cai, M., Zhou, F., Wang, Z., Zhang, L., & Zheng, Z. (2017). Formal Uncertainty and Dispersion of Single and Double Difference Models for GNSS-Based Attitude Determination. Sensors, 17(2), 408. https://doi.org/10.3390/s17020408







