Formation and Applications of the Secondary Fiber Bragg Grating †
Abstract
:1. Introduction
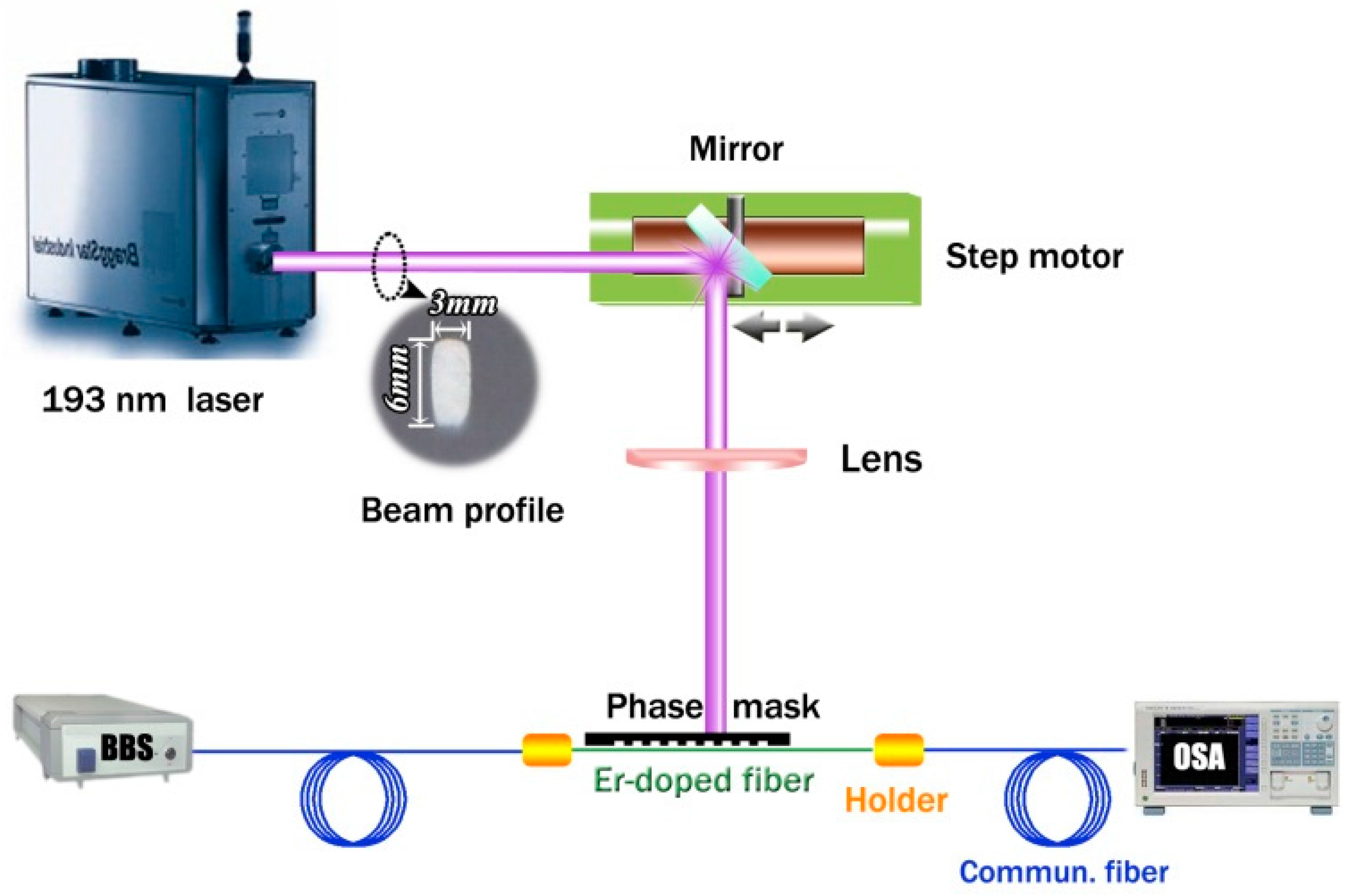
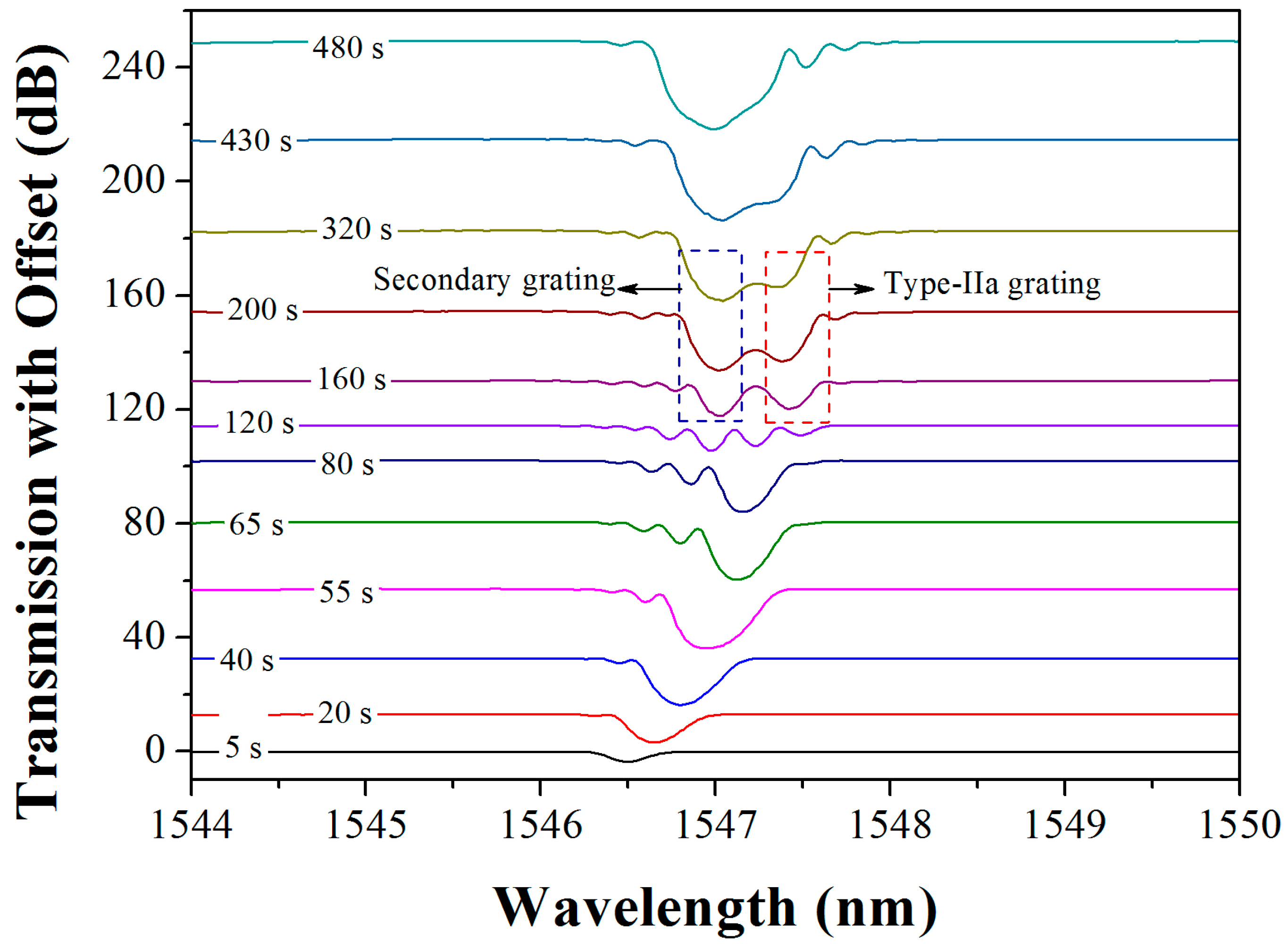
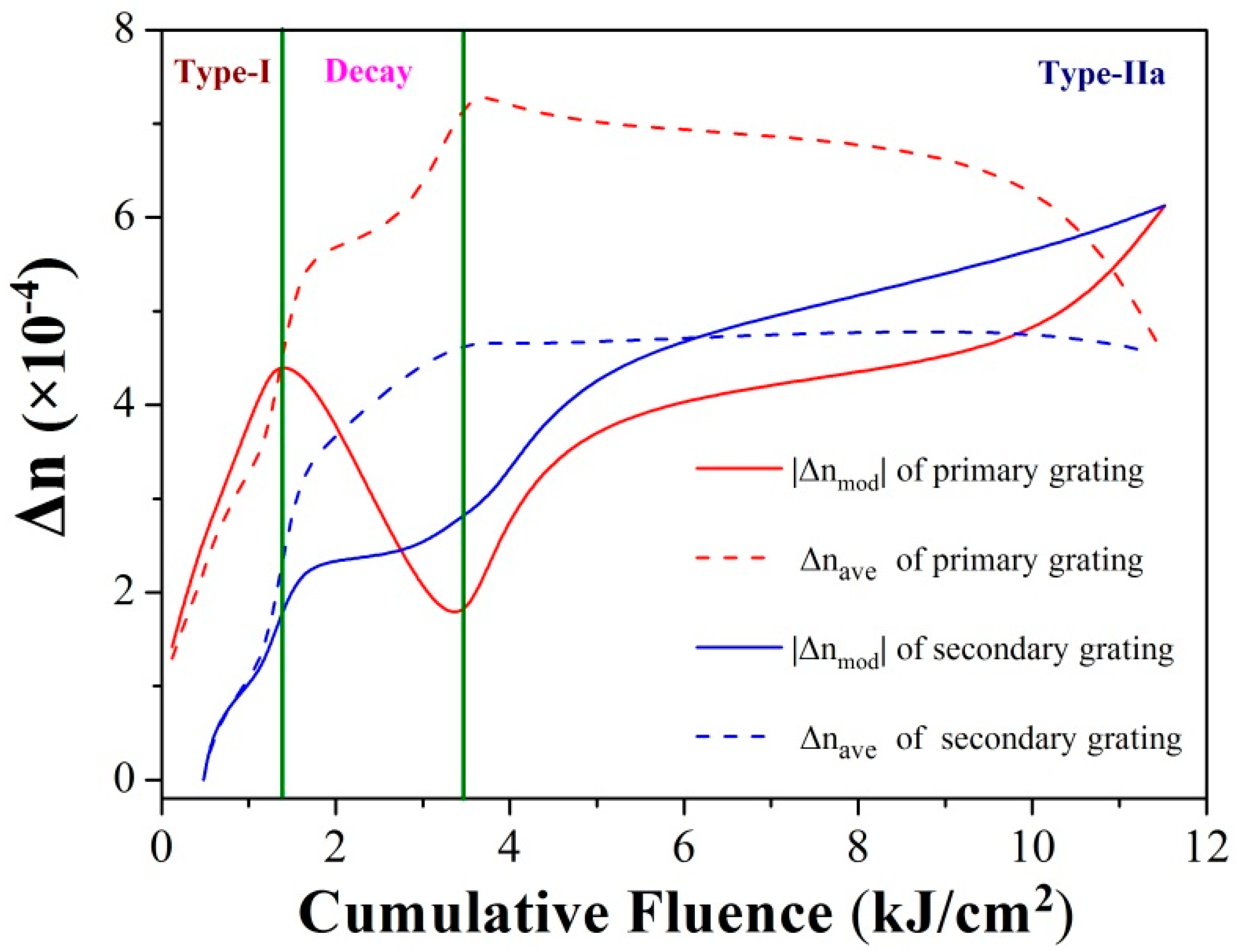
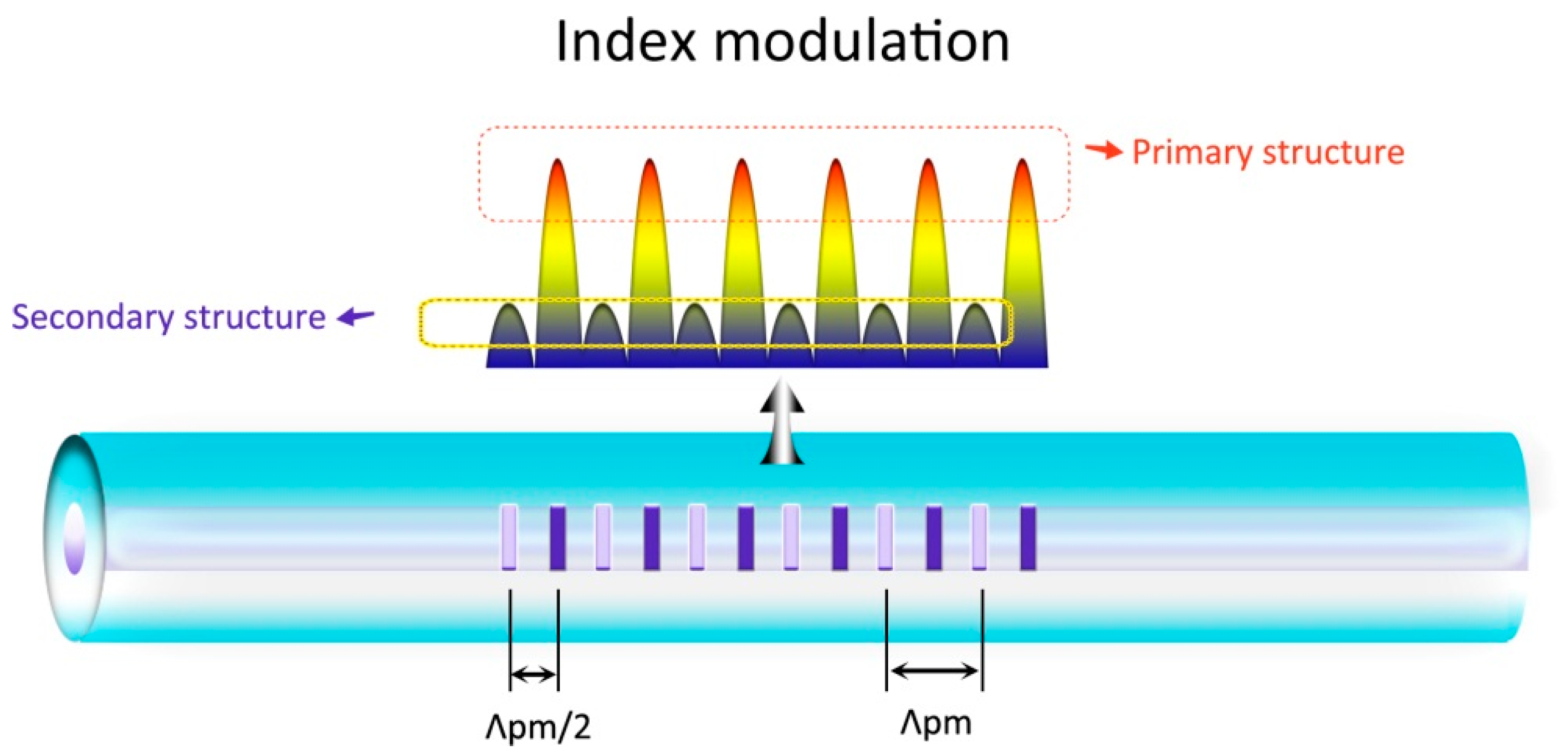
2. Formation of the SBGs
3. Applications of the SBGs
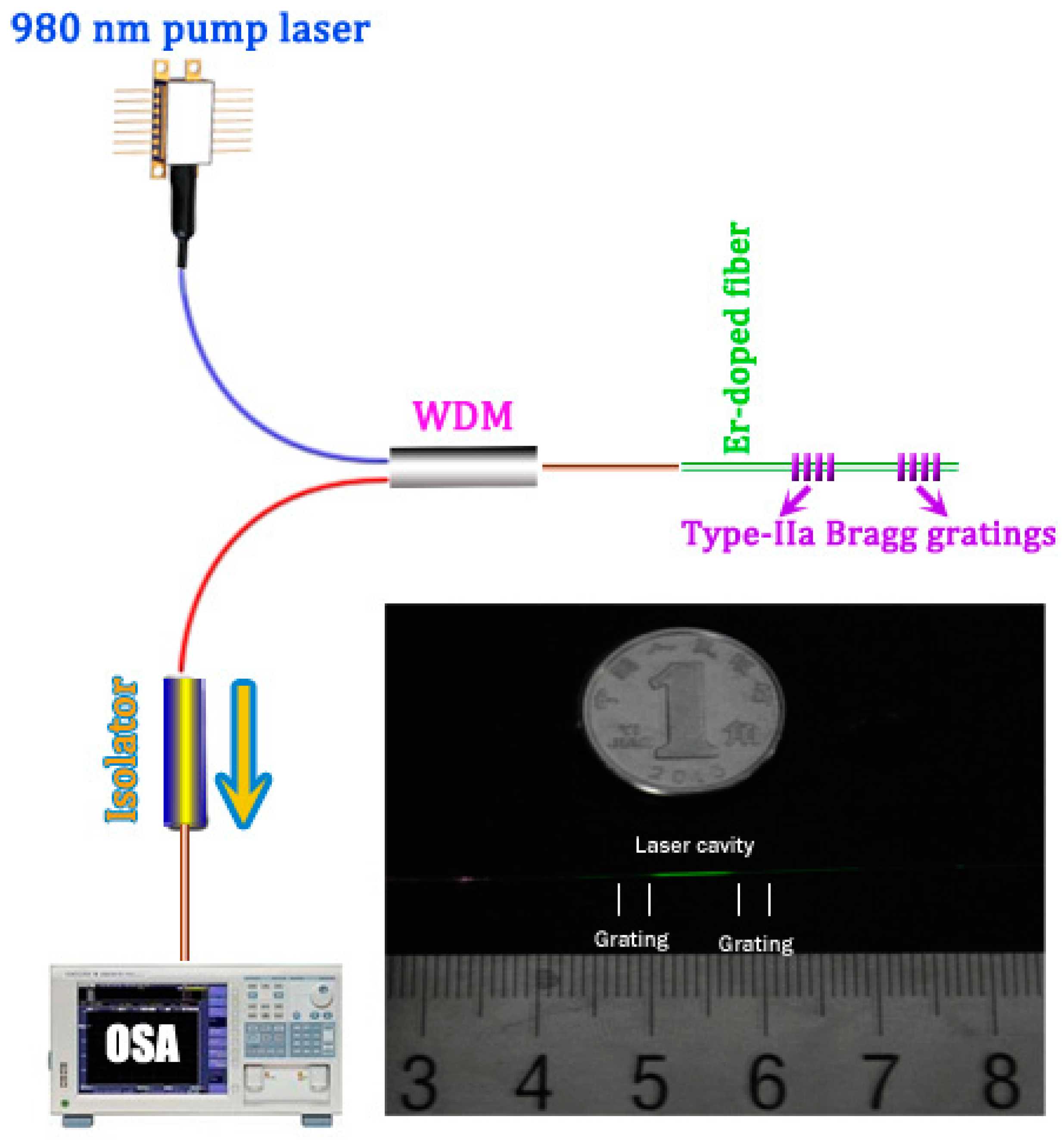
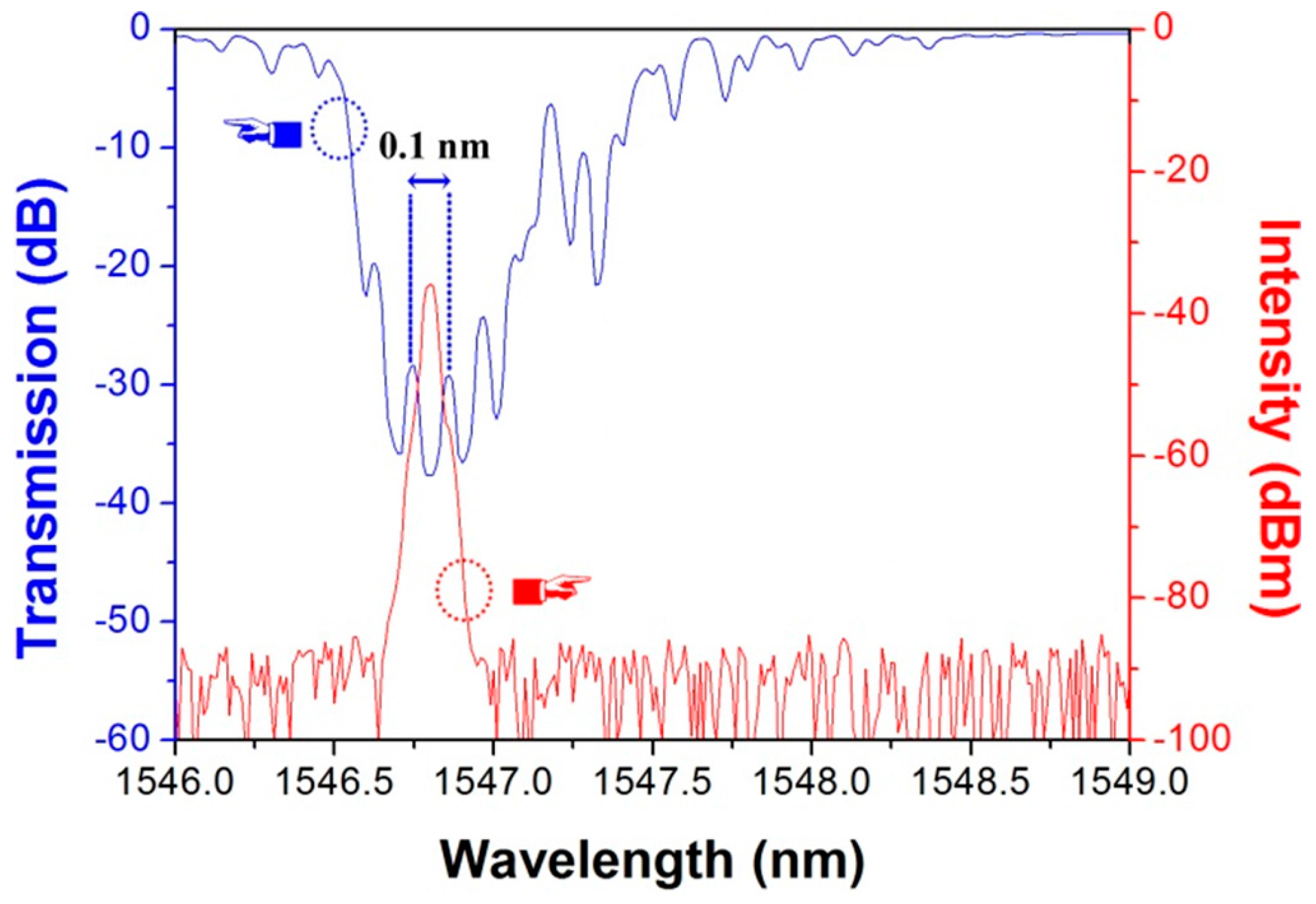
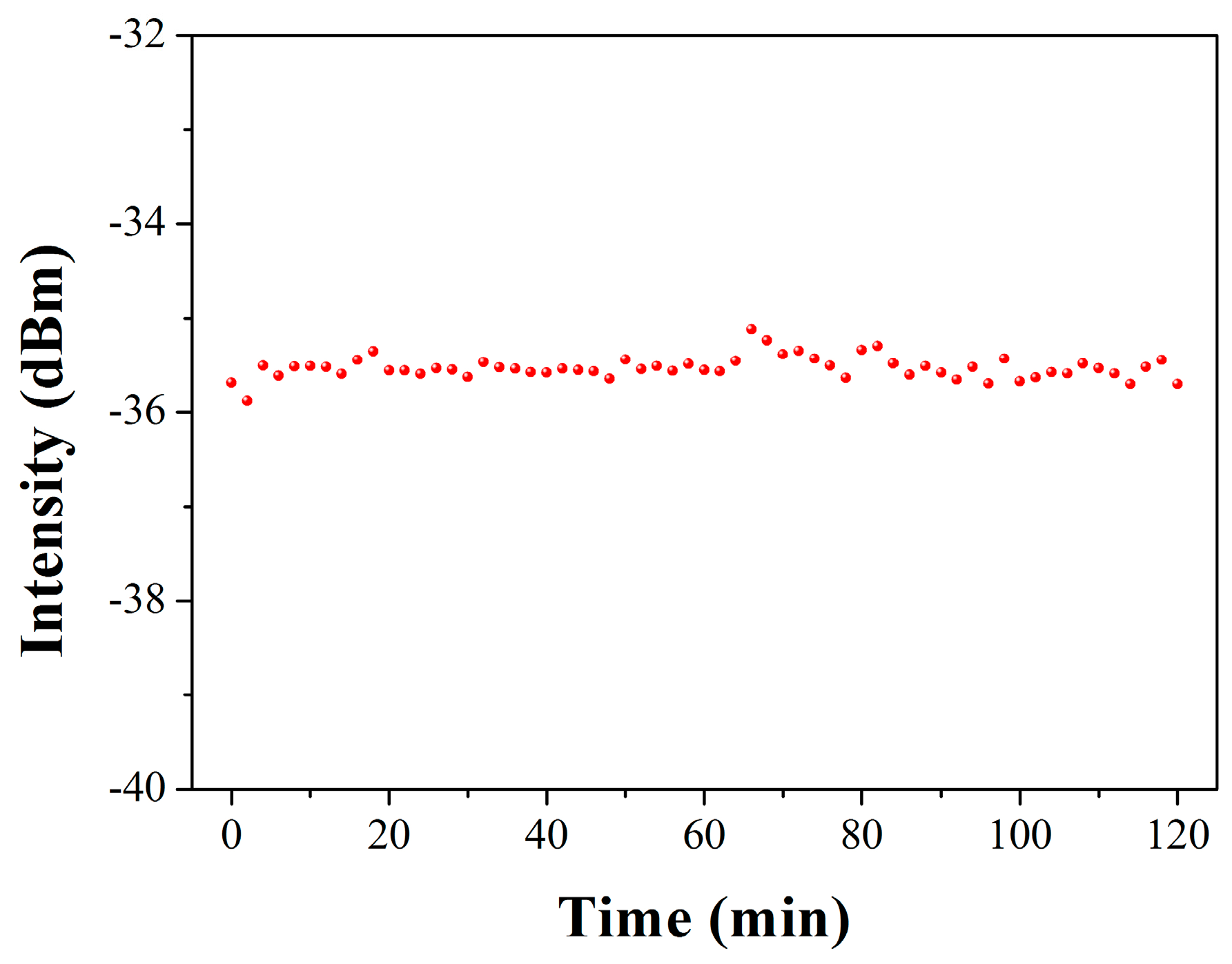
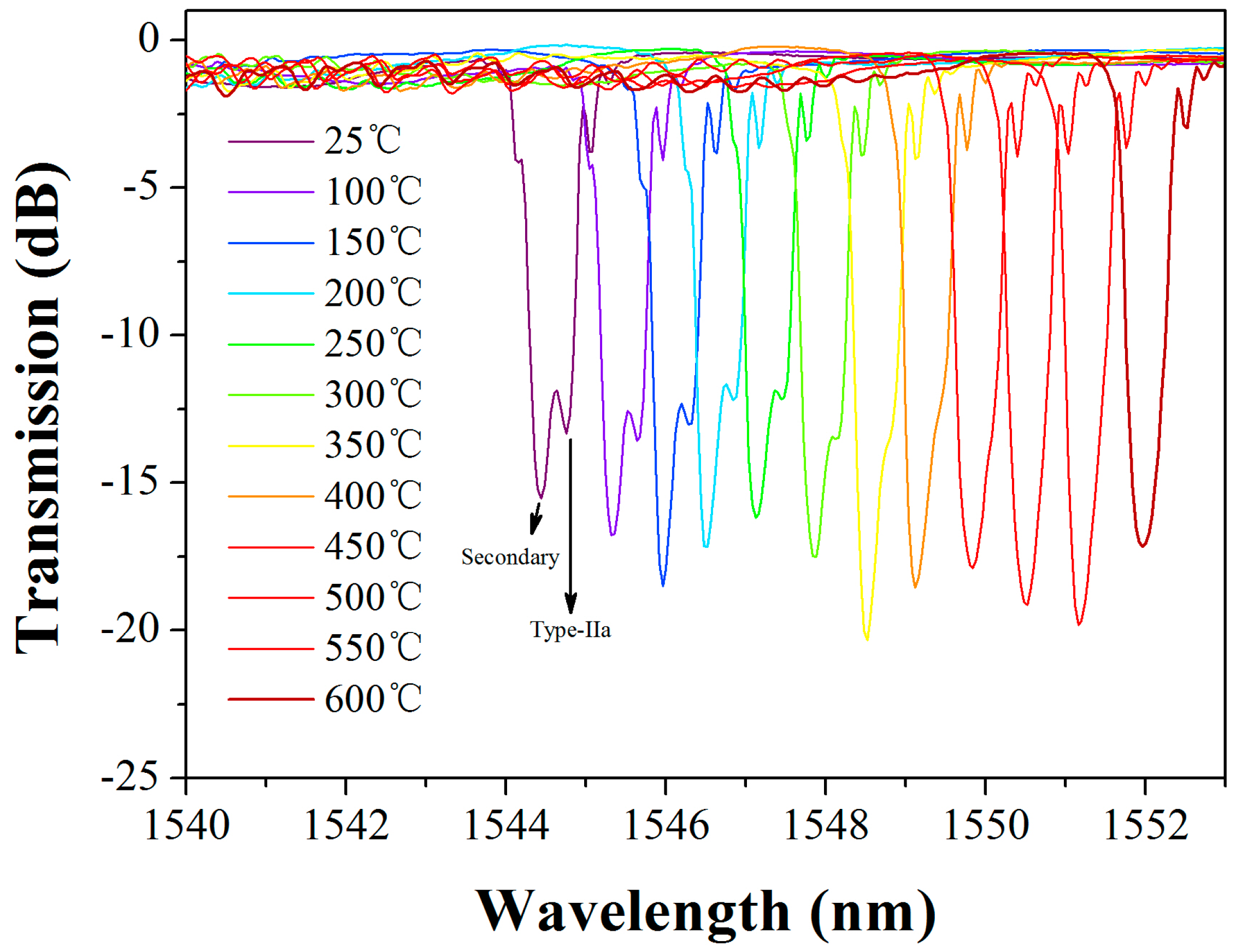
3.1. High-Temperature-Resistant Short-Cavity DBR Fiber Laser
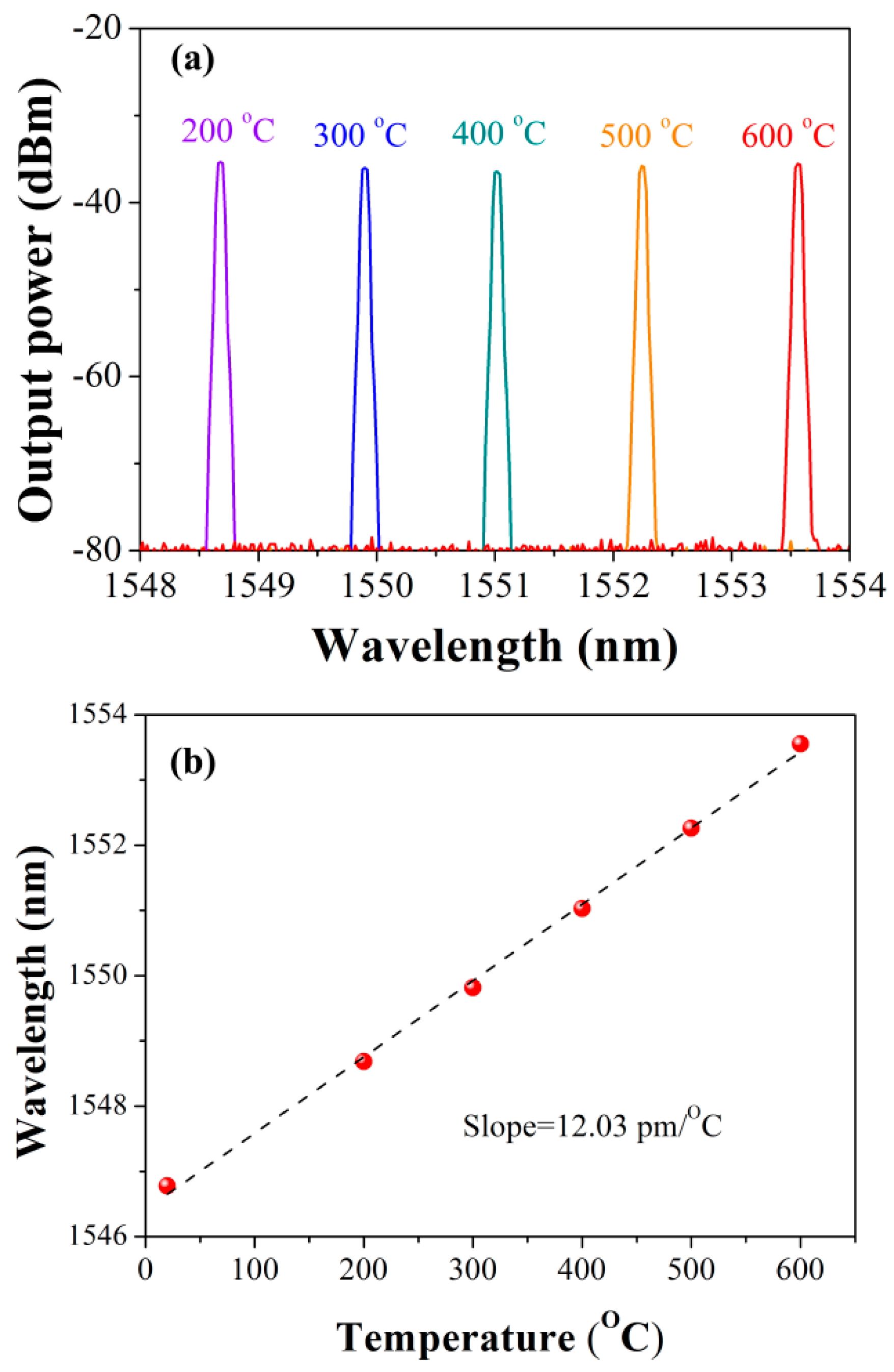
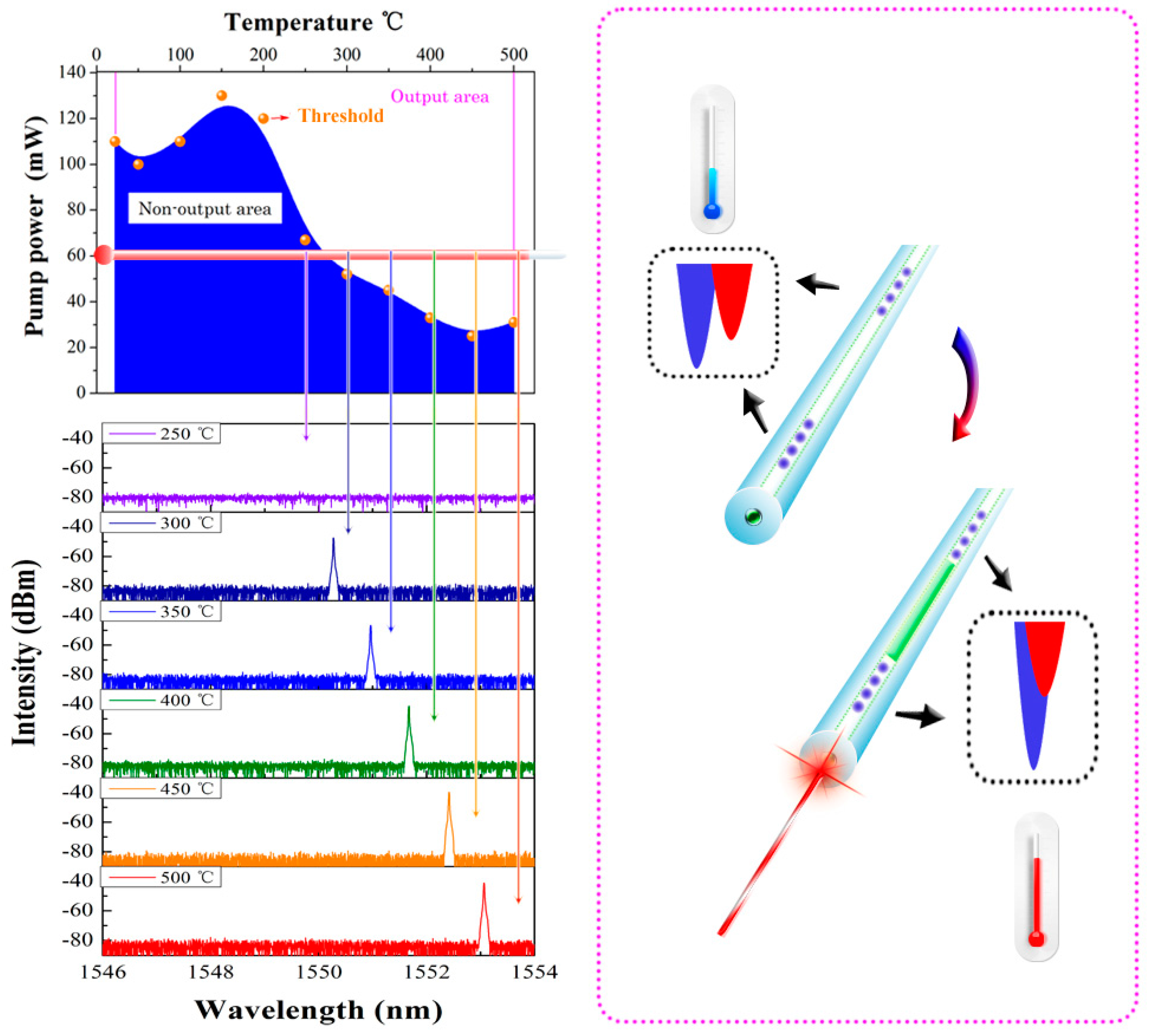
3.2. Thermally-Triggered DBR Fiber Laser
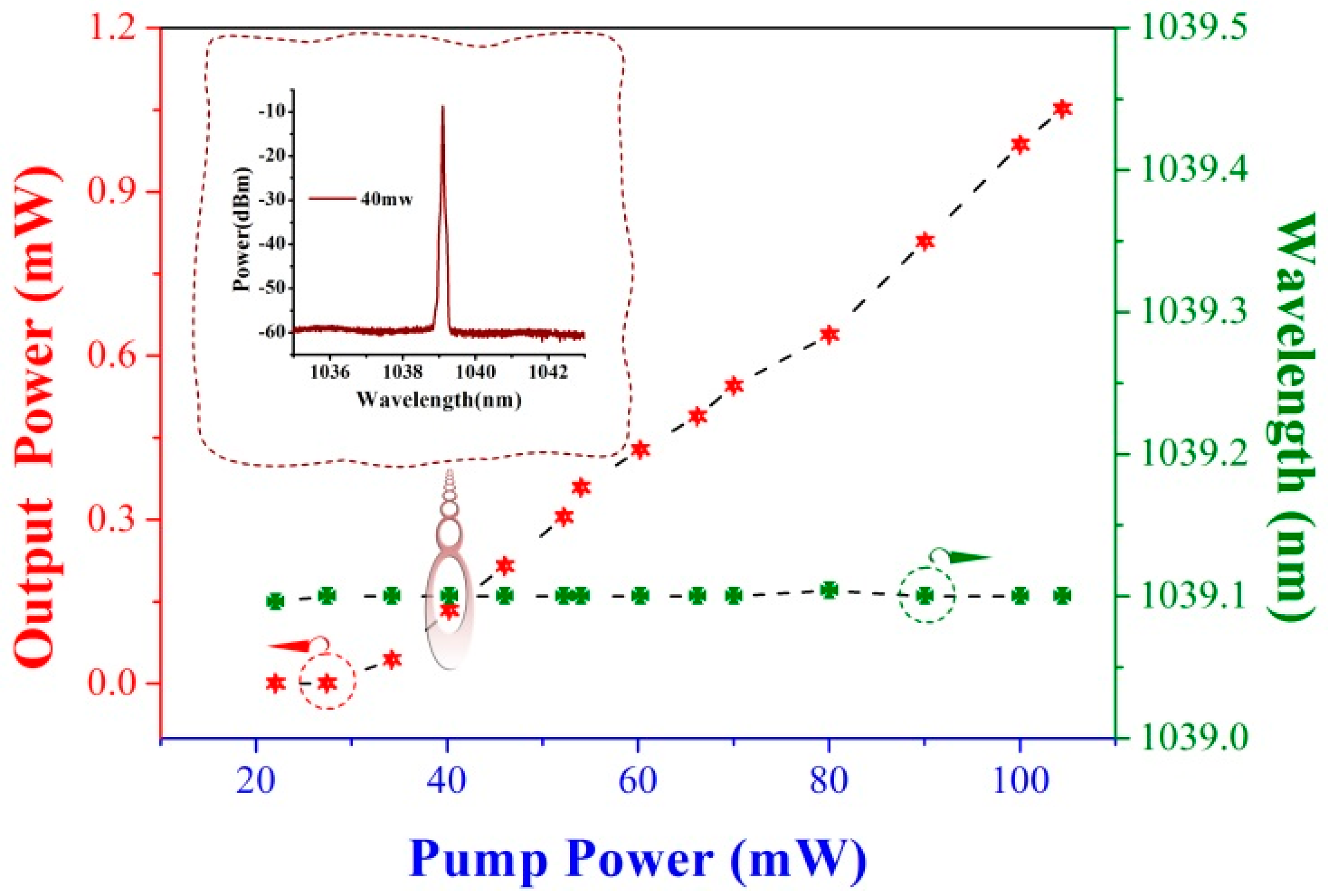
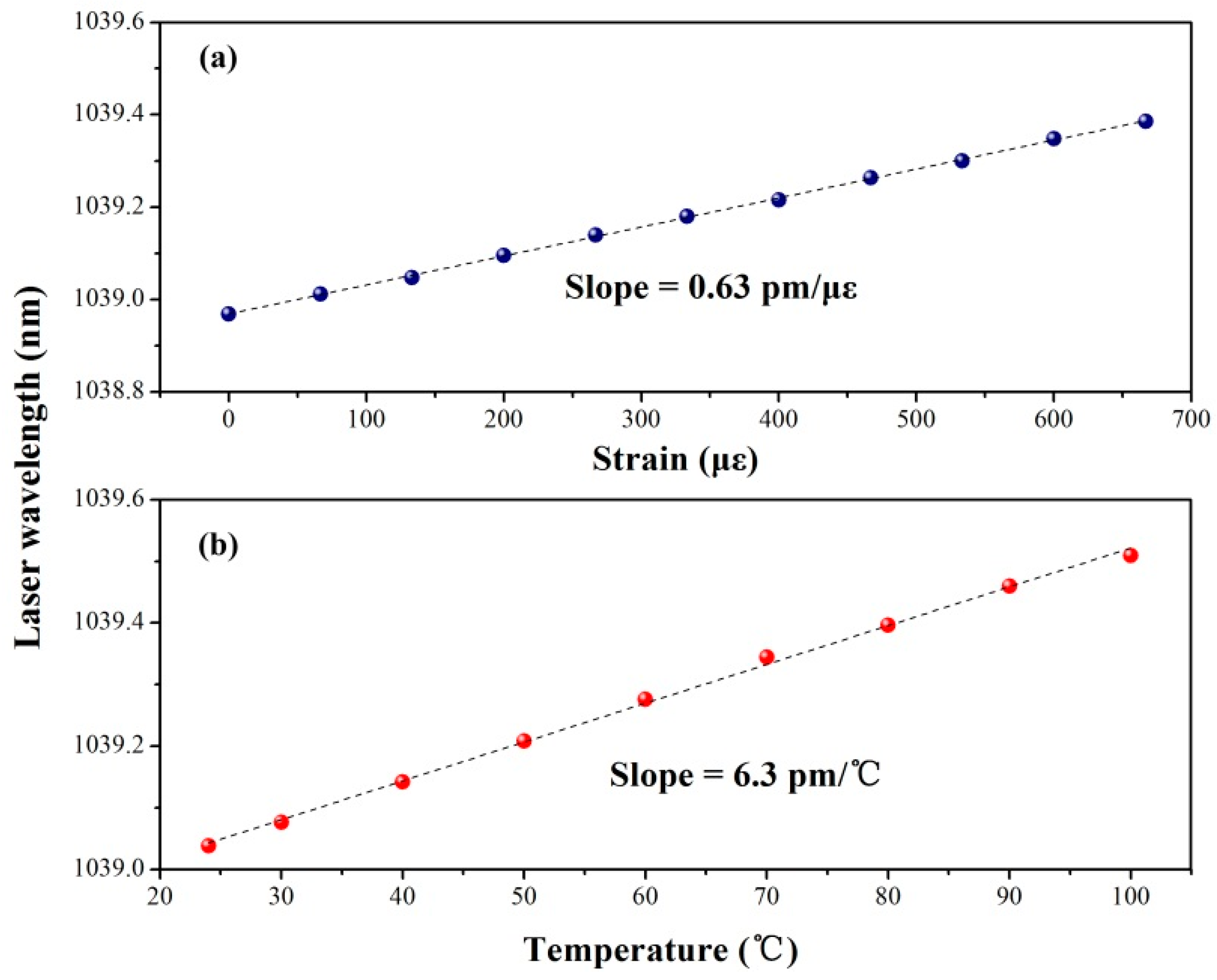
3.3. Third Harmonic Grating Fiber Laser Operating at 1-μm
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hill, K.O.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Lightwave Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Morey, W.W.; Meltz, G.; Glenn, W.H. Fibre optic Bragg grating sensors. Proc. SPIE 1989, 1169, 98–107. [Google Scholar]
- Rao, Y.J.; Ribeiro, A.B.L.; Jackson, D.A.; Zhang, L.; Bennion, I. Combined spatial- and time-division-multiplexing scheme for fibre grating sensors with drift-compensated phase-sensitive detection. Opt. Lett. 1995, 20, 2149–2151. [Google Scholar] [CrossRef] [PubMed]
- Shao, L.Y.; Xiong, L.Y.; Chen, C.K.; Laronche, A.; Albert, J. Directional bend sensor based on re-grown tilted fiber Bragg grating. J. Lightwave Technol. 2010, 28, 2681–2687. [Google Scholar] [CrossRef]
- Guo, T.; Shang, L.B.; Ran, Y.; Guan, B.O.; Albert, J. Fiber-optic vector vibroscope. Opt. Lett. 2012, 37, 2703–2705. [Google Scholar] [CrossRef] [PubMed]
- Fisher, N.E.; Webb, D.J.; Pannell, C.N.; Jackson, D.A.; Gavrilov, L.R.; Hand, J.W.; Zhang, L.; Bennion, I. Ultrasonic hydrophone based on short in-fiber Bragg gratings. Appl. Opt. 1998, 37, 8120–8128. [Google Scholar] [CrossRef] [PubMed]
- Ran, Y.; Tan, Y.N.; Sun, L.P.; Gao, S.; Li, J.; Jin, L.; Guan, B.O. 193 nm excimer laser inscribed Bragg gratings in microfibers for refractive index sensing. Opt. Express 2011, 19, 18577–18583. [Google Scholar] [CrossRef] [PubMed]
- Sun, D.D.; Guo, T.; Ran, Y.; Huang, Y.Y.; Guan, B.O. In-situ DNA hybridization detection with a reflective microfiber grating biosensor. Biosens. Bioelectron. 2014, 61, 541–546. [Google Scholar] [CrossRef] [PubMed]
- Canning, J. Fibre gratings and devices for sensors and lasers. Laser Photon. Rev. 2008, 2, 275–289. [Google Scholar] [CrossRef]
- Mihailov, S.J. Fiber Bragg grating sensors for harsh environments. Sensors 2012, 12, 1898–1918. [Google Scholar] [CrossRef] [PubMed]
- Cordier, P.; Dupont, S.; Douay, M.; Martinelli, G.; Bernage, P.; Niay, P.; Bayon, J.; Dong, L. Evidence by transmission electron microscopy of densification associated to Bragg grating photoimprinting in germanosilicate optical fibers. Appl. Phys. Lett. 1997, 70, 1204–1206. [Google Scholar] [CrossRef]
- Dianov, E.; Plotnichenko, V.; Koltashev, V.; Pyrkov, Y.N.; Ky, N.; Limberger, H.; Salathe, R. UV-irradiation-induced structural transformation of germanoscilicate glass fiber. Opt. Lett. 1997, 22, 1754–1756. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Liu, W.F.; Reekie, L. Negative-index gratings formed by a 193-nm excimer laser. Opt. Lett. 1996, 21, 2032–2034. [Google Scholar] [CrossRef] [PubMed]
- Riant, I.; Haller, F. Study of the photosensitivity at 193 nm and comparison with photosensitivity at 240 nm influence of fiber tension: Type IIa aging. J. Lightwave Technol. 1997, 15, 1464–1469. [Google Scholar] [CrossRef]
- Ky, N.H.; Limberger, H.G.; Salath, R.P.; Cochet, F.; Dong, L. UV-irradiation induced stress and index changes during the growth of Type-I and Type-IIa fiber gratings. Opt. Commun. 2003, 225, 313–318. [Google Scholar] [CrossRef]
- Groothoff, N.; Canning, J. Enhanced type IIa gratings for high-temperature operation. Opt. Lett. 2004, 29, 2360–2362. [Google Scholar] [CrossRef] [PubMed]
- Rollinson, C.; Wade, S.A.; Dragomir, N.; Baxter, G.W.; Collins, S.F.; Roberts, A. Reflections near 1030 nm from 1540 nm fibre Bragg gratings: Evidence of a complex refractive index structure. Opt. Commun. 2005, 256, 310–318. [Google Scholar] [CrossRef]
- Shu, X.; Liu, Y.; Zhao, D.; Gwandu, B.; Floreani, F.; Zhang, L.; Bennion, I. Dependence of temperature and strain coefficients on fiber grating type and its application to simultaneous temperature and strain measurement. Opt. Lett. 2002, 27, 701–703. [Google Scholar] [CrossRef] [PubMed]
- Violakis, G.; Konstantaki, M.; Pissadakis, S. Accelerated recording of negative index gratings in Ge-doped optical fibers using 248-nm 500-fs laser radiation. IEEE Photon. Technol. Lett. 2006, 18, 1182–1184. [Google Scholar] [CrossRef]
- Pissadakis, S.; Livitziis, M.; Tsibidis, G.D.; Kobelke, J.; Schuster, K. Type IIa grating inscription in a highly nonlinear microstructured optical fiber. IEEE Photon. Technol. Lett. 2009, 21, 227–229. [Google Scholar] [CrossRef]
- Prakash, O.; Kumar, J.; Mahakud, R.; Agrawal, S.K.; Dixit, S.K.; Nakhe, S.V. Enhanced temperature (~800 °C) stability of Type-IIa FBG written by 255 nm beam. IEEE Photon. Technol. Lett. 2014, 26, 93–95. [Google Scholar] [CrossRef]
- Ran, Y.; Jin, L.; Gao, S.; Sun, L.P.; Huang, Y.Y.; Li, J.; Guan, B.O. Type IIa Bragg gratings formed in microfibers. Opt. Lett. 2015, 40, 3802–3805. [Google Scholar] [CrossRef] [PubMed]
- Ran, Y.; Feng, F.R.; Liang, Y.Z.; Jin, L.; Guan, B.O. Type IIa Bragg grating based ultra-short DBR fiber laser with high temperature resistance. Opt. Lett. 2015, 40, 5706–5709. [Google Scholar] [CrossRef] [PubMed]
- Dyer, P.; Farley, R.; Giedl, R. Analysis of grating formation with excimer laser irradiated phase masks. Opt. Commun. 1995, 115, 327–334. [Google Scholar] [CrossRef]
- Rollinson, C.M.; Wade, S.A.; Kouskousis, B.P.; Kitcher, D.J.; Baxter, G.W.; Collins, S.F. Variations of the growth of harmonic reflections in fiber Bragg gratings fabricated using phase masks. J. Opt. Soc. Am. A 2012, 29, 1259–1268. [Google Scholar] [CrossRef] [PubMed]
- Mills, J.D.; Hillman, C.W.J.; Blott, B.H.; Brocklesby, W.S. Imaging of free-space interference patterns used to manufacture fiber Bragg gratings. Appl. Opt. 2000, 39, 6128–6135. [Google Scholar] [CrossRef] [PubMed]
- Feng, F.R.; Ran, Y.; Liang, Y.Z.; Gao, S.; Feng, Y.H.; Jin, L.; Guan, B.O. Thermally triggered fiber lasers based on secondary-type In Bragg gratings. Opt. Lett. 2016, 41, 2470–2473. [Google Scholar] [CrossRef] [PubMed]
- Erdogan, T. Fiber grating spectra. J. Lightwave Technol. 1997, 15, 1277–1294. [Google Scholar] [CrossRef]
- Yam, S.P.; Brodzeli, Z.; Kouskousis, B.P.; Rollinson, C.M.; Wade, S.A.; Baxter, G.W.; Collins, S.F. Fabrication of a π-phase-shifted fiber Bragg grating at twice the Bragg wavelength with the standard phase mask technique. Opt. Lett. 2009, 34, 2021–2023. [Google Scholar] [CrossRef] [PubMed]
- Feng, F.R.; Liu, T.; Xiao, P.; Ran, Y.; Liang, H.; Jin, L.; Guan, B.O. 1-μm-wavelength ytterbium-doped fiber laser based on the third harmonic reflection in secondary-Type-In Bragg gratings. Opt. Lett. 2016, 41, 4999–5002. [Google Scholar] [CrossRef] [PubMed]
- Wo, J.; Jiang, M.; Malnou, M.; Sun, Q.; Zhang, J.; Shum, P.P.; Liu, D. Twist sensor based on axial strain insensitive distributed Bragg reflector fiber laser. Opt. Express 2012, 20, 2844–2850. [Google Scholar] [CrossRef] [PubMed]
- Babin, S.A.; Churkin, D.V.; Ismagulov, A.E.; Kablukov, S.I.; Nikulin, M.A. Single frequency single polarization DFB fiber laser. Laser Phys. Lett. 2007, 4, 428–432. [Google Scholar] [CrossRef]
- Xu, S.; Yang, Z.; Zhang, W.; Wei, X.; Qian, Q.; Chen, D.; Zhang, Q.; Shen, S.; Peng, M.; Qiu, J. 400 mW ultrashort cavity low-noise single-frequency Yb3+-doped phosphate fiber laser. Opt. Lett. 2011, 36, 3708–3710. [Google Scholar] [CrossRef] [PubMed]
- Mo, S.; Xu, S.; Huang, X.; Zhang, W.; Feng, Z.; Chen, D.; Yang, T.; Yang, Z. A 1014 nm linearly polarized low noise narrow-linewidth single-frequency fiber laser. Opt. Express 2013, 21, 12419–12423. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Li, C.; Zhang, W.; Mo, S.; Yang, C.; Wei, X.; Feng, Z.; Qian, Q.; Shen, S.; Peng, M.; et al. Low noise single-frequency single-polarization ytterbium-doped phosphate fiber laser at 1083 nm. Opt. Lett. 2013, 38, 501–503. [Google Scholar] [CrossRef] [PubMed]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, B.-O.; Ran, Y.; Feng, F.-R.; Jin, L. Formation and Applications of the Secondary Fiber Bragg Grating. Sensors 2017, 17, 398. https://doi.org/10.3390/s17020398
Guan B-O, Ran Y, Feng F-R, Jin L. Formation and Applications of the Secondary Fiber Bragg Grating. Sensors. 2017; 17(2):398. https://doi.org/10.3390/s17020398
Chicago/Turabian StyleGuan, Bai-Ou, Yang Ran, Fu-Rong Feng, and Long Jin. 2017. "Formation and Applications of the Secondary Fiber Bragg Grating" Sensors 17, no. 2: 398. https://doi.org/10.3390/s17020398
APA StyleGuan, B.-O., Ran, Y., Feng, F.-R., & Jin, L. (2017). Formation and Applications of the Secondary Fiber Bragg Grating. Sensors, 17(2), 398. https://doi.org/10.3390/s17020398





