1. Introduction
The demand for a compact, portable camera is rapidly growing because of popularized consumer hand-held cameras with easy handling and compact size such as mobile cameras, digital cameras, digital camcorders, drone cameras, and wearable cameras. With the advancement of cloud services, acquisition of high quality videos becomes more important to share contents without the barriers of time and space. However, video sequences are subject to undesired vibrations due to camera shaking caused by poor handling and/or a dynamic, unstable environment. To overcome this problem, various video stabilization methods have been developed to improve the visual quality of various hand-held cameras [
1]. A mechanical video stabilization system controls the camera vibrations using the gyro sensor or accelerometer. It either moves the lens to change the light path and the optical axis or uses an internal sensor to minimize the shaky motion. In spite of the high performance, the mechanical and optical video stabilizer is not suitable for portable camera because of the increased volume and cost of the system. On the other hand, an image processing-based video stabilizer can efficiently remove the movement of video frames without extra cost of additional hardware devices.
An image processing-based video stabilization method generally consists of two steps: (i) removing undesired motion by smoothing the camera path and (ii) rendering the stabilized frames [
2]. Existing video stabilization systems can be classified by the camera path estimation method. Early two-dimensional (2D) stabilization methods used the block matching algorithm to estimate inter-frame motion vectors. Jang et al. estimated the optimal affine model between adjacent frames by using a variable block size [
3]. Xu et al. proposed a video stabilization algorithm using circular block matching and least square fitting [
4]. Since the 2D block matching-based methods can easily estimate the camera path, they are applied in various applications [
5]. However, they are sensitive to noise and produce a matching error between acquired video frames under a dynamic environment. An improved 2D video stabilization method used the optical flow to estimate the global camera path. Chang et al. used the Lucas-Kanade optical flow estimation algorithm to define an affine motion model between frames, and stabilized the camera path by motion compensation [
6]. Matsushita et al. estimated the camera path using the homography between adjacent frames and smoothed the global path using a Gaussian kernel [
7]. Xu et al. used Horn-Schunck optical flow estimation algorithm to compute an affine model between successive frames and smoothed camera path by model-fitting filter [
8]. Although optical flow-based stabilization methods can compute an affine motion model in a simple, flexible manner, they fail to stabilize multiple objects with different distances at the same time. To improve the quality of stabilized video, an alternative approach used feature points to estimate a rotation- and scale-invariant camera path. Battiato et al. used the scale invariant feature transform (SIFT) to estimate the camera path and reduce the estimation error using the least squares algorithm [
9]. Lee et al. used trajectories of SIFT feature points to estimate the camera path and minimized an energy function to smooth the camera path with reducing geometric distortion [
10]. Xu et al. estimated motion parameters of the affine model using the fast accelerated segment test (FAST) algorithm for video stabilization [
11]. Nejadasl et al. stabilized calibrated image sequence using the Kanade-Lucas-Tomasi (KLT) tracker and SIFT [
12]. Cheng et al. presented motion detection using the speeded up robust features (SURF) and modified random sample consensus (RANSAC) for video stabilization [
13]. To define a more powerful 2D camera model, the locally estimated camera path are proposed. Liu et al. modeled mesh-based 2D camera motion with bundled camera path to improve the video stabilization performance [
14], and Kim et al. classified background feature points using the KLT tracker [
15]. Although 2D video stabilization methods are faster and robust because of the use of a linear transformation, they fail to estimate the optimal camera path in textureless regions.
Currently, 3D camera motions are estimated based on the image segmentation result to improve the quality of a video. Liu et al. proposed a 3D video stabilization method using structure from motion and spatial warping to preserve 3D structures [
16]. Zhou et al. generated labeled frames using 3D point cloud and estimated the homography of each label to reduce distortion in textureless regions [
17]. The 3D stabilization methods can generate higher quality results and are suitable for an accurate video analysis [
18,
19]. However it is hard to implementation in real-time or near real-time service because of the high computational complexity, and these methods have the common problem of the parallax caused by feature tracking failure in flat region.
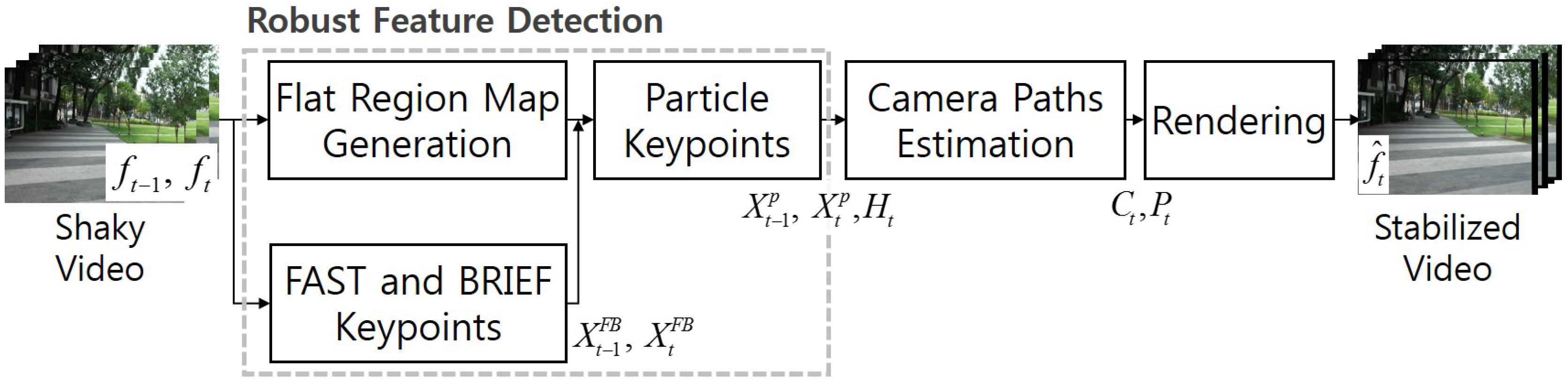
To solve these problems, this paper presents a novel video stabilization algorithm using a robust feature detection method to improve existing 2D methods instead of the less robust 3D methods. The proposed algorithm redefines important feature points using particle keypoints. The homography is accurately estimated by detecting robust particle keypoints. Undesired motions are removed by minimizing the temporal total-variation of the camera path. As a result, the proposed method provides a significantly increased visual quality of shaky video acquired by a handheld camera.
This paper is organized as follows.
Section 2 presents theoretical background of video stabilization.
Section 3 presents the robust feature extraction and matching based video stabilization and
Section 4 presents the optimal camera path estimation. Experimental results are given in
Section 5, and
Section 6 concludes the paper.
4. Estimation of the Optimal Camera Path
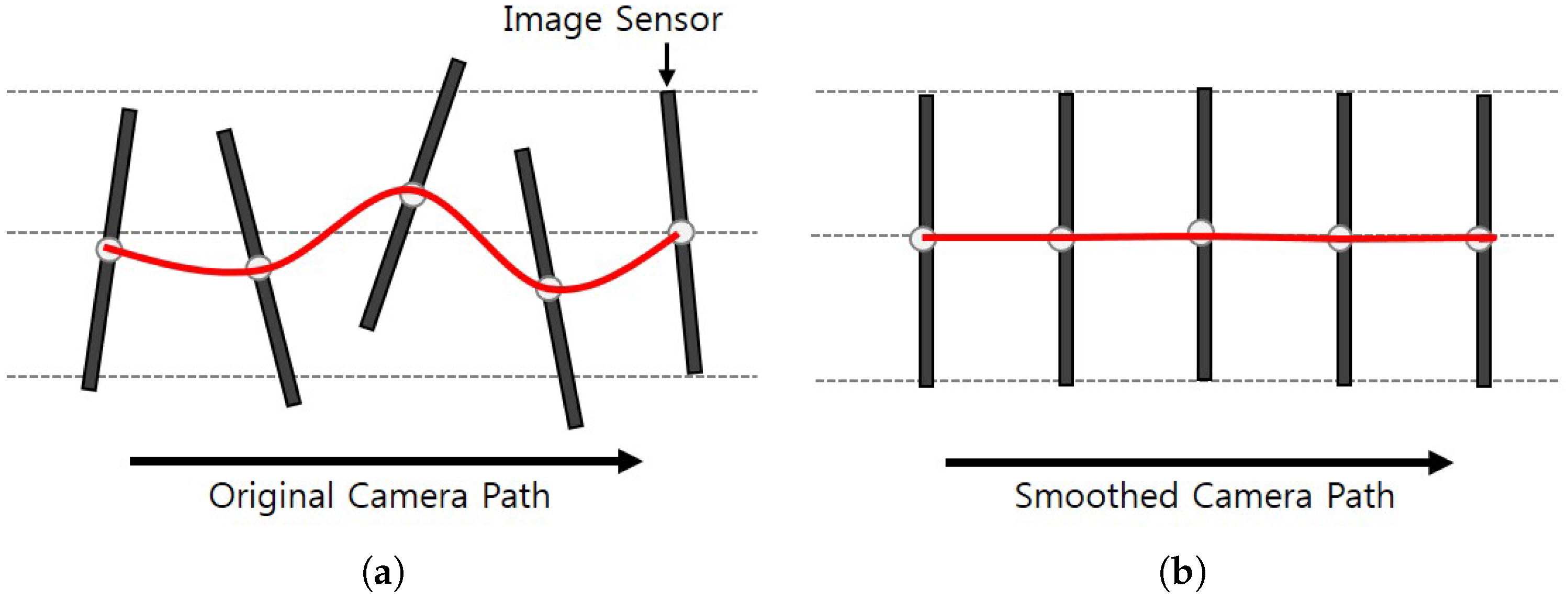
Traditional video stabilization methods use a moving average of Gaussian filter to smooth the camera path. The moving average filter can smooth the camera path using the temporal mean of neighboring frames. The Gaussian kernel can remove undesired motion using the global transformation [
7]. However, these methods fail to track a sharp change of the camera path. Furthermore, the performance of video stabilization becomes low when cropping regions and the amount of distortion increase. To solve this problem, the proposed method adaptively smooths the camera path using 1D TV algorithm [
31]. The holes represent an empty region in a video frame which is generated after moving the frame by smoothed camera path. To compensate the holes, the boundary region of a stabilized video is generally cropped out, and the remaining central region is enlarged to fill the original size of the video frame. Therefore it is important to minimize the hole region to preserve the original contents. The stabilized video has less holes since the TV method can preserve the original path and removes undesired outliers.
Given the optimal homography
between
and
, a global camera path
is generated. The corner points denoted as
in
input shaky frame
are transformed to
by
.
can be regarded as the transformation matrix of the camera movement. Therefore, the camera motion between
and
is simply considered as the difference between
and
. The global camera path
is computed by adding the movement of adjacent frames as
where
. The estimated global camera path
is smoothed by 1D TV for video stabilization. The energy function for the smoothed camera path
is defined as
where
A the temporal difference matrix
and
λ represents the weight coefficient for smoothing. The first term of Equation (
6) enforces the smoothed camera path that is close to the original path, and the second removes noisy motions by smoothing the camera path. The energy function of Equation (
6) can be minimized by the iterative clipping algorithm.
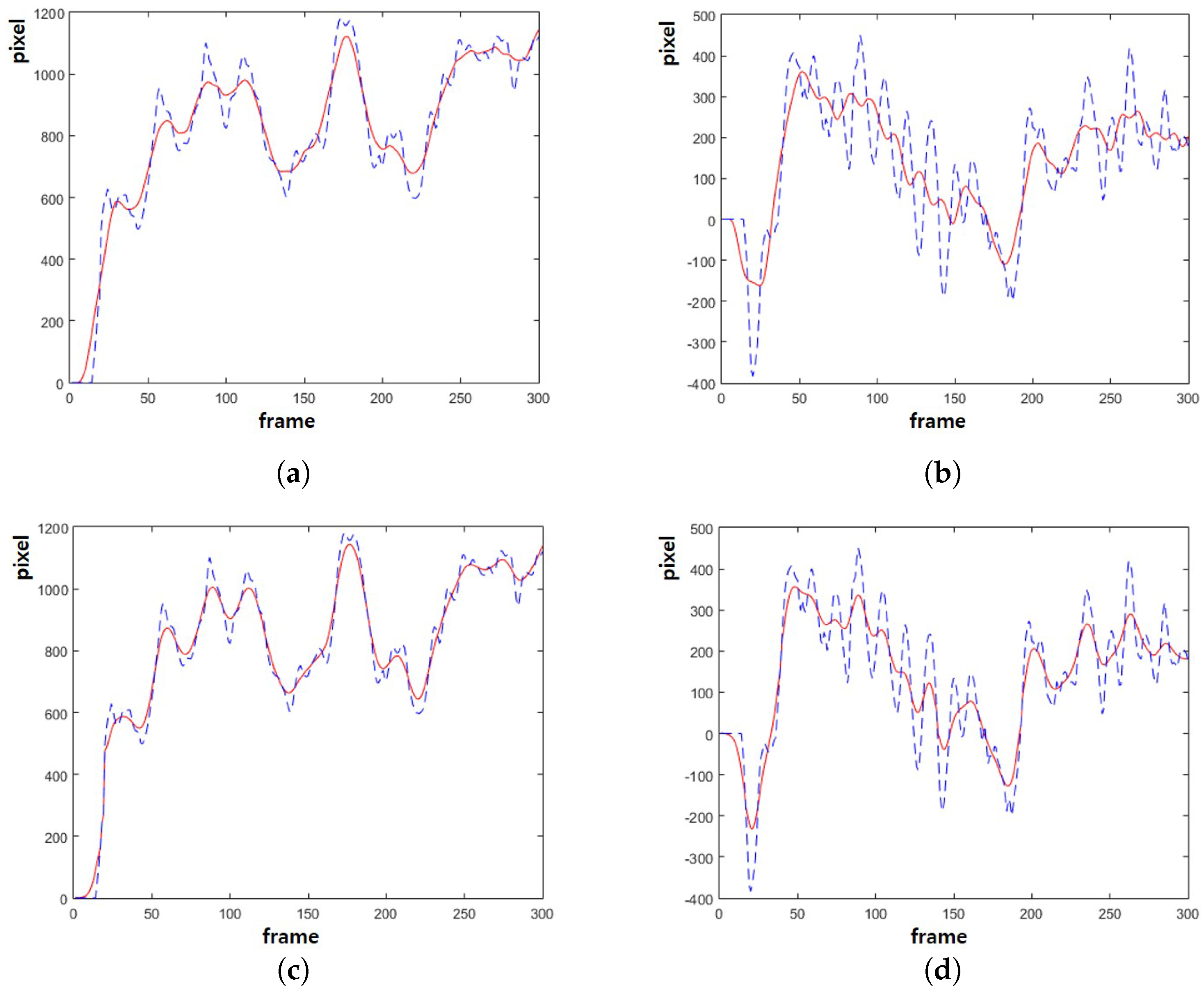
Figure 5 shows the estimated camera path using the proposed method.
Figure 5a shows the
x-coordinates of the original camera path in the dotted curve and the smoothed path using the moving average filter in the solid curve.
Figure 5b shows the
y-coordinates of the original camera path in the dotted curve and the smoothed path using the moving average filter in the solid curve.
Figure 5c shows the
x-coordinates of the original camera path in the dotted curve and the smoothed path using the proposed method in the solid curve.
Figure 5d shows the
y-coordinates of the original camera path in the dotted curve and the smoothed path using the proposed method in the solid curve. The proposed method can smooth the camera path without undesirable jitters and delay.
The final step of video stabilization is to reconstruct geometrically transformed frames using the smoothed camera path. The smoothed homography
can be estimated by the difference between the original camera path
and the smoothed path
as
where
represents the four corner points of the image. The stabilized video frame
is generated by transforming using
as
As a result, the proposed video stabilization method can successfully generate a stabilized video by estimating the optimal homography.
5. Experimental Results
This section presents experimental results and compares the performance of the proposed and existing methods. The proposed method improves the video quality by estimating the optimal homography using the particle keypoint update. To verify the accuracy of the estimated homography
of temporally adjacent frames,
and
, we tested the estimated projective transformation matrices from four feature different extraction methods, SIFT, SURF, FAST+BREIF, and the proposed method. We used SIFT and SURF algorithms with threshold values used in [
24,
25], respectively. Also, the proposed algorithm uses the intensity threshold t = 0.2 for FAST and a 256-bit string for BRIEF descriptor. After extracting feature points between
and
, each transformation matrix is estimated. By combining all correspondences from the four methods, we evaluated the motion errors between the correspondences using
l1-norm error evaluation as
where
represents the transformed feature points in the previous frame
, and
the feature points in the current frame.
Table 1 summarizes the error of estimated homography using the four feature detection algorithms. The proposed method estimates the more accurate homography than other feature extraction methods as shown in
Table 1.
Figure 6a shows the 80th, 81st, and 82nd frames in the original shaky video, and
Figure 6b the correspondingly stabilized frames using the feature-based global camera path smoothing method [
7], which cannot avoid a geometric distortion on the boundary because of the inaccurately estimated homography. We can easily find the distortion from the vertical structure on the right side of each frame. The bundled path algorithm fails in warping textureless blocks on the bottom of frame as shown in
Figure 6c [
14]. On the other hand, the proposed particle keypoint-based method can significantly enhance the shaky video with less geometric distortion on the boundary as shown in
Figure 6d.
Figure 7 shows the expanded version of an upper right region of
Figure 6 for clearer comparison. The long object at the right side of each image is observed carefully.
Figure 7a shows the expanded images of three temporally adjacent frames in original shaky video and
Figure 7b shows the results of the stabilized video with geometric distortion by feature-based global smoothed camera path estimation method [
7]. As shown in
Figure 7c, the video stabilization method based on the bundled path could not successfully stabilize the video [
14]. On the other hand, the proposed stabilized algorithm improves considerably the video quality with preserving the contents.
Figure 8 shows the difference of two temporally adjacent frames.
Figure 8a shows the differences of three pairs of original frames {(79, 80), (80, 81), (81, 82)}.
Figure 8b shows the differences of three pairs of stabilized frames {(79, 80), (80, 81), (81, 82)}. As shown in
Figure 8, the proposed method can significantly compensate the undesirable movements.
To evaluate the empty region caused by the process of frame registration for stabilization, we compared the results of the proposed stabilization method and YouTube stabilizer using the same test video as shown in
Figure 9. Stabilized frames are cropped to eliminate the missing boundaries, so it is important to have less cropping ratio to preserve the significant region of the original image. To measure the amount of cropping in various stabilization methods, tick marks are inserted on the diagonal line in the 80th input frame as shown in
Figure 9a.
Figure 9b,c respectively show the stabilized frames using auto-directed video stabilization method [
32] and the proposed video stabilization method. As shown in
Figure 9, the proposed video stabilization method can successfully preserve the contents of input frame with a reduced cropping ratio.
Figure 10 shows the same test results of
Figure 6 using different input video.
Figure 10a shows the 170th, 171st, and 172nd frames of the input shaky video captured by a mobile camera. The significant portions of the stabilized video using the existing methods in [
7,
14] are removed by cropping to eliminate holes in the boundaries as shown in
Figure 10b,c. As shown in
Figure 10d, the stabilized video using the proposed method shows significantly improved video quality by removing undesired artifacts.
As shown
Figure 11, a bottom right region of
Figure 10 is enlarged to easily compare the results.
Figure 11a shows the enlarged three original frames, and
Figure 11b shows the stabilized results using the feature-based global camera path smoothing method [
7].
Figure 11c shows the stabilized frames using the bundled path algorithm [
14]. As shown in
Figure 11d, the proposed method successfully obtains stabilized video with less holes.
Figure 12 shows the same results of
Figure 8 to demonstrate performance using the second test video.
Figure 12a shows the differences of three pairs of original frames {(169, 170), (170, 171), (171, 172)}, and
Figure 12b shows the differences of three pairs of stabilized frames {(169, 170), (170, 171), (171, 172)}.
Figure 13 compares the performance of various camera path smoothing methods. Each resulting frame is divided into sixteen rectangular grids to easily evaluate the performance of the stabilization.
Figure 13a shows the input shaky video frames acquired by a hand-held camera, and
Figure 13b shows the results of stabilized video by smoothing the camera path using a moving average filter [
7]. The stabilized frames using the proposed method that minimized the 1D TV are shown in
Figure 13c. Based on comparing each grid, the proposed method can successfully enhance the shaky video with significantly reduced holes.
Figure 14 shows the enlarged version of
Figure 13.
Figure 14a shows the first three frames in the original shaky video.
Figure 14b shows the distorted object moving back and forth in the center of each frame. On the other hand, the proposed method successfully reduces the noisy motion of the shaky video as shown in
Figure 14c.
Figure 15 shows results of the difference of the successive two frames.
Figure 15a shows the differences of three pairs of original frames {(274, 275), (275, 276), (276, 277)}.
Figure 15b shows the differences of three pairs of stabilized frames {(274, 275), (275, 276), (276, 277)}.
The difference between two successive frames is minimized since the proposed method reduces the noisy motions. To evaluate the objective performance, we used the peak signal to noise ratio (PSNR) values of the temporally adjacent frames. The PSNR is defined as
where
represents the mean square error, and
the maximum intensity value of the frames.
Table 2 summarizes the PSNR values of adjacent video frames stabilized by the proposed method. As a result, the proposed video stabilization can correct the location of the pixels in the adjacent frames.
Finally, we measured the perspective distortion for objective assessment of the proposed video stabilization method using Liu’s method [
14]. As mentioned in
Section 2, a perspective distortion generally occurs when the real world is projected onto the image sensor. An inaccurately estimated homography results in the perspective distortion that significantly degrades the geometric quality of the video. For that reason, we estimated the perspective distortion using the transformation between the original and stabilized frames. The homography of the stabilized image sequences can be defined as
where
and
respectively represent the cumulative homographies between adjacent frames of the observed shaky and stabilized videos, and
the transformation matrix. The perspective distortion is computed by averaging the perspective components in
since the homography with distortion determines the video quality.
Table 3,
Table 4 and
Table 5 summarize the perspective distortion of various video stabilization method. As shown in the Tables, the proposed video stabilization method can successfully remove the undesired motion without perspective distortion compared with conventional video stabilization algorithms.
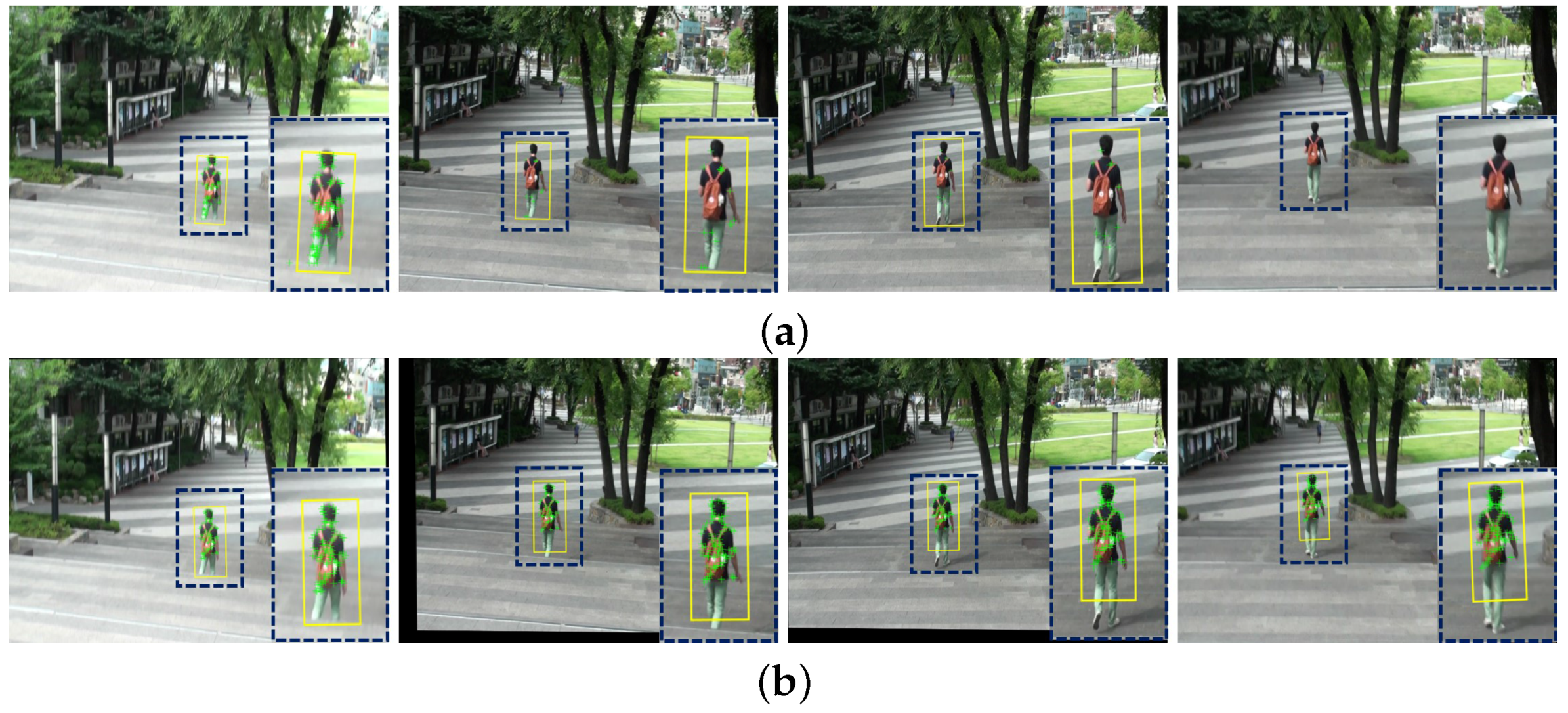
Unstable videos with undesired camera motions have the limited performance of object detection and tracking. The final experiment is performed to demonstrate whether the proposed method can play a practical role of pre-processing in various video analysis systems. We used the Lucas-Kanade feature tracker (LKT) to demonstrate the performance of the object tracking on shaky and stabilized videos.
Figure 16 illustrates the experimental results of the object tracking. The yellow boxes in
Figure 16 represent the tracking results using the LKT tracking method. Although the popular LKT algorithm tracked robust features with image rotation and view point change, it has a fundamental problem of missing the interest objects on the shaky video as shown in
Figure 16a. As shown in
Figure 16b, the proposed method can significantly improve the object tracking performance.