THz Pyro-Optical Detector Based on LiNbO3 Whispering Gallery Mode Microdisc Resonator
Abstract
:1. Introduction
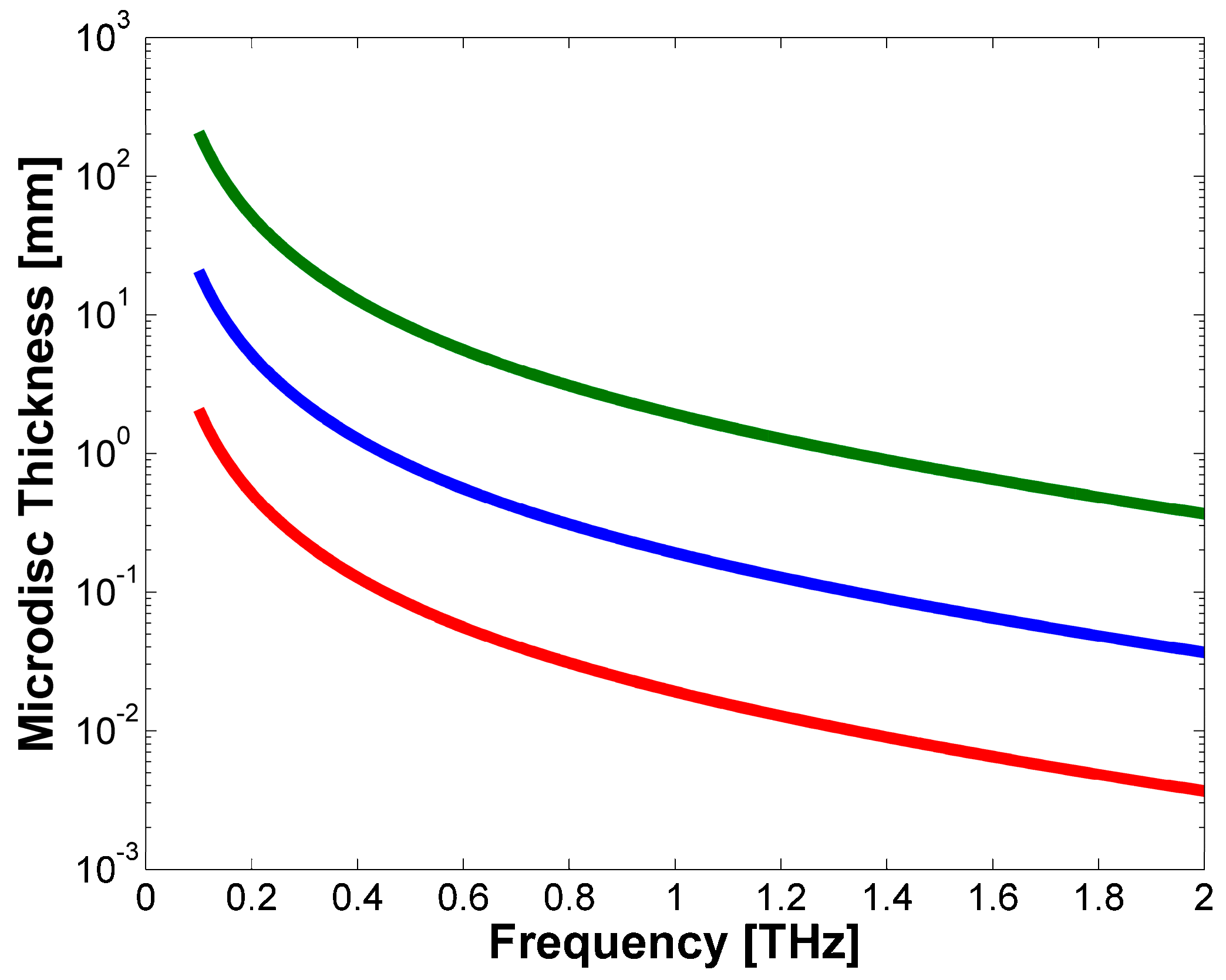
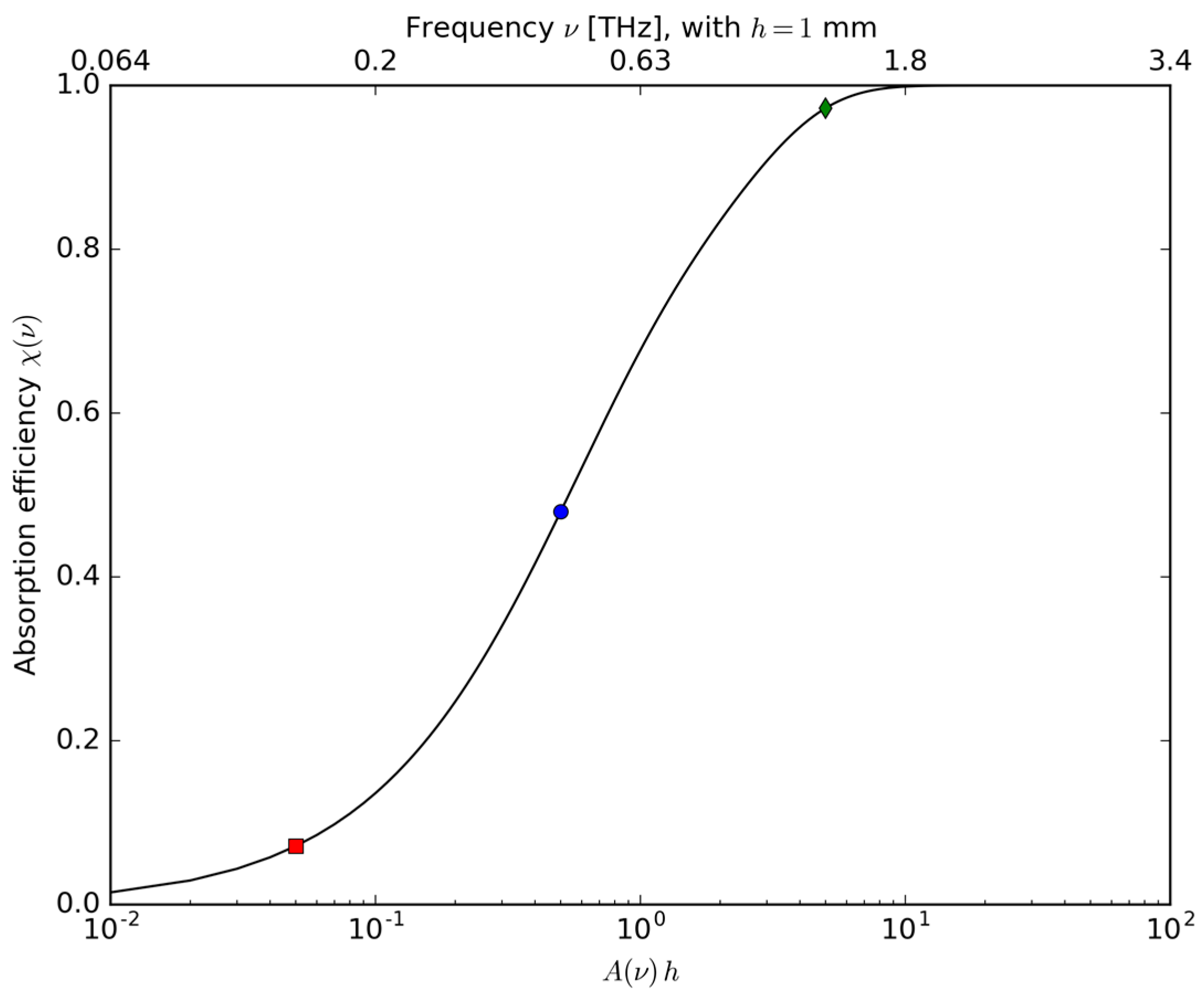
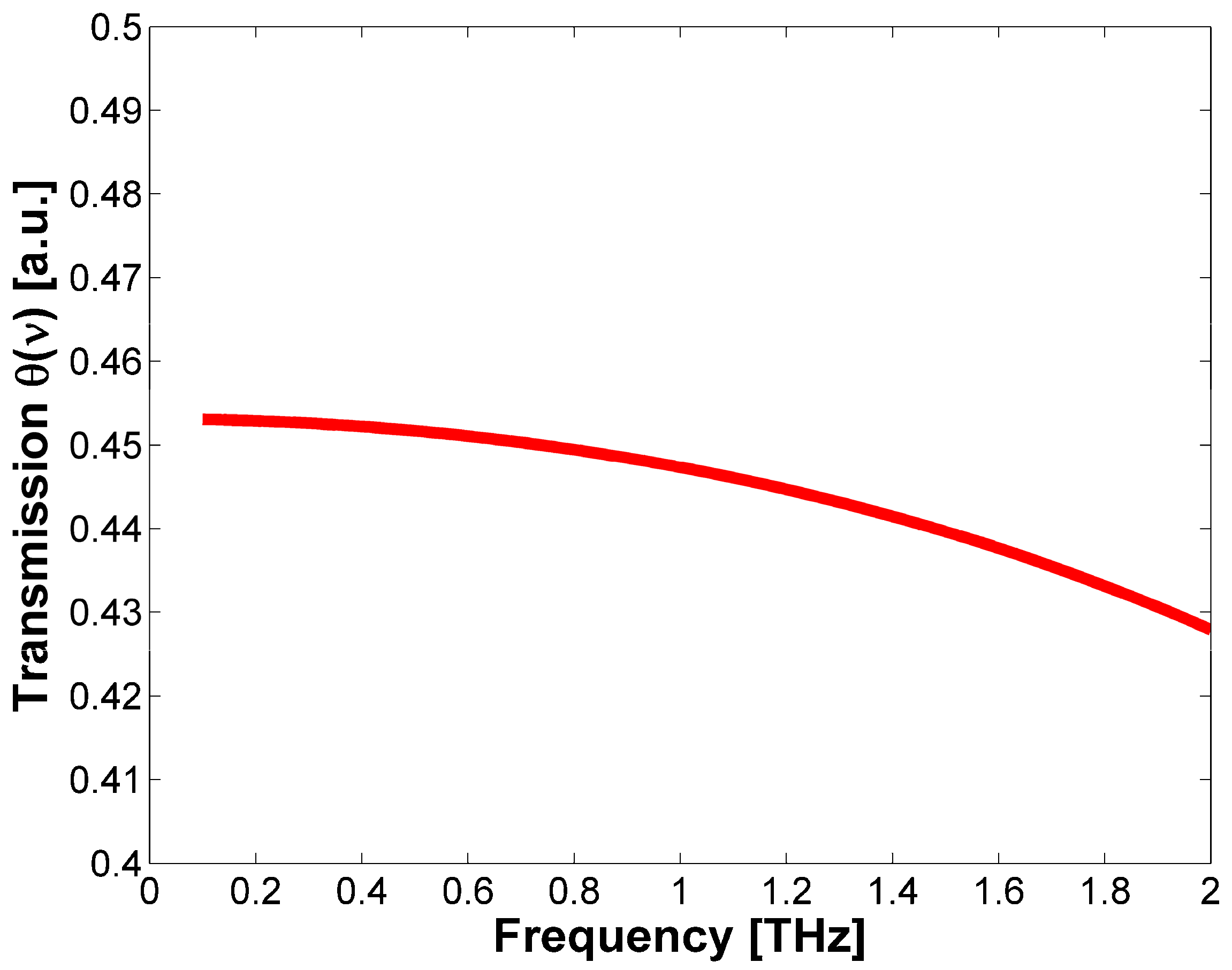
2. Theory
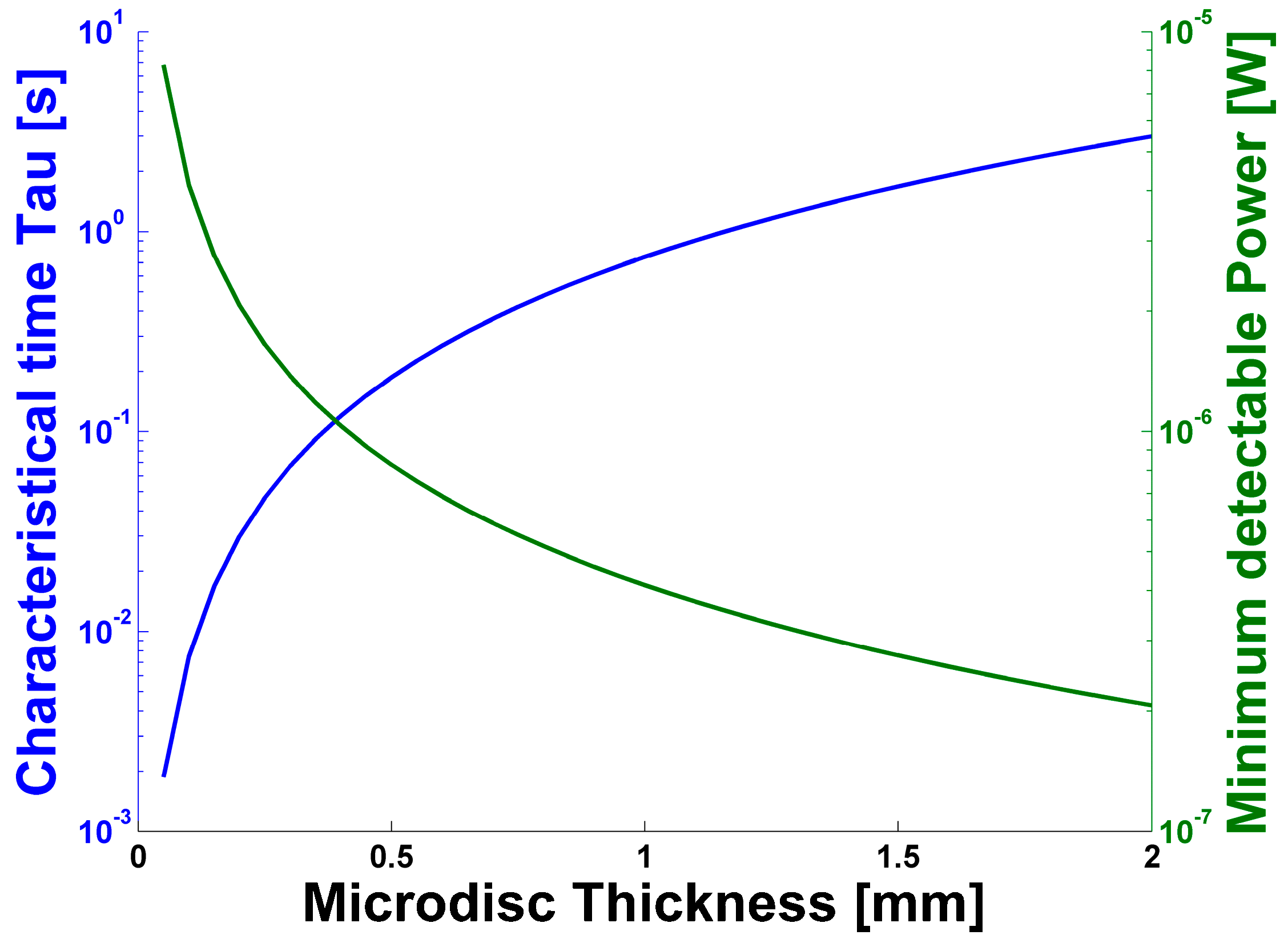
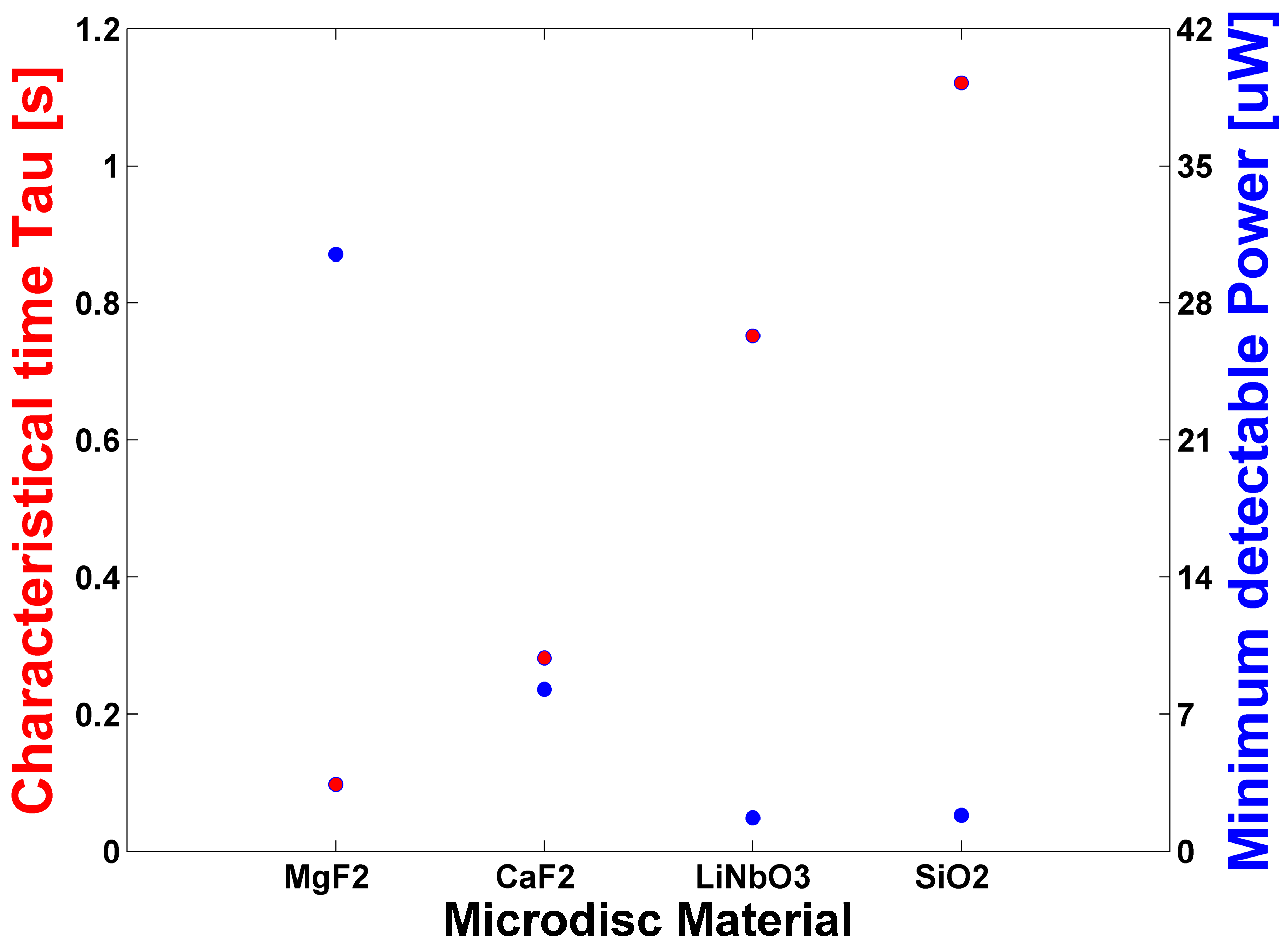
3. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Meng, C.; Chen, W.; Lv, Z.; Wang, X.; Huang, Y.; Zhang, D.; Zhao, Z.; Yuan, J. Enhancement of terahertz radiation with circularly polarized two-color fields. In Proceedings of the 2015 40th International Conference Infrared, Millimeter, Terahertz Waves (IRMMW-THz), Hong Kong, China, 23–28 August 2015.
- Minamide, H.; Hayashi, S.; Nawata, K.; Taira, T.; Shikata, J.I.; Kawase, K. Kilowatt-peak terahertz-wave generation and sub-femtojoule terahertz-wave pulse detection based on nonlinear optical wavelength-conversion at room temperature. J. Infrared Millim. Terahertz Waves 2014, 35, 25–37. [Google Scholar] [CrossRef]
- Belkin, M.A.; Capasso, F. New frontiers in quantum cascade lasers: High performance room temperature terahertz sources. Phys. Scr. 2015, 90, 118002. [Google Scholar] [CrossRef]
- Onin, A.A.; Inyaevskiy, I.O.; Limachev, Y.M.; Otkov, A.A.; Adikov, V.V. Frequency conversion of molecular gas lasers in PbIn 6 Te 10 crystal within mid-IR range. Opt. Leet. 2016, 41, 2390–2393. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.Y.; Taylor, A.J.; Glownia, J.H.; Rodriguez, G. Coherent control of terahertz supercontinuum generation in ultrafast laser–gas interactions. Nat. Photonics 2008, 2, 605–609. [Google Scholar] [CrossRef]
- Borri, S.; Patimisco, P.; Sampaolo, A.; Beere, H.E.; Ritchie, D.A.; Vitiello, M.S.; Scamarcio, G.; Spagnolo, V. Terahertz quartz enhanced photo-acoustic sensor. Appl. Phys. Lett. 2013, 103, 021105. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, Z.; Wang, T.; Jiang, Y.; Zheng, X.; Huang, Z.; Wu, X. High performance THz detector based on ultra-thin LiTaO 3 crystal. In Proceedings of the 2015 40th International Conference on the Infrared, Millimeter, and Terahertz waves (IRMMW-THz), Hong Kong, China, 23–28 August 2015.
- Degl’Innocenti, R.; Xiao, L.; Jessop, D.S.; Kindness, S.J.; Ren, Y.; Lin, H.; Zeitler, J.A.; Alexander-Webber, J.A.; Joyce, H.J.; Braeuninger-Weimer, P.; et al. Fast Room-Temperature Detection of Terahertz Quantum Cascade Lasers with Graphene-Loaded Bow-Tie Plasmonic Antenna Arrays. ACS Photonics 2016, 3, 1747–1753. [Google Scholar] [CrossRef]
- Demers, J.R.; Logan, R.T.; Brown, E.R. An optically integrated coherent frequency-domain THz spectrometer with signal-to-noise ratio up to 80 dB. MWP 2007 - 2007 IEEE Int. Top. Meet. Microw. Photonics 2007, 92–95. [Google Scholar]
- Li, W.; Liang, Z.; Wang, J.; Gou, J.; Jiang, Y. A direct method of thermal time constant measurement for lithium tantalate based terahertz pryroelectric detectors. J. Mater. Sci. Mater. Electron. 2016, 27, 1–7. [Google Scholar] [CrossRef]
- Sizov, F.; Rogalski, A. THz detectors. Prog. Quantum Electron. 2010, 34, 278–347. [Google Scholar] [CrossRef]
- Hübers, H.W. Terahertz heterodyne receivers. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 378–391. [Google Scholar] [CrossRef]
- Crowe, T.W.; Bishop, W.L.; Porterfield, D.W.; Hesler, J.L.; Weikle, R.M. Opening the terahertz window with integrated diode circuits. IEEE J. Solid-State Circuits 2005, 40, 2104–2109. [Google Scholar] [CrossRef]
- Pavel’ev, D.G.; Demarina, N.V.; Koshurinov, Y.I.; Vasil’ev, A.P.; Semenova, E.S.; Zhukov, A.E.; Ustinov, V.M. Characteristics of planar diodes based on heavily doped GaAs/AlAs superlattices in the terahertz frequency region. Semiconductors 2004, 38, 1105–1110. [Google Scholar] [CrossRef]
- Dobrovolsky, V.N.; Sizov, F.F.; Kamenev, Y.E.; Smirnov, A.B. Ambient temperature or moderately cooled semiconductor hot electron bolometer for mm and sub-mm regions. Opto-Electron. Rev. 2008, 16, 172–178. [Google Scholar] [CrossRef]
- Morf, T.; Klein, B.; Despont, M.; Drechsler, U.; Kull, L.; Corcos, D.; Elad, D.; Kaminski, N.; Pfeiffer, U.R.; Al Hadi, R.; et al. Wide bandwidth room-temperature THz imaging array based on antenna-coupled MOSFET bolometer. Sens. Actuators A Phys. 2014, 215, 96–104. [Google Scholar] [CrossRef]
- Hiromoto, N.; Tiwari, A.; Aoki, M.; Satoh, H.; Takeda, M.; Inokawa, H. Room-temperature THz antenna-coupled microbolometer with a Joule-heating resistor at the center of a half-wave antenna. In Proceedings of the 2014 39th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Tucson, AZ, USA, 14–19 September 2014.
- Hargreaves, S.; Lewis, R.A. Terahertz imaging: Materials and methods. J. Mater. Sci. Mater. Electron. 2007, 18, 299–303. [Google Scholar] [CrossRef]
- Golay, M.J.E. Theoretical consideration in heat and infra-red detection, with particular reference to the pneumatic detector. Rev. Sci. Instrum. 1947, 18, 347–356. [Google Scholar] [CrossRef] [PubMed]
- Cherednichenko, S.; Hammar, A.; Bevilacqua, S.; Drakinskiy, V.; Stake, J.; Kalabukhov, A. A room temperature bolometer for terahertz coherent and incoherent detection. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 395–402. [Google Scholar] [CrossRef]
- Nawata, K.; Notake, T.; Ishizuki, H.; Takida, Y.; Tokizane, Y.; Hayashi, S.; Han, Z.; Taira, T.; Minamide, H. Sum-frequency-generation based terahertz detection using a periodically poled lithium niobate. In Proceedings of the 2015 40th International Conference Infrared, Millimeter, Terahertz Waves (IRMMW-THz), Hong Kong, China, 23–28 August 2015.
- Ozawa, S.; Hori, T.; Azuma, S.; Funkner, S.; Niehues, G.; Yamamoto, K.; Furuya, T.; Kitahara, H.; Banciu, G.; Nedelcu, L.; et al. Electro-optic sampling of terahertz pulses using BaTiO3 in non-collinear Cherenkov phase-matching scheme. In Proceedings of the 2015 40th International Conference Infrared, Millimeter, Terahertz Waves (IRMMW-THz), Hong Kong, China, 23–28 August 2015.
- Savchenkov, A.A.; Matsko, A.B.; Ilchenko, V.S.; Maleki, L. Optical resonators with ten million finesse. Opt. Express 2007, 15, 6768–6773. [Google Scholar] [CrossRef] [PubMed]
- Foreman, M.R.; Swaim, J.D.; Vollmer, F. Whispering gallery mode sensors. Adv. Opt. Photonics 2015, 7, 168–240. [Google Scholar] [CrossRef] [PubMed]
- Moretti, L.; Iodice, M.; Della, F.G.; Corte, I. Temperature dependence of the thermo-optic coefficient of lithium niobate, from 300 to 515 k in the visible and infrared regions. J. Appl. Phys. 2005, 98, 036101. [Google Scholar] [CrossRef]
- Strekalov, D.V.; Savchenkov, A.A.; Matsko, A.B. Efficient upconversion of subterahertz radiation in a high-Q whispering gallery resonator. Opt. Lett. 2009, 34, 713–715. [Google Scholar] [CrossRef] [PubMed]
- Strekalov, D.V.; Thompson, R.J.; Baumgartel, L.M.; Grudinin, I.S. Temperature measurement and stabilization in a birefringent whispering gallery mode resonator. Opt. Express 2011, 19, 14495–14501. [Google Scholar] [CrossRef] [PubMed]
- Fescenko, I.; Alnis, J.; Schliesser, A.; Wang, C.Y.; Kippenberg, T.J.; Hansch, T.W. Dual-mode temperature compensation technique for laser stabilization to a crystalline whispering gallery mode resonator. Opt. Express 2012, 20, 19185–19193. [Google Scholar] [CrossRef] [PubMed]
- Farnesi, D.; Righini, G.C.; Barucci, A.; Berneschi, S.; Chiavaioli, F.; Cosi, F.; Pelli, S.; Soria, S.; Trono, C.; Ristic, D.; et al. Coupling light to whispering gallery mode resonators. In Proceedings of 2014 SPIE Photonics Europe, Silicon Photonics and Photonic Integrated Circuits, Brussels, Belgium, 14–17 April 2014; p. 9.
- Nunzi Conti, G.; Berneschi, S.; Cosi, F.; Pelli, S.; Soria, S.; Righini, G.C.; Dispenza, M.; Secchi, A. Planar coupling to high-Q lithium niobate disk resonators. Opt. Express 2011, 19, 3651–3656. [Google Scholar] [CrossRef] [PubMed]
- Daimon, M.; Masumura, A. High-accuracy measurements of the refractive index and its temperature coefficient of calcium fluoride in a wide wavelength range from 138 to 2326 nm. Appl. Opt. 2002, 41, 5275–5281. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Ozdemir, S.K.; Yang, L. Infrared light detection using a whispering-gallery-mode optical microcavity. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Ioppolo, T.; Rubino, E. Room-temperature micro-photonic bolome-ter based on dielectric optical resonators. Proc. SPIE 2013, 8704, 1–6. [Google Scholar]
- Kovcs, L.; Polgr, K. Density measurements on LiNbO3 crystals con- firming Nb substitution for Li. Cryst. Res. Technol. 1986, 21, K101–K104. [Google Scholar] [CrossRef]
- Nakamura, M.; Sekita, M.; Takekawa, S.; Kitamura, K. Crystal growth and characterization of Nd, Mg co-doped near-stoichiometric LiNbO3. J. Cryst. Growth 2006, 290, 144–148. [Google Scholar] [CrossRef]
- Schall, M.; Helm, H.; Keiding, S.R. Far Infrared Properties of Electro-Optic Crystals Measured by THz Time-Domain Spectroscopy. Int. J. Infrared Millim. Waves 1999, 20, 595–604. [Google Scholar] [CrossRef]
- Pignatiello, F.; De Rosa, M.; Ferraro, P.; Grilli, S.; De Natale, P.; Arie, A.; De Nicola, S. Measurement of the thermal expansion coefficients of ferroelectric crystals by a moiré interferometer. Opt. Commun. 2007, 277, 14–18. [Google Scholar] [CrossRef]
- Hanumegowda, N.M.; Stica, C.J.; Patel, B.C.; White, I.; Fan, X. Refractometric sensors based on microsphere resonators. Appl. Phys. Lett. 2005, 87, 1–3. [Google Scholar] [CrossRef]
- Ilchenko, V.S.; Savchenkov, A.A.; Matsko, A.B.; Maleki, L. Nonlinear optics and crystalline whispering gallery mode cavities. Phys. Rev. Lett. 2004, 92, 43903. [Google Scholar] [CrossRef] [PubMed]
- Richards, P.L. Bolometers for infrared and millimeter waves. J. Appl. Phys. 1994, 76, 1. [Google Scholar] [CrossRef]
- Yan, Y.-Z.; Zou, C.-L.; Yan, S.-B.; Sun, F.-W.; Ji, Z.; Liu, J.; Zhang, Y.-G.; Wang, L.; Xue, C.-Y.; Zhang, W.-D.; et al. Packaged silica microsphere-taper coupling system for robust thermal sensing application. Opt. Express 2011, 19, 5753–5759. [Google Scholar] [CrossRef] [PubMed]
- Savchenkov, A.A.; Liang, W.; Matsko, A.B.; Ilchenko, V.S.; Seidel, D.; Maleki, L. Tunable optical single-sideband modulator with complete sideband suppression. Opt. Lett. 2009, 34, 1300–1302. [Google Scholar] [CrossRef] [PubMed]
- Slack, G.A. Thermal Conductivity of CaF2, MnF2, CoF2 and ZnF2, Crystals. Phys. Rev. 1961, 122, 1451. [Google Scholar] [CrossRef]
- Leidinger, M.; Werner, C.S.; Yoshiki, W.; Buse, K.; Breunig, I. Impact of the photorefractive and pyroelectric-electro-optic effect in lithium niobate on whispering-gallery modes. Opt. Lett. 2016, 41, 5474. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cosci, A.; Cerminara, M.; Conti, G.N.; Soria, S.; Righini, G.C.; Pelli, S. THz Pyro-Optical Detector Based on LiNbO3 Whispering Gallery Mode Microdisc Resonator. Sensors 2017, 17, 258. https://doi.org/10.3390/s17020258
Cosci A, Cerminara M, Conti GN, Soria S, Righini GC, Pelli S. THz Pyro-Optical Detector Based on LiNbO3 Whispering Gallery Mode Microdisc Resonator. Sensors. 2017; 17(2):258. https://doi.org/10.3390/s17020258
Chicago/Turabian StyleCosci, Alessandro, Matteo Cerminara, Gualtiero Nunzi Conti, Silvia Soria, Giancarlo C. Righini, and Stefano Pelli. 2017. "THz Pyro-Optical Detector Based on LiNbO3 Whispering Gallery Mode Microdisc Resonator" Sensors 17, no. 2: 258. https://doi.org/10.3390/s17020258
APA StyleCosci, A., Cerminara, M., Conti, G. N., Soria, S., Righini, G. C., & Pelli, S. (2017). THz Pyro-Optical Detector Based on LiNbO3 Whispering Gallery Mode Microdisc Resonator. Sensors, 17(2), 258. https://doi.org/10.3390/s17020258









