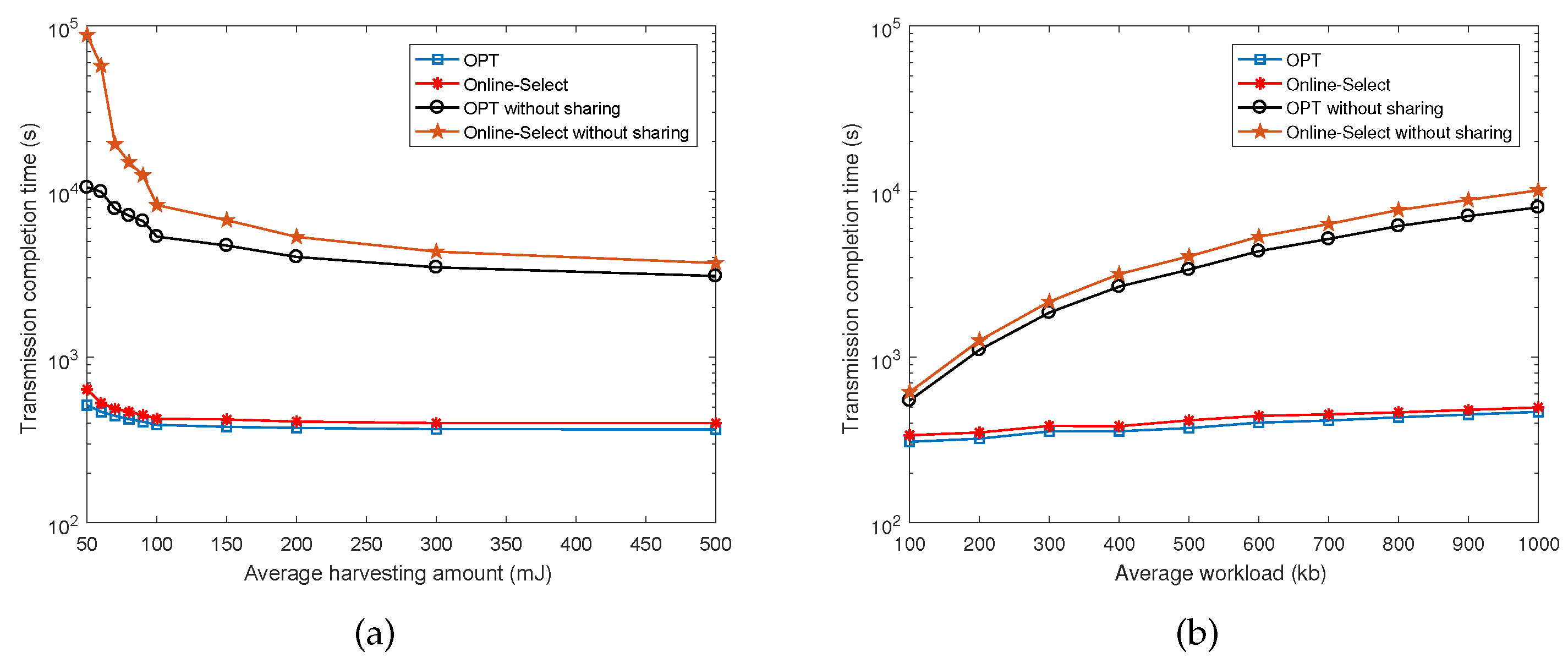
In this section, we focus on the min-E problem with a given deadline. We will first investigate some basic properties of the optimal solution. Then, we will decompose the min-E problem into two simplified models and figure out the relationship between the min-E problem and the decomposed problems. Finally, we develop an optimal algorithm to compute the optimal rate schedule for the min-E problem.
4.1. Basic Properties of Optimal Rate Schedule
Define the optimal rate scheduling policy for the min-E problem to be if it exists, which is referred to as for short. We start by introducing some optimality properties about in the following lemmas.
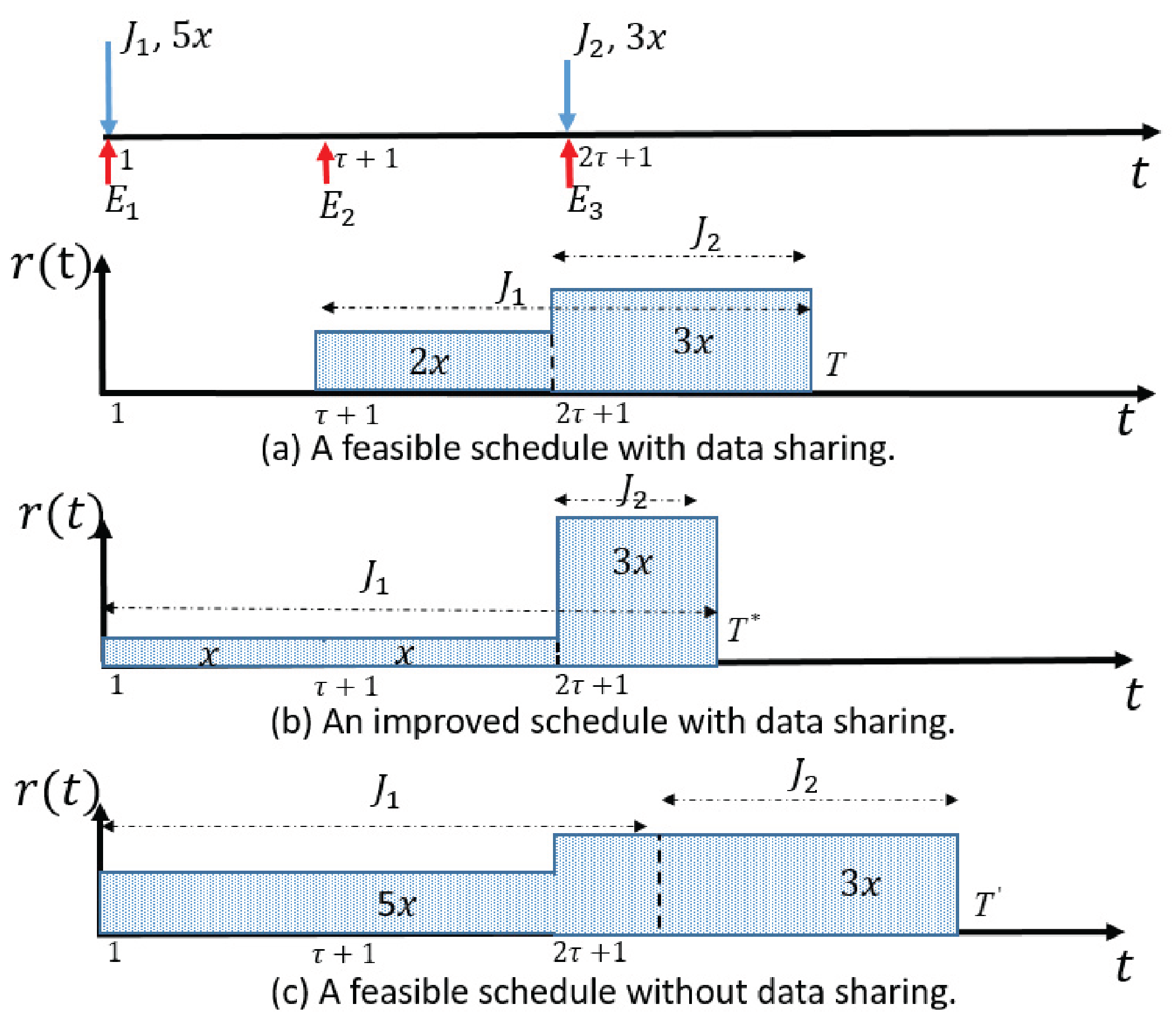
Before we start, we first introduce the concept of equalization that will be used in our proofs. Given two rates , if we can equalize the two rates to , the power consumption would decrease due to the fact that for convex rate-power functions. This method is called equalization.
We present the following two basic lemmas which can be easily extended from prior works that do not consider data sharing [
16,
20] (the detailed proof is omitted here).
Lemma 1. changes only at event points.
Lemma 2. is non-decreasing.
These two lemmas show that is a step/staircase function. In the following discussion, when we refer to a step, we mean a unique and consecutive part of a step function with constant rate. Specifically, let be the transmission rate of step i in . Accordingly, the ordered sequence of all the steps of a step function will be called a step sequence.
Then, we derive two properties of the optimal rate scheduling policy under the data sharing setting.
Lemma 3. If increases at a harvesting point at which no task arrives, then the battery must be used up right before . Viz., .
Proof. We prove the lemma by contradiction. Suppose on the contrary, increases at a harvesting point , but there remains some amount of energy at time slot . We focus on interval . Since there is no other task request arriving at , it implies that if we moved a small amount of data from time slot to be transmitted at , it would save some energy and would not violate any delay constraint, leading to a contradiction. This completes the proof. ☐
It is worth noticing that the condition that no task arrive at is necessary. Because otherwise if a task with a large workload also arrives at , say , then we cannot move some data from time slot to since the delay constraint of this task may not hold any more.
Lemma 4. If increases at an arrival point at which no energy harvesting occurs, then the total transmitted data from this point to the deadline T will be equal to the required data of task . Viz., .
Proof. First of all, we have , since the delay constraint of every task must be satisfied. Suppose is strictly greater than . Note that, we have . Moreover, is non-decreasing according to Lemma 2. Hence, we can always find an epoch in and equalize some small amount of data from that epoch to the epoch right before that has smaller rate than that one in , which would not violate the delay constraint of task since . Moreover, since no energy arrives at , moving a small amount of energy used at to the time before it would not violate the energy causality constraint. This adjustment would save some energy by the convexity of the rate-power function, resulting in a contradiction to the optimality of . Thus, under the optimal policy, the delay constraint at that point must be satisfied as an equality. ☐
Lemmas 1–4 together show that is a non-decreasing step function that changes its rate either at a harvesting point or at an arrival point.
According to Lemmas 3 and 4, we have a direct corollary for the case that both a task request and a harvesting event occur simultaneously,
Corollary 1. If increases at a point e at which both a task request and a harvesting event occur, then either the total transmitted data from e to T will be equal to , or the battery is used up just right before time slot e.
4.2. Problem Decomposition
Although a deadline is given, the min-E problem is still complex with dynamic arrivals of both energy and requests. These arrival densities together have an impact on the allocation of transmission rate. Intuitively, an efficient rate schedule in an energy harvesting communication system tends to properly use partial energy early to avoid causing high density of remained energy in late periods (which is energy inefficient by the convexity of rate-power function). However, the efficient data sharing scheduling tends to reduce the traffic transmitted in early periods and increase data transmission in late periods so as to allow more data sharing.
Observing the above dilemma in dealing with the energy harvesting and data sharing, in this work, we address the challenge/trade-off by decomposing the problem into sub-problems. We then combine their solutions to form the optimal solution for the original problem. According to the best of our knowledge, no similar method has ever been proposed in the literature.
Note that previous Lemmas 3 and 4 present properties of the optimal increasing point in terms of energy harvesting and task requesting, respectively. This implies that we may decompose the problem into two simpler models: one is the transmission only with energy harvesting, and the other is the transmission only with task requests and data sharing. Thus, before deriving the structure of the optimal solution for the min-E problem, we will introduce these two simpler models.
We first introduce the DCRS problem that does not consider energy harvesting, as defined in Definition 4.
Definition 4. Given a deadline T, the delay-constrained-only rate scheduling problem (DCRS problem) is to find a rate function such that the total energy consumption is minimized, subject to the delay constraints of all task requests described in Equation (1) under the data sharing setting. For DCRS problem, Wu et al. [
9,
26], propose an optimal algorithm called I
nterval-D
elete to search for the task with the largest average data density and then iteratively fix a part of the optimal rate function by deleting the corresponding time interval. We call the optimal rate function for DCRS problem the
ID rate schedule and use
to represent it (or
for short if there is no ambiguity).
Next, we introduce the EHRS problem that does not consider data requests and data sharing, as described in Definition 5.
Definition 5. Given a deadline T, the energy-harvesting-only rate scheduling problem (EHRS problem) is to determine a rate schedule, such that the total transmitted data is maximized before the deadline T, subject to the energy causality constraints of Equation (2). In contrast to DCRS problem, there is no concept of
data requests or
data sharing. It is assumed that there is enough data bits to be transmitted by the transmitter at the beginning of transmission, and the only objective is to send as much data bits as possible. For EHRS problem, an optimal algorithm that recursively fixes all parts of the optimal solution is provided in [
28]. We call the optimal rate function for EHRS problem the
MT rate schedule and use
(or
for short) to represent it.
It has been proved in previous work that both and are non-decreasing step functions. Specifically, the increasing point of must be a task arrival point and follows a similar property as described in Lemma 4. Also, the increasing point of must be corresponding to a harvesting event and it shares a property similar to Lemma 3.
For ease of presentation, we use or for short (and correspondingly or to denote the rate function of the i-th step of the step function (and ). We denote the step sequences of a step function as , where a triple is used to describe the i-th step of , which means the i-th step with transmission rate starts at time slot and lasts for time slots (including time slot ). Thus, the end point of the i-th step is . Specifically, we use and to represent the step sequences of and respectively, where and .
Lemma 5. If , then has the largest workload among all the tasks. That is, .
Proof. It can be proved by contradiction easily. Suppose is not the request with the largest workload. We can pick the one with largest required data, say , then it is obvious that can completely share the data of , which means there is no need to allocate a rate larger than 0 with until arrives. This leads to a contradiction and proves the lemma. ☐
Note that the same observation as the lemma above is also applicable to the optimal solution of the min-E problem.
4.3. The Bottleneck-Select Algorithm
After introducing the basic properties of and the two decomposed simple sub-problems, we are ready to examine the key properties of the min-E problem that would guide the design of our algorithm.
On one hand, if the energy is sufficient (or more precisely, if for all time slots , harvested energy is sufficient to support ), then we have , since is the optimal rate schedule that achieves the minimum energy consumption given a deadline T. On the other hand, if harvested energy is insufficient to support , the rate level must be decreased in order to avoid energy shortage. However, if the rate level is lowered down too much, then less data would be transmitted in the current epoch, which would lead to a situation that more data will be transmitted later with higher rate which is energy inefficient. Thus, we hope to reach a good trade-off between the amount of transmitted data and energy consumption, and allocate proper transmission rate to overcome the energy shortage.
Our high level idea is to compare the rates of and to help figure out what rate the optimal solution should choose.
Theorems 1 and 2 below together show the key properties that would help determine the rate.
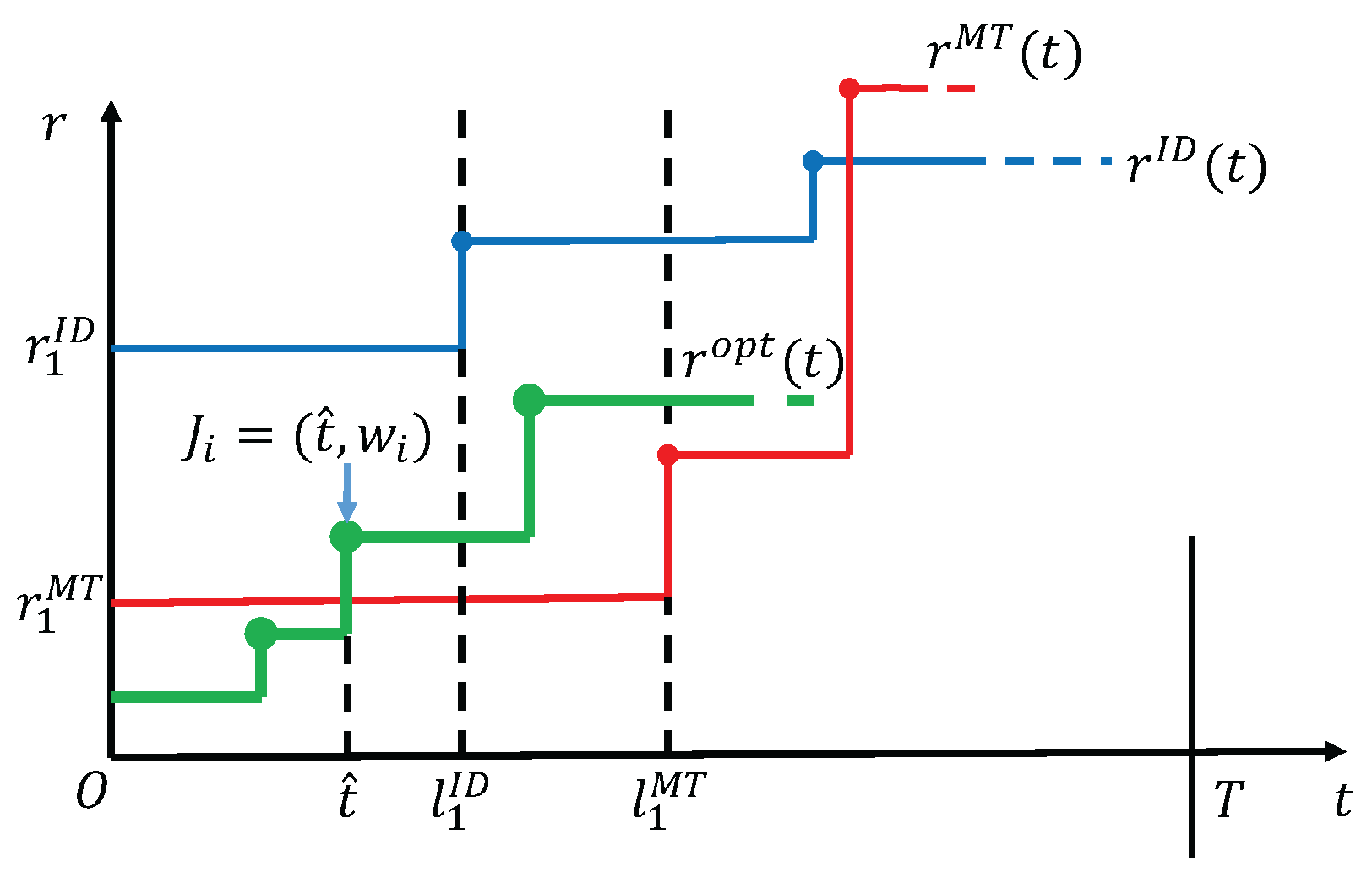
Theorem 1. If , then the optimal solution for the min-E problem exactly equals to during interval .
Proof. We prove Theorem 1 by contradiction. If is not equal to under the condition that in interval , then we consider all the possible relationships between and during interval one by one:
(1) for all t in .
According to the properties of , energy will be used up by time slot , thus cannot be supported to have larger rate in the whole interval . Therefore such a case is impossible to occur.
(2) The curve of intersects with that of in .
An examplary diagram corresponding to this case is shown in
Figure 2. By the non-decreasing property of
in Lemma 2, it is a fact that there is at most one intersection between
and
in interval
. Let the corresponding time slot of the intersection be
. Then
in
and
in
. We claim that
cannot be a harvesting point, because otherwise according to Lemma 3 energy is used up by time
, which contradicts the feasibility of
that has a larger rate than
by time
. Thus,
can only be an arrival point. Let the arrival task at
be
. Now that
is an arrival point that
increases, we have
according to Lemma 4. Meanwhile, for
, it must satisfy
to follow the delay constraint of task
. In addition, since
, which means that the first task
has the largest amount of data request among all tasks according to Lemma 5. So
and at least
. Then,
Combining Equations (
4) and (5), we have
. However, it is clear that
according to the precondition that
in interval
, which brings us a contradiction. Thus, such a case is also impossible to occur.
(3) in .
We consider two sub-cases: one is that is not constant in , the other is the constant case. For the former, we can follow the discussion similar to the proof of case (2) above, except that the intersection point in the discussion becomes the first point at which increases, thus we omit the details. For the latter, we extend the interval and can always find the first point at which increases ( cannot keep to be a constant rate during the whole transmission by time T, otherwise it will contradict the existence of , because the delay constraint will be violated). Let the first increasing point of be a time with , then must be a task arrival point or an energy harvesting point. On one hand, if is an energy harvesting point, then energy is used up by , which implies a contradiction since with a larger rate than cannot be supported in . On the other hand, if is an arrival point, then following the same proof as that of case (2) can also deduce a contradiction. These together would remove the possibilities of the case.
In summary, must be equal to in interval . ☐
Symmetrically, we have the following theorem, where the detailed proof is moved to
Appendix A.
Theorem 2. If , then the optimal solution for min-E problem exactly equals to during interval .
Based on Theorems 1 and 2, we are able to fix the rate schedule in interval or . Then, starting with the next new time slot, the same problem would repeat, if we could correctly update the sets of tasks and harvesting events, until all the tasks are finished.
First, we introduce the update module, whose function is to generate the same smaller-size problem after a part of the rate schedule is fixed. Let the rate and corresponding interval of the fixed part in be r and , respectively. Since a part of the optimal solution has been fixed, we shift the time axis by l time slots and properly update the tasks and harvestings that arrive within and after the time duration of the fixed part by treating them as new instances. The detailed implementation is presented in Algorithm 1.
| Algorithm 1 Update() |
- 1:
update the deadline T to be . - 2:
for each task with , update its arrival time to be and the remaining workload to be . - 3:
among all the tasks with , reserve the task with largest workload and remove all the others. - 4:
for each task with , update its arrival time to be . - 5:
let , remove all the harvestings with . - 6:
create a new harvesting, let its arrival time be 1 and amount of energy be . - 7:
for each harvesting with , update its arrival time to be .
|
Then, we present the final algorithm for computing the optimal schedule of the min-E problem. The idea is to compare the first steps of rates and in the two decomposed problems to find the bottleneck. If , we select as the first part of , otherwise, we select . After fixing the first part, we recursively update the problem and compute the residual part of . The detailed implementation is presented in Algorithm Bottleneck-Select.
It is worth noticing that the min-E problem with a given deadline may have no feasible solutions. This happens if the harvested energy is insufficient, or the deadline is set to be too early so that some delay constraints in Equation (
1) are impossible to be met. To detect the infeasibility of the input case, we just need to check whether there exists some task that has not been finished at the end of the while loop, as implemented in Line 15 in Algorithm 2.
Finally, we conclude that Algorithm Bottleneck-Select either returns the optimal solution or identifies the infeasibility for the min-E problem.
| Algorithm 2 Bottleneck-Select () |
- 1:
let in , . - 2:
while do - 3:
compute the first step of ID rate schedule . - 4:
compute the first step of MT rate schedule . - 5:
if then - 6:
in . - 7:
Update(). - 8:
. - 9:
else - 10:
in . - 11:
Update(). - 12:
. - 13:
end if - 14:
end while - 15:
if there exists some task that has not been finished then - 16:
return infeasible - 17:
end if - 18:
return
|
Theorem 3. Algorithm Bottleneck-Select computes the optimal rate schedule for the min-E problem when a feasible schedule exists, and determines the infeasibility of the input otherwise, in time.
Proof. We prove the optimality for minimizing the energy consumption by induction on iterations. In the first iteration, Algorithm Bottleneck-Select correctly computes and fixes the partial optimal schedule that minimizes the energy consumption by Theorems 1 and 2, which serves as the induction basis. Suppose Algorithm Bottleneck-Select fixes the optimal rate allocation in interval after the first k iterations (), we need to prove that this property also holds after the -th iteration. At the beginning of the -th iteration, all tasks with are updated by the Update operation in the k-th iteration. Specifically, each task with has workload to be finished in , and among them only the task with the largest remaining workload is retained and regarded as a new task at slot , according to the sharing nature of the data. This operation ensures that no extra workload is dealt with later. Then, in the -th iteration, it can be verified that transmitting with the computed rate (or ) is energy-optimal for the new task set and harvesting event set by similarly applying the proof of Theorems 1 and 2 to the updated instance. Finally, when the iteration terminates with , according to the correctness of hypothesis and inductions above, Algorithm Bottleneck-Select has fixed the optimal min-energy rate schedule in .
Next, we analyze the computational complexity. The
while loop repeats at most
times, since there are totally
event points and at least one event point is reached in each loop. To compute
, we only need to scan the set of harvesting events once in at most
time. However, we must construct the whole rate schedule of
before we obtain
, because Algorithm I
nterval-D
elete in [
26] partially fixes
in a back-to-front manner, which takes at most
time. The U
pdate part works with
time and is not time consuming. Therefore, the total time complexity is
. ☐