Strain Gauges Based on CVD Graphene Layers and Exfoliated Graphene Nanoplatelets with Enhanced Reproducibility and Scalability for Large Quantities
Abstract
:1. Introduction
2. Materials and Methods
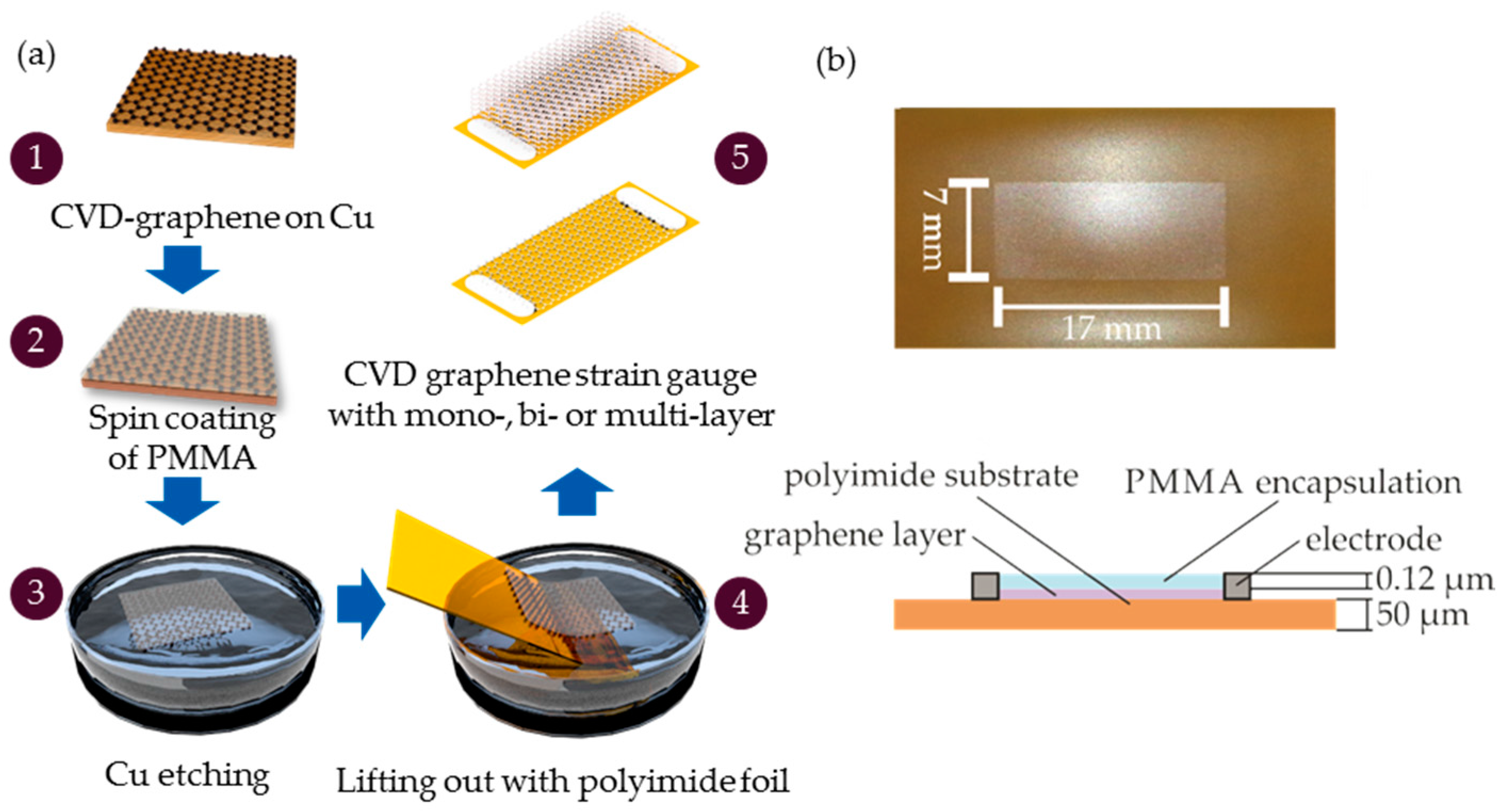
2.1. CVD Grown Graphene for Strain Gauge Application
2.1.1. Fabrication Steps of CVD Graphene Strain Gauges
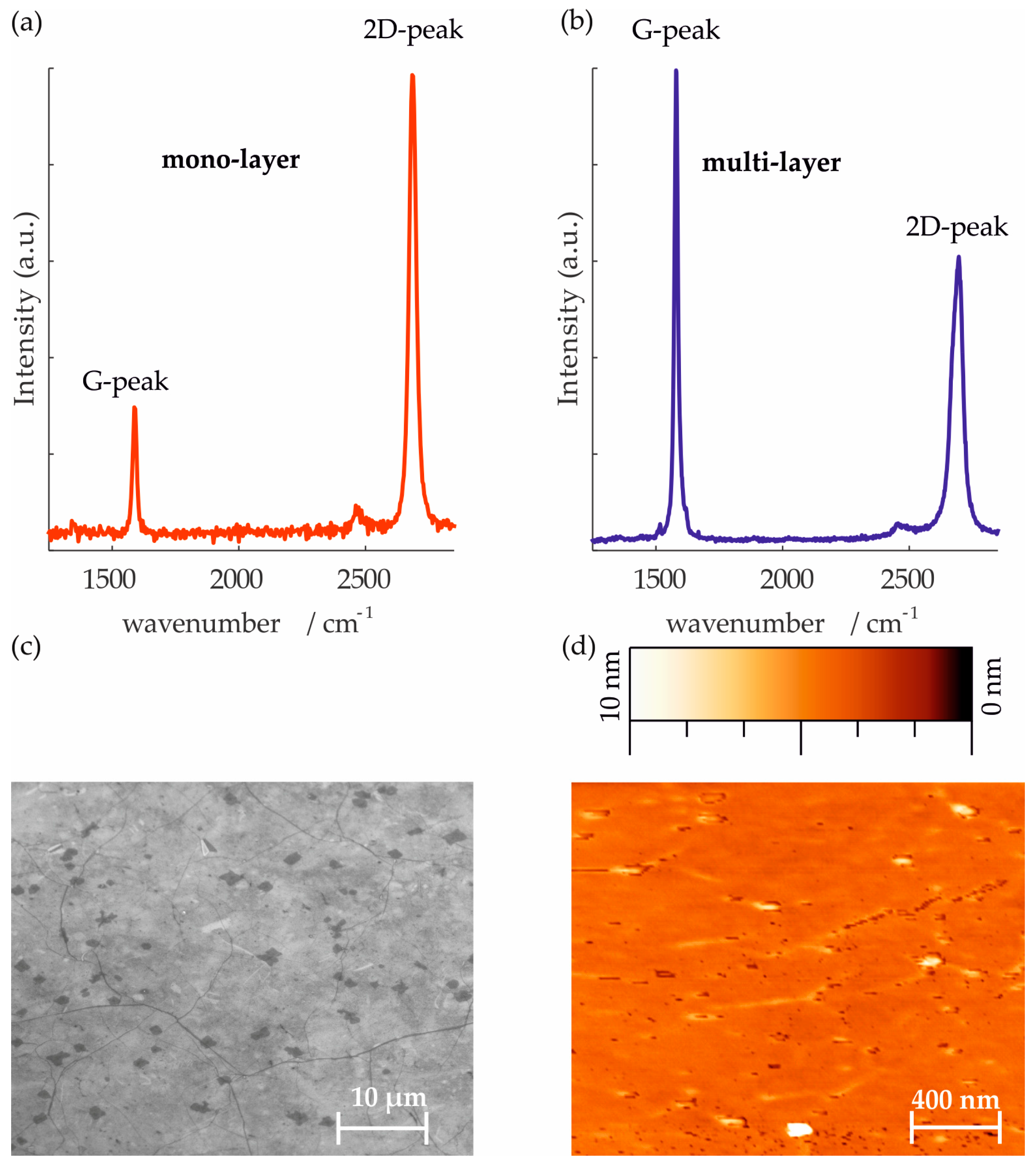
2.1.2. Characterization of CVD Graphene Layers
2.2. Liquid Exfoliated Graphene Nano Platelets (GNP) for Strain Gauge Application
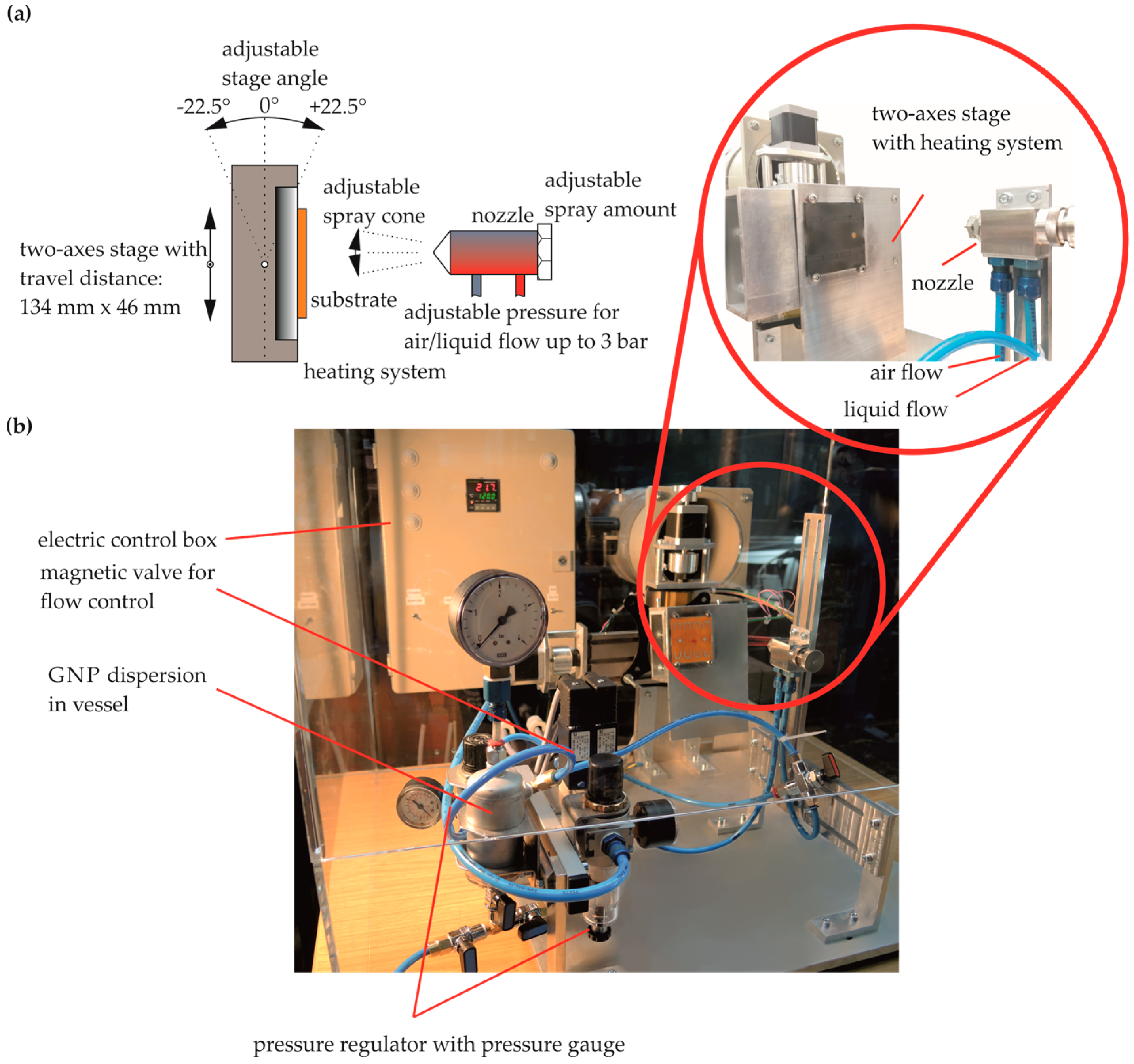
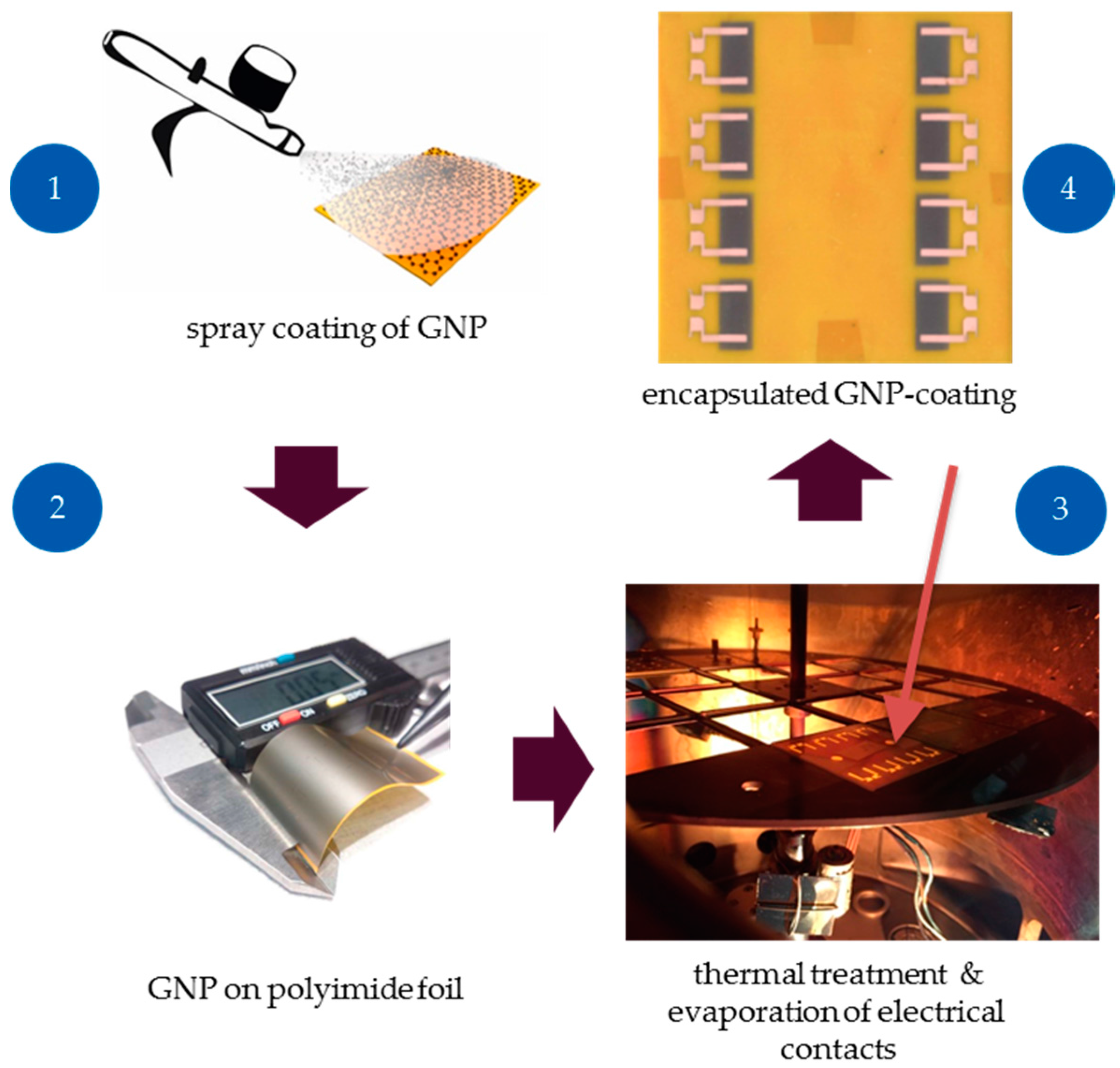
2.2.1. Fabrication Steps of GNP Strain Gauges
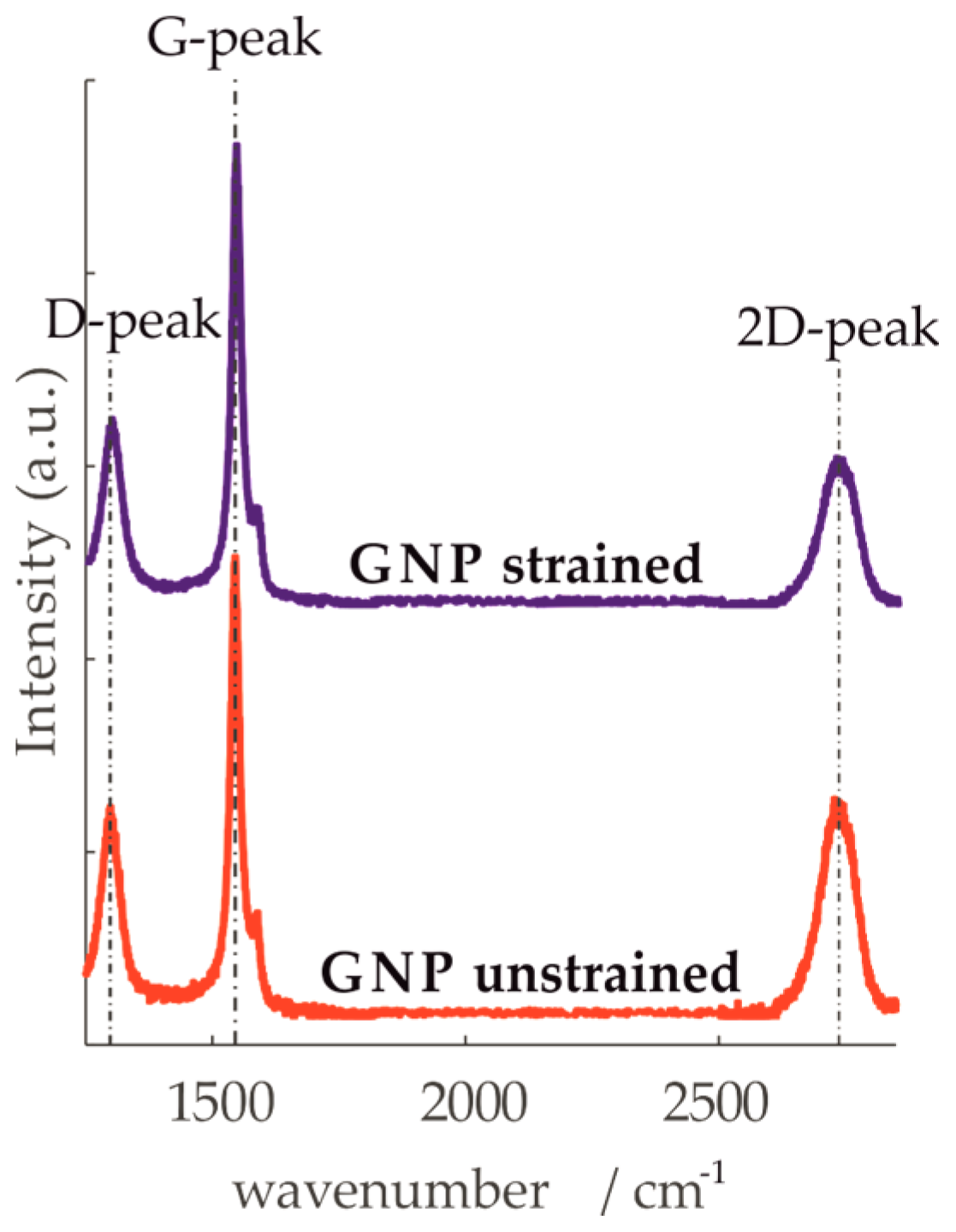
2.2.2. Characterization of Liquid Exfoliated GNP
2.2.3. Modeling Procedure
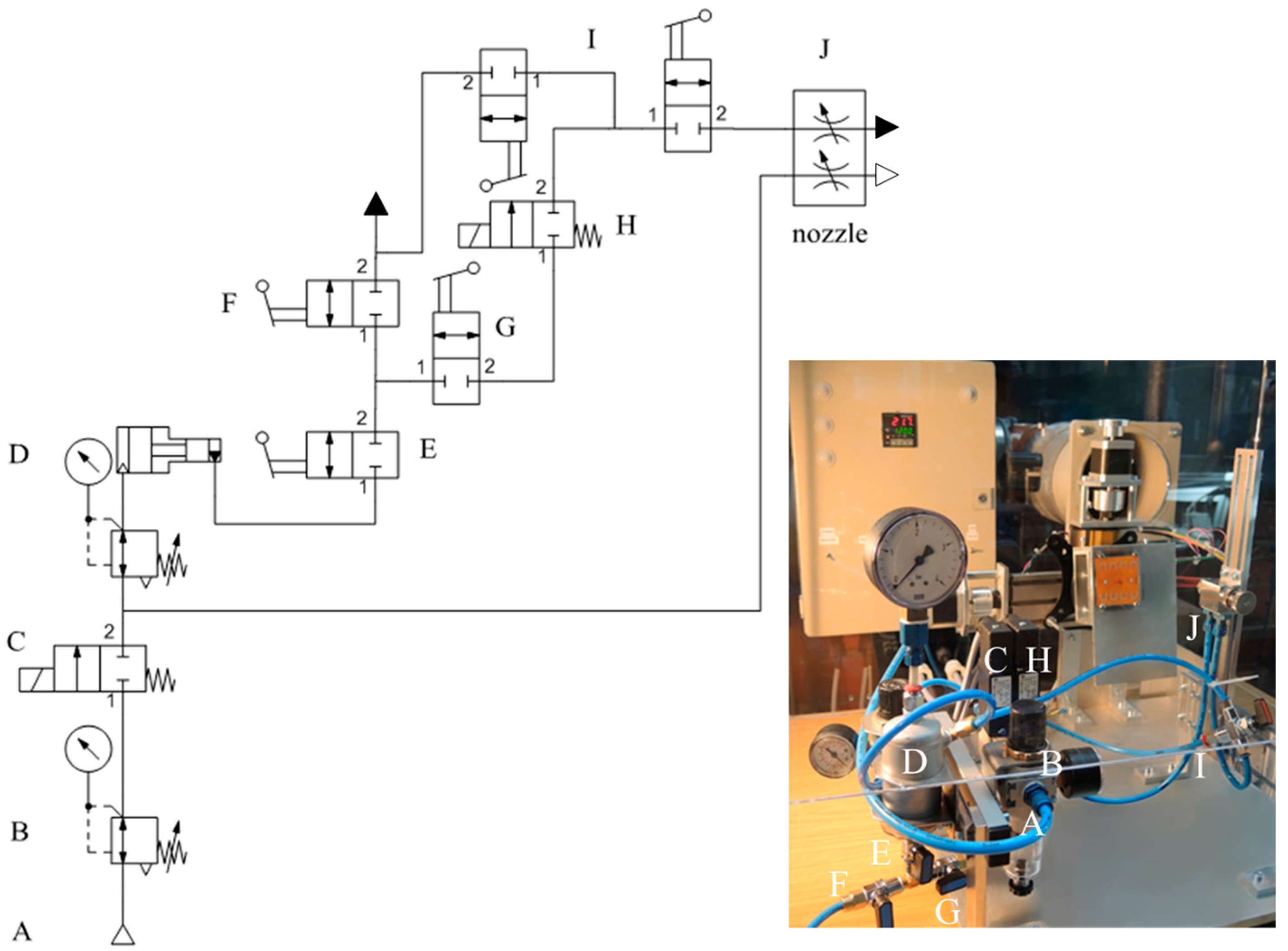
2.3. Characterization and Experimental Testing Method for Electromechanical Behaviour
3. Results and Discussion
3.1. Experimental Testings of CVD Graphene
3.1.1. Quasi-Static Load Test
3.1.2. Piezoresistive Effect
3.1.3. Discussion of the Results
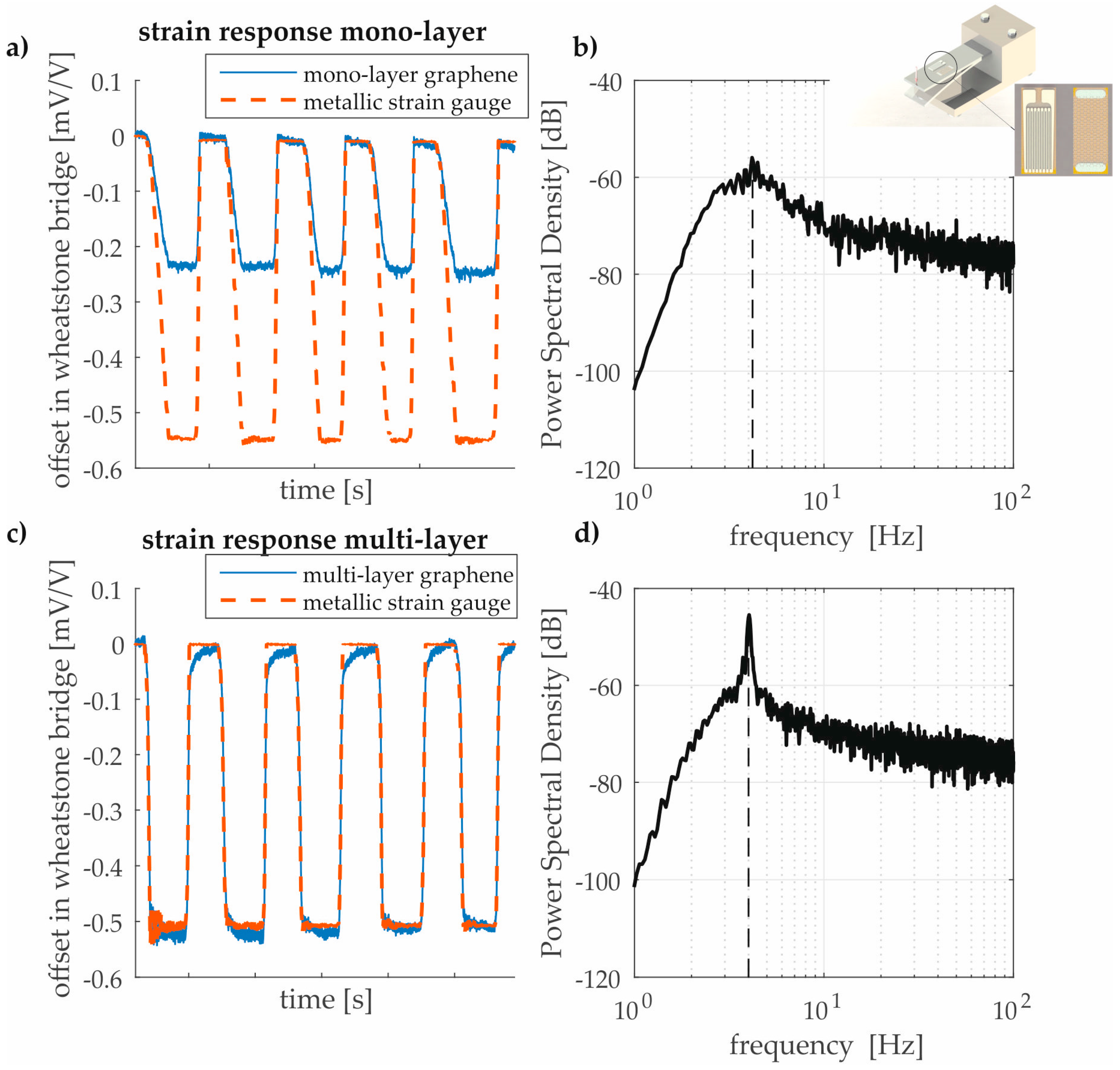
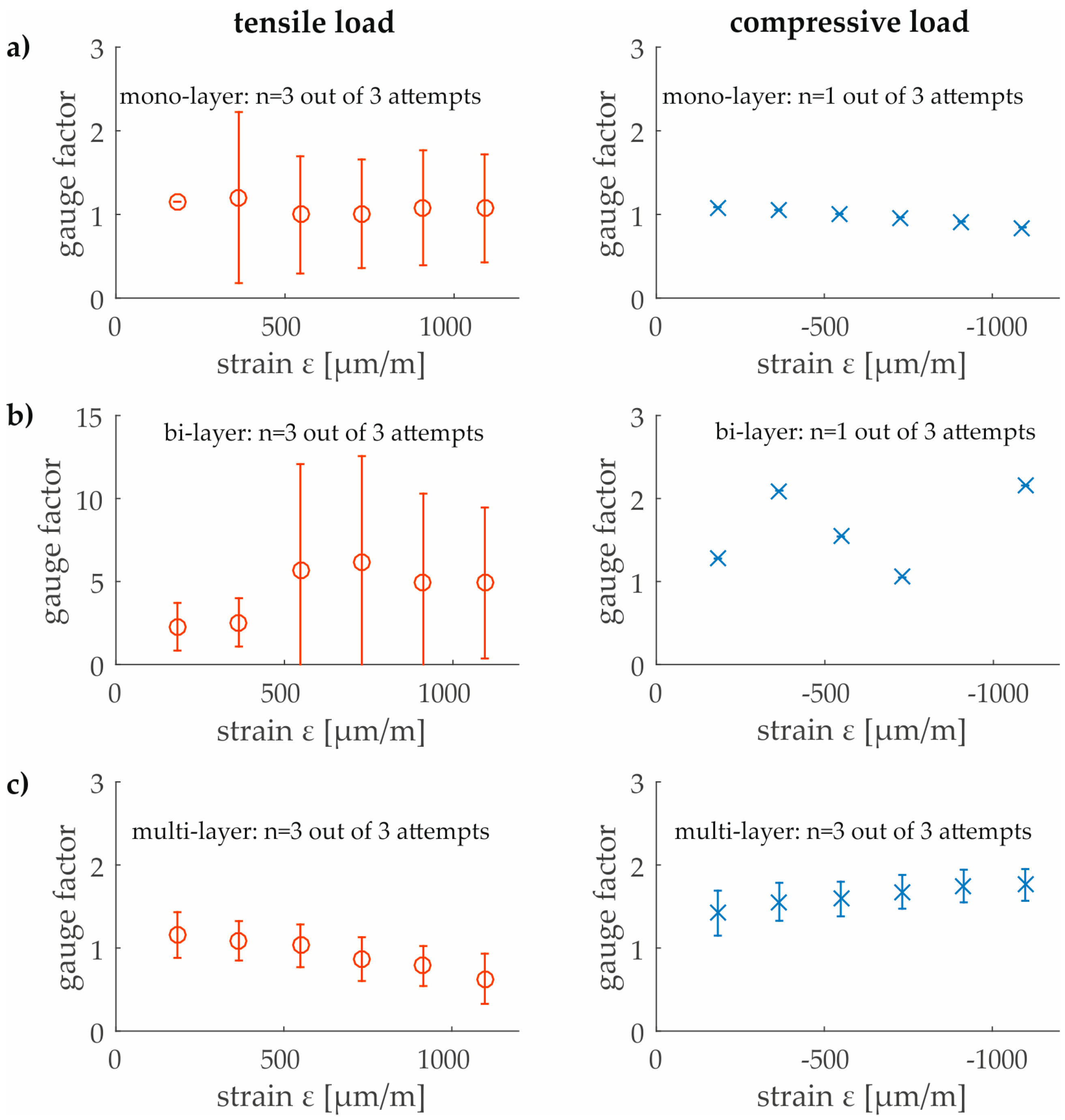
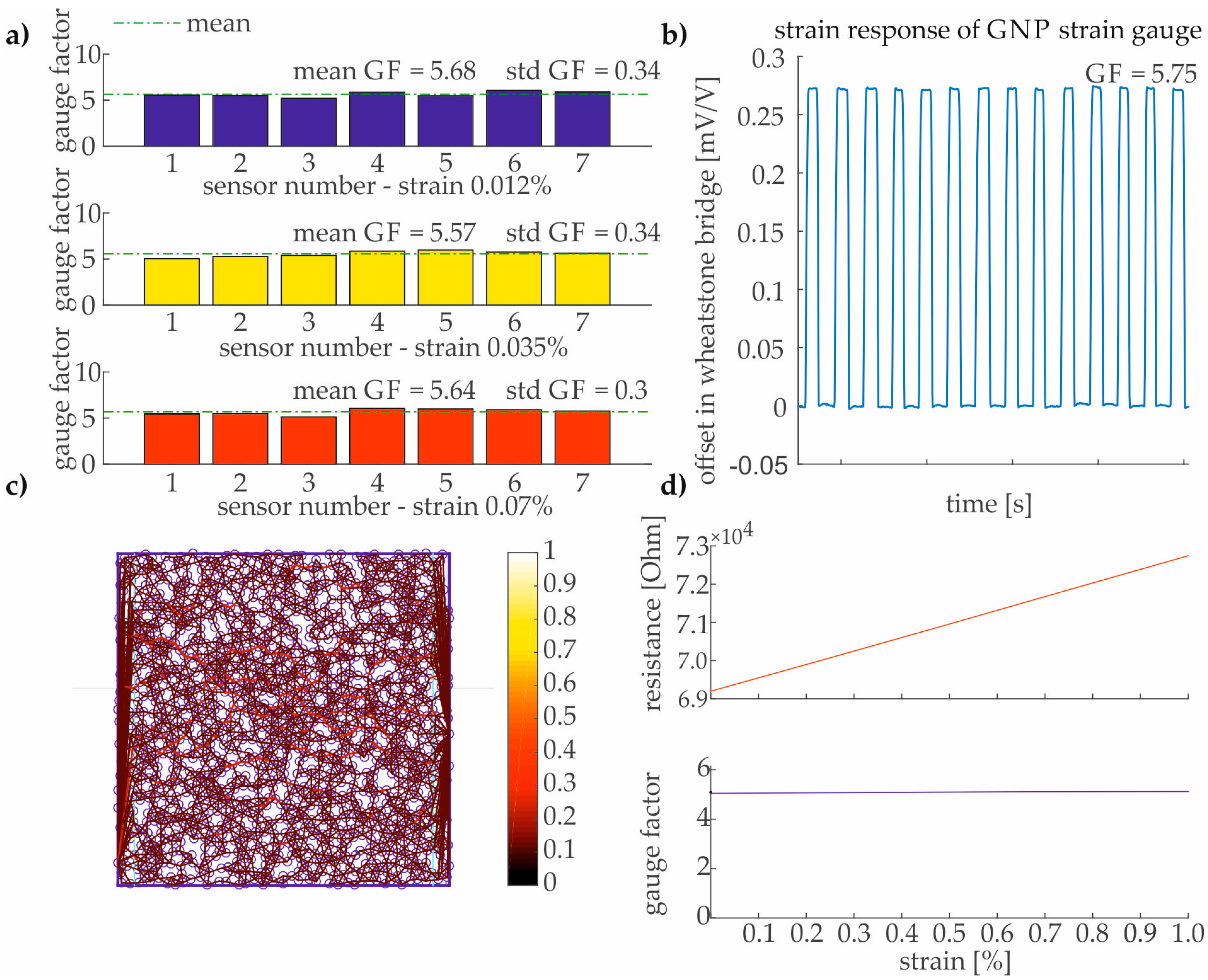
3.2. Experimental Testings of GNP
3.2.1. Quasi-Static Load Test
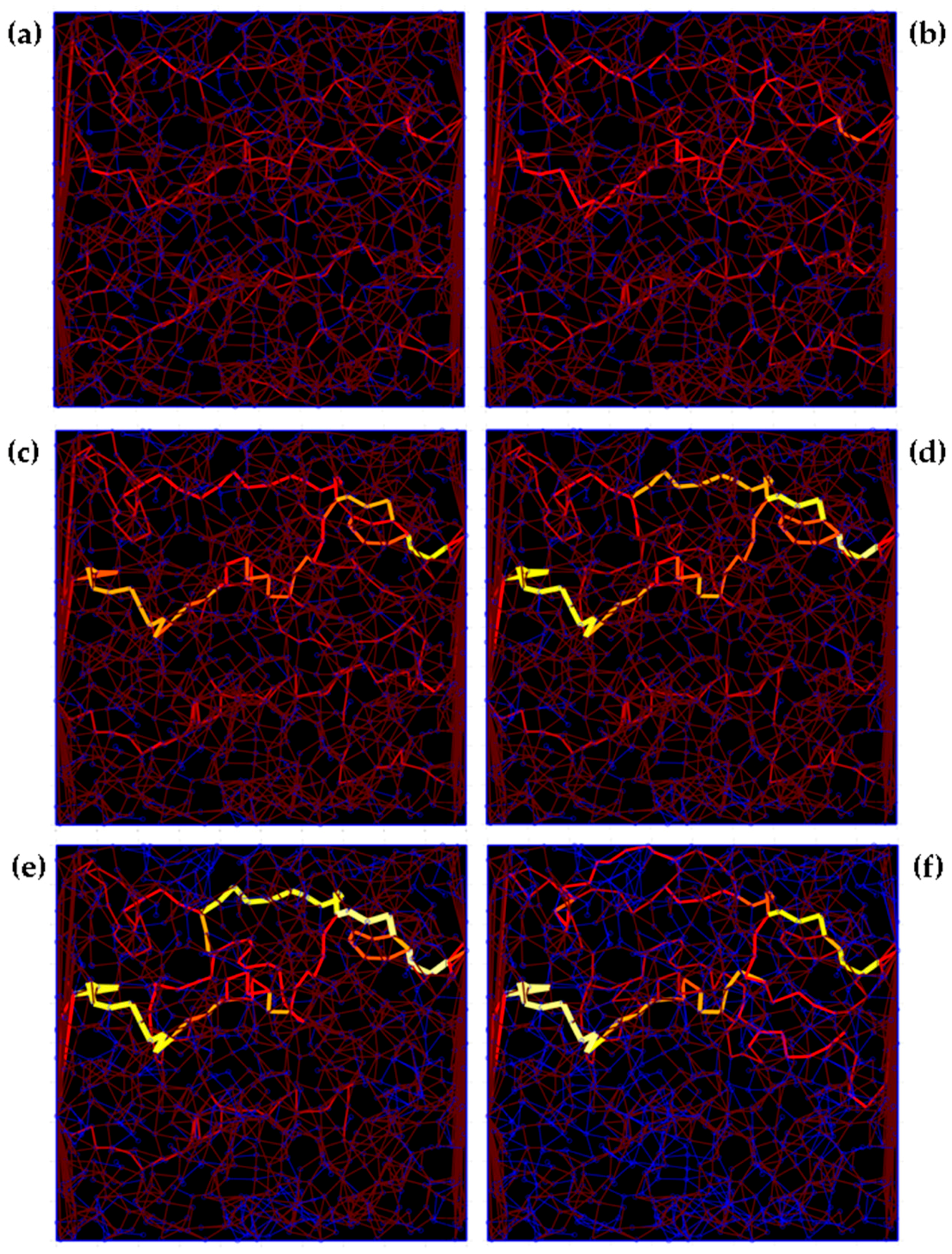
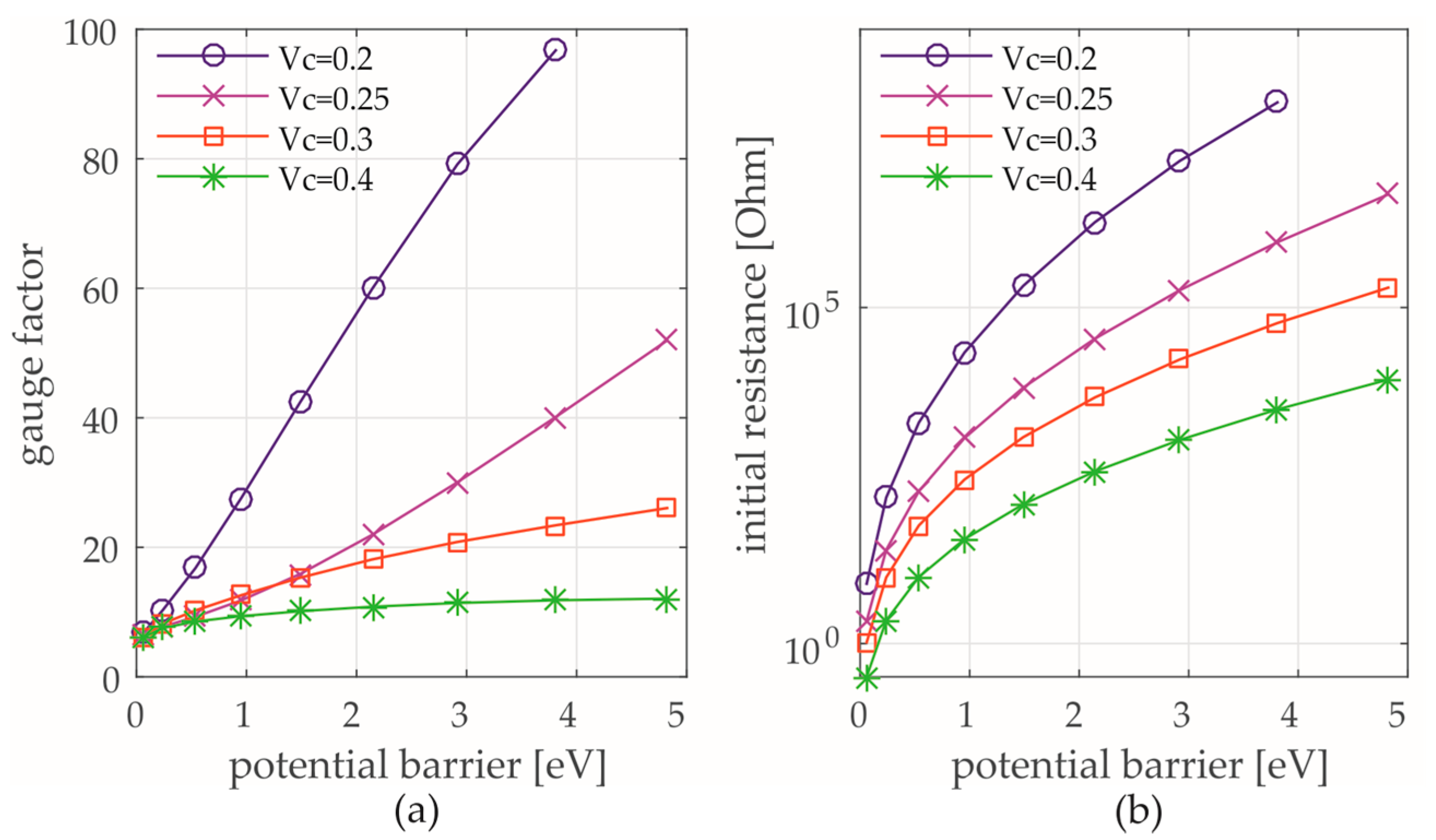
3.2.2. Numerical Investigations of Piezoresistive Effect
3.2.3. Discussion of the Results
4. Conclusions
Author Contributions
Conflicts of Interest
Appendix A
References
- Bolotin, K.I.; Sikes, K.J.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Tomori, H.; Kanda, A.; Goto, H.; Ootuka, Y.; Tsukagoshi, K.; Moriyama, S.; Watanabe, E.; Tsuya, D. Introducing Nonuniform Strain to Graphene Using Dielectric Nanopillars. Appl. Phys. Express 2011, 4, 75102. [Google Scholar] [CrossRef]
- Berger, C.; Song, Z.; Li, X.; Wu, X.; Brown, N.; Naud, C.; Mayou, D.; Li, T.; Hass, J.; Marchenkov, A.N.; et al. Electronic confinement and coherence in patterned epitaxial graphene. Science 2006, 312, 1191–1196. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Cai, W.; An, J.; Kim, S.; Nah, J.; Yang, D.; Piner, R.; Velamakanni, A.; Jung, I.; Tutuc, E.; et al. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 2009, 324, 1312–1314. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Hernandez, Y.; Nicolosi, V.; Lotya, M.; Blighe, F.M.; Sun, Z.; De, S.; McGovern, I.T.; Holland, B.; Byrne, M.; Gun’Ko, Y.K.; et al. High-yield production of graphene by liquid-phase exfoliation of graphite. Nat. Nanotechnol. 2008, 3, 563–568. [Google Scholar] [CrossRef] [PubMed]
- Ştefănescu, D.M. (Ed.) Handbook of Force Transducers; Springer: Berlin, Heidelberg, 2011. [Google Scholar]
- Wheatstone, C. The Bakerian Lecture: An Account of Several New Instruments and Processes for Determining the Constants of a Voltaic Circuit. Philos. Trans. R. Soc. Lond. 1843, 133, 303–327. [Google Scholar] [CrossRef]
- Smith, C.S. Piezoresistance Effect in Germanium and Silicon. Phys. Rev. 1954, 94, 42–49. [Google Scholar] [CrossRef]
- Rao, Y. Recent progress in applications of in-fibre Bragg grating sensors. Opt. Lasers Eng. 1999, 31, 297–324. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; Wiley: Chichester, UK, 2013. [Google Scholar]
- Chen, Z.; Ming, T.; Goulamaly, M.M.; Yao, H.; Nezich, D.; Hempel, M.; Hofmann, M.; Kong, J. Enhancing the Sensitivity of Percolative Graphene Films for Flexible and Transparent Pressure Sensor Arrays. Adv. Funct. Mater. 2016, 26, 5061–5067. [Google Scholar] [CrossRef]
- Zhao, J.; He, C.; Yang, R.; Shi, Z.; Cheng, M.; Yang, W.; Xie, G.; Wang, D.; Shi, D.; Zhang, G. Ultra-sensitive strain sensors based on piezoresistive nanographene films. Appl. Phys. Lett. 2012, 101, 63112. [Google Scholar] [CrossRef]
- Li, X.; Zhang, R.; Yu, W.; Wang, K.; Wei, J.; Wu, D.; Cao, A.; Li, Z.; Cheng, Y.; Zheng, Q.; et al. Stretchable and highly sensitive graphene-on-polymer strain sensors. Sci. Rep. 2012, 2, 870. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Zhang, G.-Y.; Shi, D.-X. Review of graphene-based strain sensors. Chin. Phys. B 2013, 22, 57701. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, R.; Shi, Z.; Zhang, L.; Shi, D.; Wang, E.; Zhang, G. Super-elastic graphene ripples for flexible strain sensors. ACS Nano 2011, 5, 3645–3650. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.-W.; Liao, Z.-M.; Zhou, J.-X.; Zhou, Y.-B.; Wu, H.-C.; Zhang, R.; Jing, G.; Xu, J.; Wu, X.; Guo, W.; et al. Strain dependent resistance in chemical vapor deposition grown graphene. Appl. Phys. Lett. 2011, 99, 213107. [Google Scholar] [CrossRef]
- Kim, K.S.; Zhao, Y.; Jang, H.; Lee, S.Y.; Kim, J.M.; Kim, K.S.; Ahn, J.-H.; Kim, P.; Choi, J.-Y.; Hong, B.H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706–710. [Google Scholar] [CrossRef] [PubMed]
- Hempel, M.; Nezich, D.; Kong, J.; Hofmann, M. A novel class of strain gauges based on layered percolative films of 2D materials. Nano Lett. 2012, 12, 5714–5718. [Google Scholar] [CrossRef] [PubMed]
- Simmons, J.G. Generalized Formula for the Electric Tunnel Effect between Similar Electrodes Separated by a Thin Insulating Film. J. Appl. Phys. 1963, 34, 1793–1803. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, G.; Yang, R.; Lu, X.; Cheng, M.; Xie, G.; Meng, J.; Shi, D.; Zhang, G. Tunable piezoresistivity of nanographene films for strain sensing. ACS Nano 2015, 9, 1622–1629. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, L.; Yang, T.; Li, X.; Zang, X.; Zhu, M.; Wang, K.; Wu, D.; Zhu, H. Wearable and Highly Sensitive Graphene Strain Sensors for Human Motion Monitoring. Adv. Funct. Mater. 2014, 24, 4666–4670. [Google Scholar] [CrossRef]
- Tung, T.T.; Nine, M.J.; Krebsz, M.; Pasinszki, T.; Coghlan, C.J.; Tran, D.N.H.; Losic, D. Recent Advances in Sensing Applications of Graphene Assemblies and Their Composites. Adv. Funct. Mater. 2017, 321, 1702891. [Google Scholar] [CrossRef]
- Wu, S.; Ladani, R.B.; Zhang, J.; Ghorbani, K.; Zhang, X.; Mouritz, A.P.; Kinloch, A.J.; Wang, C.H. Strain Sensors with Adjustable Sensitivity by Tailoring the Microstructure of Graphene Aerogel/PDMS Nanocomposites. ACS Appl. Mater. Interfaces 2016, 8, 24853–24861. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Yang, T.; Yang, Y.; Zhu, J.; Li, L.; Alam, F.E.; Li, X.; Wang, K.; Cheng, H.; Lin, C.-T.; et al. Large-Area Ultrathin Graphene Films by Single-Step Marangoni Self-Assembly for Highly Sensitive Strain Sensing Application. Adv. Funct. Mater. 2016, 26, 1322–1329. [Google Scholar] [CrossRef]
- Torrisi, F.; Hasan, T.; Wu, W.; Sun, Z.; Lombardo, A.; Kulmala, T.S.; Hsieh, G.-W.; Jung, S.; Bonaccorso, F.; Paul, P.J.; et al. Inkjet-printed graphene electronics. ACS Nano 2012, 6, 2992–3006. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Huang, Y.; Liang, J.; Wan, X.; Chen, Y. Graphene-based conducting inks for direct inkjet printing of flexible conductive patterns and their applications in electric circuits and chemical sensors. Nano Res. 2011, 4, 675–684. [Google Scholar] [CrossRef]
- Gilje, S.; Han, S.; Wang, M.; Wang, K.L.; Kaner, R.B. A chemical route to graphene for device applications. Nano Lett. 2007, 7, 3394–3398. [Google Scholar] [CrossRef] [PubMed]
- van Lam, D.; Kim, S.-M.; Cho, Y.; Kim, J.-H.; Lee, H.-J.; Yang, J.-M.; Lee, S.-M. Healing defective CVD-graphene through vapor phase treatment. Nanoscale 2014, 6, 5639–5644. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.D.; Niklaus, F.; Paussa, A.; Vaziri, S.; Fischer, A.C.; Sterner, M.; Forsberg, F.; Delin, A.; Esseni, D.; Palestri, P.; et al. Electromechanical piezoresistive sensing in suspended graphene membranes. Nano Lett. 2013, 13, 3237–3242. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Lian, J.; Siriponglert, S.; Li, H.; Chen, Y.P.; Pei, S.-S. Graphene segregated on Ni surfaces and transferred to insulators. Appl. Phys. Lett. 2008, 93, 113103. [Google Scholar] [CrossRef]
- Yu, Q.; Jauregui, L.A.; Wu, W.; Colby, R.; Tian, J.; Su, Z.; Cao, H.; Liu, Z.; Pandey, D.; Wei, D.; et al. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nat. Mater. 2011, 10, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Magnuson, C.W.; Venugopal, A.; An, J.; Suk, J.W.; Han, B.; Borysiak, M.; Cai, W.; Velamakanni, A.; Zhu, Y.; et al. Graphene films with large domain size by a two-step chemical vapor deposition process. Nano Lett. 2010, 10, 4328–4334. [Google Scholar] [CrossRef] [PubMed]
- Song, H.S.; Li, S.L.; Miyazaki, H.; Sato, S.; Hayashi, K.; Yamada, A.; Yokoyama, N.; Tsukagoshi, K. Origin of the relatively low transport mobility of graphene grown through chemical vapor deposition. Sci. Rep. 2012, 2, 337. [Google Scholar] [CrossRef] [PubMed]
- Reina, A.; Jia, X.; Ho, J.; Nezich, D.; Son, H.; Bulovic, V.; Dresselhaus, M.S.; Kong, J. Large Area, Few-Layer Graphene Films on Arbitrary Substrates by Chemical Vapor Deposition. Nano Lett. 2009, 9, 30–35. [Google Scholar] [CrossRef] [PubMed]
- ACS—Materials Advanced Chemicals Supplier. ACS Material CVD Graphene on Copper. Available online: http://www.acsmaterial.com (accessed on 13 September 2017).
- E. I. du Pont de Nemours & Co. Inc. Wilmington. Dupont™ Kapton® summary of properties. Available online: http://www.dupont.com (accessed on 7 November 2017).
- Cheng, Z.; Zhou, Q.; Wang, C.; Li, Q.; Wang, C.; Fang, Y. Toward intrinsic graphene surfaces: A systematic study on thermal annealing and wet-chemical treatment of SiO2-supported graphene devices. Nano Lett. 2011, 11, 767–771. [Google Scholar] [CrossRef] [PubMed]
- Kataria, S.; Wagner, S.; Ruhkopf, J.; Gahoi, A.; Pandey, H.; Bornemann, R.; Vaziri, S.; Smith, A.D.; Ostling, M.; Lemme, M.C. Chemical vapor deposited graphene: From synthesis to applications. Phys. Status Solidi A 2014, 211, 2439–2449. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F.; Piscanec, S.; Jiang, D.; Novoselov, K.S.; Roth, S.; et al. Raman spectrum of graphene and graphene layers. Phys. Rev. Lett. 2006, 97, 187401. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, A.C. Raman spectroscopy of graphene and graphite: Disorder, electron–phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007, 143, 47–57. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Jorio, A.; Hofmann, M.; Dresselhaus, G.; Saito, R. Perspectives on carbon nanotubes and graphene Raman spectroscopy. Nano Lett. 2010, 10, 751–758. [Google Scholar] [CrossRef] [PubMed]
- Wallace, P.R. The Band Theory of Graphite. Phys. Rev. 1947, 71, 622–634. [Google Scholar] [CrossRef]
- Paton, K.R.; Varrla, E.; Backes, C.; Smith, R.J.; Khan, U.; O’Neill, A.; Boland, C.; Lotya, M.; Istrate, O.M.; King, P.; et al. Scalable production of large quantities of defect-free few-layer graphene by shear exfoliation in liquids. Nat. Mater. 2014, 13, 624–630. [Google Scholar] [CrossRef] [PubMed]
- Krueger, M.; Berg, S.; Stone, D.; Strelcov, E.; Dikin, D.A.; Kim, J.; Cote, L.J.; Huang, J.; Kolmakov, A. Drop-casted self-assembling graphene oxide membranes for scanning electron microscopy on wet and dense gaseous samples. ACS Nano 2011, 5, 10047–10054. [Google Scholar] [CrossRef] [PubMed]
- Kong, B.-S.; Geng, J.; Jung, H.-T. Layer-by-layer assembly of graphene and gold nanoparticles by vacuum filtration and spontaneous reduction of gold ions. Chem. Commun 2009, 2174–2176. [Google Scholar] [CrossRef] [PubMed]
- Lotya, M.; Hernandez, Y.; King, P.J.; Smith, R.J.; Nicolosi, V.; Karlsson, L.S.; Blighe, F.M.; De, S.; Wang, Z.; McGovern, I.T.; et al. Liquid phase production of graphene by exfoliation of graphite in surfactant/water solutions. J. Am. Chem. Soc. 2009, 131, 3611–3620. [Google Scholar] [CrossRef] [PubMed]
- Wiedemann, M.; Melz, T. (Eds.) Smarte Strukturen und Systeme: Tagungsband des 4SMARTS-Symposiums, 21–22 June 2017, Braunschweig, 1st ed.; Shaker: Aachen, Germany, 2017. [Google Scholar]
- Modesto-López, L.B.; Miettinen, M.; Riikonen, J.; Torvela, T.; Pfüller, C.; Lehto, V.-P.; Lähde, A.; Jokiniemi, J. Films of Graphene Nanomaterials Formed by Ultrasonic Spraying of Their Stable Suspensions. Aerosol Sci. Technol. 2015, 49, 45–56. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and Conduction. Rev. Mod. Phys. 1973, 45, 574–588. [Google Scholar] [CrossRef]
- Stauffer, D. Introduction to Percolation Theory: Revised Second Edition, 2nd ed.; Taylor and Francis: Hoboken, NJ, USA, 2014. [Google Scholar]
- Mohiuddin, T.M.G.; Lombardo, A.; Nair, R.R.; Bonetti, A.; Savini, G.; Jalil, R.; Bonini, N.; Basko, D.M.; Galiotis, C.; Marzari, N.; et al. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Grüneisen parameters, and sample orientation. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Lu, Z.; Dunn, M.L. van der Waals adhesion of graphene membranes. J. Appl. Phys. 2010, 107, 44301. [Google Scholar] [CrossRef]
- Oskouyi, A.; Sundararaj, U.; Mertiny, P. Tunneling Conductivity and Piezoresistivity of Composites Containing Randomly Dispersed Conductive Nano-Platelets. Materials 2014, 7, 2501–2521. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Pascal, T.A.; Kim, H.; Goddard, W.A.; Greer, J.R. Electronic—Mechanical coupling in graphene from in situ nanoindentation experiments and multiscale atomistic simulations. Nano Lett. 2011, 11, 1241–1246. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.D.; Niklaus, F.; Paussa, A.; Schroder, S.; Fischer, A.C.; Sterner, M.; Wagner, S.; Vaziri, S.; Forsberg, F.; Esseni, D.; et al. Piezoresistive Properties of Suspended Graphene Membranes under Uniaxial and Biaxial Strain in Nanoelectromechanical Pressure Sensors. ACS Nano 2016, 10, 9879–9886. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Low, T.; Perebeinos, V.; Bol, A.A.; Zhu, Y.; Yan, H.; Tersoff, J.; Avouris, P. Structure and electronic transport in graphene wrinkles. Nano Lett. 2012, 12, 3431–3436. [Google Scholar] [CrossRef] [PubMed]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural defects in graphene. ACS Nano 2011, 5, 26–41. [Google Scholar] [CrossRef] [PubMed]
- Hirai, H.; Tsuchiya, H.; Kamakura, Y.; Mori, N.; Ogawa, M. Electron mobility calculation for graphene on substrates. J. Appl. Phys. 2014, 116, 83703. [Google Scholar] [CrossRef]
- Babichev, A.V.; Rykov, S.A.; Tchernycheva, M.; Smirnov, A.N.; Davydov, V.Y.; Kumzerov, Y.A.; Butko, V.Y. Influence of Substrate Microstructure on the Transport Properties of CVD-Graphene. ACS Appl. Mater. Interfaces 2016, 8, 240–246. [Google Scholar] [CrossRef] [PubMed]
- Alamusi; Hu, N.; Fukunaga, H.; Atobe, S.; Liu, Y.; Li, J. Piezoresistive strain sensors made from carbon nanotubes based polymer nanocomposites. Sensors 2011, 11, 10691–10723. [Google Scholar] [CrossRef] [PubMed]

| Potential Barrier (eV) | Std GF (%) | Std Initial Resistance (%) |
|---|---|---|
| 0.04 | 6.2% | 4.1% |
| 0.24 | 9.9% | 8.0% |
| 0.95 | 22.0% | 17.6% |
| 2.14 | 25.1% | 20.8% |
| 3.81 | 37.0% | 39.4% |
| 8.57 | 101.8% | 66.6% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yokaribas, V.; Wagner, S.; Schneider, D.S.; Friebertshäuser, P.; Lemme, M.C.; Fritzen, C.-P. Strain Gauges Based on CVD Graphene Layers and Exfoliated Graphene Nanoplatelets with Enhanced Reproducibility and Scalability for Large Quantities. Sensors 2017, 17, 2937. https://doi.org/10.3390/s17122937
Yokaribas V, Wagner S, Schneider DS, Friebertshäuser P, Lemme MC, Fritzen C-P. Strain Gauges Based on CVD Graphene Layers and Exfoliated Graphene Nanoplatelets with Enhanced Reproducibility and Scalability for Large Quantities. Sensors. 2017; 17(12):2937. https://doi.org/10.3390/s17122937
Chicago/Turabian StyleYokaribas, Volkan, Stefan Wagner, Daniel S. Schneider, Philipp Friebertshäuser, Max C. Lemme, and Claus-Peter Fritzen. 2017. "Strain Gauges Based on CVD Graphene Layers and Exfoliated Graphene Nanoplatelets with Enhanced Reproducibility and Scalability for Large Quantities" Sensors 17, no. 12: 2937. https://doi.org/10.3390/s17122937
APA StyleYokaribas, V., Wagner, S., Schneider, D. S., Friebertshäuser, P., Lemme, M. C., & Fritzen, C.-P. (2017). Strain Gauges Based on CVD Graphene Layers and Exfoliated Graphene Nanoplatelets with Enhanced Reproducibility and Scalability for Large Quantities. Sensors, 17(12), 2937. https://doi.org/10.3390/s17122937





