Towards Realistic Urban Traffic Experiments Using DFROUTER: Heuristic, Validation and Extensions
Abstract
:1. Introduction
2. Related Works
3. Overview of the Simulation Tools Adopted
3.1. SUMO Overview
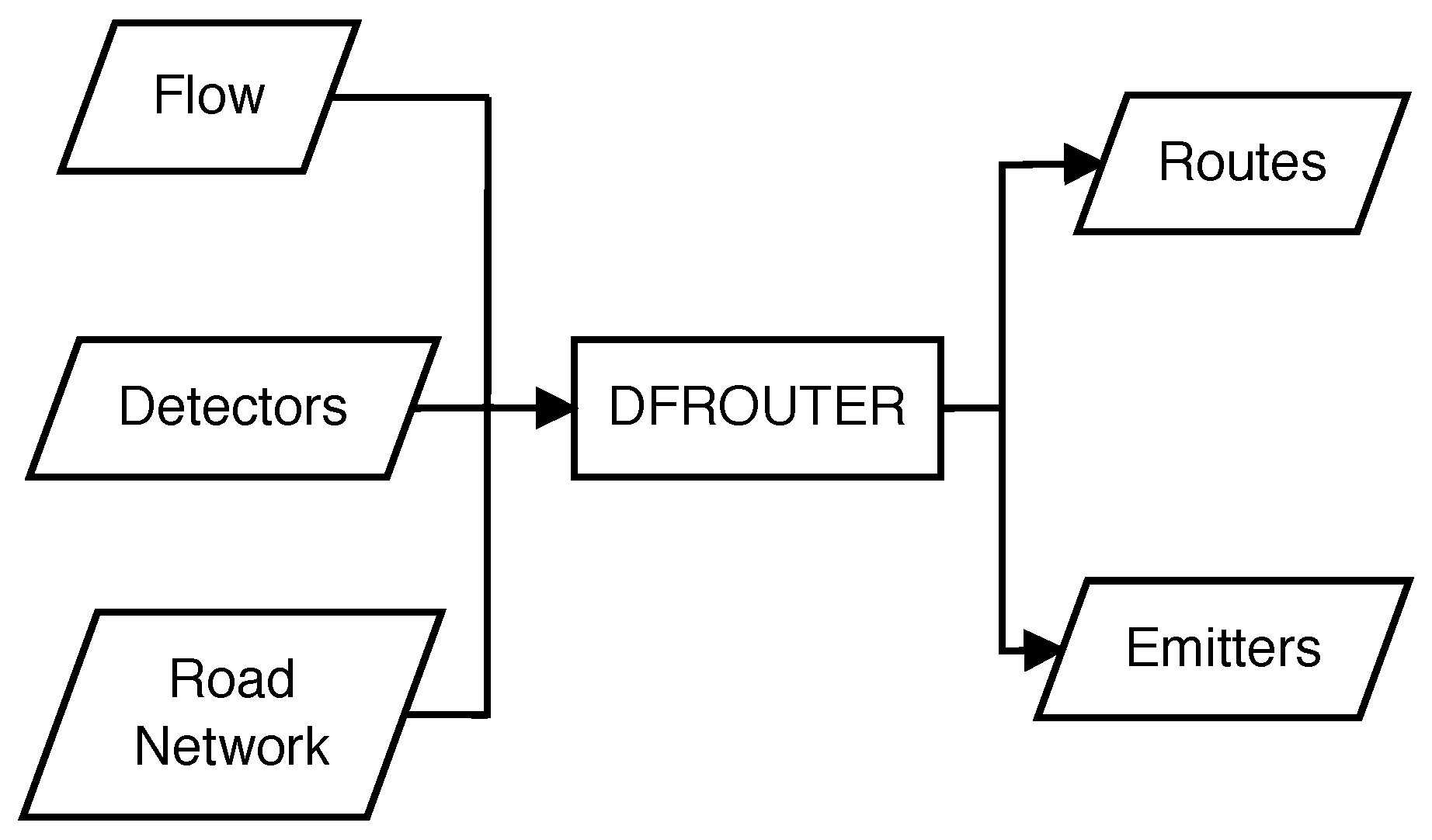
3.2. DFROUTER Operation
- Importing the road network, including the detector positions and associated measurements.
- Applying the detector classification for the following categories: source detectors (starting points of routes), in-between detectors and sink detectors (ending points of routes).
- Calculate the vehicle flow between consecutive detectors.
- Compute the route usage probabilities. Usually, measurements are provided on a per-lane basis, and they need to be summarized for each cross-section.
4. Traffic Flow Generation Methodology
4.1. DFROUTER Output Analysis
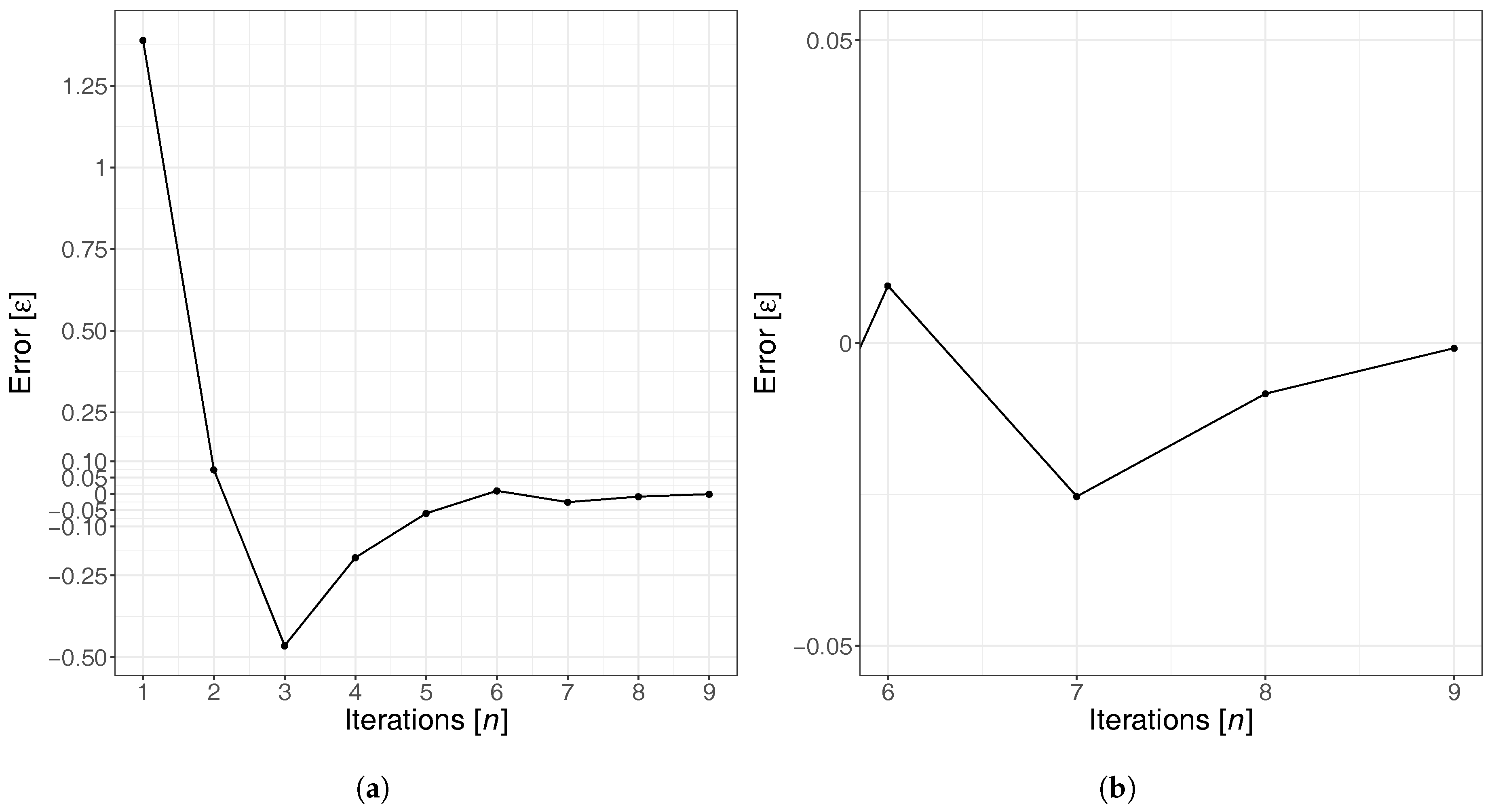
4.2. Proposed Iterative Heuristic
| Algorithm 1 Iterative heuristic. |
|
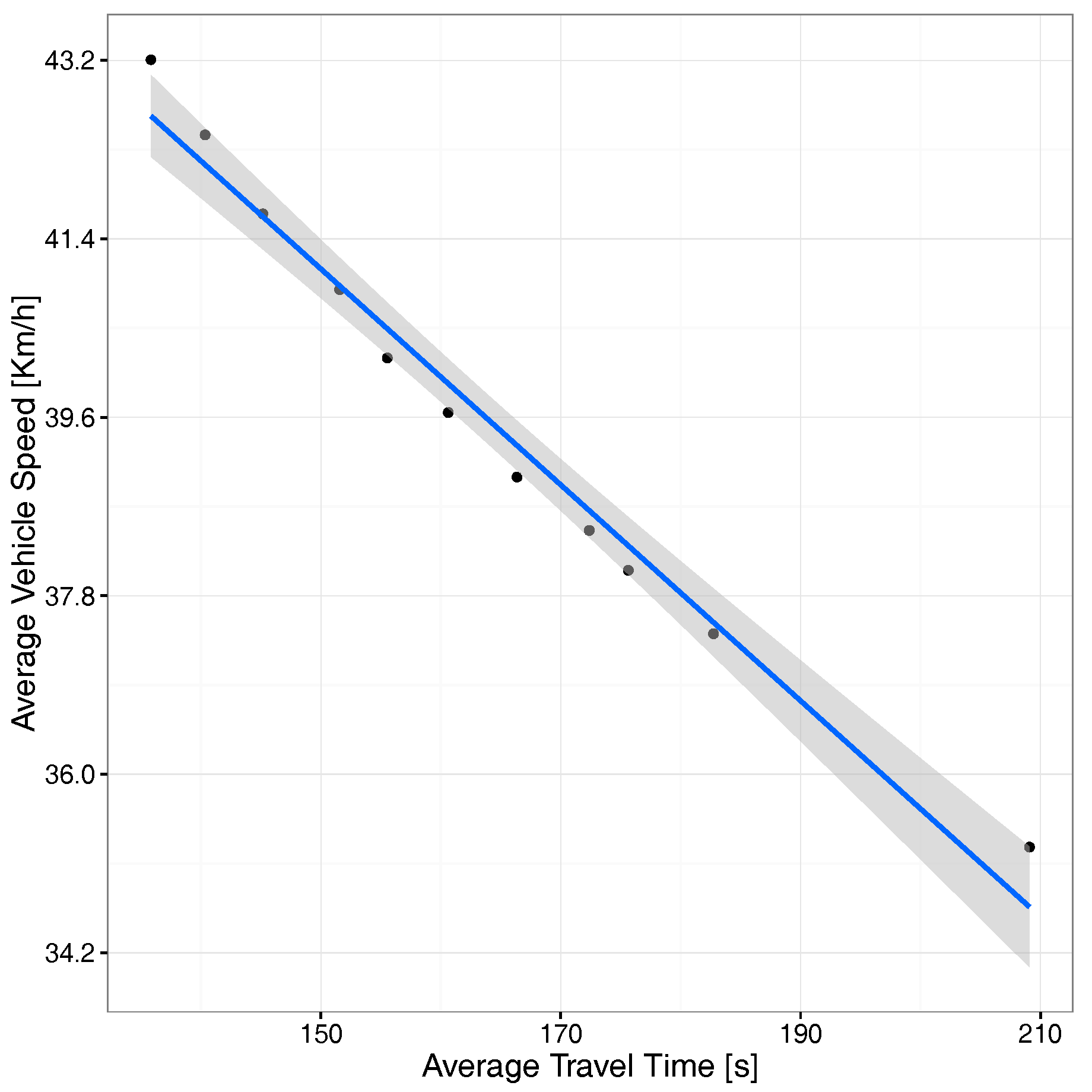
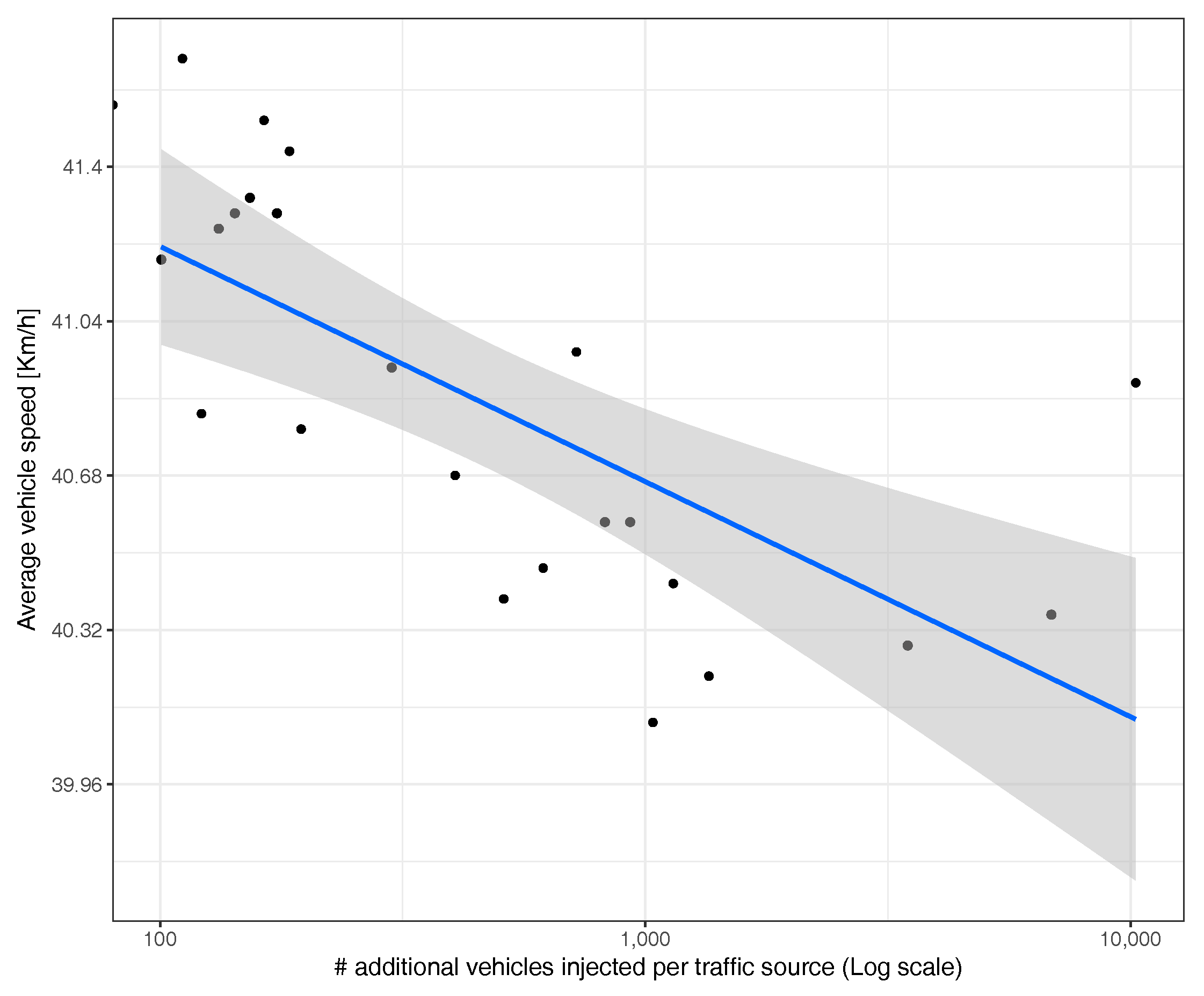
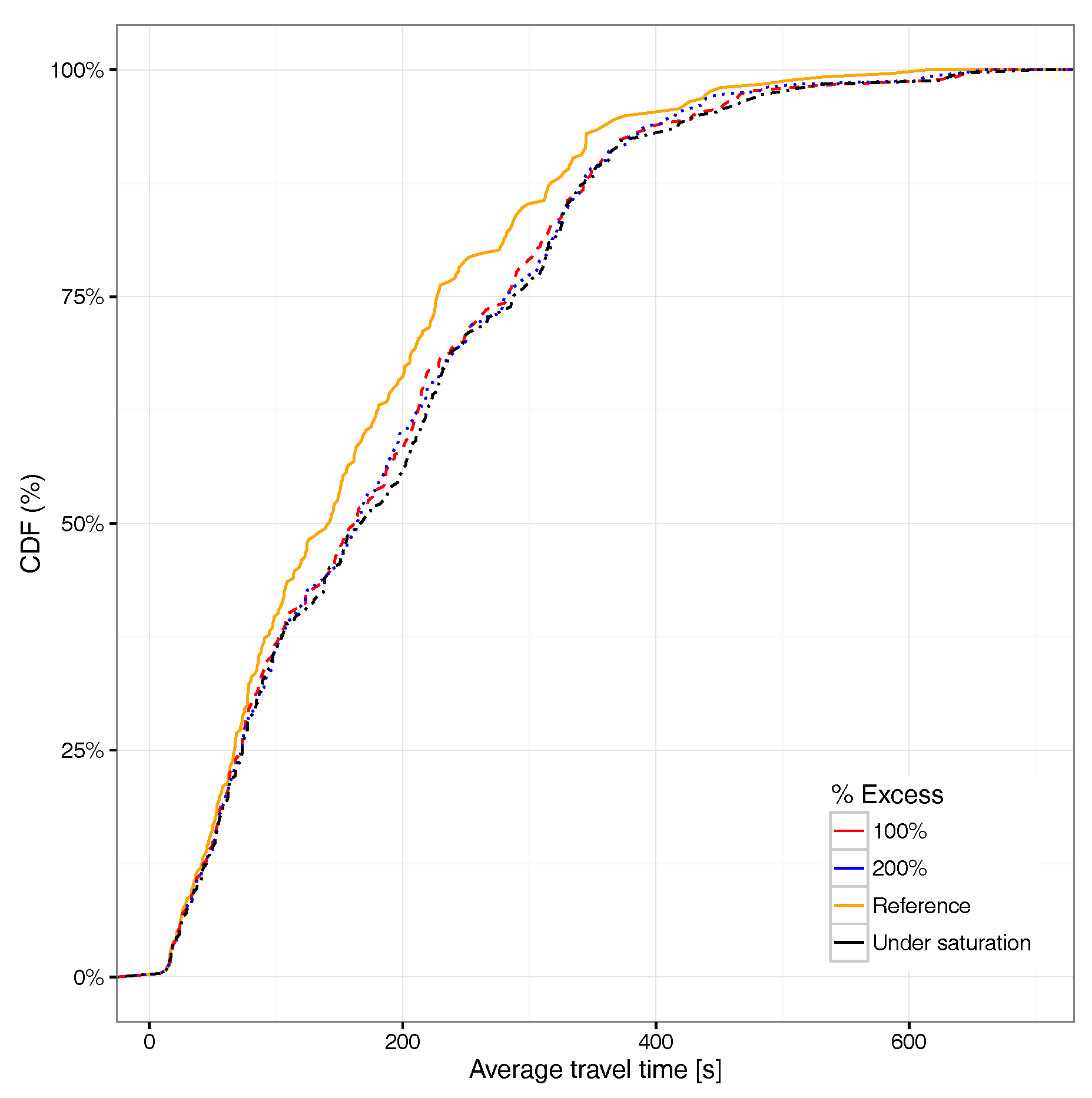
4.3. Goodness of Fit Achieved by the Proposed Heuristic
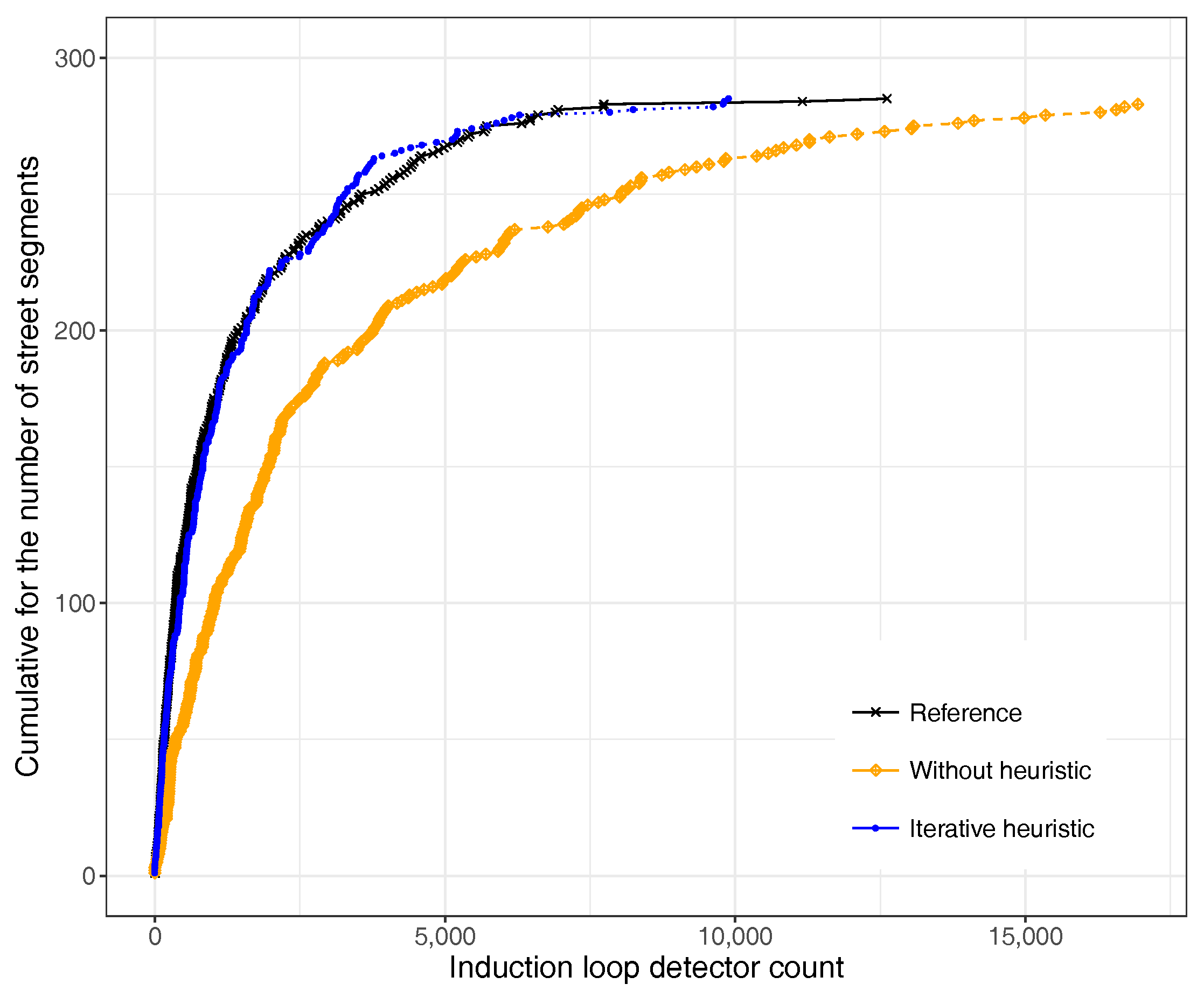
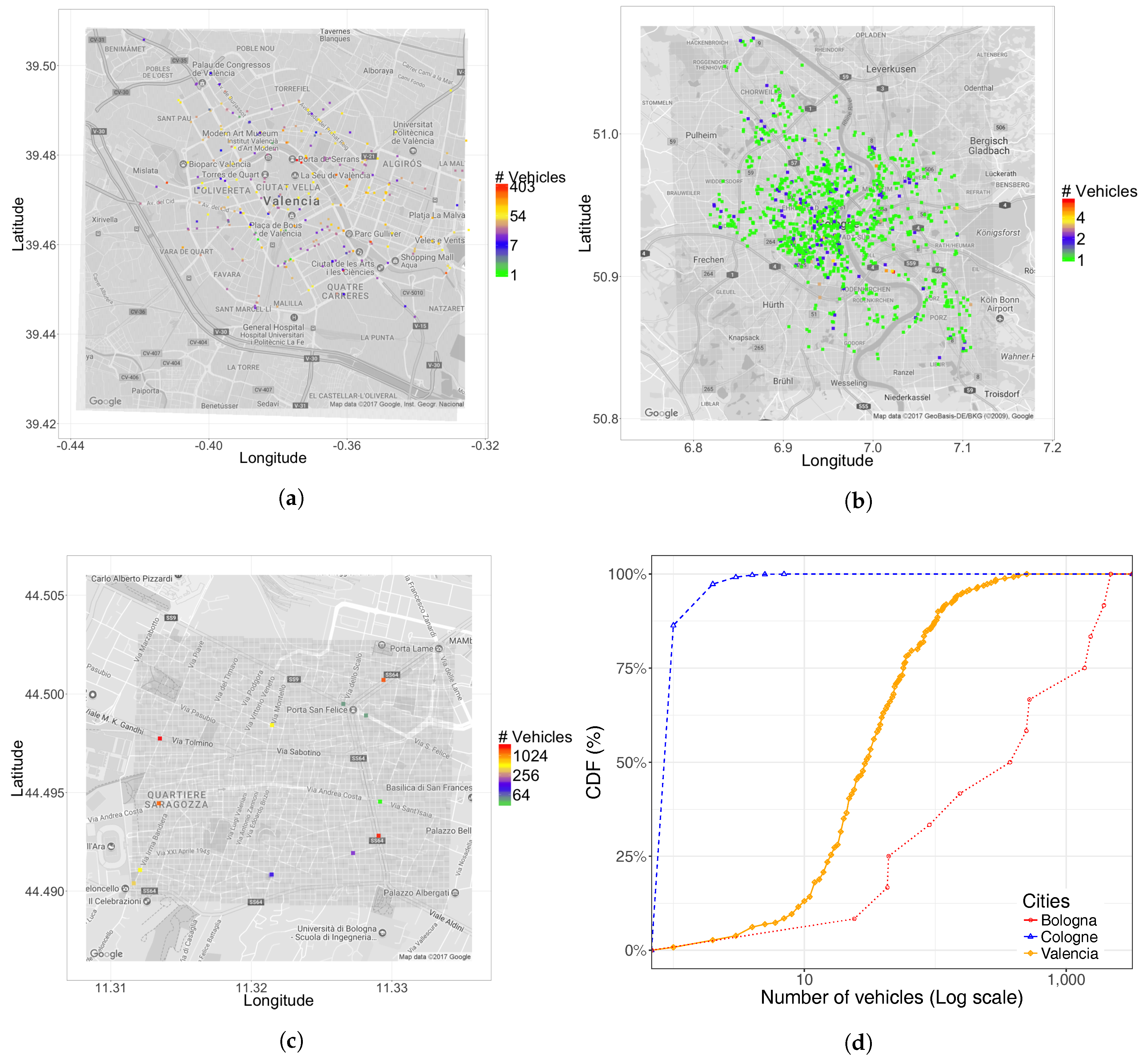
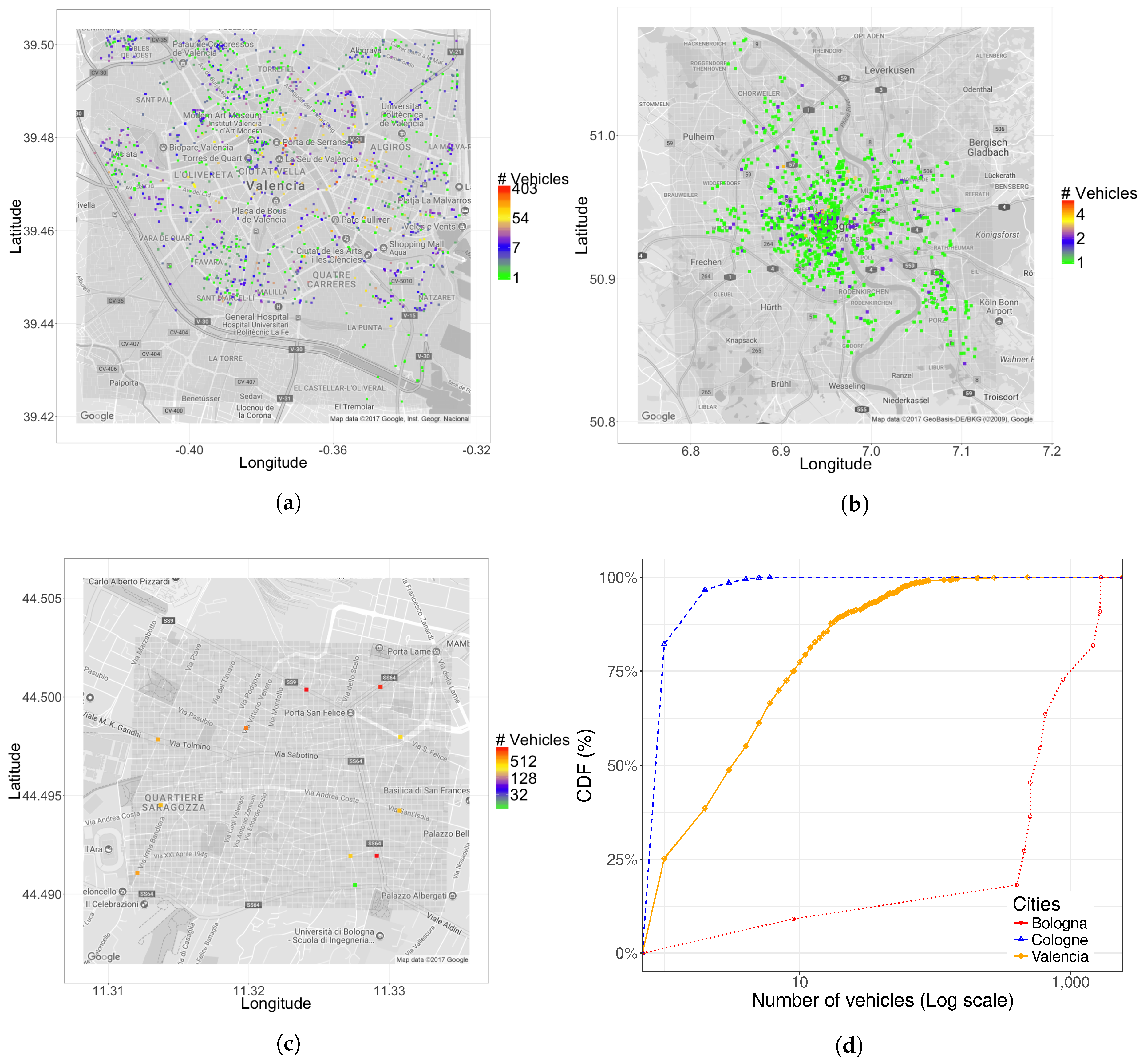
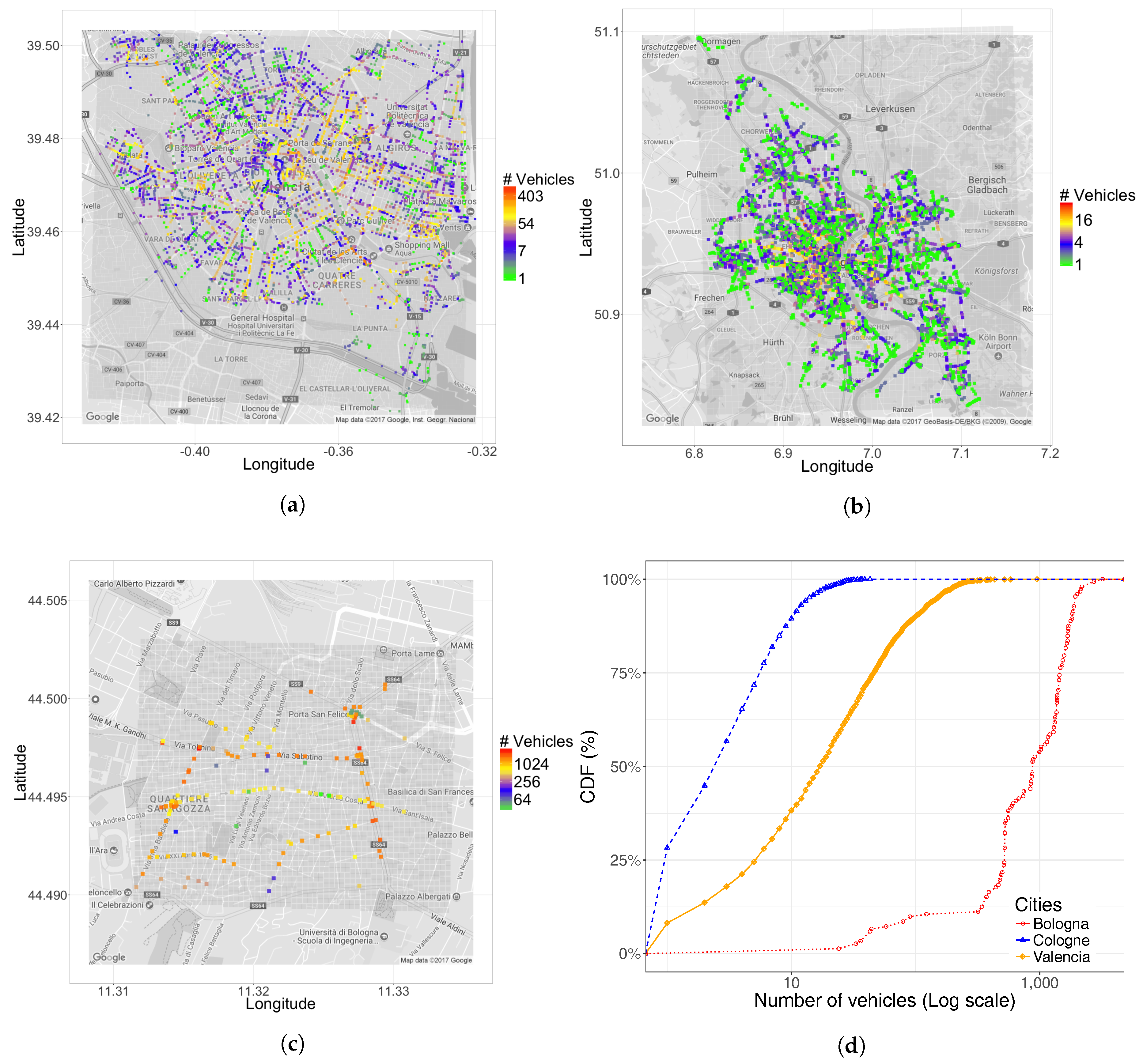
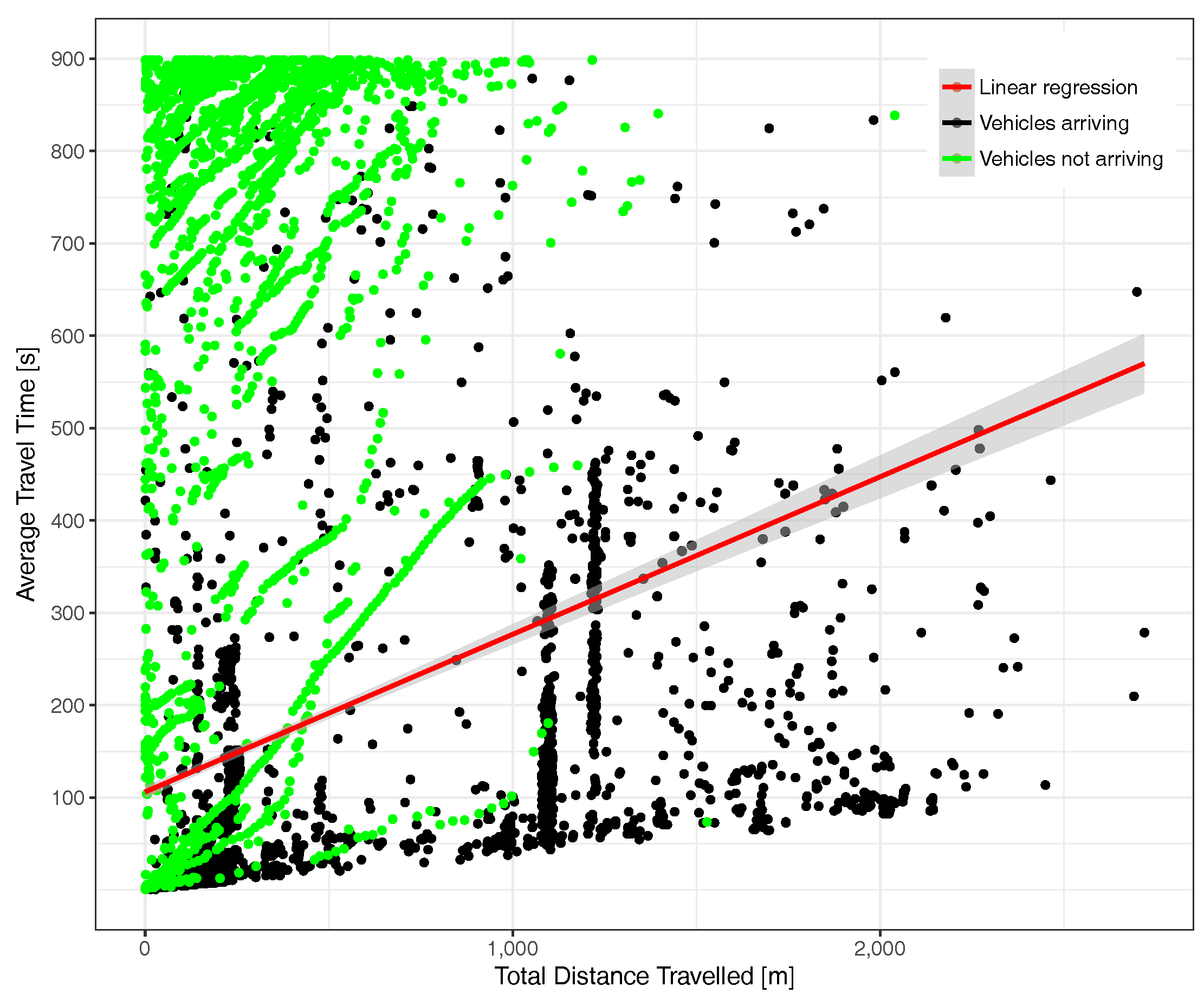
5. Simulation Results
- The vehicle density per km.
- Percentage of street segments affected.
- The distribution along a map.
- The Cumulative Distribution Function (CDF) of vehicles per segment.
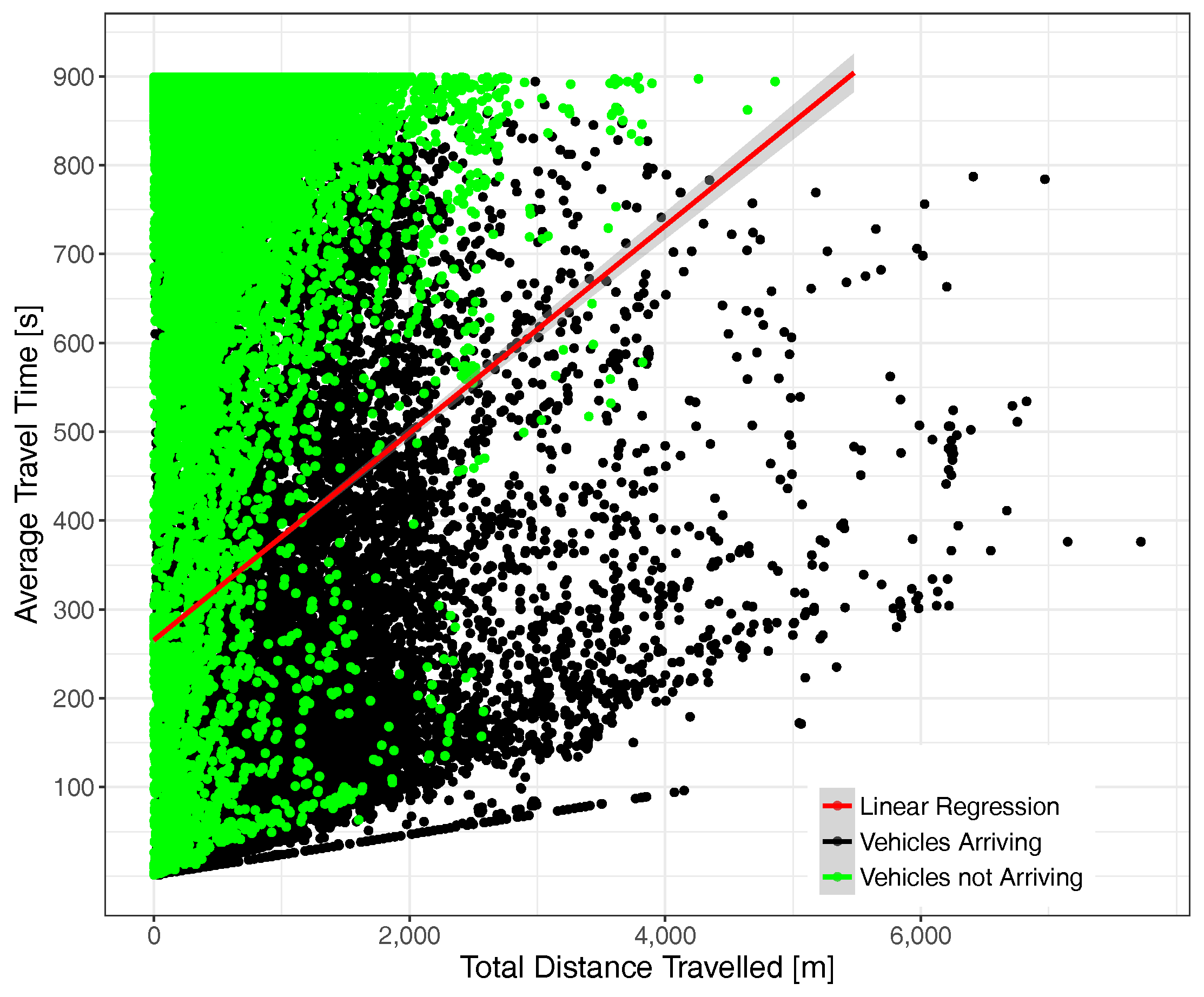
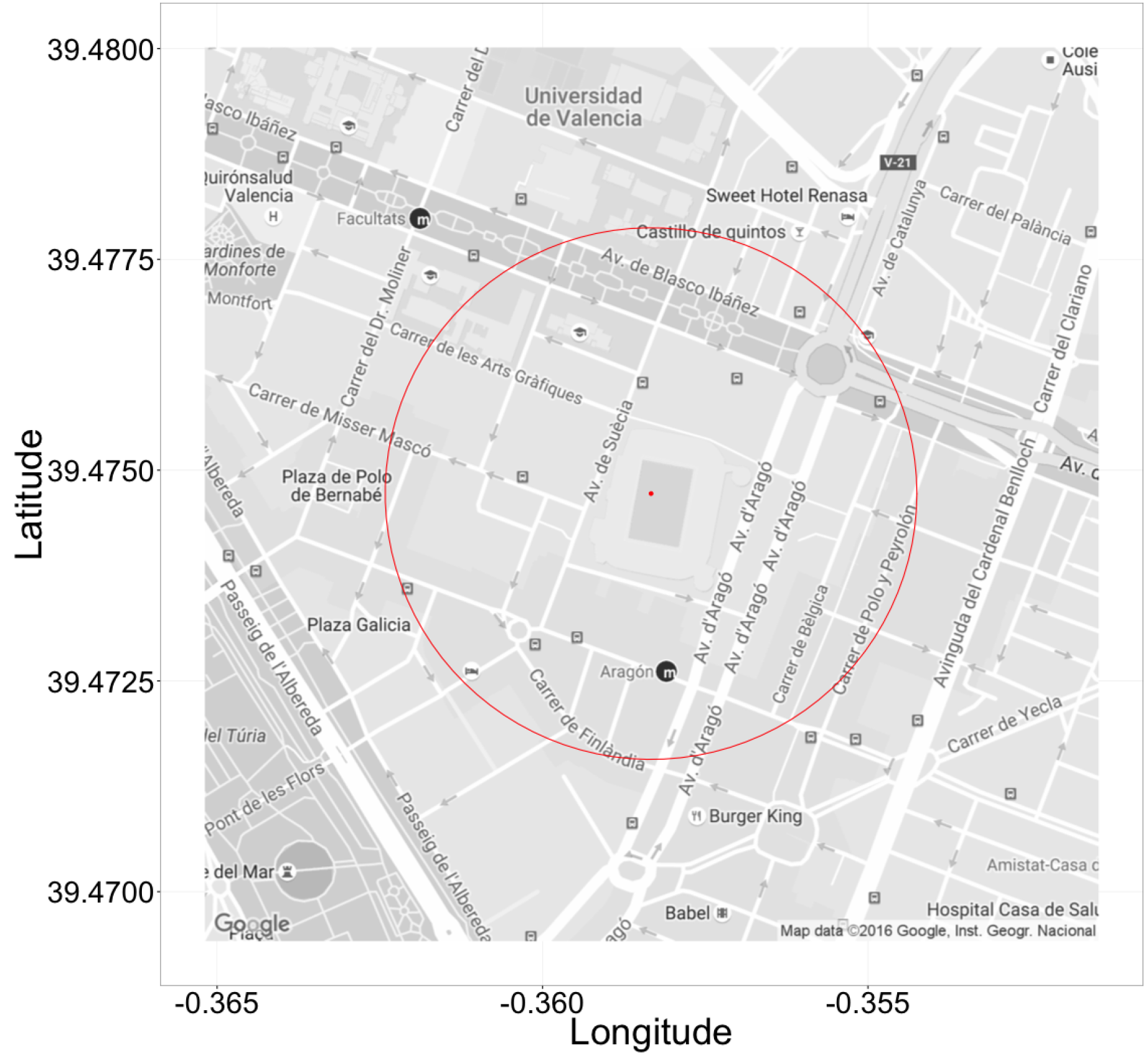
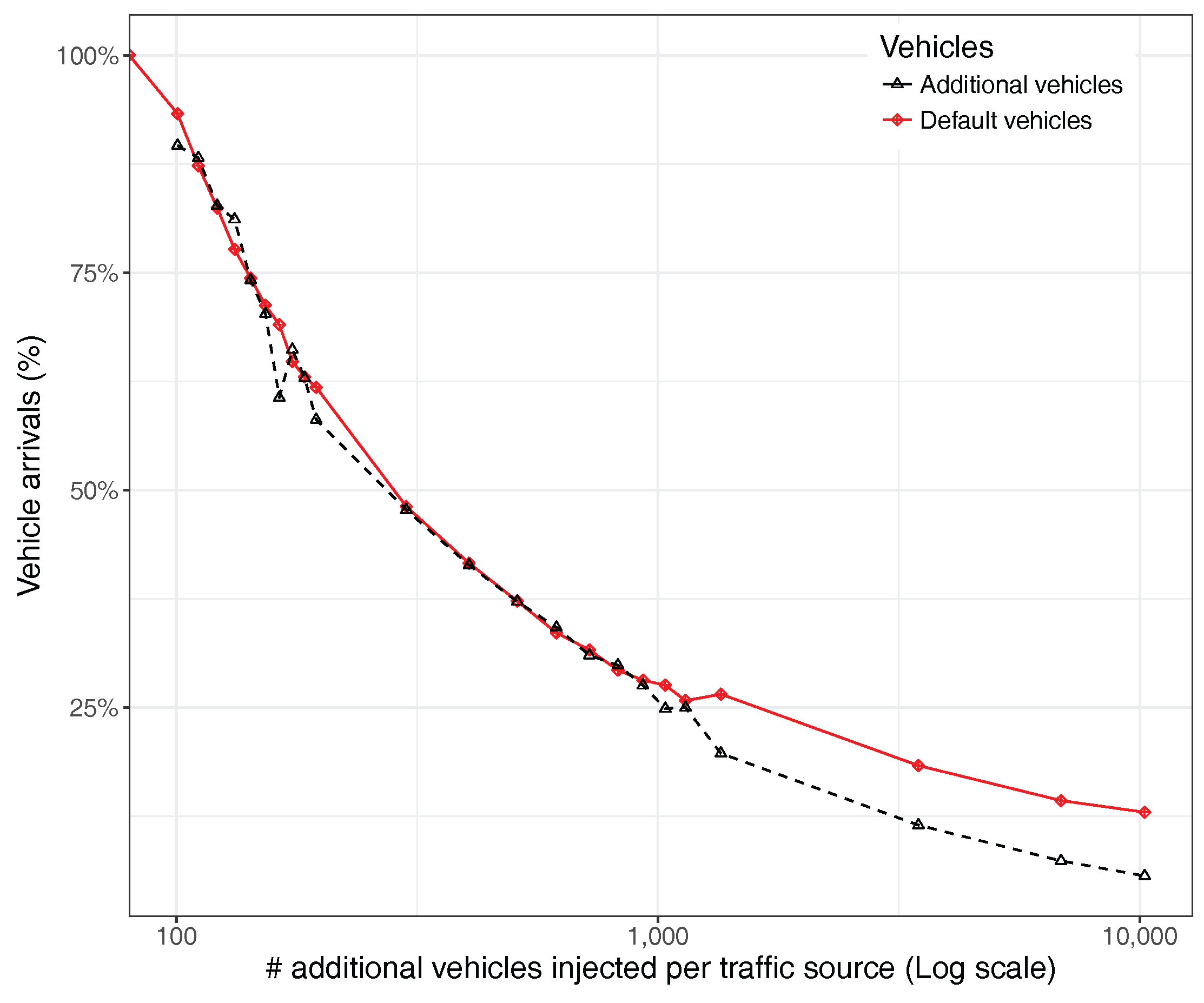
5.1. Traffic Destination Analysis
5.2. Traffic Dispersion Analysis
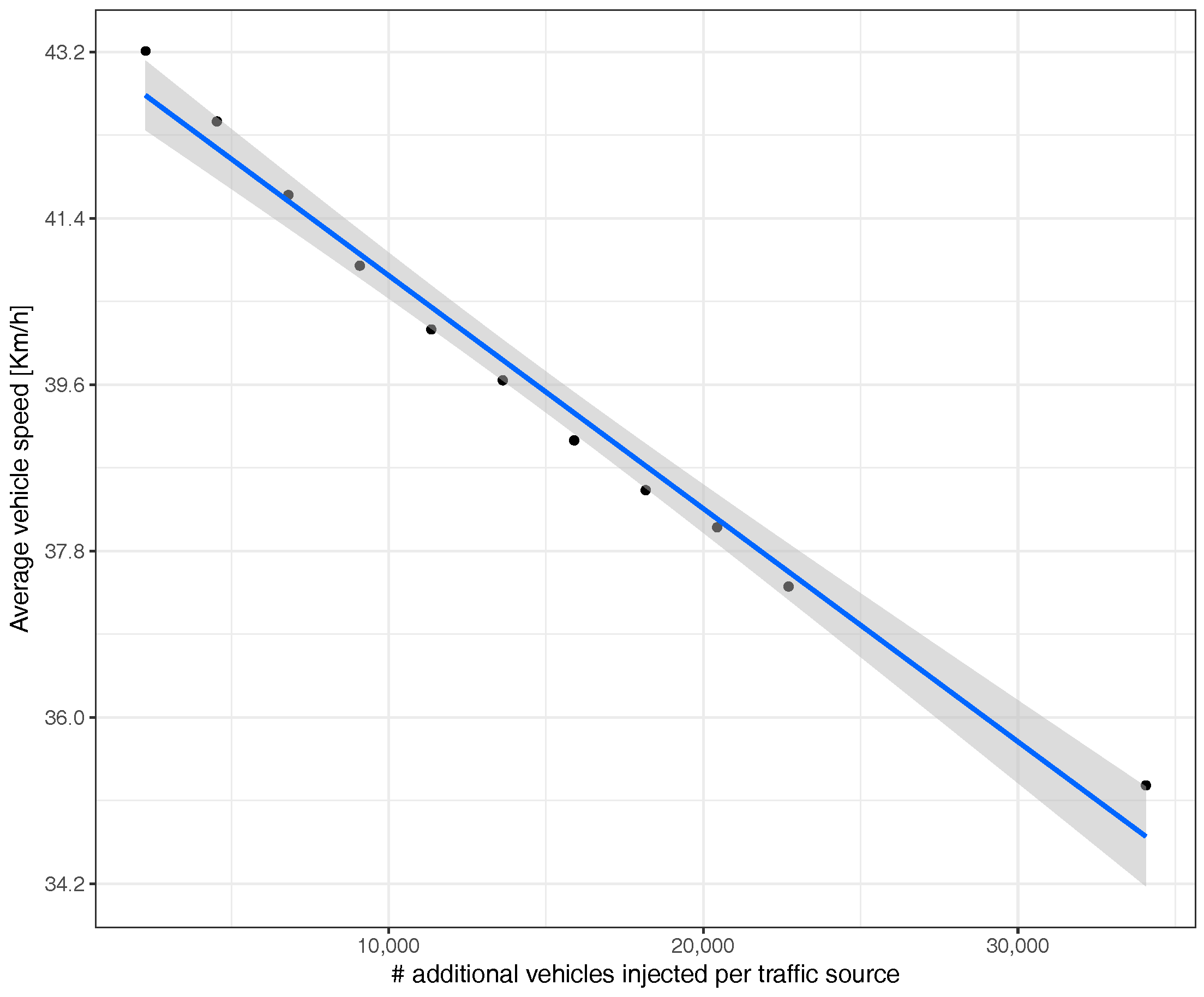
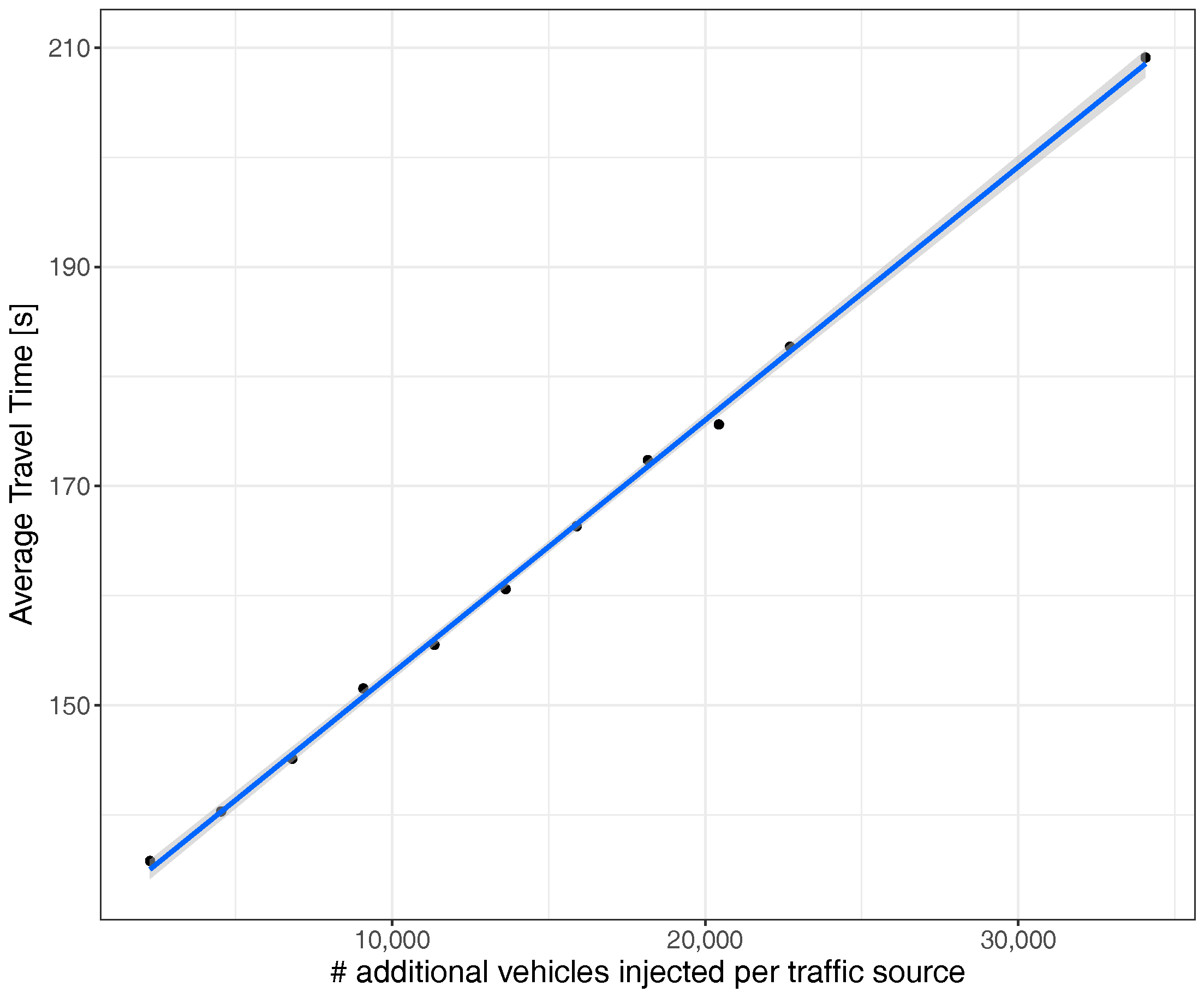
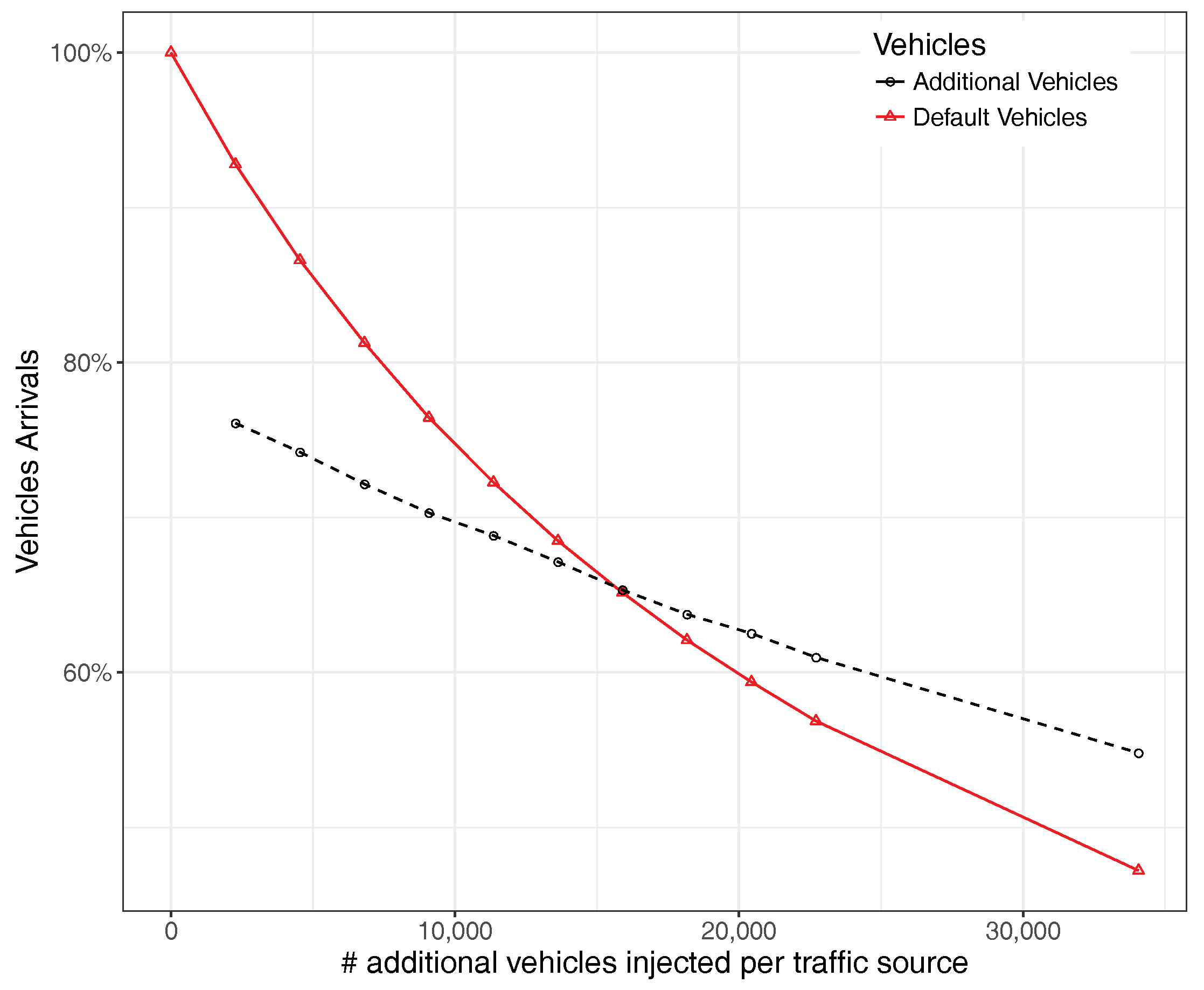
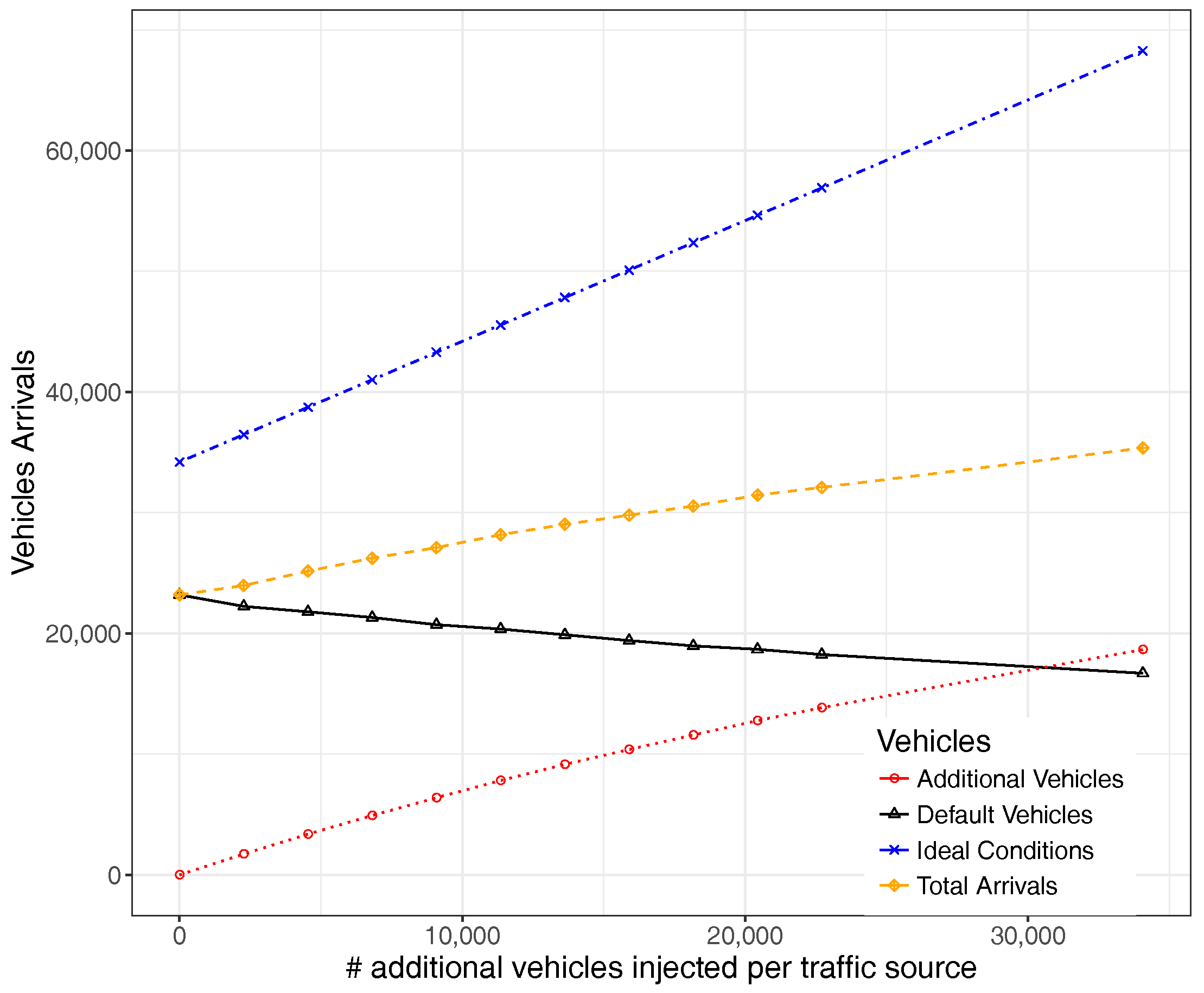
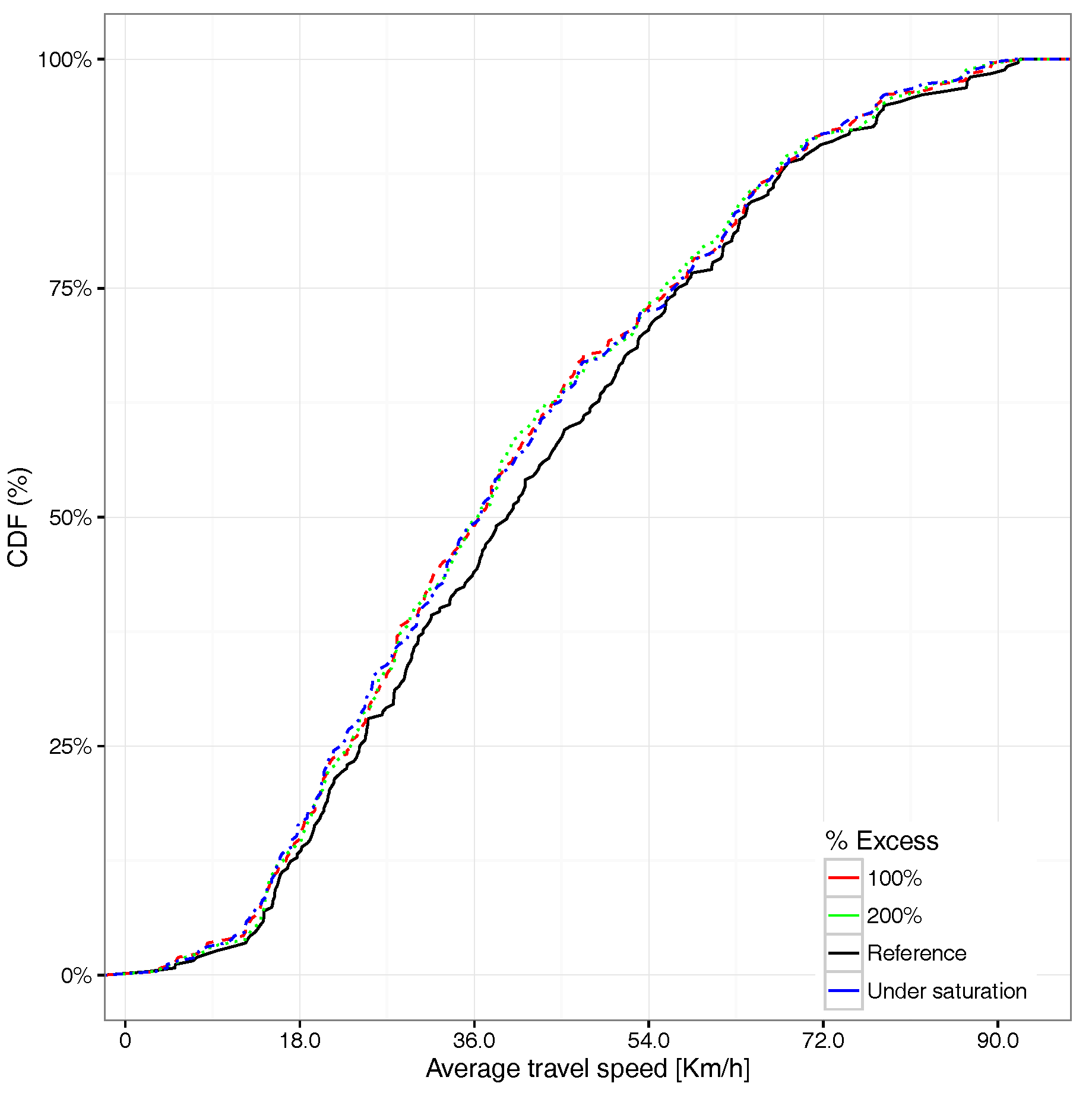
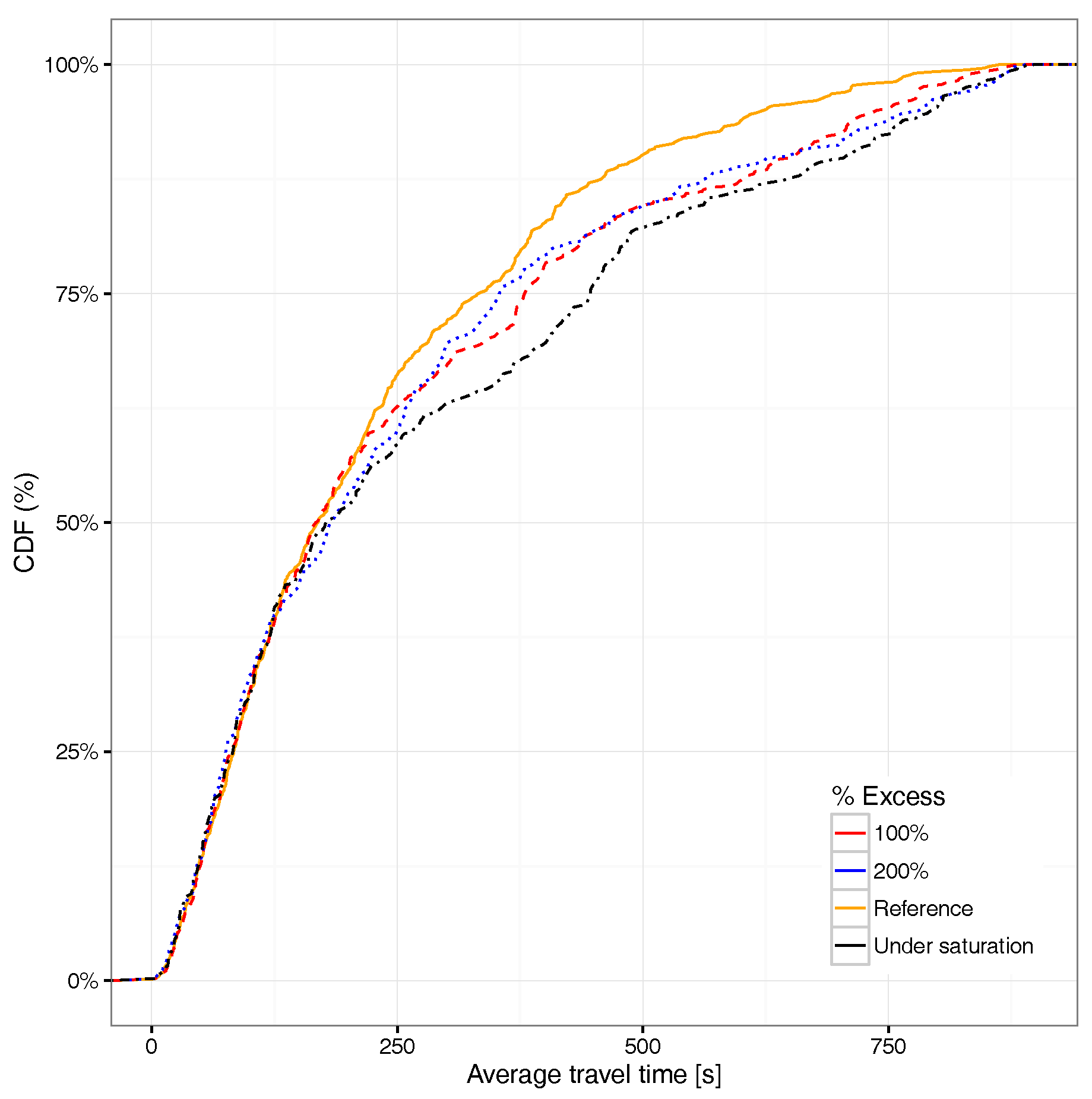
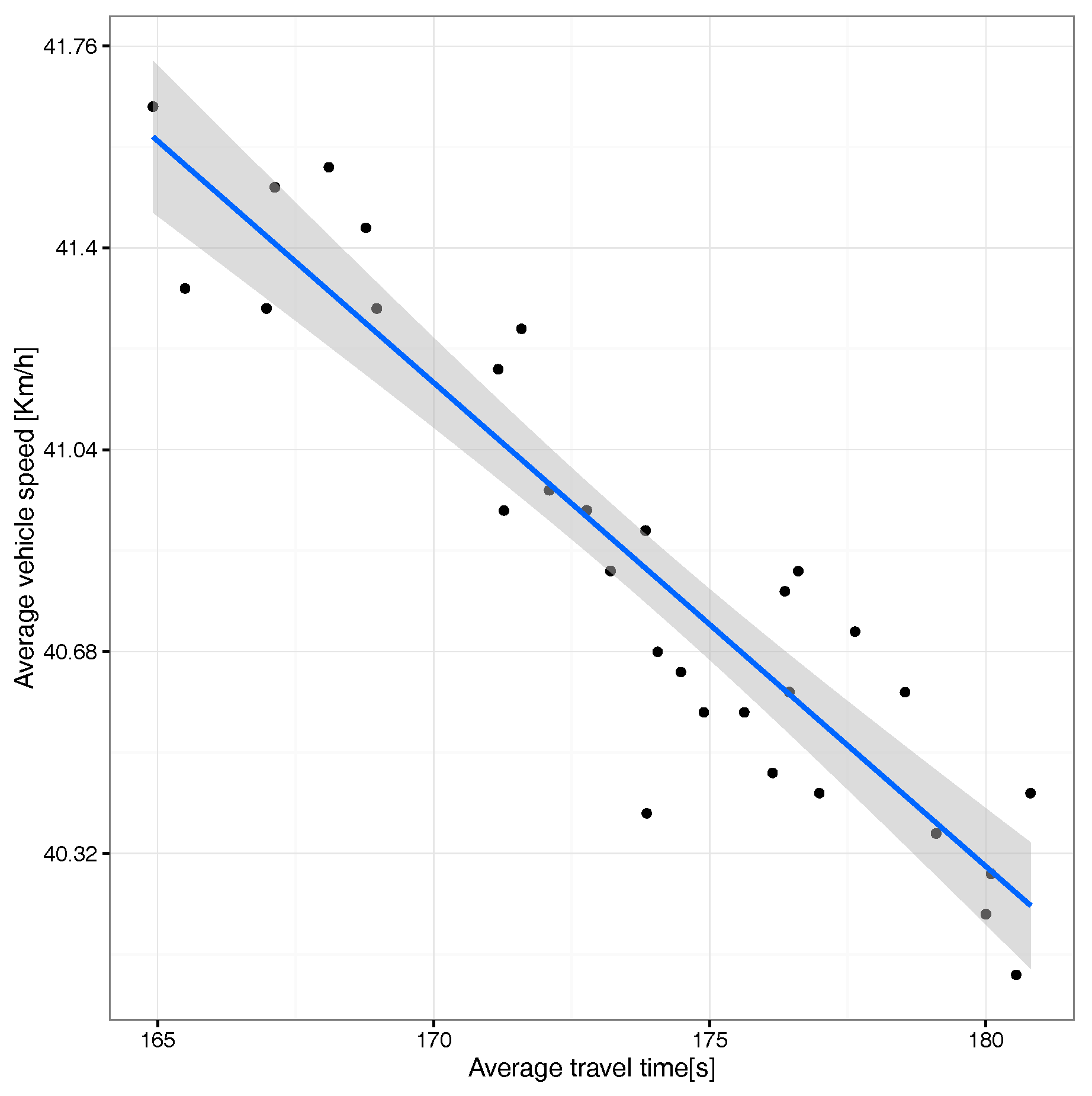
6. Traffic Congestion Analysis
6.1. Uniform Traffic Load Regulation
6.2. Hotspot-Based Traffic Load Regulation
7. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hoogendoorn, S.P.; Bovy, P.H. State-of-the-art of vehicular traffic flow modelling. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2001, 215, 283–303. [Google Scholar] [CrossRef]
- Härri, J.; Filali, F.; Bonnet, C. Mobility models for vehicular ad hoc networks: A survey and taxonomy. Commun. Surv. Tutor. 2009, 11, 19–41. [Google Scholar] [CrossRef]
- Krajzewicz, D.; Hertkorn, G.; Rössel, C.; Wagner, P. SUMO (Simulation of Urban MObility)-an open-source traffic simulation. In Proceedings of the 4th Middle East Symposium on Simulation and Modelling (MESM20002), Sharjah, United Arab Emirates, 28–30 September 2002; pp. 183–187, ISBN 90-77039-09-0. [Google Scholar]
- Zambrano, J.L.; Calafate, C.T.; Soler, D.; Cano, J.C.; Manzoni, P. Using Real Traffic Data for ITS Simulation: Procedure and Validation. In Proceedings of the 2016 International IEEE Conferences UIC/ATC/ScalCom/CBDCom/IoP/SmartWorld, Toulouse, France, 18–21 July 2016; pp. 161–170. [Google Scholar] [CrossRef]
- Calafate, C.T.; Soler, D.; Cano, J.C.; Manzoni, P. Traffic Management as a Service: The Traffic Flow Pattern Classification Problem. Math. Probl. Eng. 2015, 716598. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Krajzewicz, D.; Fullerton, M.; Nicolay, E. DFROUTER—Estimation of Vehicle Routes from Cross-Section Measurements. In Modeling Mobility with Open Data; Springer: Cham, Switzerland, 2015; pp. 3–23. [Google Scholar]
- Nguyen, T.; Fullerton, M.; Krajzewicz, D.; Mai, S.T. DFROUTER-Route estimate methods based on detector data. In SUMO2014-Modeling Mobility with Open Data; Springer: Berlin, Germany, 2014. [Google Scholar]
- Qiu, Z.; Cheng, P. State of the art and practice: Cellular probe technology applied in advanced traveler information system. In Proceedings of the 86th Annual Meeting Transportation Research Board, Washington, DC, USA, 21–25 January 2007; Volume 07-0223. [Google Scholar]
- Ma, X.; Yu, H.; Wang, Y.; Wang, Y. Large-scale transportation network congestion evolution prediction using deep learning theory. PLoS ONE 2015, 10, e0119044. [Google Scholar] [CrossRef] [PubMed]
- Cascetta, E. Estimation of trip matrices from traffic counts and survey data: A generalized least squares estimator. Transp. Res. B Methodol. 1984, 18, 289–299. [Google Scholar] [CrossRef]
- Caceres, N.; Wideberg, J.P.; Benitez, F.G. Deriving origin destination data from a mobile phone network. Inst. Eng. Technol. 2007, 1, 15–26. [Google Scholar] [CrossRef]
- Sohn, K.; Kim, D. Dynamic origin–destination flow estimation using cellular communication system. IEEE Trans. Veh. Technol. 2008, 57, 2703–2713. [Google Scholar] [CrossRef]
- Pan, C.; Lu, J.; Di, S.; Ran, B. Cellular-based data-extracting method for trip distribution. Transp. Res. Rec. 2006, 1945, 33–39. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, X.; Liu, Y.; Gong, K.; Henricakson, K.C.; Xu, M.; Wang, Y. A Two-Stage Algorithm for Origin-Destination Matrices Estimation Considering Dynamic Dispersion Parameter for Route Choice. PLoS ONE 2006, 11, e0146850. [Google Scholar] [CrossRef]
- Castillo, E.; Conejo, A.J.; Menéndez, J.M.; Jiménez, P. The observability problem in traffic network models. Comput. Aided Civ. Inf. 2008, 23, 208–222. [Google Scholar] [CrossRef]
- Castillo, E.; Gallego, I.; Sánchez-Cambronero, S.; Rivas, A. Matrix tools for general observability analysis in traffic networks. IEEE Trans. Intell. Transp. Syst. 2010, 11, 799–813. [Google Scholar] [CrossRef]
- Hamedi, M.; Fish, R.L.W.; Haghani, A. Freeway dynamic message sign evaluation using bluetooth sensors: A case study. In Proceedings of the 17th ITS World Congress, Busan, Korea, 25–29 October 2010. [Google Scholar]
- Fernández-Lozano, J.J.; Martín-Guzmán, M.; Martín-Ávila, J.; García-Cerezo, A. A wireless sensor network for urban traffic characterization and trend monitoring. Sensors 2015, 15, 26143–26169. [Google Scholar] [CrossRef] [PubMed]
- Lees-Miller, J.; Wilson, R.E.; Box, S. Hidden Markov models for vehicle tracking with bluetooth. In Proceedings of the 92nd Annual Meeting Transportation Research Board, Washington, DC, USA, 13–17 January 2013; p. 14. [Google Scholar]
- Chakraborty, G.; Naik, K.; Chakraborty, D.; Shiratori, N.; Wei, D. Analysis of the Bluetooth device discovery protocol. Wirel. Netw. 2010, 16, 421–436. [Google Scholar] [CrossRef]
- Zhu, S.; Guo, Y.; Chen, J.; Li, D.; Cheng, L. Integrating Optimal Heterogeneous Sensor Deployment and Operation Strategies for Dynamic Origin-Destination Demand Estimation. Sensors 2017, 17, 1767. [Google Scholar] [CrossRef] [PubMed]
- Van Der Zijpp, N. Dynamic origin-destination matrix estimation from traffic counts and automated vehicle identification data. J. Transp. Res. Rec. 1997, 1607, 87–94. [Google Scholar] [CrossRef]
- Barceló Bugeda, J.; Montero Mercadé, L.; Bullejos, M.; Serch, O.; Carmona, C. A Kalman filter approach for the estimation of time dependent od matrices exploiting bluetooth traffic data collection. In Proceedings of the 91st TRB Annual Meeting Compendium of Papers DVD, Washington, DC, USA, 22–26 January 2012; pp. 1–16. [Google Scholar] [CrossRef]
- Yang, X.; Lu, Y.; Hao, W. Origin Destination (O-D) Estimation using Probe Vehicle Trajectory and Link Counts. J. Adv. Trasnsp. 2017, 4341532. [Google Scholar] [CrossRef]
- Xie, X.F.; Smith, S.F.; Barlow, G.J. Schedule-Driven Coordination for Real-Time Traffic Network Control. In Proceedings of the Twenty-Second International Conference on Automated Planning and Scheduling, Sao Paulo, Brazil, 25–29 June 2012; pp. 323–331. [Google Scholar]
- McCluskey, T.L.; Vallati, M.; Franco, S. Automated planning for urban traffic management. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence (IJCAI-17), Melbourne, Australia, 19–25 August 2017; pp. 5238–5240. [Google Scholar]
- Shehata, M.S.; Cai, J.; Badawy, W.M.; Burr, T.W.; Pervez, M.S.; Johannesson, R.J.; Radmanesh, A. Video-based automatic incident detection for smart roads: The outdoor environmental challenges regarding false alarms. IEEE Trans. Intell. Transp. Syst. 2008, 9, 349–360. [Google Scholar] [CrossRef]
- Kastrinaki, V.; Zervakis, M.; Kalaitzakis, K. A survey of video processing techniques for traffic applications. Image Vis. Comput. 2003, 21, 359–381. [Google Scholar] [CrossRef]
- Fu, T.; Stipancic, J.; Zangenehpour, S.; Miranda-Moreno, L.; Saunier, N. Automatic Traffic Data Collection under Varying Lighting and Temperature Conditions in Multimodal Environments: Thermal versus Visible Spectrum Video-Based Systems. J. Adv. Trasnsp. 2017, 5142732. [Google Scholar] [CrossRef]
- Varga, A. The OMNeT++ discrete event simulation system. Eur. Stab. Mech. 2005, 9, 65. [Google Scholar]
- Krajzewicz, D. Traffic simulation with SUMO–simulation of urban mobility. In Fundamentals of Traffic Simulation; Springer: New York, NY, USA, 2010; pp. 269–293. ISBN 978-1-4419-6141-9. [Google Scholar]
- Behrisch, M.; Bieker, L.; Erdmann, J.; Krajzewicz, D. Sumo–simulation of urban mobility: An Overview. In Proceedings of the SIMUL 2011 The Third International Conference on Advances in System Simulation, Barcelona, Spain, 23–28 October 2011; ISBN 978-1-61208-169-4. [Google Scholar]
- Bieker, L.; Krajzewicz, D.; Morra, A.; Michelacci, C.; Cartolano, F. Traffic simulation for all: A real world traffic scenario from the city of Bologna. In Modeling Mobility with Open Data; Springer: Berlin, Germany, 2015; pp. 47–60. ISBN 978-3-319-15023-9. [Google Scholar]
- National Research Counci. Highway Capacity Manual; HCM2010. In Transportation Research Board (TRB); National Research Council: Washington, DC, USA, 2010; pp. 31–96. ISBN 978-0-309-16077-3. [Google Scholar]




| n | ||||||
|---|---|---|---|---|---|---|
| 0 | - | - | - | 0 | 1 | 1 |
| 1 | 409,499 | 978,339 | 1.38926 | 0 | 1 | 0.41857 |
| 2 | 409,499 | 439,738 | 0.07384 | 0 | 0.41857 | 0.20928 |
| 3 | 409,499 | 219,071 | −0.46503 | 0.20938 | 0.41857 | 0.31393 |
| 4 | 409,499 | 329,609 | −0.19509 | 0.31393 | 0.41857 | 0.36625 |
| 5 | 409,499 | 385,108 | −0.05956 | 0.36625 | 0.41857 | 0.39241 |
| 6 | 409,499 | 413,368 | 0.00945 | 0.36625 | 0.39241 | 0.37933 |
| 7 | 409,499 | 399,120 | −0.02535 | 0.37933 | 0.39241 | 0.38587 |
| 8 | 409,499 | 406,074 | −0.00836 | 0.38587 | 0.39241 | 0.38914 |
| 9 | 409,499 | 409,153 | −0.00084 | - | - | - |
| City | Area (km) | # Street Segments | # Segment per km | Vehicle Density (per km) |
|---|---|---|---|---|
| Valencia | 77.43 | 11,418 | 147.46 | 173.886991 |
| Cologne | 595.9 | 21,953 | 36.84 | 2.31794261 |
| Bologna | 2.34 | 337 | 144.02 | 3,751.71 |
| City | # Source Positions per km | % of Street Segments Used |
|---|---|---|
| Valencia | 3.36 | 2.28 |
| Cologne | 1.82 | 4.71 |
| Bologna | 5.13 | 3.56 |
| City | # Destinations per km | % of Street Segments Used |
|---|---|---|
| Valencia | 17.13 | 11.61 |
| Cologne | 1.74 | 4.71 |
| Bologna | 4.70 | 3.26 |
| City | # Occupied Street Segments per km | % of Street Segments Used |
|---|---|---|
| Valencia | 95.08 | 64.48 |
| Cologne | 12.88 | 34.97 |
| Bologna | 64.96 | 45.10 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zambrano-Martinez, J.L.; Calafate, C.T.; Soler, D.; Cano, J.-C. Towards Realistic Urban Traffic Experiments Using DFROUTER: Heuristic, Validation and Extensions. Sensors 2017, 17, 2921. https://doi.org/10.3390/s17122921
Zambrano-Martinez JL, Calafate CT, Soler D, Cano J-C. Towards Realistic Urban Traffic Experiments Using DFROUTER: Heuristic, Validation and Extensions. Sensors. 2017; 17(12):2921. https://doi.org/10.3390/s17122921
Chicago/Turabian StyleZambrano-Martinez, Jorge Luis, Carlos T. Calafate, David Soler, and Juan-Carlos Cano. 2017. "Towards Realistic Urban Traffic Experiments Using DFROUTER: Heuristic, Validation and Extensions" Sensors 17, no. 12: 2921. https://doi.org/10.3390/s17122921
APA StyleZambrano-Martinez, J. L., Calafate, C. T., Soler, D., & Cano, J.-C. (2017). Towards Realistic Urban Traffic Experiments Using DFROUTER: Heuristic, Validation and Extensions. Sensors, 17(12), 2921. https://doi.org/10.3390/s17122921








