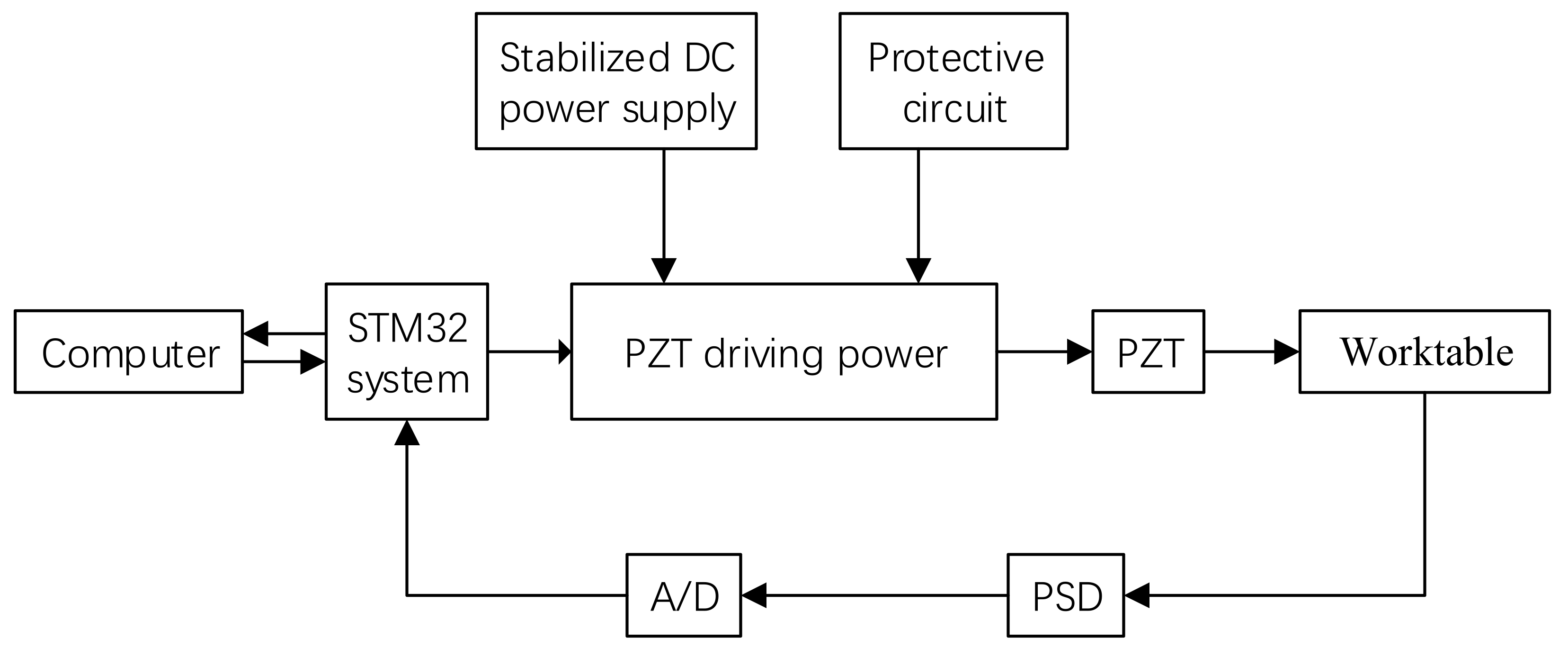
3.1. Control System Modeling
To better analyze the system, mathematical modeling was required for the precision elements, PZT, and driving power of the control system.
The PZT micro-actuator can be considered equivalent to a capacitor in the circuit. With a stack structure, the equivalent capacitance of a PZT can reach as high as several microfarads. When a step voltage is applied to both ends of the PZT, it shows some features that are similar to capacitance charge-discharge. Therefore, a transient process is needed for the PZT to reach a stable state. The voltage applied is linearly correlated with the output displacement of the PZT to some degree. The PZT and power-driven equivalent resistance constitute an RC loop that is a first-order inertial loop in automatic control, as shown in
Figure 5:
where Δ
x is the variation of displacement (μm); Δ
U1 is the voltage (V) variation;
km is the displacement-voltage conversion coefficient;
Tm is the time constant; and
Tm =
RC C.Measured by the precision capacitance meter, the equivalent capacitance of the PZT is
µF. In consideration of the complexity of the driving power circuit, its output impedance was not a theoretical value; instead, it was measured throughout the experiment, during which an external slide rheostat was used to adjust the value of resistance, with the voltage at both ends measured according to the calculation
= 199.98. Thus, the time constant
=
. The PZT displacement-voltage conversion coefficient was determined by multiple metering of the PZT displacement, i.e.,
= 0.175:
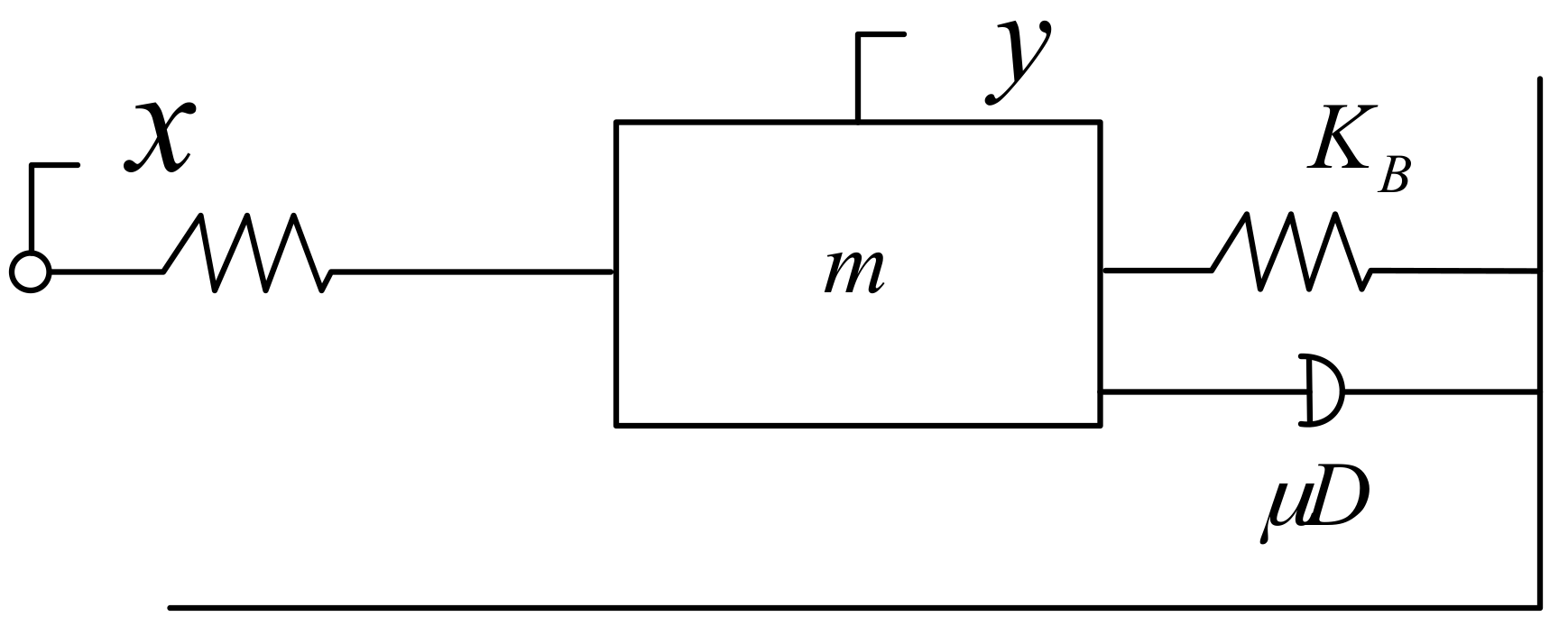
The PZT precision worktable could be deemed as a mass-spring-damper second-order system based on its own structure and features, as shown in
Figure 6:
Here,
m is the mass of the platform,
μD is the damper, and
KB is the elastic coefficient of the spring. According to the reference manual of the platform and relevant tests,
m = 0.5 kg,
KB = 0.83 × 10
6 N/m, and
μD = 249.2 Ns/m. Force analysis of the spring-mass-damping system suggested that the displacement output by the platform is
y(
t) in the presence of force
f(
t). According to Newton’s second law, there is an acceleration speed on the platform in the presence of force. The force on the platform is given as follows:
where
is the damping force;
is the spring’s resilience; and
is the resilience when the displacement is zero. With this formula, the following formula could be derived:
After Laplace transformation of this formula, we obtain:
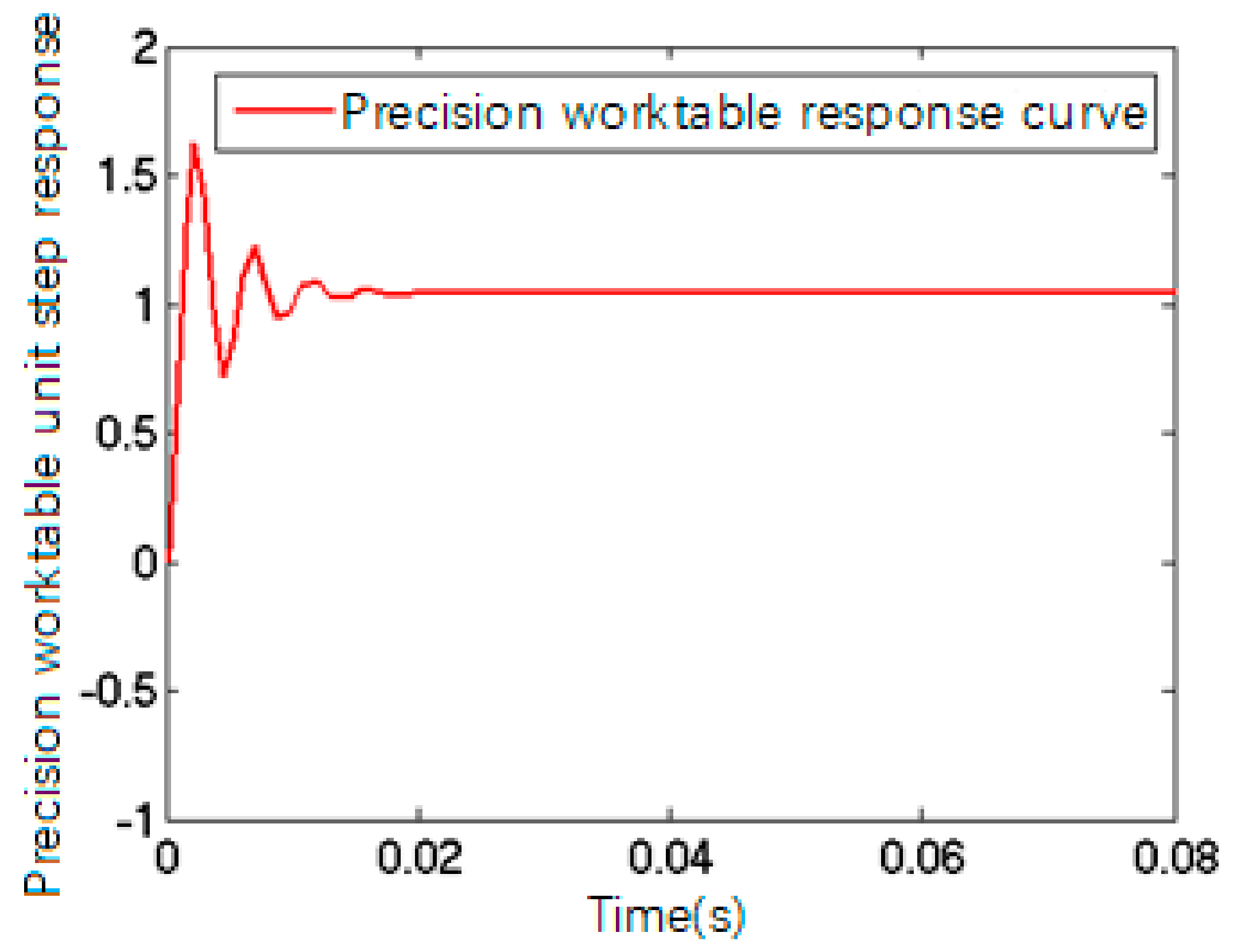
When the formula above was converted into a standard second-order oscillation loop, its step response output could be described by
Figure 7. Its transfer function with micron output is:
where
is the undamped natural angular frequency of the system;
is the amplification coefficient;
is the damping ratio.
Digital signals that needed to be converted were sent to the D/A converter through the interface circuit by the single chip computer and then converted into corresponding DC voltage analog signals. In the high voltage amplifier, low voltage output by D/A was converted into a high voltage available for PZT operation in order to control the PZT’s displacement and, thus, realize the platform positioning. The DC high voltage amplification circuit was able to amplify the analog voltage signal output by a D/A converter, which was simplified into a proportional amplifier loop under automatic control. As a result, its transfer function could be determined:
The amplification coefficient was consistent with the multiples of an actual operational amplifier. In this test, it was required to convert 0–5 V into 0–60 V. Therefore, .
The proportional amplifier loop, the first-order RC inertial loop, and the second-order oscillation loop in the PZT precision worktable were connected serially, i.e., the output of the last loop served as the input of the next loop. The transfer function could be established by multiplication of the transfer functions of the various loops. The transfer coefficients of the first-order and the second-order systems suggested that the transfer function of the system is:
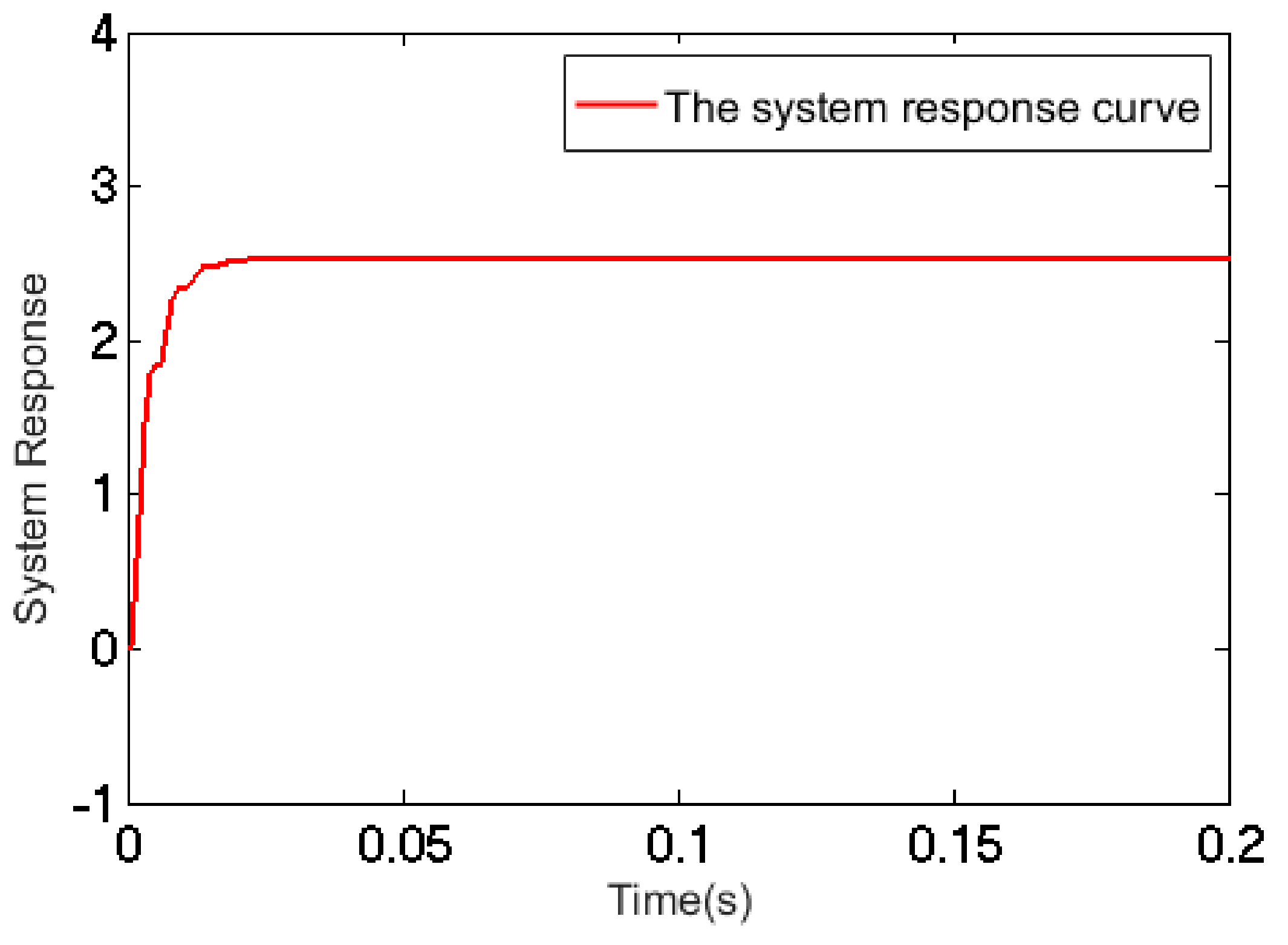
Here, . The open-loop transfer function of the PZT precision worktable was a third-order system whose response could be deemed as the combined action of two parts, i.e., components of the first-order inertial loop response and the second-order oscillation loop response.
The system response curve depicting the effect of a step signal is shown in
Figure 8.
3.2. Algorithm of the Control System
The impact of creep, one of the inherent characteristics of PZTs, on PZT positioning precision could not be neglected. When a step voltage was applied to the PZT actuator, an instantaneous step response that was generally several milliseconds was generated within the time scale determined by its mechanical resonance, followed by a slow creep response. It was generally assumed that the creep process of PZT took on a logarithmic form:
where
is the total displacement of the PZT with a given voltage,
is the PZT displacement with a given voltage in time
,
is the PZT creep coefficient,
is the step response time, which is generally
,
t is the creep time, and
is the zero timing point of
t.
When voltage was applied , the PZT started the creep process, with the creep rate varying with the voltage difference and with the voltage course.
It could be assumed that it was the input voltage that led to a certain creep displacement of PZT according to the contravariant relationship between electric energy and mechanical energy, whereas constant strain could also result in the voltage creep of the PZT. Therefore, voltage creep could be analyzed by the law of displacement creep. The voltage creep model is given as:
where
is the input voltage at time
t,
is the input voltage corresponding to constant strain
,
and is the voltage creep coefficient.
, , and were determined by various factors, such as PZT materials, experiment conditions, driving voltage and velocity, etc. As differences of piezoelectric materials, PZT aging, and experiment condition variations made it difficult for precise determination of the three model parameters in PZT creep formula, it is advisable to use the least square method.
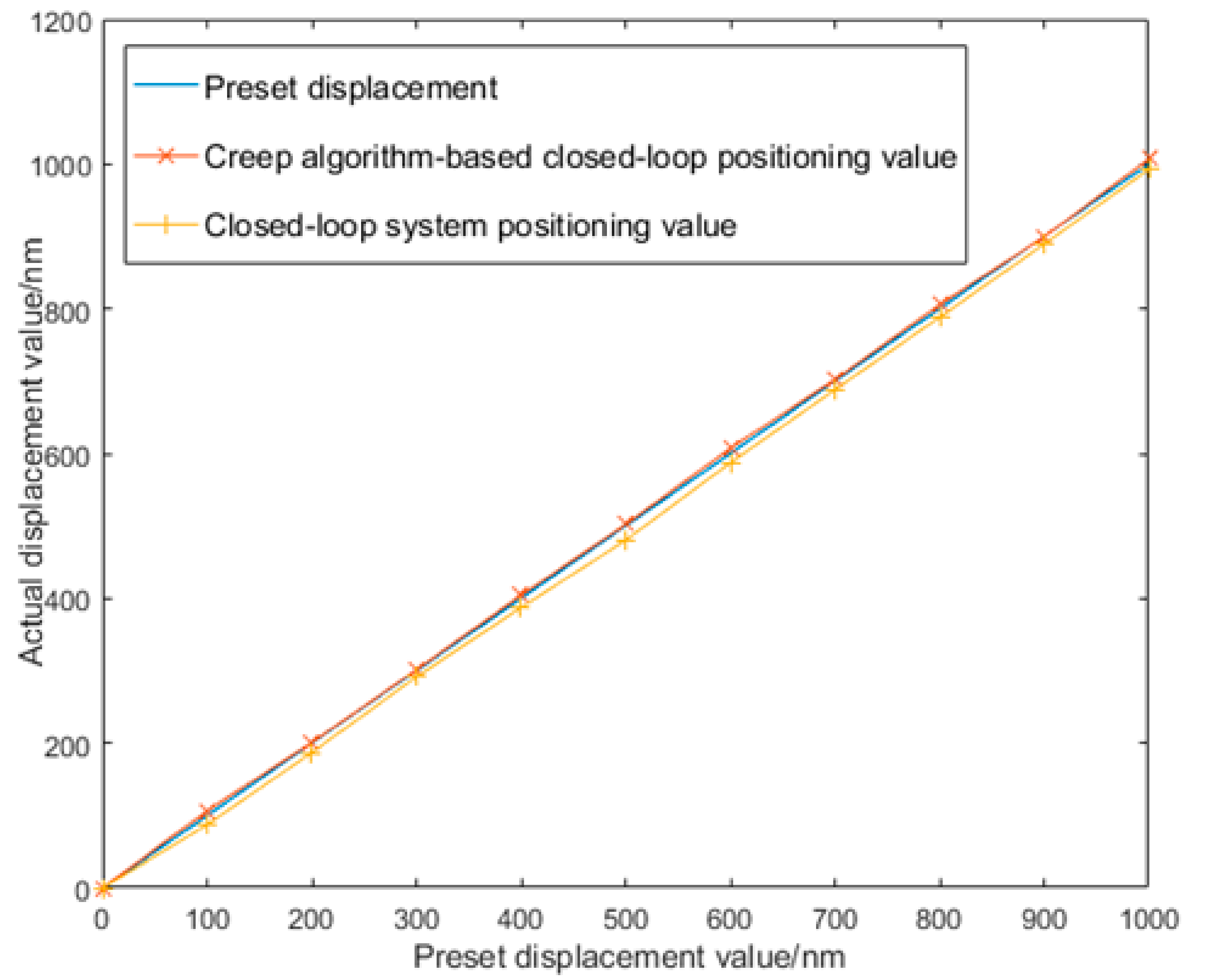
A creep model-based feed-forward control based on a proportional–integral–derivative controller (PID) closed-loop control was able to further reduce the impact of creep on displacement.
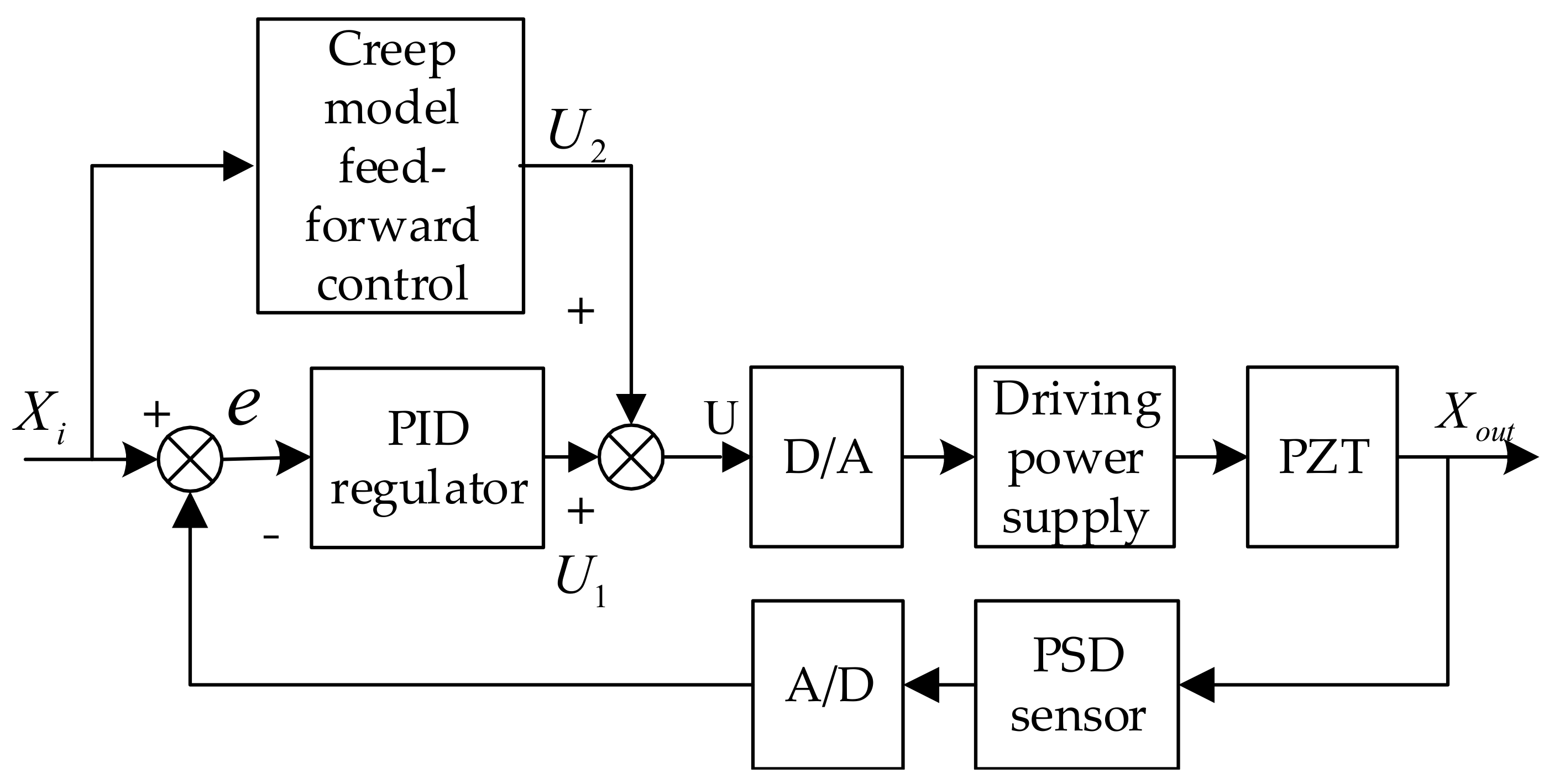
Figure 9 shows the structure of a voltage creep model-based closed-loop control system:
In this study, a PSD feedback-based PID algorithm implementation was designed. in the control block diagram was the displacement required to be output with a certain voltage; was the output displacement of the micro-displacement platform; the deviation value between the voltage value generated by the PSD feedback displacement and input voltage was ; the voltage value was obtained from deviation after scale, integral, and differential operations by the PID regulator. Next, this voltage value underwent D/A where it was converted into a low-voltage control signal that was then amplified into the driving power of PZT particles, so that PZT deforms to drive the precision worktable. Displacement output by the micro-displacement platform was converted into voltage signals by the PSD sensor and was then sent to a single chip computer via an A/D converter.
Deviation was the voltage value obtained from PSD feedback subtracting the voltage value corresponding to the displacement that was required to be output. In the event that this value lay in the deviation area, the PID control process was completed; otherwise, PID control was repeated until it fell within the designated range, i.e., the precision requirement was satisfied.
Controller tuning, also known as “optimal tuning”, is essentially matching its characteristics and controlled characteristics by adjusting the controller’s parameters, so that the PID controller is able to perform effectively. The controller parameters obtained with this method are designated “optimal tuning parameters”. Of all tuning methods, Ziegler-Nichols tuning and the performance index setting are the most widely used. Manual tuning of PID parameters using the add-up method was implemented in this test. Given that
,
increased until there was system oscillation, then the value of this critical state was denoted as
and oscillation period as
, as shown in
Table 1.
PID parameters obtained by Ziegler-Nichols tuning method were
KP = 7.8,
Ki = 0.0029 and
KD = 0.000725.
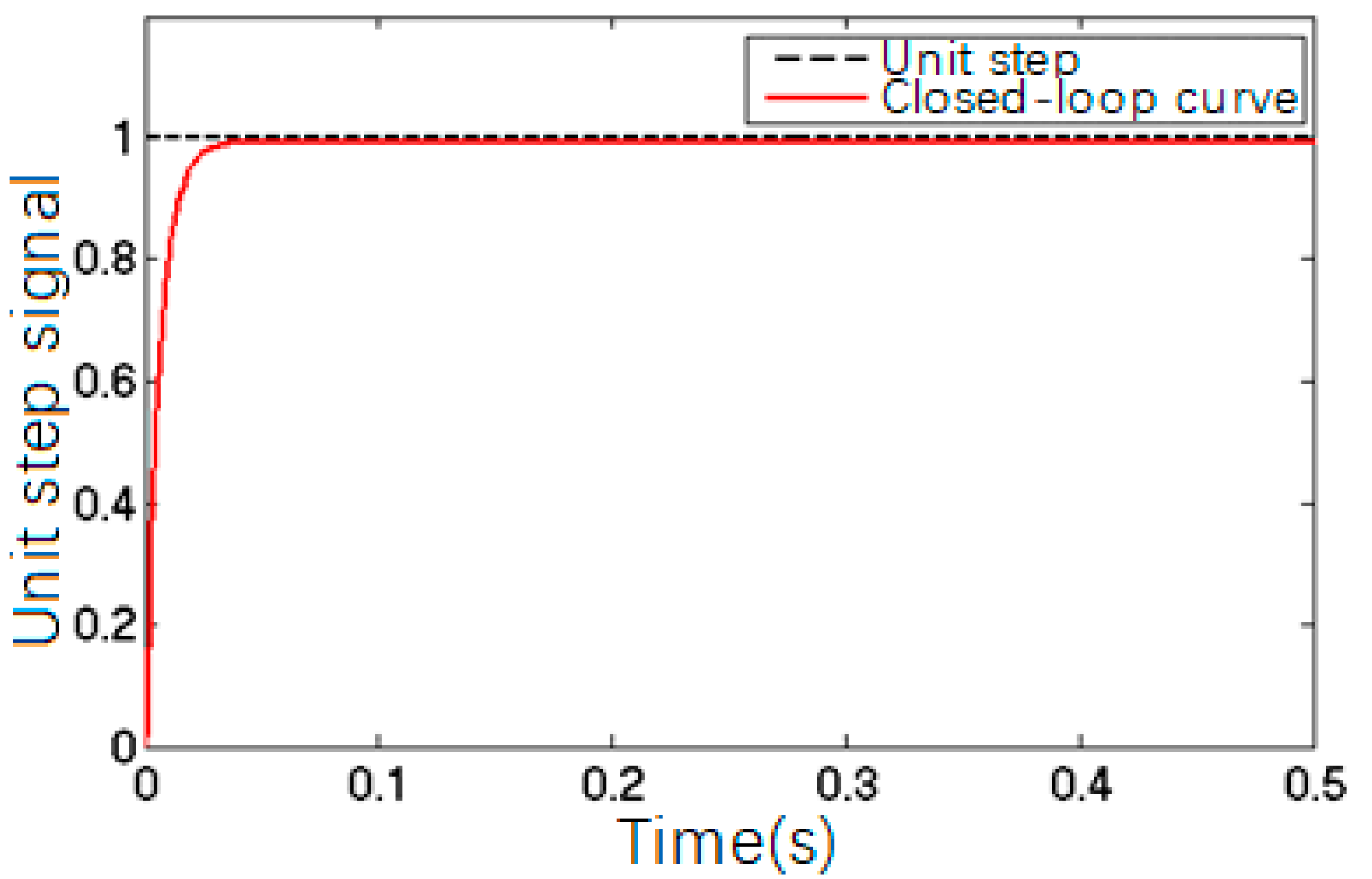
Figure 10 shows the closed-loop response of the precision worktable with these PID parameters;
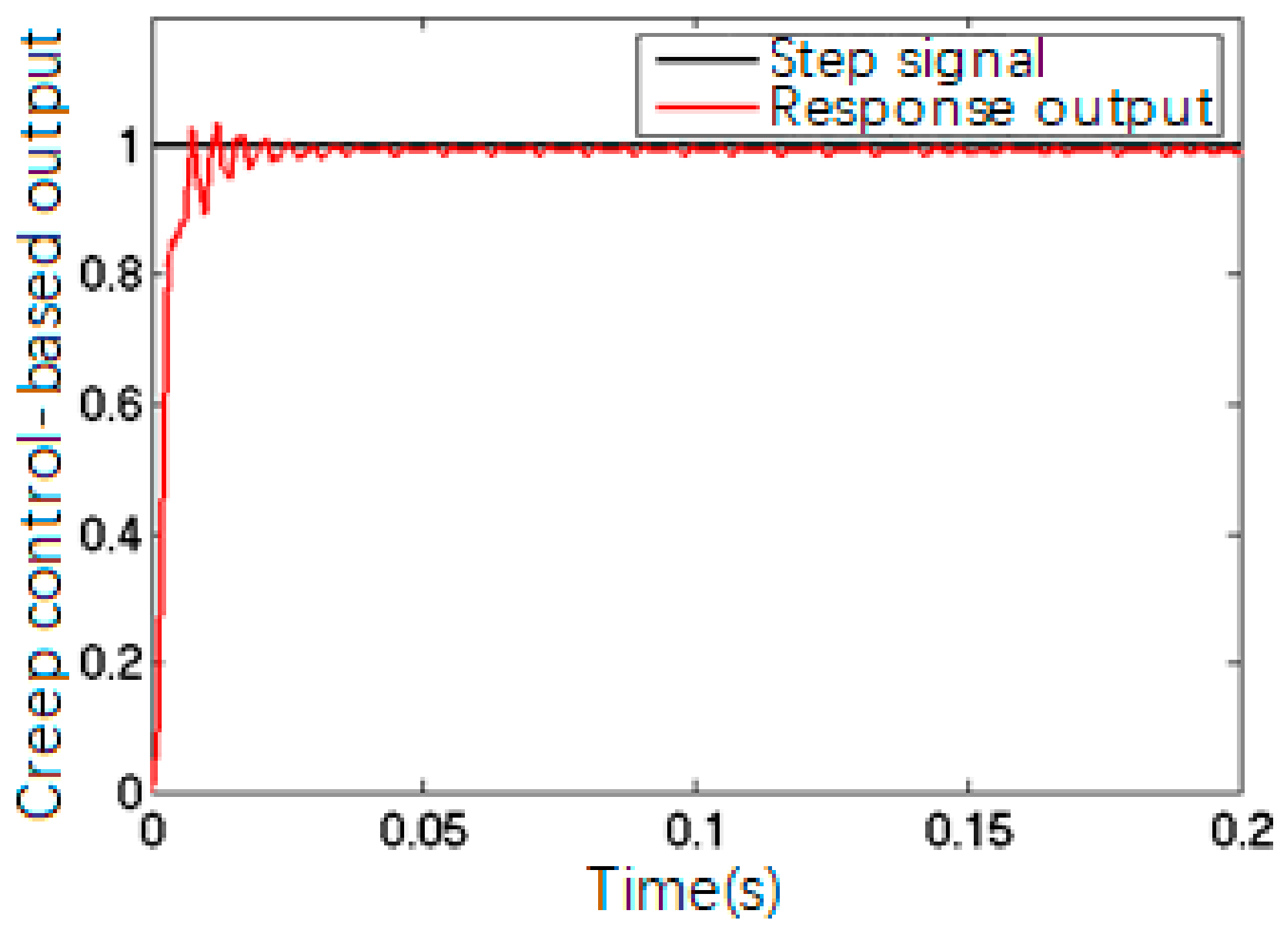
Figure 11 shows the creep-based system closed-loop response.
The comparison between
Figure 10 and
Figure 11 suggested that the closed-loop control of a precision control system was able to trace and execute the input and output effectively with precise positioning, but the system still showed creep features, which could be solved by adding a feed-forward model to the closed-loop algorithm to eliminate the impact of PZT creep.