Optimal Quantization Scheme for Data-Efficient Target Tracking via UWSNs Using Quantized Measurements
Abstract
:1. Introduction
2. Related Work
3. Problem Formulation
3.1. System Model
3.2. Distributed Fusion Architectures with Quantized Measurements
3.3. State Estimation with Quantized Measurements
3.4. PCRLB with Quantized Measurements
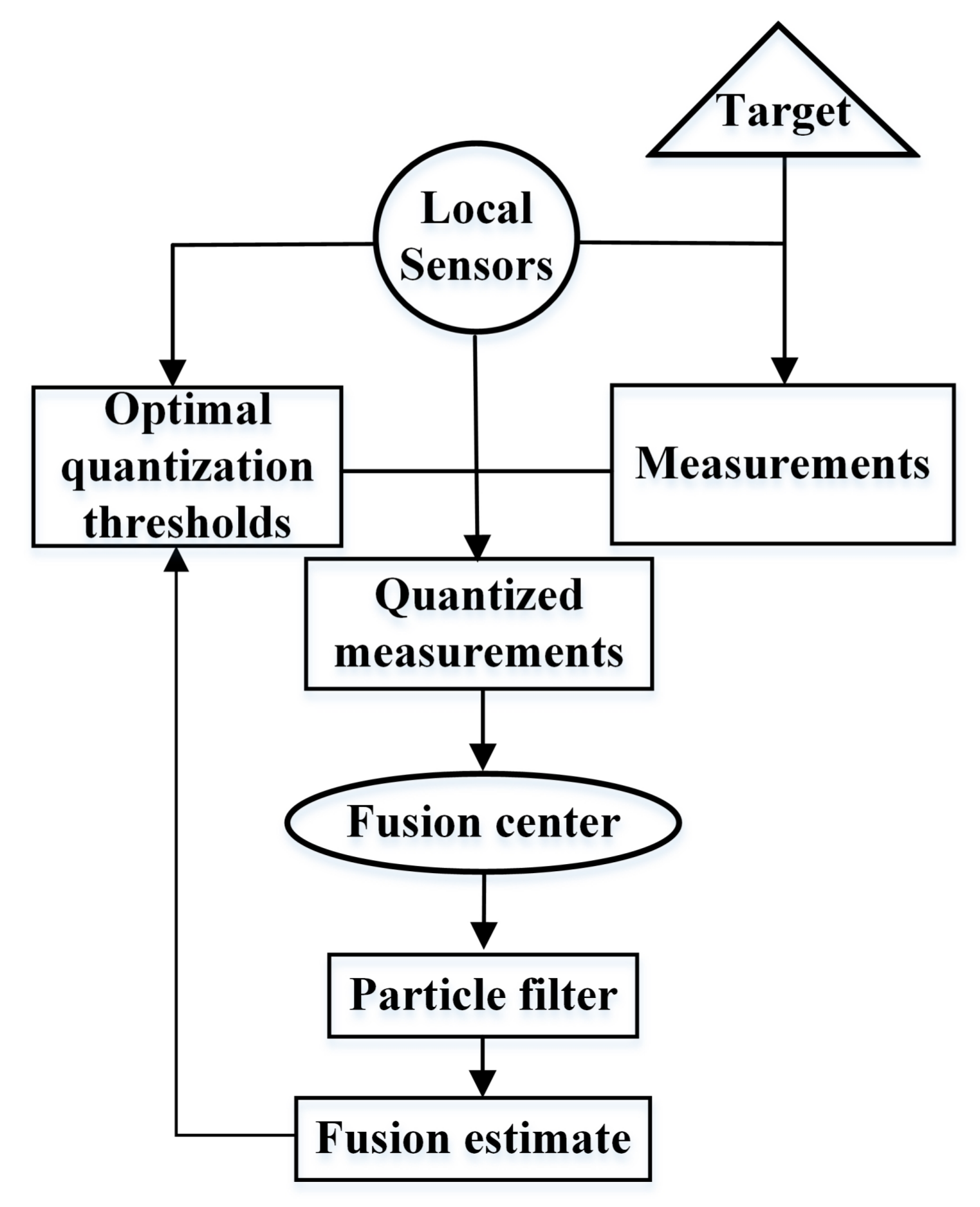
4. Optimal Quantization-Based Target Tracking Scheme
4.1. Optimal Quantization Thresholds Determination
4.2. Optimal Quantization-Based Target Tracking Scheme
5. Simulation and Results
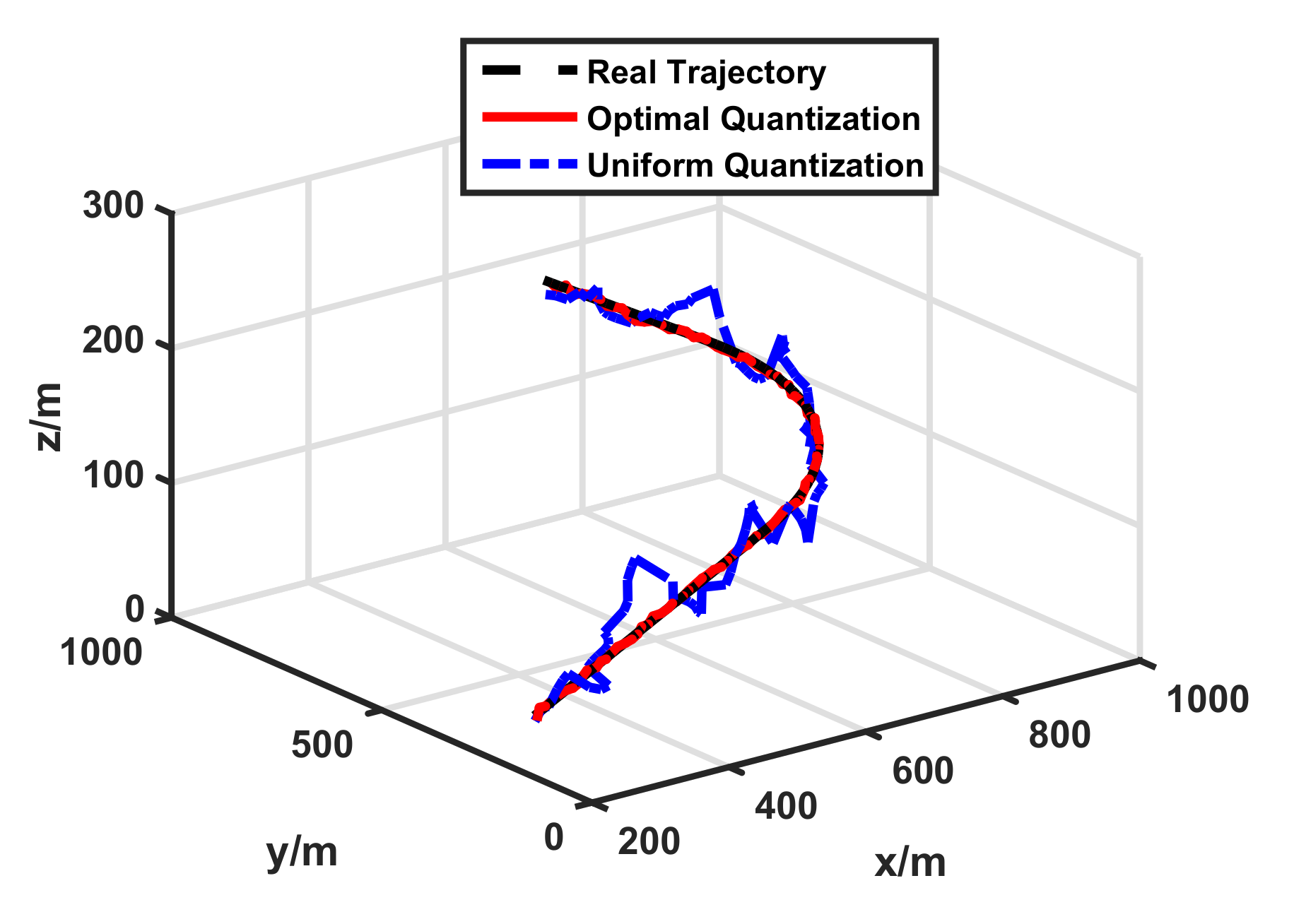
5.1. Simulation Scenario
5.2. Performance Verification
5.2.1. Performance Comparison
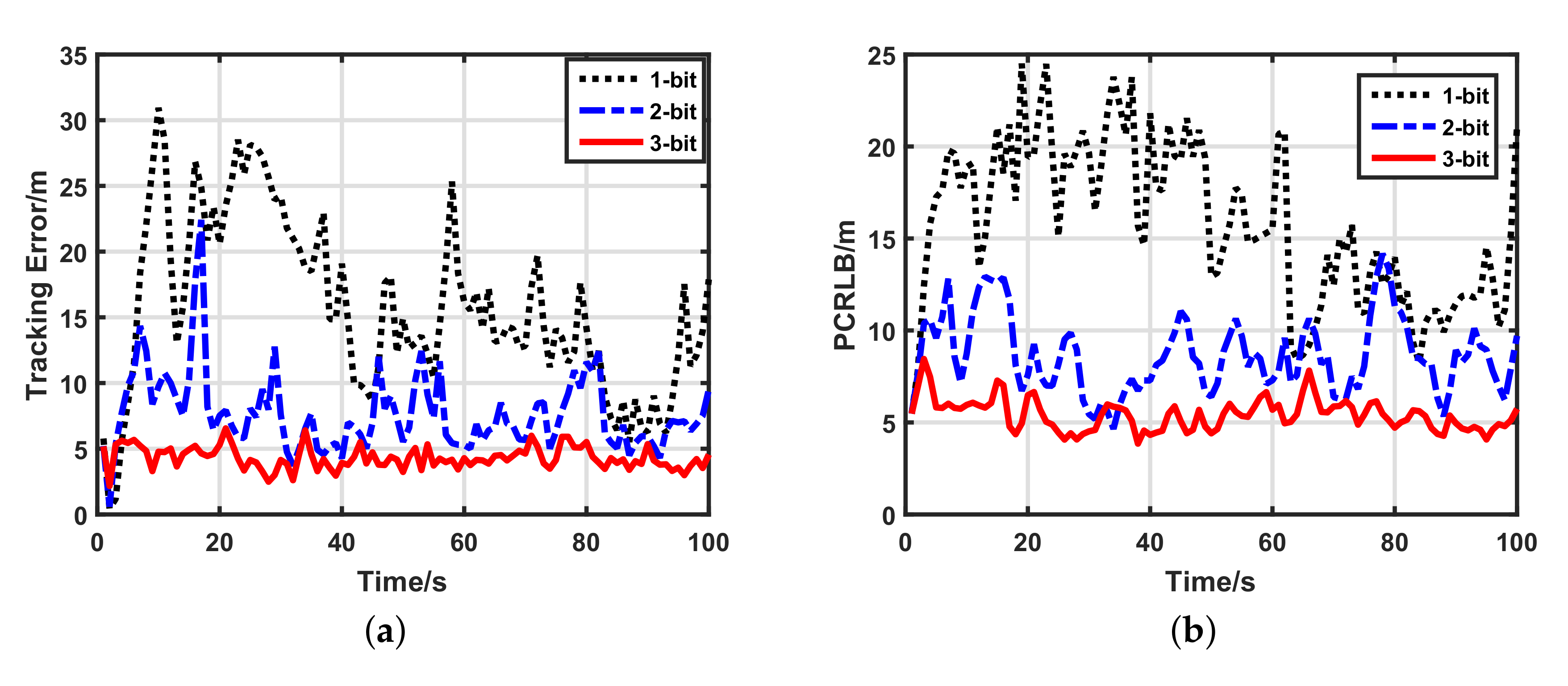
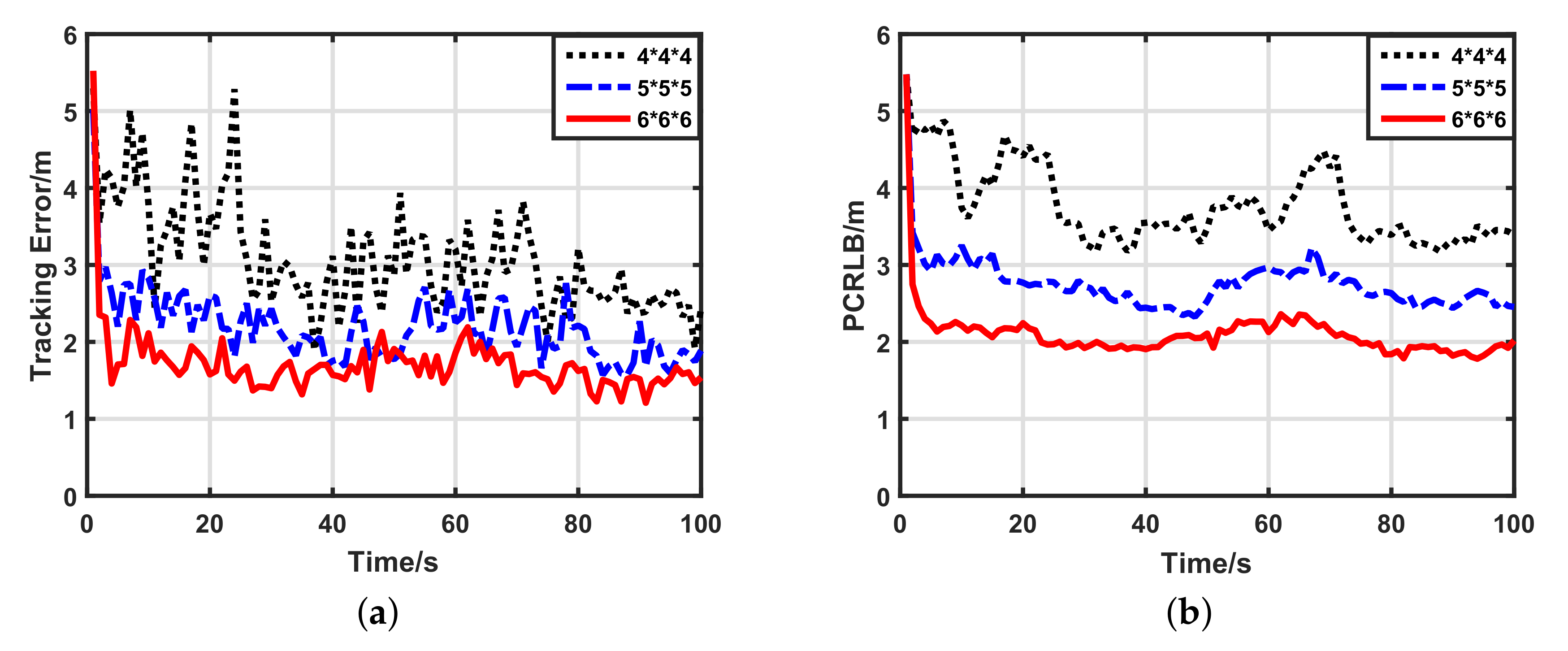
5.2.2. Impacts of Data Lengths
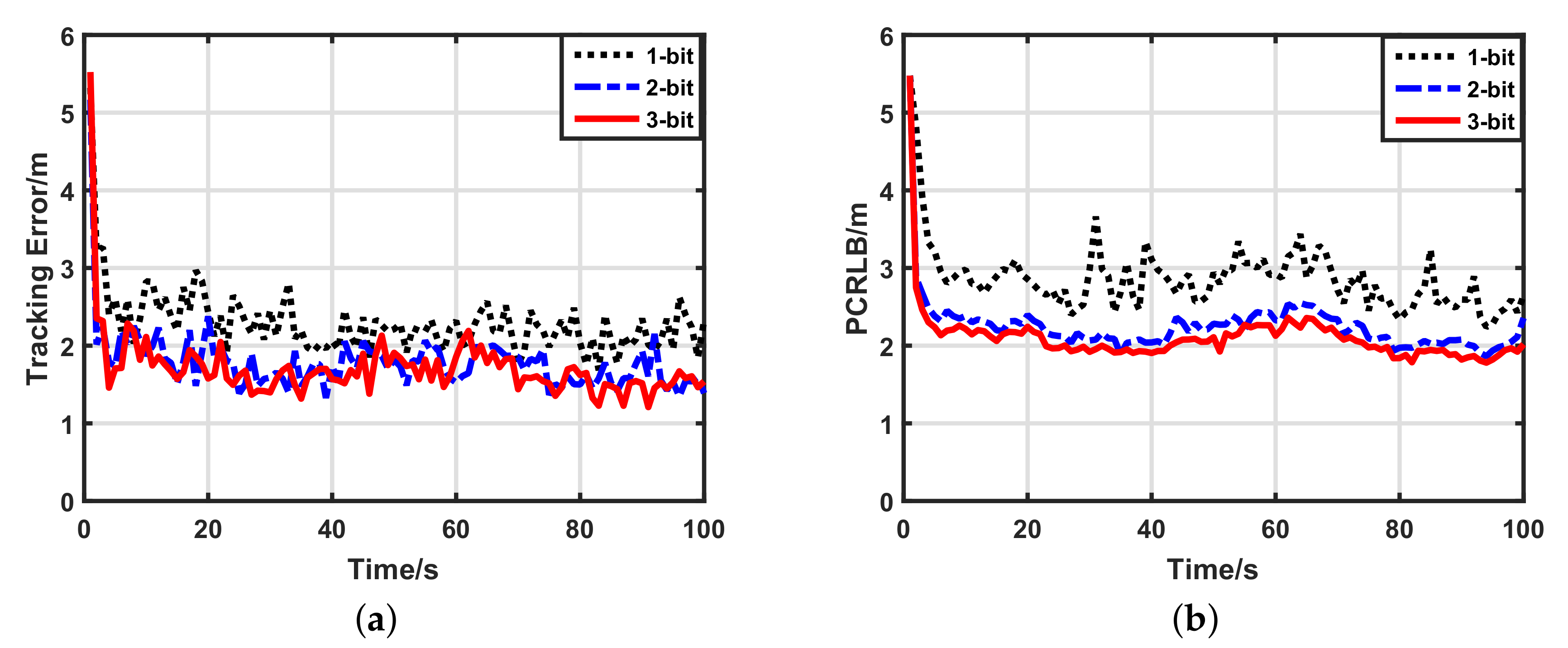
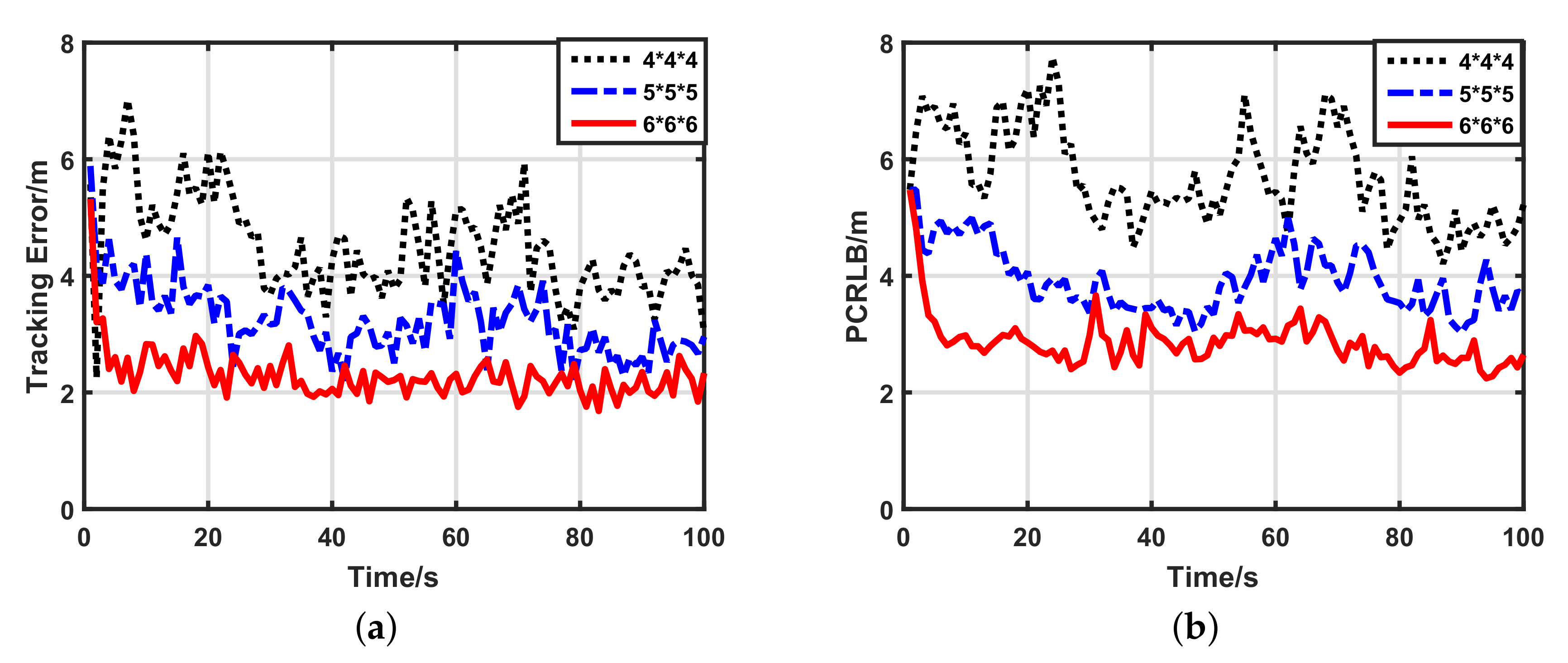
5.2.3. Impacts of Network Density
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jaime, L. Underwater sensor nodes and networks. Sensors 2013, 13, 11782–11796. [Google Scholar]
- Sandeep, D.N.; Kumar, V. Review on Clustering, Coverage and Connectivity in Underwater Wireless Sensor Networks: A Communication Techniques Perspective. IEEE Access 2017, 5, 11176–11199. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Cui, J.H.; Zhou, S.; Yang, B. A joint time synchronization and localization design for mobile underwater sensor networks. IEEE Trans. Mob. Comput. 2016, 15, 530–543. [Google Scholar] [CrossRef]
- Climent, S.; Sanchez, A.; Capella, J.V.; Meratnia, N.; Serrano, J.J. Underwater acoustic wireless sensor networks: Advances and future trends in physical, MAC and routing layers. Sensors 2014, 14, 795–833. [Google Scholar] [CrossRef] [PubMed]
- Jindal, V.; Verma, A.K.; Bawa, S. Current scenario in WSNs. Int. J. Adv. Res. Comput. Eng. Technol. 2012, 1, 55–60. [Google Scholar]
- Calafate, C.T.; Lino, C.; Diaz-Ramire, A.; Cano, J.C.; Manzoni, P. An integral model for target tracking based on the use of a WSN. Sensors 2013, 13, 7250–7278. [Google Scholar] [CrossRef] [PubMed]
- Xu, N.; Zhang, Y.; Zhang, D.; Zhao, S.; Fu, W. Moving Target Tracking in Three Dimensional Space with Wireless Sensor Network. Wirel. Pers. Commun. 2017, 94, 3403–3413. [Google Scholar] [CrossRef]
- Catipovic, J. Performance limitations in underwater acoustic telemetry. IEEE J. Ocean. Eng. 1990, 15, 205–216. [Google Scholar] [CrossRef]
- Felemban, E.; Shaikh, F.K.; Qureshi, U.M.; Sheikh, A.A.; Qaisar, S.B. Underwater sensor network applications: A comprehensive survey. Int. J. Distrib. Sens. Netw. 2015, 11, 1–14. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Pompili, D.; Melodia, T. Underwater acoustic sensor networks: Research challenges. Ad Hoc Netw. 2005, 3, 257–279. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, M.; Zhang, S. Node Topology Effect on Target Tracking Based on UWSNs Using Quantized Measurements. IEEE Trans. Cybern. 2015, 45, 2323–2335. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Wang, D.; Pei, T.; Lan, Y. Energy-Efficient Target Tracking in Wireless Sensor Networks: A Quantized Measurement Fusion Framework. Int. J. Distrib. Sensor Netw. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Huang, Y.; Liang, W.; Yu, H.B.; Xiao, Y. Target tracking based on a distributed particle filter in underwater sensor networks. Wirel. Commun. Mob. Comput. 2008, 8, 1023–1033. [Google Scholar] [CrossRef]
- Isbitiiren, G.; Akan, O.B. Three-dimensional underwater target tracking with acoustic sensor networks. IEEE Trans. Veh. Technol. 2011, 60, 3897–3906. [Google Scholar] [CrossRef]
- Wang, X.; Xu, M.; Wang, H. Combination of interacting multiple models with the particle filter for three-dimensional target tracking in underwater wireless sensor networks. Math. Probl. Eng. 2012, 2012, 1–16. [Google Scholar] [CrossRef]
- Yu, C.H.; Lee, J.C.; Choi, J.W.; Park, M.K.; Kang, D.J. Energy efficient distributed interacting multiple model filter in UWSNs. In Proceedings of the International Conference on Control, Automation and Systems, Jeju Island, Korea, 17–21 October 2012; pp. 1093–1098. [Google Scholar]
- Zhang, S.; Chen, H.; Liu, M. Adaptive sensor scheduling for target tracking in underwater wireless sensor networks. In Proceedings of the 2014 International Conference on Mechatronics and Control (ICMC), Jinzhou, China, 3–5 July 2014; pp. 55–60. [Google Scholar]
- Chen, H.; Zhang, S.; Liu, M.; Zhang, Q. An Artificial Measurements-Based Adaptive Filter for Energy-Efficient Target Tracking via Underwater Wireless Sensor Networks. Sensors 2017, 17, 971. [Google Scholar] [CrossRef] [PubMed]
- Niu, R.; Varshney, P.K. Target location estimation in sensor networks with quantized data. IEEE Trans. Signal Process. 2006, 54, 4519–4528. [Google Scholar] [CrossRef]
- Li, H.; Fang, J. Distributed adaptive quantization and estimation for wireless sensor networks. IEEE Signal Process. Lett. 2007, 14, 669–672. [Google Scholar] [CrossRef]
- Mansouri, M.; Ouachani, I.; Snoussi, H.; Richard, C. Cramer-Rao Bound-based adaptive quantization for target tracking in wireless sensor networks. In Proceedings of the 2009 IEEE/SP 15th Workshop on Statistical Signal Processing, Cardiff, UK, 31 August–3 September 2009; pp. 693–696. [Google Scholar]
- Liu, S.; Masazade, E.; Shen, X.; Varshney, P.K. Adaptive non-myopic quantizer design for target tracking in wireless sensor networks. In Proceedings of the 2013 Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 2013; pp. 1085–1089. [Google Scholar]
- Kose, A.; Masazade, E. A multiobjective optimization approach for adaptive binary quantizer design for target tracking in wireless sensor networks. In Proceedings of the 2015 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), San Diego, CA, USA, 14–16 September 2015; pp. 31–36. [Google Scholar]
- Feng, X.; Pan, F.; Gao, Q.; Li, W. Gaussian likelihood based Bernoulli particle filter for non-uniformly quantized interval measurement. In Proceedings of the 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 5–8 July 2016; pp. 298–303. [Google Scholar]
- Duan, Z.; Jilkov, V.P.; Li, X.R. State estimation with quantized measurements: Approximate MMSE approach. In Proceedings of the 2008 11th International Conference on Information Fusion (FUSION), Cologne, Germany, 30 June–3 July 2008; pp. 1–6. [Google Scholar]
- Masazade, E.; Niu, R.; Varshney, P.K. Dynamic bit allocation for object tracking in wireless sensor networks. IEEE Trans. Signal Process. 2012, 60, 5048–5063. [Google Scholar] [CrossRef]
- Cao, N.; Choi, S.; Masazade, E.; Varshney, P.K. Sensor selection for target tracking in wireless sensor networks with uncertainty. IEEE Trans. Signal Process. 2016, 64, 5191–5204. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ruan, Y.; Willett, P.; Marrs, A.; Palmieri, F.; Marano, S. Practical fusion of quantized measurements via particle filtering. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 15–29. [Google Scholar] [CrossRef]



| b-Bit Quantized Measurement | Optimal Quantization Factor m |
|---|---|
| Quantization Methods | 1-Bit | 2-Bit | 3-Bit |
|---|---|---|---|
| Uniform quantization | 15.6724 | 7.6371 | 4.3038 |
| Optimal quantization | 2.2887 | 1.7847 | 1.7063 |
| Networks | 1-Bit | 2-Bit | 3-Bit | Participant Sensors |
|---|---|---|---|---|
| 4.5077 | 3.3834 | 3.0779 | 5.87 | |
| 3.2378 | 2.3898 | 2.1845 | 11.17 | |
| 2.2887 | 1.7847 | 1.7063 | 19.66 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Chen, H.; Liu, M.; Zhang, Q. Optimal Quantization Scheme for Data-Efficient Target Tracking via UWSNs Using Quantized Measurements. Sensors 2017, 17, 2565. https://doi.org/10.3390/s17112565
Zhang S, Chen H, Liu M, Zhang Q. Optimal Quantization Scheme for Data-Efficient Target Tracking via UWSNs Using Quantized Measurements. Sensors. 2017; 17(11):2565. https://doi.org/10.3390/s17112565
Chicago/Turabian StyleZhang, Senlin, Huayan Chen, Meiqin Liu, and Qunfei Zhang. 2017. "Optimal Quantization Scheme for Data-Efficient Target Tracking via UWSNs Using Quantized Measurements" Sensors 17, no. 11: 2565. https://doi.org/10.3390/s17112565
APA StyleZhang, S., Chen, H., Liu, M., & Zhang, Q. (2017). Optimal Quantization Scheme for Data-Efficient Target Tracking via UWSNs Using Quantized Measurements. Sensors, 17(11), 2565. https://doi.org/10.3390/s17112565





