Efficient Graph-Based Resource Allocation Scheme Using Maximal Independent Set for Randomly- Deployed Small Star Networks
Abstract
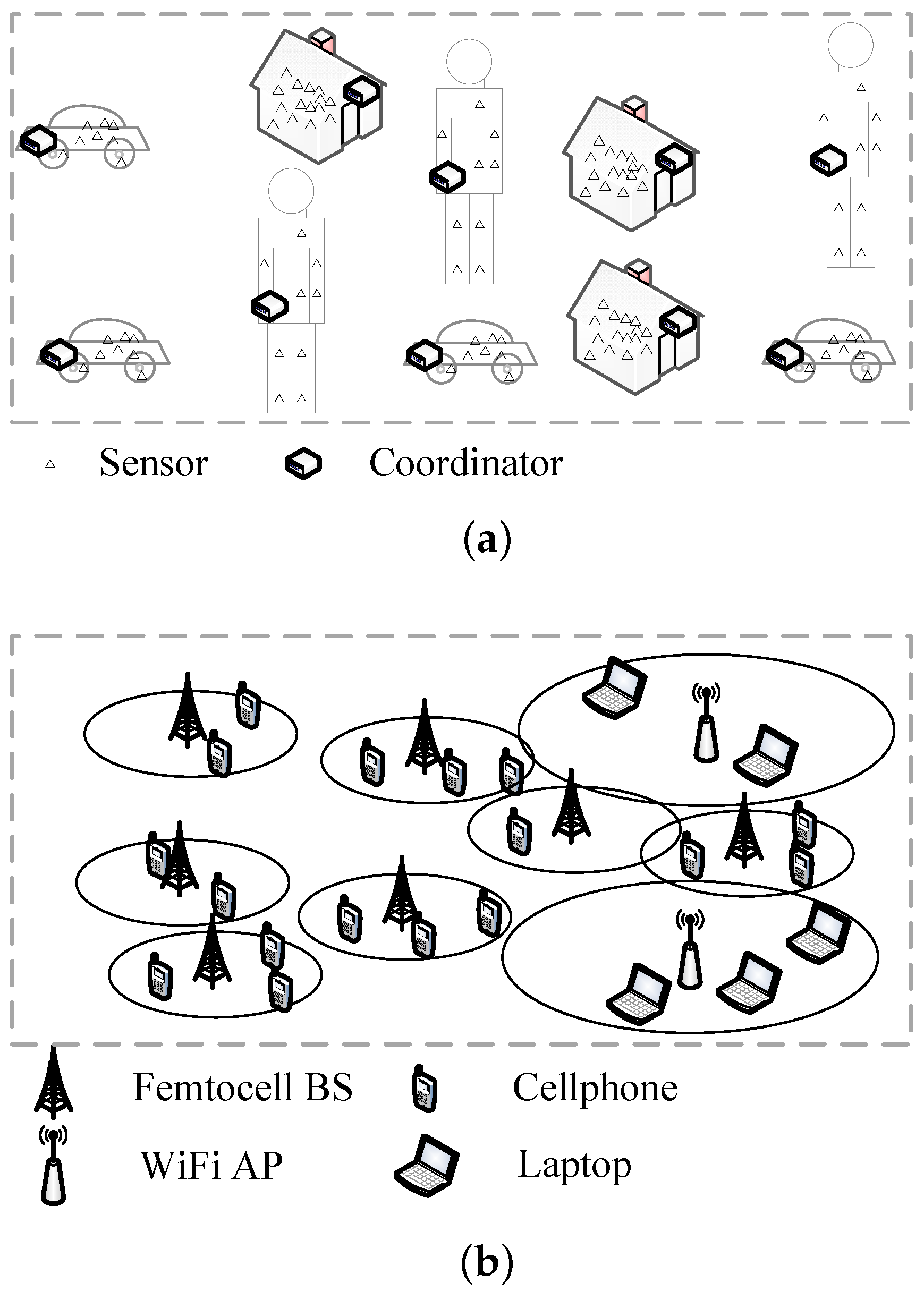
:1. Introduction
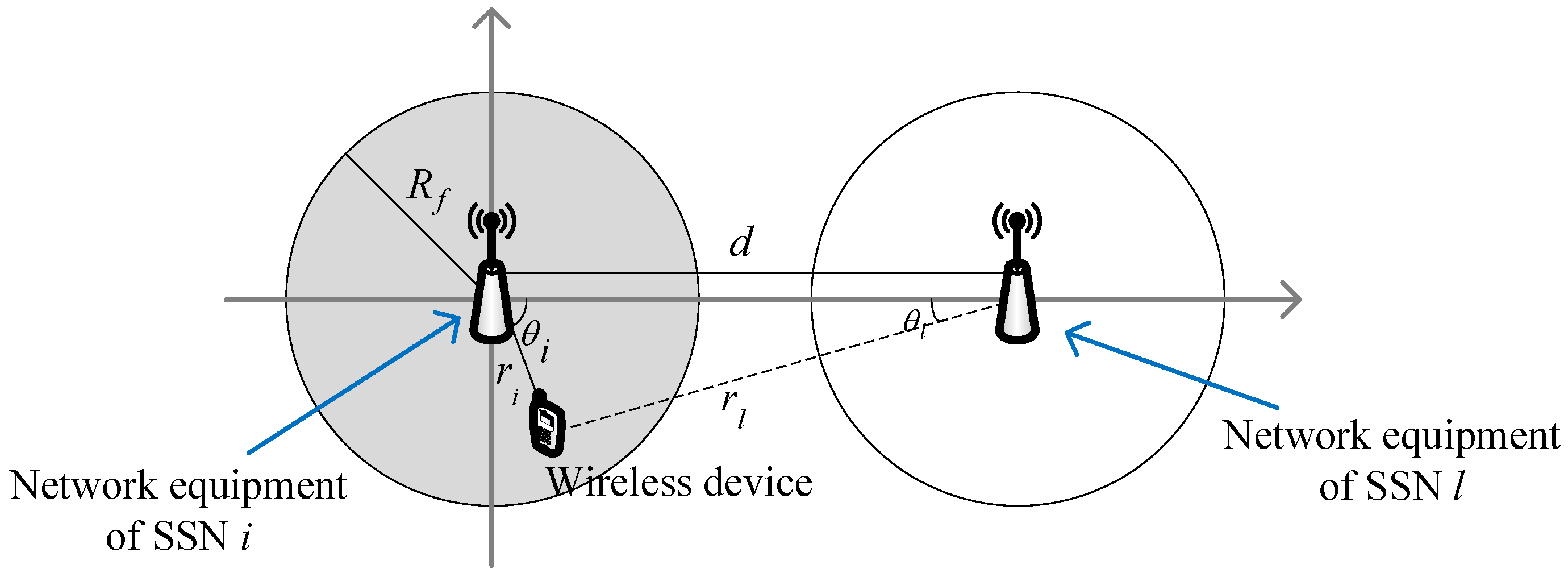
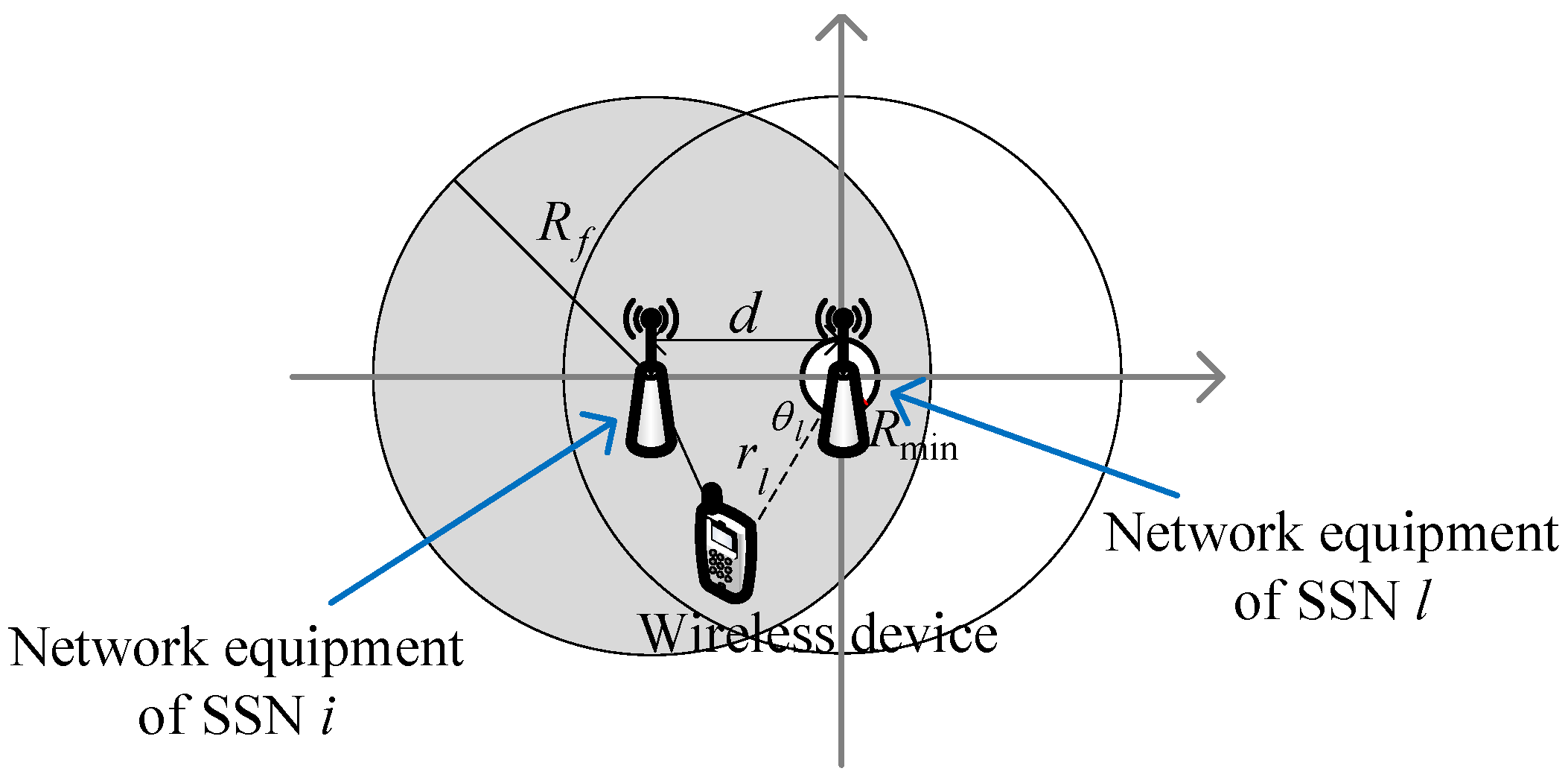
2. System Model
3. The Proposed Graph-Based Scheme
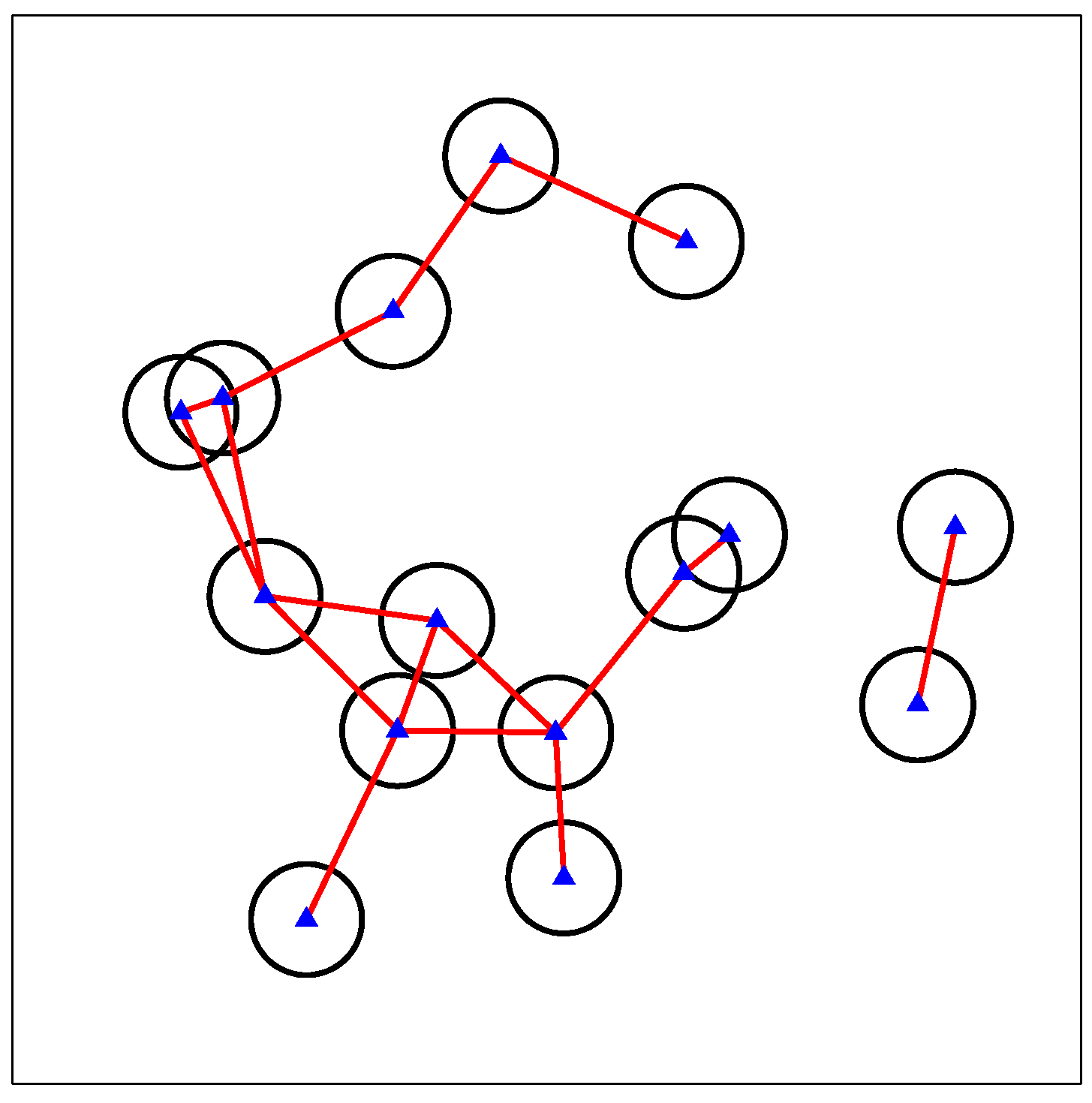
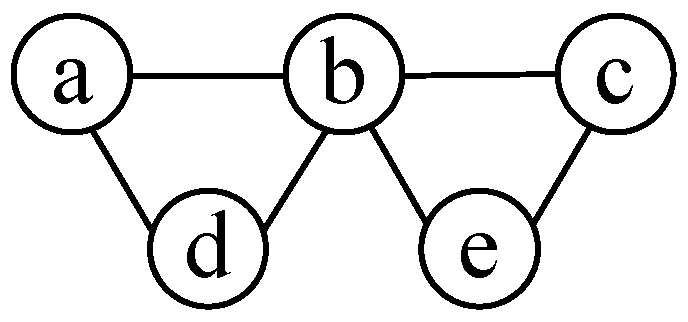
3.1. Interference Graph
3.2. MIS
| Algorithm 1 Obtaining one random MIS. |
| Input: , Output:
|
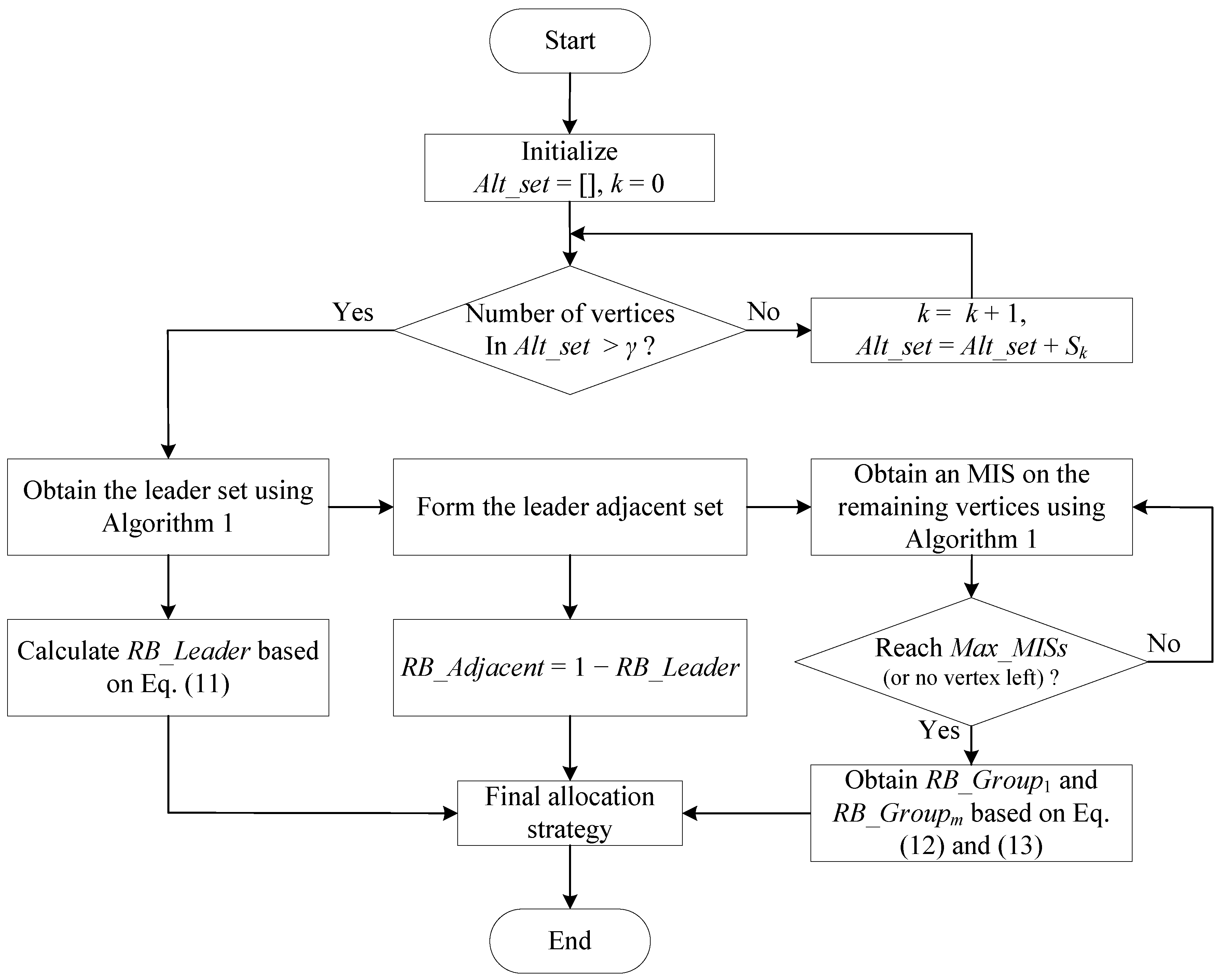
3.3. Proposed Scheme
4. Performance Evaluation
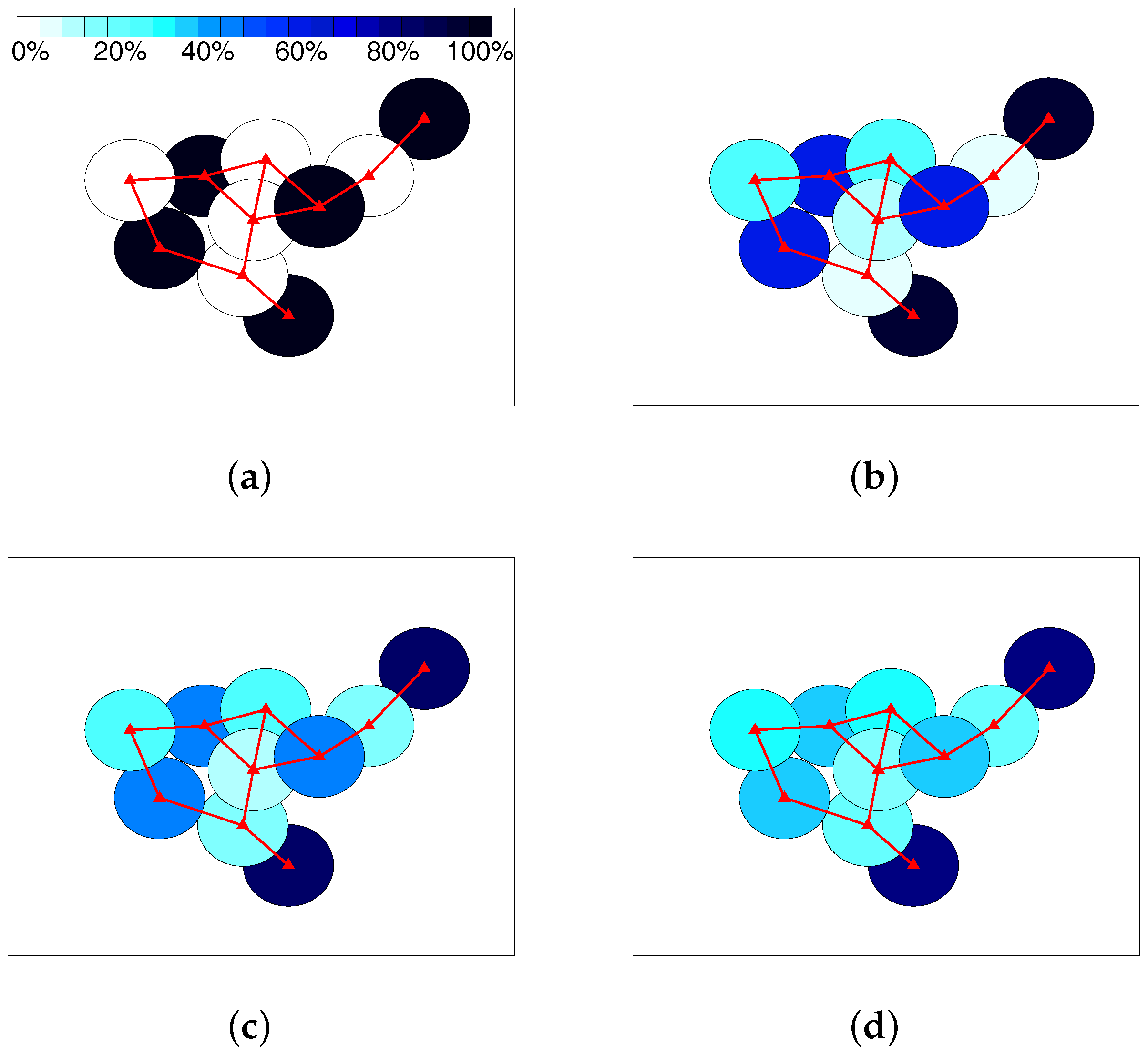
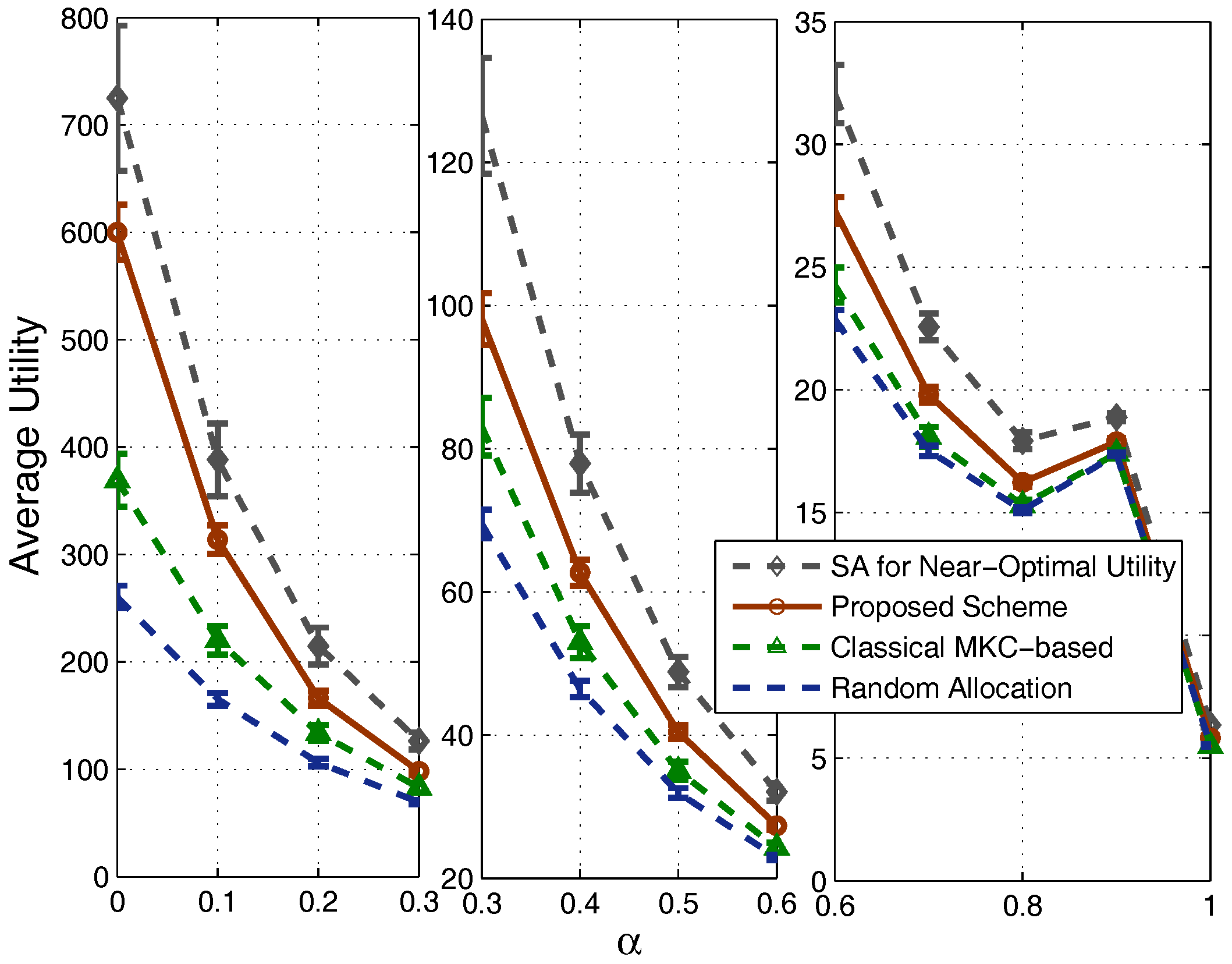
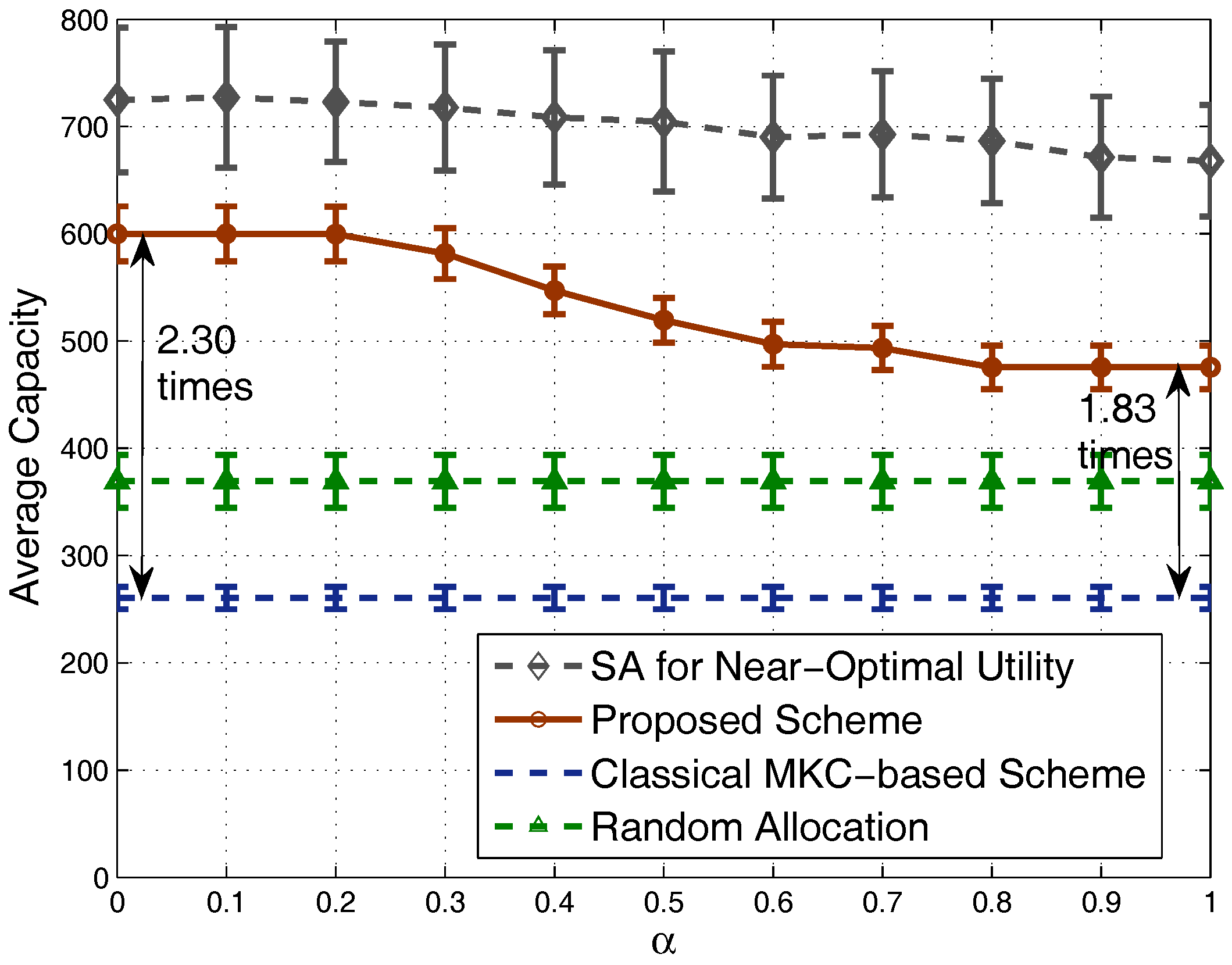
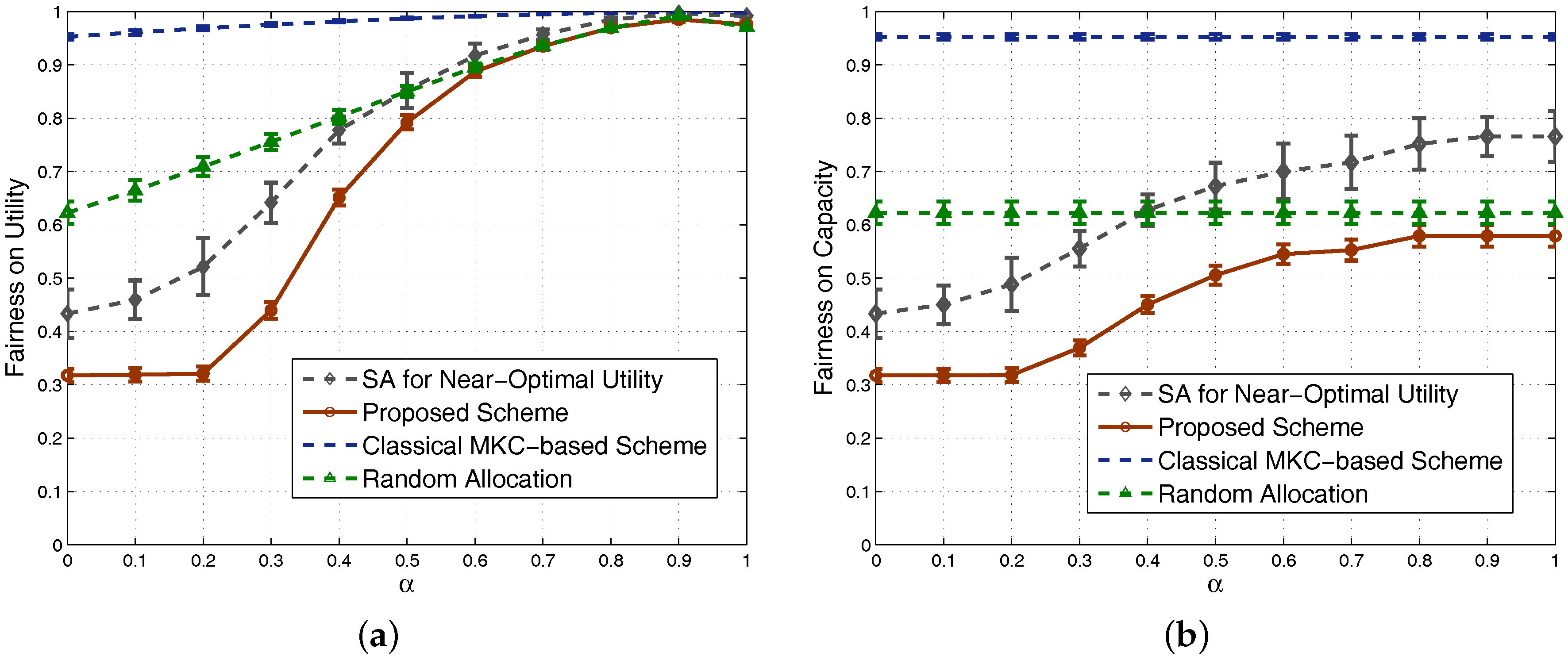
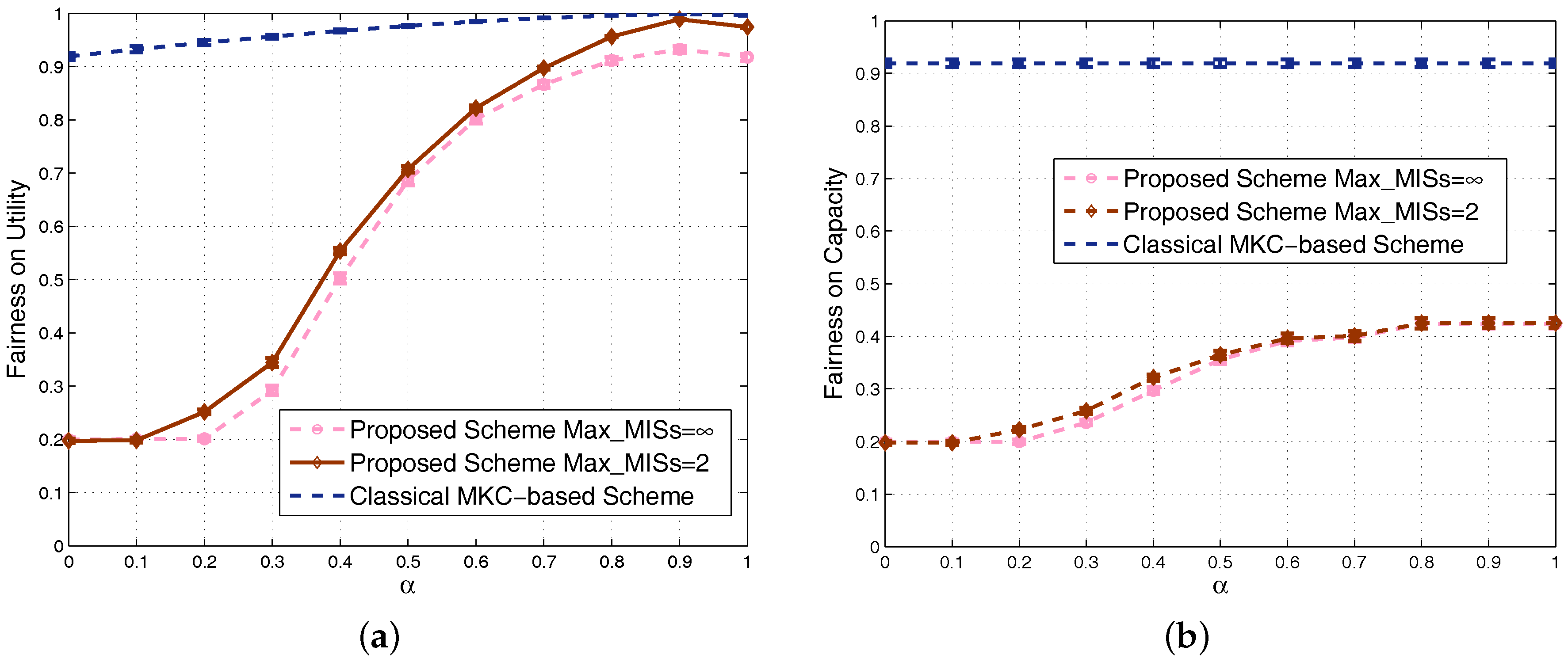
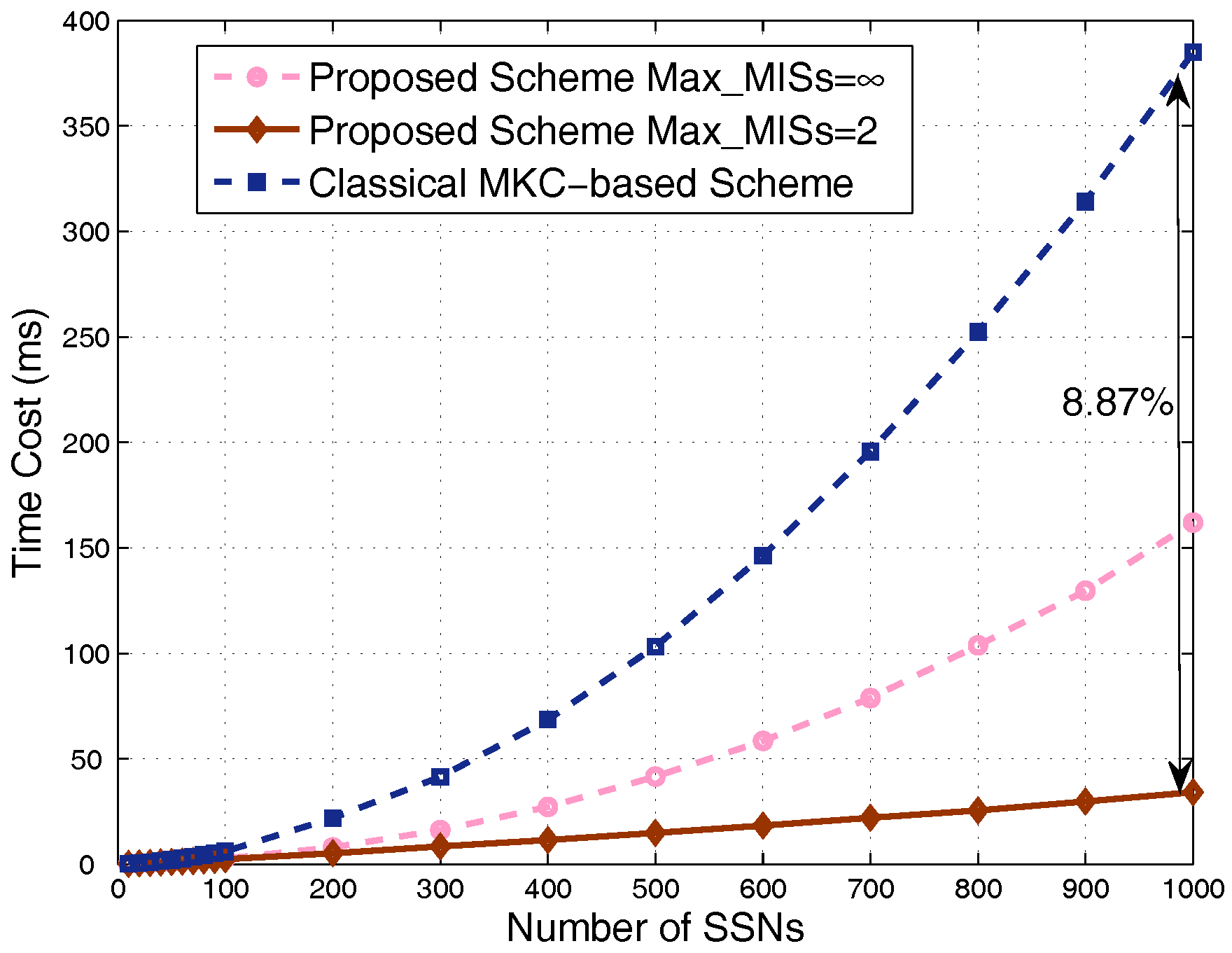
4.1. Results in Nondense Scenarios
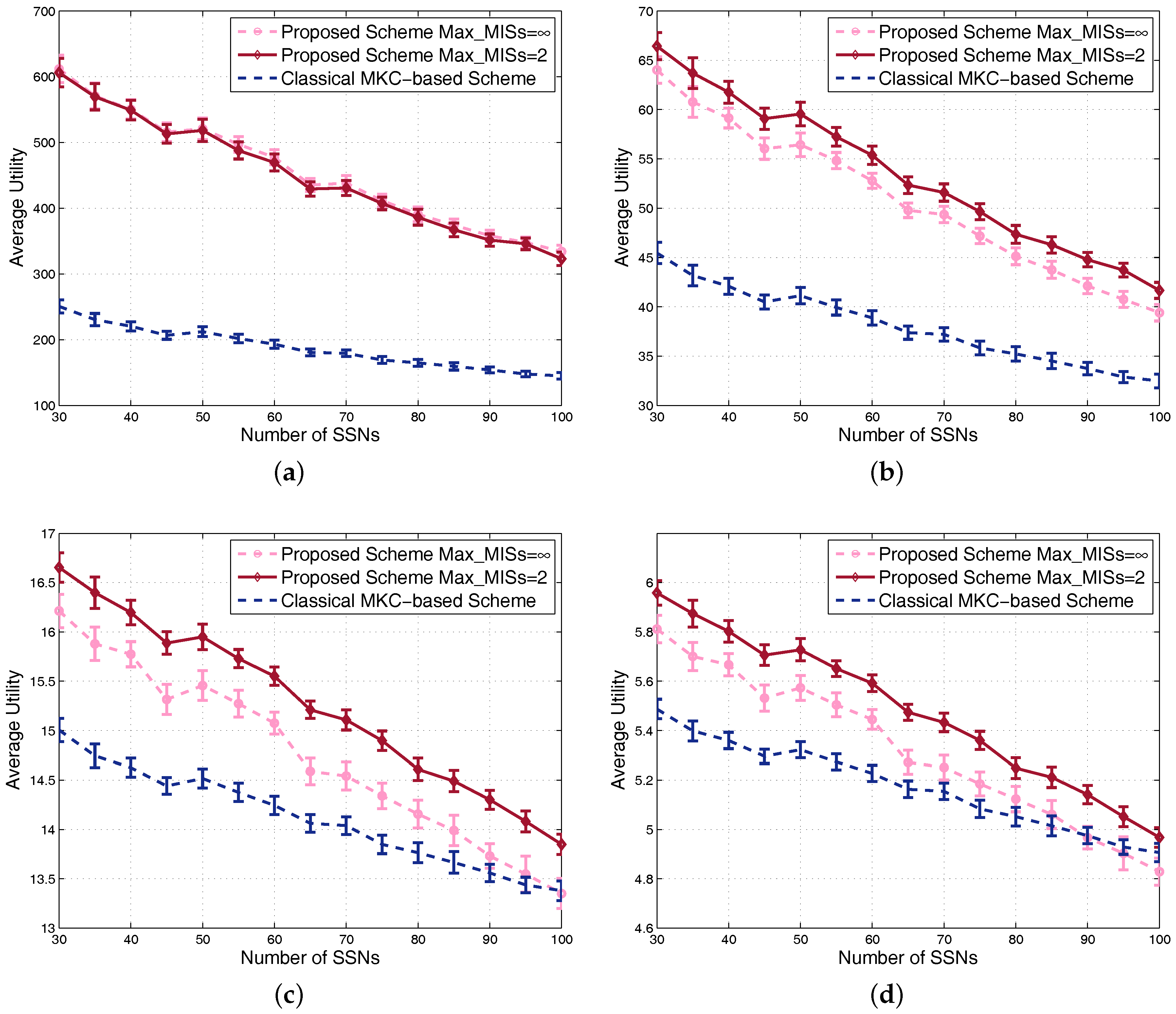
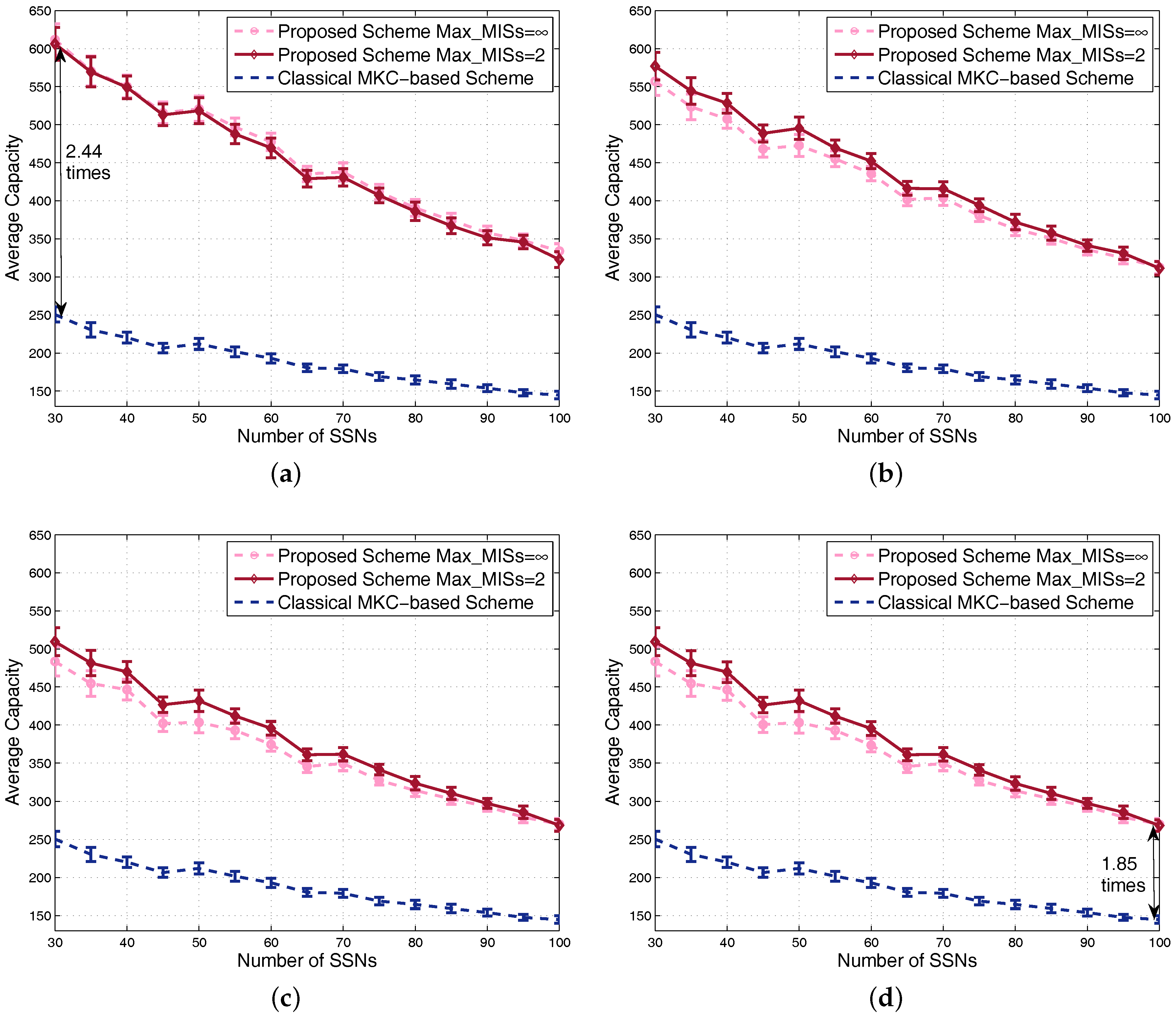
4.2. Results in Dense Scenarios
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Andrews, J. Seven ways that HetNets are a cellular paradigm shift. IEEE Commun. Mag. 2013, 15, 136–144. [Google Scholar] [CrossRef]
- Kamel, M.; Hamouda, W.; Youssef, A. Ultra-dense networks: A survey. IEEE Commun. Surv. Tutor. 2016, 18, 2522–2545. [Google Scholar] [CrossRef]
- Lin, H.; Wang, L.; Kong, R. Energy efficient clustering protocol for large-scale sensor networks. IEEE Sens. J. 2015, 15, 7150–7160. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Han, D.; Wu, H.; Zhou, R. Fuzzy-logic based distributed energy-efficient clustering algorithm for wireless sensor networks. Sensors 2017, 17, 1554. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Quek, T. On constructing interference free schedule for coexisting wireless body area networks using distributed coloring algorithm. In Proceedings of the IEEE International Conference on Wearable and Implantable Body Sensor Networks, Cambridge, MA, USA, 9–12 June 2015; pp. 1–6. [Google Scholar]
- Cheng, S.; Huang, C. Coloring-based inter-WBAN scheduling for mobile wireless body area networks. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 250–259. [Google Scholar] [CrossRef]
- Lin, P.; Zhang, J.; Chen, Y.; Zhang, Q. Macro-femto heterogeneous network deployment and management: From business models to technical solutions. IEEE Wirel. Commun. 2011, 18, 64–70. [Google Scholar] [CrossRef]
- Patel, C.; Yavuz, M.; Nanda, S. Femtocells: Industry perspectives. IEEE Wirel. Commun. 2010, 17, 6–7. [Google Scholar] [CrossRef]
- Omar, H.; Abboud, K.; Cheng, N.; Malekshan, K.; Gamage, A.; Zhuang, W. A survey on high efficiency wireless local area networks: Next generation WiFi. IEEE Commun. Surv. Tutor. 2016, 18, 2315–2344. [Google Scholar] [CrossRef]
- Dhillon, H.; Ganti, R.; Baccelli, F.; Andrews, J. Modeling and analysis of k-tier downlink heterogeneous cellular networks. IEEE J. Sel. Areas Commun. 2012, 30, 550–560. [Google Scholar] [CrossRef]
- Kosta, C.; Hunt, B.; Auddus, A.; Tafazolli, R. On interference avoidance through inter-cell interference coordination (ICIC) based on OFDMA mobile systems. IEEE Commun. Surv. Tutor. 2013, 15, 973–995. [Google Scholar] [CrossRef]
- Hamza, A.S.; Khalifa, S.S.; Hamza, H.S.; Elsayed, K. A survey on inter-cell interference coordination techniques in OFDMA-based cellular networks. IEEE Commun. Surv. Tutor. 2013, 15, 1642–1670. [Google Scholar] [CrossRef]
- Wang, L.; Fang, F.; Cottatellucci, L.; Nikaein, N. An analytical framework for multilayer partial frequency reuse scheme design in mobile communication systems. IEEE Trans. Veh. Technol. 2016, 65, 7593–7605. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Chen, W.; Kai, C.; Wu, L. Dynamic interference coordination with analytical near-optimum of power allocation toward high user fairness. China Commun. 2016, 13, 37–48. [Google Scholar] [CrossRef]
- Lopez-Perez, D.; Guvenc, I.; Roche, G.; Kountouris, M.; Quek, T.; Zhang, J. Enhanced intercell interference coordination challenges in heterogeneous networks. IEEE Wirel. Commun. 2011, 18, 22–30. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, S.; Li, X.; Ji, H.; Du, X. Interference management for heterogeneous networks with spectral efficiency improvement. IEEE Wirel. Commun. 2015, 22, 101–107. [Google Scholar] [CrossRef]
- Chieochan, S.; Hossain, E.; Diamond, J. Channel assignment schemes for infrastructure-based 802.11 WLANs: A survey. IEEE Commun. Surv. Tutor. 2010, 12, 124–136. [Google Scholar] [CrossRef]
- Joo, C.; Lin, X.; Ryu, J.; Shroff, N. Distributed greedy approximation to maximum weighted independent set for scheduling with fading channels. IEEE/ACM Trans. Netw. 2016, 24, 1476–1488. [Google Scholar] [CrossRef]
- Bai, S.; Che, X.; Bai, X.; Wei, X. Maximal independent sets in heterogeneous wireless ad hoc networks. IEEE Trans. Mob. Comput. 2016, 15, 2023–2033. [Google Scholar] [CrossRef]
- Marshoud, H.; Otrok, H.; Barada, H.; Estrada, R.; Dziong, Z. Genetic algorithm based resource allocation and interference mitigation for OFDMA macrocell-femtocells networks. In Proceedings of the 6th Joint IFIP WMNC, Dubai, United Arab Emirates, 23–25 April 2013; pp. 1–7. [Google Scholar]
- Li, H.; Chen, X.; Xiang, X. An intelligent optimization algorithm for joint MCS and resource block allocation in LTE femtocell downlink with QoS guarantees. In Proceedings of the International Conference on Game Theory for Networks, Beijing, China, 25–27 November 2014; pp. 1–6. [Google Scholar]
- Sadr, S.; Adve, R. Hierarchical resource allocation in femtocell networks using graph algorithms. In Proceedings of the IEEE ICC, Ottawa, ON, Canada, 10–15 June 2012; pp. 4416–4420. [Google Scholar]
- Chang, Y.; Tao, Z.; Zhang, J.; Kuo, C.J. Multicell OFDMA downlink resource allocation using a graphic framework. IEEE Trans. Veh. Technol. 2009, 58, 3494–3507. [Google Scholar] [CrossRef]
- Pateromichelakis, E.; Shariat, M.; Quddus, A.U. Graph-Based multicell scheduling in ofdma-based small cell networks. IEEE Access 2014, 2, 897–908. [Google Scholar] [CrossRef]
- Li, Y.; Luo, J.; Xu, W.; Vucic, N.; Pateromichelakis, E.; Caire, G. A joint scheduling and resource allocation scheme for millimeter wave heterogeneous networks. In Proceedings of the IEEE WCNC, San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Chen, Q.; Zhang, Q.; Niu, Z. A graph theory based opportunistic link scheduling for wireless ad hoc network. IEEE Trans. Wirel. Commun. 2009, 8, 5075–5085. [Google Scholar] [CrossRef]
- Pang, Q.; Leung, V.C.M. Channel clustering and probabilistic channel visiting techniques for WLAN interference mitigation in Bluetooth devices. IEEE Trans. Electromagn. Compat. 2007, 49, 914–923. [Google Scholar] [CrossRef]
- Lan, T.; Kao, D.; Chiang, M.; Sabharwal, A. An axiomatic theory of fairness in network resource allocation. In Proceedings of the IEEE InfoCom, San Diego, CA, USA, 14–19 March 2010; pp. 1–9. [Google Scholar]
- Yang, J.; Draper, S.; Nowak, R. Learning the interference graph of a wireless networks. IEEE Trans. Signal Inf. Process. Netw. 2017, 3, 631–646. [Google Scholar] [CrossRef]
- Luby, M. A simple parallel algorithm for the maximal independent set problem. SIAM J. Comput. 1986, 15, 1036–1053. [Google Scholar] [CrossRef]
- Alon, N.; Babai, L.; Itai, A. A fast and simple randomized parallel algorithm for the maximal independent set problem. J. Algorithm. 1986, 7, 567–583. [Google Scholar] [CrossRef]
- Bondy, J.; Murty, U. Independent sets and cliques. In Graph Theory with Applications; Macmillan Press Ltd.: London, UK, 1976; pp. 101–113. [Google Scholar]
- Weber, A.; Agyapong, P.; Rosowski, T.; Zimmerman, G.; Fallgren, M.; Sharma, S.; Kousaridas, A.; Yang, C.; Karls, I.; Maternia, M.; et al. Performance Evaluation Framework. Deliverable 2.1, METIS Project: Mobile and Wireless Communications Enablers for the Twenty-Twenty Information Society-II. 2016. Available online: http://www.metis2020.com (accessed on 25 July 2017).
- Special Interest Group (SIG) on 5G Channel Model, 5G Channel Model for Bands up to 100 GHz. IEEE Globecom White Paper. 2015. Available online: http://www.5gworkshops.com/5GCM.html (accessed on 25 July 2017).
- Jain, R.; Chiu, D.; Hawe, W. A Quantitative Measure of Fairness and Discrimination for Resource Allocation in Shared System; DEC Research Report TR-301; Digital Equipment Corporation: Hudson, MA, USA, 1984. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Wang, L.; Wang, W.; Zhou, Q. Efficient Graph-Based Resource Allocation Scheme Using Maximal Independent Set for Randomly- Deployed Small Star Networks. Sensors 2017, 17, 2553. https://doi.org/10.3390/s17112553
Zhou J, Wang L, Wang W, Zhou Q. Efficient Graph-Based Resource Allocation Scheme Using Maximal Independent Set for Randomly- Deployed Small Star Networks. Sensors. 2017; 17(11):2553. https://doi.org/10.3390/s17112553
Chicago/Turabian StyleZhou, Jian, Lusheng Wang, Weidong Wang, and Qingfeng Zhou. 2017. "Efficient Graph-Based Resource Allocation Scheme Using Maximal Independent Set for Randomly- Deployed Small Star Networks" Sensors 17, no. 11: 2553. https://doi.org/10.3390/s17112553
APA StyleZhou, J., Wang, L., Wang, W., & Zhou, Q. (2017). Efficient Graph-Based Resource Allocation Scheme Using Maximal Independent Set for Randomly- Deployed Small Star Networks. Sensors, 17(11), 2553. https://doi.org/10.3390/s17112553



