Motion-Blur-Free High-Speed Video Shooting Using a Resonant Mirror
Abstract
:1. Introduction
2. Related Works
2.1. Image Stabilization
2.2. High-Speed Vision
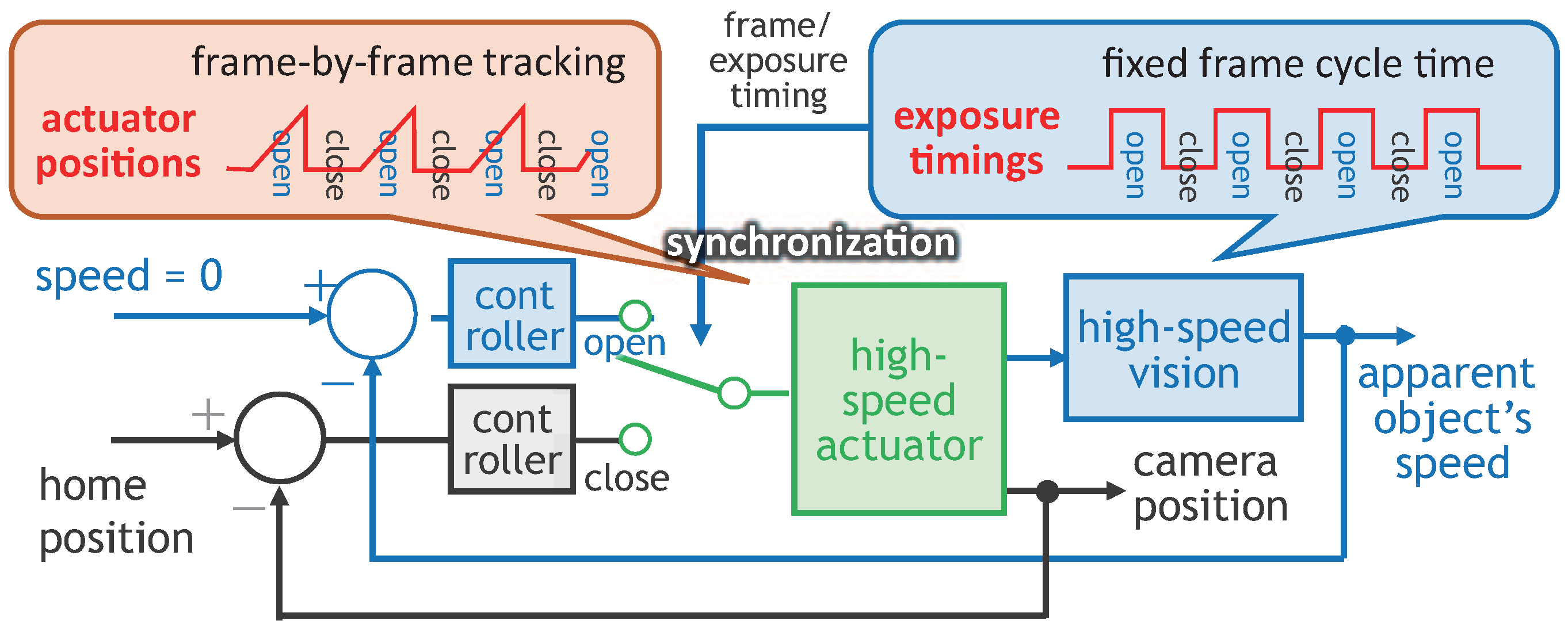
2.3. Camera-Driven Frame-By-Frame Intermittent Tracking
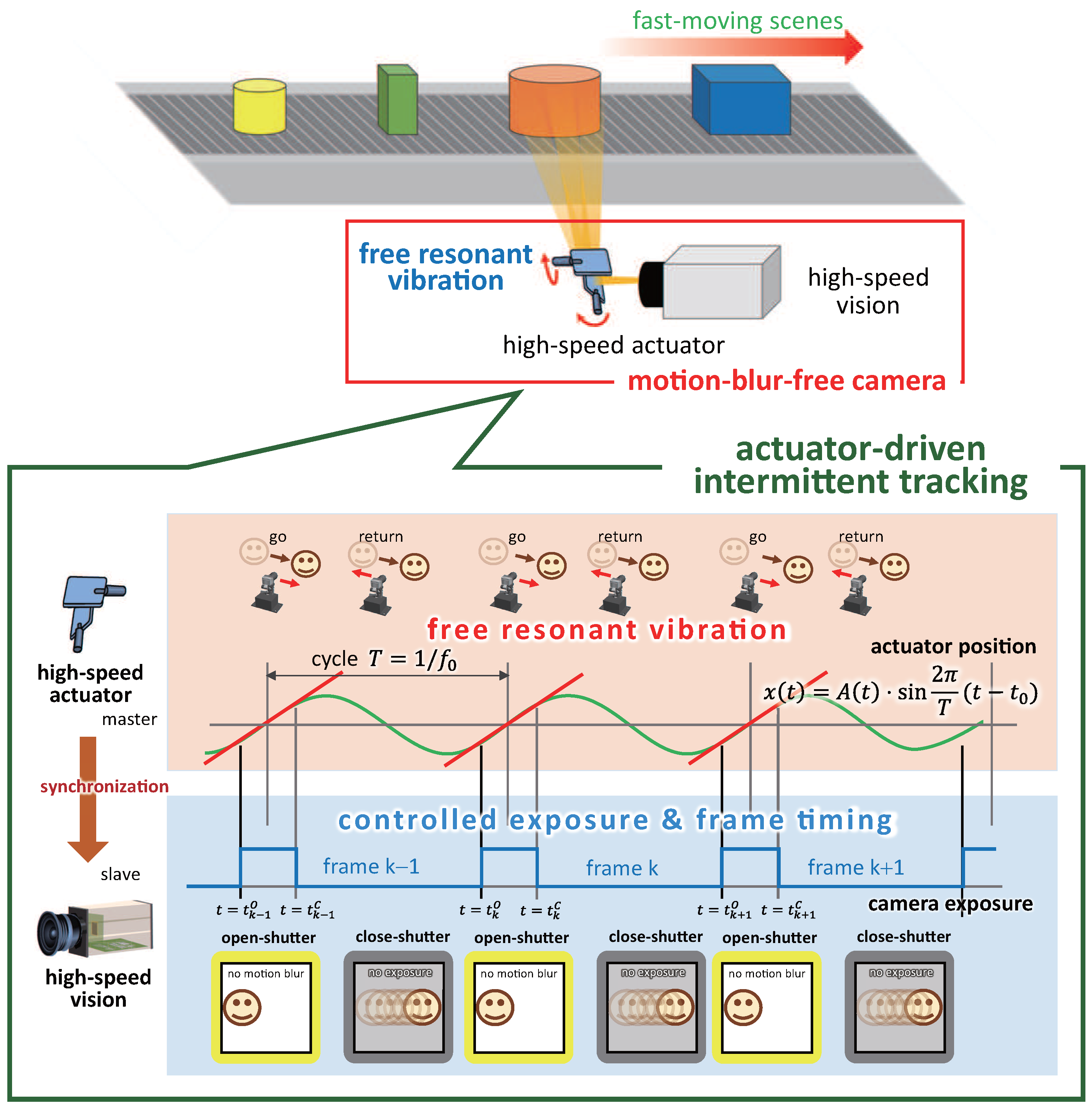
3. Actuator-Driven Frame-By-Frame Intermittent Tracking
3.1. Concept
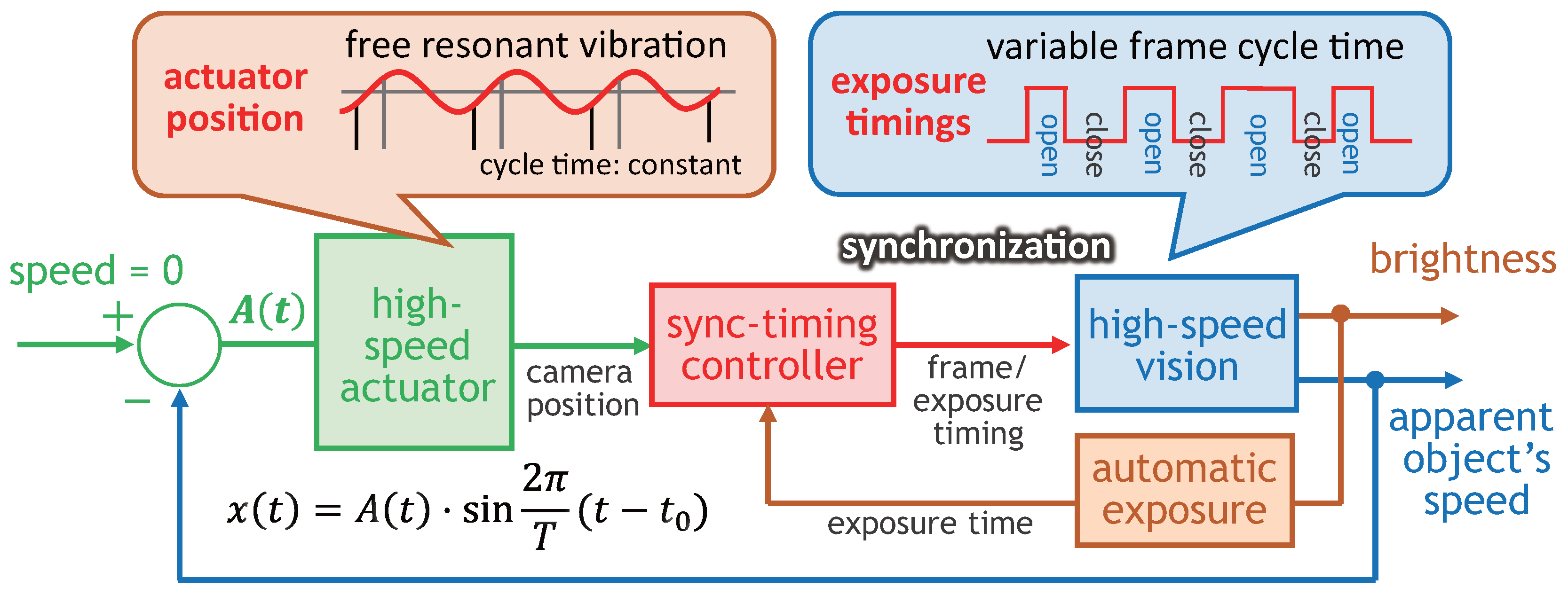
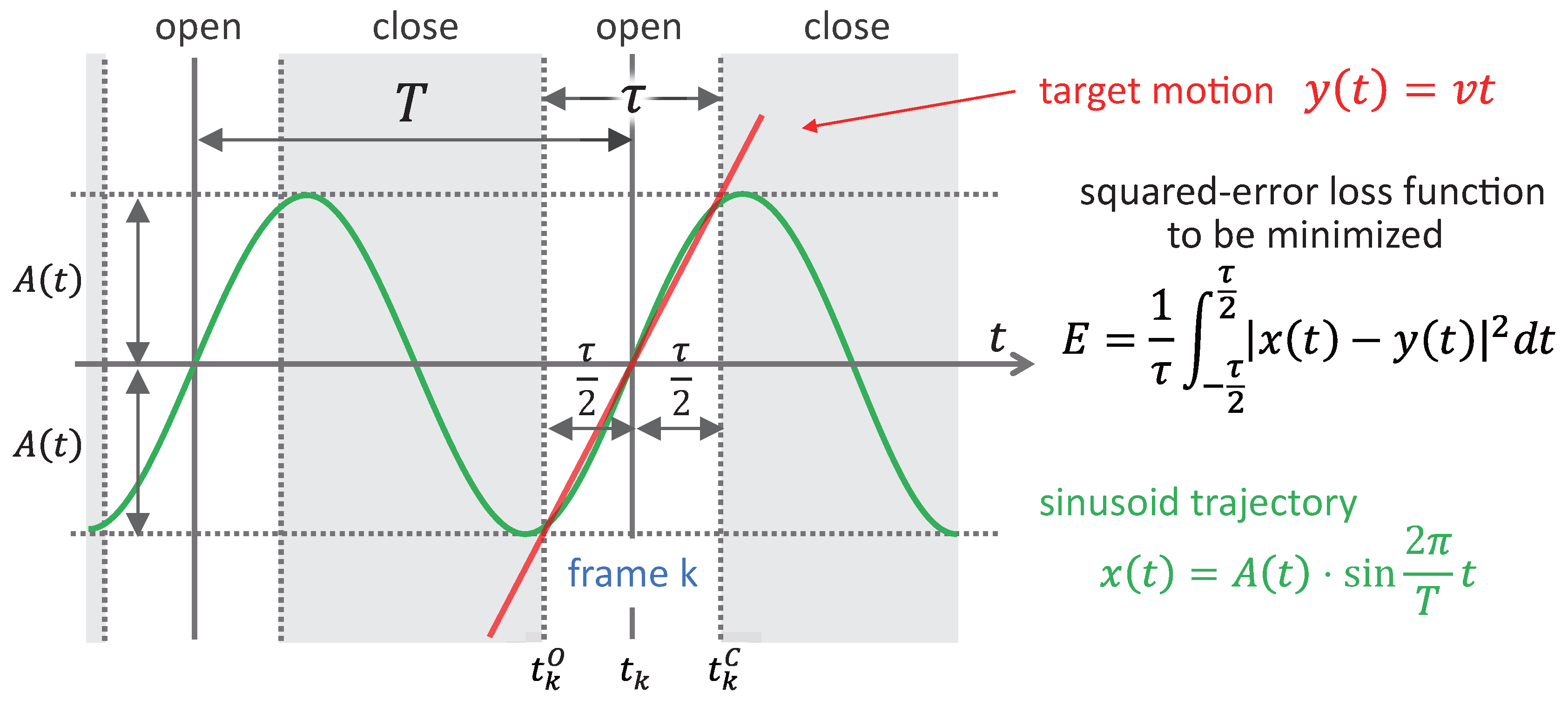
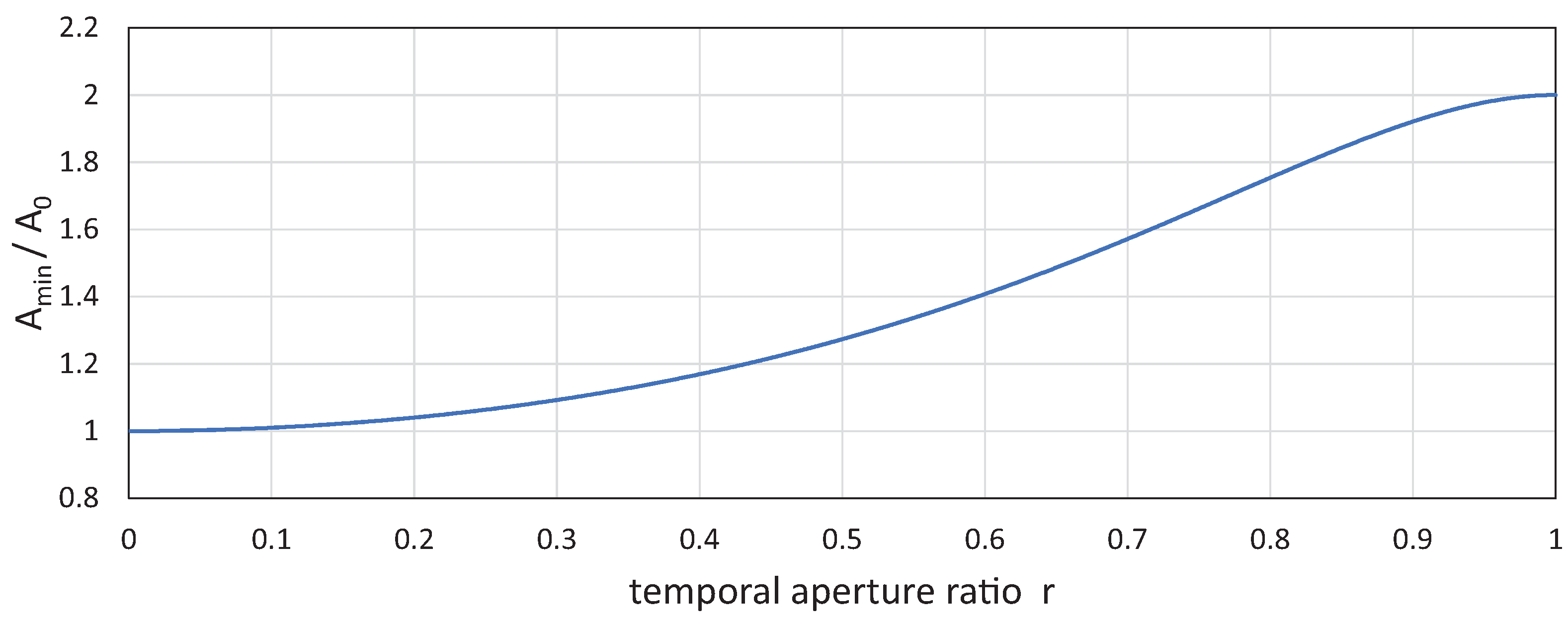
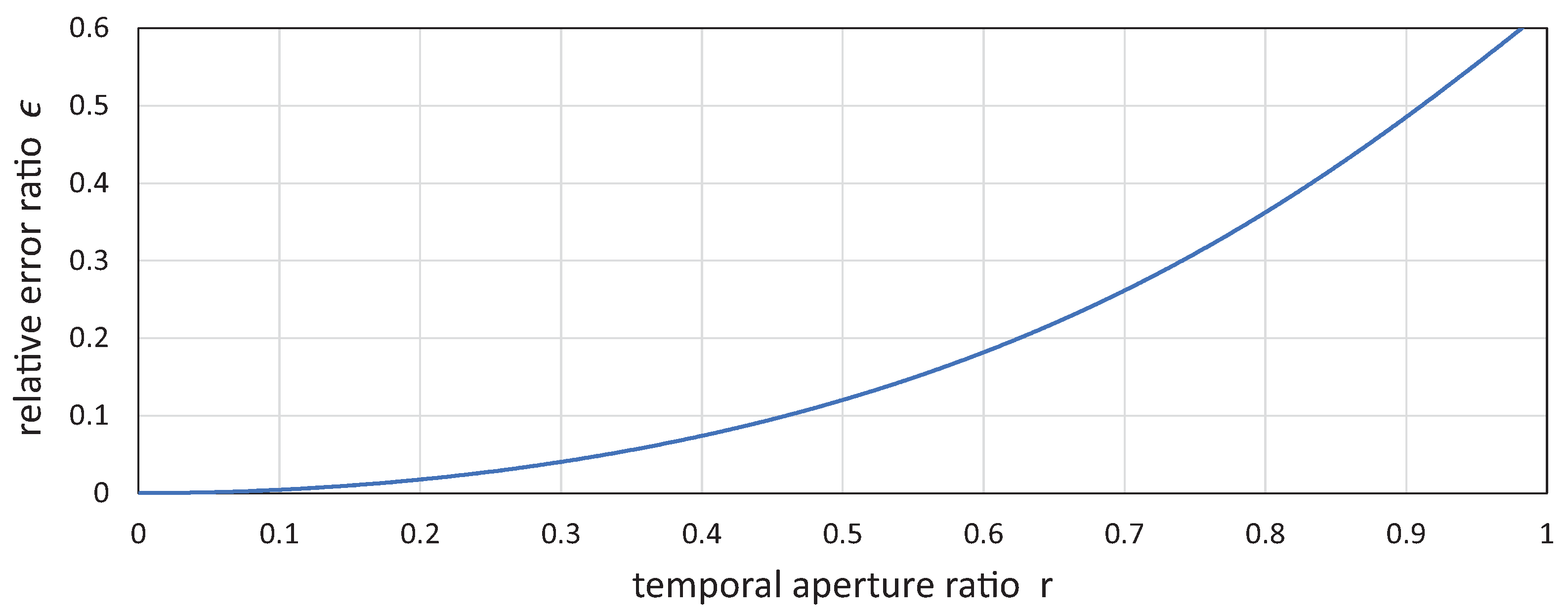
3.2. Camera Shutter Timings and Vibration Amplitude
4. Motion-Blur-Free HFR Video Shooting System
5. Preliminary Experiments
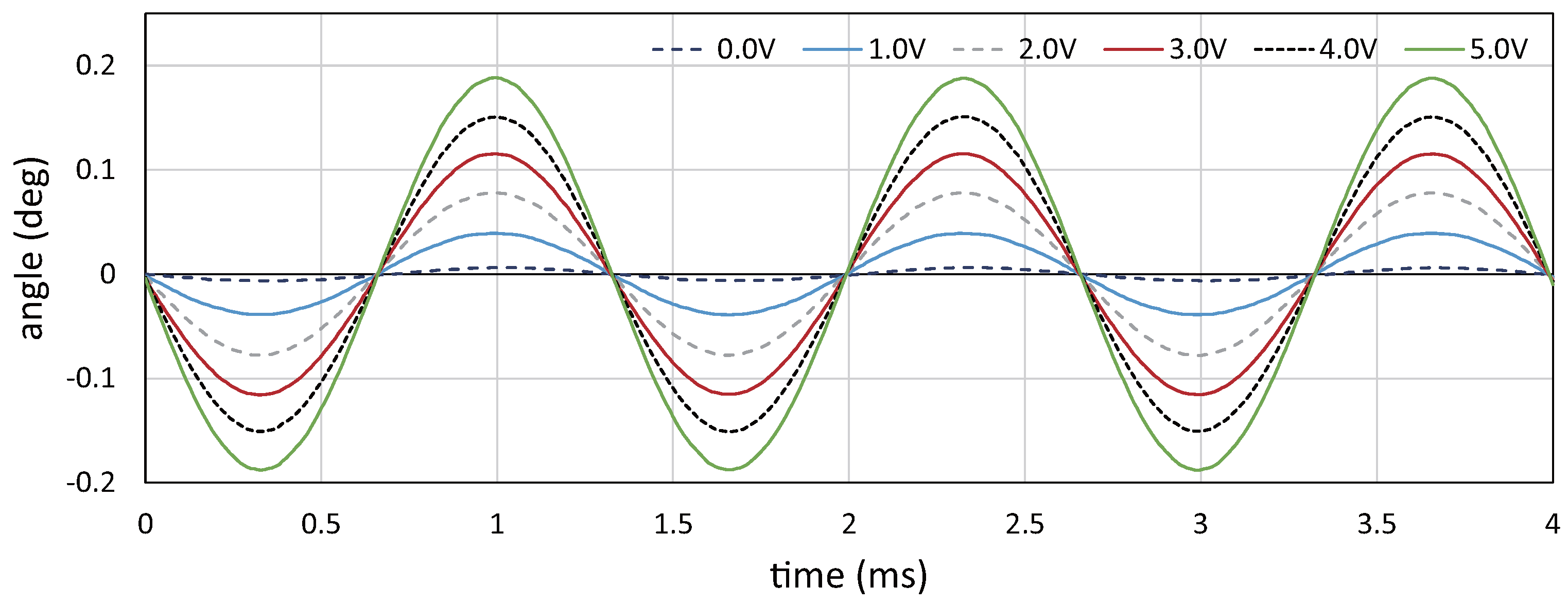
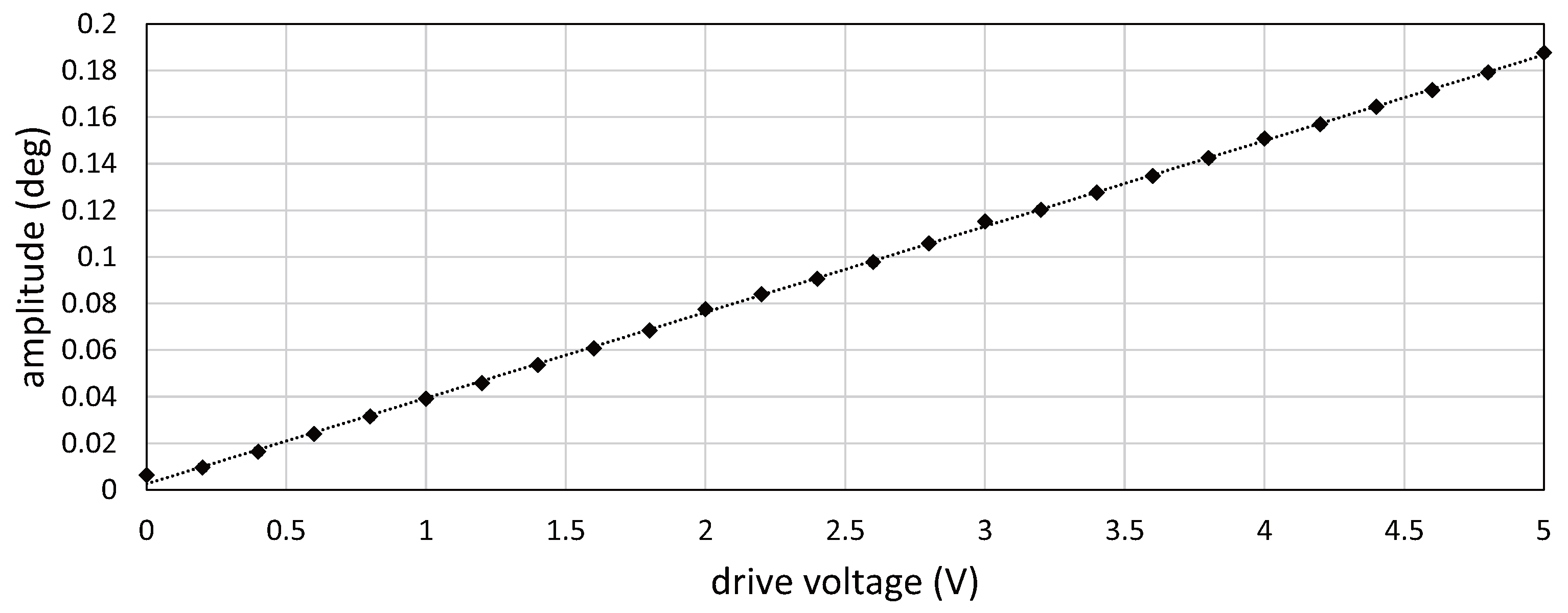
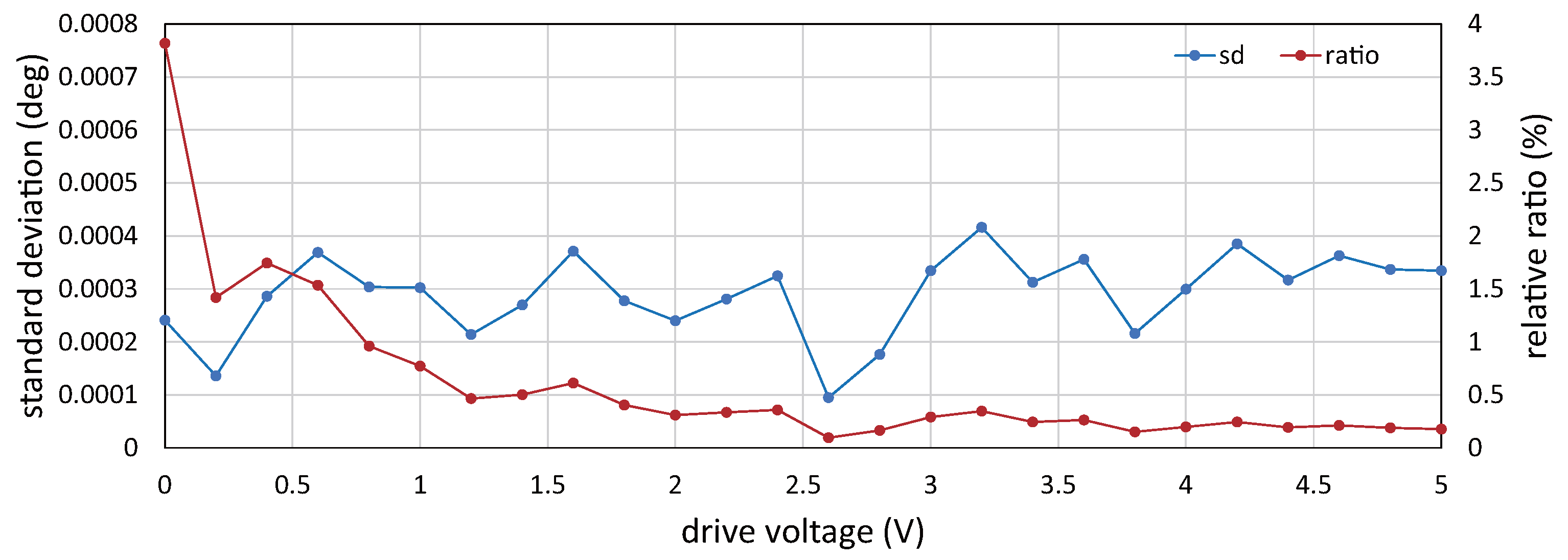
5.1. Relationship between Drive Voltage and Vibration Amplitude
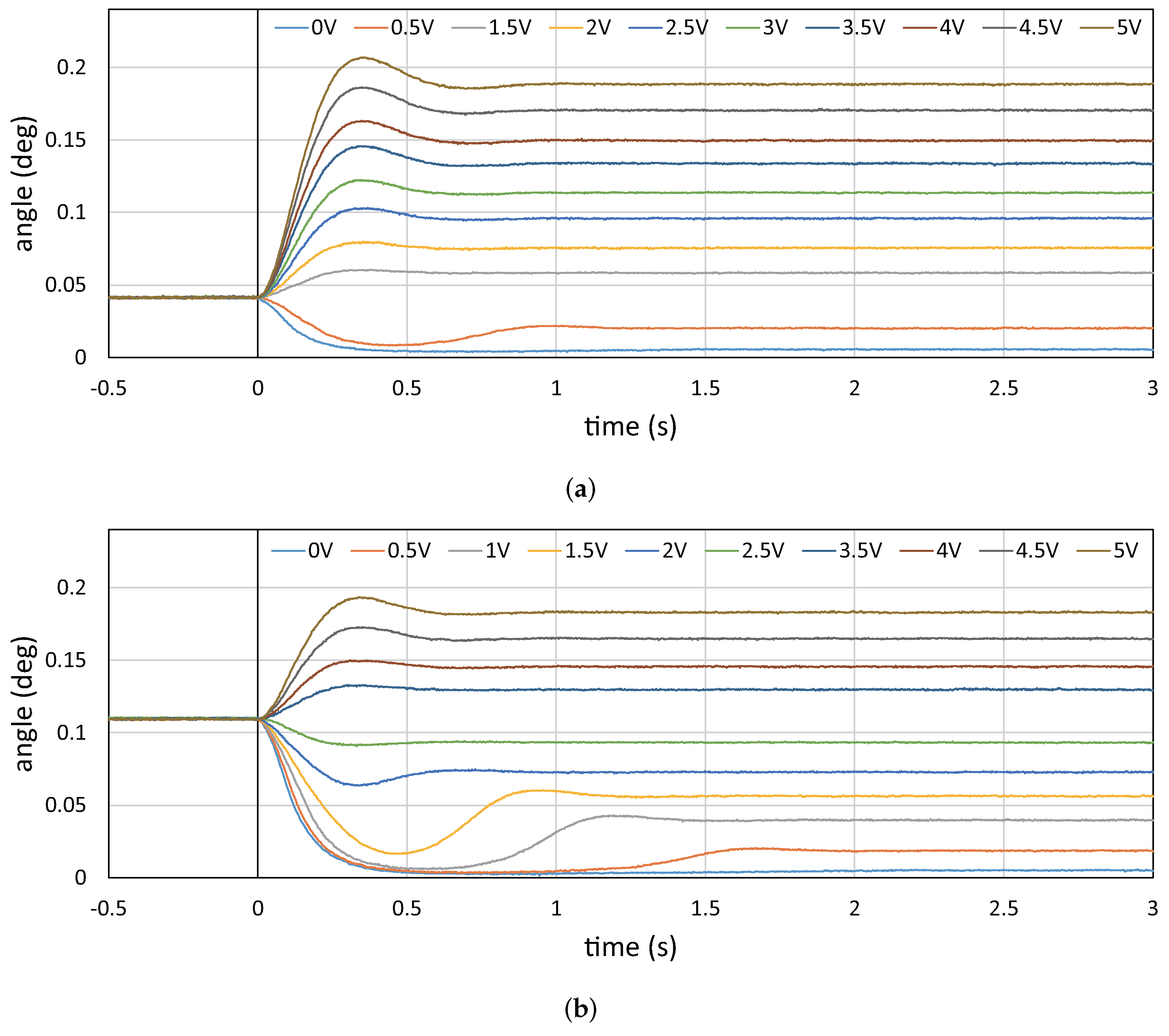
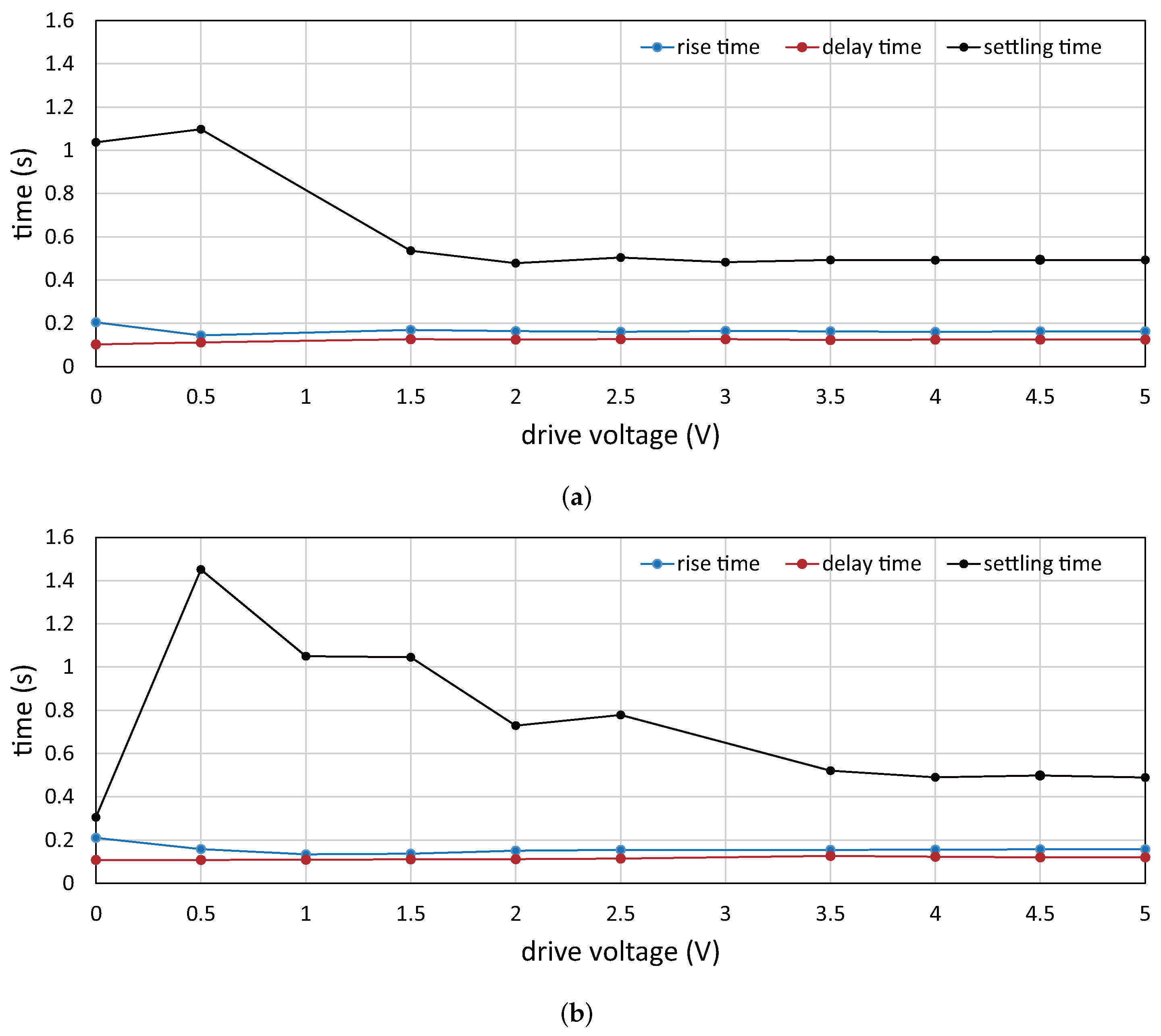
5.2. Step Responses of Vibration Amplitude
6. Video Shooting Experiments
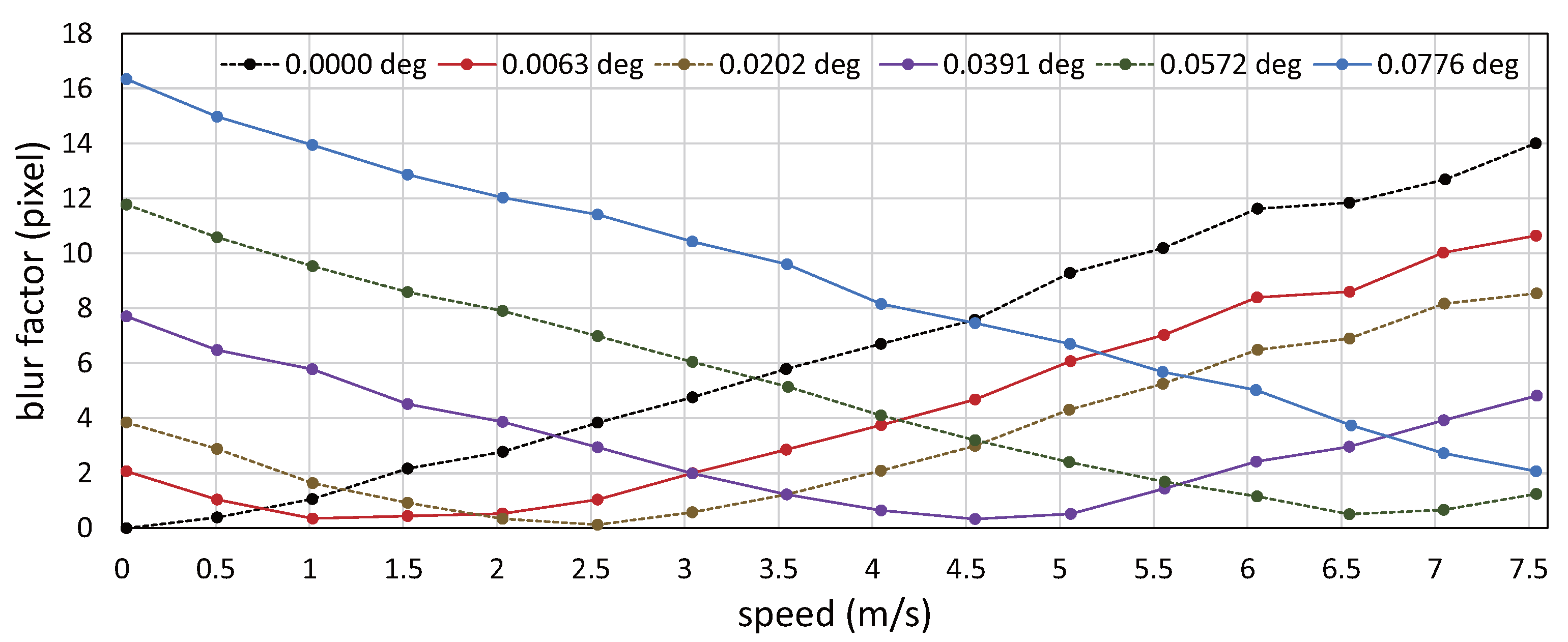
6.1. Video Shooting without Amplitude Control for Circle-Dots Moving at Constant Speeds
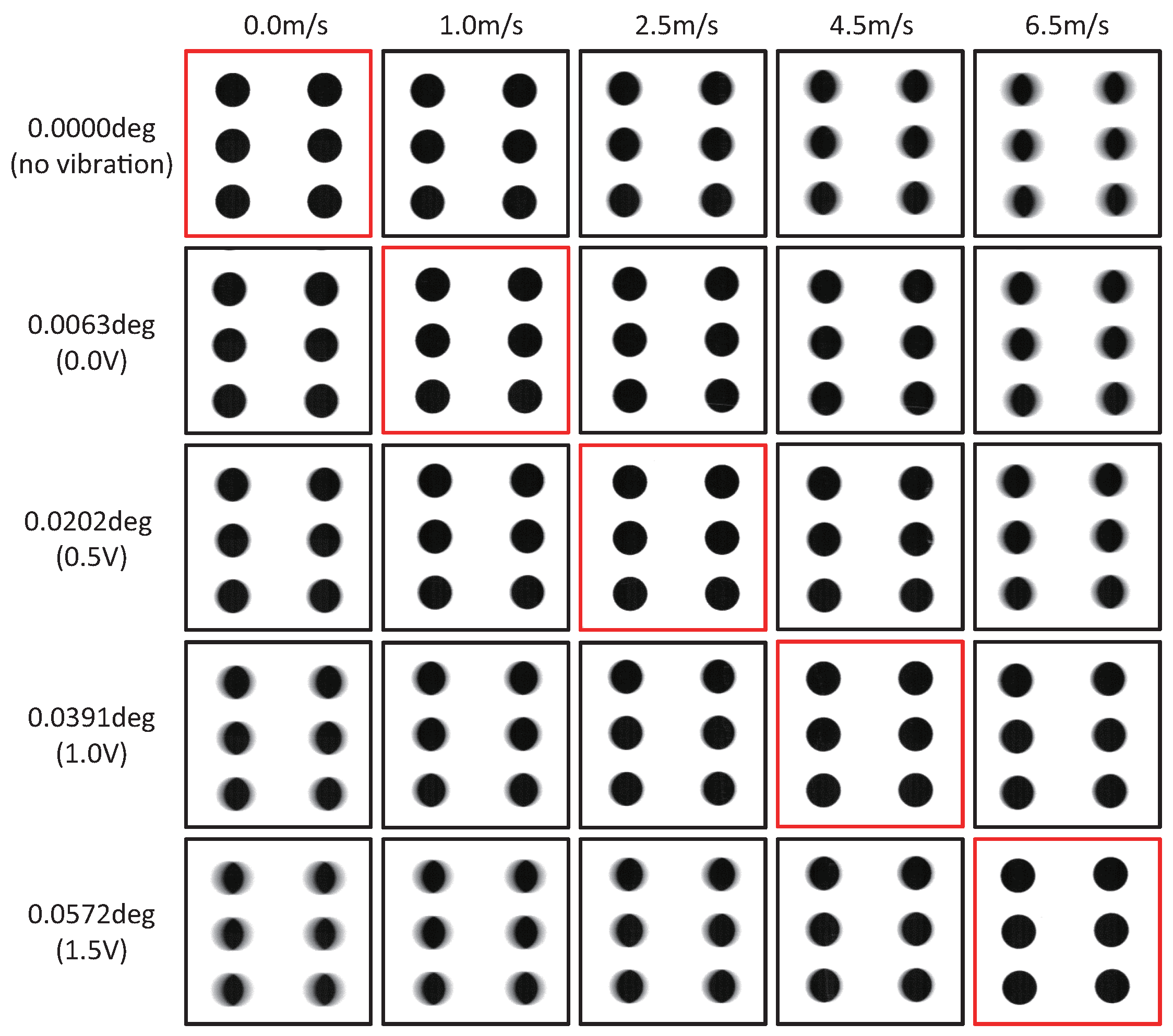
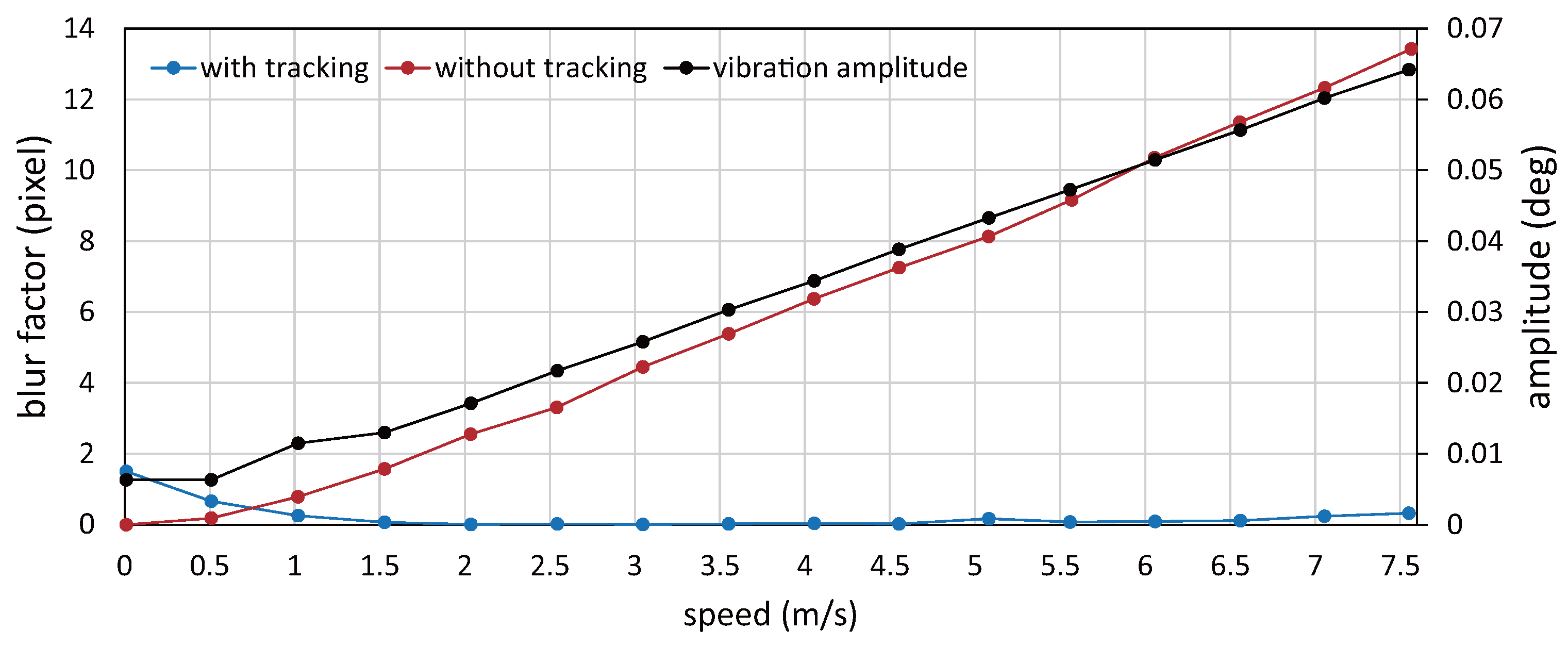
6.2. Video Shooting with Amplitude Control for Circle-Dots Moving at Constant Speeds
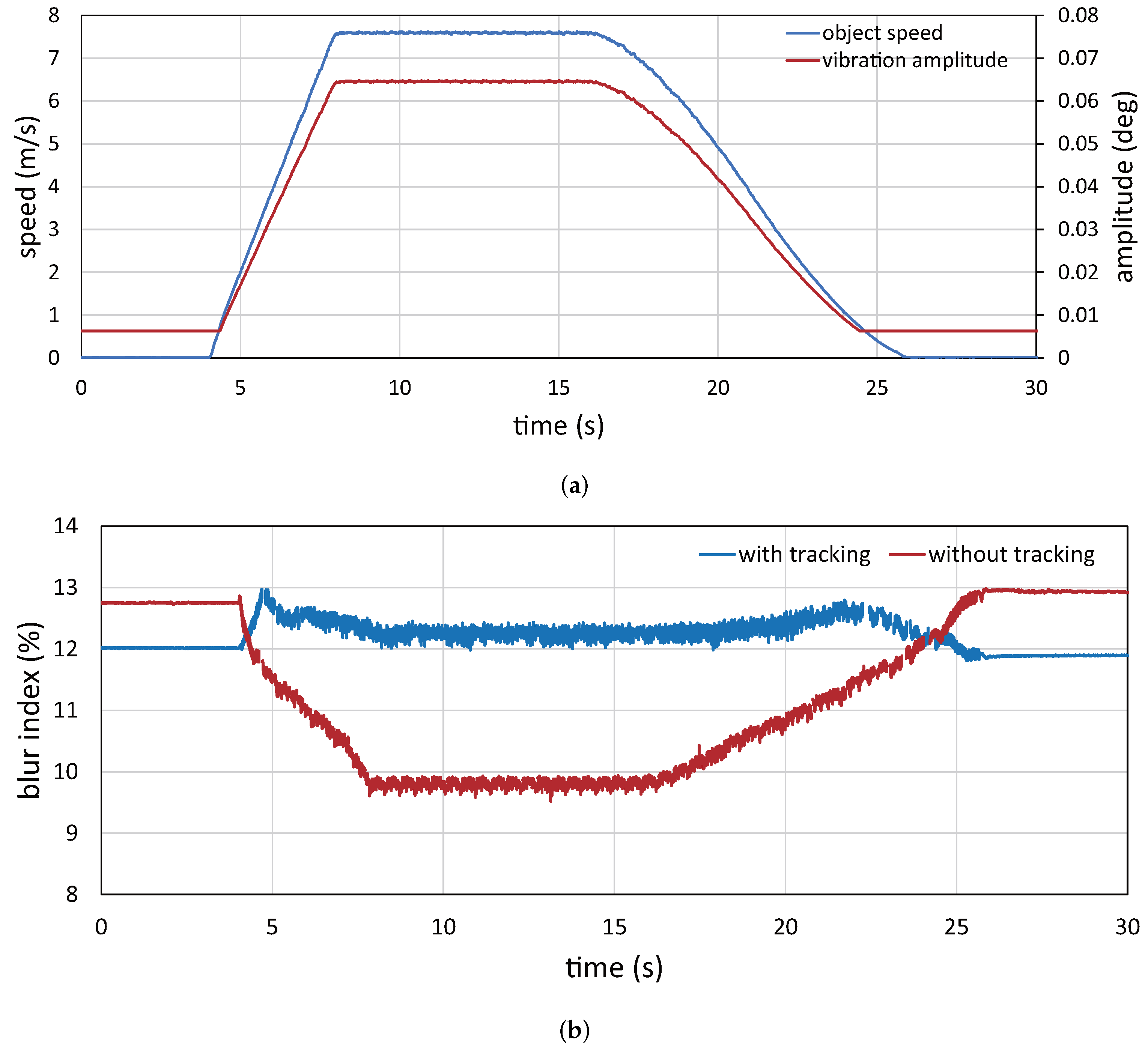
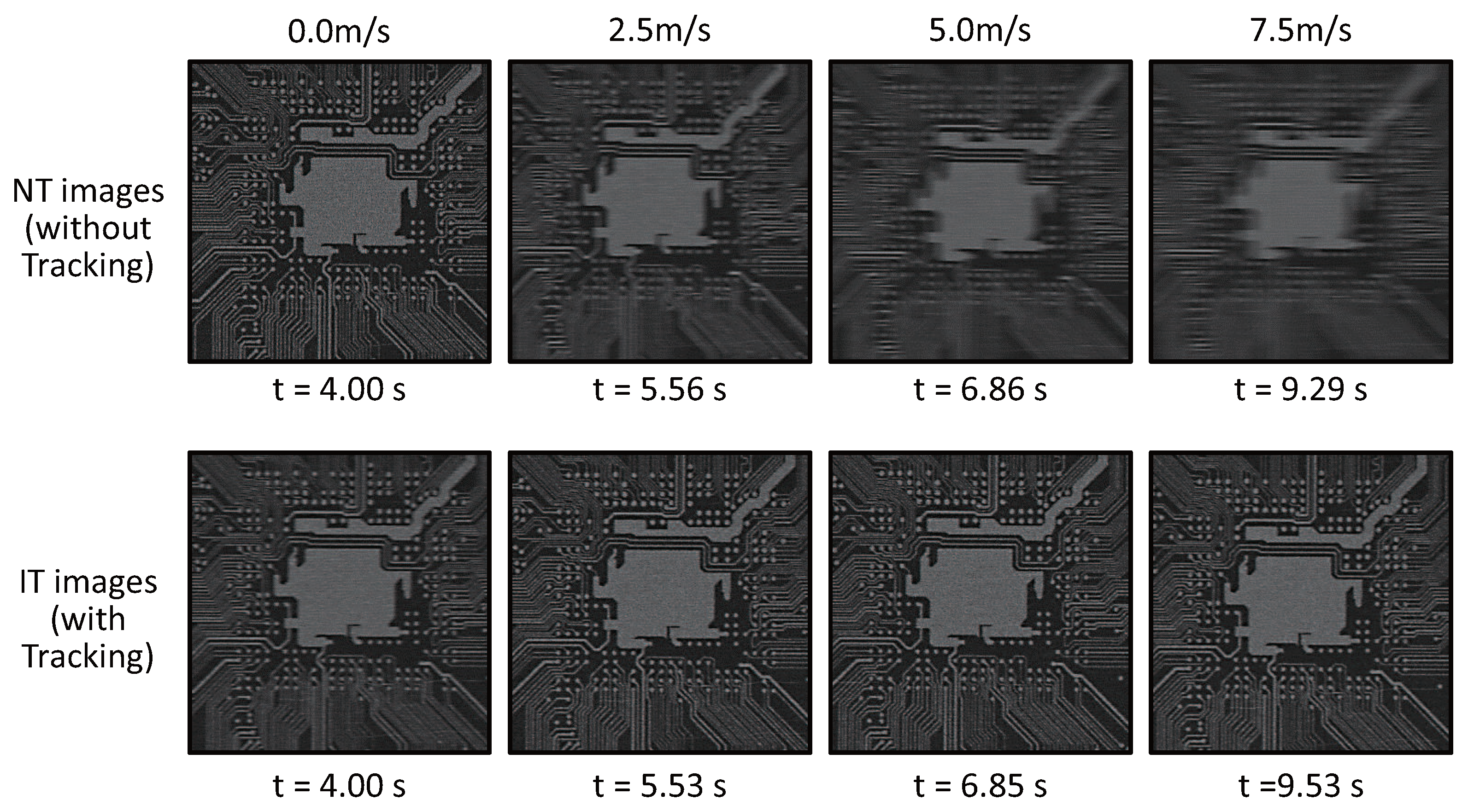
6.3. Video Shooting with Amplitude Control for Patterned Objects at Variable Speeds
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kundur, D.; Hatzinakos, D. Blind image deconvolution. IEEE Signal Proc. Mag. 1996, 13, 43–64. [Google Scholar] [CrossRef]
- Campisi, P.; Egiazarian, K. Blind Image Deconvolution: Theory and Applications; CRC Press: New York, NY, USA, 2007. [Google Scholar]
- KuKim, S.; KiPaik, J. Out-of-focus blur estimation and restoration for digital auto-focusing system. Electron. Lett. 1998, 34, 1217–1219. [Google Scholar] [CrossRef]
- Fergus, R.; Singh, B.; Hertzbann, A.; Roweis, S.T.; Freeman, W.T. Removing camera shake from a single photograph. ACM Trans. Graph. 2006, 25, 787–794. [Google Scholar] [CrossRef]
- Levin, A.; Weiss, Y.; Durand, F.; Freeman, W.T. Efficient marginal likelihood optimization in blind deconvolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 2657–2664. [Google Scholar]
- Joshi, N.; Szeliski, R.; Kriegman, D.J. PSF estimation using sharp edge prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Cho, S.; Lee, S. Fast motion deblurring. ACM Trans. Graph. 2009, 28, 145. [Google Scholar] [CrossRef]
- Xu, L.; Jia, J. Two-phase kernel estimation for robust motion deblurring. In Proceedings of the European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; pp. 157–170. [Google Scholar]
- Yang, F.; Huang, Y.; Luo, Y.; Li, L.; Li, H. Robust image restoration for motion blur of image sensors. Sensors 2016, 16, 845. [Google Scholar] [CrossRef] [PubMed]
- Xiong, N.; Liu, R.W.; Liang, M.; Wu, D.; Liu, Z.; Wu, H. Effective alternating direction optimization methods for sparsity-constrained blind image deblurring. Sensors 2017, 17, 174. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, D.; Tay, T.; Fergus, R. Blind deconvolution using a normalized sparsity measure. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 230–240. [Google Scholar]
- Joshi, N.; Zitnick, C.L.; Szeliski, R.; Kriegman, D.J. Image deblurring and denoising using color priors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 1550–1557. [Google Scholar]
- Sun, L.; Cho, S.; Wang, J.; Hays, J. Edge-based blur kernel estimation using patch priors. In Proceedings of the IEEE Conference on Computational Photography, Cambridge, MA, USA, 19–21 April 2013; pp. 1–8. [Google Scholar]
- Pan, J.; Sun, D.; Pfister, H.; Yang, M.-H. Blind image deblurring using dark channel prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1628–1636. [Google Scholar]
- Shan, Q.; Jia, J.; Agarwala, A. High-quality motion deblurring from a single image. ACM Trans. Graph. 2008, 27, 73. [Google Scholar] [CrossRef]
- Bascle, B.; Blake, A.; Zisserman, A. Motion deblurring and super-resolution from an image sequence. In Proceedings of the European Conference on Computer Vision, Cambridge, UK, 15–18 April 1996; pp. 571–582. [Google Scholar]
- Chen, J.; Yuan, L.; Tang, C.-K.; Quan, L. Robust dual motion deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Farsiu, S.; Robinson, M.D.; Elad, M.; Milanfar, P. Fast and robust multiframe super resolution. IEEE Trans. Image Process. 2004, 13, 1327–1344. [Google Scholar] [CrossRef] [PubMed]
- Nayar, S.K.; Ben-Ezra, M. Motion-based motion deblurring. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 689–698. [Google Scholar] [CrossRef] [PubMed]
- Tai, Y.-W.; Du, H.; Brown, M.S.; Lin, S. Image/video deblurring using a hybrid camera. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Rav-Acha, A.; Peleg, S. Two motion-blurred images are better than one. Pattern Recognit. Lett. 2005, 26, 311–317. [Google Scholar] [CrossRef]
- Yuan, L.; Sun, J.; Quan, L.; Shum, H.-Y. Image deblurring with blurred/noisy image pairs. ACM Trans. Graph. 2007, 26, 1. [Google Scholar] [CrossRef]
- Tai, Y.-W.; Tan, P.; Brown, M.S. Richardson-Lucy deblurring for scenes under projective motion path. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1603–1618. [Google Scholar] [PubMed]
- Whyte, O.; Sivic, J.; Zisserman, A.; Ponce, J. Non-uniform deblurring for shaken images. Int. J. Comput. Vis. 2012, 98, 168–186. [Google Scholar] [CrossRef]
- Gupta, A.; Joshi, N.; Zitnick, C.L.; Cohen, M.; Curless, B. Single image deblurring using motion density functions. In Proceedings of the European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; pp. 171–184. [Google Scholar]
- Joshi, N.; Kang, S.B.; Zitnick, C.L.; Szeliski, R. Image deblurring using inertial measurement sensors. ACM Trans. Graphics 2010, 29, 30. [Google Scholar] [CrossRef]
- Kim, M.D.; Ueda, J. Dynamics-based motion de-blurring for a PZT-driven, compliant camera orientation mechanism. Int. J. Robot. Res. 2015, 34, 653–673. [Google Scholar] [CrossRef]
- Inoue, M.; Jiang, M.; Matsumoto, Y.; Takaki, T.; Ishii, I. Motion-blur-free video shooting system based on frame-by-frame intermittent tracking. ROBOMECH J. 2017, Submitted. [Google Scholar]
- Kusaka, H.; Tsuchida, Y.; Shimohata, T. Control technology for optical image stabilization. SMPTE Motion Imaging J. 2002, 111, 609–615. [Google Scholar] [CrossRef]
- Cardani, B. Optical image stabilization for digital cameras. IEEE Control Syst. 2006, 26, 21–22. [Google Scholar] [CrossRef]
- Sato, K.; Ishizuka, S.; Nikami, A.; Sato, M. Control techniques for optical image stabilizing system. IEEE Trans. Consum. Electron. 1993, 39, 461–466. [Google Scholar] [CrossRef]
- Pournazari, P.; Nagamune, R.; Chiao, M. A concept of a magnetically-actuated optical image stabilizer for mobile applications. IEEE Trans. Consum. Electron. 2014, 60, 10–17. [Google Scholar] [CrossRef]
- Hao, Q.; Cheng, X.; Kang, J.; Jiang, Y. An image stabilization optical system using deformable freeform mirrors. Sensors 2015, 15, 1736–1749. [Google Scholar] [CrossRef] [PubMed]
- Chiu, C.-W.; Chao, P.C.-P.; Wu, D.-Y. Optimal design of magnetically actuated optical image stabilizer mechanism for cameras in mobile phones via genetic algorithm. IEEE Trans. Magn. 2007, 43, 2582–2584. [Google Scholar] [CrossRef]
- Moon, J.-H.; Jung, S.Y. Implementation of an image stabilization system for a small digital camera. IEEE Trans. Consum. Electron. 2008, 54. [Google Scholar] [CrossRef]
- Song, M.-G.; Hur, Y.-J.; Park, N.-C.; Park, K.-S.; Park, Y.-P.; Lim, S.-C.; Park, J.-H. Design of a voice-coil actuator for optical image stabilization based on genetic algorithm. IEEE Trans. Magn. 2009, 45, 4558–4561. [Google Scholar] [CrossRef]
- Song, M.-G.; Baek, H.-W.; Park, N.-C.; Park, K.-S.; Yoon, T.; Park, Y.-P.; Lim, S.-C. Development of small sized actuator with compliant mechanism for optical image stabilization. IEEE Trans. Magn. 2010, 46, 2369–2372. [Google Scholar] [CrossRef]
- Li, T.-H.S.; Chen, C.-C.; Su, Y.-T. Optical image stabilizing system using fuzzy sliding-mode controller for digital cameras. IEEE Trans. Consum. Electron. 2012, 58, 237–245. [Google Scholar] [CrossRef]
- Wang, J.H.-S.; Qiu, K.-F.; Chao, P.C.-P. Control design and digital implementation of a fast 2-degree-of-freedom translational optical image stabilizer for image sensors in mobile camera phones. Sensors 2017, 17, 2333. [Google Scholar] [CrossRef] [PubMed]
- Walrath, C.D. Adaptive bearing friction compensation based on recent knowledge of dynamic friction. Automatica 1984, 20, 717–727. [Google Scholar] [CrossRef]
- Ekstrand, B. Equations of motion for a two-axes gimbal system. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1083–1091. [Google Scholar] [CrossRef]
- Kennedy, P.J.; Kennedy, R.L. Direct versus indirect line of sight (LOS) stabilization. IEEE Trans. Control Syst. Technol. 2003, 11, 3–15. [Google Scholar] [CrossRef]
- Zhou, X.; Jia, Y.; Zhao, Q.; Yu, R. Experimental validation of a compound control scheme for a two-axis inertially stabilized platform with multi-sensors in an unmanned helicopter-based airborne power line inspection system. Sensors 2016, 16, 366. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xiao, Y.; Zhuang, Z.; Zhou, L.; Liu, F.; He, Y. Development of a near ground remote sensing system. Sensors 2016, 16, 648. [Google Scholar] [CrossRef] [PubMed]
- Jang, S.-W.; Pomplun, M.; Kim, G.-Y.; Choi, H.-I. Adaptive robust estimation of affine parameters from block motion vectors. Image Vis. Comput. 2005, 23, 1250–1263. [Google Scholar] [CrossRef]
- Xu, L.; Lin, X. Digital image stabilization based on circular block matching. IEEE Trans. Consum. Electron 2006, 52, 566–574. [Google Scholar]
- Chantara, W.; Mun, J.-H.; Shin, D.-W.; Ho, Y.-S. Object tracking using adaptive template matching. IEIE Trans. Smart Process. Comput. 2015, 4, 1–9. [Google Scholar] [CrossRef]
- Ko, S.-J.; Lee, S.-H.; Lee, K.-H. Digital image stabilizing algorithms based on bit-plane matching. IEEE Trans. Consum. Electron. 1998, 44, 617–622. [Google Scholar]
- Ko, S.-J.; Lee, S.-H.; Jeon, S.-W.; Kang, E.-S. Fast digital image stabilizer based on gray-coded bit-plane matching. IEEE Trans. Consum. Electron 1999, 45, 598–603. [Google Scholar]
- Shen, Y.; Guturu, P.; Damarla, T.; Buckles, B.P.; Namuduri, K.R. Video stabilization using principal component analysis and scale invariant feature transform in particle filter framework. IEEE Trans. Consum. Electron. 2009, 55. [Google Scholar] [CrossRef]
- Xu, J.; Chang, H.; Yang, S.; Wang, M. Fast feature-based video stabilization without accumulative global motion estimation. IEEE Trans. Consum. Electron. 2012, 58, 993–999. [Google Scholar] [CrossRef]
- Liu, S.; Yuan, L.; Tan, P.; Sun, J. Bundled camera paths for video stabilization. ACM Trans. Graphics 2013, 32, 78. [Google Scholar] [CrossRef]
- Kim, S.-K.; Kang, S.-J.; Wang, T.-S.; Ko, S.-J. Feature point classification based global motion estimation for video stabilization. IEEE Trans. Consum. Electron. 2013, 59, 267–272. [Google Scholar] [CrossRef]
- Cheng, X.; Hao, Q.; Xie, M. A comprehensive motion estimation technique for the improvement of EIS Methods based on the SURF algorithm and Kalman filter. Sensors 2016, 16, 486. [Google Scholar] [CrossRef] [PubMed]
- Jeon, S.; Yoon, I.; Jang, J.; Yang, S.; Kim, J.; Paik, J. Robust video stabilization using particle keypoint update and l1-optimized camera path. Sensors 2017, 17, 337. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.-Y.; Hu, W.-F.; Cheng, M.-H.; Chang, B.-S. Digital image translational and rotational motion stabilization using optical flow technique. IEEE Trans. Consum. Electron. 2002, 48, 108–115. [Google Scholar] [CrossRef]
- Matsushita, Y.; Ofek, E.; Ge, W.; Tang, X.; Shum, H.-Y. Full-frame video stabilization with motion inpainting. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1150–1163. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Lai, X.; Xu, D.; Tsoligkas, N.A. An integrated new scheme for digital video stabilization. Adv. Multimed. 2013, 2013, 8. [Google Scholar] [CrossRef]
- Pathak, S.; Moro, A.; Fujii, H.; Yamashita, A.; Asama, H. Spherical video stabilization by estimating rotation from dense optical flow fields. J. Robot. Mechatron., 2017, 29, 566–579. [Google Scholar] [CrossRef]
- Edgerton, H.E.; Germeshausen, K.J. Stroboscopic-light high-speed motion pictures. J. Soc. Motion Pict. Eng. 1934, 23, 284–298. [Google Scholar] [CrossRef]
- Bradley, D.; Atcheson, B.; Ihrke, I.; Heidrich, W. Synchronization and rolling shutter compensation for consumer video camera arrays. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Boden, F.; Bodensiek, K.; Stasicki, B. Application of image pattern correlation for non-intrusive deformation measurements of fast rotating objects on aircrafts. In Proceedings of the Fourth International Conference on Experimental Mechanics, Singapore, 18–20 November 2009. [Google Scholar]
- Theobalt, C.; Albrecht, I.; Haber, J.; Magnor, M.; Seidel, H.-P. Pitching a baseball: Tracking high-speed motion with multi-exposure images. In Proceedings of the ACM SIGGRAPH 2004, Los Angeles, CA, USA, 8–12 August 2004; pp. 540–547. [Google Scholar]
- Borsato, F.H.; Aluani, F.O.; Morimoto, C.H. A fast and accurate eye tracker using stroboscopic differential lighting. In Proceedings of the IEEE International Conference on Computer Vision Workshop, Santiago, Chile, 7–13 December 2015; pp. 110–118. [Google Scholar]
- Watanabe, Y.; Komura, T.; Ishikawa, M. 955-fps real-time shape measurement of a moving/deforming object using high-speed vision for numerous-point analysis. In Proceedings of the IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 3192–3197. [Google Scholar]
- Ishii, I.; Taniguchi, T.; Sukenobe, R.; Yamamoto, K. Development of high-speed and real-time vision platform, H3 Vision. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 3671–3678. [Google Scholar]
- Ishii, I.; Tatebe, T.; Gu, Q.; Moriue, Y.; Takaki, T.; Tajima, K. 2000 fps Real-time vision system with high-frame-rate video recording. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 1536–1541. [Google Scholar]
- Yamazaki, T.; Katayama, H.; Uehara, S.; Nose, A.; Kobayashi, M.; Shida, S.; Odahara, M.; Takamiya, K.; Hisamatsu, Y.; Matsumoto, S.; et al. A 1ms high-Speed vision chip with 3D-stacked 140GOPS column-parallel PEs for spatio-temporal image processing. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 5–9 February 2017; pp. 82–83. [Google Scholar]
- Ishii, I.; Taniguchi, T.; Yamamoto, K.; Takaki, T. High-frame-rate optical flow system. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 105–112. [Google Scholar] [CrossRef]
- Ishii, I.; Tatebe, T.; Gu, Q.; Takaki, T. Color-histogram-based tracking at 2000 fps. J. Electron. Imaging 2012, 21, 013010. [Google Scholar] [CrossRef]
- Gu, Q.; Takaki, T.; Ishii, I. Fast FPGA-based multiobject feature extraction. IEEE Trans. Circuits Syst. Video Technol. 2013, 23, 30–45. [Google Scholar] [CrossRef]
- Gu, Q.; Raut, S.; Okumura, K.; Aoyama, T.; Takaki, T.; Ishii, I. Real-time image mosaicing system using a high-frame-rate video sequence. J. Robot. Mechatron. 2015, 27, 12–23. [Google Scholar] [CrossRef]
- Ishii, I.; Ichida, T.; Gu, Q.; Takaki, T. 500-fps face tracking system. J. Real-Time Image Proc. 2013, 8, 379–388. [Google Scholar] [CrossRef]
- Namiki, A.; Hashimoto, K.; Ishikawa, M. A hierarchical control architecture for high-speed visual servoing. Int. J. Robot. Res. 2003, 22, 873–888. [Google Scholar] [CrossRef]
- Senoo, T.; Namiki, A.; Ishikawa, M. Ball control in high-speed batting motion using hybrid trajectory generator. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 1762–1767. [Google Scholar]
- Namiki, A.; Ito, N. Ball catching in Kendama game by estimating grasp conditions based on a high-speed vision system and tactile sensors. In Proceedings of the IEEE Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; pp. 634–639. [Google Scholar]
- Aoyama, T.; Takaki, T.; Miura, T.; Gu, Q.; Ishii, I. Realization of flower stick rotation using robotic arm. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Hamburg, Germany, 28 September–2 October 2015; pp. 5648–5653. [Google Scholar]
- Jiang, M.; Aoyama, T.; Takaki, T.; Ishii, I. Pixel-level and robust vibration source sensing in high-frame-rate video analysis. Sensors 2016, 16, 1842. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Gu, Q.; Aoyama, T.; Takaki, T.; Ishii, I. Real-time vibration source tracking using high-speed vision. IEEE Sens. J. 2017, 17, 1513–1527. [Google Scholar] [CrossRef]
- Oku, H.; Ishii, I.; Ishikawa, M. Tracking a protozoon using high-speed visual feedback. In Proceedings of the International IEEE-EMBS Conference on Microtechnologies in Medicine and Biology, Lyon, France, 12–14 October 2000; pp. 156–159. [Google Scholar]
- Sakuma, S.; Kuroda, K.; Tsai, C.-H.D.; Fukui, W.; Arai, F.; Kaneko, M. Red blood cell fatigue evaluation based on the close-encountering point between extensibility and recoverability. Lab Chip 2014, 14, 1135–1141. [Google Scholar] [CrossRef] [PubMed]
- Gu, Q.; Aoyama, T.; Takaki, T.; Ishii, I. Simultaneous vision-based shape and motion analysis of cells fast-flowing in a microchannel. IEEE Trans. Autom. Sci. Eng. 2015, 12, 204–215. [Google Scholar] [CrossRef]
- Gu, Q.; Kawahara, T.; Aoyama, T.; Takaki, T.; Ishii, I.; Takemoto, A.; Sakamoto, N. LOC-based high-throughput cell morphology analysis system. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1346–1356. [Google Scholar] [CrossRef]
- Yang, H.; Gu, Q.; Aoyama, T.; Takaki, T.; Ishii, I. Dynamics-based stereo visual inspection using multidimensional modal analysis. IEEE Sens. J. 2013, 13, 4831–4843. [Google Scholar] [CrossRef]
- Okumura, K.; Yokoyama, K.; Oku, H.; Ishikawa, M. 1 ms auto pan-tilt—Video shooting technology for objects in motion based on Saccade Mirror with background subtraction. Adv. Robot. 2015, 29, 457–468. [Google Scholar] [CrossRef]
- Li, L.; Aoyama, T.; Takaki, T.; Ishii, I.; Yang, H.; Umemoto, C.; Matsuda, H.; Chikaraishi, M.; Fujiwara, A. Vibration distribution measurement using a high-speed multithread active vision. In Proceedings of the IEEE Conference on Advanced Intelligent Mechatronics, Munich, Germany, 3–7 July 2017; pp. 400–405. [Google Scholar]
- Inoue, M.; Gu, Q.; Aoyama, T.; Takaki, T.; Ishii, I. An intermittent frame-by-frame tracking camera for motion-blur-free video shooting. In Proceedings of the 2015 IEEE/SICE International Symposium on System Integration, Nagoya, Japan, 11–13 December 2015; pp. 241–246. [Google Scholar]
- Ueno, T.; Gu, Q.; Aoyama, T.; Takaki, T.; Ishii, I.; Kawahara, T. Motion-blur-free microscopic video shooting based on frame-by-frame intermittent tracking. In Proceedings of the IEEE Conference on Automation Science and Engineering, Gothenburg, Sweden, 24–28 August 2015; pp. 837–842. [Google Scholar]
- Hayakawa, T.; Watanabe, T.; Ishikawa, M. Real-time high-speed motion blur compensation system based on back-and-forth motion control of galvanometer mirror. Opt. Express 2015, 23, 31648–31661. [Google Scholar] [CrossRef] [PubMed]
- Hayakawa, T.; Ishikawa, M. Development of motion-blur-compensated high-speed moving visual inspection vehicle for tunnels. Int. J. Civ. Struct. Eng. Res. 2016, 5, 151–155. [Google Scholar]






© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inoue, M.; Gu, Q.; Jiang, M.; Takaki, T.; Ishii, I.; Tajima, K. Motion-Blur-Free High-Speed Video Shooting Using a Resonant Mirror. Sensors 2017, 17, 2483. https://doi.org/10.3390/s17112483
Inoue M, Gu Q, Jiang M, Takaki T, Ishii I, Tajima K. Motion-Blur-Free High-Speed Video Shooting Using a Resonant Mirror. Sensors. 2017; 17(11):2483. https://doi.org/10.3390/s17112483
Chicago/Turabian StyleInoue, Michiaki, Qingyi Gu, Mingjun Jiang, Takeshi Takaki, Idaku Ishii, and Kenji Tajima. 2017. "Motion-Blur-Free High-Speed Video Shooting Using a Resonant Mirror" Sensors 17, no. 11: 2483. https://doi.org/10.3390/s17112483
APA StyleInoue, M., Gu, Q., Jiang, M., Takaki, T., Ishii, I., & Tajima, K. (2017). Motion-Blur-Free High-Speed Video Shooting Using a Resonant Mirror. Sensors, 17(11), 2483. https://doi.org/10.3390/s17112483




