3-Axis Fully-Integrated Capacitive Tactile Sensor with Flip-Bonded CMOS on LTCC Interposer †
Abstract
:1. Introduction
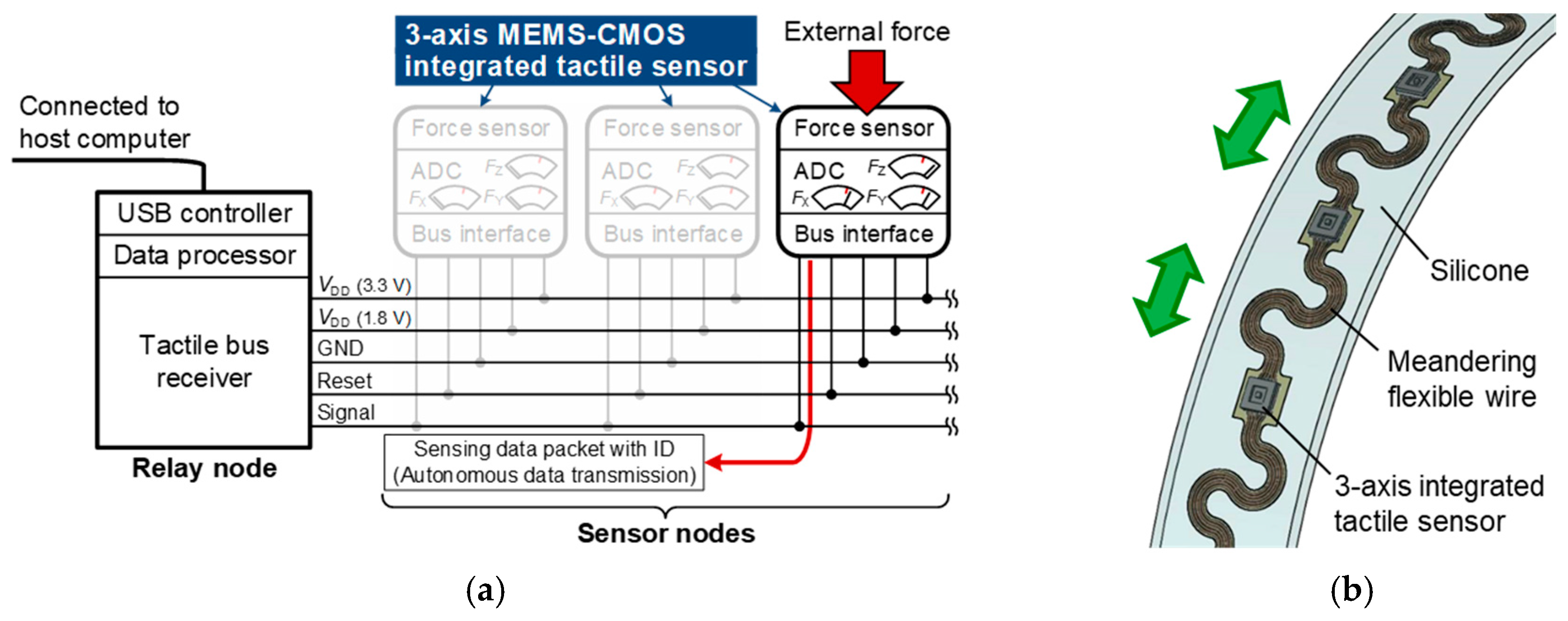
2. Design
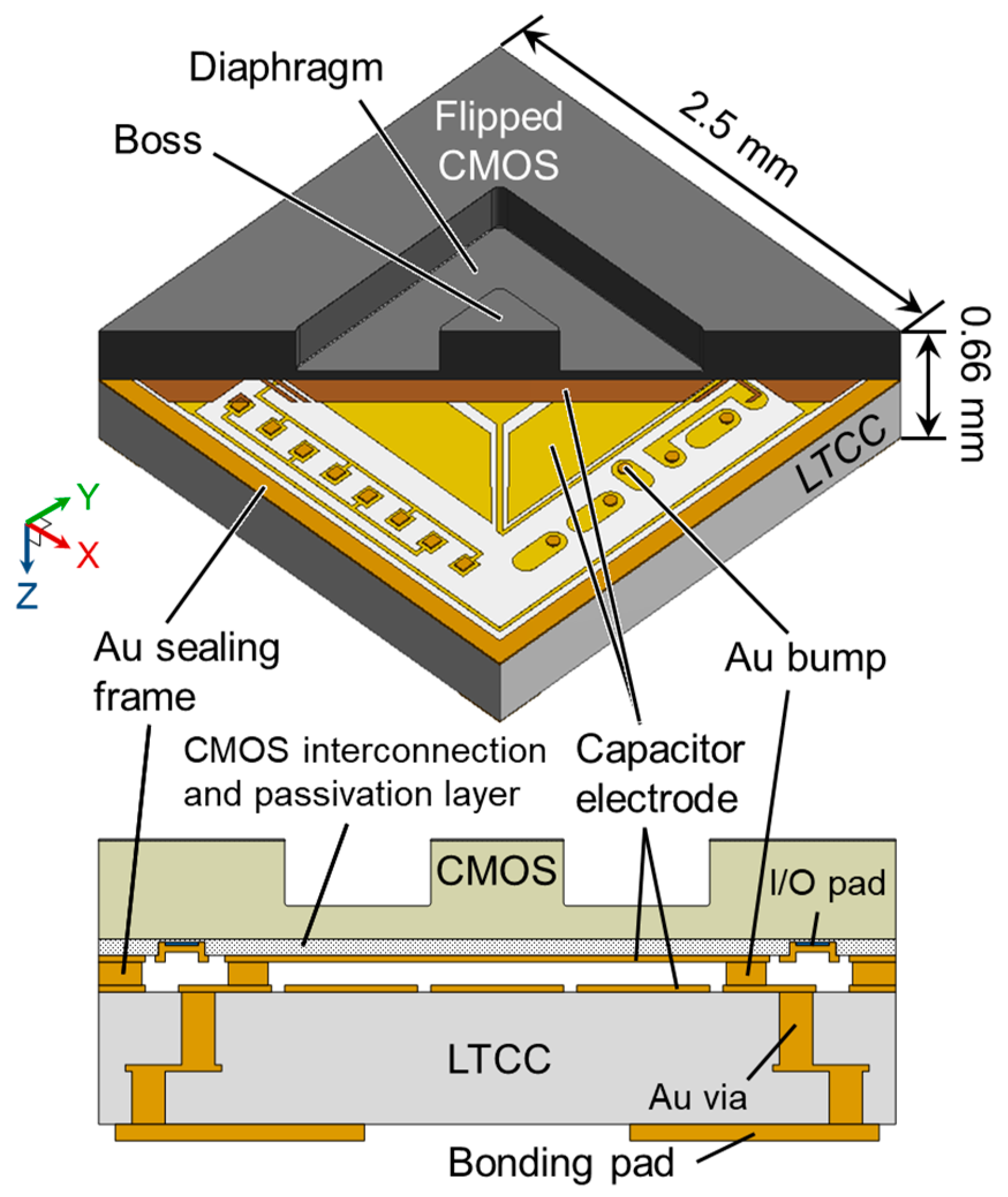
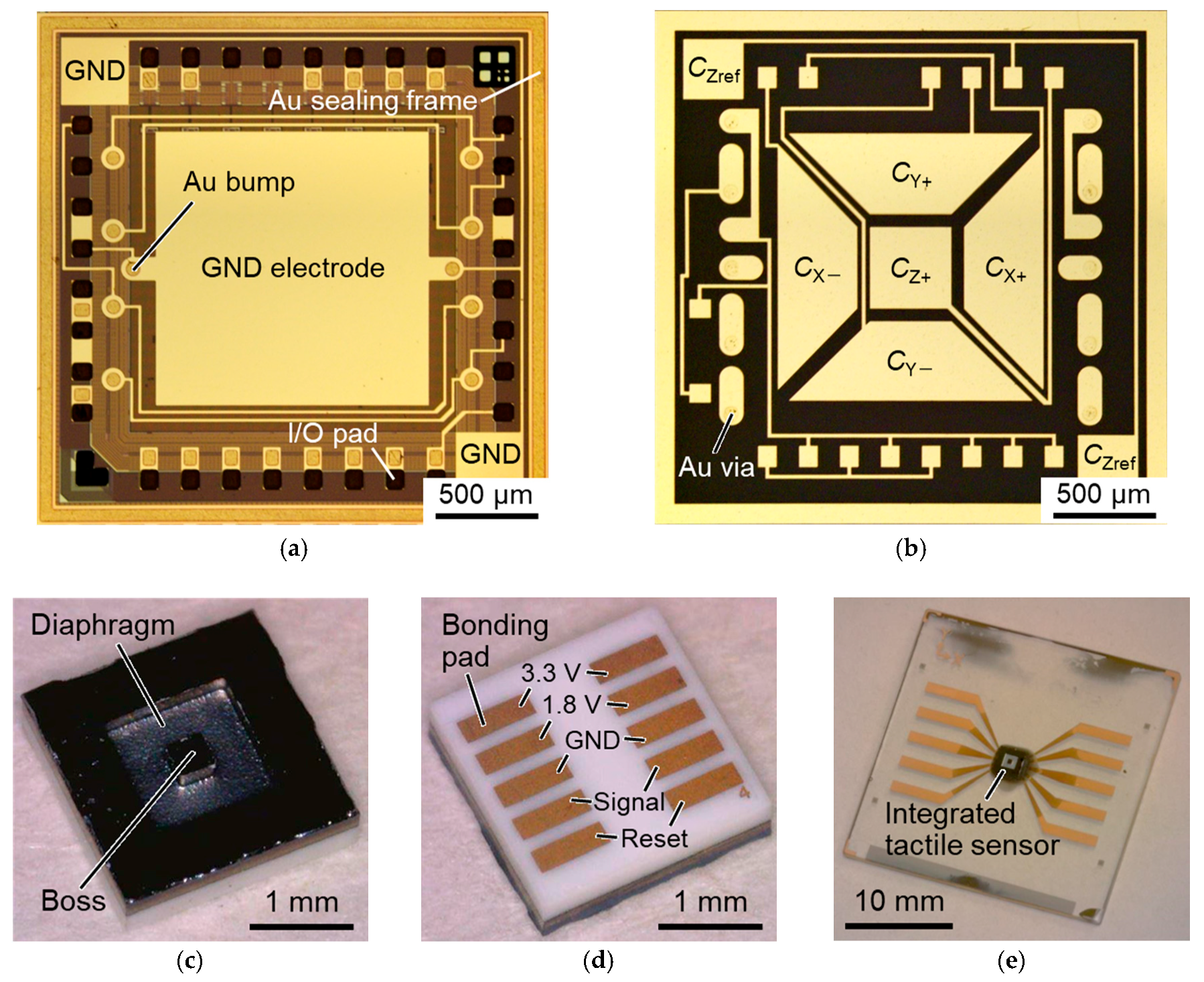
2.1. Sensor Structure
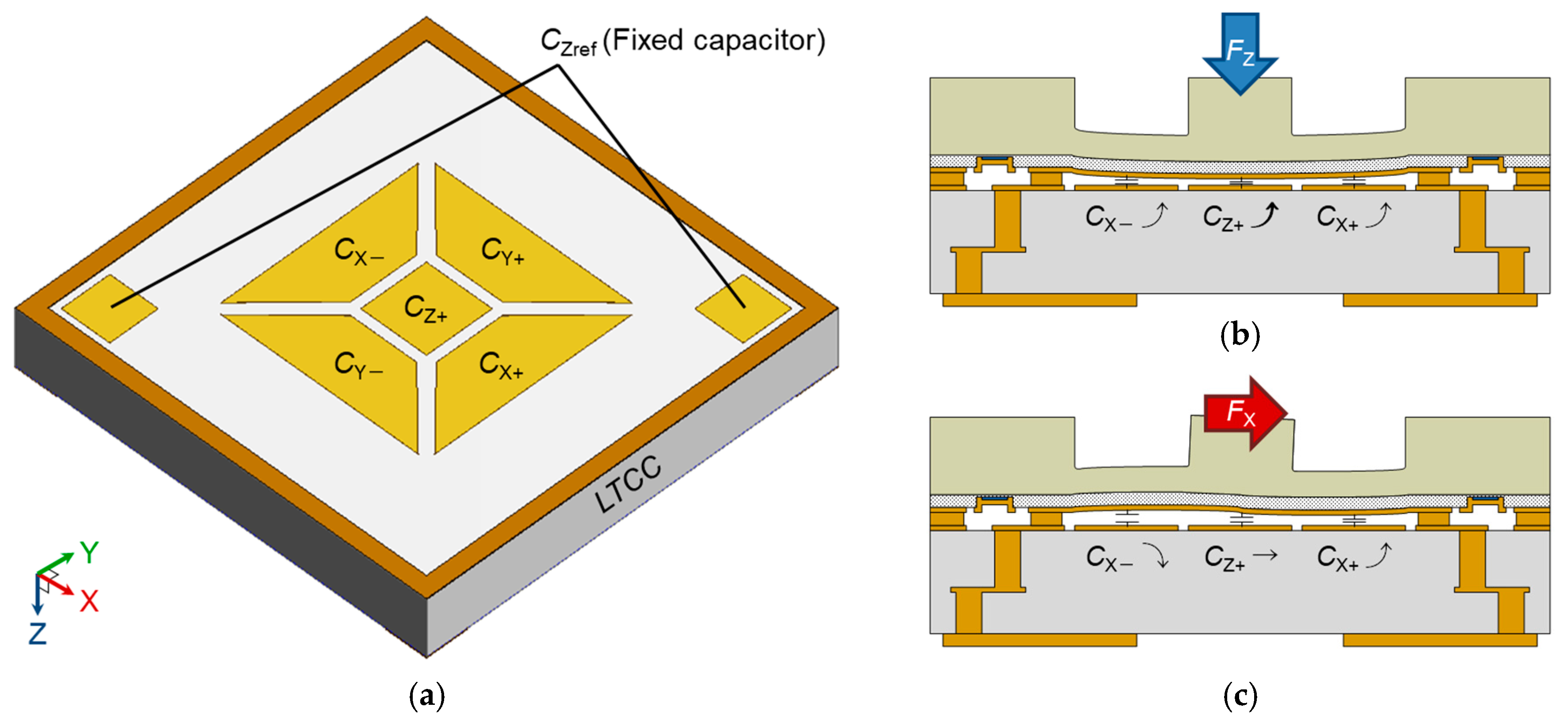
2.2. Working Principle
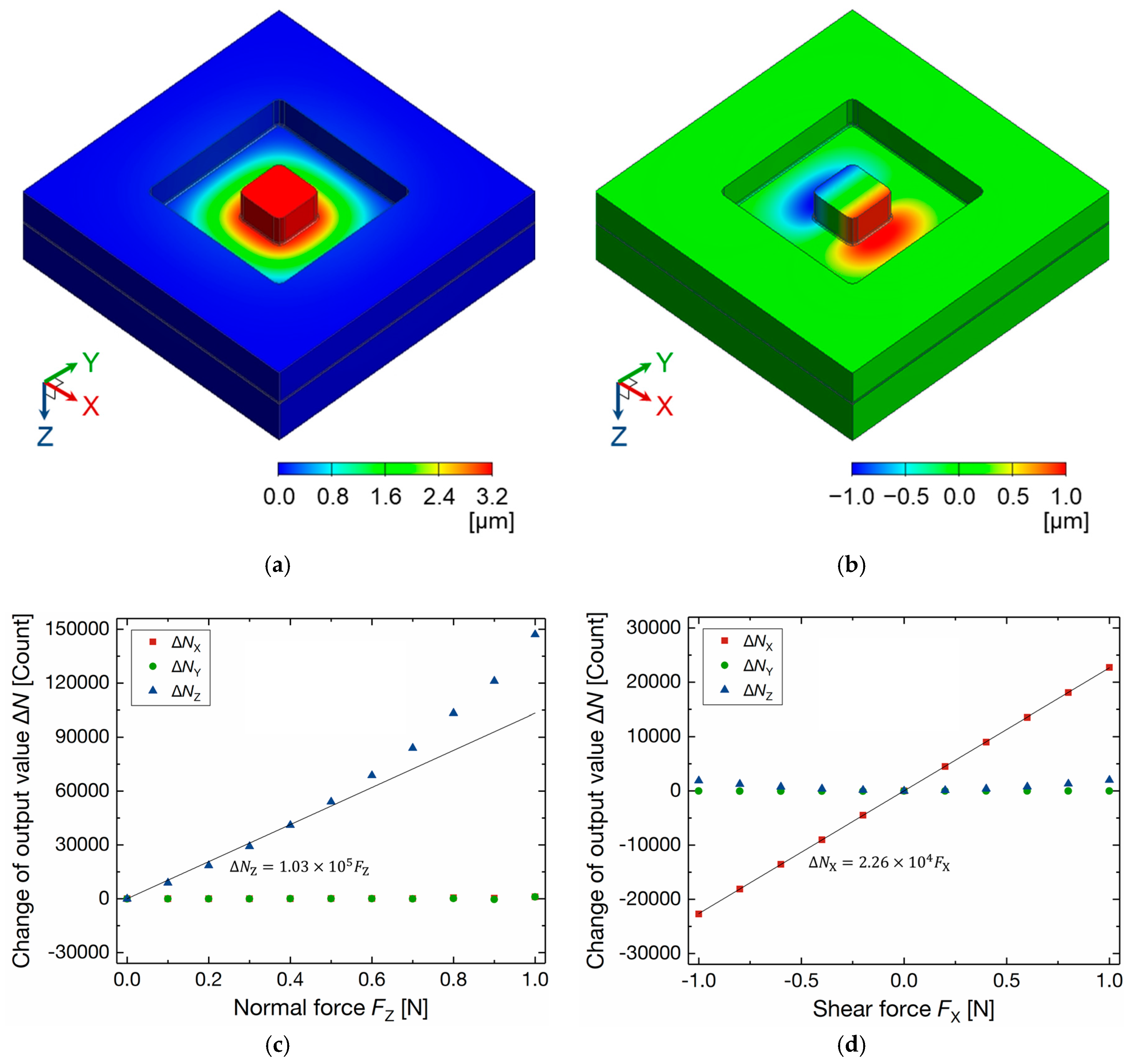
2.3. FEM Simulation
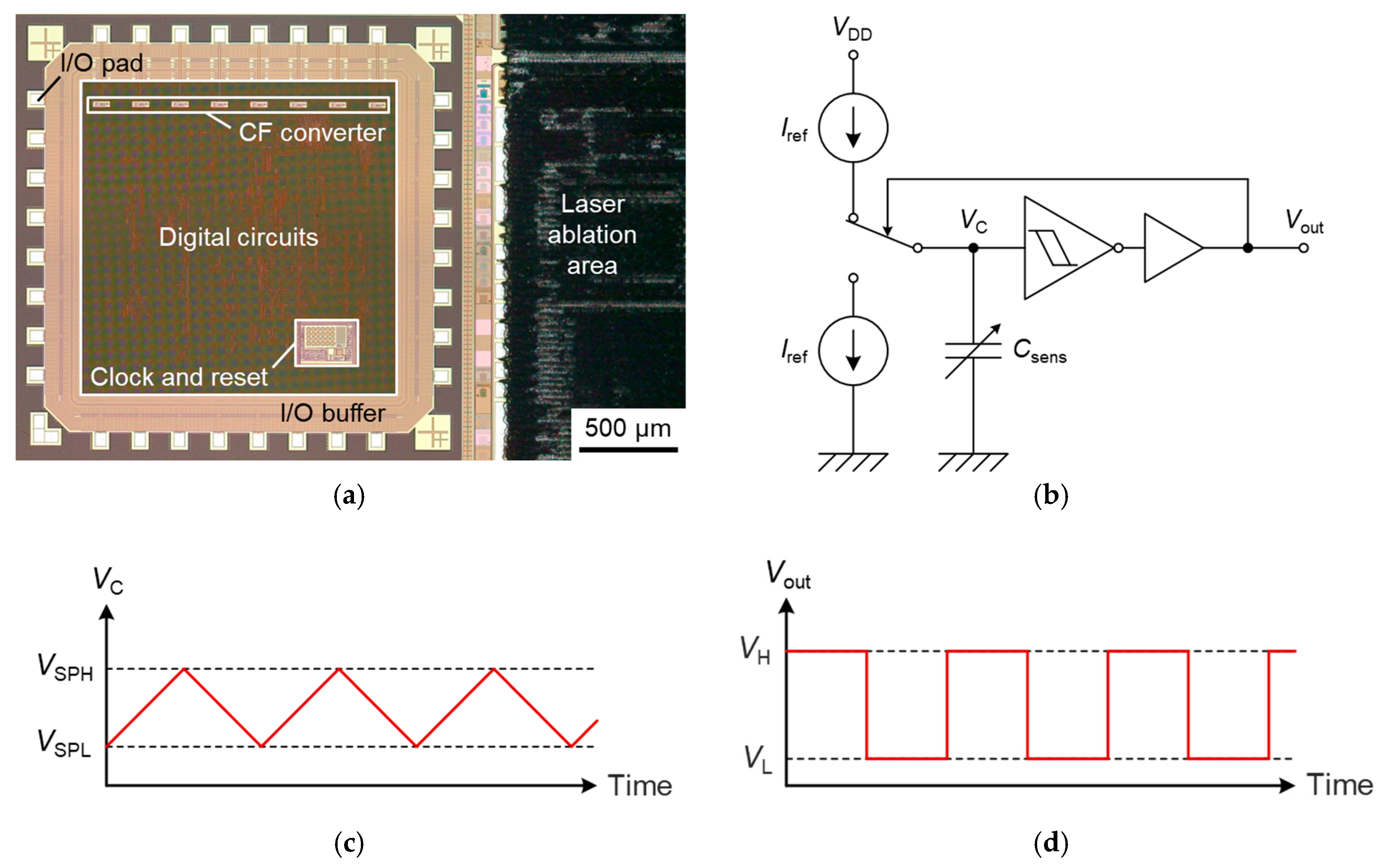
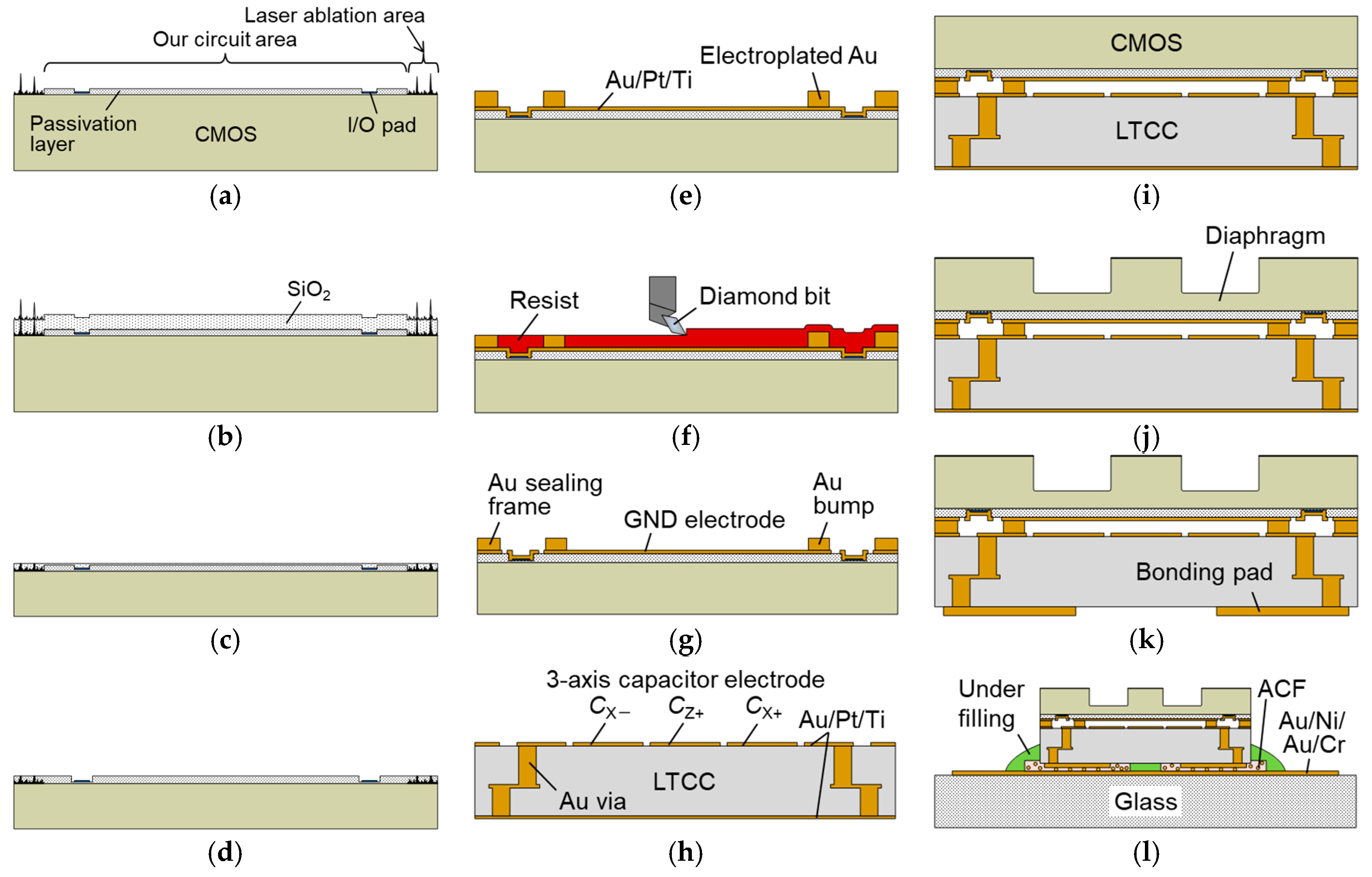
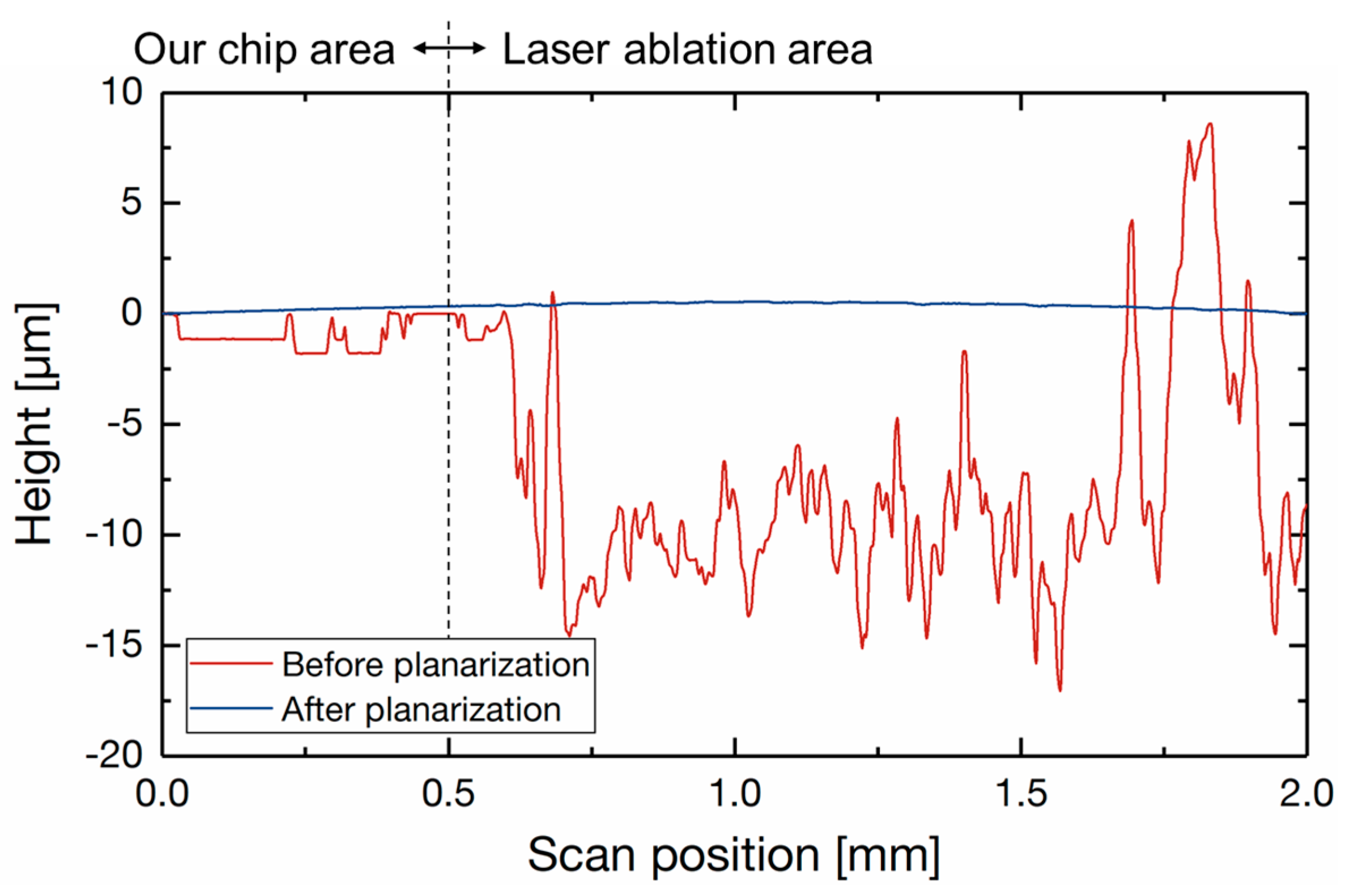
3. Fabrication
4. Experiments and Results
4.1. Experimental Method
4.2. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kappassov, Z.; Corrales, J.-A.; Perdereau, V. Tactile sensing in dexterous robot hands—Review. Robot. Auton. Syst. 2015, 74, 195–220. [Google Scholar] [CrossRef]
- Dahiya, R.S.; Mittendorfer, P.; Valle, M.; Cheng, G.; Lumelsky, V.J. Directions toward effective utilization of tactile skin: A review. IEEE Sens. J. 2013, 13, 4121–4138. [Google Scholar] [CrossRef]
- Kumagai, I.; Kobayashi, K.; Nozawa, S.; Kakiuchi, Y.; Yoshikai, T.; Okada, K.; Inaba, M. Development of a full body multi-axis soft tactile sensor suit for life sized humanoid robot and an algorithm to detect contact states. In Proceedings of the 12th IEEE-RAS International Conference on Humanoid Robots, Osaka, Japan, 29 November–1 December 2012; pp. 526–531. [Google Scholar]
- Schmitz, A.; Maiolino, P.; Maggiali, M.; Natale, L.; Cannata, G.; Metta, G. Methods and technologies for the implementation of large-scale robot tactile sensors. IEEE Trans. Robot. 2011, 27, 389–400. [Google Scholar] [CrossRef]
- Mukai, T.; Onishi, M.; Odashima, T.; Hirano, S.; Luo, Z. Development of the tactile sensor system of a human-interactive robot “RI-MAN”. IEEE Trans. Robot. 2008, 24, 505–512. [Google Scholar] [CrossRef]
- Yousef, H.; Boukallel, M.; Althoefer, K. Tactile sensing for dexterous in-hand manipulation in robotics—A review. Sens. Actuators A Phys. 2011, 167, 171–187. [Google Scholar] [CrossRef]
- Dahiya, R.S.; Metta, G.; Valle, M.; Sandini, G. Tactile sensing—From humans to humanoids. IEEE Trans. Robot. 2010, 26, 1–20. [Google Scholar] [CrossRef]
- Takahashi, H.; Nakai, A.; Thanh-Vinh, N.; Matsumoto, K.; Shimoyama, I. A triaxial tactile sensor without crosstalk using pairs of piezoresistive beams with sidewall doping. Sens. Actuators A Phys. 2013, 199, 43–48. [Google Scholar] [CrossRef]
- Sohgawa, M.; Hirashima, D.; Moriguchi, Y.; Uematsu, T.; Mito, W.; Kanashima, T.; Okuyama, M.; Noma, H. Tactile sensor array using microcantilever with nickel-chromium alloy thin film of low temperature coefficient of resistance and its application to slippage detection. Sens. Actuators A Phys. 2012, 186, 32–37. [Google Scholar] [CrossRef]
- Hwang, E.-S.; Seo, J.-H.; Kim, Y.-J. A polymer-based flexible tactile sensor for both normal and shear load detections and its application for robotics. J. Microelectromech. Syst. 2007, 16, 556–563. [Google Scholar] [CrossRef]
- Lee, H.-K.; Chung, J.; Chang, S.I.; Yoon, E. Normal and shear force measurement using a flexible polymer tactile sensor with embedded multiple capacitors. J. Microelectromech. Syst. 2008, 17, 934–942. [Google Scholar]
- Dahiya, R.S.; Adami, A.; Collini, C.; Lorenzelli, L. POSFET tactile sensing arrays using CMOS technology. Sens. Actuators A Phys. 2013, 202, 226–232. [Google Scholar] [CrossRef]
- Takao, H.; Yawata, M.; Sawada, K.; Ishida, M. A multifunctional integrated silicon tactile imager with arrays of strain and temperature sensors on single crystal silicon diaphragm. Sens. Actuators A Phys. 2010, 160, 69–77. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Sun, C.-M.; Lin, L.-Y.; Tsai, M.-H.; Fang, W. Development of a CMOS-based capacitive tactile sensor with adjustable sensing range and sensitivity using polymer fill-in. J. Microelectromech. Syst. 2011, 20, 119–127. [Google Scholar] [CrossRef]
- Asano, S.; Muroyama, M.; Bartley, T.; Kojima, T.; Nakayama, T.; Yamaguchi, U.; Yamada, H.; Nonomura, Y.; Hata, Y.; Funabashi, H.; et al. Surface-mountable capacitive tactile sensors with flipped CMOS-diaphragm on a flexible and stretchable bus line. Sens. Actuators A Phys. 2016, 240, 167–176. [Google Scholar] [CrossRef]
- Asano, S.; Muroyama, M.; Bartley, T.; Nakayama, T.; Yamaguchi, U.; Yamada, H.; Hata, Y.; Nonomura, Y.; Tanaka, S. 3-axis fully-integrated surface-mountable differential capacitive sensor by CMOS flip-bonding. In Proceedings of the 29th IEEE International Conference on Micro Electro Mechanical Systems (MEMS 2016), Shanghai, China, 24–28 January 2016; pp. 850–853. [Google Scholar]
- Hata, Y.; Suzuki, Y.; Muroyama, M.; Nakayama, T.; Nonomura, Y.; Chand, R.; Hirano, H.; Omura, Y.; Fujiyoshi, M.; Tanaka, S. Fully-integrated, fully-differential 3-axis tactile sensor on platform LSI with TSV-based surface-mountable structure. In Proceedings of the 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; pp. 500–503. [Google Scholar]
- Yokoyama, H.; Sohgawa, M.; Kanashima, T.; Azuma, T.; Okuyama, M.; Noma, H. Fabrication and noise reduction of the miniature tactile sensor using through-silicon-via connection with signal amplifier. Jpn. J. Appl. Phys. 2013, 52, 06GL08. [Google Scholar] [CrossRef]
- Makihata, M.; Tanaka, S.; Muroyama, M.; Matsuzaki, S.; Yamada, H.; Nakayama, T.; Yamaguchi, U.; Mima, K.; Nonomura, Y.; Fujiyoshi, M.; et al. Integration and packaging technology of MEMS-on-CMOS capacitive tactile sensor for robot application using thick BCB isolation layer and backside-grooved electrical connection. Sens. Actuators A Phys. 2012, 188, 103–110. [Google Scholar] [CrossRef]
- Tanaka, S.; Mohri, M.; Ogashiwa, T.; Fukushi, H.; Tanaka, K.; Nakamura, D.; Nishimori, T.; Esashi, M. Electrical interconnection in anodic bonding of silicon wafer to LTCC wafer using highly compliant porous bumps made from submicron gold particles. Sens. Actuators A Phys. 2012, 188, 198–202. [Google Scholar] [CrossRef]
- Chen, K.-S.; Ayon, A.; Spearing, S.M. Controlling and testing the fracture strength of silicon on the mesoscale. J. Am. Ceram. Soc. 2000, 83, 1476–1484. [Google Scholar] [CrossRef]
- Suzuki, Y.; Fukushi, H.; Muroyama, M.; Hata, Y.; Nakayama, T.; Chand, R.; Hirano, H.; Nonomura, Y.; Funabashi, H.; Tanaka, S. 300 μm deep through silicon via in laser-ablated CMOS multi-project wafer for cost-effective development of integrated MEMS. In Proceedings of the 30th IEEE International Conference on Micro Electro Mechanical Systems (MEMS 2017), Las Vegas, NV, USA, 22–26 January 2017; pp. 744–748. [Google Scholar]
- Al Farisi, M.S.; Hirano, H.; Frömel, J.; Tanaka, S. Wafer-level hermetic thermo-compression bonding using electroplated gold sealing frame planarized by fly-cutting. J. Micromech. Microeng. 2017, 27, 015029. [Google Scholar] [CrossRef]
- Kim, S.-C.; Kim, Y.-H. Flip chip bonding with anisotropic conductive film (ACF) and nonconductive adhesive (NCA). Curr. Appl. Phys. 2013, 13, S14–S25. [Google Scholar] [CrossRef]
- Bartley, T.; Tanaka, S.; Nonomura, Y.; Nakayama, T.; Hata, Y.; Muroyama, M. Sensor network serial communication system with high tolerance to timing and topology variations. In Proceedings of the IEEE SENSORS 2015, Busan, Korea, 1–4 November 2015; pp. 362–365. [Google Scholar]
- Bartley, T.; Tanaka, S.; Nonomura, Y.; Nakayama, T.; Muroyama, M. Delay window blind oversampling clock and data recovery algorithm with wide tracking range. In Proceedings of the IEEE International Symposium on Circuits and Systems, Lisbon, Portugal, 24–27 May 2015; pp. 1598–1601. [Google Scholar]
- Yoshiyuki Hata, Y.; Nonomura, Y.; Omura, Y.; Nakayama, T.; Fujiyoshi, M.; Funabashi, H.; Akashi, T.; Muroyama, M.; Tanaka, S. Quad-seesaw-electrode type 3-axis tactile sensor with low nonlinearities and low cross-axis sensitivities. Sens. Actuators A Phys. 2017, in press. [Google Scholar]
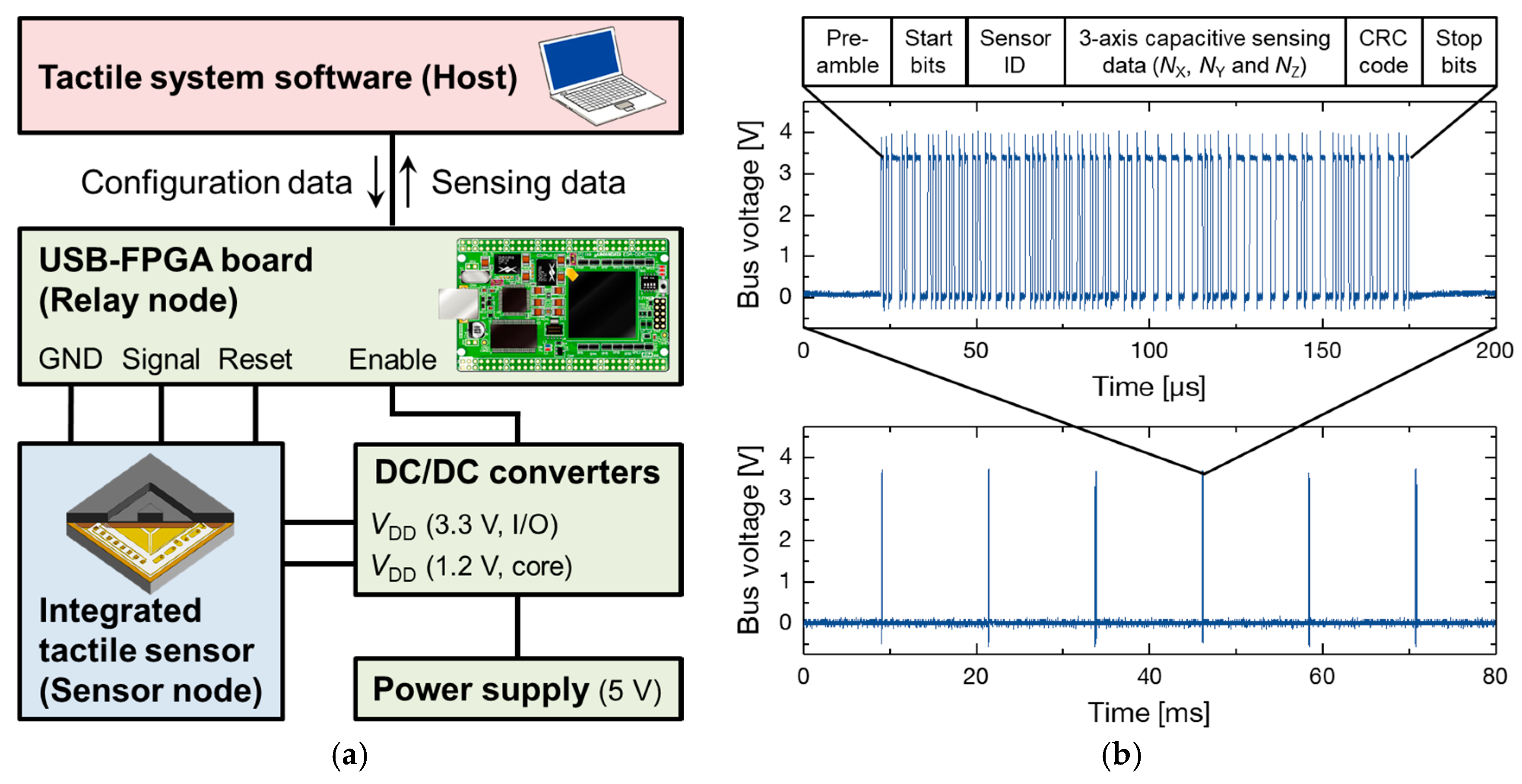
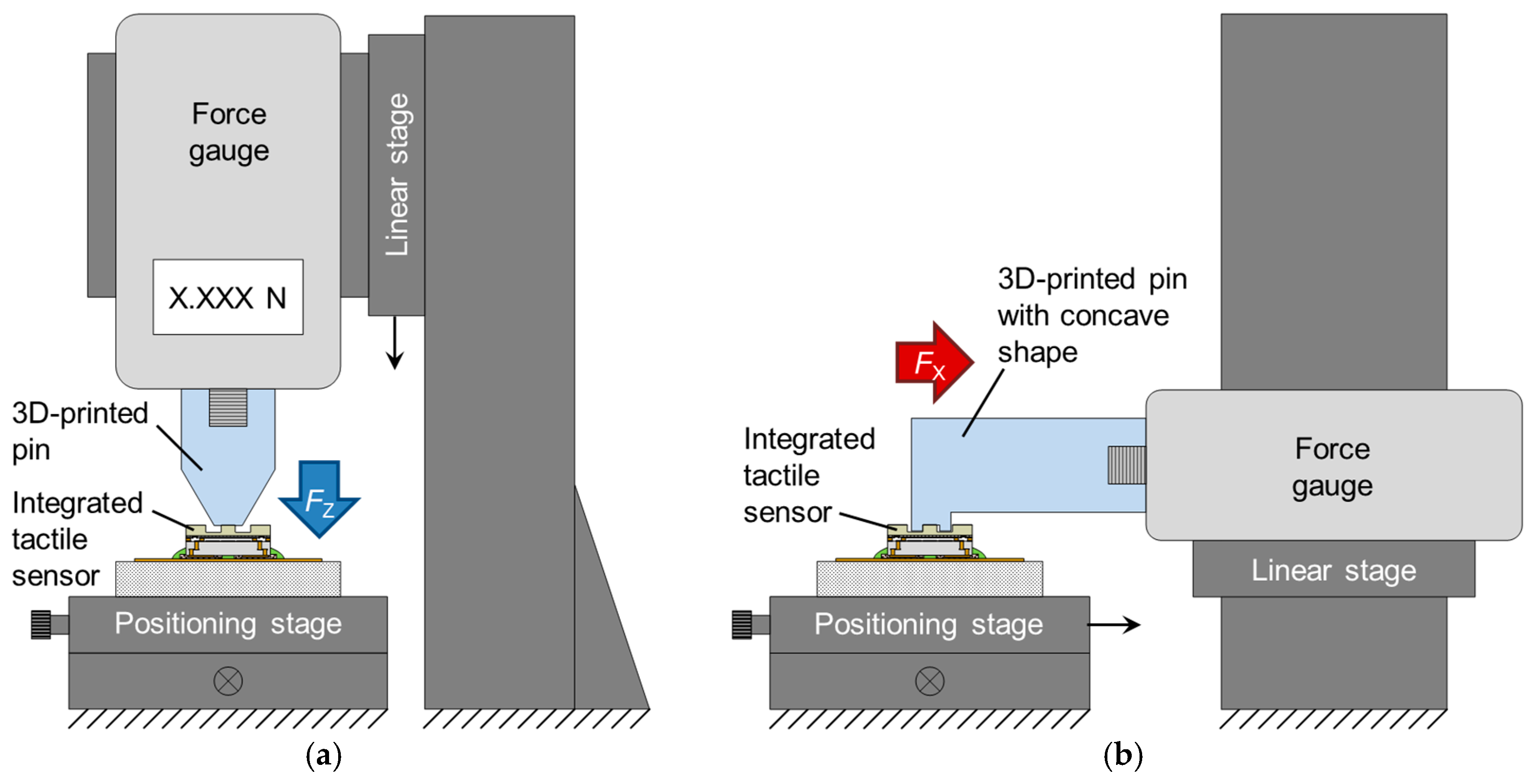
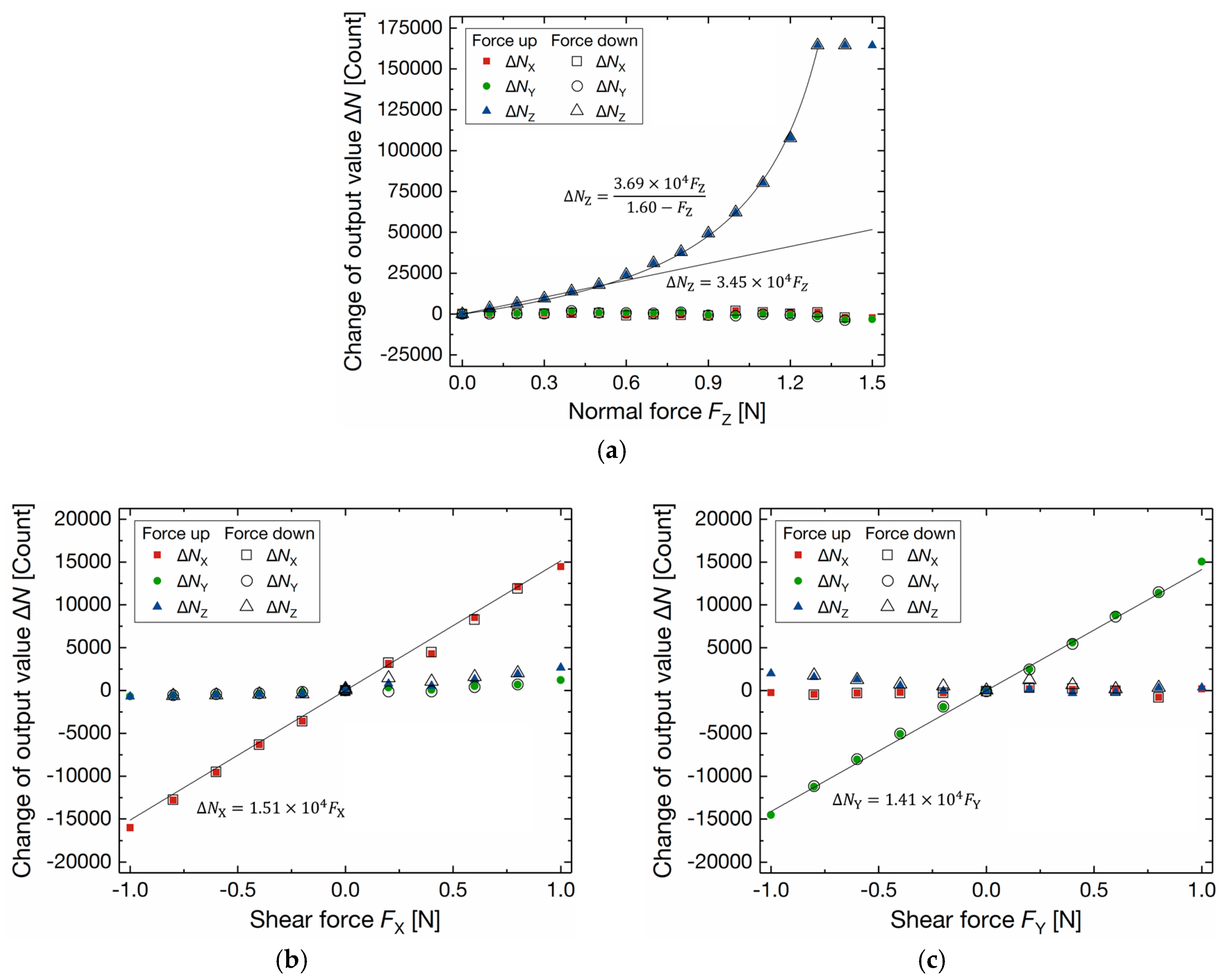
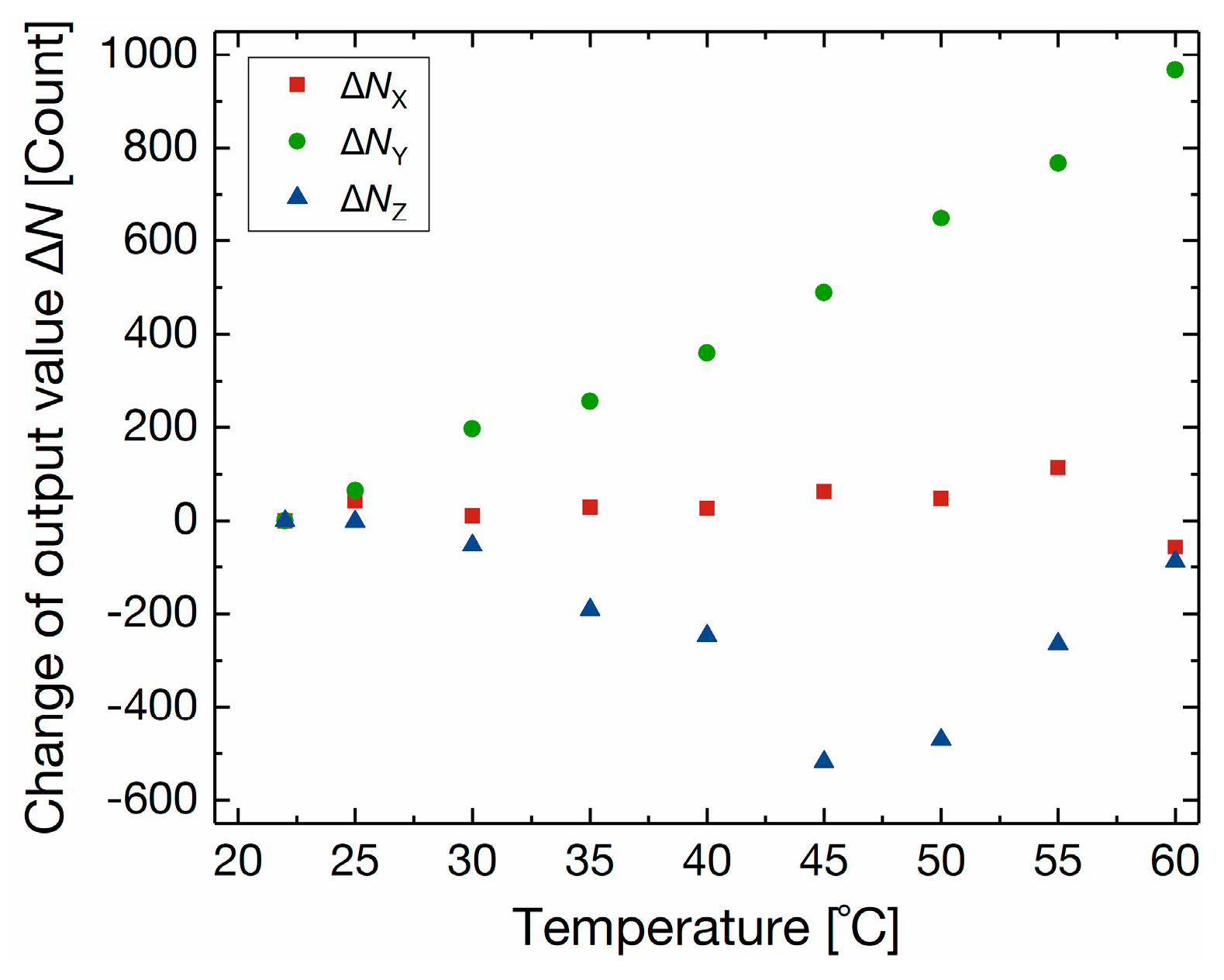
| Force | Sensitivity [Count/mN] | Noise [Count] | Hysteresis [%] | Average Cross-Axis Sensitivity [%] | ||
|---|---|---|---|---|---|---|
| X-Axis | Y-Axis | Z-Axis | ||||
| FX (−1 to 1 N) | 15.1 | 12.4 | ≤ 1.7 | - | 5.5 | 9.0 |
| FY (−1 to 1 N) | 14.1 | 7.6 | ≤ 1.1 | 5.2 | - | 7.2 |
| FZ (0 to 1.3 N 1) | ≥ 34.5 | 3.5 | ≤ 0.3 | 8.2 | 10.4 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asano, S.; Muroyama, M.; Nakayama, T.; Hata, Y.; Nonomura, Y.; Tanaka, S. 3-Axis Fully-Integrated Capacitive Tactile Sensor with Flip-Bonded CMOS on LTCC Interposer. Sensors 2017, 17, 2451. https://doi.org/10.3390/s17112451
Asano S, Muroyama M, Nakayama T, Hata Y, Nonomura Y, Tanaka S. 3-Axis Fully-Integrated Capacitive Tactile Sensor with Flip-Bonded CMOS on LTCC Interposer. Sensors. 2017; 17(11):2451. https://doi.org/10.3390/s17112451
Chicago/Turabian StyleAsano, Sho, Masanori Muroyama, Takahiro Nakayama, Yoshiyuki Hata, Yutaka Nonomura, and Shuji Tanaka. 2017. "3-Axis Fully-Integrated Capacitive Tactile Sensor with Flip-Bonded CMOS on LTCC Interposer" Sensors 17, no. 11: 2451. https://doi.org/10.3390/s17112451
APA StyleAsano, S., Muroyama, M., Nakayama, T., Hata, Y., Nonomura, Y., & Tanaka, S. (2017). 3-Axis Fully-Integrated Capacitive Tactile Sensor with Flip-Bonded CMOS on LTCC Interposer. Sensors, 17(11), 2451. https://doi.org/10.3390/s17112451





