Robust Stereo Visual Odometry Using Improved RANSAC-Based Methods for Mobile Robot Localization
Abstract
:1. Introduction
2. Related Work
- Detect features in each image.
- Match them in two consecutive frames and remove the wrong matches.
- Estimate the ego-motion of the cameras.
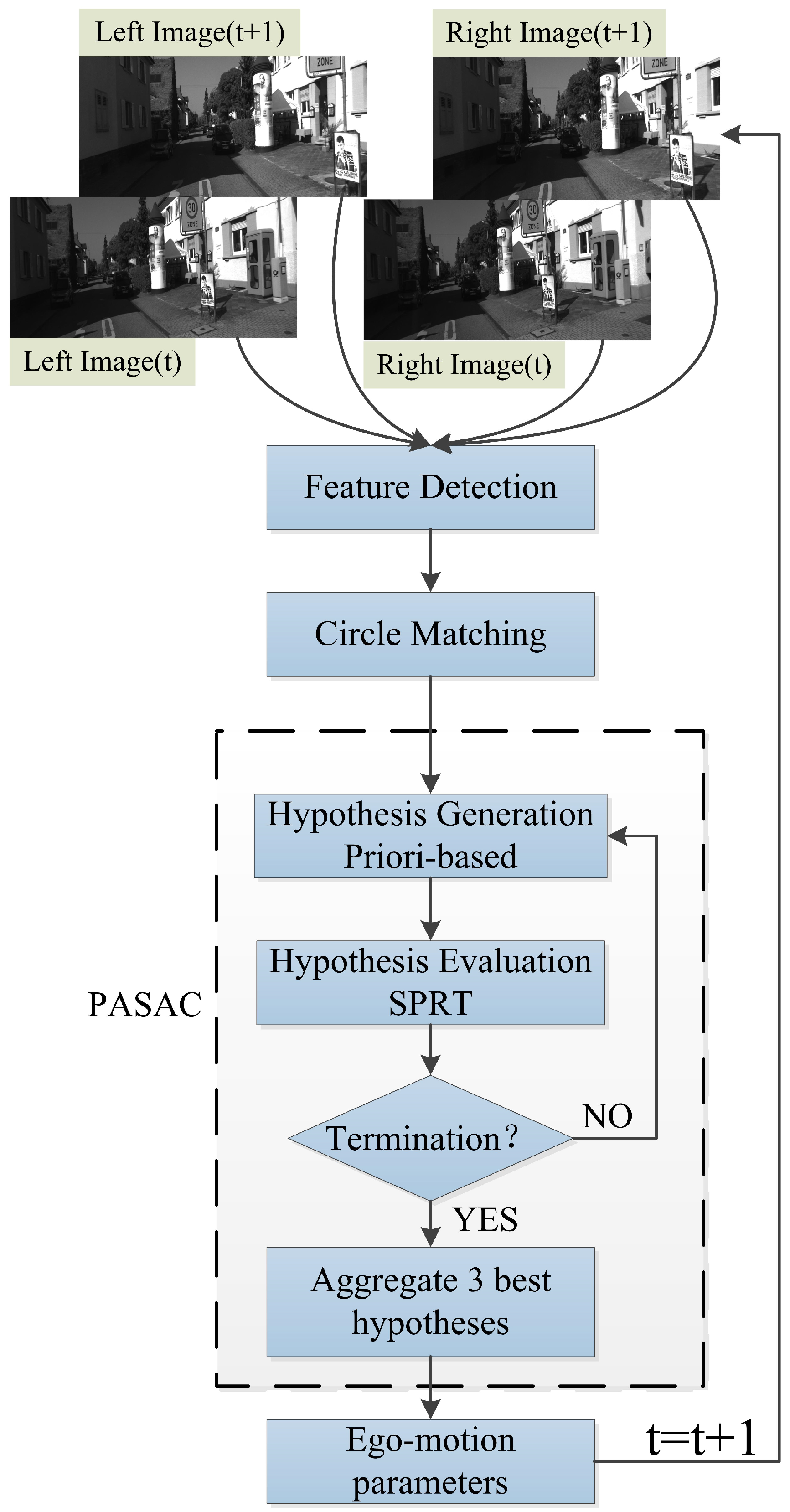
3. Proposed Method
3.1. Robust Feature Detection
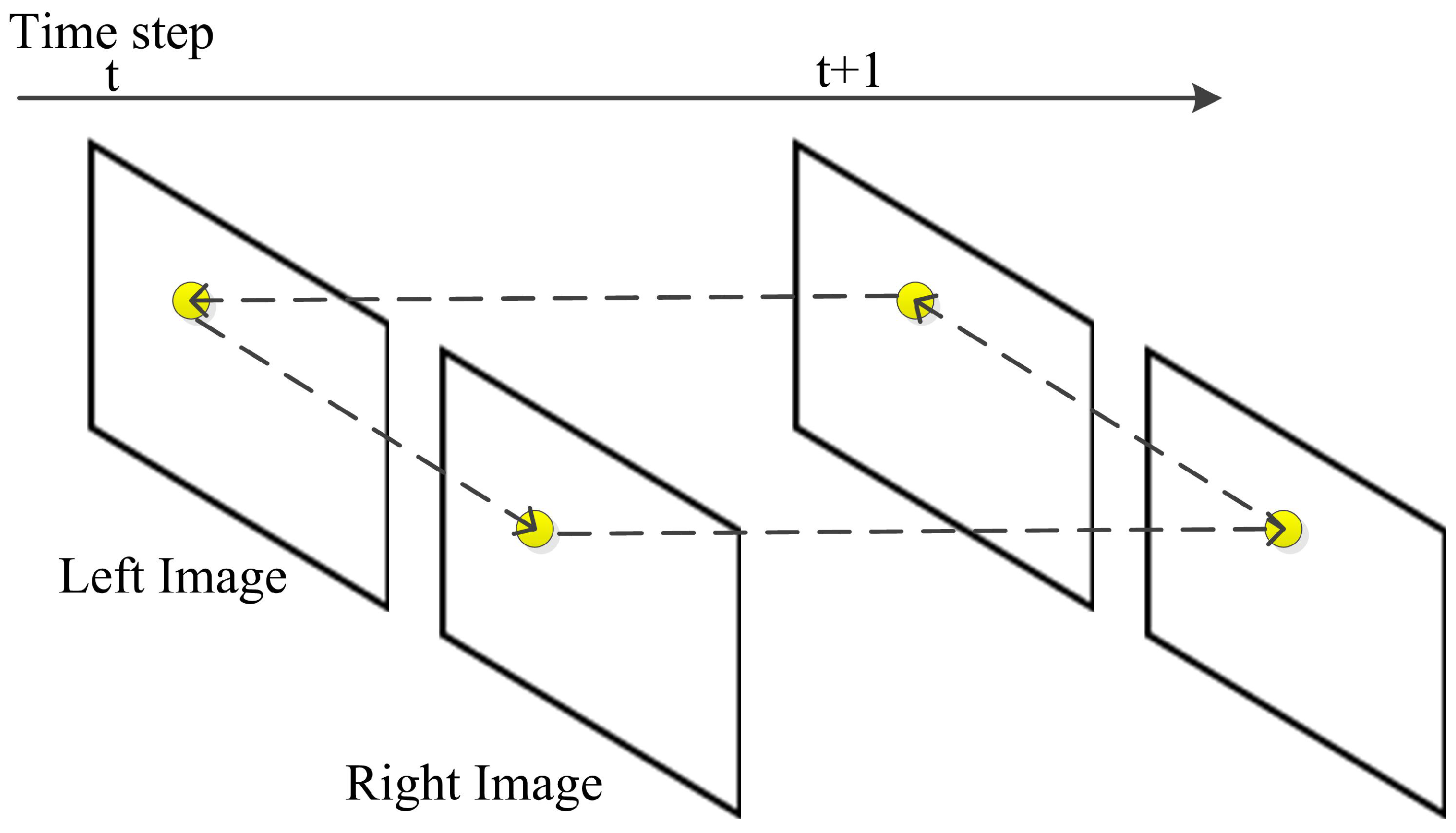
3.2. Feature Circle Matching
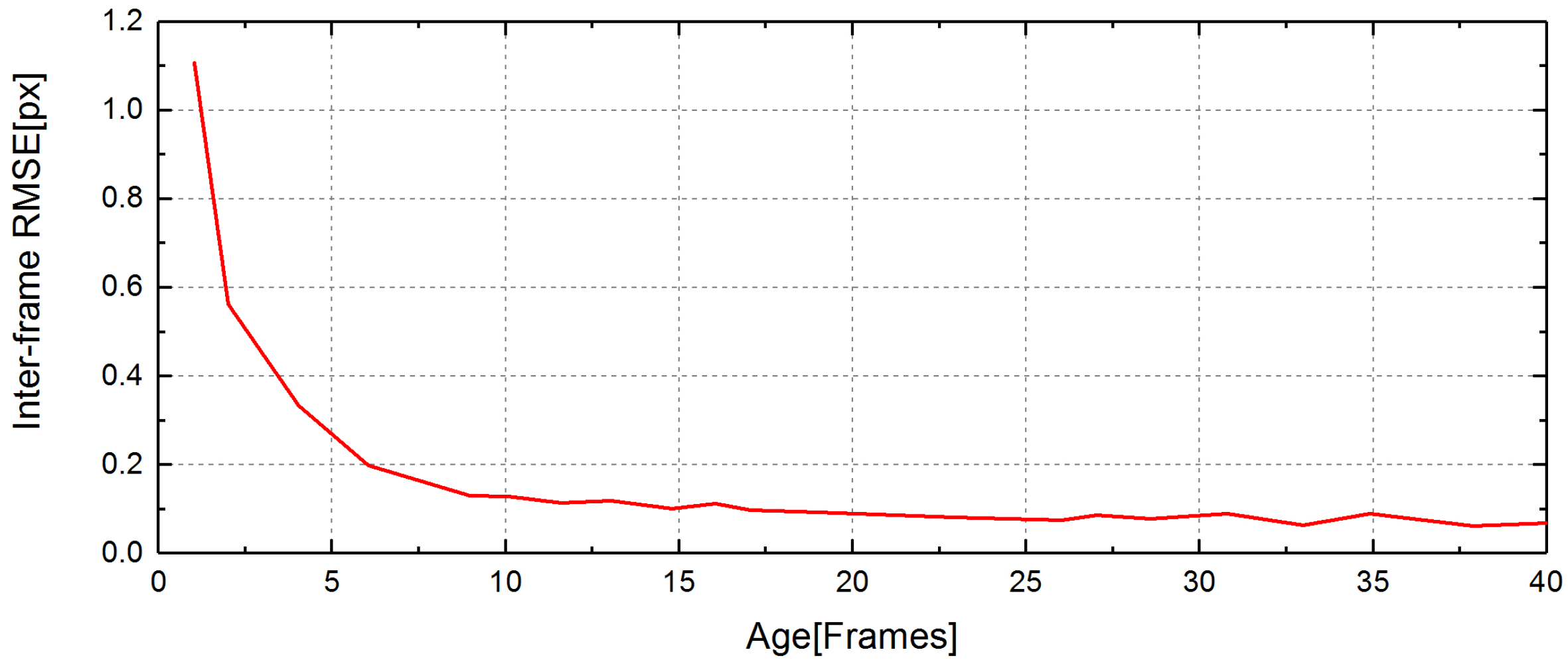
3.3. Feature Tracking
3.4. Robust Motion Estimation
3.4.1. Modeling
3.4.2. Hypothesis Generation
3.4.3. Hypothesis Evaluation
| Algorithm 1: The adaptive SPRT |
 |
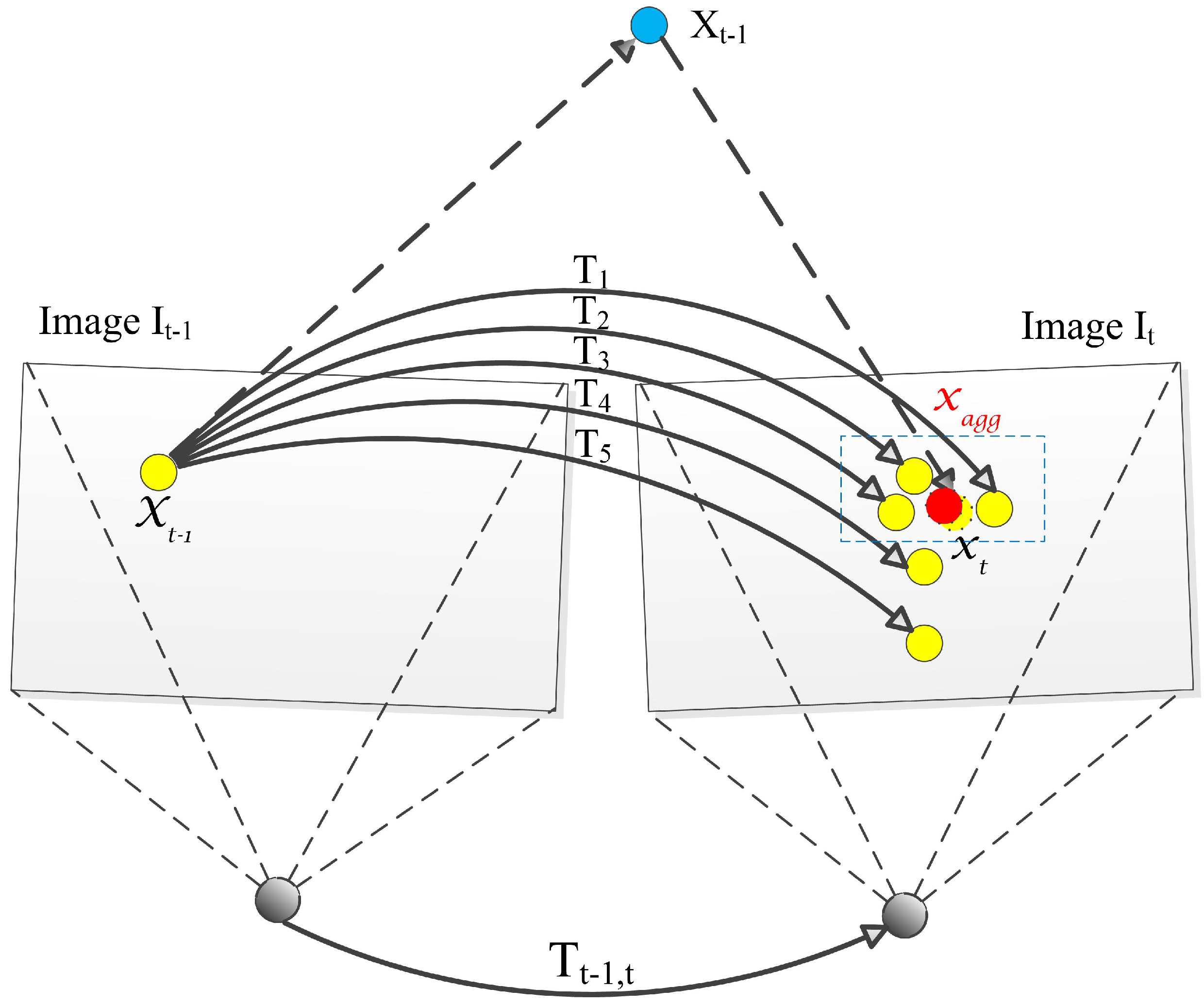
3.4.4. Hypothesis Aggregation
| Algorithm 2: Robust motion estimation PASAC |
 |
4. Results
4.1. Datasets
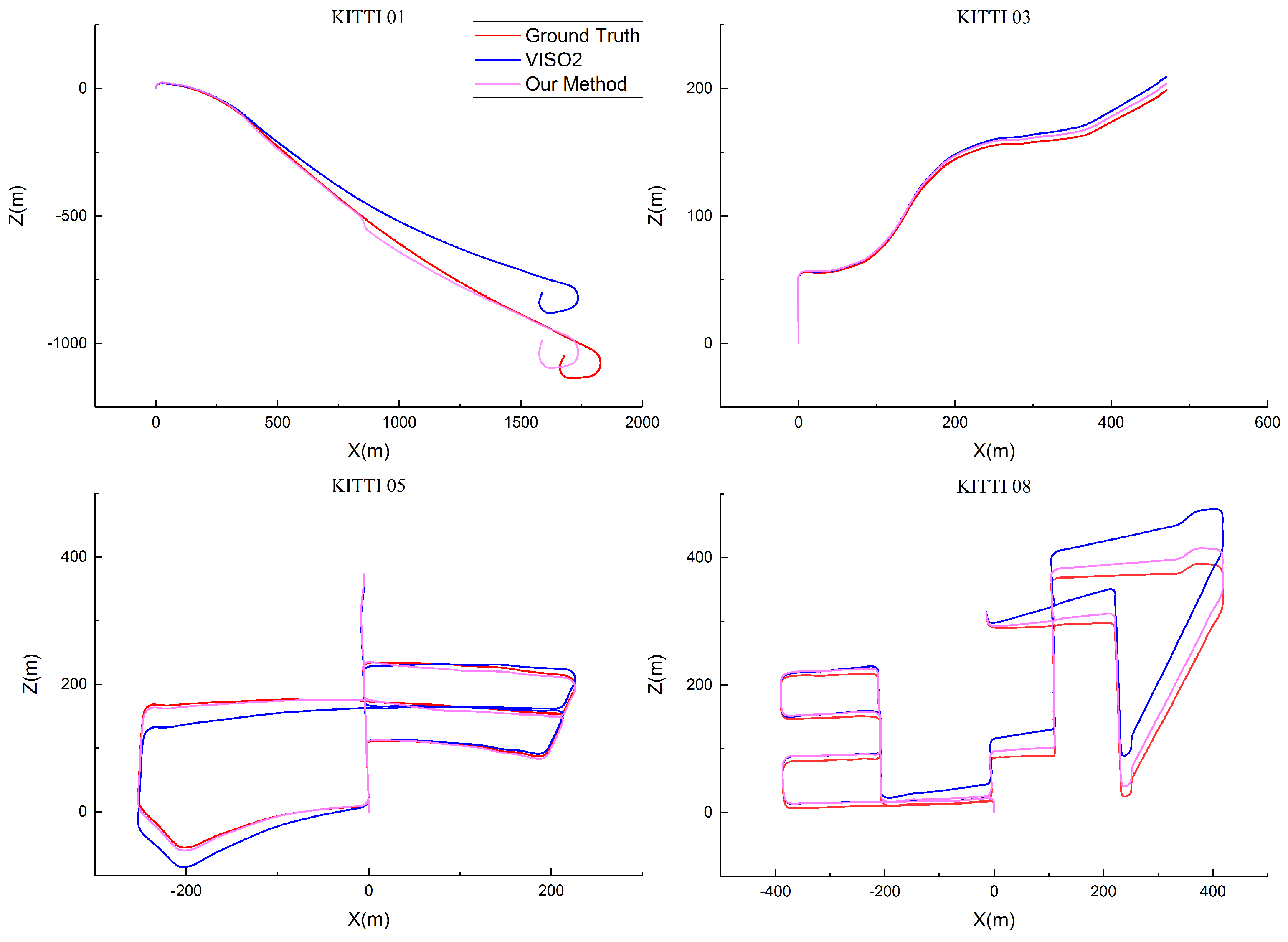
4.2. Evaluation on the KITTI Dataset
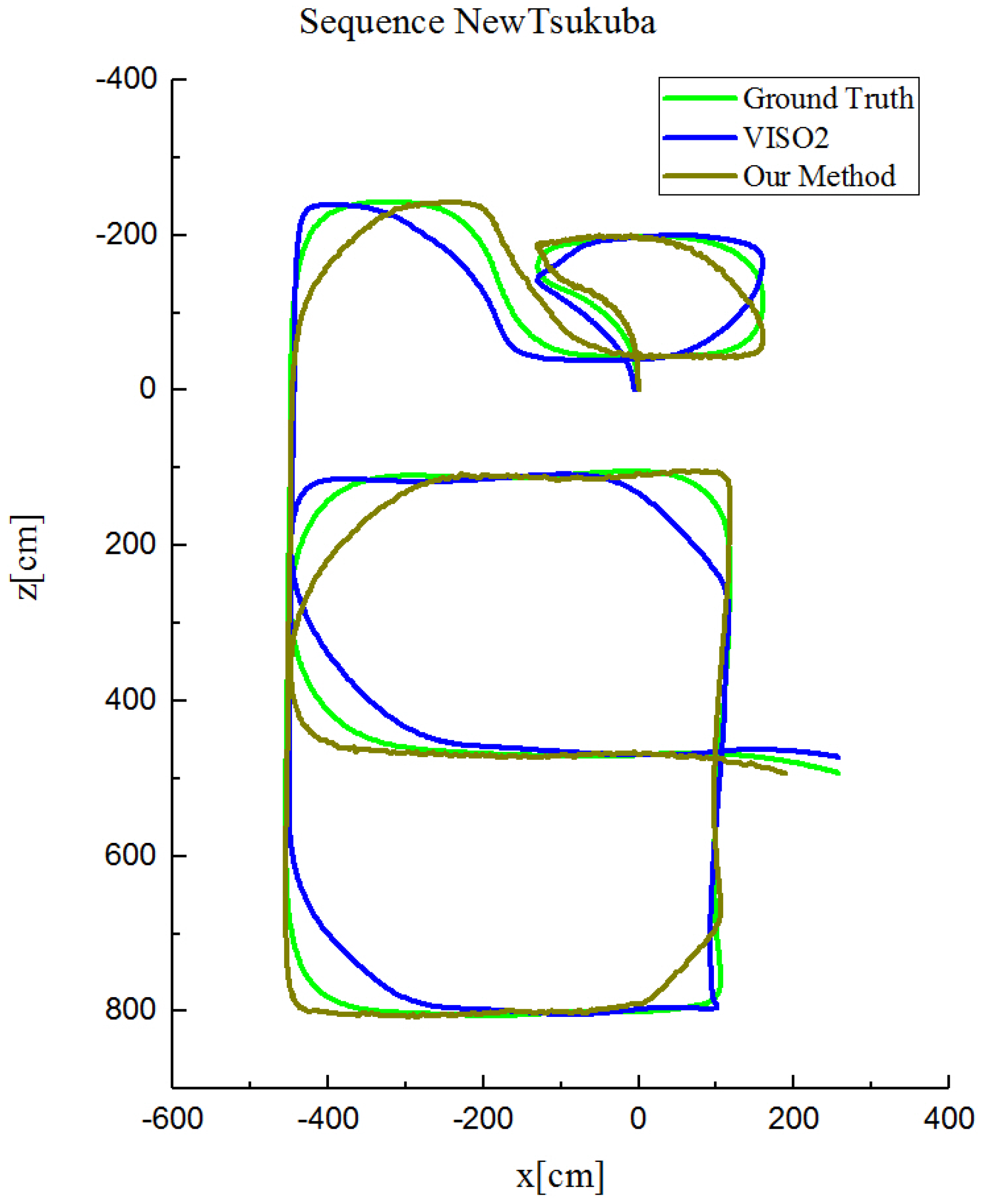
4.3. Evaluation on the New Tsukuba Dataset
4.4. Running Time
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| VO | Visual Odometry |
| VSLAM | Visual Simultaneous Localization and Mapping |
| RANSAC | Random Sample Consensus |
| SPRT | Sequential Probability Ratio Test |
| KLT | Kanade–Lucas–Tomasi Feature Tracker |
| SAD | Sum of Absolute Differences |
| LM | Levenberg–Marquardt |
References
- Nistér, D.; Naroditsky, O.; Bergen, J. Visual odometry. In Proceedings of the Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; pp. 652–659. [Google Scholar]
- Cvišić, I.; Petrović, I. Stereo odometry based on careful feature selection and tracking. In Proceedings of the European Conference on Mobile Robots, Lincoln, UK, 2–4 September 2015; pp. 1–6. [Google Scholar]
- Persson, M.; Piccini, T.; Felsberg, M.; Mester, R. Robust stereo visual odometry from monocular techniques. In Proceedings of the IEEE Intelligent Vehicles Symposium, Seoul, Korea, 28 June–1 July 2015; pp. 686–691. [Google Scholar]
- Cain, C.; Leonessa, A. Validation of underwater sensor package using feature based slam. Sensors 2016, 16, 380. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.K.; Yoon, K.J. Three-Point Direct Stereo Visual Odometry. In Proceedings of the British Machine Vision Conference, York, UK, 19 – 22 September 2016. [Google Scholar] [CrossRef]
- Newcombe, R.A.; Lovegrove, S.J.; Davison, A.J. DTAM: Dense tracking and mapping in real-time. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2320–2327. [Google Scholar]
- Engel, J.; Stückler, J.; Cremers, D. Large-scale direct SLAM with stereo cameras. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and System, Hamburg, Germany, 28 September–2 October 2015; pp. 1935–1942. [Google Scholar]
- Moravec, H.P. Obstacle Avoidance and Navigation in the Real World by a Seeing Robot Rover; Technical report; Robotics Institute, Carnegie Mellon University and doctoral dissertation, Stanford University, 1980. [Google Scholar]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; Volume 15, pp. 10–5244. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 430–443. [Google Scholar]
- Shi, J. Good features to track. In Proceedings of the IEEE Computer Thus, ciety Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994; pp. 593–600. [Google Scholar]
- Schmidt, A.; Kraft, M.; Kasiński, A. An evaluation of image feature detectors and descriptors for robot navigation. In Proceedings of the International Conference on Computer Vision and Graphics; Warsaw, Poland, 20–22 September 2010; pp. 251–259. [Google Scholar]
- Govender, N. Evaluation of feature detection algorithms for structure from motion. In Proceedings of the 3rd Robotics and Mechatronics Symposium (ROBMECH 2009), Pretoria, Thus, South Africa, 8–10 November 2009. [Google Scholar]
- Othón, E.J.J.; Michel, D.; Gordillo, J.L. Visual EKF-SLAM from Heterogeneous Landmarks. Sensors 2016, 16, 489. [Google Scholar]
- Kottas, D.G.; Roumeliotis, S.I. Efficient and consistent vision-aided inertial navigation using line observations. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 1540–1547. [Google Scholar]
- Badino, H.; Yamamoto, A.; Kanade, T. Visual odometry by multi-frame feature integration. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Sydney, Australia, 1–8 December 2013; pp. 222–229. [Google Scholar]
- Pollefeys, M.; Nistér, D.; Frahm, J.M.; Akbarzadeh, A.; Mordohai, P.; Clipp, B.; Engels, C.; Gallup, D.; Kim, S.J.; Merrell, P.; et al. Detailed real-time urban 3d reconstruction from video. Int. J. Comput. Vis. 2008, 78, 143–167. [Google Scholar] [CrossRef]
- Alcantarilla, P.F.; Yebes, J.J.; Almazán, J.; Bergasa, L.M. On combining visual SLAM and dense scene flow to increase the robustness of localization and mapping in dynamic environments. In Proceedings of the IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 1290–1297. [Google Scholar]
- Song, Y.; Nuske, S.; Scherer, S. A Multi-Sensor Fusion MAV State Estimation from Long-Range Stereo, IMU, GPS and Barometric Sensors. Sensors 2016, 17, 11. [Google Scholar]
- Kitt, B.; Geiger, A.; Lategahn, H. Visual odometry based on stereo image sequences with ransac-based outlier rejection scheme. In Proceedings of the IEEE Intelligent Vehicles Symposium, San Diego, CA, USA, 21–24 June 2010; pp. 486–492. [Google Scholar]
- Nistér, D. Preemptive RANSAC for live structure and motion estimation. Mach. Vis. Appl. 2005, 16, 321–329. [Google Scholar] [CrossRef]
- Tan, W.; Liu, H.; Dong, Z.; Zhang, G.; Bao, H. Robust monocular SLAM in dynamic environments. In Proceedings of the IEEE International Symposium on Mixed and Augmented Reality, Adelaide, Australia, 10–12 September 2013; pp. 209–218. [Google Scholar]
- Geiger, A.; Ziegler, J.; Stiller, C. Stereoscan: Dense 3d reconstruction in real-time. In Proceedings of the IEEE Intelligent Vehicles Symposium, Baden-Baden, Germany, 5–9 June 2011; pp. 963–968. [Google Scholar]
- Neubeck, A.; Van Gool, L. Efficient non-maximum suppression. In Proceedings of the International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; Volume 3, pp. 850–855. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Chum, O.; Matas, J. Matching with PROSAC-progressive sample consensus. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–26 June 2005; Volume 1, pp. 220–226. [Google Scholar]
- Chum, O.; Matas, J. Optimal randomized RANSAC. IEEE Trans. Pattern. Anal. Mach. Intell. 2008, 30, 1472–1482. [Google Scholar] [CrossRef] [PubMed]
- Rais, M.; Facciolo, G.; Meinhardt-Llopis, E.; Morel, J.M.; Buades, A.; Coll, B. Accurate motion estimation through random sample aggregated consensus. arXiv, 2017; arXiv:1701.05268. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Martull, S.; Peris, M.; Fukui, K. Realistic CG Stereo Image Dataset with Ground Truth Disparity Maps. In Proceedings of the International Conference on Pattern Recognition, Tsukuba Science City, Japan, 11–15 November 2012; pp. 117–118. [Google Scholar]
- Kreso, I.; Segvic, S. Improving the egomotion estimation by correcting the calibration bias. In Proceedings of the International Conference on Computer Vision Theory and Applications, Vilamoura, Algarve, 11–14 August 2015; pp. 347–356. [Google Scholar]





| (a) | (b) |
| (c) | (d) |
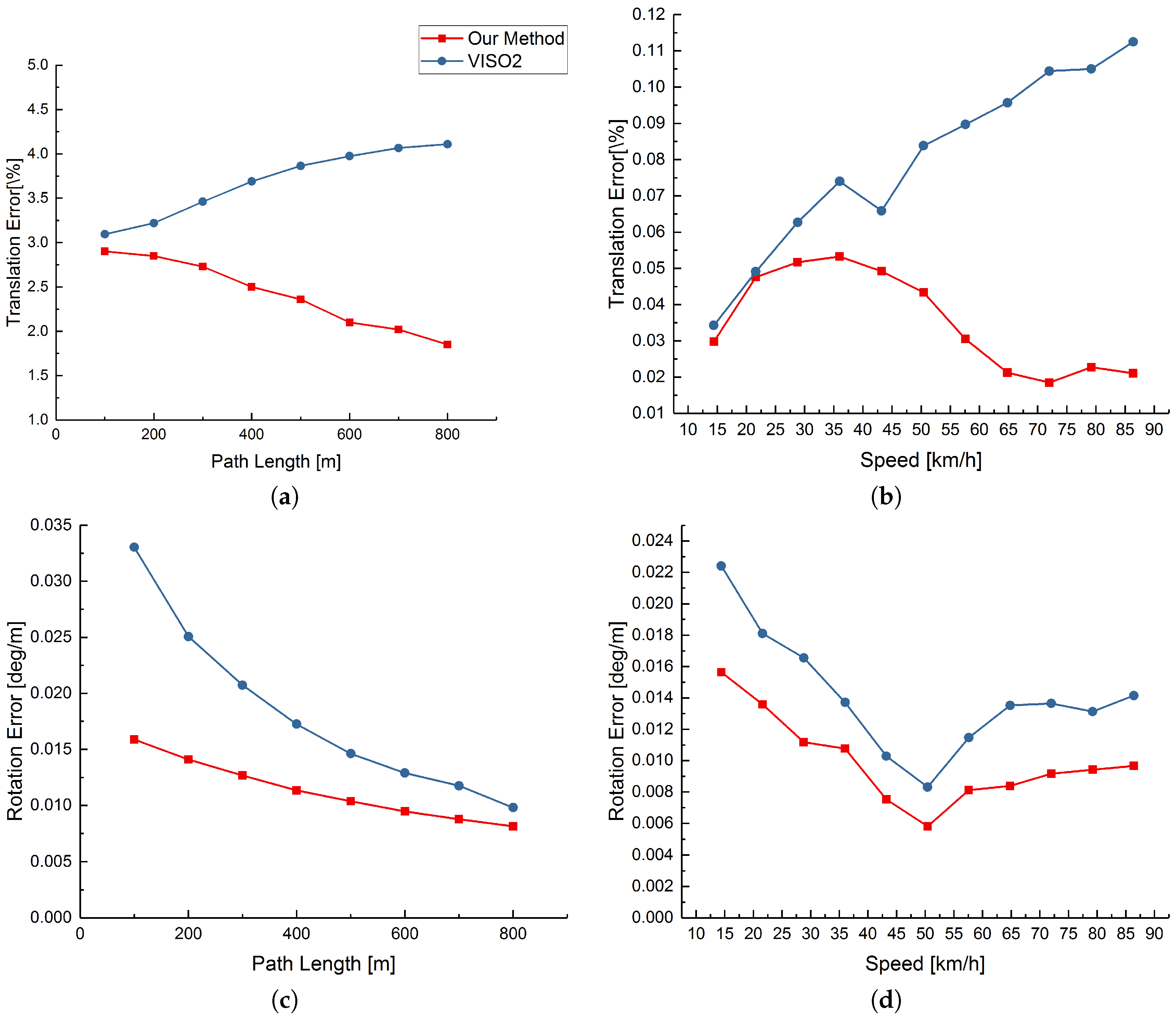
| (a) | (b) |
| (c) | (d) |
| KITTI Dataset | I | KV | T (ms) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RANSAC | PROSAC | Our Method | RANSAC | PROSAC | Our Method | RANSAC | PROSAC | Our Method | |
| 00 | 75.6 | 85.2 | 89.8 | 41520 | 1520 | 845 | 72.5 | 15.3 | 8.5 |
| 01 | 76.4 | 88.6 | 92.2 | 34508 | 1400 | 950 | 70.3 | 17.5 | 10.5 |
| 02 | 80.4 | 86.5 | 95.5 | 25004 | 750 | 788 | 65.2 | 12.3 | 15.2 |
| 03 | 78.8 | 84.4 | 90.3 | 32075 | 1004 | 850 | 67.5 | 21.2 | 9.5 |
| 04 | 82.7 | 82.1 | 89.2 | 30258 | 950 | 787 | 62.3 | 20.1 | 6.5 |
| 05 | 85.5 | 89.3 | 93.1 | 33382 | 1045 | 920 | 51.5 | 16.5 | 5.7 |
| Avg. | 79.9 | 86.0 | 91.7 | 32791 | 1112 | 857 | 64.9 | 17.2 | 9.3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Gu, Y.; Li, J.; Zhang, X. Robust Stereo Visual Odometry Using Improved RANSAC-Based Methods for Mobile Robot Localization. Sensors 2017, 17, 2339. https://doi.org/10.3390/s17102339
Liu Y, Gu Y, Li J, Zhang X. Robust Stereo Visual Odometry Using Improved RANSAC-Based Methods for Mobile Robot Localization. Sensors. 2017; 17(10):2339. https://doi.org/10.3390/s17102339
Chicago/Turabian StyleLiu, Yanqing, Yuzhang Gu, Jiamao Li, and Xiaolin Zhang. 2017. "Robust Stereo Visual Odometry Using Improved RANSAC-Based Methods for Mobile Robot Localization" Sensors 17, no. 10: 2339. https://doi.org/10.3390/s17102339
APA StyleLiu, Y., Gu, Y., Li, J., & Zhang, X. (2017). Robust Stereo Visual Odometry Using Improved RANSAC-Based Methods for Mobile Robot Localization. Sensors, 17(10), 2339. https://doi.org/10.3390/s17102339




