Adaptive Integration of the Compressed Algorithm of CS and NPC for the ECG Signal Compressed Algorithm in VLSI Implementation
Abstract
:1. Introduction
2. Proposed Architecture
2.1. Compressed Sensing
2.1.1. Measurement Matrix
2.1.2. Discrete Cosine Transform (DCT)
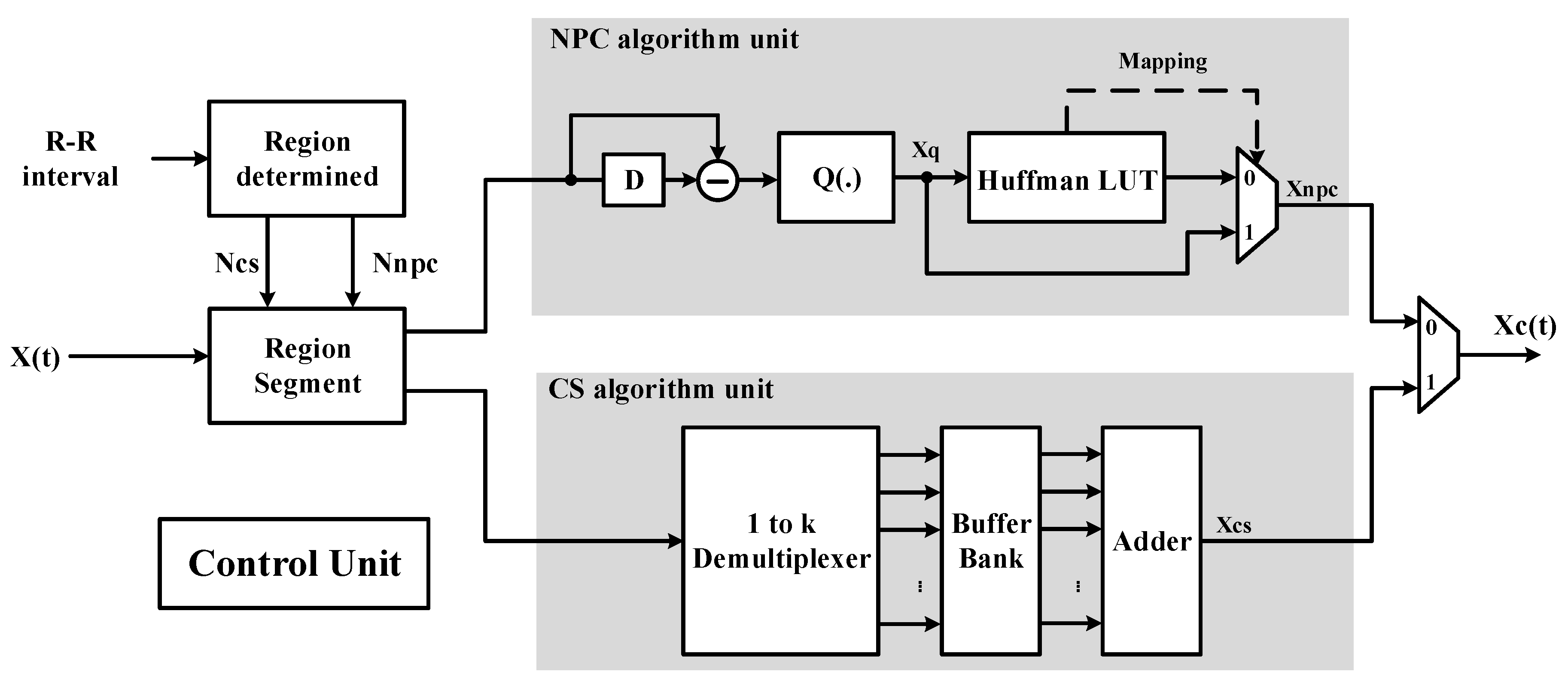
2.2. Near-Precise Compressed Algorithm
- Differences between adjacent signals are first calculated to reduce the amplitude scale of the signal. Thus, there is a greater probability of the same different result, which makes it possible to increase the compression ratio using methods based on Huffman coding theory.
- Generally, quantifying differences between adjacent signals requires an infinite number of bits; however, that is impossible to implement in VLSI. Thus, we perform quantization to the eighth decimal place in the NPC algorithm.
- Huffman coding utilizes symbols that vary in repetition to map bits of different lengths. If the symbol Xq is repeated frequently, then the output data Xnpc will have fewer bits after Huffman mapping. Consequently, symbol Xq (repeating infrequently) is mapped to data of a longer length. To increase the compression ratio and restrict the number of output bits, a multiplexer is switched according to whether the input data are mapped in a Huffman Look-Up Table (LUT). If the input data are mapped in a Huffman LUT, then Mapping = 0 and output data Xnpc are equal to the Huffman LUT mapping results. If the input data are not included in the Huffman LUT, then Mapping = 1 and the output Xnpc is equal to the quantification results.
- When the symbol Xq is repeated frequently, it is compressed via Huffman coding and the compressed data is restricted to fewer than 8 bits. ECG signals in the QRS region can be compressed with almost no loss using the proposed NPC algorithm.
- The Huffman LUT can be implemented using low-cost hardware because we map only the portion of the data that appears frequently. This reduces the size of the LUT by 82%.
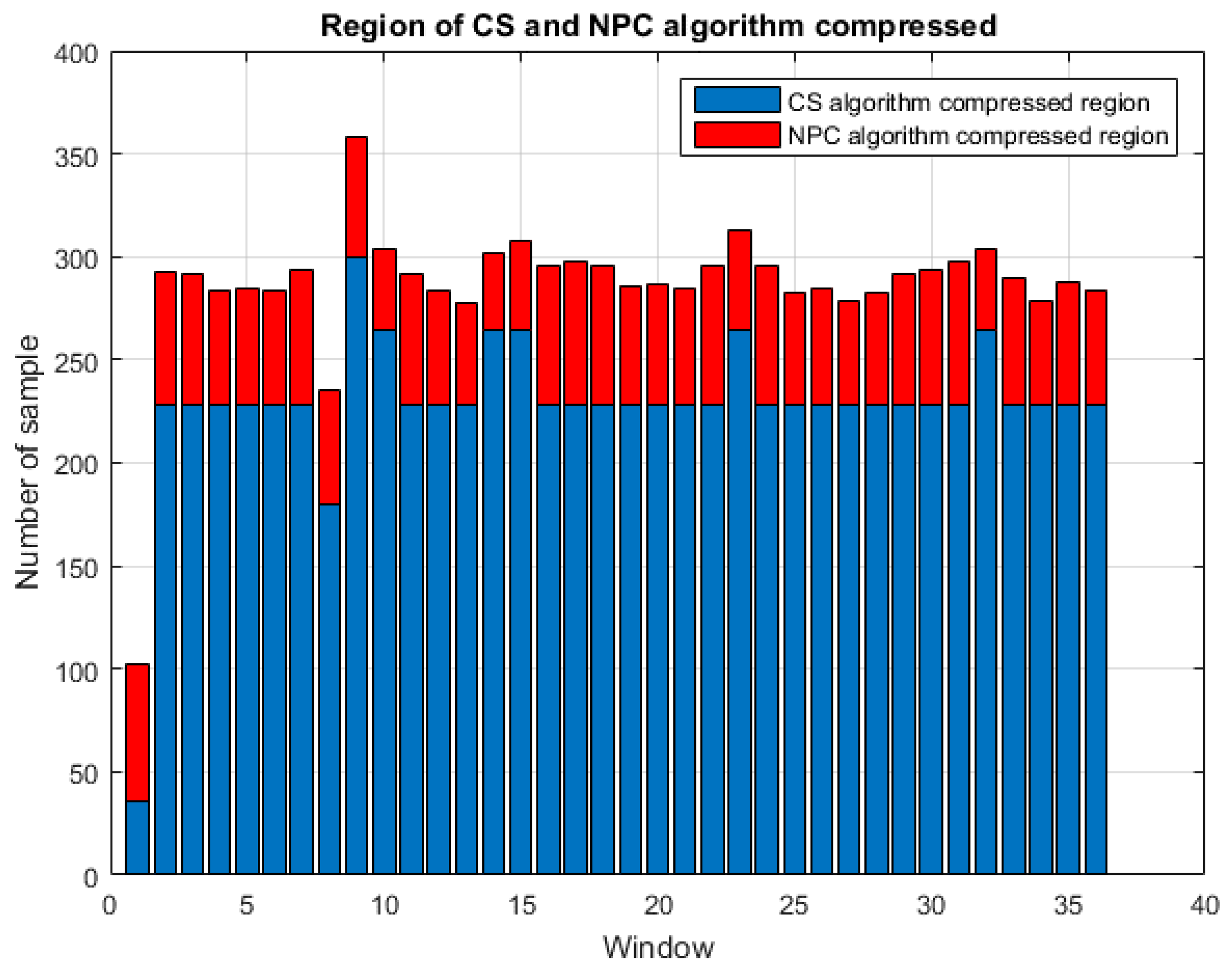
2.3. Adaptive Compression Algorithm Integrating CS and NPC
| Algorithm 1. Proposed Adaptive Compressed Algorithm. |
| Input: Input data ; R–R information |
| Output: Compressed data |
| 1. Initialization: s = 0; i = 0; j = 0; is decomposed to , where |
| 2. while () |
| 3. (NPC algorithm) |
| 4. while () |
| 5. Adjacent signals difference: If (k = 0), , else |
| 6. Quantification: |
| 7. Huffman mapping: If ( maps to Huffman LUT ) , mapping = 0 |
| 8. else , mapping = 1 |
| 9. Update NPC output format: |
| 10. end while |
| 11. (CS algorithm) |
| 12. while () |
| 13. if (), , else |
| 14. if (j = ) |
| 15. , where |
| 16. else |
| 17. , |
| 18. end while |
| 19. Index update: s = s + 1 |
| 20. Output data: |
| 21. end while |
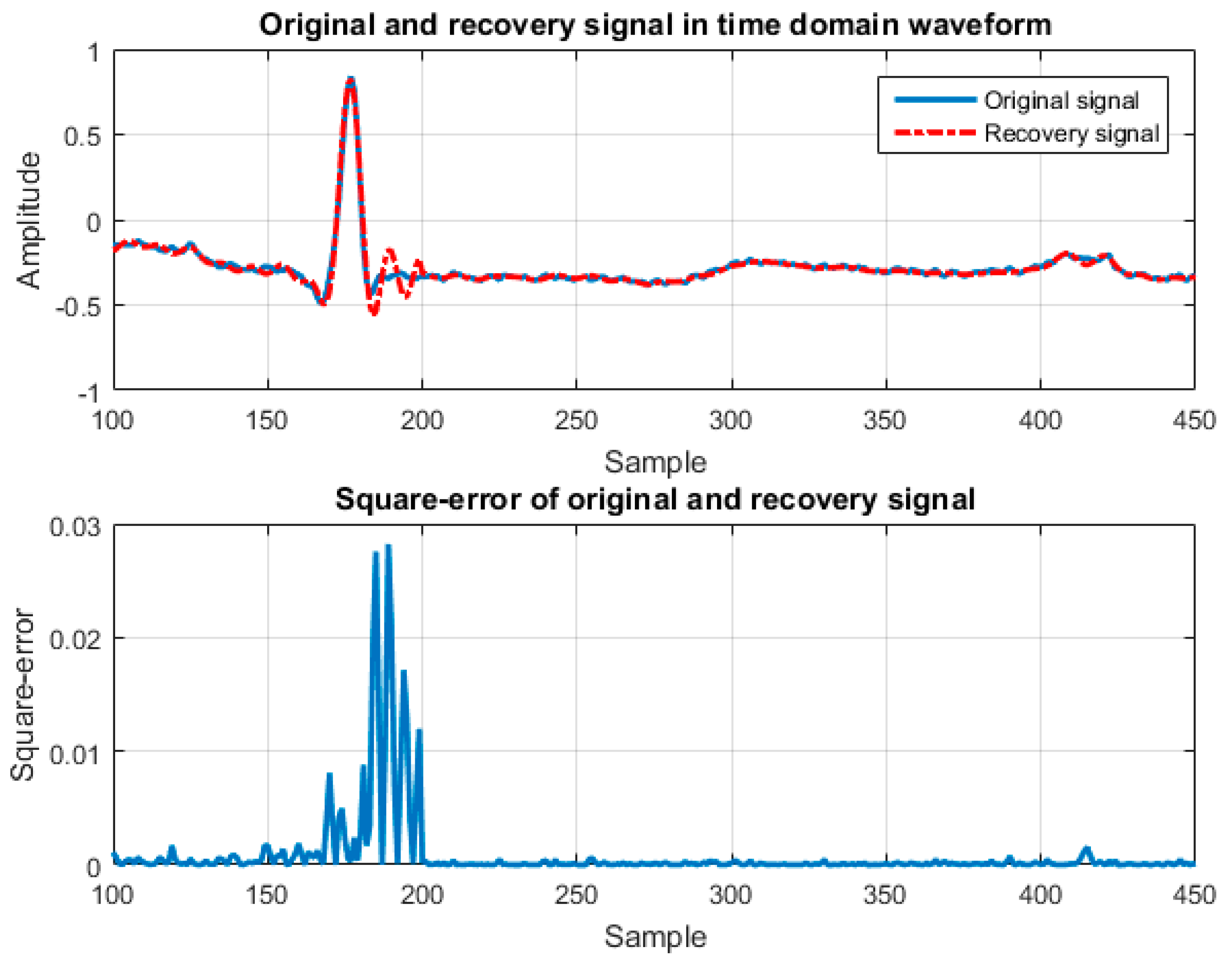
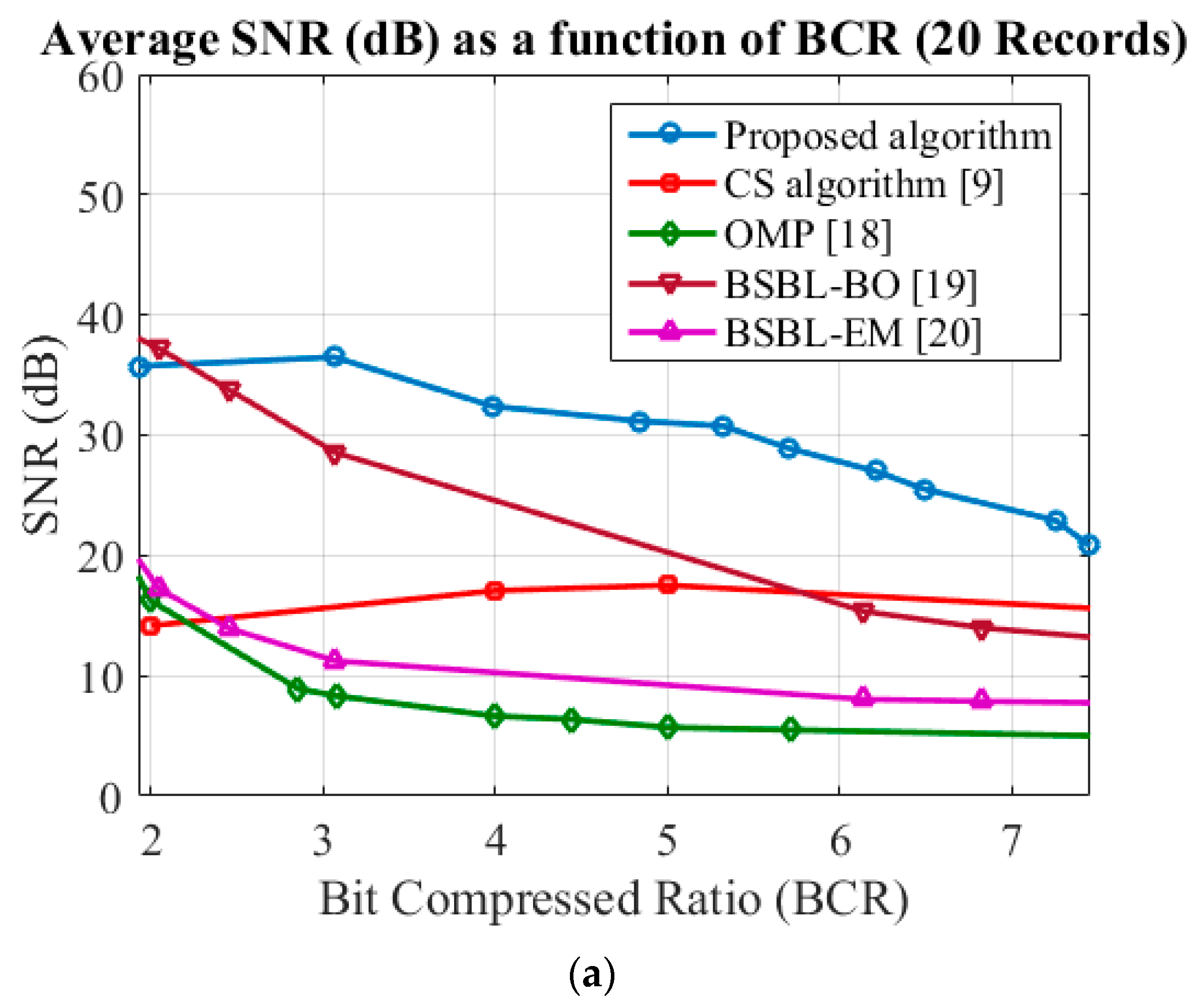
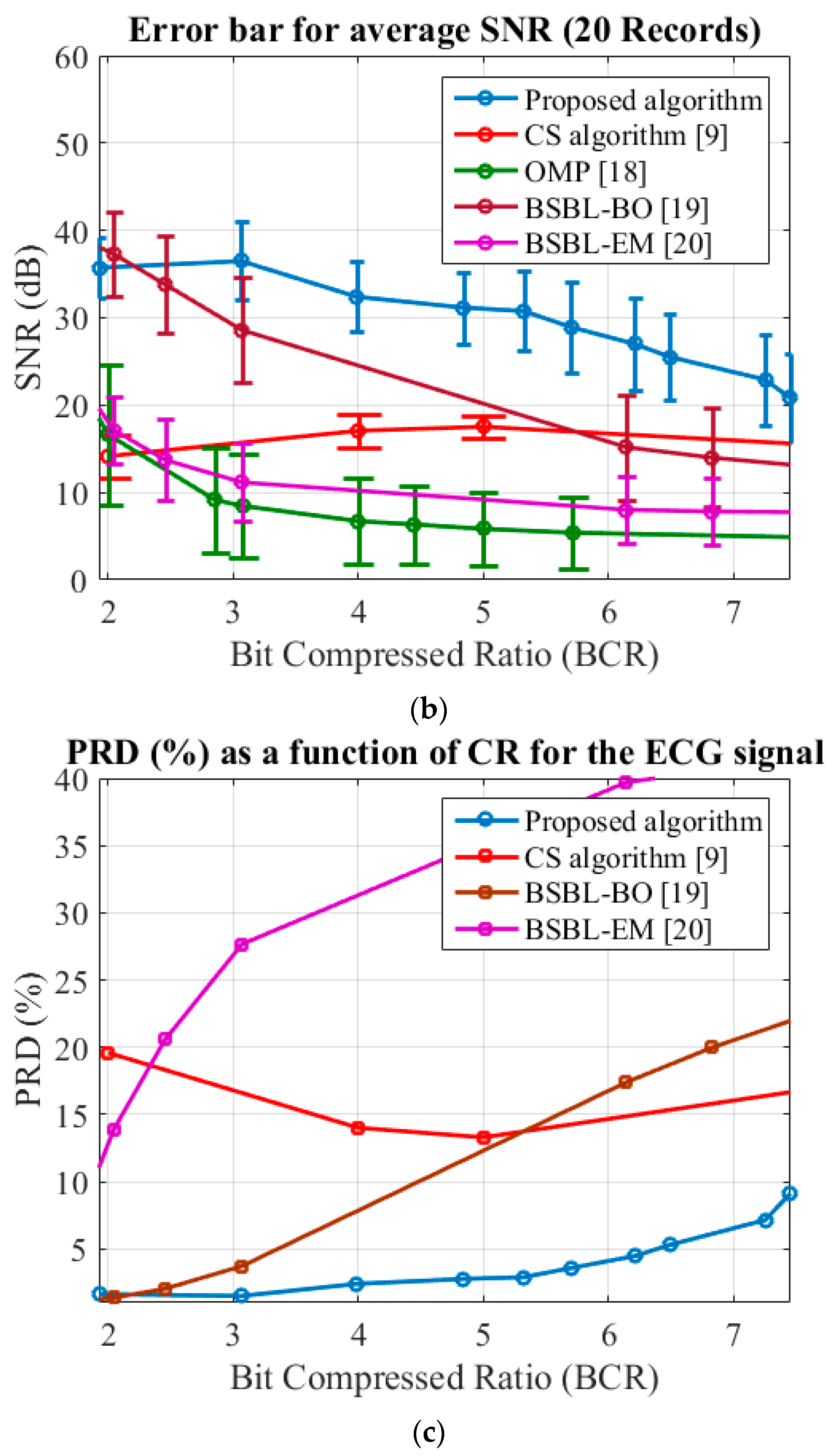
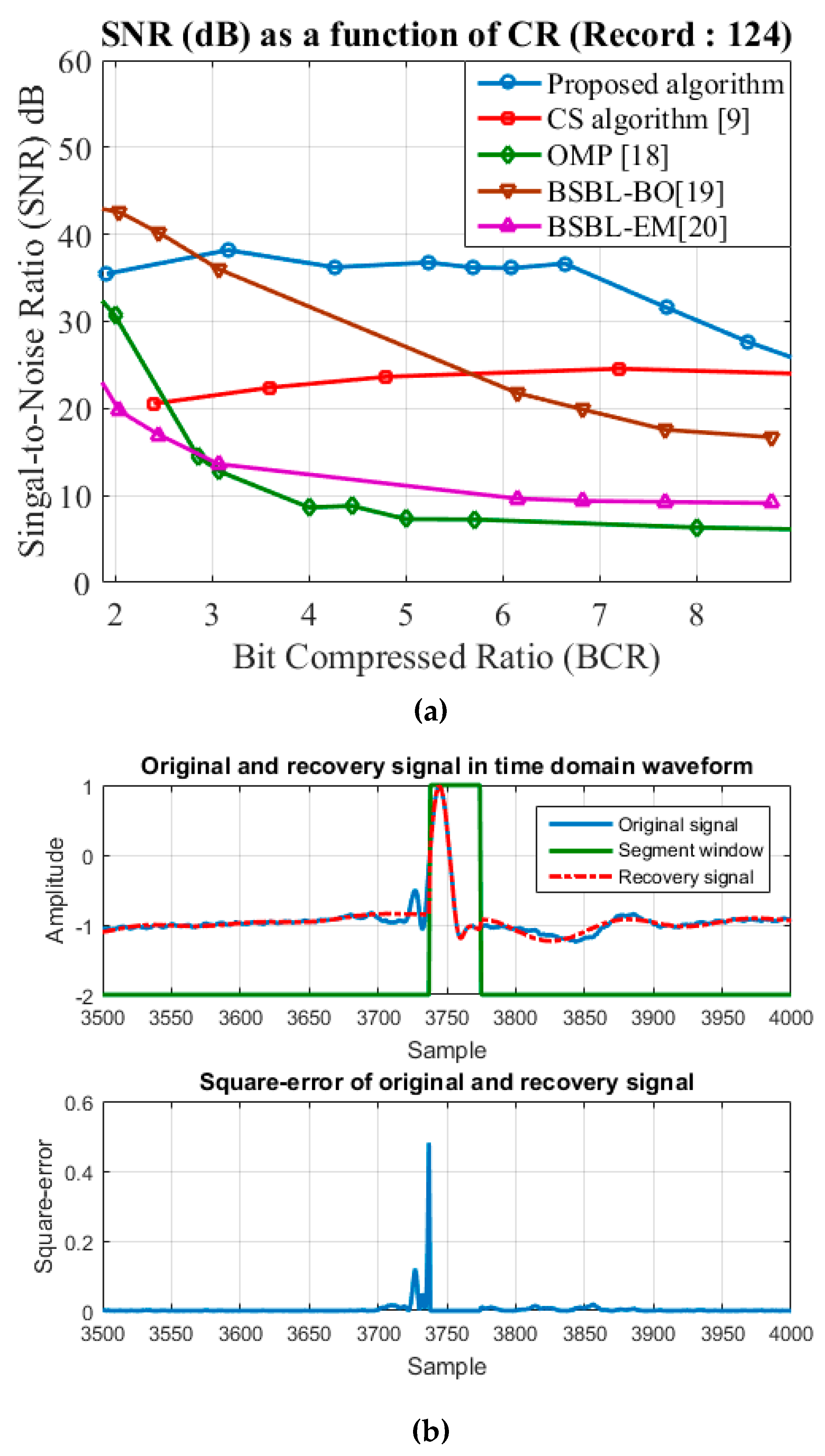
3. Simulation Results
4. Discussion
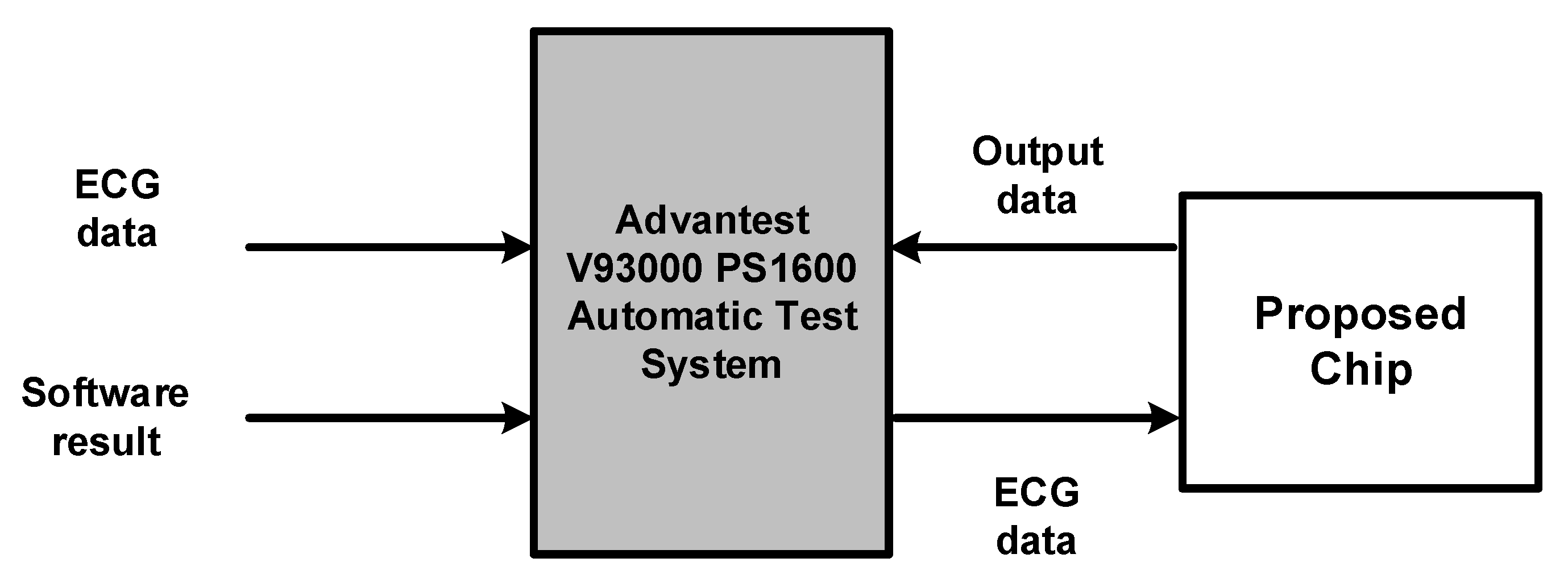
5. Hardware Implementation
5.1. Chip Implementation
5.2. FPGA Implementation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- WHO. Global Status Report on Noncommunicable Disease 2014; World Health Organization: Geneva, Switzerland, 2015. [Google Scholar]
- Chen, S.L.; Wang, J.G. VLSI implementation of low-power cost-efficient lossless ECG encoder design for wireless healthcare monitoring application. Electron. Lett. 2013, 49, 91–93. [Google Scholar] [CrossRef]
- Chen, S.L.; Lo, K.A.; Lin, T.L. Efficient fuzzy-controlled and hybrid entropy coding strategy lossless ECG encoder VLSI design for wireless body sensor networks. Electron. Lett. 2013, 49, 1058–1060. [Google Scholar] [CrossRef]
- Chen, S.L.; Tuan, M.C.; Chi, T.K.; Lin, T.L. VLSI architecture of lossless ECG compression design based on fuzzy decision and optimization method for wearable devices. Electron. Lett. 2015, 51, 1409–1411. [Google Scholar] [CrossRef]
- Deepu, C.J.; Zhang, X.; Liew, W.S.; Wong, D.L.T.; Lian, Y. An ECG-on-Chip with 535 nW/Channel Integrated Lossless Data Compressor for Wireless Sensors. IEEE J. Solid-State Circuits 2014, 49, 2435–2448. [Google Scholar] [CrossRef]
- Zhang, J.; Gu, Z.; Yu, Z.; Li, Y. Energy-efficient ECG compression on wireless biosensors via minimal coherence sensing and weighted l1 minimization reconstruction. IEEE J. Biomed. Health Inform. 2015, 19, 520–528. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.C.; Tsai, P.Y.; Huang, M.H. Matrix-Inversion-Free Compressed Sensing with Variable Orthogonal Multi-Matching Pursuit Based on Prior Information for ECG Signals. IEEE Tran. Biomed. Circuit Syst. 2016, 10, 864–873. [Google Scholar] [CrossRef] [PubMed]
- Craven, D.; McGinley, B.; Kilmartin, L.; Glavin, M.; Jones, E. Adaptive Dictionary Reconstruction for Compressed Sensing of ECG Signals. IEEE J. Biomed. Health Inform. 2017, 21, 645–654. [Google Scholar] [CrossRef] [PubMed]
- Ravelomanantsoa, A.; Rabah, H.; Rouane, A. Compressed sensing: A simple deterministic measurement matrix and a fast recovery algorithm. IEEE Trans. Instrum. Meas. 2015, 64, 3405–3413. [Google Scholar] [CrossRef]
- Candès, E.J.; Wakin, M.B. An introduction to Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Wang, J.; Kwon, S.; Shim, B. Generalized orthogonal matching pursuit. IEEE Trans. Signal Process. 2012, 60, 6202–6216. [Google Scholar] [CrossRef]
- Sahoo, S.; Makur, A. Signal recovery from random measurements via extended orthogonal matching pursuit. IEEE Signal Process. Soc. 2015, 63, 2572–2581. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Normalized iterative hard thresholding: Guaranteed stability and performance. IEEE J. Sel. Top. Signal Process. 2010, 4, 298–309. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Stagewise weak gradient pursuits. IEEE Trans. Signal Process. 2009, 57, 4333–4346. [Google Scholar] [CrossRef]
- Chen, Y.H.; Chang, T.Y.; Li, C.Y. A high performance video where transform engine by using space-time scheduling strategy. IEEE Trans. VLSI Syst. 2012, 20, 655–664. [Google Scholar] [CrossRef]
- Lee, H.; Buckley, K.M. ECG data compression using cut and align beats approach and 2-D transforms. IEEE Trans. Biomed. Eng. 1999, 46, 556–564. [Google Scholar] [PubMed]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH arrhythmia database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Zhang, Z.; Jung, T.-P.; Makeig, S.; Rao, B. Compressed sensing for energy-efficient wireless telemonitoring of noninvasive fetal ECG via block sparse bayesian learning. IEEE Trans. Biomed. Eng. 2013, 60, 300–309. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wei, S.; Wei, D.; Lin, L.; Liu, F.; Liu, C. Comparison of Four Recovery Algorithms Used in Compressed Sensing for ECG Signal Processing. In Proceedings of the Computing in Cardiology Conference (CinC), Vancouver, BC, Canada, 11–14 September 2016. [Google Scholar]


| CR | 2 | 4 | 8 | 10 | 12 | 15 | 20 | 25 | 30 | 40 |
| QS | 1.50 | 2.01 | 1.87 | 2.07 | 2.12 | 1.85 | 1.55 | 1.31 | 0.99 | 0.85 |
| Process Technology | TSMC 0.18 μm CMOS |
| Supply Voltage | 1.8 V |
| Maximum Frequency | 60 MHz |
| Core Area | 831 827 |
| Power Consumption | 2.1 mW |
| Gate Count (K) | 2.69 |
| Bits-Compressed Ratio | 5.05 |
| FPGA Chip | XC7K325T | |
|---|---|---|
| Used | Available | |
| # of Slices Registers | 126 | 407,600 |
| # of Slices LUTs | 428 | 203,800 |
| # of Fully-Used LUT-FF Pairs | 102 | 452 |
| Clock Frequency | 131 MHz | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tseng, Y.-H.; Chen, Y.-H.; Lu, C.-W. Adaptive Integration of the Compressed Algorithm of CS and NPC for the ECG Signal Compressed Algorithm in VLSI Implementation. Sensors 2017, 17, 2288. https://doi.org/10.3390/s17102288
Tseng Y-H, Chen Y-H, Lu C-W. Adaptive Integration of the Compressed Algorithm of CS and NPC for the ECG Signal Compressed Algorithm in VLSI Implementation. Sensors. 2017; 17(10):2288. https://doi.org/10.3390/s17102288
Chicago/Turabian StyleTseng, Yun-Hua, Yuan-Ho Chen, and Chih-Wen Lu. 2017. "Adaptive Integration of the Compressed Algorithm of CS and NPC for the ECG Signal Compressed Algorithm in VLSI Implementation" Sensors 17, no. 10: 2288. https://doi.org/10.3390/s17102288
APA StyleTseng, Y.-H., Chen, Y.-H., & Lu, C.-W. (2017). Adaptive Integration of the Compressed Algorithm of CS and NPC for the ECG Signal Compressed Algorithm in VLSI Implementation. Sensors, 17(10), 2288. https://doi.org/10.3390/s17102288






