Pose Estimation of a Mobile Robot Based on Fusion of IMU Data and Vision Data Using an Extended Kalman Filter
Abstract
:1. Introduction
2. Related Work
2.1. Inertial Sensor-Based Methods
2.2. Vision Based Methods
Object Recognition and Feature Matching
- Draw a minimal number of randomly selected correspondences Sk (random sample);
- Compute the pose from these minimal set of point correspondences using direct linear transform (DLT);
- Determine the number Ck of points from the whole set of all correspondence that are consistent with the estimated parameters with a predefined tolerance. If Ck > C* then we retain the randomly selected set of correspondences Sk as the best one: S* equal Sk and C* equal Ck;
- Repeat first step to third step.
- Load training image;
- Convert the image to grayscale;
- Remove lens distortions from images;
- Initialize match object;
- Detect feature points using SURF;
- Check the image pixels;
- Extract feature descriptor;
- Match query image with training image using RANSAC;
- If inliers > threshold then compute homograph transform box;
- Draw box on object and display.
2.3. Fusion of Inertial-Vision Sensor-Based Methods
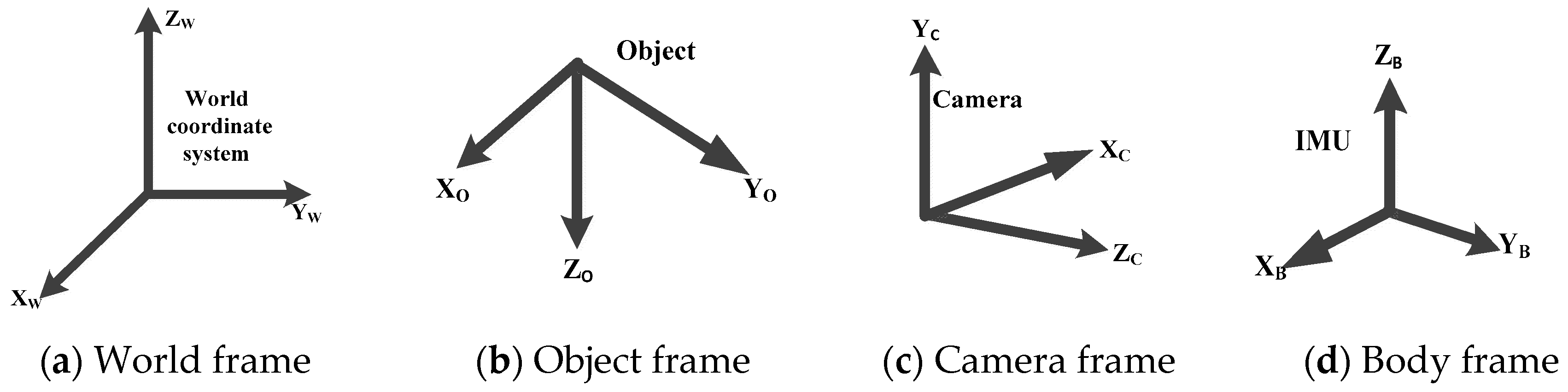
3. Proposed Modeling Method
- Global frame/world frame {w}: This frame aids the user to navigate and determine the pose estimation in relative to IMU and camera frames.
- IMU/body frame {b}: This frame is attached to the IMU (accelerometer and gyroscope) on the mobile robot.
- Object coordinate frame {o}: This frame is attached to the object (a 4WD mobile robot).
- Camera frame {c}: This frame is attached to the camera on the mobile robot with the x-axis pointing to the image plane in the right direction and z-axis pointing along the optical axis and origin located at the camera optical center.
3.1. IMU-Based Pose Estimation
3.2. Vision Based Pose Estimation Method
Projection of Object Reference Points to Image Plane
3.3. Fusion Based on IMU and Vision Pose Estimation Method
3.4. EKF Implementation
4. System Hardware and Experimental Setup
5. Results and Discussion
5.1. Simulated Results of Object Detection and Recognition in an Image
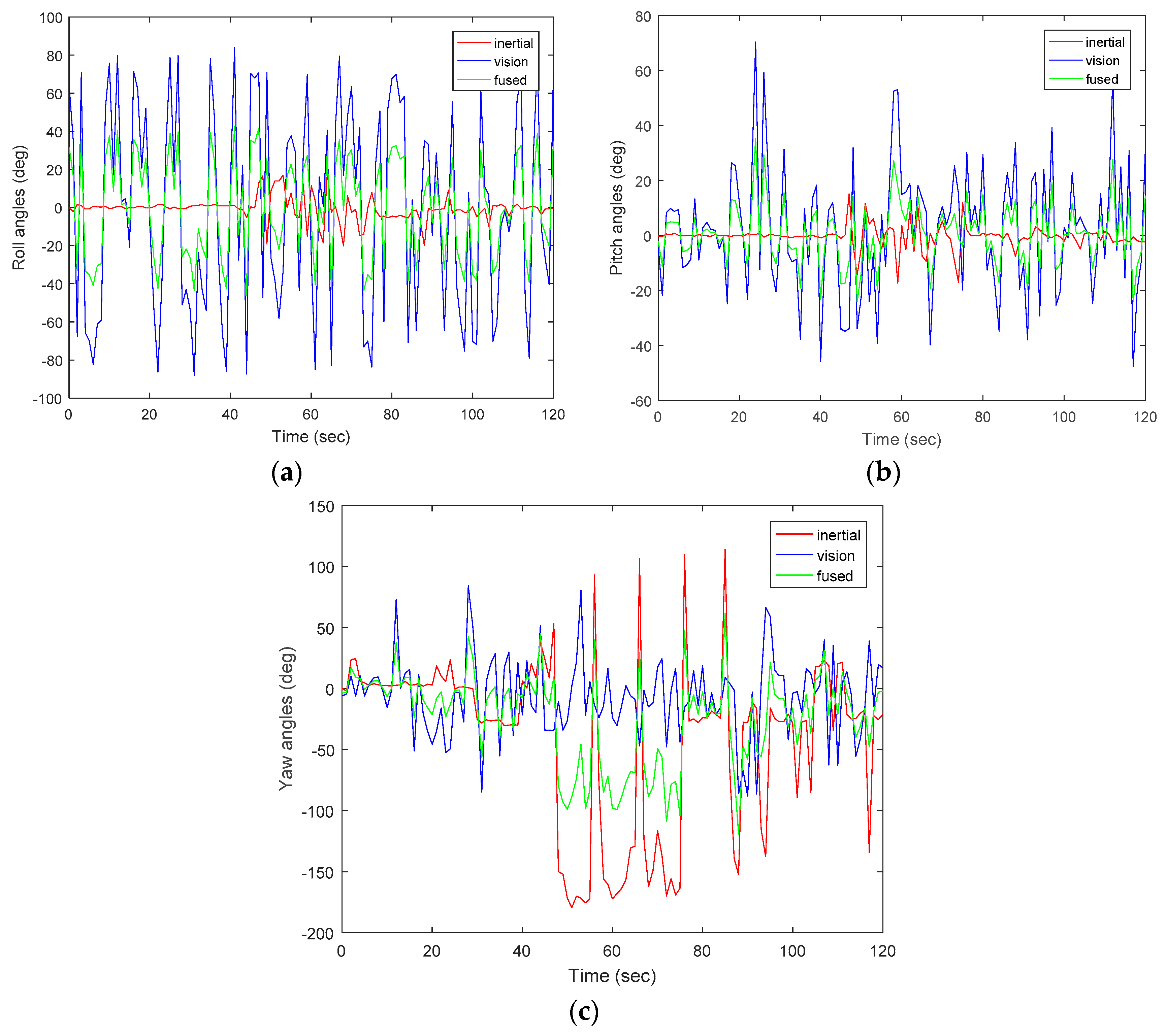
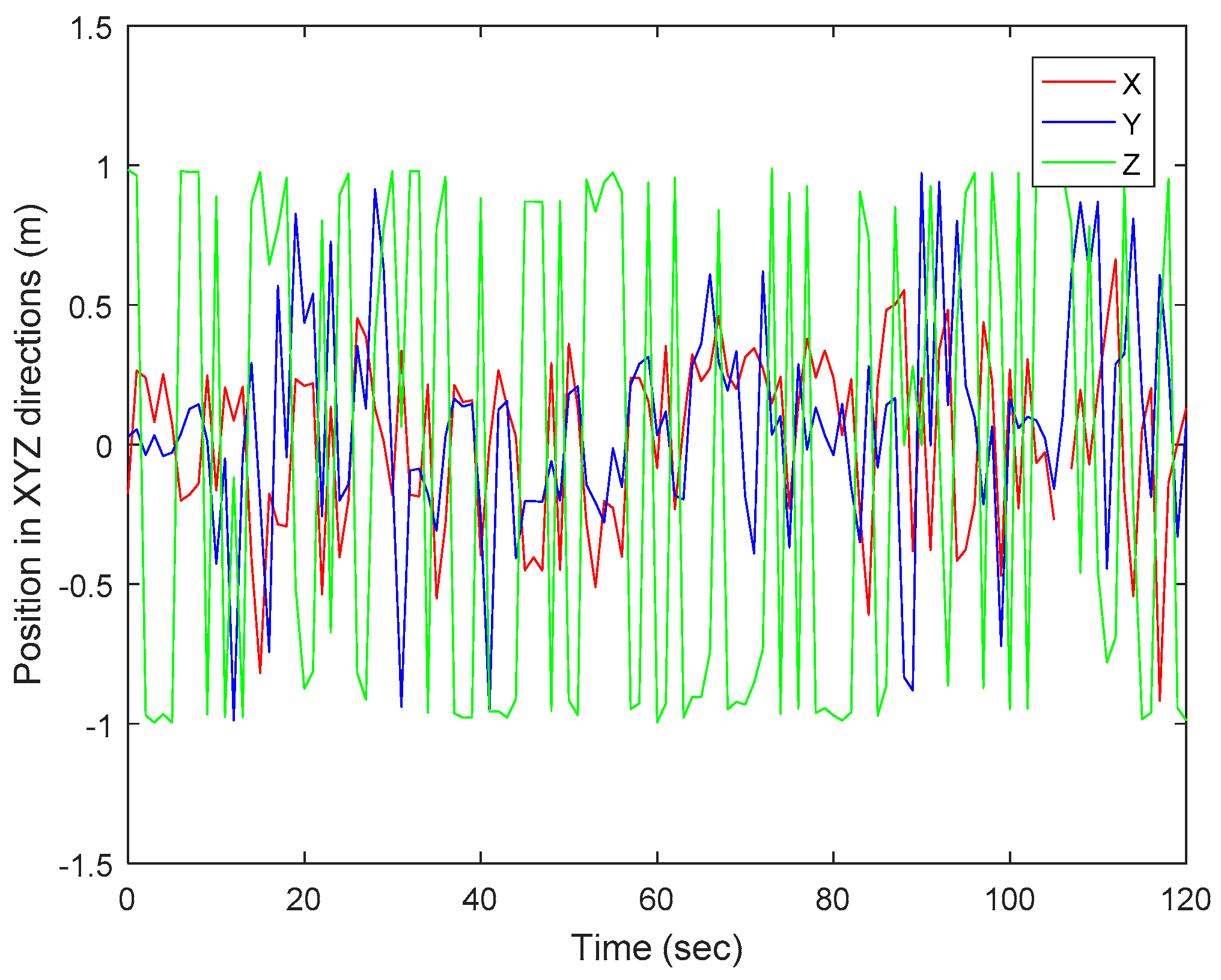
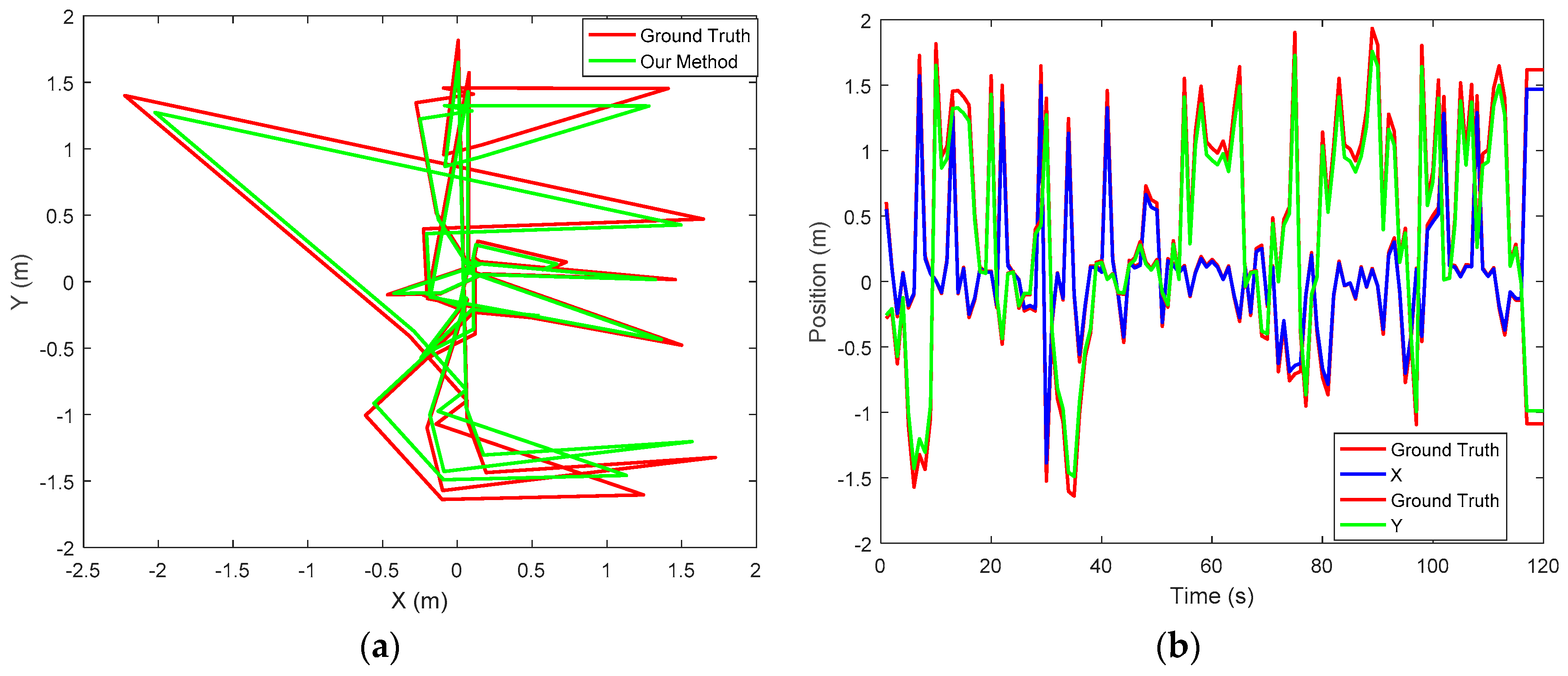
5.2. Simulated Results of Object Analysis of Experimental Results
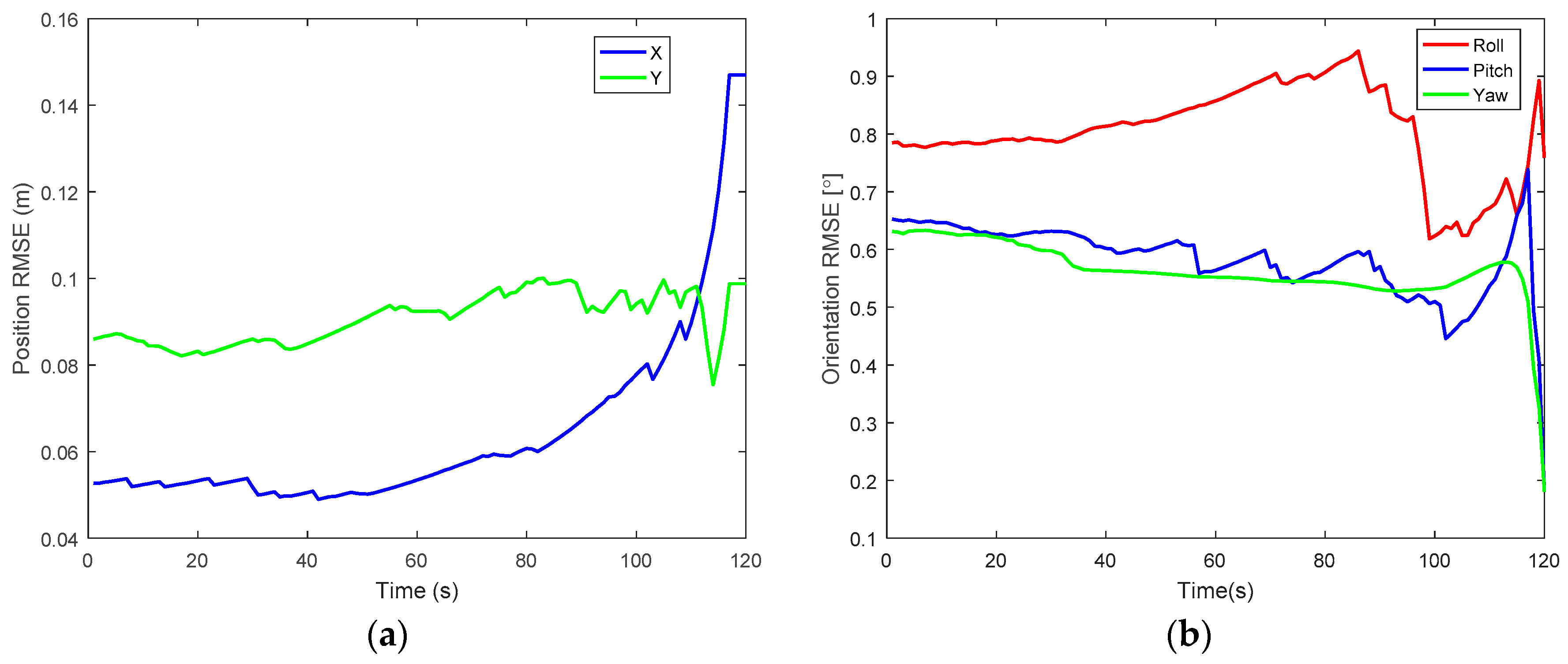
5.3. Performance: Accuracy
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Röwekämper, J.; Sprunk, C.; Tipaldi, G.D.; Stachniss, C.; Pfaff, P.; Burgard, W. On the position accuracy of mobile robot localization based on particle filters combined with scan matching. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 3158–3164. [Google Scholar]
- Alomari, A.; Phillips, W.; Aslam, N.; Comeau, F. Dynamic fuzzy-logic based path planning for mobility-assisted localization in wireless sensor networks. Sensors 2017, 17, 1904. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, H.; Moussa, A.; Elhabiby, M.; El-Sheimy, N.; Sesay, A. A novel real-time reference key frame scan matching method. Sensors 2017, 17, 1060. [Google Scholar] [CrossRef] [PubMed]
- Gregory Dudek, M.J. Inertial sensors, GPS and odometry. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 446–490. [Google Scholar]
- Jinglin, S.; Tick, D.; Gans, N. Localization through fusion of discrete and continuous epipolar geometry with wheel and imu odometry. In Proceedings of the American Control Conference (ACC), San Francisco, CA, USA, 29 June–1 July 2010. [Google Scholar]
- Weng, E.N.G.; Khan, R.U.; Adruce, S.A.Z.; Bee, O.Y. Objects tracking from natural features in mobile augmented reality. Procedia Soc. Behav. Sci. 2013, 97, 753–760. [Google Scholar] [CrossRef]
- Li, J.; Besada, J.A.; Bernardos, A.M.; Tarrío, P.; Casar, J.R. A novel system for object pose estimation using fused vision and inertial data. Inf. Fusion 2017, 33, 15–28. [Google Scholar] [CrossRef]
- Chen, P.; Peng, Z.; Li, D.; Yang, L. An improved augmented reality system based on andar. J. Vis. Commun. Image Represent. 2016, 37, 63–69. [Google Scholar] [CrossRef]
- Daponte, P.; De Vito, L.; Picariello, F.; Riccio, M. State of the art and future developments of the augmented reality for measurement applications. Measurement 2014, 57, 53–70. [Google Scholar] [CrossRef]
- Khandelwal, P.; Swarnalatha, P.; Bisht, N.; Prabu, S. Detection of features to track objects and segmentation using grabcut for application in marker-less augmented reality. Procedia Comput. Sci. 2015, 58, 698–705. [Google Scholar] [CrossRef]
- Potter, C.H.; Hancke, G.P.; Silva, B.J. Machine-to-machine: Possible applications in industrial networks. In Proceedings of the 2013 IEEE International Conference on Industrial Technology (ICIT), Cape Town, South Africa, 25–28 February 2013; pp. 1321–1326. [Google Scholar]
- Opperman, C.A.; Hancke, G.P. Using NFC-enabled phones for remote data acquisition and digital control. In Proceedings of the AFRICON, 2011, Livingstone, Zambia, 13–15 September 2011; pp. 1–6. [Google Scholar]
- Kumar, A.; Hancke, G.P. An energy-efficient smart comfort sensing system based on the IEEE 1451 standard for green buildings. IEEE Sens. J. 2014, 14, 4245–4252. [Google Scholar] [CrossRef]
- Silva, B.; Fisher, R.M.; Kumar, A.; Hancke, G.P. Experimental link quality characterization of wireless sensor networks for underground monitoring. IEEE Trans. Ind. Inform. 2015, 11, 1099–1110. [Google Scholar] [CrossRef]
- Kruger, C.P.; Abu-Mahfouz, A.M.; Hancke, G.P. Rapid prototyping of a wireless sensor network gateway for the internet of things using off-the-shelf components. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 1926–1931. [Google Scholar]
- Phala, K.S.E.; Kumar, A.; Hancke, G.P. Air quality monitoring system based on ISO/IEC/IEEE 21451 standards. IEEE Sens. J. 2016, 16, 5037–5045. [Google Scholar] [CrossRef]
- Cheng, B.; Cui, L.; Jia, W.; Zhao, W.; Hancke, G.P. Multiple region of interest coverage in camera sensor networks for tele-intensive care units. IEEE Trans. Ind. Inform. 2016, 12, 2331–2341. [Google Scholar] [CrossRef]
- Ben-Afia, A.; Deambrogio, D.; Escher, C.; Macabiau, C.; Soulier, L.; Gay-Bellile, V. Review and classification of vision-based localization technoques in unknown environments. IET Radar Sonar Navig. 2014, 8, 1059–1072. [Google Scholar] [CrossRef]
- Lee, T.J.; Bahn, W.; Jang, B.M.; Song, H.J.; Cho, D.I.D. A new localization method for mobile robot by data fusion of vision sensor data and motion sensor data. In Proceedings of the 2012 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China, 11–14 December 2012; pp. 723–728. [Google Scholar]
- Tian, Y.; Jie, Z.; Tan, J. Adaptive-frame-rate monocular vision and imu fusion for robust indoor positioning. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 2257–2262. [Google Scholar]
- Borenstein, J.; Everett, H.R.; Feng, L.; Wehe, D. Navigating mobile robots: Systems and techniques. J. Robot. Syst. 1997, 14, 231–249. [Google Scholar] [CrossRef]
- Persa, S.; Jonker, P. Real-time computer vision system for mobile robot. In SPIE, Intelligent Robots and Computer Vision XX: Algorithms, Techniques, and Active Vision; David, P.C., Ernest, L.H., Eds.; SPIE: Bellingham, WA, USA, 2001; pp. 105–114. [Google Scholar]
- Goel, P.; Roumeliotis, S.I.; Sukhatme, G.S. Robust localization using relative and absolute position estimates. In Proceedings of the 1999 IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS ‘99, Kyongju, Korea, 17–21 October 1999; pp. 1134–1140. [Google Scholar]
- Fantian, K.; Youping, C.; Jingming, X.; Gang, Z.; Zude, Z. Mobile robot localization based on extended kalman filter. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 9242–9246. [Google Scholar]
- Alatise, M.; Hancke, G.P. Pose estimation of a mobile robot using monocular vision and inertial sensors data. In Proceedings of the IEEE AFRICON 2017, Cape Town, South Africa, 18–20 September 2017. [Google Scholar]
- Kumar, K.; Reddy, P.K.; Narendra, N.; Swamy, P.; Varghese, A.; Chandra, M.G.; Balamuralidhar, P. An improved tracking using IMU and vision fusion for mobile augemented reality applications. Int. J. Multimed. Appl. (IJMA) 2014, 6, 13–29. [Google Scholar]
- Erdem, A.T.; Ercan, A.O. Fusing inertial sensor data in an extended kalman filter for 3D camera tracking. IEEE Trans. Image Process. 2015, 24, 538–548. [Google Scholar] [CrossRef] [PubMed]
- Azuma, R.T. A survey of augmented reality. Presence Teleoper. Virtual Environ. 1997, 6, 355–385. [Google Scholar] [CrossRef]
- Nasir, A.K.; Hille, C.; Roth, H. Data fusion of stereo vision and gyroscope for estimation of indoor mobile robot orientation. IFAC Proc. Vol. 2012, 45, 163–168. [Google Scholar] [CrossRef]
- Bird, J.; Arden, D. Indoor navigation with foot-mounted strapdown inertial navigation and magnetic sensors [emerging opportunities for localization and tracking]. IEEE Wirel. Commun. 2011, 18, 28–35. [Google Scholar] [CrossRef]
- Sibai, F.N.; Trigui, H.; Zanini, P.C.; Al-Odail, A.R. Evaluation of indoor mobile robot localization techniques. In Proceedings of the 2012 International Conference on Computer Systems and Industrial Informatics, Sharjah, UAE, 18–20 December 2012; pp. 1–6. [Google Scholar]
- Aggarwal, P.; Syed, Z.; Niu, X.; El-Sheimy, N. A standard testing and calibration procedure for low cost mems inertial sensors and units. J. Navig. 2008, 61, 323–336. [Google Scholar] [CrossRef]
- Genc, Y.; Riedel, S.; Souvannavong, F.; Akınlar, C.; Navab, N. Marker-less tracking for AR: A learning-based approach. In Proceedings of the 2002 International Symposium on Mixed and Augmented Reality, ISMAR 2002, Darmstadt, Germany, 1 October 2002. [Google Scholar] [CrossRef]
- Ozuysal, M.; Fua, P.; Lepetit, V. Fast keypoint recognition in ten lines of code. In Proceedings of the IEEE International Conference on Computer Visionand Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (surf). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Loncomilla, P.; Ruiz-del-Solar, J.; Martínez, L. Object recognition using local invariant features for robotic applications: A survey. Pattern Recognit. 2016, 60, 499–514. [Google Scholar] [CrossRef]
- Farooq, J. Object detection and identification using surf and bow model. In Proceedings of the 2016 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 11–12 April 2016; pp. 318–323. [Google Scholar]
- Hol, J.; Schön, T.; Gustafsson, F. Modeling and calibration of inertial and vision sensors. Int. J. Robot. Res. 2010, 2, 25. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M.C. A combined corner and edge detector. Proc. Alvey Vis. Conf. 1988, 15, 147–151. [Google Scholar]
- Tomasi, C.; Kanade, T. Shape and Motion from Image Streams: A Factorization Method—Part 3: Detection and Tracking of Point Features; Technical Report CMU-CS-91-132; Carnegie Mellon University: Pittsburgh, PA, USA, 1991. [Google Scholar]
- Mikolajczyk, K.; Schmid, C. Scale & affine invariant interest point detectors. Int. J. Comput. Vis. 2004, 60, 63–86. [Google Scholar]
- Fischler, M.; Bolles, R. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Serradell, E.; Ozuysal, M.; Lepetit, V.; Fua, P.; Moreno-Noquer, F. Combining geometric and appearance prioris for robust homography estimation. In Proceedings of the 11th European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; pp. 58–72. [Google Scholar]
- Zhai, M.; Shan, F.; Jing, Z. Homography estimation from planar contours in image sequence. Opt. Eng. 2010, 49, 037202. [Google Scholar]
- Cheng, C.-M.; Lai, S.-H. A consensus sampling technique for fast and robust model fitting. Pattern Recognit. 2009, 42, 1318–1329. [Google Scholar] [CrossRef]
- Torr, P.H.; Murray, D.W. The development and comparison of robust methods for estimating the fundamental matrix. Int.J. Comput. Vis. 1997, 24, 271–300. [Google Scholar] [CrossRef]
- Chen, C.-S.; Hung, Y.-P.; Cheng, J.-B. Ransac-based darces: A new approach to fast automatic registration of partially range images. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 1229–1234. [Google Scholar] [CrossRef]
- Gonzalez-Ahuilera, D.; Rodriguez-Gonzalvez, P.; Hernandez-Lopez, D.; Lerma, J.L. A robust and hierchical approach for the automatic co-resgistration of intensity and visible images. Opt. Laser Technol. 2012, 44, 1915–1923. [Google Scholar] [CrossRef]
- Lv, Y.; Feng, J.; Li, Z.; Liu, W.; Cao, J. A new robust 2D camera calibration method using ransac. Opt. Int. J. Light Electron Opt. 2015, 126, 4910–4915. [Google Scholar] [CrossRef]
- Zhou, F.; Cui, Y.; Wang, Y.; Liu, L.; Gao, H. Accurate and robust estimation of camera parameters using ransac. Opt. Lasers Eng. 2013, 51, 197–212. [Google Scholar] [CrossRef]
- Marchand, E.; Uchiyama, H.; Spindler, F. Pose estimation for augmented reality: A hands-on survey. IEEE Trans. Vis. Comput. Graph. 2016, 22, 2633–2651. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Hu, H.; Zhou, H. Integration of vision and inertial sensors for 3D arm motion tracking in home-based rehabilitation. Int. J. Robot. Res. 2007, 26, 607–624. [Google Scholar] [CrossRef]
- Suya, Y.; Neumann, U.; Azuma, R. Hybrid inertial and vision tracking for augmented reality registration. In Proceedings of the IEEE Virtual Reality (Cat. No. 99CB36316), Houston, TX, USA, 13–17 March 1999; pp. 260–267. [Google Scholar]
- You, S.; Neumann, U. Fusion of vision and gyro tracking for robust augmented reality registration. In Proceedings of the IEEE Virtual Reality 2001, Yokohama, Japan, 13–17 March 2001; pp. 71–78. [Google Scholar]
- Nilsson, J.; Fredriksson, J.; Ödblom, A.C. Reliable vehicle pose estimation using vision and a single-track model. IEEE Trans. Intell. Transp. Syst. 2014, 15, 14. [Google Scholar] [CrossRef]
- Fox, D.; Thrun, S.; Burgard, W.; Dellaert, F. Particle filters for mobile robot localization. In Sequential Monte Carlo Methods in Practice; Springer: New York, NY, USA, 2001; Available online: http://citeseer.nj.nec.com/fox01particle.html (accessed on 15 September 2016).
- Wan, E.A.; Merwe, R.V.D. The unscented kalman filter for nonlinear estimation. In Proceedings of the Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000 (AS-SPCC), Lake Louise, AB, Canada, 4 October 2000; pp. 153–158. [Google Scholar]
- Jing, C.; Wei, L.; Yongtian, W.; Junwei, G. Fusion of inertial and vision data for accurate tracking. Proc. SPIE 2012, 8349, 83491D. [Google Scholar]
- Ligorio, G.; Sabatini, A. Extended kalman filter-based methods for pose estimation using visual, inertial and magnetic sensors: Comparative analysis and performance evaluation. Sensors 2013, 13, 1919–1941. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, N.; Ghazilla, R.A.R.; Khairi, N.M.; Kasi, V. Reviews on various inertial measurement unit (IMU) sensor applications. Int. J. Signal Process. Syst. 2013, 1, 256–262. [Google Scholar] [CrossRef]
- Diebel, J. Representing attitude: Euler angles, unit quaternions, and rotation vectors. Matrix 2006, 58, 1–35. [Google Scholar]
- Zhao, H.; Wang, Z. Motion measurement using inertial sensors, ultrasonic sensors, and magnetometers with extended kalman filter for data fusion. IEEE Sens. J. 2012, 12, 943–953. [Google Scholar] [CrossRef]
- Choi, S.; Joung, J.H.; Yu, W.; Cho, J.I. What does ground tell us? Monocular visual odometry under planar motion constraint. In Proceedings of the 2011 11th International Conference on Control, Automation and Systems (ICCAS), Gyeonggi-do, Korea, 26–29 October 2011; pp. 1480–1485. [Google Scholar]
- Caballero, F.; Merino, L.; Ferruz, J.; Ollero, A. Unmanned aerial vehicle localization based on monocular vision and online mosaicking. J. Intell. Robot. Syst. 2009, 55, 323–343. [Google Scholar] [CrossRef]
- Chaolei, W.; Tianmiao, W.; Jianhong, L.; Yang, C.; Yongliang, W. Monocular vision and IMU based navigation for a small unmanned helicopter. In Proceedings of the 2012 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 1694–1699. [Google Scholar]
- Dementhon, D.F.; Davis, L.S. Model-based object pose in lines of code. Int. J. Comput. Vis. 1995, 15, 123–141. [Google Scholar] [CrossRef]
- Zhengyou, Z. Flexible camera calibration by viewing a plane from unknown orientations. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 666–673. [Google Scholar]
- Park, J.; Hwang, W.; Kwon, H.I.; Kim, J.H.; Lee, C.H.; Anjum, M.L.; Kim, K.S.; Cho, D.I. High performance vision tracking system for mobile robot using sensor data fusion with kalman filter. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 3778–3783. [Google Scholar]
- Delaune, J.; Le Besnerais, G.; Voirin, T.; Farges, J.L.; Bourdarias, C. Visual–inertial navigation for pinpoint planetary landing using scale-based landmark matching. Robot. Auton. Syst. 2016, 78, 63–82. [Google Scholar] [CrossRef]
- Bleser, G.; Stricker, D. Advanced tracking through efficient image processing and visual–inertial sensor fusion. Comput. Graph. 2009, 33, 59–72. [Google Scholar] [CrossRef]
- Linksprite Technologies, Inc. Linksprite JPEG Color Camera Serial UART Interface. Available online: www.linksprite.com (accessed on 12 October 2016).






| Variables | Meanings |
|---|---|
| Sampling interval of IMU sensor | 100 Hz |
| Gyroscope measurement noise variance, | 0.001 rad2/s2 |
| Accelerometer measurement noise variance, | 0.001 m/s2 |
| Camera measurement noise variance, | 0.9 |
| Sampling interval between image frames | 25 Hz |
| Time (s) | Position Error (m) | Orientation Error (Degree) | |||
|---|---|---|---|---|---|
| x | y | Roll | Pitch | Yaw | |
| 20 | 0.05 | 0.08 | 0.78 | 0.62 | 0.62 |
| 40 | 0.05 | 0.08 | 0.81 | 0.60 | 0.56 |
| 60 | 0.07 | 0.09 | 0.85 | 0.56 | 0.55 |
| 80 | 0.06 | 0.09 | 0.90 | 0.56 | 0.54 |
| 100 | 0.07 | 0.09 | 0.62 | 0.50 | 0.53 |
| 120 | 0.14 | 0.09 | 0.75 | 0.18 | 0.18 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alatise, M.B.; Hancke, G.P. Pose Estimation of a Mobile Robot Based on Fusion of IMU Data and Vision Data Using an Extended Kalman Filter. Sensors 2017, 17, 2164. https://doi.org/10.3390/s17102164
Alatise MB, Hancke GP. Pose Estimation of a Mobile Robot Based on Fusion of IMU Data and Vision Data Using an Extended Kalman Filter. Sensors. 2017; 17(10):2164. https://doi.org/10.3390/s17102164
Chicago/Turabian StyleAlatise, Mary B., and Gerhard P. Hancke. 2017. "Pose Estimation of a Mobile Robot Based on Fusion of IMU Data and Vision Data Using an Extended Kalman Filter" Sensors 17, no. 10: 2164. https://doi.org/10.3390/s17102164
APA StyleAlatise, M. B., & Hancke, G. P. (2017). Pose Estimation of a Mobile Robot Based on Fusion of IMU Data and Vision Data Using an Extended Kalman Filter. Sensors, 17(10), 2164. https://doi.org/10.3390/s17102164





