Hyperspectral Imagery Super-Resolution by Adaptive POCS and Blur Metric
Abstract
:1. Introduction
2. Projection onto Convex Set-Based Super-Resolution Reconstruction (SRR)
3. Hyperspectral Imagery Super-Resolution by Adaptive Projection onto Convex Sets (APOCS) and Blur Metric
3.1. Image Blur Metric Based on Gabor Wavelet Transform
| Algorithm 1. Steps of the image blur metric assessment method: |
| Step 1: Set the initial value of p (Equation (5)); |
| Step 2: Compute the Gabor feature GF(m1,m2) via Equation (4); |
| Step 3: Compute the mean value m(m1,m2) and variance value ε(m1,m2) of the Gabor feature with Equations (5) and (6); |
| Step 4: Compute the adaptive threshold t(m1,m2) (Equation (7)) and achieve the Gabor feature classification (Equation (8)); |
| Step 5: Gain the separated frequency information HFR(m1,m2) and LFR(m1,m2) via Equation (9); |
| Step 6: Extract the statistical features HFRhad(m1,m2), HFRmhad, HFRvad(m1,m2), HFRmvad and LFRhad(m1,m2), LFRmhad, LFRvad(m1,m2), LFRmvad from the separated frequency information (Equations (10) and (11)); |
| Step 7: Compute the image blur metric assessment AIBM via statistical features (Equation (12)). |
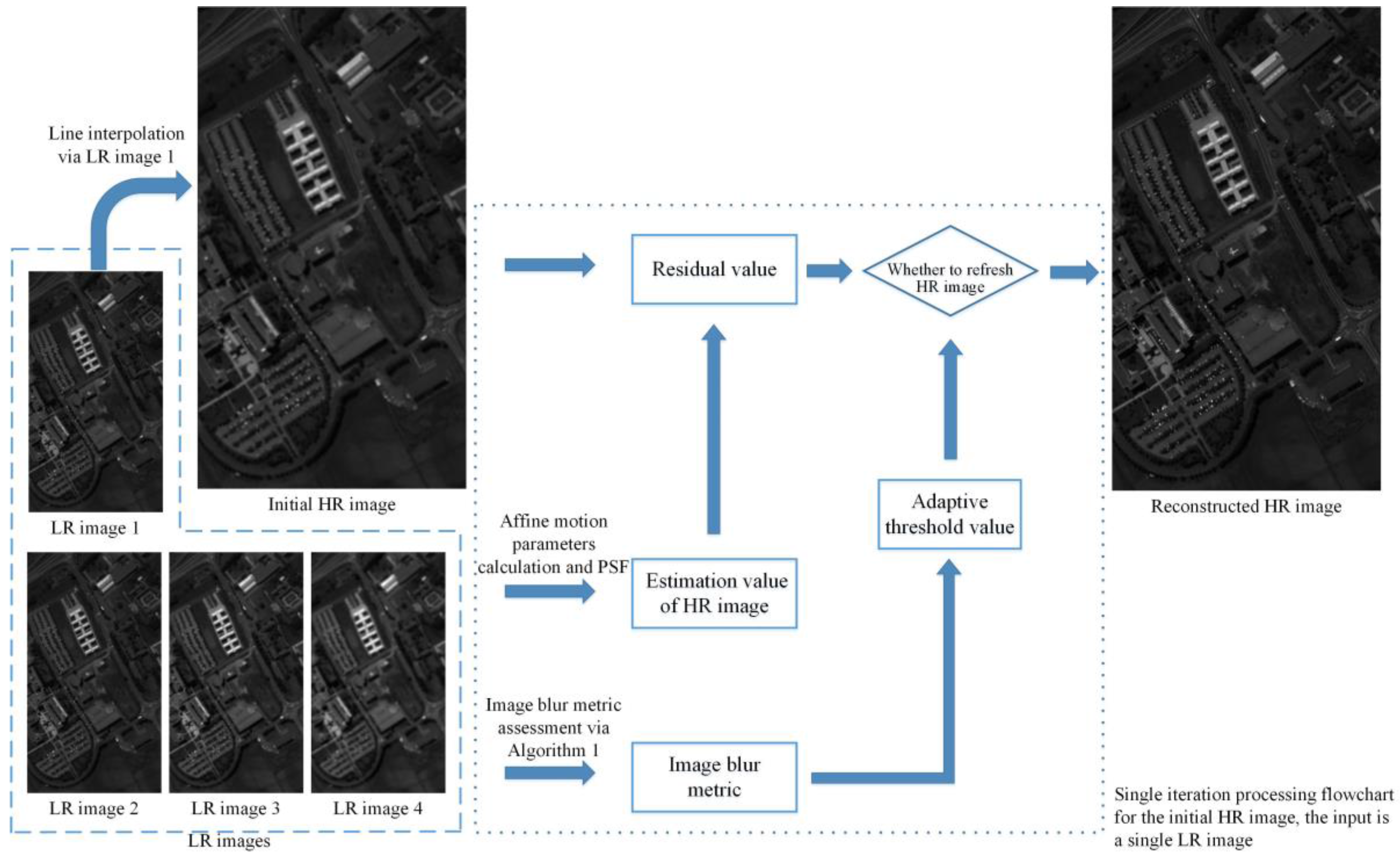
3.2. Proposed APOCS-Blur Metrics (BM) Method
| Algorithm 2. Steps of the proposed APOCS-BM method: |
| Step 1: Set the initial value of p (Equation (5)), α, β, t0 (Equation (13)) and iteration number Itn; |
| Step 2: Gain the initial HR image H from the LR image L1 by linear interpolation, calculate the AIBM[m1,m2] and for each LR image L1~L4; |
| Step 3: For i = 1,2, …, Itn |
| for j = 1,2, 3, 4 |
| Step 3.1: Calculate the affine motion parameters for LR image Lj; |
| Step 3.2: Gain the estimation value Hes of H via the affine motion parameters and point spread function; |
| Step 3.3: Calculate the residual Rj(i); |
| Step 3.4: Calculate the adaptive threshold value δk[m1,m2]; |
| Step 3.5: If Rj(i) > δk[m1,m2] or Rj(i) < −δk[m1,m2] |
| Step 3.5.1: refresh H with the estimation value Hes; |
| end If |
| end for |
| end for |
| Step 4: output the reconstructed HR image H. |
4. Experiments and Results
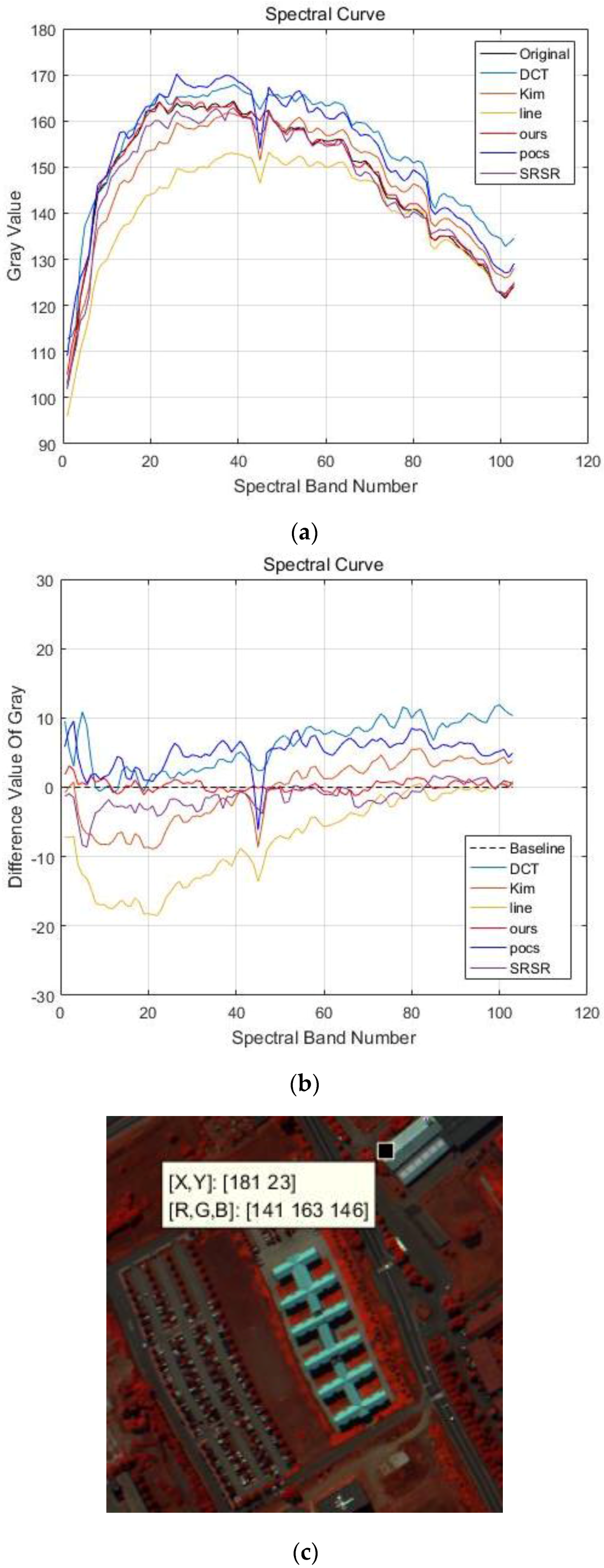
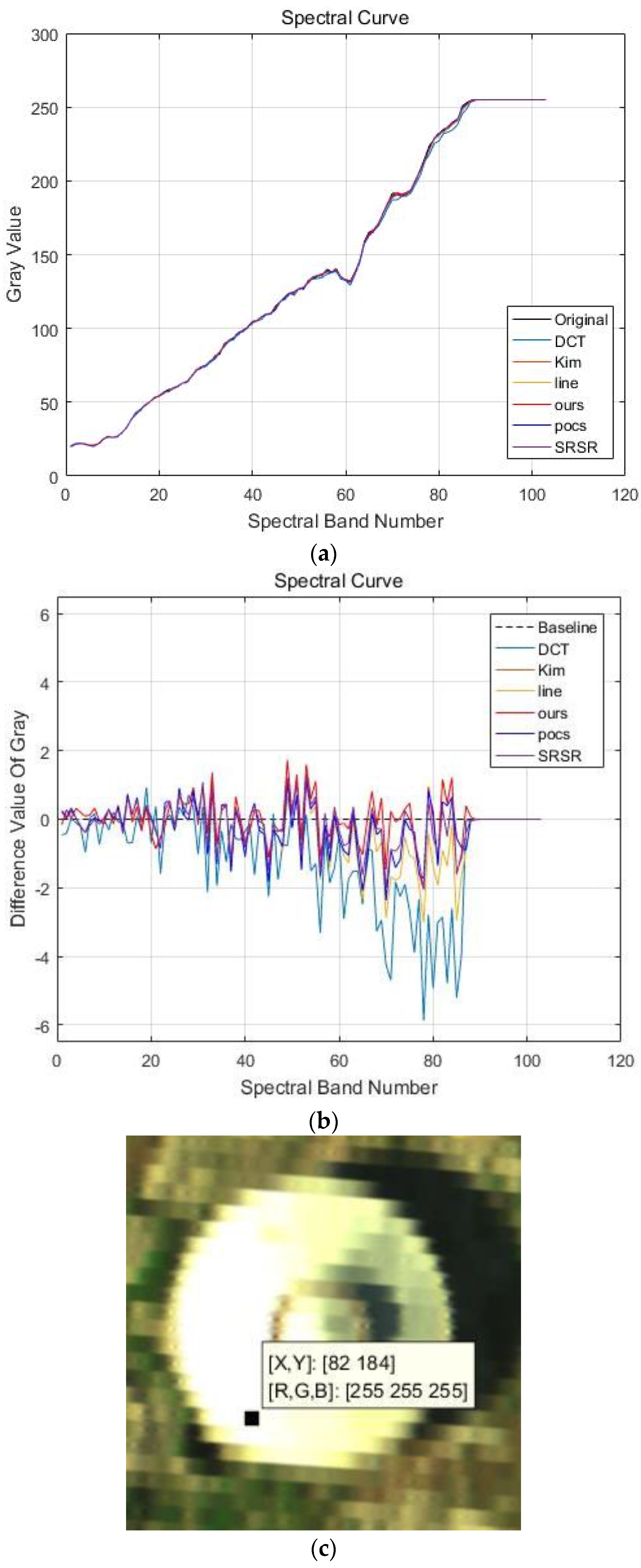
4.1. PaviaU and PaviaC Dataset
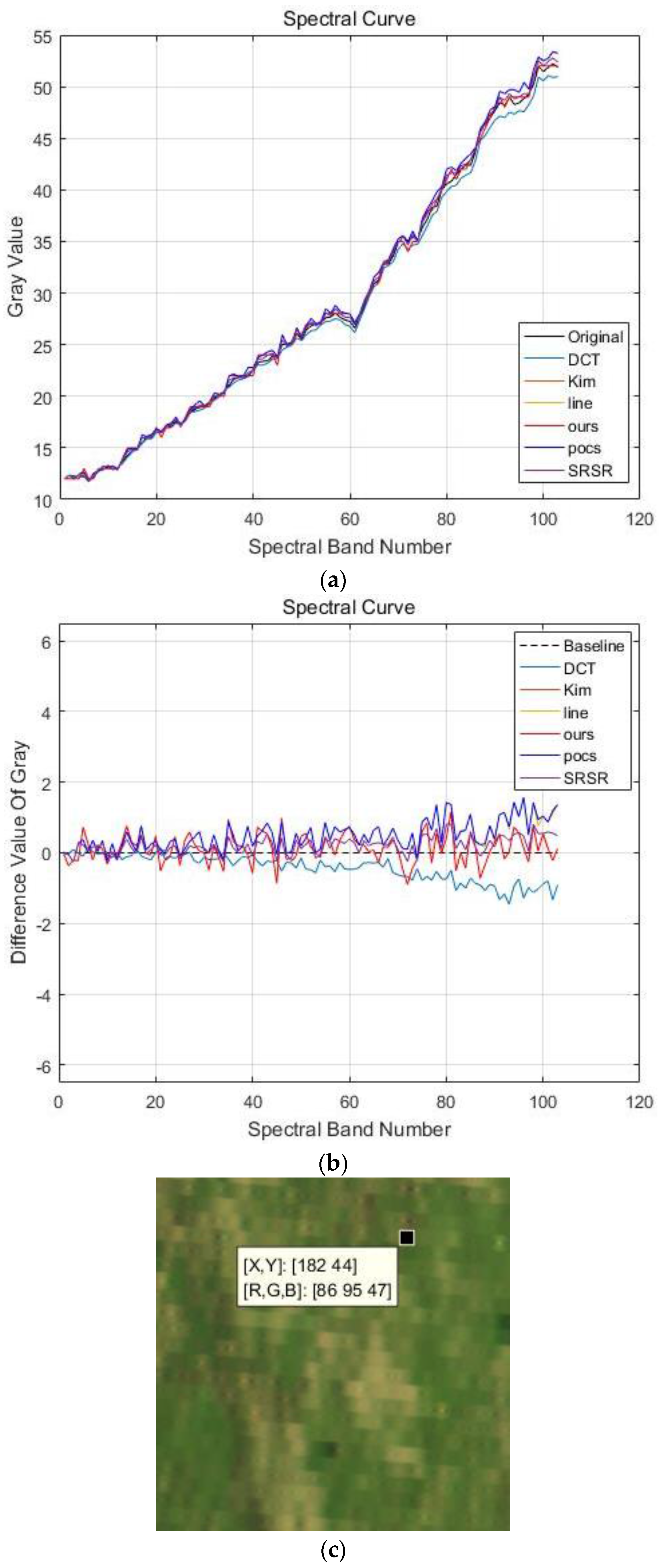
4.2. Jinyin Tan Dataset
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bioucas-Dias, J.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Thomas, C.; Ranchin, T.; Wald, L.; Chanussot, J. Synthesis of multispectral images to high spatial resolution: A critical review of fusion methods based on remote sensing physics. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1301–1312. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; ElMasry, G.; Sun, D.W.; Allen, P. Non-destructive prediction and visualization of chemical composition in lamb meat using NIR hyperspectral imaging and multivariate regression. Innov. Food Sci. Emerg. Technol. 2012, 16, 218–226. [Google Scholar] [CrossRef]
- Granero-Montagud, L.; Portalés, C.; Pastor-Carbonell, B.; Ribes-Gómez, E.; Gutiérrez-Lucas, A.; Tornari, V.; Papadakis, V.; Groves, R.M.; Sirmacek, B.; Bonazza, A.; et al. Deterioration estimation of paintings by means of combined 3D and hyperspectral data analysis. Proc. SPIE 2013, 8790. [Google Scholar] [CrossRef]
- Scafutto, R.D.P.M.; de Souza Filho, C.R.; Rivard, B. Characterization of mineral substrates impregnated with crude oils using proximal infrared hyperspectral imaging. Remote Sens. Environ. 2016, 179, 116–130. [Google Scholar] [CrossRef]
- Calin, M.A.; Parasca, S.V.; Savastru, R.; Manea, D. Characterization of burns using hyperspectral imaging technique–A preliminary study. Burns 2015, 41, 118–124. [Google Scholar] [CrossRef] [PubMed]
- Goto, A.; Nishikawa, J.; Kiyotoki, S.; Nakamura, M.; Nishimura, J.; Okamoto, T.; Ogihara, H.; Fujita, Y.; Hamamoto, Y.; Sakaida, I. Use of hyperspectral imaging technology to develop a diagnostic support system for gastric cancer. J. Biomed. Opt. 2015, 20. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, L.; Shen, H.A. Super-resolution reconstruction algorithm for hyperspectral images. Signal Process. 2012, 92, 2082–2096. [Google Scholar] [CrossRef]
- Tsai, R.Y.; Huang, T.S. Multiple Frame Image Restoration and Registration. In Advances in Computer Vision and Image Processing; JAI Press Inc.: Greenwich, CT, USA, 1984; pp. 317–339. [Google Scholar]
- Yaroslavsky, L.; Happonen, A.; Katyi, Y. Signal discrete sinc-interpolation in DCT domain: Fast algorithms; SMMSP: Toulouse, France, 2002; pp. 7–9. [Google Scholar]
- Anbarjafari, G.; Demirel, H. Image super resolution based on interpolation of wavelet domain high frequency subbands and the spatial domain input image. ETRI J. 2010, 32, 390–394. [Google Scholar] [CrossRef]
- Ji, H.; Fermüller, C. Robust wavelet-based super-resolution reconstruction: Theory and algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 649–660. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Xu, Z.; Shum, H.Y. Image Super-Resolution Using Gradient Profile Prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8.
- Irani, M.; Peleg, S. Improving Resolution by Image Registration. CVGIP Graph. Models Image Process. 1991, 53, 231–239. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L.; Huang, B.; Li, P. A MAP approach for joint motion estimation, segmentation, and super resolution. IEEE Trans. Image Process. 2007, 16, 479–490. [Google Scholar] [CrossRef] [PubMed]
- Elad, M.; Feuer, A. Superresolution restoration of an image sequence: Adaptive filtering approach. IEEE Trans. Image Process. 1999, 8, 387–395. [Google Scholar] [CrossRef] [PubMed]
- Stark, H.; Oskoui, P. High-resolution image recovery from image-plane arrays, using convex projections. JOSA A 1989, 6, 1715–1726. [Google Scholar] [CrossRef]
- Xu, Z.Q.; Zhu, X.C. Super-Resolution Reconstruction of Compressed Video Based on Adaptive Quantization Constraint Set. In Proceedings of the First International Conference on Innovative Computing, Information and Control, Beijing, China, 30 August–1 September 2006; pp. 281–284.
- Kim, K.I.; Kwon, Y. Example-Based Learning for Single-Image Super-Resolution, Joint Pattern Recognition Symposium; Springer: Berlin/Heidelberg, Germany, 2008; pp. 456–465. [Google Scholar]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image super-resolution via sparse representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Marcia, R.F.; Willett, R.M. Compressive Coded Aperture Super Resolution Image Reconstruction. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 833–836.
- Pan, Z.; Yu, J.; Huang, H.; Hu, S.; Zhang, A.; Ma, H.; Sun, W. Super-resolution based on compressive sensing and structural self-similarity for remote sensing images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4864–4876. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Cho, S.; Finkelstein, A.; Rusinkiewicz, S. A no-reference metric for evaluating the quality of motion deblurring. ACM Trans. Graph. 2013, 32. [Google Scholar] [CrossRef]
- Kerouh, F.; Serir, A. A no reference quality metric for measuring image blur in wavelet domain. Int. J. Digit. Inf. Wirel. Commun. 2012, 4, 767–776. [Google Scholar]
- Li, H.; Zhang, A.; Hu, S. A Multispectral Image Creating Method for a New Airborne Four-Camera System with Different Bandpass Filters. Sensors 2015, 15, 17453–17469. [Google Scholar] [CrossRef] [PubMed]
- Zhang, A.; Hu, S.; Meng, X.; Yang, L.; Li, H. Toward High Altitude Airship Ground-Based Boresight Calibration of Hyperspectral Pushbroom Imaging Sensors. Remote Sens. 2015, 7, 17297–17311. [Google Scholar] [CrossRef]








| Measures | Linear Interpolation | DCT-Based Method [10] | Kim [19] | POCS [17] | SR-SR Method [20] | Proposed Method |
|---|---|---|---|---|---|---|
| A-PSNR | 20.8478 | 24.9727 | 25.1193 | 25.7390 | 26.9570 | 28.5050 |
| A-SSIM | 0.5347 | 0.6824 | 0.7108 | 0.7161 | 0.8069 | 0.8435 |
| SAM | 0.2148 | 0.1192 | 0.1100 | 0.1002 | 0.1016 | 0.0817 |
| Measures | Linear Interpolation | DCT-Based Method [10] | Kim [19] | POCS [17] | SR-SR Method [20] | Proposed Method |
|---|---|---|---|---|---|---|
| A-PSNR | 21.4309 | 25.6022 | 25.7052 | 26.3187 | 27.3867 | 29.0013 |
| A-SSIM | 0.4959 | 0.6539 | 0.6761 | 0.6816 | 0.7916 | 0.8292 |
| SAM | 0.2633 | 0.1333 | 0.1225 | 0.1093 | 0.1208 | 0.0949 |
| Measures | Linear Interpolation | DCT-Based Method [10] | Kim [19] | POCS [17] | SR-SR Method [20] | Proposed Method |
|---|---|---|---|---|---|---|
| A-PSNR | 37.9661 | 40.0457 | 40.0424 | 40.1739 | 43.8014 | 44.7879 |
| A-SSIM | 0.9608 | 0.9696 | 0.9720 | 0.9727 | 0.9869 | 0.9885 |
| SAM | 0.0876 | 0.0621 | 0.0600 | 0.0572 | 0.0588 | 0.0411 |
| Measures | Line Interpolation | DCT-Based Method [10] | Kim [19] | POCS [17] | SR-SR Method [20] | Proposed Method |
|---|---|---|---|---|---|---|
| A-PSNR | 47.3629 | 52.4696 | 50.7218 | 50.7808 | 51.1665 | 55.5370 |
| A-SSIM | 0.9897 | 0.9905 | 0.9910 | 0.9914 | 0.9947 | 0.9966 |
| SAM | 0.0610 | 0.0544 | 0.0474 | 0.0488 | 0.0448 | 0.0405 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Zhang, S.; Zhang, A.; Chai, S. Hyperspectral Imagery Super-Resolution by Adaptive POCS and Blur Metric. Sensors 2017, 17, 82. https://doi.org/10.3390/s17010082
Hu S, Zhang S, Zhang A, Chai S. Hyperspectral Imagery Super-Resolution by Adaptive POCS and Blur Metric. Sensors. 2017; 17(1):82. https://doi.org/10.3390/s17010082
Chicago/Turabian StyleHu, Shaoxing, Shuyu Zhang, Aiwu Zhang, and Shatuo Chai. 2017. "Hyperspectral Imagery Super-Resolution by Adaptive POCS and Blur Metric" Sensors 17, no. 1: 82. https://doi.org/10.3390/s17010082
APA StyleHu, S., Zhang, S., Zhang, A., & Chai, S. (2017). Hyperspectral Imagery Super-Resolution by Adaptive POCS and Blur Metric. Sensors, 17(1), 82. https://doi.org/10.3390/s17010082





