A Truthful Incentive Mechanism for Online Recruitment in Mobile Crowd Sensing System
Abstract
:1. Introduction
- To the best of our knowledge, this is the first truthful incentive based on auction theory with consideration of ex post service qualities and dynamically-arriving users in a new MCS system without requiring previous knowledge of users. In TOAM, the platform learns users’ expected service qualities and makes sequential online decisions on winner selections with an exploration-exploitation trade-off.
- To achieve truthfulness with the consideration of computational efficiency in our situation, we adopt a framework proposed in [12] and design a novel ex post monotone allocation rule to select proper winners.
- We analyze if TOAM possesses truthfulness, individual rationality and computational efficiency theoretically. Besides, extensive simulation results on both real and synthetic traces verify the efficient of our incentive TOAM, which can decrease the payments, improve the utility of the platform and social welfare.
2. System Model, Technical Preliminaries and Problem Formulation
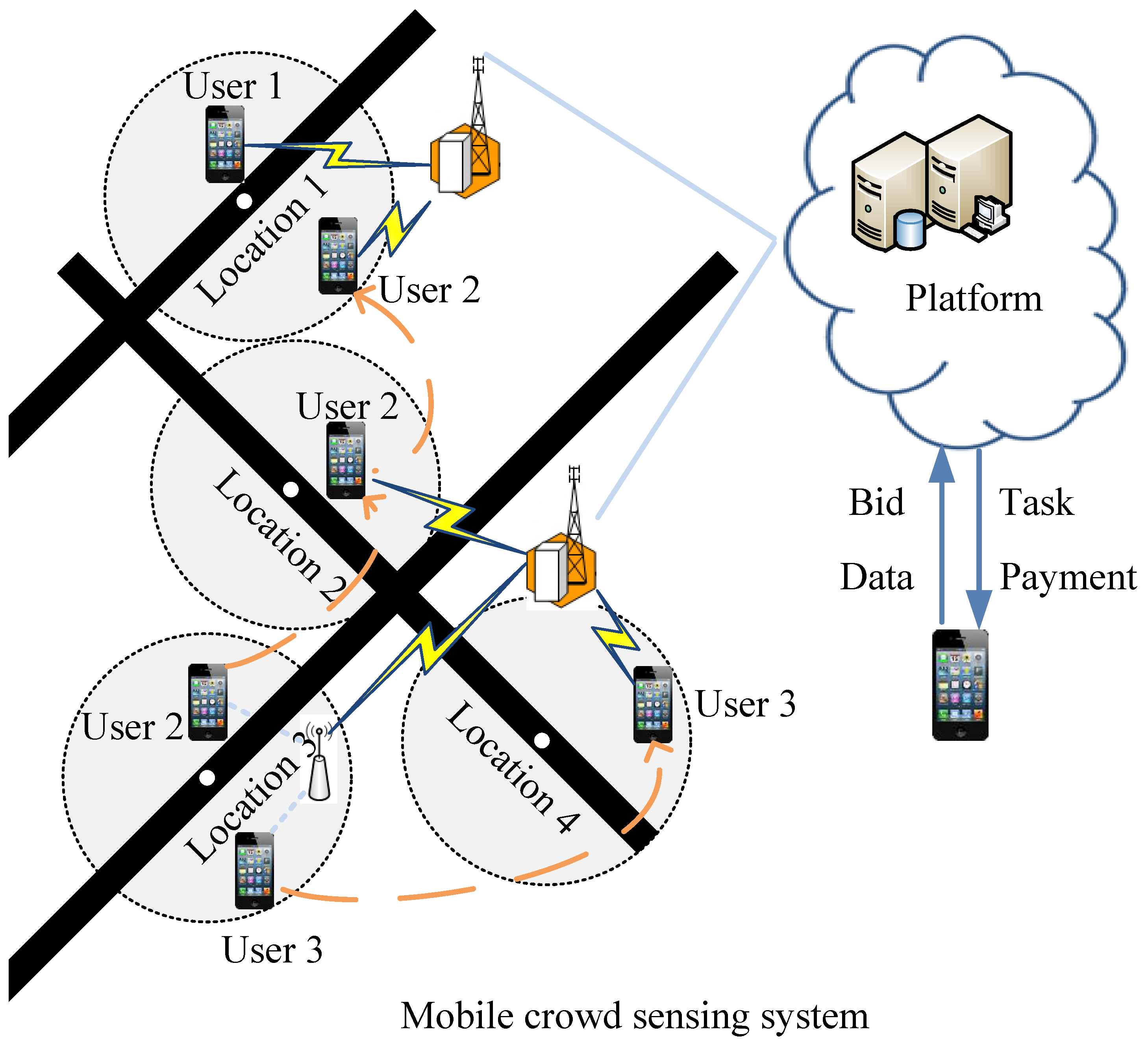
2.1. System Model
2.2. Technical Preliminaries
2.3. Problem Formulation
- User i submits his or her bidding price (i.e., when he or she participates in the system for the first time.
- The platform computes user i’s new bidding price for allocation as follows. With probability , ; else, ,where is picked uniformly at random.
- For every time slot t, the platform assigns sensing jobs to users for every sensing location according to the allocation rule , where consists of new bidding prices for all users in .
- The platform calculates users’ payments as follows. For every selected user i, if ; otherwise . For any other unselected user k, .
3. Incentive Mechanism Design
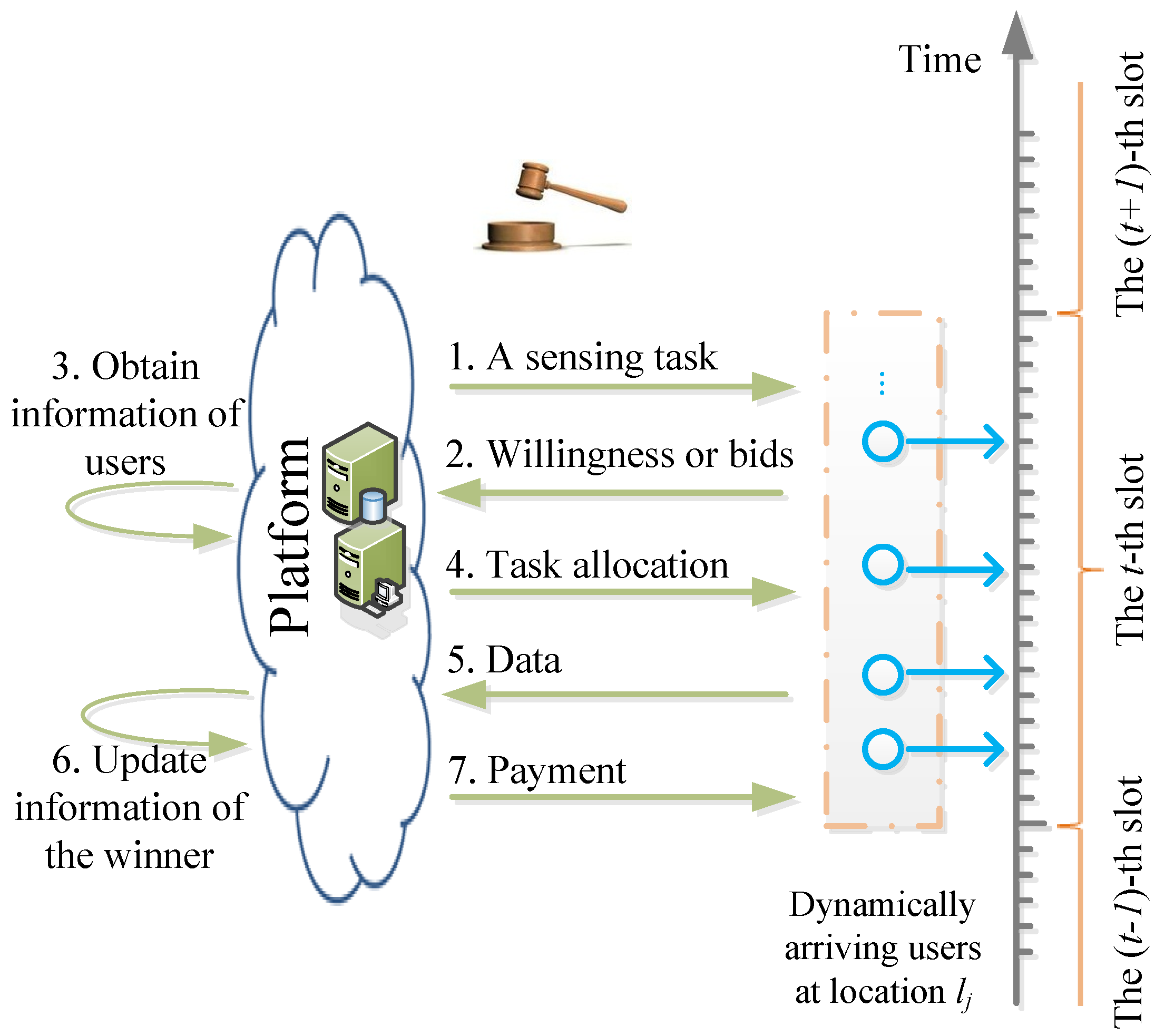
3.1. System Overview
- The platform announces the sensing job when users arrive at location .
- If users are new in the system, they create and submit their optimal bidding prices for this job to the platform independently. Otherwise, users are just required to show their willingness of participation.
- The platform obtains users’ information for this allocation. If users are new, the platform gets and records their bidding prices from their bids. Otherwise, the system obtains users’ information from the storage, including users’ bidding prices, estimated expected service qualities, and so on.
- Based on users’ new bidding prices perturbed by the platform randomly and users’ expected service qualities observed by the platform, the platform selects a winner to perform this job.
- At the end of time t, the winner submits sensory data to the platform.
- The platform updates the information of the winner if necessary according to the allocation rule.
- The platform pays the winner with a rational price.
3.2. Allocation Algorithm
- For one job, construct an active set of users according to a bidding bound (reserve price) for a later random selection. In order to decrease the winning probability of the liar, we select a bidding bound from the arriving bidding prices with some probabilities. If users’ bidding prices are higher than the bidding bound, remove these users from the set of arriving users. The rest of arriving users construct the active set. To avoid removing too many users at the beginning of the system, the probability of selecting a low bidding bound increases with the passage of time.
- With the increasing updated number, we estimate users’ expected service qualities in the non-decreasing trend. By doing so, it reduces the uncertain influence of being selected on the learned expected service qualities.
- Update winners’ information (including the expected service qualities) if they are selected randomly. Due to the liar’s overstated bidding price, some others may win instead of the liar. We call these winners direct-winners. These direct-winners’ expected service qualities may be improved in this way. Thus, the liar’s winning probability can be reduced to a certain extent in the future.
- Do not update winners’ information if they are selected according to the price-quality ratios. If winners are selected according to price-quality ratios, the updated information of direct-winners may affect the results. However, as winners’ information remains the same in this way, the direct-winners will not disturb others more. Therefore, the influence of the liar is controlled.
- : We randomly select a new user as the winner from . We call users who have joined the system, but have not undertaken sensory jobs new users. The platform updates the winner’s corresponding information with the observed winner’s actual service quality at the end of time slot t by calling updating Algorithm 2 (UpdateInformationofWinner).
- : The platform selects the winner randomly with the bidding bound limitation. There are three steps. Firstly, we randomly designate a user from . Secondly, construct an active set of users with the bidding bound limitation. Thirdly, if the designated user is in the active set , he or she is the winner. Then, update the winner’s corresponding information at the end of time slot t by calling updating Algorithm 2 (UpdateInformationofWinner).
- : If the randomly-designated user is not in , the platform optimistically picks the user with the highest estimated price-quality ratio among the users in .
| Algorithm 1: Allocation algorithm. |
 |
| Algorithm 2: UpdateInformationofWinner. |
| 1 //Input: user i; 2 Update the number of being randomly selected ; 3 Add the observed service quality to the total service quality ; 4 Update the learned expected service quality ); |
4. Theoretic Analysis
- : It is easy to see with different bid vectors if he or she is new in the system at . Therefore, the lemma is true.
- : User i can be selected if user i is designated and stays in the active set. Now, we analyze user i’s probability of satisfying these two conditions. (1) As the random designated user is irrelevant with respect to his or her bidding price, user i’s probability of being designated is not related to the bid vector. (2) The selection of the ranking index bound is independent of the users’ bidding prices. Therefore, the ranking index bound is the same with different bid vectors. Since , the ranking index of user i with bid vector B is not larger than that with bid vector . Therefore, user i’s probability of staying in the active set with bid vector B is not lower than that with bid vector . To sum up, . Since the service quality increases with the updated number and , we can get .
- : From the proof of Lemma 1, we can see, .
- : User j can be selected if user j is the designated user and remains in the active set. As shown in the proof of Lemma 1, user j’s probability of being randomly designated with bid vector B is equal to that with bid vector . Now, we compute user j’s probability of being in the active set. Since users join the system dynamically, user j may meet with user i at time . If user j and user i come across at time , the ranking index of user j with bid vector B is not smaller than that with bid vector due to . If user j does not meet with user i at time , the ranking index of user j with B equals that with . Therefore, user j’s probability of staying in the active set with B is not higher than that with . From the above analysis, we can see . Since the service quality increases with the updated number and , we can derive at the end of time .
- User g () is the designated one, but user g is not in active set . As shown in the case of Lemma 2, user g’s probability of being in active set with B is not lower than that with .
- User i is in active set . As shown in the case of Lemma 1, user i’s probability of being in with B is not lower than that with .
- User i has the highest estimated price-quality ratio among active users in . Since is known from Lemma 1 and , we can derive . For any other competitor g (), we can derive due to , which is known from Lemma 2. Therefore, the probability of having the highest estimated price-quality ratio with bid vector B is not lower than that with .
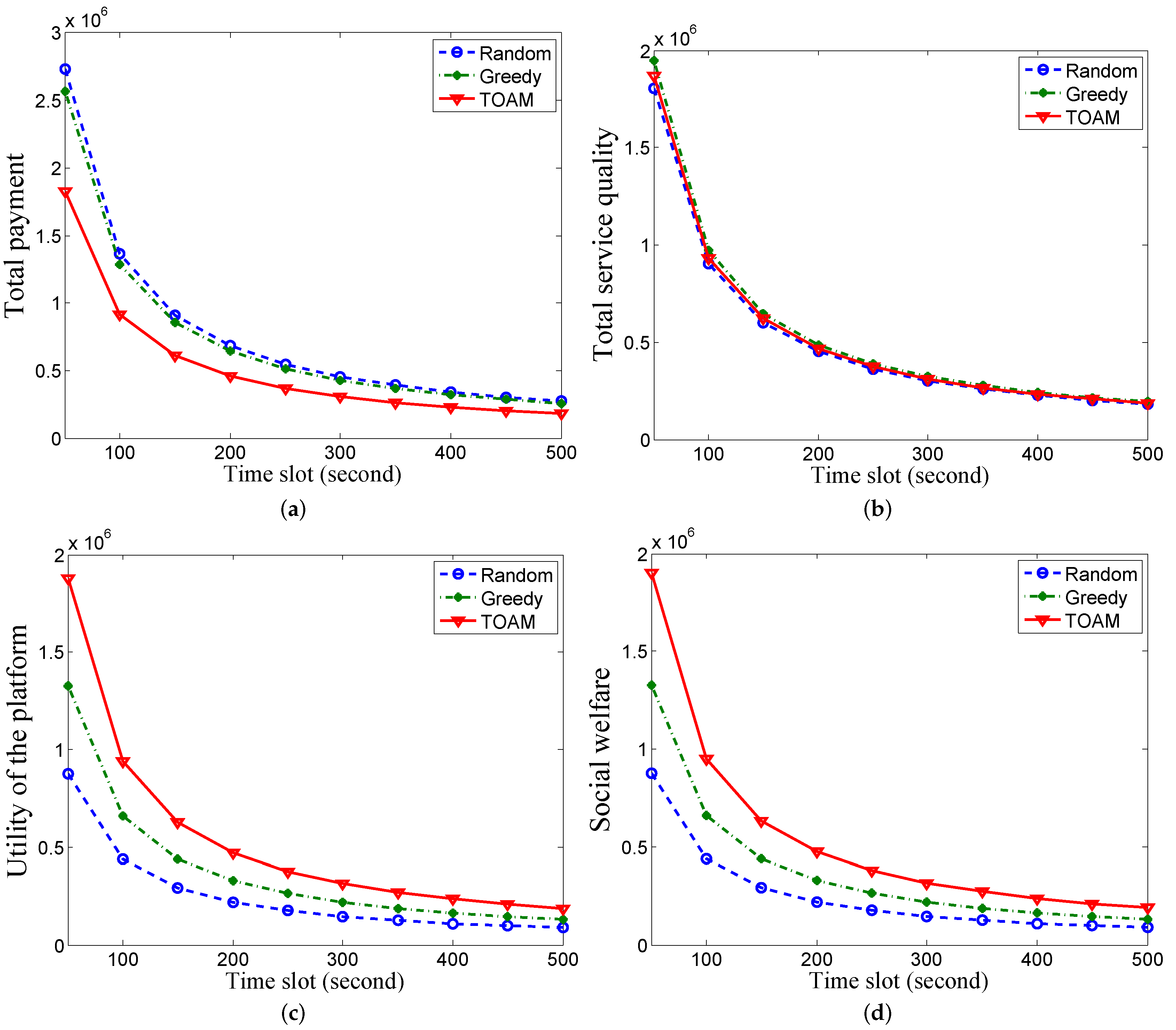
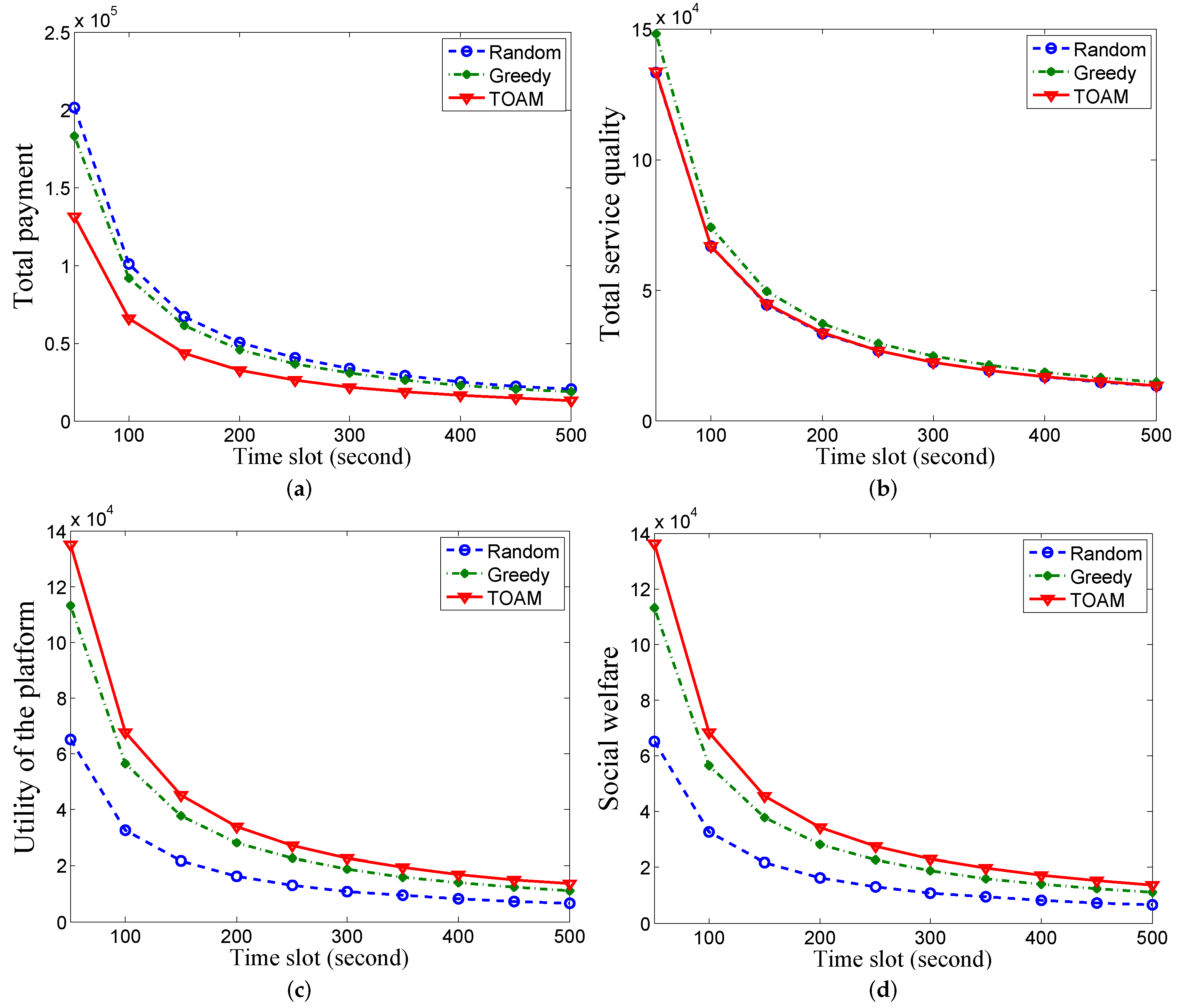
5. Performance Evaluation
5.1. Simulation Setup
5.2. Comparing Algorithms
5.3. Performance Comparison
6. Related Work
6.1. Incentive Mechanisms for the Mobile Crowd Sensing System
6.2. Truthful Single-Parameter Mechanisms
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sensorly. Available online: http://www.sensorly.com/ (accessed on 1 August 2016).
- Mobile Millennium. Available online: http://traffic.berkeley.edu/ (accessed on 2 August 2016).
- WeatherLah. Available online: http://www.weatherlah.com/ (accessed on 2 August 2016).
- Mathur, S.; Jin, T.; Kasturirangan, N.; Chandrasekaran, J.; Xue, W.; Gruteser, M.; Trappe, W. Parknet: Drive-by sensing of road-side parking statistics. In Proceedings of the 8th International Conference on Mobile Systems, Applications, and Services, San Francisco, CA, USA, 15–18 June 2010.
- Koutsopoulos, I. Optimal incentive-driven design of participatory sensing systems. In Proceedings of the 2013 IEEE International Conference on Computer Communications, Turin, Italy, 14–19 April 2013.
- Jin, H.; Su, L.; Chen, D.; Nahrstedt, K.; Xu, J. Quality of information aware incentive mechanisms for mobile crowdsensing systems. In Proceedings of the 16th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Hangzhou, China, 22–25 June 2015.
- Wen, Y.; Shi, J.; Zhang, Q.; Tian, X.; Huang, Z.; Yu, H.; Cheng, Y.; Shen, X. Quality-driven auction-based incentive mechanism for mobile crowd sensing. IEEE Trans. Veh. Technol. 2015, 64, 4203–4214. [Google Scholar] [CrossRef]
- Tham, C.K.; Luo, T. Quality of contributed service and market equilibrium for participatory sensing. IEEE Trans. Mobile Comput. 2013, 14, 133–140. [Google Scholar]
- Kawajiri, R.; Shimosaka, M.; Kashima, H. Steered crowdsensing: Incentive design towards quality-oriented place-centric crowdsensing. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle, WA, USA, 13–17 September 2014.
- Song, Z.; Liu, C.H.; Wu, J.; Ma, J.; Wang, W. QoI-aware multitask-oriented dynamic participant selection with budget constraints. IEEE Trans. Veh. Technol. 2014, 63, 4618–4632. [Google Scholar] [CrossRef]
- Klemperer, P. What really matters in auction design. J. Econ. Perspect. 2002, 16, 169–189. [Google Scholar] [CrossRef]
- Babaioff, M.; Kleinberg, R.D.; Slivkins, A. Truthful mechanisms with implicit payment computation. In Proceedings of the 11th ACM conference on Electronic Commerce, Cambridge, MA, USA, 7–11 June 2010.
- Paladi, N.; Gehrmann, C.; Michalas, A. Providing end-user security guarantees in public infrastructure clouds. IEEE Trans. Cloud Comput. 2016. [Google Scholar] [CrossRef]
- Yun, C.; Li, X.C.; Li, Z.J.; Jiang, S.X.; Li, Y.L.; Ji, J.; Jiang, X.F. AirCloud: A cloud-based air-quality monitoring system for everyone. In Proceedings of the 12th ACM Conference on Embedded Network Sensor Systems, Memphis, TN, USA, 3–6 November 2014.
- Li, Q.; Li, Y.; Gao, J.; Zhao, B.; Fan, W.; Han, J. Resolving conflicts in heterogeneous data by truth discovery and source reliability estimation. In Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data, Snowbird, UT, USA, 22–27 June 2014.
- Su, L.; Li, Q.; Hu, S.; Wang, S. Generalized decision aggregation in distributed sensing systems. In Proceedings of the 2014 IEEE Real-Time Systems Symposium, Rome, Italy, 2–5 December 2014.
- Wang, S.; Wang, D.; Su, L.; Kaplan, L. Towards cyber-physical systems in social spaces: The data reliability challenge. In Proceedings of the Real-Time Systems Symposium, Rome, Italy, 2–5 December 2014.
- Myerson, R.B. Optimal auction design. Math. Oper. Res. 1981, 6, 58–73. [Google Scholar] [CrossRef]
- Shnayder, V.; Parkes, D.C.; Kawadia, V.; Hoon, J. Truthful prioritization for dynamic bandwidth sharing. In Proceedings of the 15th International Symposium on Mobile Ad Hoc Networking and Computing, Philadelphia, PA, USA, 11–14 August 2014.
- Wang, J.; Tang, J.; Yang, D.; Wang, E.; Xue, G. Quality-aware and fine-grained incentive mechanisms for mobile crowdsensing. In Proceedings of the 2014 IEEE 36th International Conference on Distributed Computing Systems, Nara, Japan, 27–30 June 2016.
- Kotz, D.; Henderson, T.; Abyzov, I.; Yeo, J. CRAWDAD Data Set Dartmouth/Campus/Movement. Available online: http://crawdad.org/dartmouth/campus/ (accessed on 8 March 2005).
- Hsu, W.J.; Spyropoulos, T.; Psounis, K.; Helmy, A. Modeling time-variant user mobility in wireless mobile networks. In Proceedings of the 2013 IEEE International Conference on Computer Communications, Anchorage, AL, USA, 6–12 May 2007.
- Balazinska, M.; Castro, P. Characterizing mobility and network usage in a corporate wireless local-area network. In Proceedings of the 2nd International Conference on Mobile Systems, Applications, and Services, San Francisco, CA, USA, 5–8 May 2003.
- Mukherjee, T.; Chander, D.; Mondal, A.; Dasgupta, K.; Kumar, A.; Venkat, A. CityZen: A cost-effective city management system with incentive-driven resident engagement. In Proceedings of the 2014 IEEE 15th International Conference on Mobile Data Management, Brisbane, Australia, 15–18 July 2014.
- Peng, D.; Wu, F.; Chen, G. Pay as how well you do: A quality based incentive mechanism for crowdsensing. In Proceedings of the 16th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Hangzhou, China, 22–25 June 2015.
- Han, Y.; Zhu, Y. Profit-maximizing stochastic control for mobile crowd sensing platforms. In Proceedings of the 2014 IEEE 11th International Conference on Mobile Ad Hoc and Sensor Systems, Philadelphia, PA, USA, 27–30 October 2014.
- Karaliopoulos, M.; Telelis, O.; Koutsopoulos, I. User recruitment for mobile crowdsensing over opportunistic networks. In Proceedings of the 2015 IEEE International Conference on Computer Communications, Hong Kong, China, 26 April–1 May 2015.
- Xiao, M.; Wu, J.; Huang, L.; Wang, Y.; Liu, C. Multi-task assignment for crowdsensing in mobile social networks. In Proceedings of the 2015 IEEE International Conference on Computer Communications, Hong Kong, China, 26 April–May 2015.
- Yang, D.; Xue, G.; Fang, X.; Tang, J. Crowdsourcing to smartphones: Incentive mechanism design for mobile phone sensing. In Proceedings Of the 18th Annual International Conference on Mobile Computing and Networking, Istanbul, Turkey, 22–26 August 2012.
- Feng, Z.; Zhu, Y.; Zhang, Q.; Ni, L.M.; Vasilakos, A.V. TRAC: Truthful auction for location-aware collaborative sensing in mobile crowdsourcing. In Proceedings of the 2014 IEEE International Conference on Computer Communication, Toronto, ON, Canada, 27 April–2 May 2014.
- Zeng, Y.; Li, D. A self-adaptive behavior-aware recruitment scheme for participatory sensing. Sensors 2015, 15, 23361–23375. [Google Scholar] [CrossRef] [PubMed]
- Michalas, A.; Komninos, N. The lord of the sense: A privacy preserving reputation system for participatory sensing applications. In Proceedings of 2014 the IEEE Symposium on Computers and Communications, Madeira, Portugal, 23–26 June 2014.
- Zhang, X.; Yang, Z.; Zhou, Z.; Cai, H.; Chen, L.; Li, X. Free market of crowdsourcing: Incentive mechanism design for mobile sensing. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 3190–3200. [Google Scholar] [CrossRef]
- Zhao, D.; Li, X.Y.; Ma, H. How to crowdsource tasks truthfully without sacrificing utility: Online incentive mechanisms with budget constraint. In Proceedings of the 2014 IEEE International Conference on Computer Communication, Toronto, ON, Canada, 27 April–2 May 2014.
- Feng, Z.; Zhu, Y.; Zhang, Q.; Zhu, H.; Yu, J.; Cao, J.; Ni, L.M. Towards truthful mechanisms for mobile crowdsourcing with dynamic smartphones. In Proceedings of the 2014 IEEE 34th International Conference on Distributed Computing Systems, Madrid, Spain, 30 June–3 July 2014.
- Gao, L.; Hou, F.; Huang, J. Providing long-term participation incentive in participatory sensing. In Proceedings of the 2015 IEEE International Conference on Computer Communication, Hong Kong, China, 26 April–1 May 2015.
- Archer, A.; Tardos, E. Truthful mechanism for one-parameter agents. In Proceedings of the 2001 IEEE Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 14–17 October 2001.
- Jain, S.; Gujar, S.; Bhat, S.; Zoeter, O.; Narahari, Y. An incentive compatible multi-armed-bandit crowdsourcing mechanism with quality assurance. Arx. Prepr. 2014; arXiv:1406.7157. [Google Scholar]
| Notation | Description |
|---|---|
| N, i | Set of users and a user. |
| n | Number of users. |
| T, t | Deadline and a time slot. |
| L, | Set of locations and the j-th location. |
| Set of arriving users at a location at time slot t. | |
| , | User i’s cost and bidding price. |
| User i’s new bidding price for allocation. | |
| , | Maximum and minimum cost. |
| , , | User i’s service quality at time slot t, expected service quality and learned expected service quality. |
| , | User i’s payment and utility at time slot t. |
| Utility of the platform. | |
| Active set of users at location at time slot t. | |
| User i’s number of being randomly selected. | |
| , | User i’s total observed service quality and observed service quality at time slot t. |
| Others’ bidding prices, except user i. | |
| User i’s alternate bidding price that is higher than . | |
| B | Bid vector of all users with and . |
| Alternate bid vector of all users with and . | |
| , | User i’s learned expected service quality at time slot t with the bid vector B and . |
| , | User i’s probability of being selected at time slot t with the bid vector B and . |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Liu, M.; Zhou, Y.; Li, Z.; Chen, S.; He, X. A Truthful Incentive Mechanism for Online Recruitment in Mobile Crowd Sensing System. Sensors 2017, 17, 79. https://doi.org/10.3390/s17010079
Chen X, Liu M, Zhou Y, Li Z, Chen S, He X. A Truthful Incentive Mechanism for Online Recruitment in Mobile Crowd Sensing System. Sensors. 2017; 17(1):79. https://doi.org/10.3390/s17010079
Chicago/Turabian StyleChen, Xiao, Min Liu, Yaqin Zhou, Zhongcheng Li, Shuang Chen, and Xiangnan He. 2017. "A Truthful Incentive Mechanism for Online Recruitment in Mobile Crowd Sensing System" Sensors 17, no. 1: 79. https://doi.org/10.3390/s17010079
APA StyleChen, X., Liu, M., Zhou, Y., Li, Z., Chen, S., & He, X. (2017). A Truthful Incentive Mechanism for Online Recruitment in Mobile Crowd Sensing System. Sensors, 17(1), 79. https://doi.org/10.3390/s17010079





