Local Coverage Optimization Strategy Based on Voronoi for Directional Sensor Networks †
Abstract
:1. Introduction
- We transform the network area coverage problem into cell coverage problems by exploiting the Voronoi diagram, which only needs to optimize local coverage for each cell. The proposed approach solves the problem in a decentralized way.
- By adopting a node’s moving or rotation actions, we propose three local coverage optimization algorithms to improve the cell coverage, i.e., Move Inside Cell Algorithm (MIC), Rotate Working Direction Algorithm (RWD), Rotation based on boundary (RB), respectively.
- We use extensive simulations to prove the effectiveness of our proposed algorithms in terms of the coverage ratio. Specifically, compared to the benchmark algorithm Distributed Voronoi-Based SelRedeployment algorithm (DVSA) proposed in [8], our algorithm MIC shows a shorter moving distance and lower energy consumption.
2. Related Work
3. System Model and Problem Statement
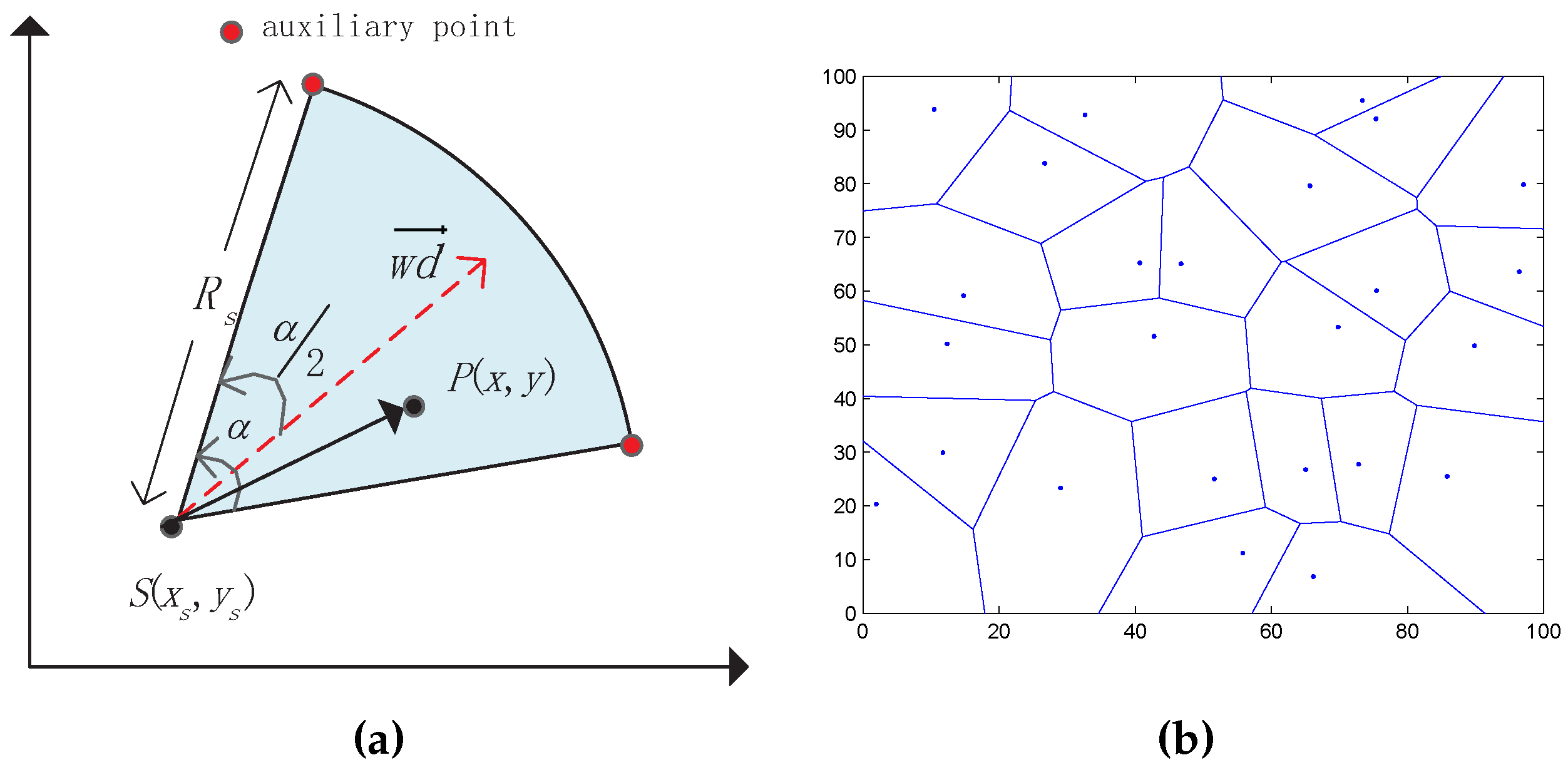
3.1. DSN Sensing Model
- Euclidean distance between p and s must be smaller than sensing radius , i.e., :
- The absolute included angle between and must be smaller then :
3.2. Voronoi Diagram and Some Assumptions
- All of the directional sensors are homogeneous, that is to say, every sensor has the same sensing radius , viewing angle α, rotation ability and mobility.
- We can obtain an accurate coordinate of every sensor node by using Global Position System (GPS) or other alternative localization algorithms such as DV-hop, Amorphous, etc.
- All of the sensor nodes have strong transmission ability to ensure the network connectivity and Voronoi diagram constructed successfully.
3.3. Problem Statement
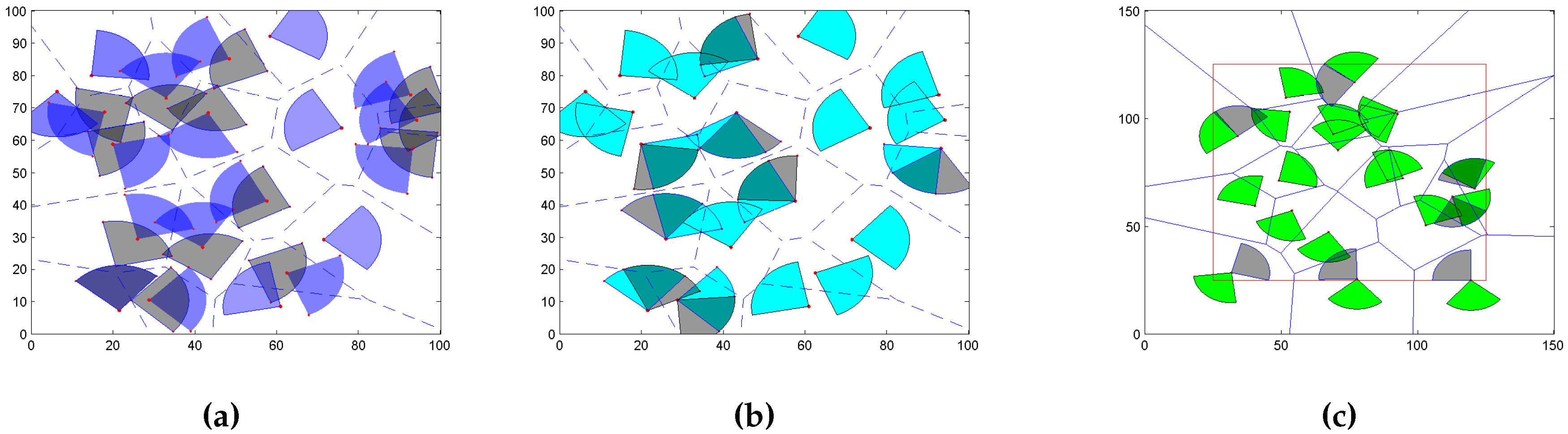
- Restrict the sensor node’s moving trace in its corresponding cell.
- Get maximal coverage in each cell and minimum overlap with another cell’s sensor fan.
- Maximize the cell coverage under the constraints of minimized moving distance.
4. Theoretical Analysis and Algorithms
4.1. To Determine Whether a Sensor’s Sector Area is Wrapped in the Cell (Gets Full Coverage)
4.2. Move and Rotate inside the Cell Based on the Vertex
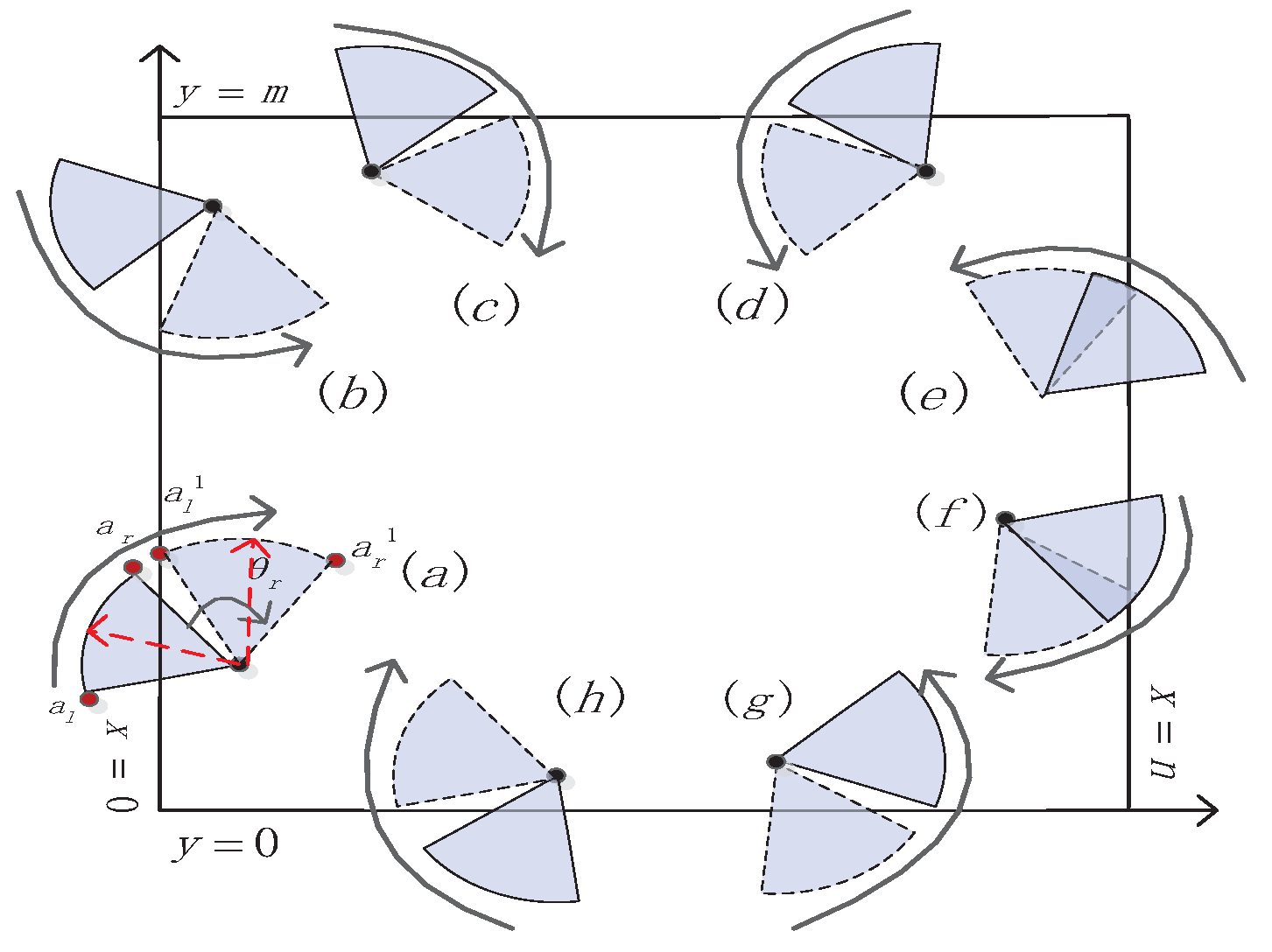
4.2.1. Case 1: Rotate Working Direction Algorithm (RWD)
4.2.2. Case 2: Move Inside Cell Algorithm (MIC)
| Algorithm 1 Rotate Working Direction Algorithm (RWD) |
|
| Algorithm 2 Move Inside Cell Algorithm (MIC) |
|
4.3. Rotation Based on Boundary (RB)
- for boundary ,
- for boundary ,
- for boundary
- for boundary
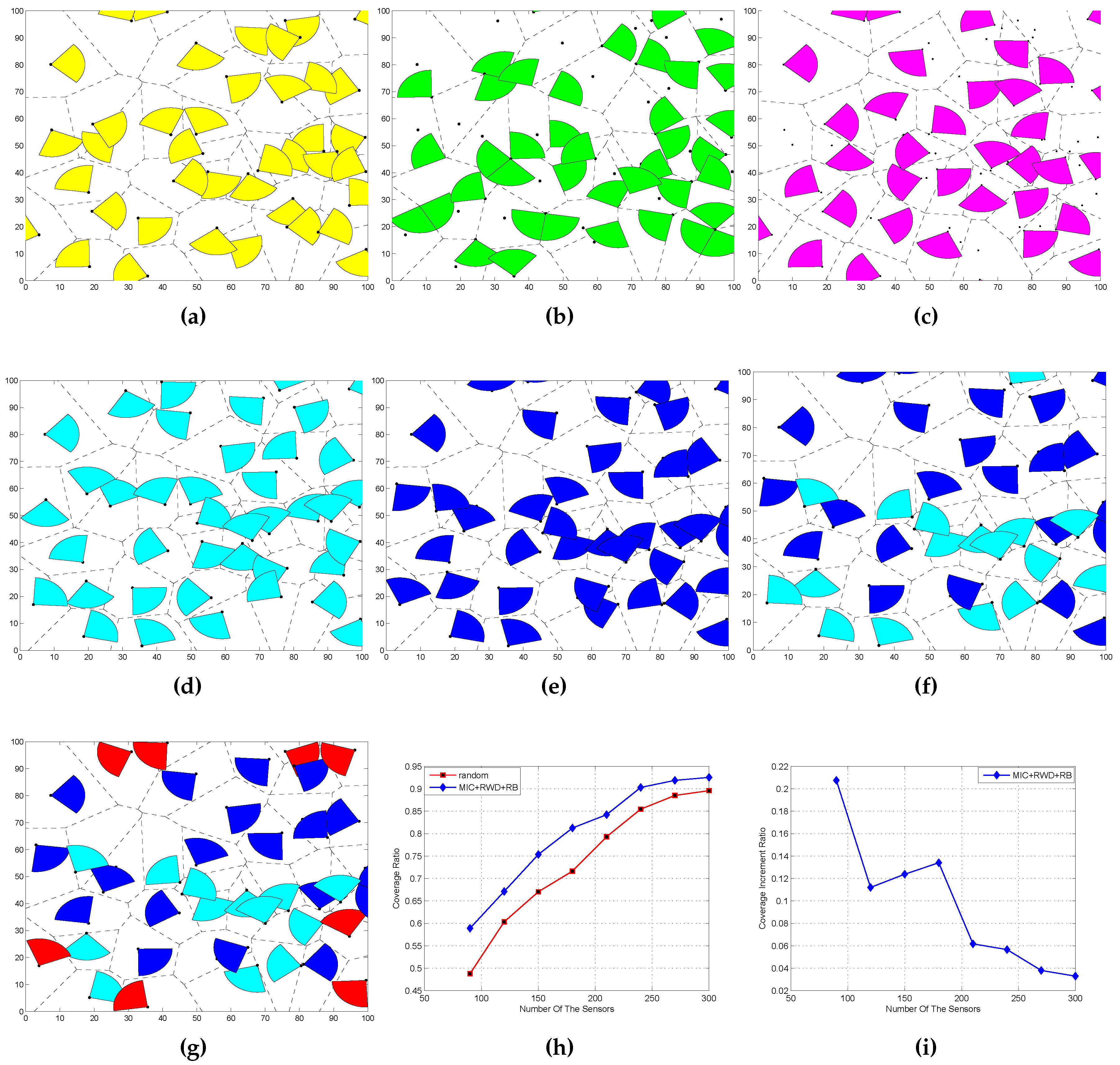
5. Performance Evaluation
5.1. Sensing Coverage
5.2. Comparison from Moving Distance
5.3. Coverage Ratios with Different and AoV
5.4. Coverage Ratio
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cardei, M.; Thai, M.T.; Li, Y.S.; Wu, W.L. Energy-efficient target coverage in wireless sensor networks. In Proceedings of the 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, FL, USA, 13–17 March 2005; pp. 1976–1984.
- Megerian, S.; Koushanfar, F.; Potkonjak, M.; Srivastava, M. Worst and best-case coverage in sensor networks. IEEE Trans. Mob. Comput. 2005, 4, 84–92. [Google Scholar] [CrossRef]
- Liang, C.K.; Chung, C.Y.; Li, C.F. A virtual force based movement scheme for area coverage in directional sensor networks. In Proceedings of the 2014 Tenth International Conference on Intelligent Information Hiding and Multimedia Signal Processing, Kitakyushu, Japan, 27–29 August 2014; pp. 718–722.
- Tao, D.; Ma, H.D.; Liu, L. A Virtual Potential Field Based Coverage-Enhancing Algorithm for Directional Sensor Networks. J. Software 2007, 18, 1152–1163. [Google Scholar] [CrossRef]
- Li, J.; Wang, R.H.; Huang, H.P.; Sun, L.G. Voronoi-Based Coverage Optimization for Directional Sensor Networks. Wirel. Sens. Netw. 2009, 1, 417–424. [Google Scholar] [CrossRef]
- Stergiopoulos, J.; Tzes, A. Voronoi based coverage optimization for mobile networks with limited sensing range: A directional search approach. In Proceedings of the 2009 American Control Conference, St. Louis, Mo, USA, 10–12 June 2009; pp. 1427–1436.
- You, S.; Zhang, G.L.; Li, D.M. Coverage improvement strategy based on Voronoi for directional sensor networks. In Proceedings of the EAI International Conference on Machine Learning and Intelligent Communications, Shanghai, China, 27–28 August 2016.
- Sung, T.W.; Yang, C.S. Distributed Voronoi-Based Self-Redeployment for Coverage Enhancement in a Mobile Directional Sensor Network. Int. J. Distrib. Sens. Netw. 2013, 6, 1456–1459. [Google Scholar] [CrossRef]
- Wang, B.; Lim, H.B.; Ma, D. A survey of movement strategies for improving network coverage in wireless sensor networks. Comput. Commun. 2009, 32, 1427–1436. [Google Scholar] [CrossRef]
- Guvensan, M.A.; Yavuz, A.G. On coverage issues in directional sensor networks: A survey. Ad Hoc Netw. 2011, 9, 1238–1255. [Google Scholar] [CrossRef]
- Wang, G.; Cao, G.; Berman, P.; Porta, T.F.L. Bidding protocols for deploying mobile sensors. IEEE Trans. Mob. Comput. 2007, 6, 515–528. [Google Scholar] [CrossRef]
- Ghosh, A. Estimating coverage holes and enhancing coverage in mixed sensor networks. In Proceedings of the IEEE International Conference on Local Computer Networks, Alberta, Canada; 2014; pp. 68–76. [Google Scholar]
- Liang, C.K.; He, M.C.; Tsai, C.H. Movement assisted sensor deployment in directional sensor networks. In Proceedings of the Sixth International Conference on Mobile Ad-Hoc Sensor Networks, Hangzhou, China, 20–22 December 2010; pp. 226–230.
- Lin, T.Y.; Santoso, H.A.; Wu, K.R.; Wang, G.L. Enhanced Deployment Algorithms for Heterogeneous Directional Mobile Sensors in a Bounded Monitoring Area. IEEE Trans. Mob. Comput. 2016, PP. [Google Scholar] [CrossRef]
- Sung, T.W.; Yang, C.S. Localised sensor direction adjustments with geometric structures of Voronoi diagram and Delaunay triangulation for directional sensor networks. Int. J. Ad Hoc Ubiquitous Comput. 2015, 20, 91–106. [Google Scholar] [CrossRef]
- Bash, B.A.; Desnoyers, P.J. Exact distributed voronoi cell computation in sensor networks. In Proceedings of the 6th International Conference on Information Processing in Sensor Networks, Cambridge, MA, USA, 25–27 April 2007; pp. 236–243.
- Kalantari, B. Voronoi diagram properties in polynomials with polynomiography applications and extensions. In Proceedings of the 2012 Ninth International Symposium on Voronoi Diagrams in Science and Engineering, Saint Petersburg, Russia, 27–29 August 2012; pp. 32–40.



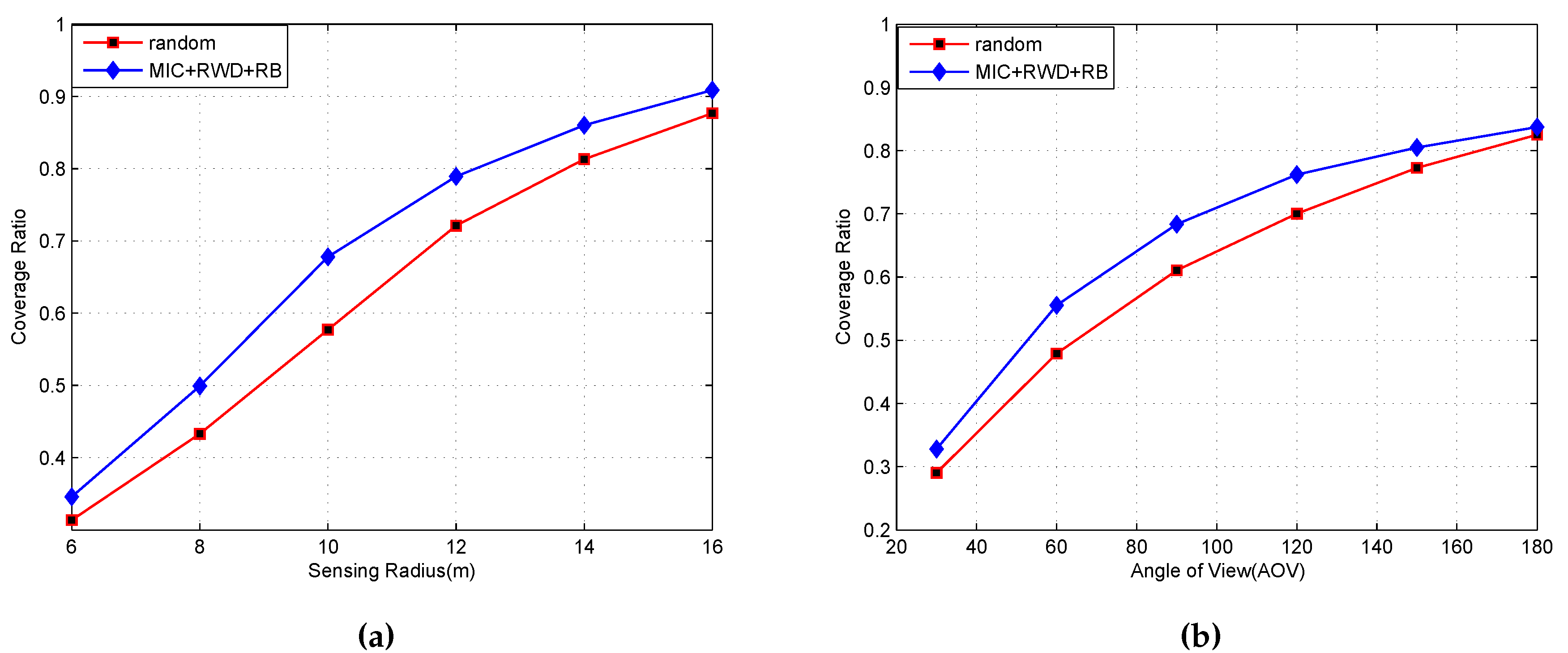
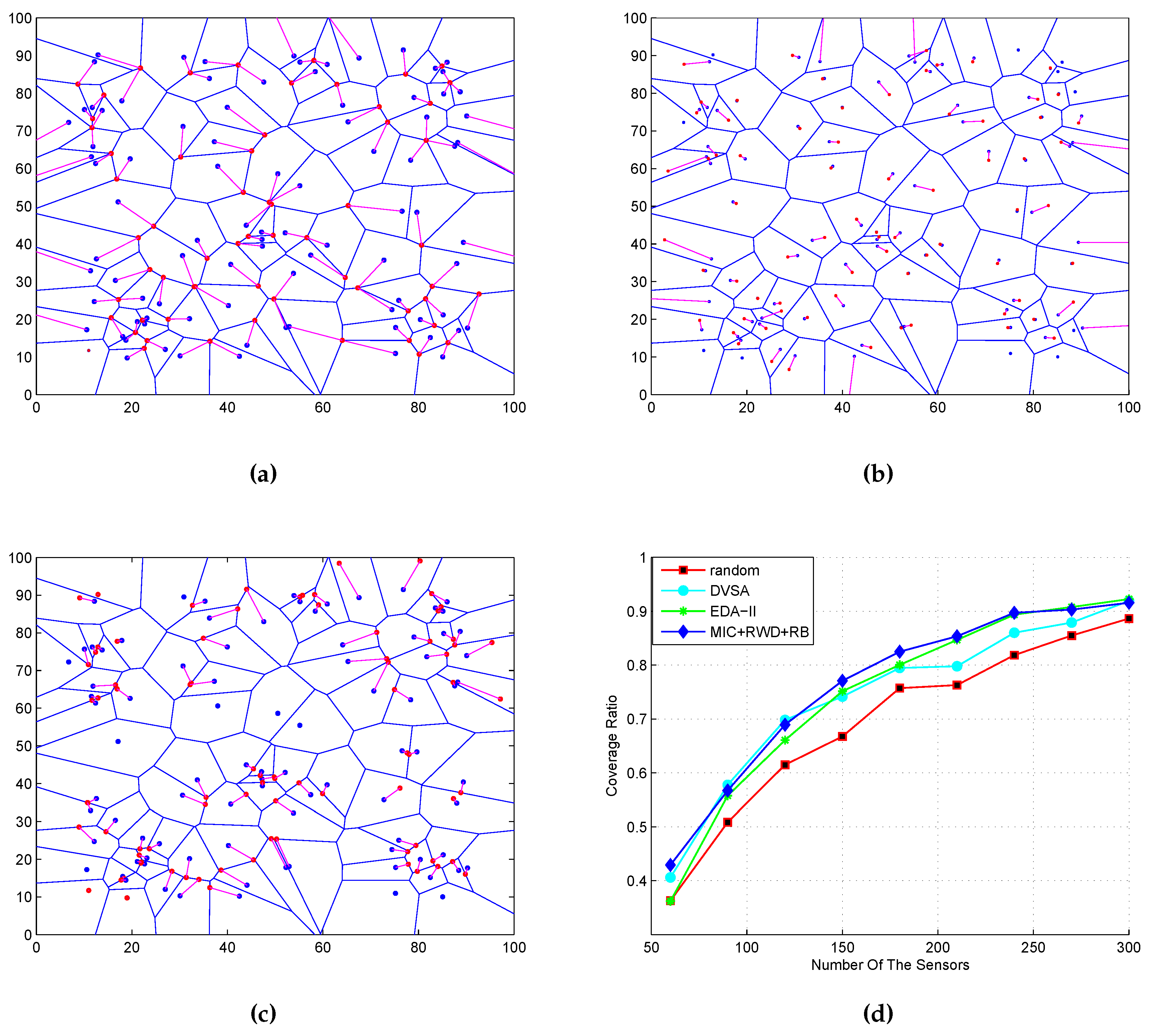
| Parameters | Value |
|---|---|
| sensing radius | = 6 m, 8 m, ..., 12 m |
| angle of view (AoV) | AoV = |
| size of monitoring area | Area = 100 m m |
| the number of sensors, N | N = 40, 60, 90, ..., 300 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; You, S.; Ren, J.; Li, D.; Wang, L. Local Coverage Optimization Strategy Based on Voronoi for Directional Sensor Networks. Sensors 2016, 16, 2183. https://doi.org/10.3390/s16122183
Zhang G, You S, Ren J, Li D, Wang L. Local Coverage Optimization Strategy Based on Voronoi for Directional Sensor Networks. Sensors. 2016; 16(12):2183. https://doi.org/10.3390/s16122183
Chicago/Turabian StyleZhang, Guanglin, Shan You, Jiajie Ren, Demin Li, and Lin Wang. 2016. "Local Coverage Optimization Strategy Based on Voronoi for Directional Sensor Networks" Sensors 16, no. 12: 2183. https://doi.org/10.3390/s16122183
APA StyleZhang, G., You, S., Ren, J., Li, D., & Wang, L. (2016). Local Coverage Optimization Strategy Based on Voronoi for Directional Sensor Networks. Sensors, 16(12), 2183. https://doi.org/10.3390/s16122183







