Line-Based Registration of Panoramic Images and LiDAR Point Clouds for Mobile Mapping
Abstract
:1. Introduction
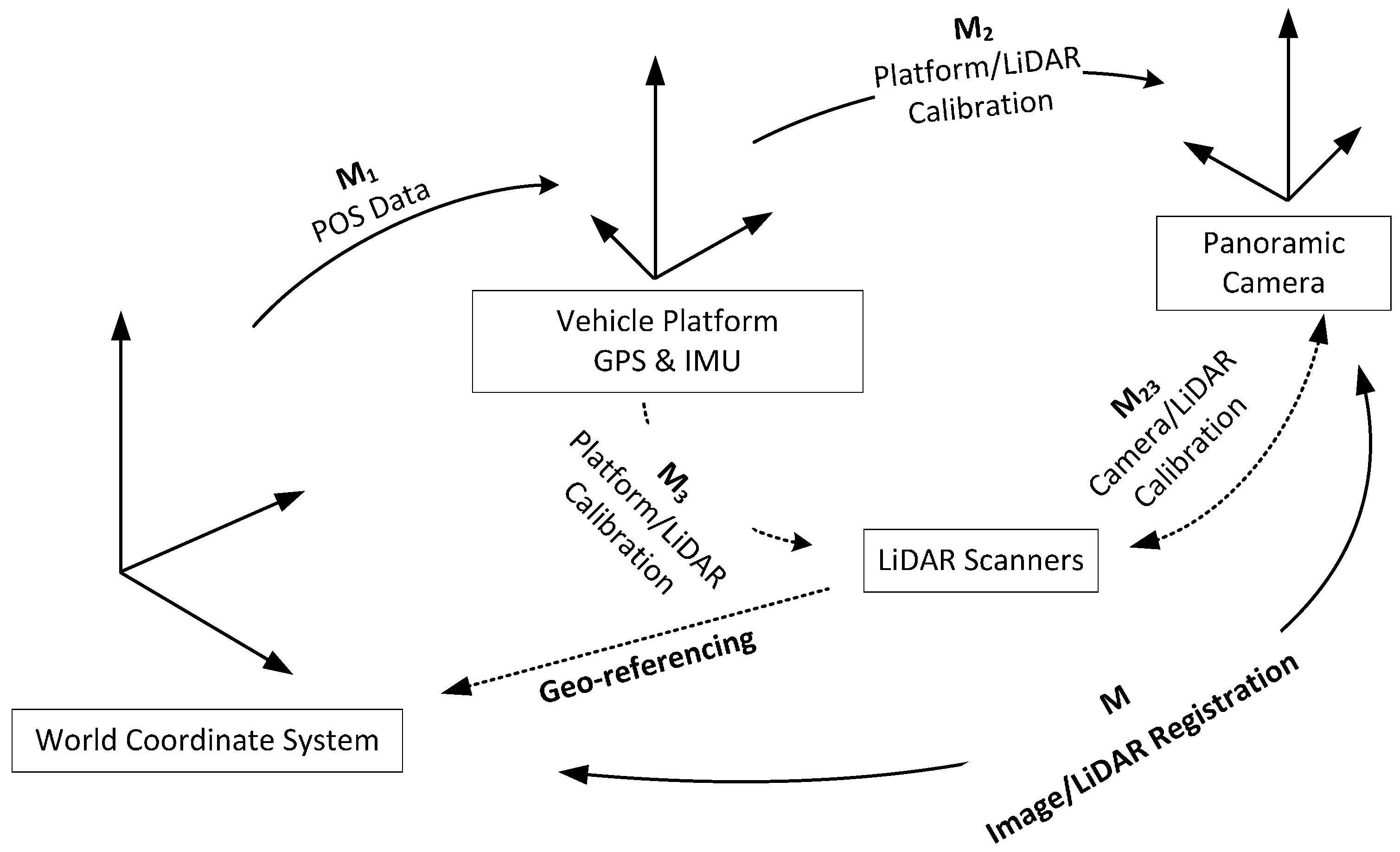
2. The Mobile Mapping System and Sensor Configuration
2.1. Coordinate Systems
2.2. Geo-Refereneced LiDAR
2.3. Multi-Camera Rig Models
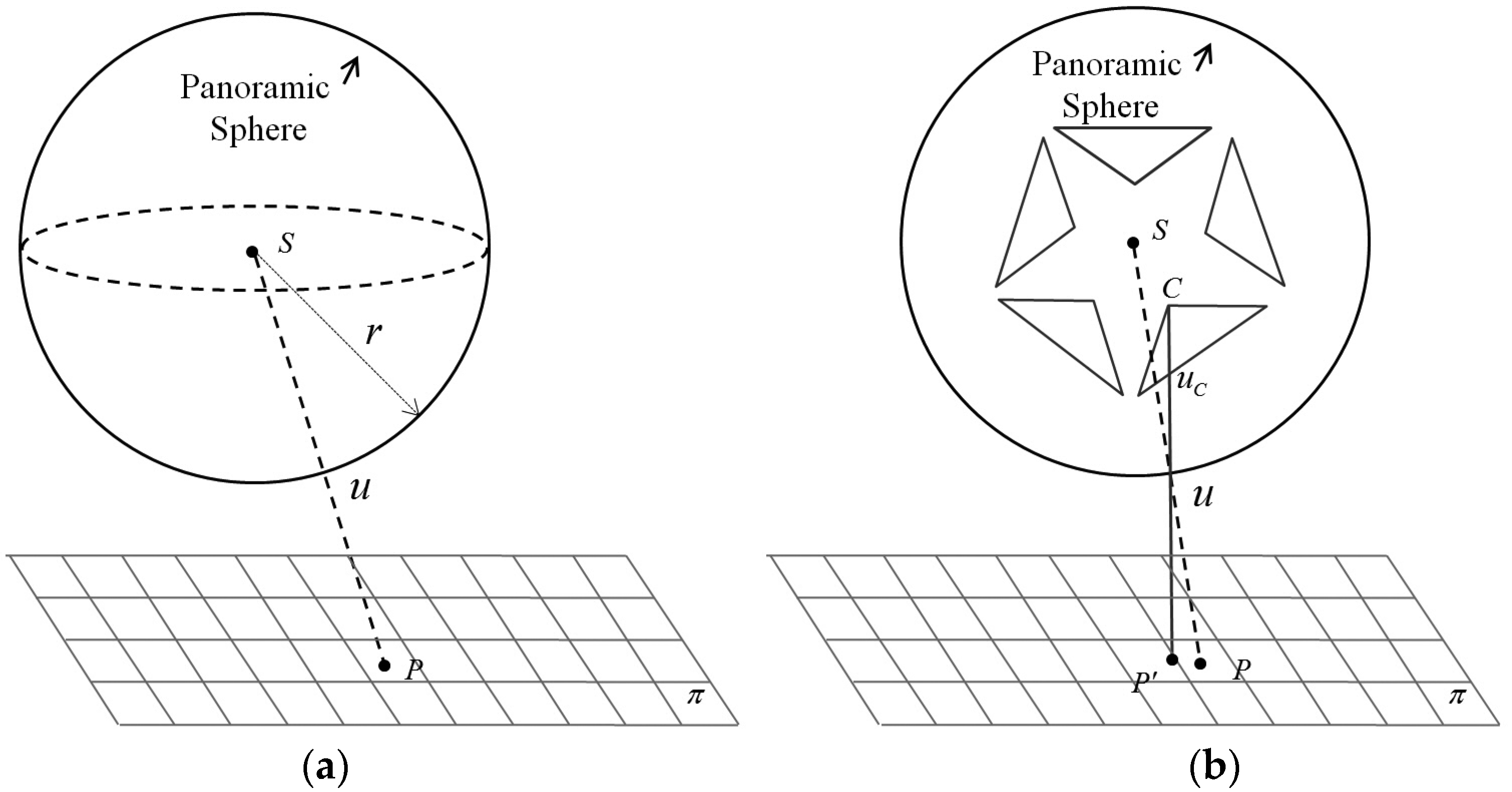
2.3.1. Spherical Camera Model
2.3.2. Panoramic Camera Model
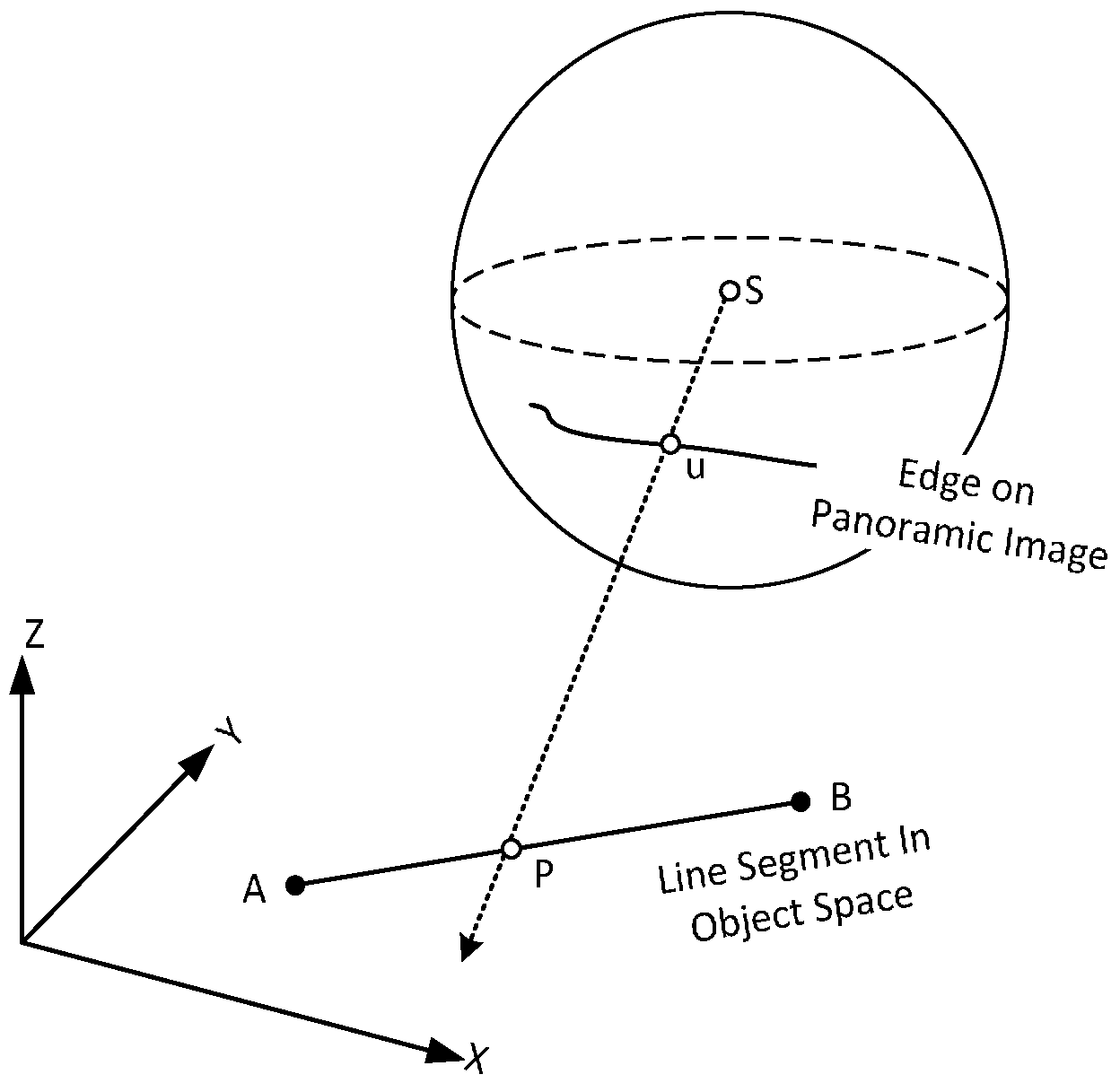
3. Line-Based Registration Method
3.1. Transformation Model
3.2. Solution
4. Line Feature Extraction from LiDAR
4.1. Buildings
4.2. Street Light Poles
4.3. Curbs
5. Experiments and Results
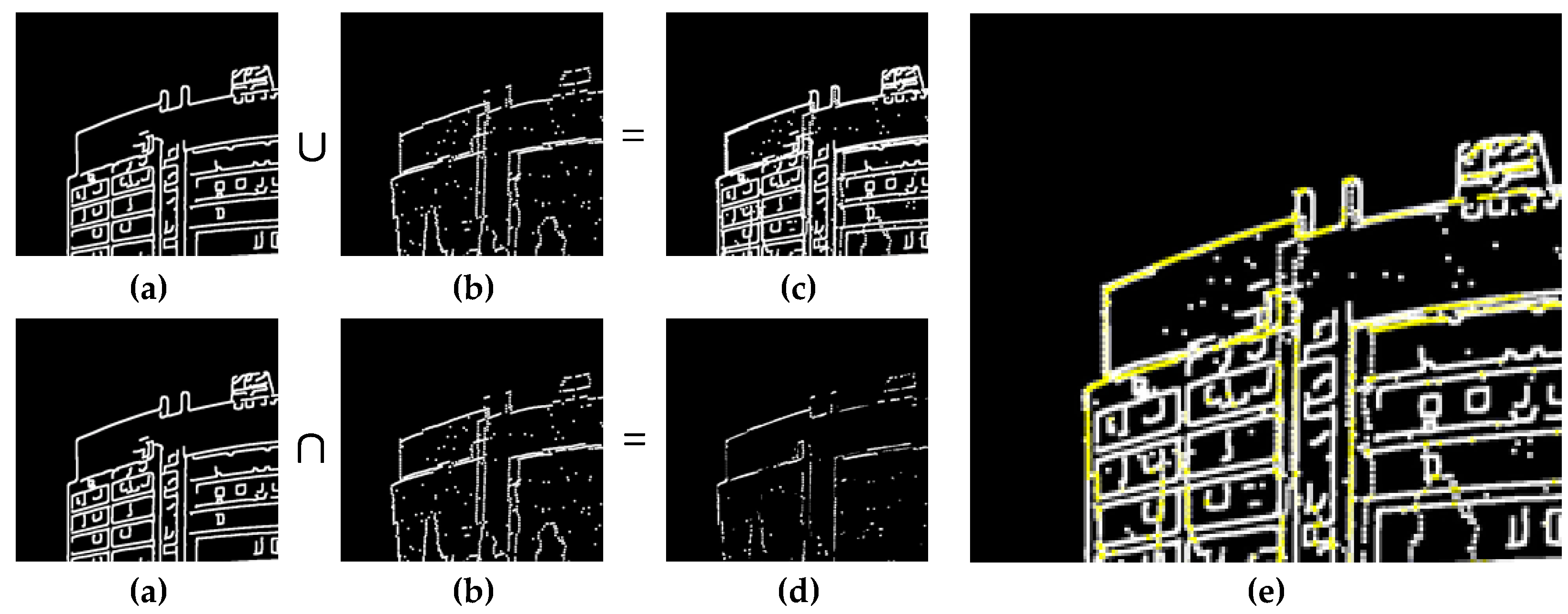
5.1. Datasets
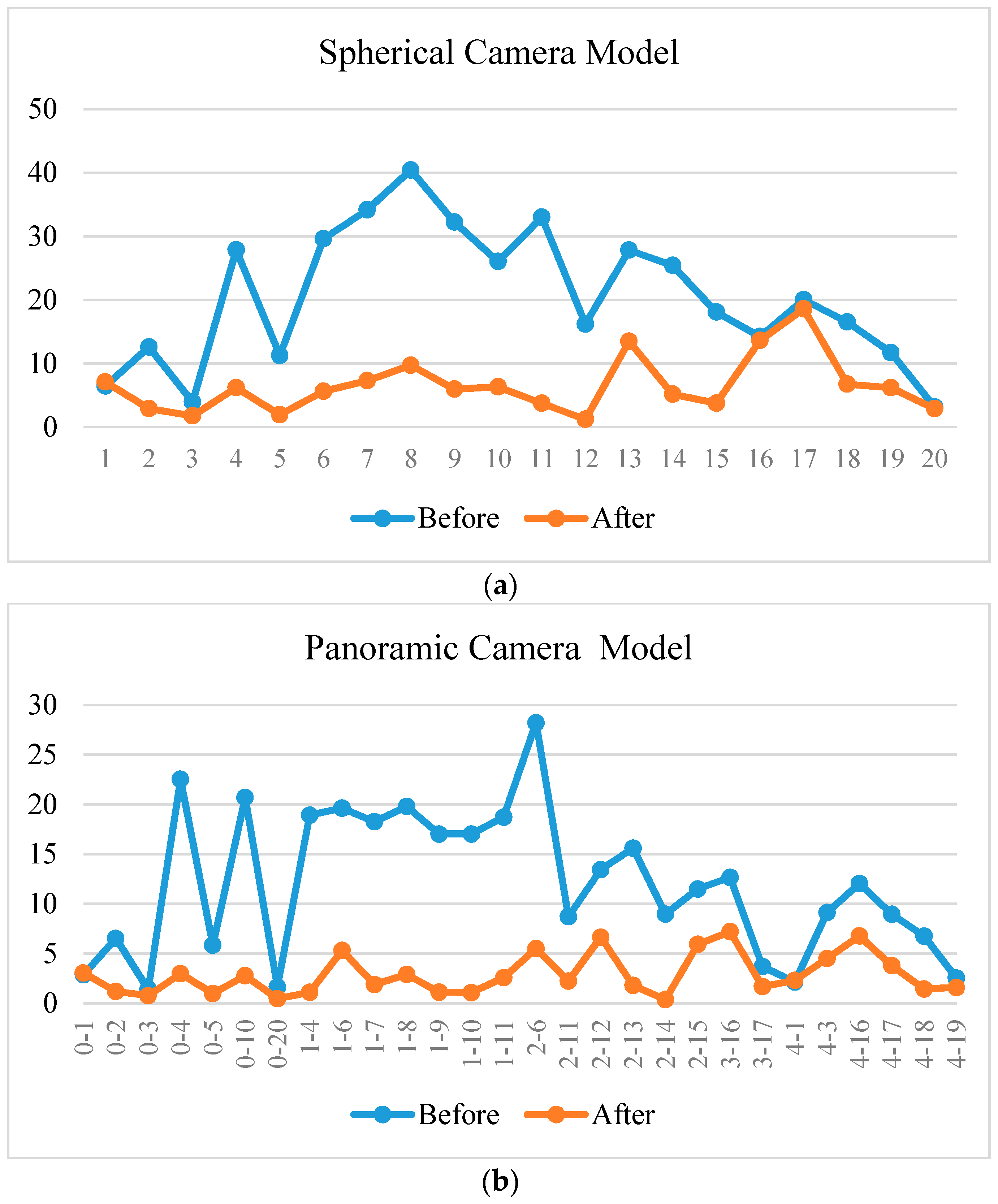
5.2. Registration Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cornelis, N.; Leibe, B.; Cornelis, K.; Van Gool, L. 3D urban scene modeling integrating recognition and reconstruction. Int. J. Comput. Vis. 2008, 78, 121–141. [Google Scholar] [CrossRef]
- Wonka, P.; Muller, P.; Watson, B.; Fuller, A. Urban design and procedural modeling. In ACM SIGGRAPH 2007 Courses; ACM: San Diego, CA, USA, 2007. [Google Scholar]
- Zhuang, Y.; He, G.; Hu, H.; Wu, Z. A novel outdoor scene-understanding framework for unmanned ground vehicles with 3d laser scanners. Trans. Inst. Meas. Control 2015, 37, 435–445. [Google Scholar] [CrossRef]
- Li, D. Mobile mapping technology and its applications. Geospat. Inf. 2006, 4, 125. [Google Scholar]
- Pu, S.; Vosselman, G. Building facade reconstruction by fusing terrestrial laser points and images. Sensors 2009, 9, 4525–4542. [Google Scholar] [PubMed]
- Brenner, C. Building reconstruction from images and laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2005, 6, 187–198. [Google Scholar] [CrossRef]
- Pu, S. Knowledge Based Building Facade Reconstruction from Laser Point Clouds and Images; University of Twente: Enschede, The Netherlands, 2010. [Google Scholar]
- Wang, R. Towards Urban 3d Modeling Using Mobile Lidar and Images; McGill University: Montreal, QC, Canada, 2011. [Google Scholar]
- Park, Y.; Yun, S.; Won, C.S.; Cho, K.; Um, K.; Sim, S. Calibration between color camera and 3d lidar instruments with a polygonal planar board. Sensors 2014, 14, 5333–5353. [Google Scholar] [CrossRef] [PubMed]
- Naroditsky, O.; Patterson, A.; Daniilidis, K. Automatic alignment of a camera with a line scan lidar system. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 3429–3434.
- Gong, X.; Lin, Y.; Liu, J. 3d lidar-camera extrinsic calibration using an arbitrary trihedron. Sensors 2013, 13, 1902–1918. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, Y.; Yan, F.; Hu, H. Automatic extrinsic self-calibration for fusing data from monocular vision and 3-d laser scanner. IEEE Trans. Instrum. Meas. 2014, 63, 1874–1876. [Google Scholar] [CrossRef]
- Levinson, J.; Thrun, S. Automatic Online Calibration of Cameras and Lasers. Robot. Sci. Syst. 2013, 2013, 24–28. [Google Scholar]
- Mishra, R.; Zhang, Y. A review of optical imagery and airborne lidar data registration methods. Open Remote Sens. J. 2012, 5, 54–63. [Google Scholar] [CrossRef]
- Habib, A.; Ghanma, M.; Morgan, M.; Al-Ruzouq, R. Photogrammetric and lidar data registration using linear features. Photogramm. Eng. Remote Sens. 2005, 71, 699–707. [Google Scholar] [CrossRef]
- Brown, L. A Survey of Image Registration Techniques. ACM Comput. Surv. 1992, 24, 325–376. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef] [PubMed]
- Ballard, D.H. Generalizing the hough transform to detect arbitrary shapes. Pattern Recognit. 1981, 13, 111–122. [Google Scholar] [CrossRef]
- Von Gioi, R.G.; Jakubowicz, J.; Morel, J.-M.; Randall, G. LSD: A line segment detector. Image Process. Line 2012, 2, 35–55. [Google Scholar] [CrossRef]
- Liu, L.; Stamos, I. Automatic 3d to 2d registration for the photorealistic rendering of urban scenes. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2005), San Diego, CA, USA, 20–25 June 2005; pp. 137–143.
- Liu, L.; Stamos, I. A systematic approach for 2d-image to 3d-range registration in urban environments. Comput. Vis. Image Underst. 2012, 116, 25–37. [Google Scholar] [CrossRef]
- Moghadam, P.; Bosse, M.; Zlot, R. Line-based extrinsic calibration of range and image sensors. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3685–3691.
- Borges, P.; Zlot, R.; Bosse, M.; Nuske, S.; Tews, A. Vision-based localization using an edge map extracted from 3d laser range data. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 4902–4909.
- Lin, Y.; Wang, C.; Cheng, J.; Chen, B.; Jia, F.; Chen, Z.; Li, J. Line segment extraction for large scale unorganized point clouds. ISPRS J. Photogramm. Remote Sens. 2015, 102, 172–183. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Guan, H.; Wang, C.; Yu, J. Semiautomated extraction of street light poles from mobile lidar point-clouds. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1374–1386. [Google Scholar] [CrossRef]
- Yokoyama, H.; Date, H.; Kanai, S.; Takeda, H. Pole-Like Objects Recognition from Mobile Laser Scanning Data Using Smoothing and Principal Component Analysis. Int. Archives Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, 115–120. [Google Scholar] [CrossRef]
- El-Halawany, S.; Moussa, A.; Lichti, D.D.; El-Sheimy, N. Detection of Road Curb from Mobile Terrestrial Laser Scanner Point Cloud. In Proceedings of the 2011 ISPRS Workshop om Laser Scanning, Calgary, AB, Canada, 29–31 August 2011.
- Tan, J.; Li, J.; An, X.; He, H. Robust curb detection with fusion of 3d-lidar and camera data. Sensors 2014, 14, 9046–9073. [Google Scholar] [CrossRef] [PubMed]
- Ronnholm, P. Registration Quality-Towards Integration of Laser Scanning and Photogrammetry; European Spatial Data Research Network: Leuven, Belgium, 2011. [Google Scholar]
- Patias, P.; Petsa, E.; Streilein, A. Digital Line Photogrammetry: Concepts, Formulations, Degeneracies, Simulations, Algorithms, Practical Examples; ETH Zürich: Zürich, Switzerland, 1995. [Google Scholar]
- Schenk, T. From point-based to feature-based aerial triangulation. ISPRS J. Photogramm. Remote Sens. 2004, 58, 315–329. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Zhang, J.; Zhang, H. Photogrammetric modeling of linear features with generalized point photogrammetry. Photogramm. Eng. Remote Sens. 2008, 74, 1119–1127. [Google Scholar] [CrossRef]
- Mastin, A.; Kepner, J.; Fisher, J. Automatic Registration of Lidar and Optical Images of Urban Scenes. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 2639–2646.
- Parmehr, E.G.; Fraser, C.S.; Zhang, C.; Leach, J. Automatic registration of optical imagery with 3d lidar data using statistical similarity. ISPRS J. Photogramm. Remote Sen. 2014, 88, 28–40. [Google Scholar] [CrossRef]
- Wang, R.; Ferrie, F.P.; Macfarlane, J. Automatic registration of mobile lidar and spherical panoramas. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Providence, RI, USA, 18–20 June 2012; pp. 33–40.
- Torii, A.; Havlena, M.; Pajdla, T. From google street view to 3d city models. In Proceedings of the IEEE 12th International Conference on Computer Vision Workshops (ICCV Workshops), Kyoto, Japan, 29 September–2 October 2009; pp. 2188–2195.
- Micusik, B.; Kosecka, J. Piecewise planar city 3d modeling from street view panoramic sequences. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 2906–2912.
- Shi, Y.; Ji, S.; Shi, Z.; Duan, Y.; Shibasaki, R. GPS-supported visual slam with a rigorous sensor model for a panoramic camera in outdoor environments. Sensors 2013, 13, 119–136. [Google Scholar] [CrossRef] [PubMed]
- Ji, S.; Shi, Y.; Shi, Z.; Bao, A.; Li, J.; Yuan, X.; Duan, Y.; Shibasaki, R. Comparison of two panoramic sensor models for precise 3d measurements. Photogramm. Eng. Remote Sens. 2014, 80, 229–238. [Google Scholar] [CrossRef]
- PointGrey. Ladybug 3. Available online: https://www.ptgrey.com/ladybug3-360-degree-firewire-spherical-camera-systems (accessed on 28 December 2016).
- SICK. Lms5xx. Available online: https://www.sick.com/de/en/product-portfolio/detection-and-ranging-solutions/2d-laser-scanners/lms5xx/c/g179651 (accessed on 28 December 2016).
- Sairam, N.; Nagarajan, S.; Ornitz, S. Development of mobile mapping system for 3d road asset inventory. Sensors 2016, 16, 367. [Google Scholar] [CrossRef] [PubMed]
- Point Grey Research, I. Geometric Vision Using Ladybug Cameras. Available online: http://www.ptgrey.com/tan/10621 (accessed on 28 December 2016).
- Rabbani, T.; van Den Heuvel, F.; Vosselmann, G. Segmentation of point clouds using smoothness constraint. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 248–253. [Google Scholar]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient Ransac for Point-Cloud Shape Detection. Comput. Graph. Forum 2007, 24, 214–226. [Google Scholar] [CrossRef]
- Pu, S.; Rutzinger, M.; Vosselman, G.; Oude Elberink, S. Recognizing basic structures from mobile laser scanning data for road inventory studies. ISPRS J. Photogramm. Remote Sens. 2011, 66, S28–S39. [Google Scholar] [CrossRef]
- Meguro, J.; Hashizume, T.; Takiguchi, J.; Kurosaki, R. Development of an autonomous mobile surveillance system using a network-based rtk-GPS. In Proceedings of the International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005.
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]












| POS | EOP | |
|---|---|---|
| X (m) | 38,535,802.519 | −0.3350 |
| Y (m) | 3,400,240.762 | −0.8870 |
| Z (m) | 762,11.089 | 0.4390 |
| () | 0.2483 | −1.3489 |
| () | 0.4344 | 0.6250 |
| () | 87.5076 | 1.2000 |
| Lens ID | Rx (Radians) | Ry (Radians) | Rz (Radians) | Tx (m) | Ty (m) | Tz (m) | x0 (Pixels) | y0 (Pixels) | f (Pixels) |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 2.1625 | 1.5675 | 2.1581 | 0.0416 | −0.0020 | −0.0002 | 806.484 | 639.546 | 400.038 |
| 1 | 1.0490 | 1.5620 | −0.2572 | 0.0114 | −0.0400 | 0.0002 | 794.553 | 614.885 | 402.208 |
| 2 | 0.6134 | 1.5625 | −1.9058 | −0.0350 | −0.0229 | 0.0006 | 783.593 | 630.813 | 401.557 |
| 3 | 1.7005 | 1.5633 | −2.0733 | −0.0328 | 0.0261 | −0.0003 | 790.296 | 625.776 | 400.521 |
| 4 | −2.2253 | 1.5625 | −0.9974 | 0.0148 | 0.0388 | −0.0003 | 806.926 | 621.216 | 406.115 |
| 5 | −0.0028 | 0.0052 | 0.0043 | 0.0010 | −0.0006 | 0.06202 | 776.909 | 589.499 | 394.588 |
| Model | Spherical | Panoramic | ||
|---|---|---|---|---|
| Deltas | Errors | Deltas | Errors | |
| X (m) | −3.4372 × 10−2 | 1.1369 × 10−3 | 3.4328 × 10−2 | 1.0373 × 10−3 |
| Y (m) | 1.0653 | 1.2142 × 10−3 | 1.0929 | 1.0579 × 10−3 |
| Z (m) | 1.9511 × 10−1 | 9.9237 × 10−4 | 2.2075 × 10−1 | 8.0585 × 10−4 |
| () | −1.2852 × 10−2 | 1.4211 × 10−3 | −1.4731 × 10−2 | 1.0920 × 10−3 |
| () | 5.8824 × 10−4 | 1.4489 × 10−4 | 1.5866 × 10−3 | 1.2430 × 10−3 |
| () | −7.9019 × 10−3 | 8.4789 × 10−4 | −6.7691 × 10−3 | 7.7509 × 10−4 |
| RMSE (pixels) | 4.718 | 4.244 | ||
| Lens ID | Before (%) | After (%) |
|---|---|---|
| 0 | 7.80 | 8.29 |
| 1 | 8.31 | 10.30 |
| 2 | 11.32 | 11.83 |
| 3 | 9.84 | 9.90 |
| 4 | 7.42 | 7.54 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, T.; Ji, S.; Shan, J.; Gong, J.; Liu, K. Line-Based Registration of Panoramic Images and LiDAR Point Clouds for Mobile Mapping. Sensors 2017, 17, 70. https://doi.org/10.3390/s17010070
Cui T, Ji S, Shan J, Gong J, Liu K. Line-Based Registration of Panoramic Images and LiDAR Point Clouds for Mobile Mapping. Sensors. 2017; 17(1):70. https://doi.org/10.3390/s17010070
Chicago/Turabian StyleCui, Tingting, Shunping Ji, Jie Shan, Jianya Gong, and Kejian Liu. 2017. "Line-Based Registration of Panoramic Images and LiDAR Point Clouds for Mobile Mapping" Sensors 17, no. 1: 70. https://doi.org/10.3390/s17010070
APA StyleCui, T., Ji, S., Shan, J., Gong, J., & Liu, K. (2017). Line-Based Registration of Panoramic Images and LiDAR Point Clouds for Mobile Mapping. Sensors, 17(1), 70. https://doi.org/10.3390/s17010070






