Statistical Modeling of Indirect Paths for UWB Sensors in an Indoor Environment
Abstract
:1. Introduction
2. Measurement Campaign
3. Indirect Path Model
- Captured energy is greater than 90% of the total energy.
- Path strength is less than four times the noise standard deviation.
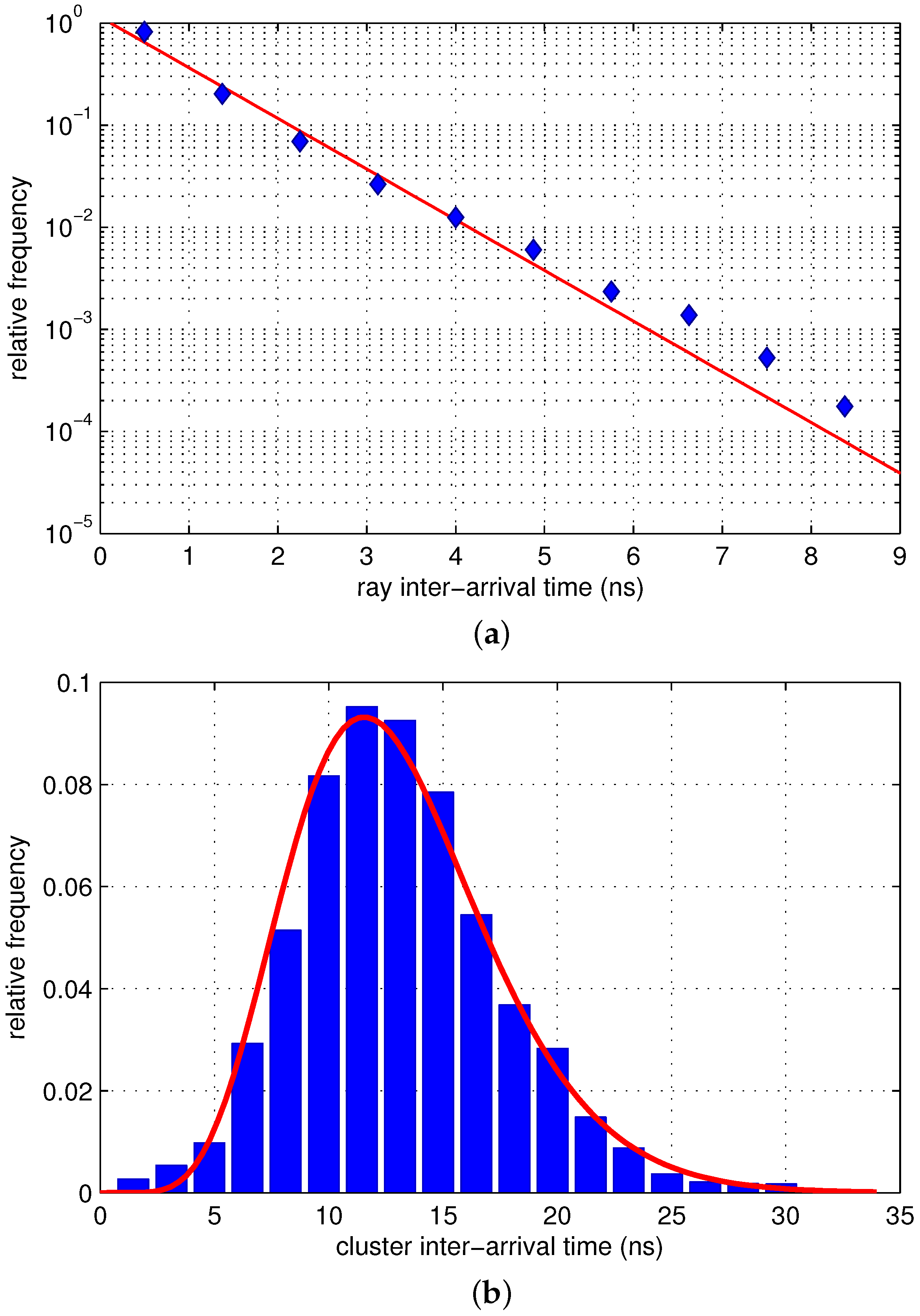
3.1. Path Arrivals
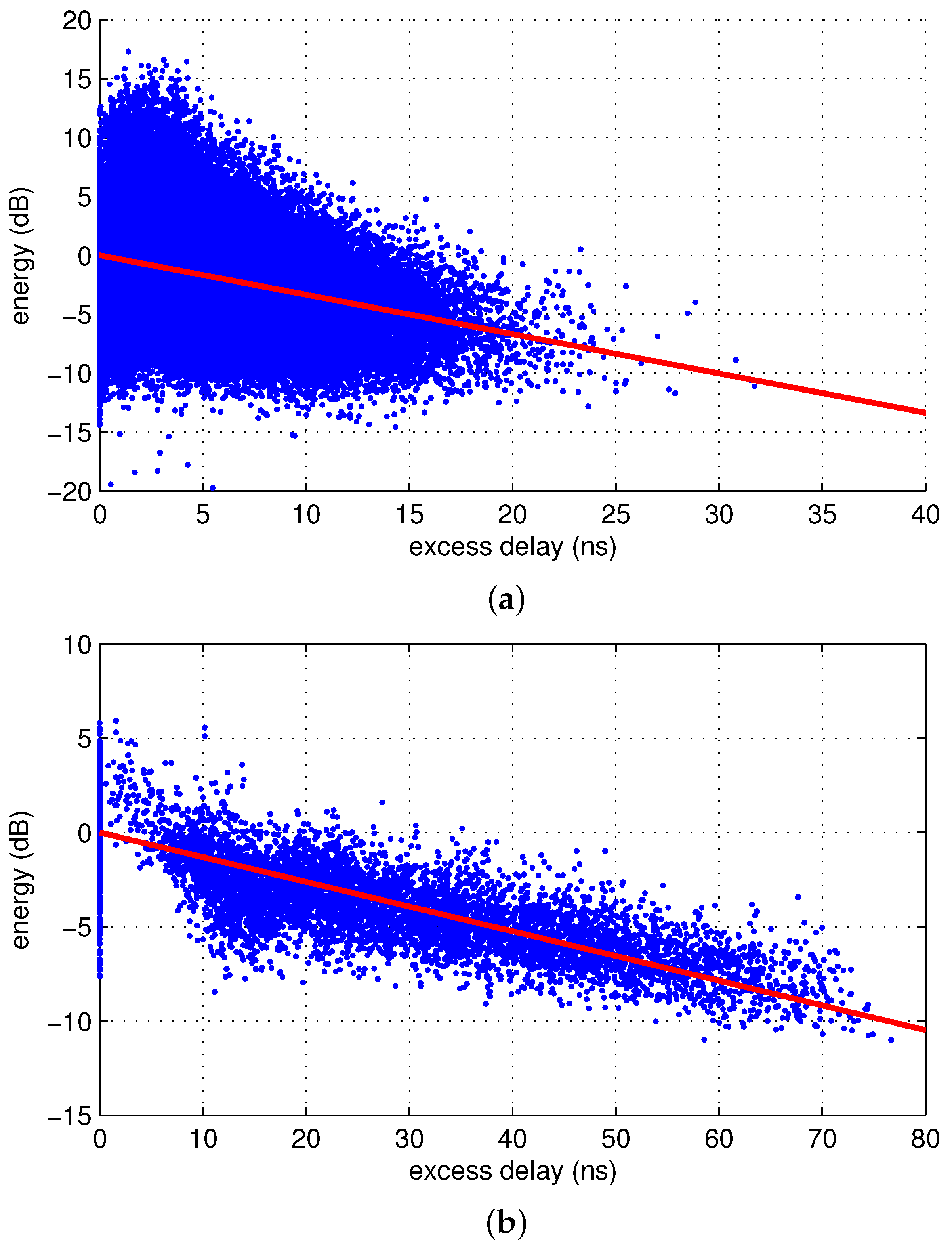
3.2. Path Strengths
4. Application of the Indirect Path Model to Two-Target Tracking
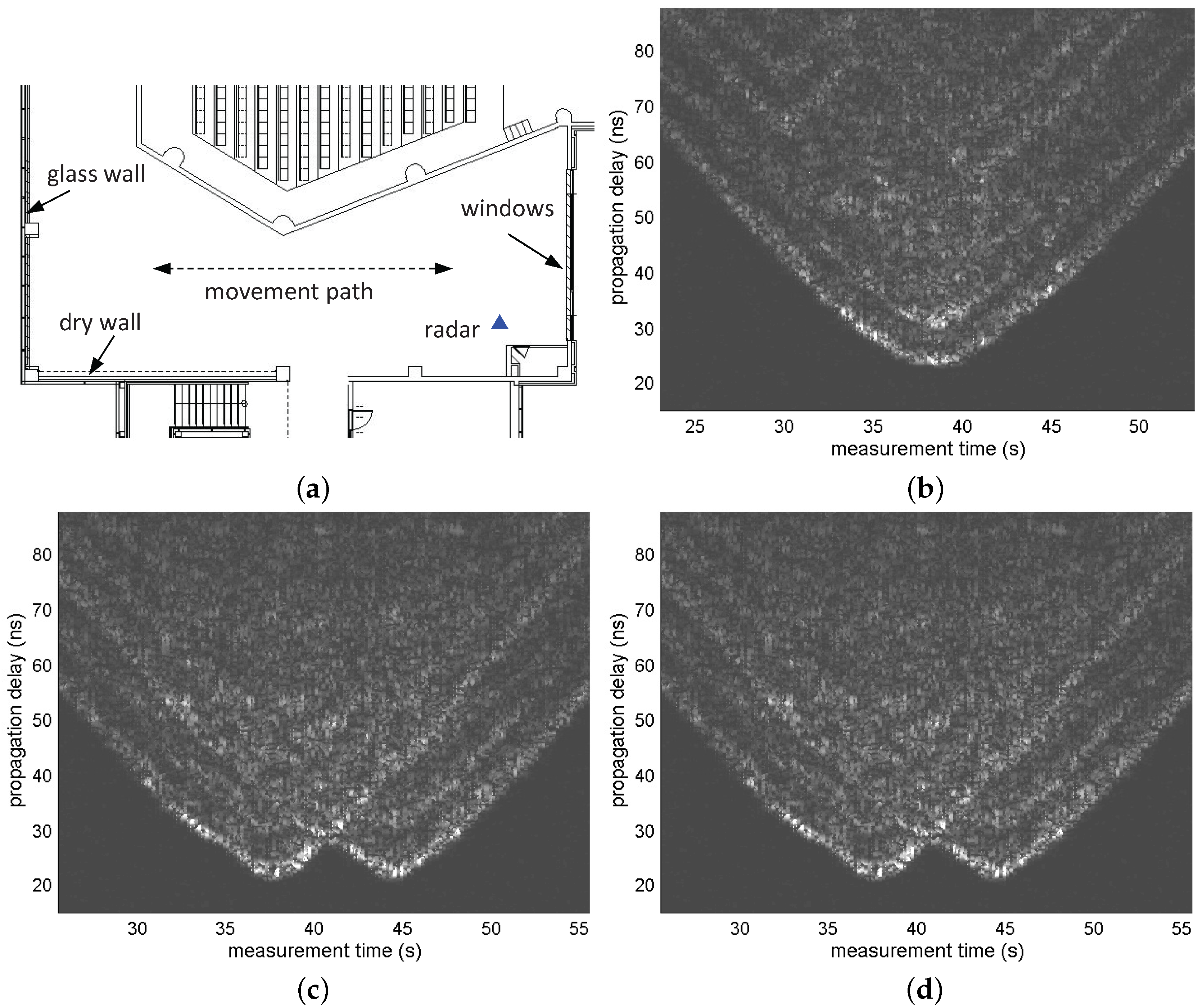
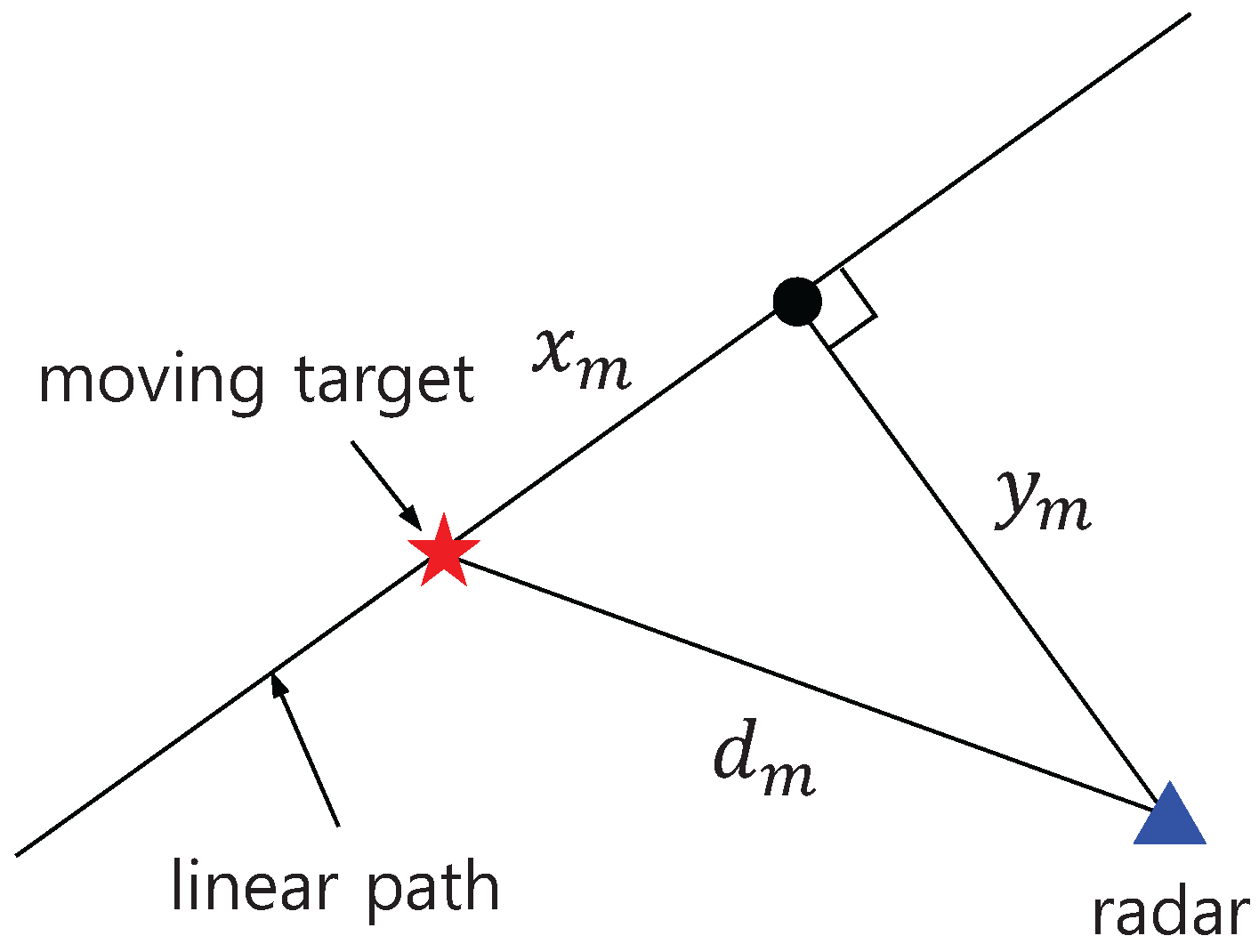
4.1. Test Scenario
4.2. Screening Algorithm
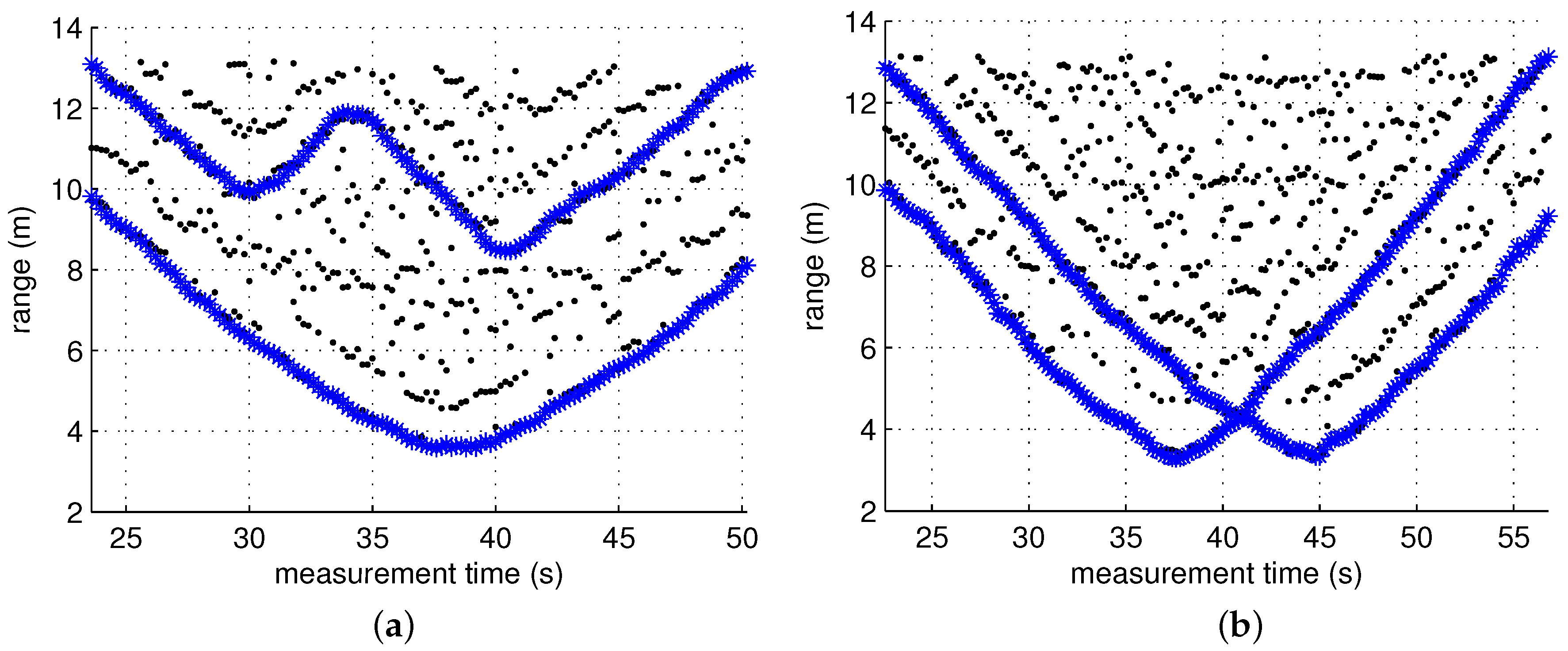
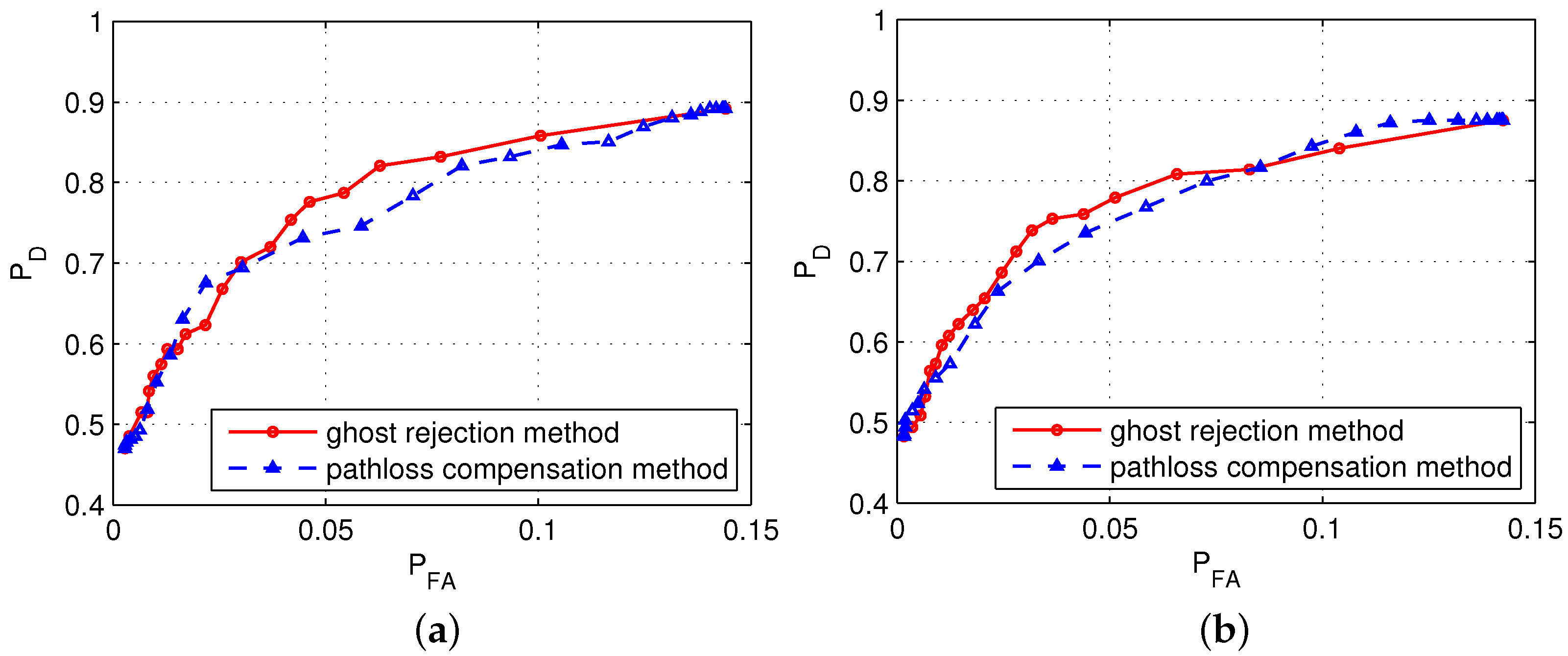
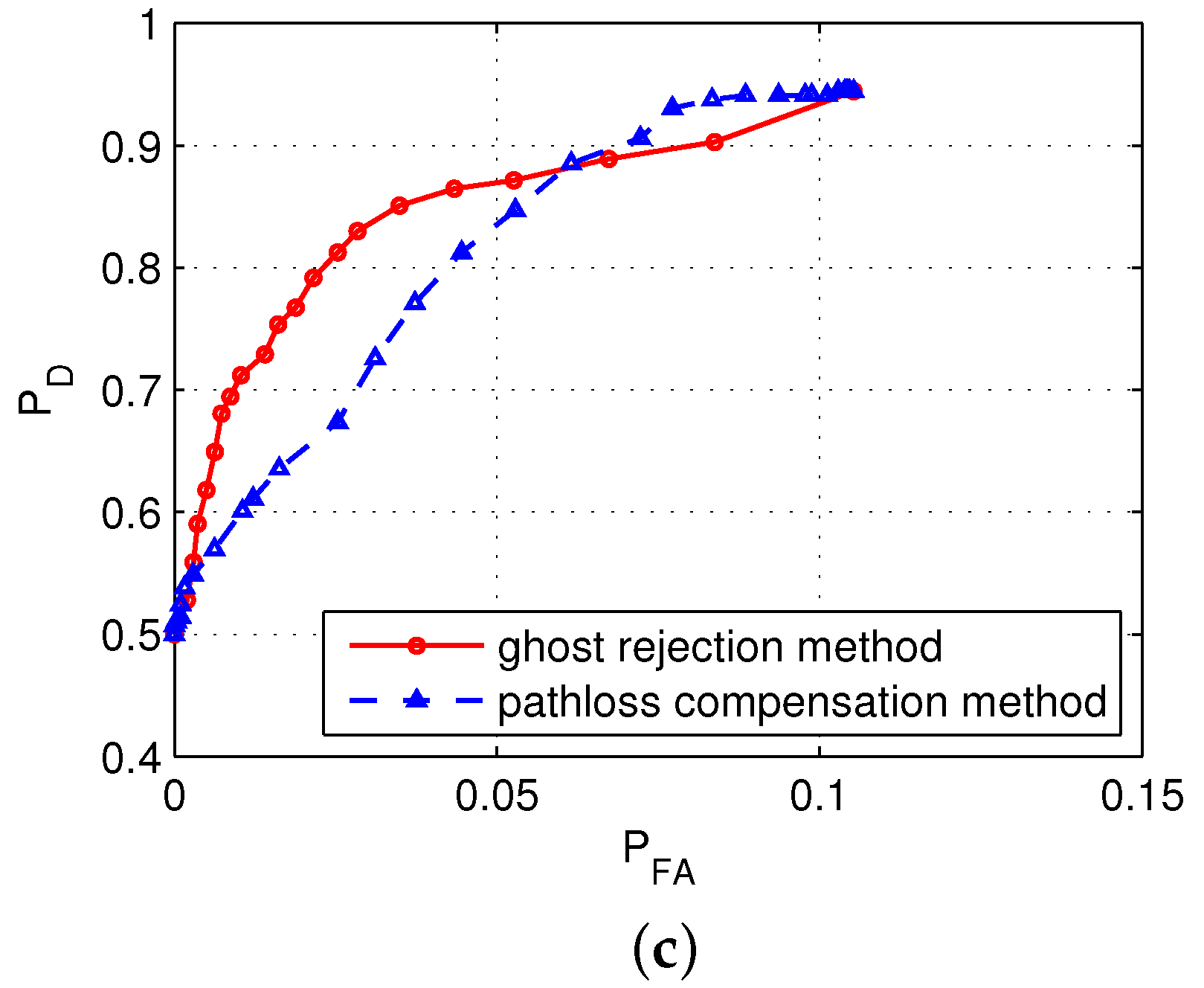
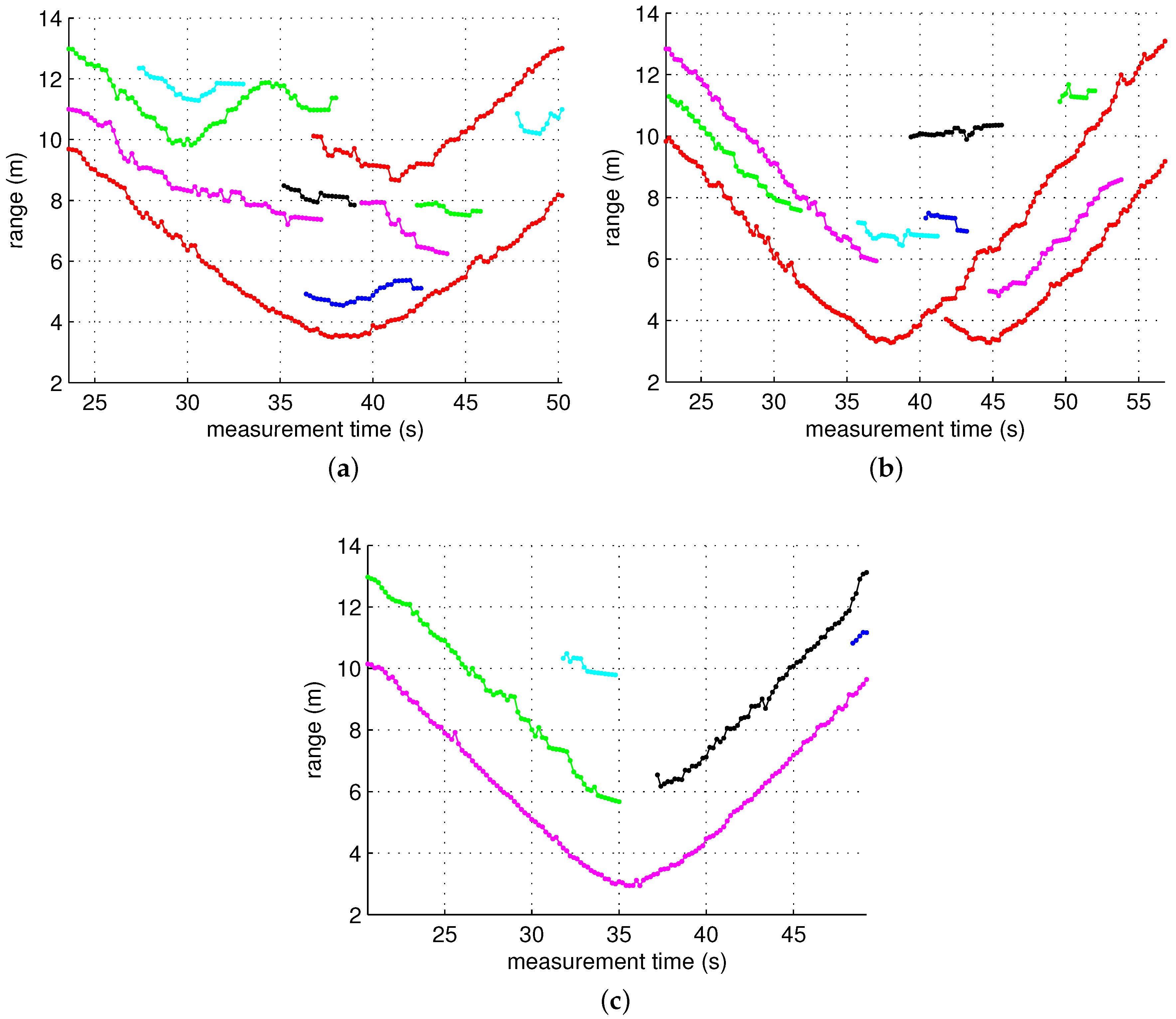
4.3. Test Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Bartoletti, S.; Conti, A.; Giorgetti, A.; Win, M.Z. Sensor Radar Networks for Indoor Tracking. IEEE Wirel. Commun. Lett. 2014, 3, 157–160. [Google Scholar]
- Bartoletti, S.; Giorgetti, A.; Win, M.Z.; Conti, A. Blind Selection of Representative Observations for Sensor Radar Networks. IEEE Transa. Veh. Technol. 2015, 64, 1388–1400. [Google Scholar] [CrossRef]
- Sobhani, B.; Paolini, E.; Giorgetti, A.; Mazzotti, M.; Chiani, M. Target Tracking for UWB Multistatic Radar Sensor Networks. IEEE J. Sel. Top. Signal Process. 2014, 8, 125–136. [Google Scholar] [CrossRef]
- Shen, J.; Molisch, A.F. Indirect Path Detection Based on Wireless Propagation Measurements. IEEE Trans. Wirel. Commun. 2012, 11, 4482–4493. [Google Scholar] [CrossRef]
- Kim, C.; Lee, J.Y. ToA-based multi-target localization and respiration detection using UWB radars. EURASIP J. Wirel. Commun. Netw. 2014, 2014. [Google Scholar] [CrossRef]
- Smith, G.E.; Mobasseri, B.G. Analysis and Exploitation of Multipath Ghosts in Radar Target Image Classification. IEEE Trans. Image Process. 2014, 23, 1581–1592. [Google Scholar] [CrossRef] [PubMed]
- Cramer, J.M.; Scholtz, R.A.; Win, M.Z. Evaluation of an Ultra-Wideband Propagation Channel. IEEE Trans. Antennas Propag. 2002, 50, 561–570. [Google Scholar] [CrossRef]
- Molisch, A.F.; Cassioli, D.; Chong, C.C.; Emami, S.; Fort, A.; Kannan, B.; Karedal, J.; Kunisch, J.; Schantz, H.G.; Siwiak, K.; et al. A Comprehensive Standardized Model for Ultrawideband Propagation Channels. IEEE J. Sel. Areas Commun. 2006, 54, 3151–3166. [Google Scholar] [CrossRef]
- Lee, J.Y. UWB Channel Modeling in Roadway and Indoor Parking Environments. IEEE Trans. Veh. Technol. 2010, 59, 3171–3180. [Google Scholar] [CrossRef]
- Rovnakova, J.; Kocur, D. Weak signal enhancement in radar signal processing. In Proceedings of the 20th International Conference, Radioelektronika (RADIOELEKTRONIKA), Brno, Czech Republic, 19–21 April 2010; pp. 1–4.
- Kim, J.; Baek, I.; Cho, S. Compensation of recieved signal attenuation by distance using UWB radar. In Proceedings of the 2012 Winter Conference of Korea Information and Communications Society, Pyeongchang, Korea, 8–10 February 2012; pp. 282–283.
- Blackman, S.S. Multiple hypothesis tracking for multiple target tracking. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 5–18. [Google Scholar] [CrossRef]


| Measurement Set | Location | Number of Scans |
|---|---|---|
| 1 | lecture room, 3rd floor, Main Library | 187 |
| 2 | lecture room, 3rd floor, Main Library | 178 |
| 3 | #313, 3rd floor, Newton Hall | 287 |
| 4 | lobby, 4th floor, Newton Hall | 238 |
| 5 | lobby, 4th floor, Newton Hall | 275 |
| 6 | lobby, 3rd floor, All Nations Hall | 166 |
| 7 | lobby, 3rd floor, All Nations Hall | 227 |
| 8 | hallway, 3rd floor, Nehemiah Hall | 125 |
| 9 | hallway, 3rd floor, Nehemiah Hall | 111 |
| 10 | hallway, 1st floor, Nehemiah Hall | 108 |
| 11 | hallway, 1st floor, Nehemiah Hall | 80 |
| 12 | lobby, 1st floor, Nehemiah Hall | 143 |
| 13 | lobby, 1st floor, Nehemiah Hall | 168 |
| total | 2293 |
| Parameters | Symbol | Value |
|---|---|---|
| cluster arrival | K | 8.4476 |
| θ | 1.5510 | |
| ray arrival rate (1/ns) | λ | 1.1521 |
| cluster decay time constant (ns) | Γ | 33.1268 |
| ray decay time constant (ns) | γ | 12.9967 |
| standard deviation of cluster fading | 1.6605 | |
| standard deviation of ray fading | 3.9038 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.; Lee, J.-Y. Statistical Modeling of Indirect Paths for UWB Sensors in an Indoor Environment. Sensors 2017, 17, 43. https://doi.org/10.3390/s17010043
Lee M, Lee J-Y. Statistical Modeling of Indirect Paths for UWB Sensors in an Indoor Environment. Sensors. 2017; 17(1):43. https://doi.org/10.3390/s17010043
Chicago/Turabian StyleLee, Moona, and Joon-Yong Lee. 2017. "Statistical Modeling of Indirect Paths for UWB Sensors in an Indoor Environment" Sensors 17, no. 1: 43. https://doi.org/10.3390/s17010043
APA StyleLee, M., & Lee, J.-Y. (2017). Statistical Modeling of Indirect Paths for UWB Sensors in an Indoor Environment. Sensors, 17(1), 43. https://doi.org/10.3390/s17010043






