Measurement Matrix Optimization and Mismatch Problem Compensation for DLSLA 3-D SAR Cross-Track Reconstruction
Abstract
:1. Introduction
2. DLSLA 3-D SAR Signal Model and Sparse Reconstruction Conditions Analysis
2.1. DLSLA 3-D SAR Imaging Geometry and Signal Model
2.2. Sparse Reconstruction Conditions Analysis
3. Measurement Matrix Optimization
3.1. Worst-Case Mutual Coherence Based Deterministic Sampling Strategy
3.1.1. Analytical Sampling Strategy Based on Cyclic Different Set
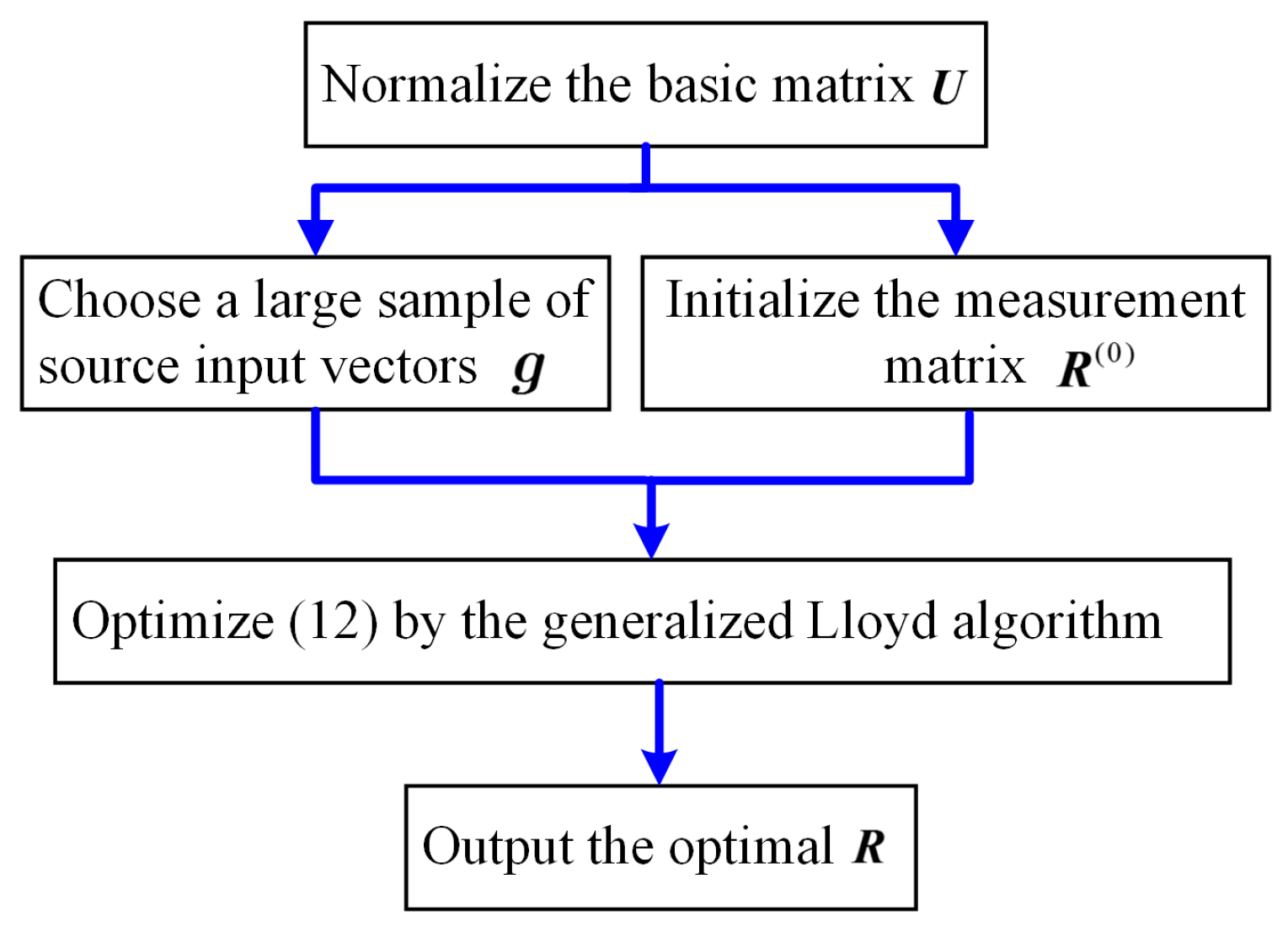
3.1.2. Numerical Sampling Strategy Based on Lloyd Search Algorithm
3.2. Modified Average Mutual Coherence Based Sampling Strategy
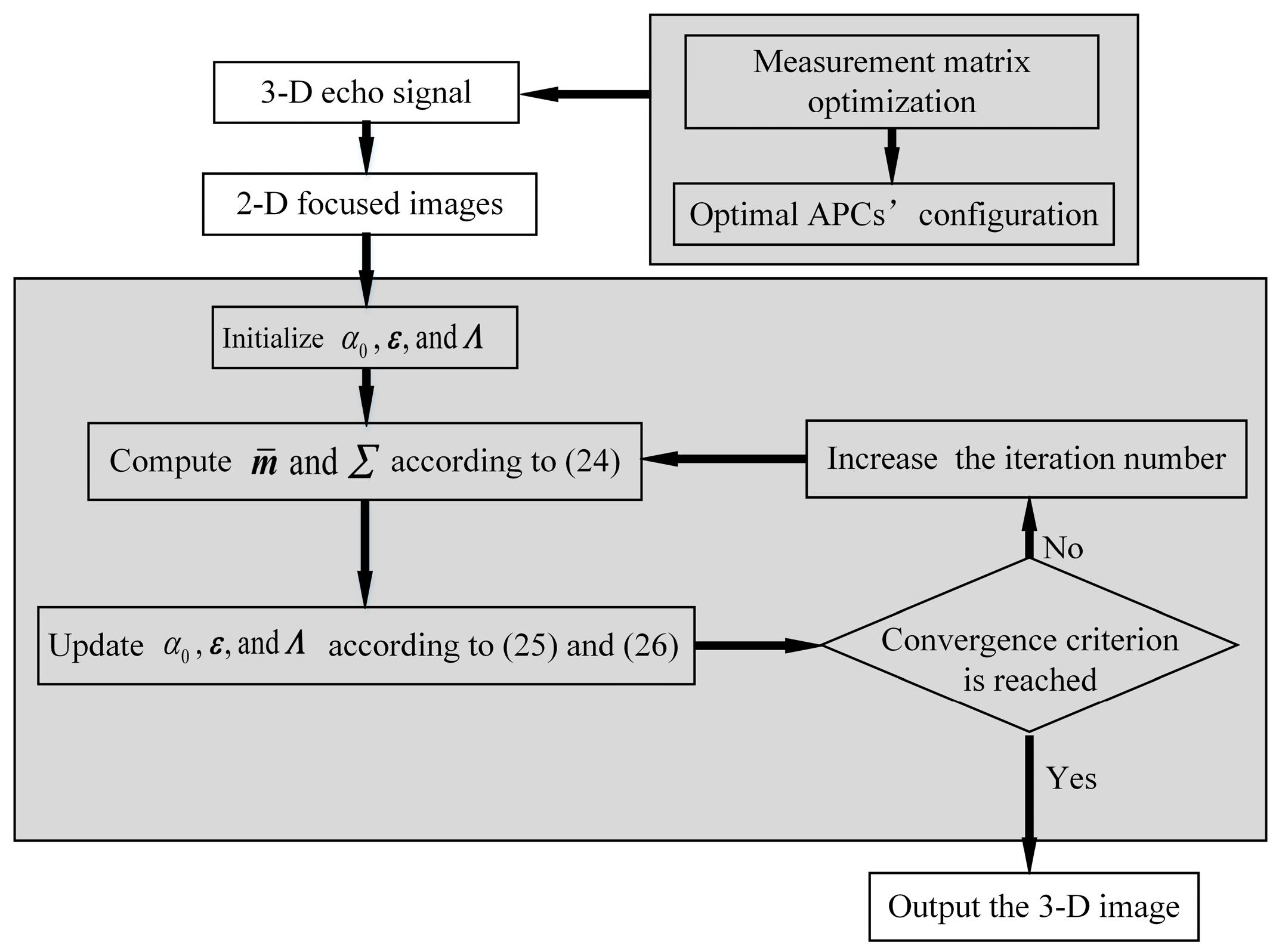
4. Cross-Track Reconstruction Based on Sparse Bayesian Inference
4.1. Cross-Track Reconstruction Model with Measurement Matrix Mismatch
4.2. Bayesian Formulation and Sparseness Prior
4.3. Bayesian Inference
5. Experiments and Results
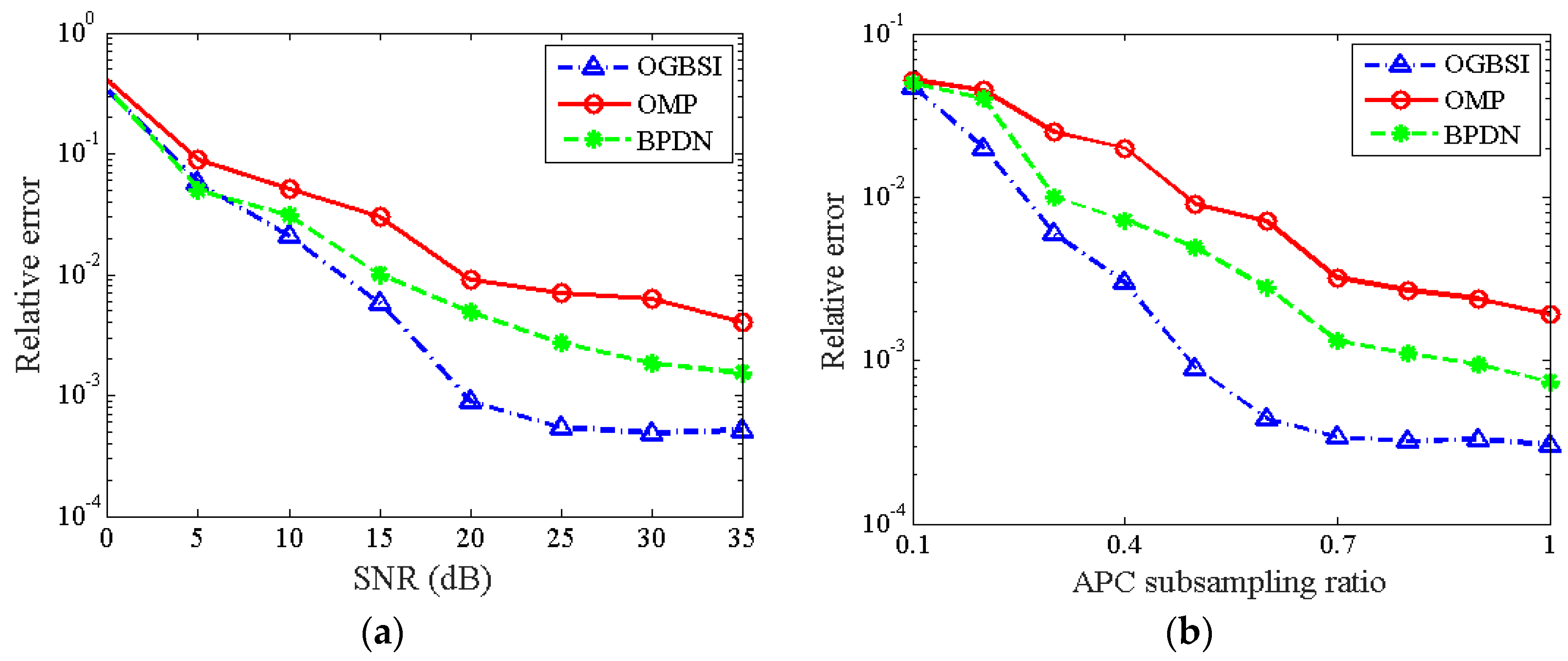
5.1. Performance Comparison of Measurement Matrix Optimization Schemes
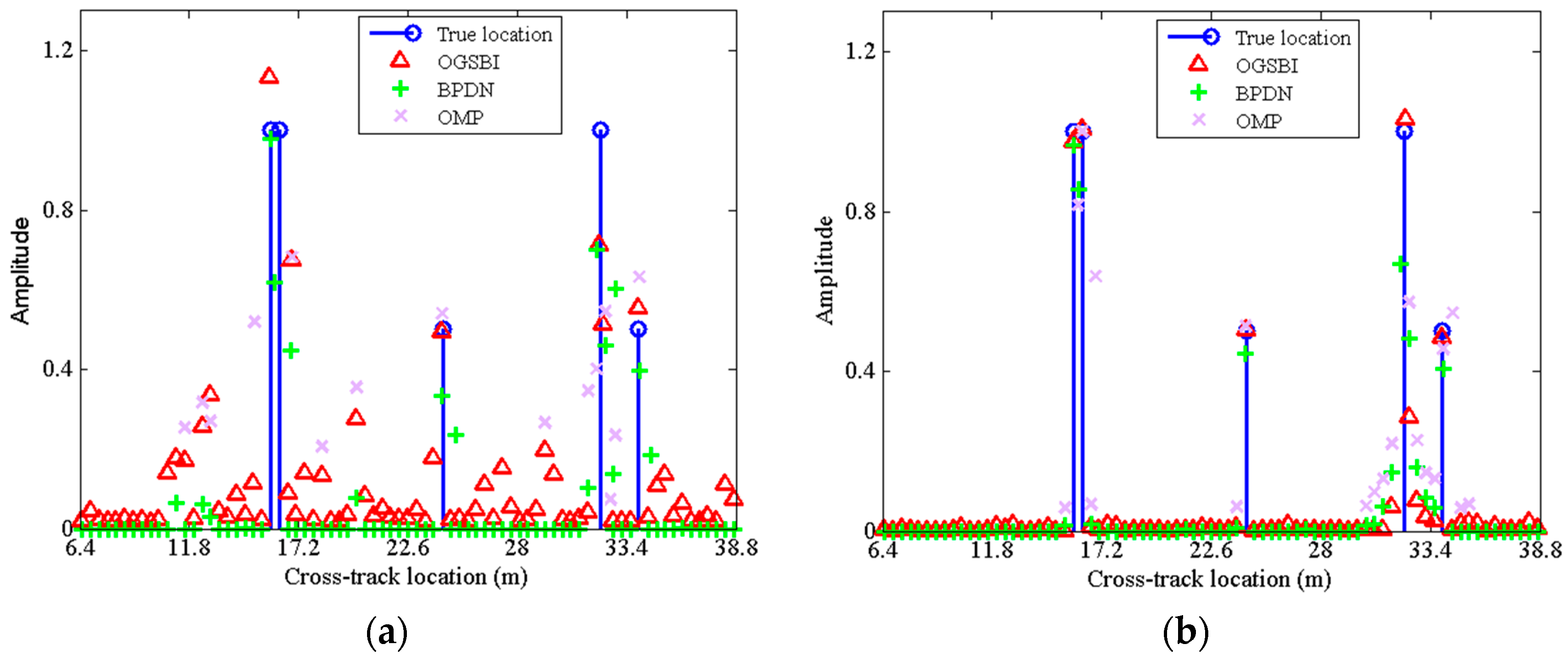
5.2. Reconstruction Performance for Off-Grid Scatterers
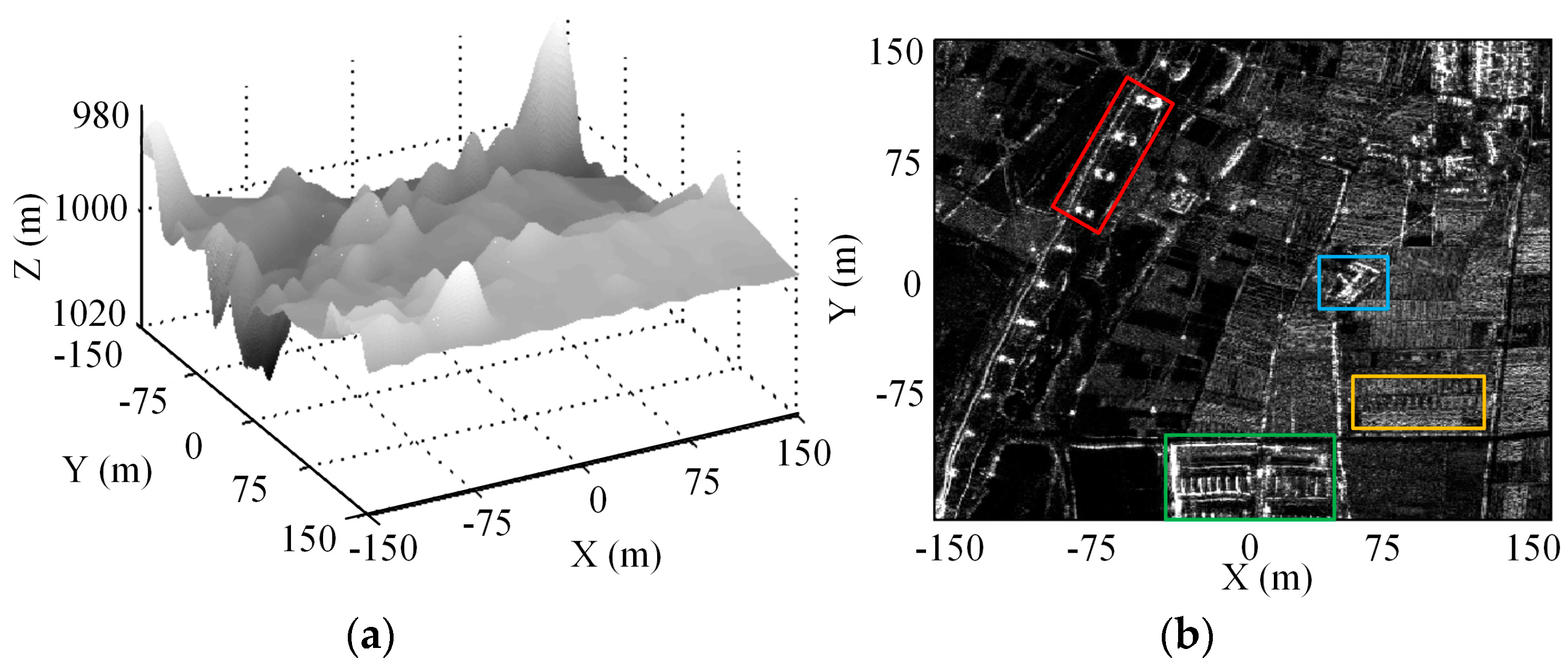
5.3. Experiment for Distributed 3-D Imaging Scene
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DLSLA 3-D SAR | Downward looking sparse linear array three-dimensional synthetic aperture radar |
| CS | Compressive sensing |
| APC | Antenna phase centers |
| RIP | Restricted isometry property |
| CDS | Cyclic difference sets |
| OGSBI | Off-grid sparse Bayesian inference |
| MAP | Maximum a posteriori |
| MIMO | Multiple-input multiple-out |
| SVQ | Sphere vector quantization |
| Probability distribution function | |
| EM | Expectation-maximization |
| BPDN | Basis pursuit denoise |
| RMSE | Relative mean square error |
| OMP | Orthogonal matching pursuit |
| CSAR | Circular SAR |
References
- Klare, J.; Cerutti-Maori, D.; Brenner, A.; Ender, J. Image quality analysis of the vibrating sparse MIMO antenna array of the airborne 3D imaging radar ARTINO. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 5310–5314.
- Shi, J.; Zhang, X.; Gao, X.; Jianyu, J. Signal Processing for Microwave Array Imaging: TDC and Sparse Recovery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4584–4598. [Google Scholar]
- Peng, X.; Wang, Y.; Hong, W.; Tan, W.; Wu, Y. Airborne Downward Looking Sparse Linear Array 3-D SAR Heterogeneous Parallel Simulation. Remote Sens. 2013, 5, 5304–5329. [Google Scholar] [CrossRef]
- Ren, X.; Chen, L.; Yang, J. 3D Imaging Algorithm for Down-Looking MIMO Array SAR Based on Bayesian Compressive Sensing. Int. J. Antennas Propag. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, Y.; Dong, G.; Kuang, G. Truncated SVD-Based Compressive Sensing for Downward-Looking Three-Dimensional SAR Imaging with Uniform/Nonuniform Linear Array. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1853–1857. [Google Scholar] [CrossRef]
- Wei, S.J.; Zhang, X.L. Sparse Autofocus Recovery for Under-sampled Linear Array SAR 3-D Imaing. Progr. Electromagn. Res. 2013, 140, 43–62. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An Introduction To Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Bajwa, W.U.; Calderbank, R.; Jafarpour, S. Why Gabor frames? Two fundamental measures of coherence and their role in model selection. J. Commun. Netw. 2010, 12, 289–307. [Google Scholar] [CrossRef]
- Bajwa, W.U.; Calderbank, R.; Mixon, D.G. Two are better than one: Fundamental parameters of frame coherence. Appl. Comput. Harmonic Anal. 2011, 33, 58–78. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L.; Zhang, C. Off-grid Direction of Arrival Estimation Using Sparse Bayesian Inference. IEEE Trans. Signal Process. 2011, 61, 38–43. [Google Scholar] [CrossRef]
- Si, W.; Qu, X.; Qu, Z. Off-Grid DOA Estimation Using Alternating Block Coordinate Descent in Compressed Sensing. Sensors 2015, 15, 21099–21113. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Lu, X.; Yu, X.; Xi, Z.; Chen, W. A fast and accurate sparse continuous signal reconstruction by homotopy DCD with non-convex regularization. Sensors 2014, 14, 5929–5951. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Liu, C.; Liu, B.; Wang, D. Sparse Frequency Diverse MIMO Radar Imaging for Off-Grid Target Based on Adaptive Iterative MAP. Remote Sens. 2013, 5, 631–647. [Google Scholar] [CrossRef]
- Xia, P.; Zhou, S.; Giannakis, G.B. Achieving the Welch bound with difference sets. IEEE Trans. Inf. Theory 2005, 51, 1900–1907. [Google Scholar] [CrossRef]
- Stahl, H.; Mietzner, J.; Fischer, R.F.H. A Sub-Nyquist radar system based on optimized sensing matrices derived via sparse rulers. In Proceedings of the 3rd International Workshop on Compressed Sensing Theory and Its Applications to Radar, Sonar and Remote Sensing (CoSeRa), Pisa, Italy, 16–19 June 2015; pp. 42–46.
- Ji, S.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Stojanovic, I.; Cetin, M.; Karl, W.C. Compressed Sensing of Monostatic and Multistatic SAR. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1444–1448. [Google Scholar] [CrossRef]
- Yu, N.Y.; Li, Y. Deterministic construction of Fourier-based compressed sensing matrices from an almost difference set. J. Adv. Signal Process. 2013, 2013, 1–14. [Google Scholar]
- Xia, P.; Giannakis, G.B. Design and analysis of transmit-beamforming based on limited-rate feedback. IEEE Trans. Signal Process. 2006, 54, 1853–1863. [Google Scholar]
- Gordon, D. La Jolla Difference Set Repository. Available online: http://www.ccrwest.org/diffsets.html (accessed on 2 August 2016).
- Linde, B.Y.; Buzo, A.; Gray, R.M. An algorithm for vector quantizer desig. IEEE Trans. Commun. 2012, 28, 84–95. [Google Scholar] [CrossRef]
- Granville, V.; Krivánek, M.; Rasson, J.P. Simulated Annealing: A Proof of Convergence. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 652–656. [Google Scholar] [CrossRef]
- Liu, H.; Bo, J.; Liu, H.; Bao, Z. Superresolution ISAR Imaging Based on Sparse Bayesian Learning. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5005–5013. [Google Scholar]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Lin, Y.; Hong, W.; Tan, W.; Wang, Y.; Xiang, M. Airborne circular SAR imaging: Results at P-band. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5594–5597.




| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Center Wavelength | 8 mm | Frequency Points | 1600 | AT 2 Sampling Number | 261 |
| Signal Bandwidth | 300 MHz | Platform Flying Height | 1000 m | AT Sampling Interval | 0.01 m |
| A/D Sampling Frequency | 360 MHz | CT 1 APC Number | 261 | CT Beam Width | 14° |
| Signal Pulse Width | 4 μs | CT Sampling Interval | 0.01 m | AT Beam Width | 14° |
| Region I | Region II | Region III | Region IV | |
|---|---|---|---|---|
| OGSBI | 0.21 | 0.33 | 0.24 | 0.41 |
| BPDN | 0.26 | 0.42 | 0.32 | 0.56 |
| OMP | 0.33 | 0.47 | 0.51 | 0.72 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, Q.; Jiang, C.; Lin, Y.; Tan, W.; Wang, Z.; Hong, W. Measurement Matrix Optimization and Mismatch Problem Compensation for DLSLA 3-D SAR Cross-Track Reconstruction. Sensors 2016, 16, 1333. https://doi.org/10.3390/s16081333
Bao Q, Jiang C, Lin Y, Tan W, Wang Z, Hong W. Measurement Matrix Optimization and Mismatch Problem Compensation for DLSLA 3-D SAR Cross-Track Reconstruction. Sensors. 2016; 16(8):1333. https://doi.org/10.3390/s16081333
Chicago/Turabian StyleBao, Qian, Chenglong Jiang, Yun Lin, Weixian Tan, Zhirui Wang, and Wen Hong. 2016. "Measurement Matrix Optimization and Mismatch Problem Compensation for DLSLA 3-D SAR Cross-Track Reconstruction" Sensors 16, no. 8: 1333. https://doi.org/10.3390/s16081333
APA StyleBao, Q., Jiang, C., Lin, Y., Tan, W., Wang, Z., & Hong, W. (2016). Measurement Matrix Optimization and Mismatch Problem Compensation for DLSLA 3-D SAR Cross-Track Reconstruction. Sensors, 16(8), 1333. https://doi.org/10.3390/s16081333






