Data-Aware Retrodiction for Asynchronous Harmonic Measurement in a Cyber-Physical Energy System
Abstract
:1. Introduction
2. Preliminaries
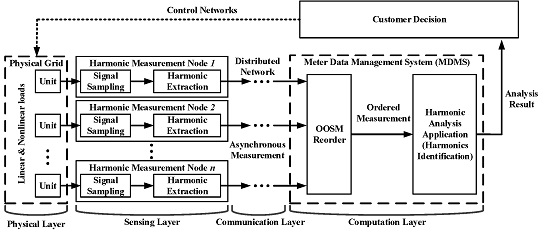
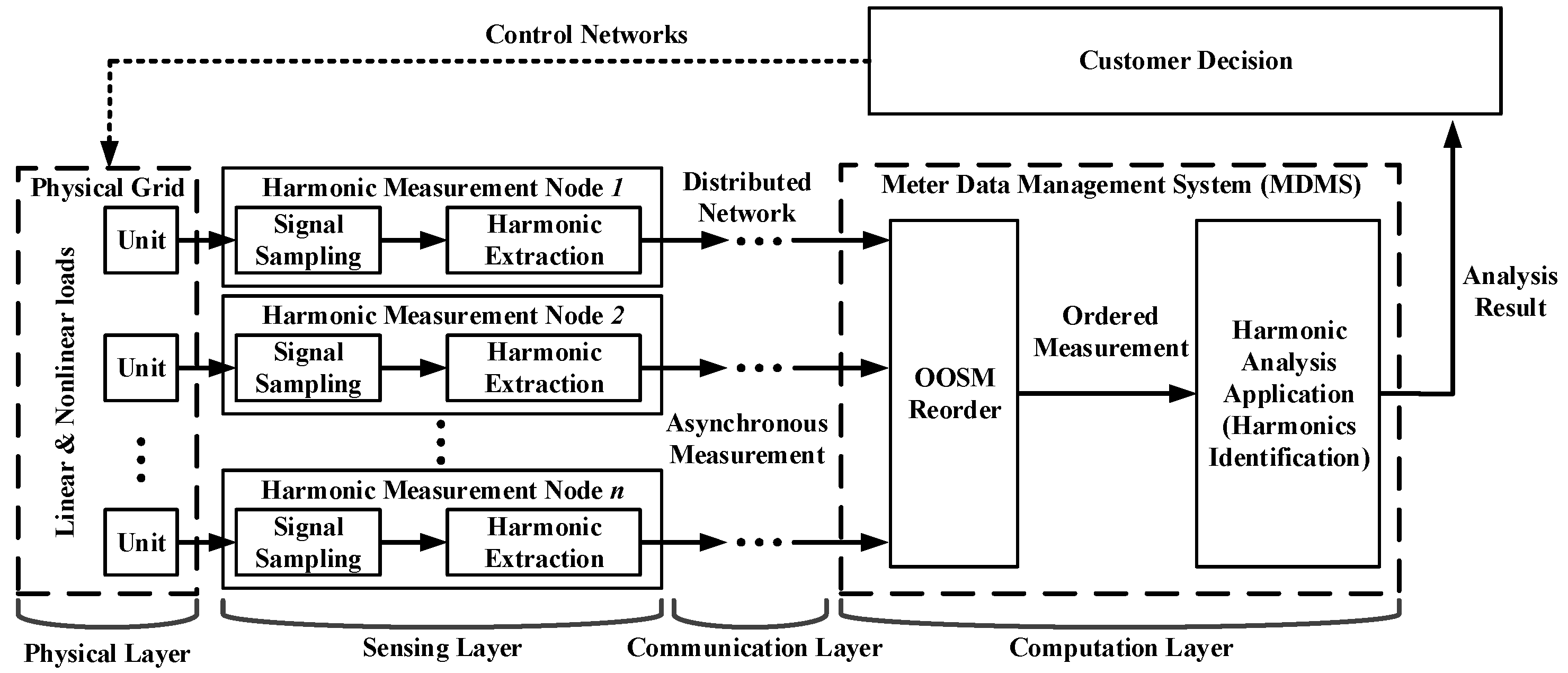
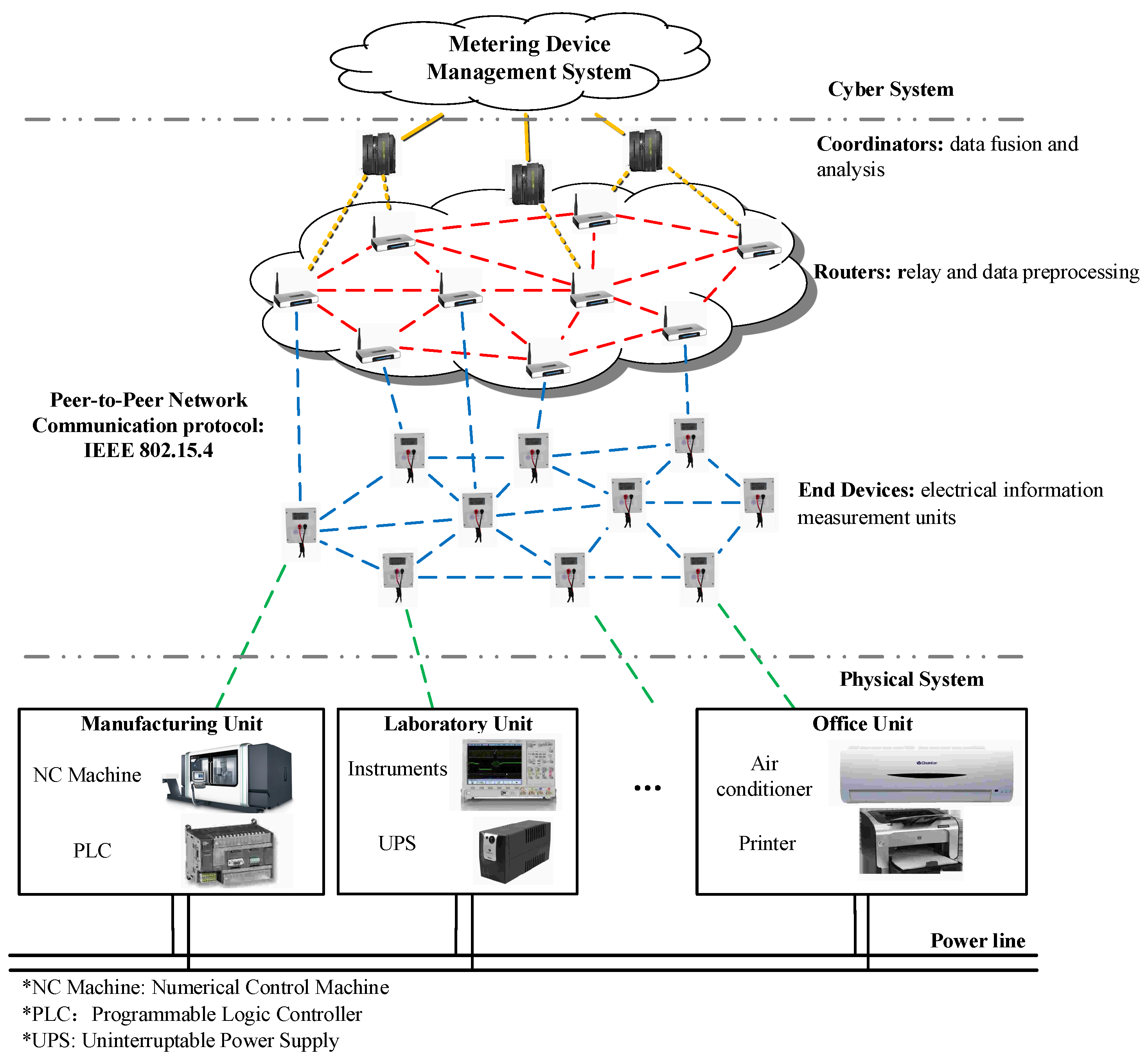
2.1. Distributed Metering Framework in a Cyber-Physical Energy System
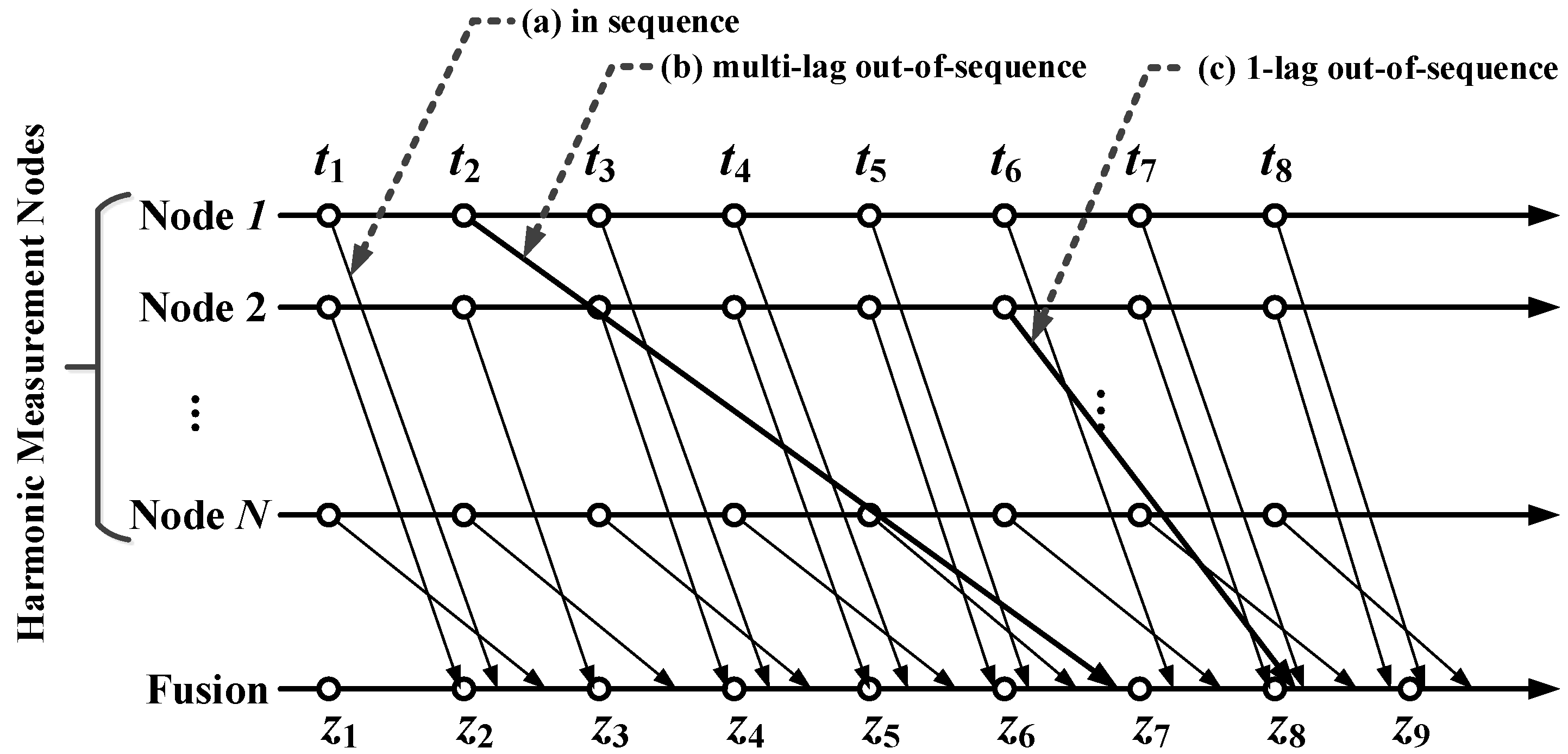
2.2. Out-of-Sequence Measurement Problem Formulation
- Prediction:
- combine the evolution model :where
- Filtering:
- the filtering density is obtained by combining the sensor model and the prediction density:
- Retrodiction:
- the retrodiction density is obtained by combing the object evolution model with the previous prediction and filter densities:
3. Data-Aware Retrodiction for Out-of-Sequence Measurement
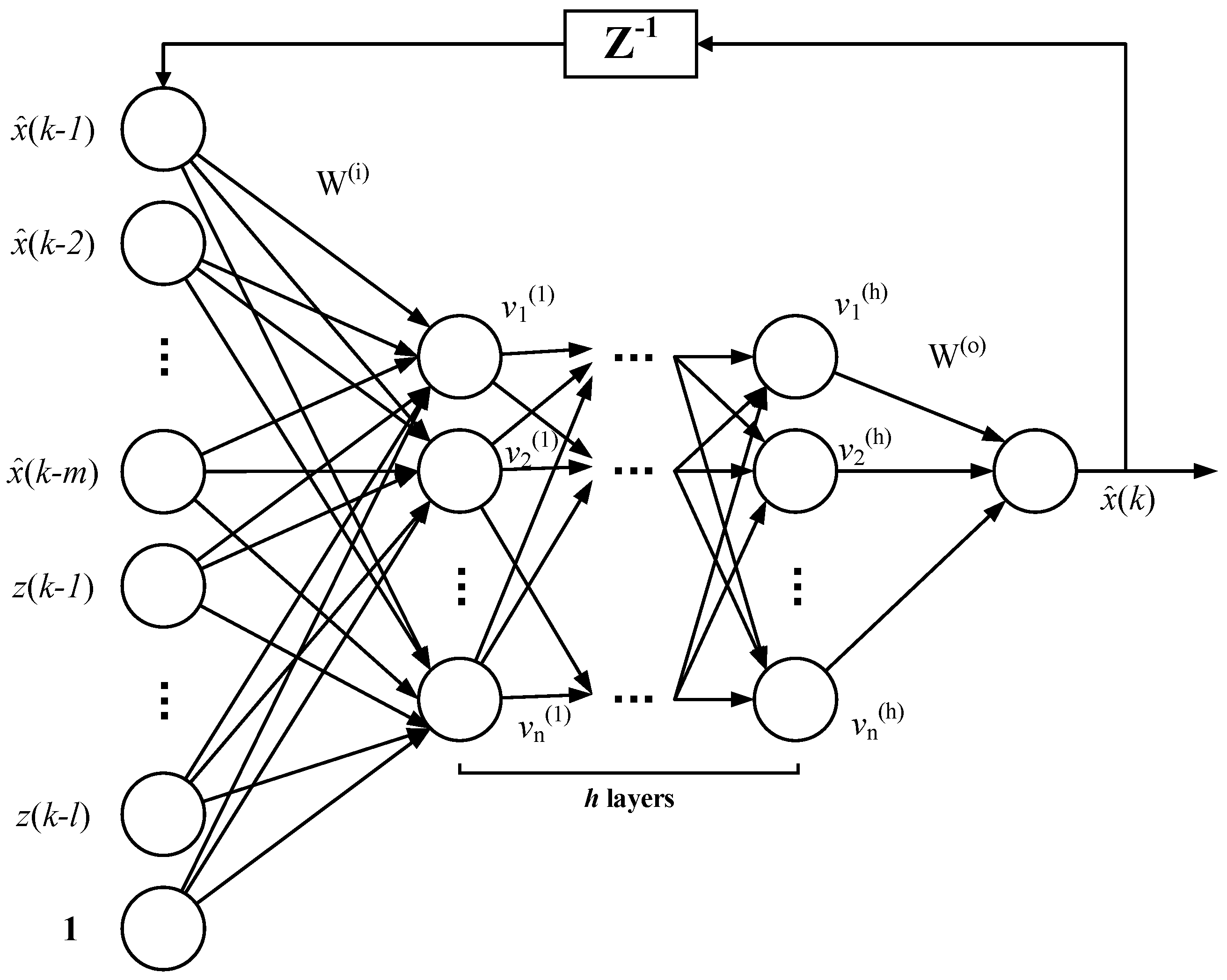
3.1. Harmonic Modeling Based on a Nonlinear Autoregressive Exogenous Model Neural Network
3.2. Data-Aware Retrodiction Based on the NARX Neural Network
3.2.1. Single-Lag Out-of-Sequence Measurement Solution
- Step 1:
- Step 2:
- Step 3:
- Step 4:
- Update the weights with:
- Step 5:
- Update the estimation of .
3.2.2. Multi-Lag Out-of-Sequence Measurement Solution
- Step 1:
- Calculate , and initialize , ;
- Step 2:
- Perform the single-lag OOSM algorithm with , and set ;
- Step 3:
- Update ;
- Step 4:
- Go back to Step 2 until .
- Step 5:
- Update the latest estimation .
- Step 1:
- Sensor nodes of the electric monitoring network measure the harmonics in each branch. The harmonic measurement algorithm is ADALINE [45]. The distributed nodes calculate the amplitudes and phases of each order of harmonics in their branches and send the harmonic data up to the data management system through the two-way sensing network.
- Step 2:
- Upon the arrival of the harmonic information of the network, the data management system updates the cached electrical state. If harmonic data of certain branches are late, update the harmonic parameter with the former estimate value and go on measuring.
- Step 3:
- When the out-of-sequence measurement arrives, the OOSM algorithm retrodicts the transmission error of the end notes using the multi-lag out-of-sequence measurement method and updates the latest estimation of the harmonic information of the grid.
- Step 4:
- The harmonic analysis applications, such as harmonic sources identification, are processed with the updated harmonic estimation result.
3.3. Evaluation of Data-Aware Retrodiction for Harmonics Measurement
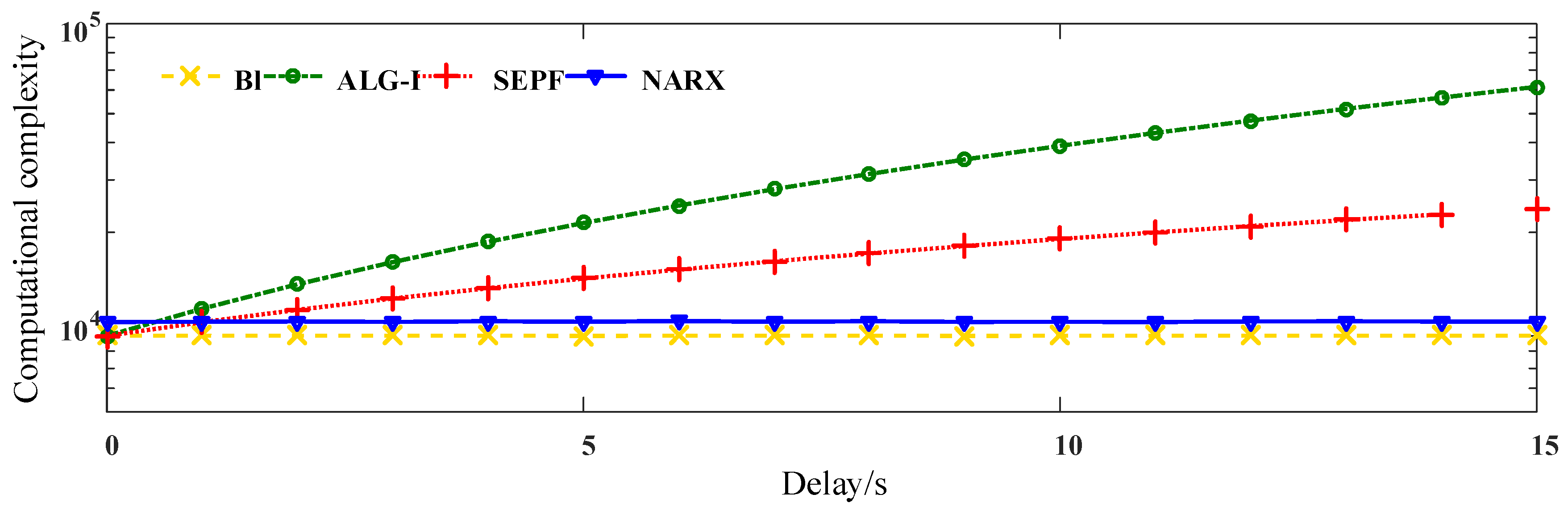
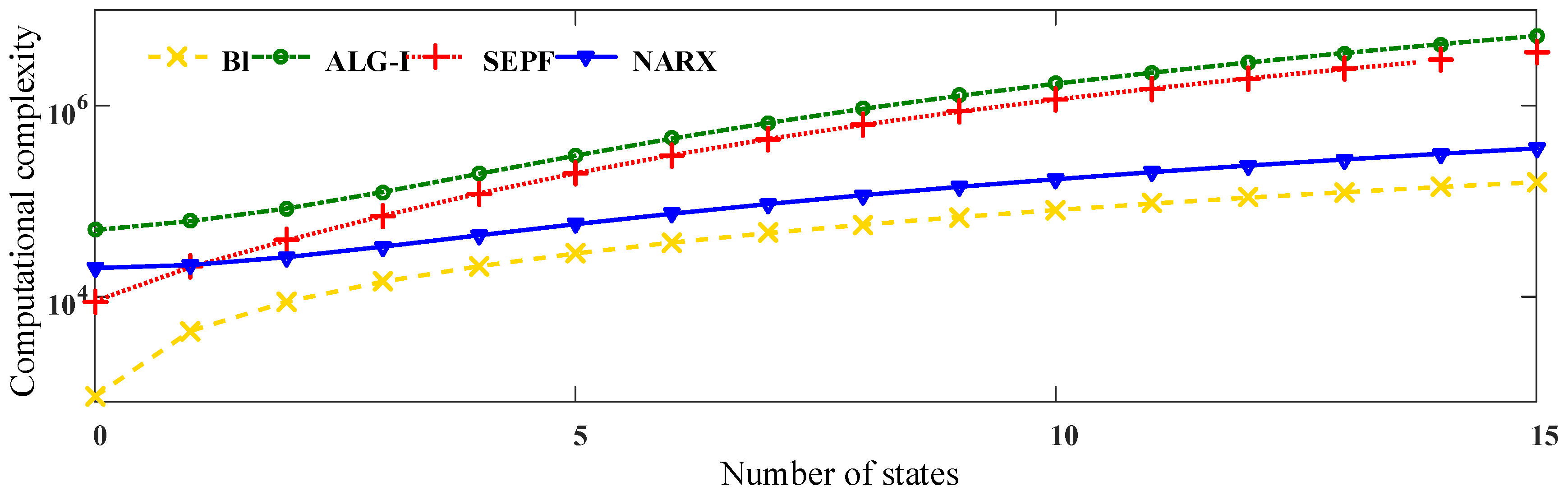
3.3.1. Computational Complexity Evaluation
3.3.2. Memory Consumption
4. Experiments and Analysis
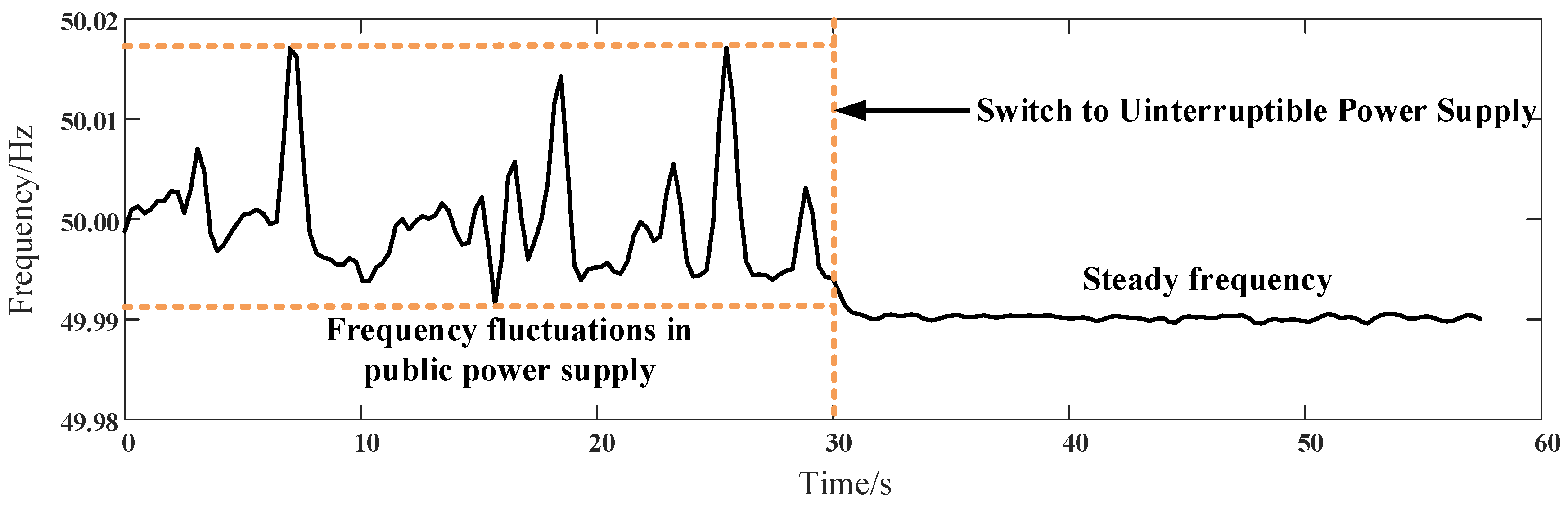
4.1. Experiment Setup
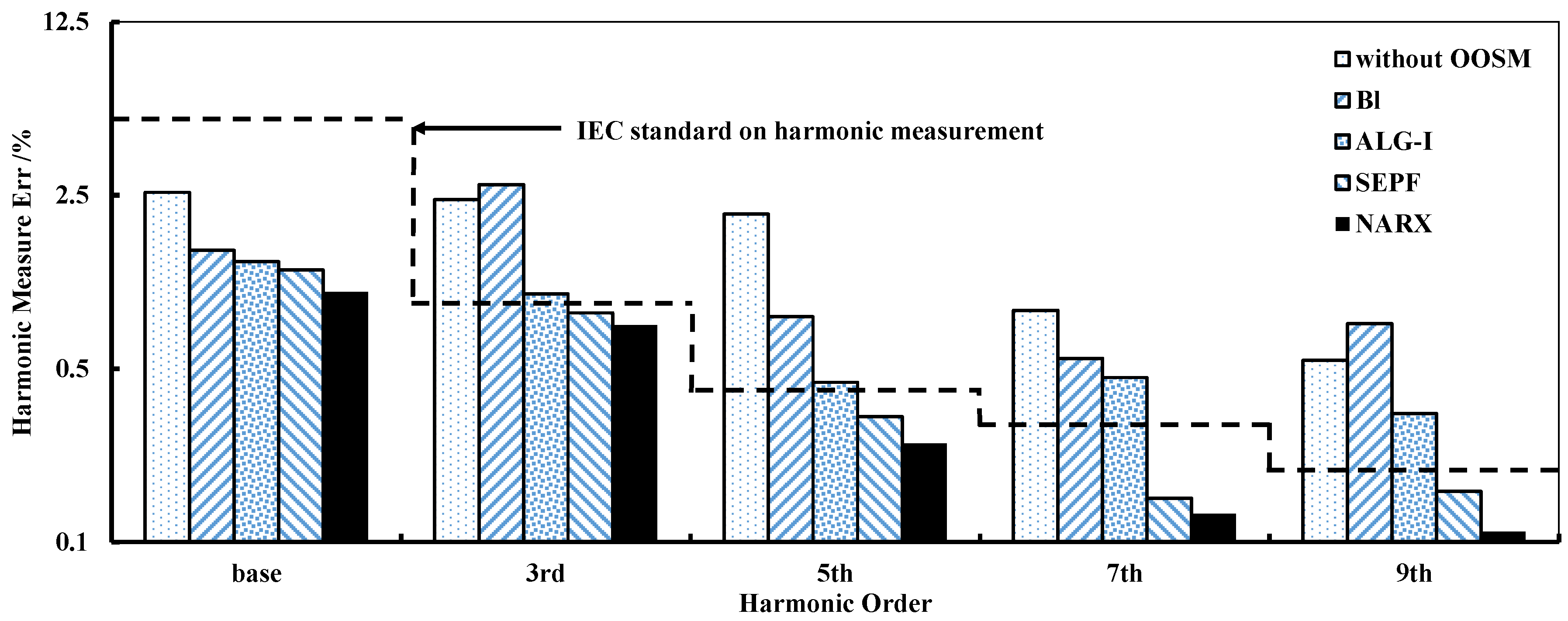
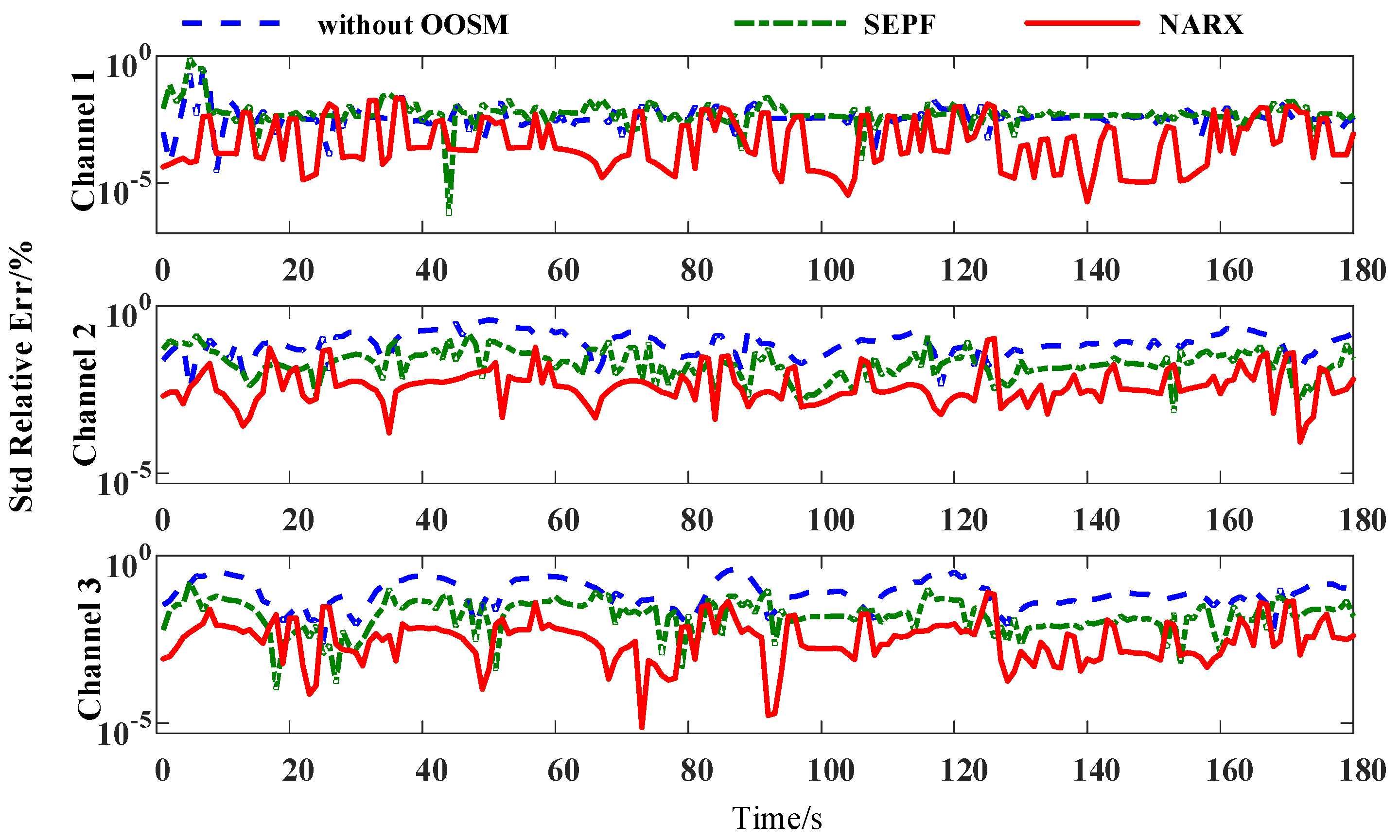
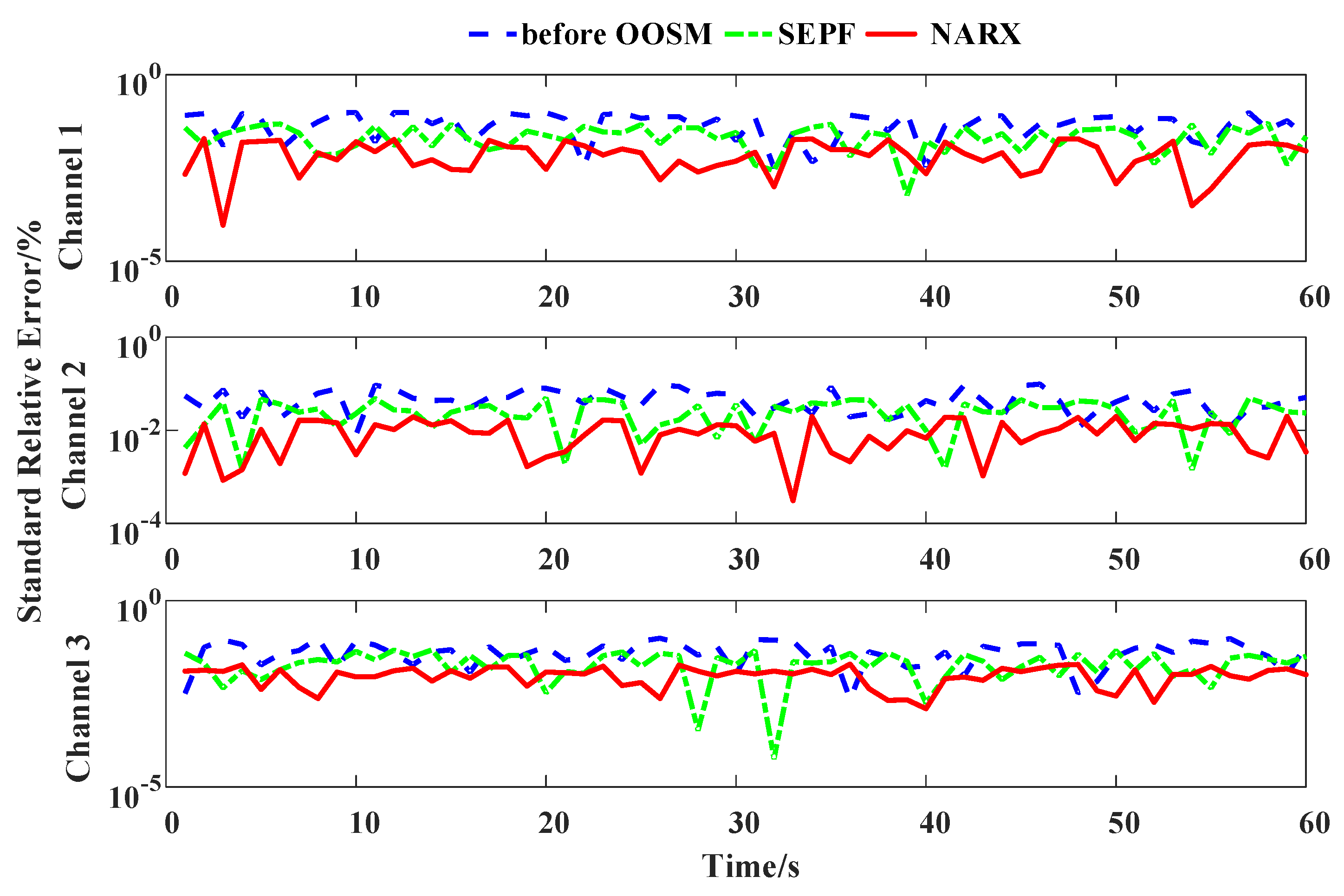
4.2. Measurement Precision Comparison
4.3. Computational Complexity Comparison
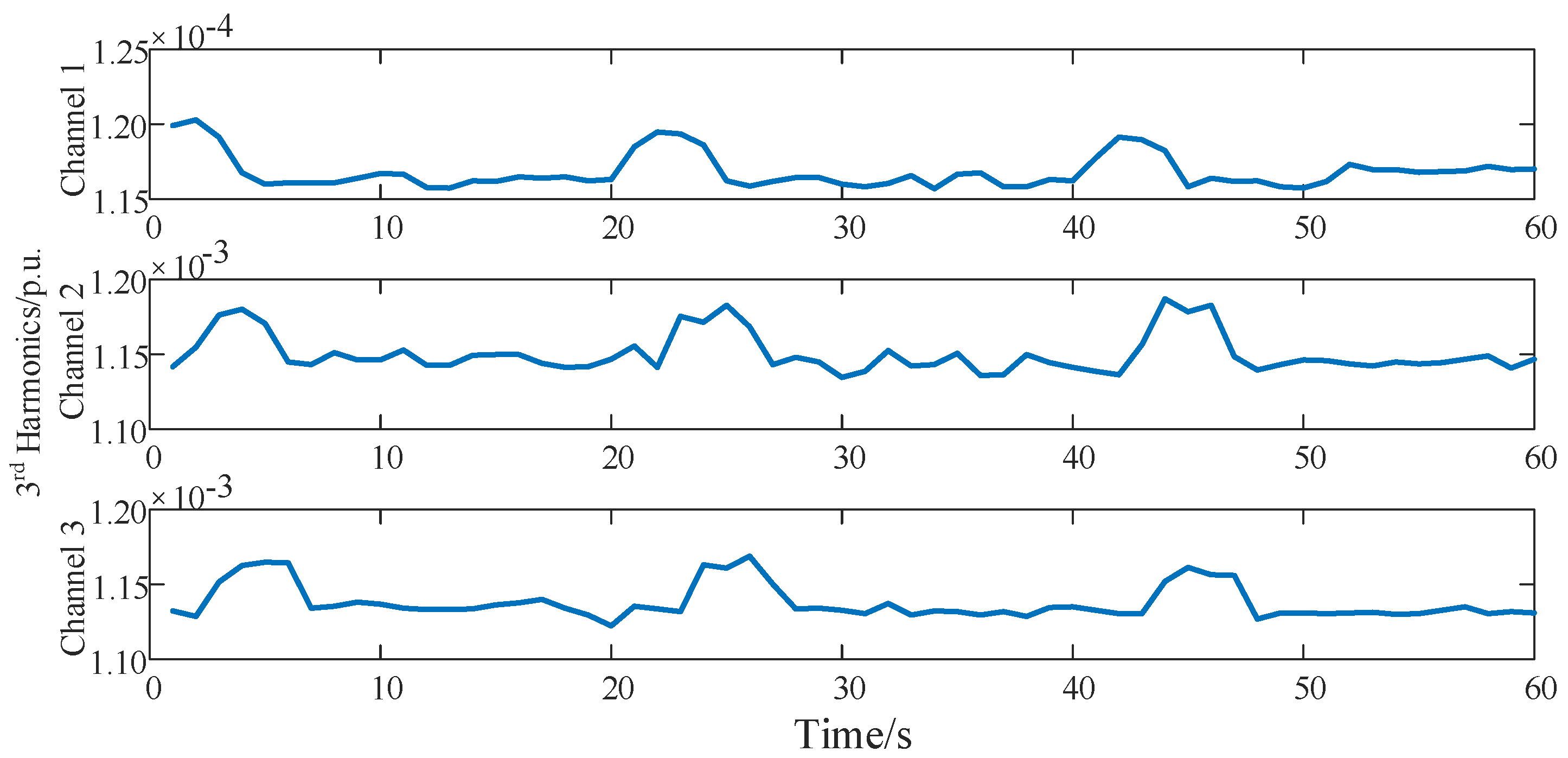
4.4. Case I: Data-Aware Retrodiction for Non-Stationary Harmonic Measurement
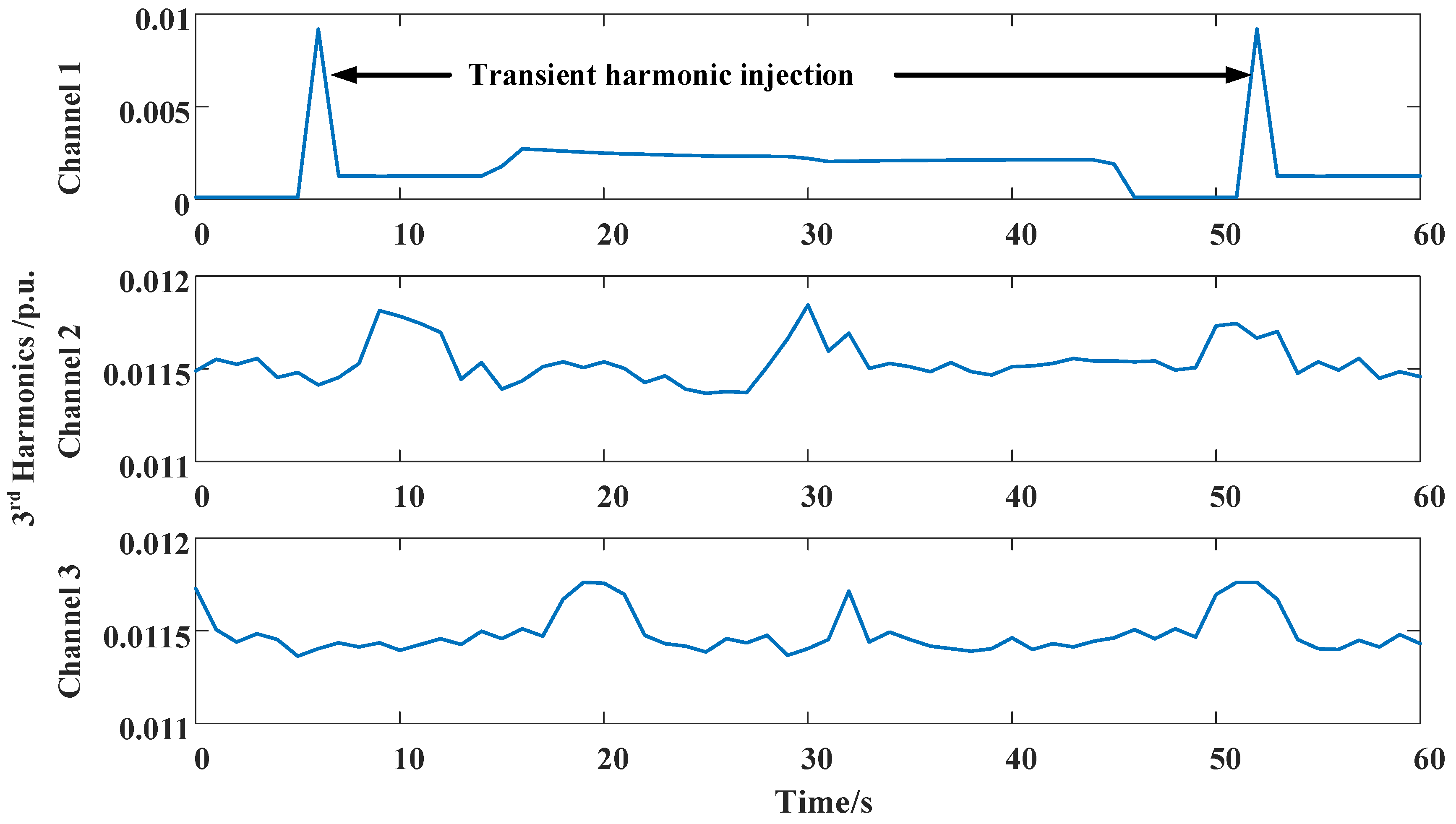
4.5. Case II: Data-Aware Retrodiction for Transient Harmonic Measurement
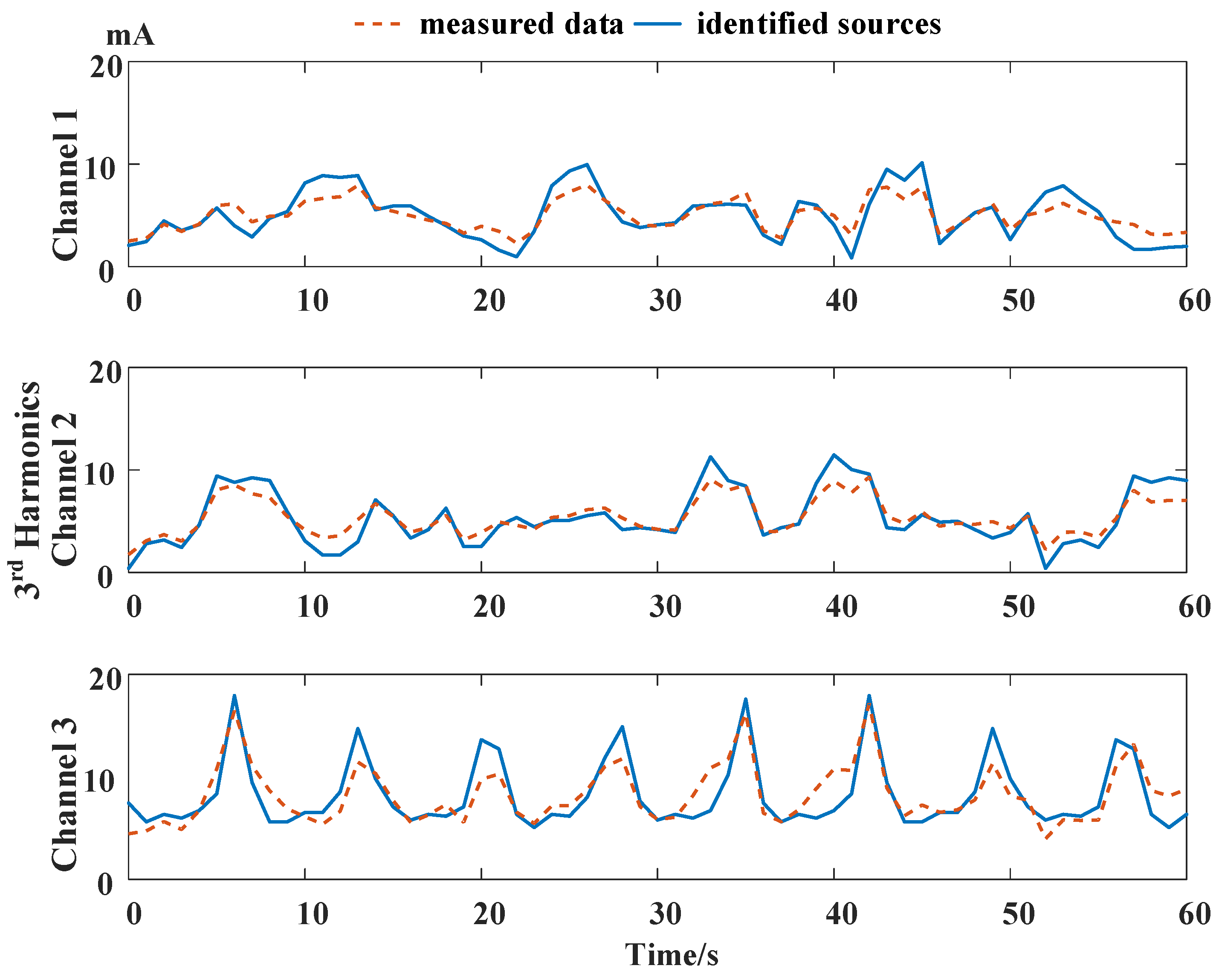
4.6. Case III: Data-Aware Retrodiction-Based Harmonic Identification
4.7. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| OOSM | Out-of-sequence measurement |
| CPES | Cyber-physical energy systems |
| AMI | Advanced infrastructure |
| NARX | Nonlinear autoregressive model with exogenous inputs |
References
- Silva, L.C.; Almeida, H.O.; Perkusich, A.; Perkusich, M. A model-based approach to support validation of medical cyber-physical systems. Sensors 2015, 15, 27625–27670. [Google Scholar] [CrossRef] [PubMed]
- Horvath, P.; Yampolskiy, M.; Koutsoukos, X. Efficient evaluation of wireless real-time control networks. Sensors 2015, 15, 4134–4153. [Google Scholar] [CrossRef] [PubMed]
- Facchinetti, T.; Vedova, M.L.D. Real-time modeling for direct load control in cyber-physical power systems. IEEE Trans. Ind. Inf. 2011, 7, 689–698. [Google Scholar] [CrossRef]
- Ilic, M.D.; Xie, L.; Khan, U.A.; Moura, J.M.F. Modeling of future cyber-physical energy systems for distributed sensing and control. IEEE Trans. Syst. Man Cybern. 2010, 40, 825–838. [Google Scholar] [CrossRef]
- Liu, N.; Chen, J.; Zhu, L.; Zhang, J.; He, Y. A key management scheme for secure communications of advanced metering infrastructure in smart grid. IEEE Trans. Ind. Electron. 2013, 60, 4746–4756. [Google Scholar]
- Westenberger, A.; Duraisamy, B.; Munz, M.; Muntzinger, M.; Fritzsche, M.; Dietmayer, K. Impact of out-of-sequence measurements on the joint integrated probabilistic data association filter for vehicle safety systems. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Alcala de Henares, Spain, 3–7 June 2012; pp. 438–443.
- Zhang, S.; Bar-Shalom, Y. Particle filter processing of out-of-sequence measurements: Exact bayesian solution. IEEE Trans. Aerosp. Electron. Syst. 2011, 48, 2818–2831. [Google Scholar] [CrossRef]
- Bar-Shalom, Y. Update with out-of-sequence measurements in tracking: Exact solution. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 769–777. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Mallick, M. One-step solution for the multistep out-of-sequence-measurement problem in tracking. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 27–37. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Mallick, M.; Chen, H.; Washburn, R. One-step solution for the general out-of-sequence-measurement problem in tracking. IEEE Aerosp. Conf. Proc. 2002, 4, 1551–1559. [Google Scholar]
- Mallick, M.; Coraluppi, S.; Carthel, C. Advances in asynchronous and decentralized estimation. In Proceedings of the 2001 IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 10–17 March 2001; pp. 1873–1888.
- Lanzkron, P.; Bar-Shalom, Y. A two-step method for out-of-sequence measurements. IEEE Aerosp. Conf. Proc. 2004, 3, 2036–2041. [Google Scholar]
- Challa, S.; Evans, R.J.; Wang, X. A bayesian solution and its approximations to out-of-sequence measurement problems. Inf. Fusion 2003, 4, 185–199. [Google Scholar] [CrossRef]
- Zhang, K.; Li, X.; Zhu, Y. Optimal update with out-of-sequence measurements. IEEE Trans. Signal Proc. 2005, 53, 1992–2004. [Google Scholar] [CrossRef]
- Mallick, M.; Kirubarajan, T.; Arulampalam, S. Out-of-sequence measurement processing for tracking ground target using particle filters. IEEE Aerosp. Conf. Proc. 2002, 4. [Google Scholar] [CrossRef]
- Orton, M.; Marrs, A. Particle filters for tracking with out-of-sequence measurements. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 693–702. [Google Scholar] [CrossRef]
- Zhang, S.; Bar-Shalom, Y. Out-of-sequence measurement processing for particle filter: Exact bayesian solution. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2818–2831. [Google Scholar] [CrossRef]
- Shen, X.; Zhu, Y.; Song, E.; Luo, Y. Optimal centralized update with multiple local out-of-sequence measurements. IEEE Trans. Signal Proc. 2009, 57, 1551–1562. [Google Scholar] [CrossRef]
- Orguner, U.; Fredrik, G. Storage efficient particle filters for the out of sequence measurement problem. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–6.
- Oreshkin, B.N.; Coates, M.J. Efficient delay-tolerant particle filtering. IEEE Trans. Signal Proc. 2011, 59, 3369–3381. [Google Scholar] [CrossRef]
- Berntorp, K.; Robertsson, A.; Arzen, K.E. Rao-blackwellized particle filters with out-of-sequence measurement processing. IEEE Trans. Signal Proc. 2014, 62, 6454–6467. [Google Scholar] [CrossRef]
- Zhu, C.; Xia, Y.; Xie, L.; Yan, L. Optimal linear estimation for systems with transmission delays and packet dropouts. IET Signal Proc. 2013, 7, 814–823. [Google Scholar] [CrossRef]
- Kim, T.H.; Song, T.L.; Musicki, D. Out-of-sequence measurements update using the information filter with reduced data storage. In Proceedings of the 2014 Sensor Data Fusion: Trends, Solutions, Applications (SDF), Bonn, Germany, 8–10 October 2014; pp. 1–6.
- Zachariah, D.; Skog, I.; Jansson, M.; Handel, P. Bayesian estimation with distance bounds. IEEE Signal Proc. Lett. 2012, 19, 880–883. [Google Scholar] [CrossRef]
- Zhang, S.; Bar-Shalom, Y. Optimal update with multiple out-of-sequence measurements with arbitrary arriving order. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3116–3132. [Google Scholar] [CrossRef]
- Besada-Portas, E.; Lopez-Orozco, J.A.; Lanillos, P.; de la Cruz, J.M. Localization of non-linearly modeled autonomous mobile robots using out-of-sequence measurements. Sensors 2012, 12, 2487–2518. [Google Scholar] [CrossRef] [PubMed]
- Brahmi, M.; Schueler, K.; Bouzouraa, S.; Maurer, M.; Siedersberger, K.H.; Hofmann, U. Timestamping and latency analysis for multi-sensor perception systems. In Proceedings of the 2013 IEEE Sensors, Baltimore, MD, USA, 3–6 November 2013; pp. 1–4.
- Liu, Y.Y.; Wang, X.; Liu, Y.Y. Asynchronous harmonic analysis based on out-of-sequence measurement for large-scale residential power network. In Proceedings of the 2015 IEEE International Instrumentation and Measurement Technology Conference (I2MTC) Proceedings, Pisa, Italy, 11–14 May 2015; pp. 1693–1698.
- Qasim, M.; Khadkikar, V. Application of artificial neural networks for shunt active power filter control. IEEE Trans. Ind. Inf. 2014, 10, 1765–1774. [Google Scholar] [CrossRef]
- Marks, J.H.; Green, T.C. Predictive transient-following control of shunt and series active power filters. IEEE Trans. Power Electron. 2002, 17, 574–584. [Google Scholar] [CrossRef]
- Anh, H.P.H.; Ahn, K.K. Hybrid control of a pneumatic artificial muscle (PAM) robot arm using an inverse NARX fuzzy model. Eng. Appl. Artif. Intell. 2011, 24, 697–716. [Google Scholar] [CrossRef]
- Ardalani-Farsa, M.; Zolfaghari, S. Chaotic time series prediction with residual analysis method using hybrid Elman-NARX neural networks. Neurocomputing 2010, 73, 2540–2553. [Google Scholar] [CrossRef]
- Li, G.; Wen, C.; Zheng, W.X.; Chen, Y. Identification of a class of nonlinear autoregressive models with exogenous inputs based on kernel machines. IEEE Trans. Signal Proc. 2011, 59, 2146–2159. [Google Scholar] [CrossRef]
- Samara, P.A.; Sakellariou, J.S.; Fouskitakis, G.N.; Hios, J.D.; Fassois, S.D. Aircraft virtual sensor design via a time-dependent functional pooling NARX methodology. Aerosp. Sci. Technol. 2013, 29, 114–124. [Google Scholar] [CrossRef]
- Jaiswal, S.; Wath, M.G.; Ballal, M.S. Modeling the measurement error of energy meter using NARX model. In Proceedings of the 2016 IEEE International Instrumentation and Measurement Technology Conference, Taipei, Taiwan, 23–26 May 2016; pp. 1–6.
- Wang, X.; Wang, S.; Ma, J.J. An improved co-evolutionary particle swarm optimization for wireless sensor networks with dynamic deployment. Sensors 2007, 7, 354–370. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S. Collaborative signal processing for target tracking in distributed wireless sensor networks. J. Parallel Distrib. Comput. 2007, 67, 501–515. [Google Scholar] [CrossRef]
- Lim, Y.; Kim, H.M.; Kang, S.; Science, C.; Engineering, I. A reliable data delivery mechanism for grid power quality using neural networks in wireless sensor networks. Sensors 2010, 10, 9349–9358. [Google Scholar] [CrossRef] [PubMed]
- Turrado, C.C.; Lasheras, F.S.; Calvo-rollé, J.L.; Piñón-pazos, A.J.; Javier, F.; Juez, D.C. A new missing data imputation algorithm applied to electrical data loggers. Sensors 2015, 15, 31069–31082. [Google Scholar] [CrossRef] [PubMed]
- Granados-lieberman, D.; Valtierra-rodriguez, M.; Morales-hernandez, L.A.; Romero-troncoso, R.J.; Osornio-rios, R.A. A hilbert transform-based smart sensor for detection, classification, and quantification of power quality disturbances. Sensors 2013, 13, 5507–5527. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Wang, X.; Sun, X.; Liu, Y. Pure harmonics extracting from time-varying power signal based on improved empirical mode decomposition. Measurement 2014, 49, 216–225. [Google Scholar] [CrossRef]
- Kennedy, K.; Lightbody, G.; Yacamini, R. Power system harmonic analysis using the Kalman filter. IEEE Power Eng. Soc. Gen. Meet. 2003, 2, 752–757. [Google Scholar]
- Rosendo Macías, J.A.; Expósito, A.G. Self-tuning of Kalman filters for harmonic computation. IEEE Trans. Power Deliv. 2006, 21, 501–503. [Google Scholar] [CrossRef]
- Xiao, Z.; Jing, X.; Cheng, L. Parameterized convergence bounds for volterra series expansion of NARX models. IEEE Trans. Signal Proc. 2013, 61, 5026–5038. [Google Scholar] [CrossRef]
- Garanayak, P.; Panda, G. Fast and accurate measurement of harmonic parameters employing hybrid adaptive linear neural network and filtered-x least mean square algorithm. IET Gener. Transm. Distrib. 2016, 10, 421–436. [Google Scholar] [CrossRef]
- Besada-Portas, E.; Lopez-Orozco, J.A.; Besada, J.; de la Cruz, J.M. Multisensor fusion for linear control systems with asynchronous, out-of-sequence and erroneous data. Automatica 2011, 47, 1399–1408. [Google Scholar] [CrossRef]
- Williams, R.J.; Zipser, D.; Backpropagation, L. Gradient-Based Learning Algorithms for Recurrent Networks and Their Computational Complexity; Erlbaum Associates Inc.: Hillsdale, NJ, USA, 1995; pp. 433–486. [Google Scholar]
- Shi, Y.; Cui, A.; Ge, Q. Multisensor estimation fusion for wireless networks with mixed data delays. In Proceedings of the 2010 2nd International Workshop on Database Technology and Applications 2010, Wuhan, China, 27–28 November 2010; pp. 1–4.
- Wang, H.; Liu, S. Adaptive Kalman filter for harmonic detection in active power filter application. In Proceedings of the 2015 IEEE on Electrical Power and Energy Conference (EPEC), London, UK, 26–28 October 2015; pp. 227–232.
- Tsakonas, E.E.; Sidiropoulos, N.D.; Swami, A. Optimal particle filters for tracking a time-varying harmonic or chirp signal. IEEE Trans. Signal Proc. 2008, 56, 4598–4610. [Google Scholar] [CrossRef]

| Algorithm | Computation Complexity Level |
|---|---|
| Bl | |
| Lanzkron | |
| ALG-S | |
| ALG-I | |
| A-PF | |
| SERBPF | |
| NARX |
| Algorithm | Memory Consumption |
|---|---|
| Bl | |
| Lanzkron | |
| ALG-S | |
| ALG-I | |
| A-PF | |
| SERBPF | |
| NARX |
| Harmonics Order | Base | 3rd | 5th | 7th | 9th | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| without OOSM | 2.57 | 1.66 | 2.40 | 2.43 | 2.12 | 1.02 | 3.40 | 2.08 | 1.45 | 1.63 |
| Bl | 1.50 | 1.74 | 2.76 | 1.88 | 1.21 | 1.22 | 1.02 | 1.66 | 1.00 | 1.42 |
| ALG-I | 1.35 | 1.42 | 1.60 | 1.34 | 1.02 | 1.34 | 0.92 | 1.33 | 0.92 | 1.21 |
| SEPF | 1.25 | 1.32 | 1.50 | 1.24 | 0.90 | 1.08 | 0.90 | 1.12 | 0.87 | 0.97 |
| NARX | 1.02 | 1.21 | 1.33 | 0.95 | 0.92 | 1.23 | 0.90 | 1.01 | 0.88 | 0.95 |
| Harmonics Order | Base | 3rd | 5th | 7th | 9th | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| Bl | 0.82 | 0.93 | 1.54 | 1.09 | 0.76 | 0.74 | 0.60 | 0.99 | 0.61 | 0.95 |
| ALG-I | 0.73 | 0.79 | 1.00 | 0.82 | 0.58 | 0.78 | 0.57 | 0.68 | 0.54 | 0.72 |
| SEPF | 0.65 | 0.71 | 0.91 | 0.63 | 0.59 | 0.59 | 0.55 | 0.61 | 0.47 | 0.55 |
| NARX | 0.55 | 0.62 | 0.87 | 0.60 | 0.61 | 0.65 | 0.57 | 0.62 | 0.55 | 0.59 |
| Harmonics Order | Base | 3rd | 5th | 7th | 9th | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| Bl | 10.75 | 11.38 | 15.92 | 12.57 | 7.33 | 10.39 | 6.20 | 11.17 | 5.33 | 8.55 |
| ALG-I | 8.27 | 10.64 | 9.36 | 7.85 | 7.41 | 8.51 | 7.33 | 9.36 | 5.55 | 8.77 |
| SEPF | 7.27 | 7.54 | 9.82 | 8.76 | 7.28 | 6.70 | 5.99 | 9.13 | 5.96 | 7.24 |
| NARX | 5.57 | 8.70 | 7.45 | 6.83 | 7.37 | 8.59 | 6.09 | 7.49 | 5.59 | 6.88 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wang, X.; Liu, Y.; Cui, S. Data-Aware Retrodiction for Asynchronous Harmonic Measurement in a Cyber-Physical Energy System. Sensors 2016, 16, 1316. https://doi.org/10.3390/s16081316
Liu Y, Wang X, Liu Y, Cui S. Data-Aware Retrodiction for Asynchronous Harmonic Measurement in a Cyber-Physical Energy System. Sensors. 2016; 16(8):1316. https://doi.org/10.3390/s16081316
Chicago/Turabian StyleLiu, Youda, Xue Wang, Yanchi Liu, and Sujin Cui. 2016. "Data-Aware Retrodiction for Asynchronous Harmonic Measurement in a Cyber-Physical Energy System" Sensors 16, no. 8: 1316. https://doi.org/10.3390/s16081316
APA StyleLiu, Y., Wang, X., Liu, Y., & Cui, S. (2016). Data-Aware Retrodiction for Asynchronous Harmonic Measurement in a Cyber-Physical Energy System. Sensors, 16(8), 1316. https://doi.org/10.3390/s16081316