Robust Pedestrian Classification Based on Hierarchical Kernel Sparse Representation
Abstract
:1. Introduction
2. Related Work
2.1. CENTRIST Features
2.2. Sparse Representation Classifier
3. Hierarchical Kernel Sparse Representation
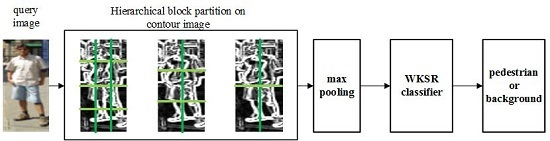
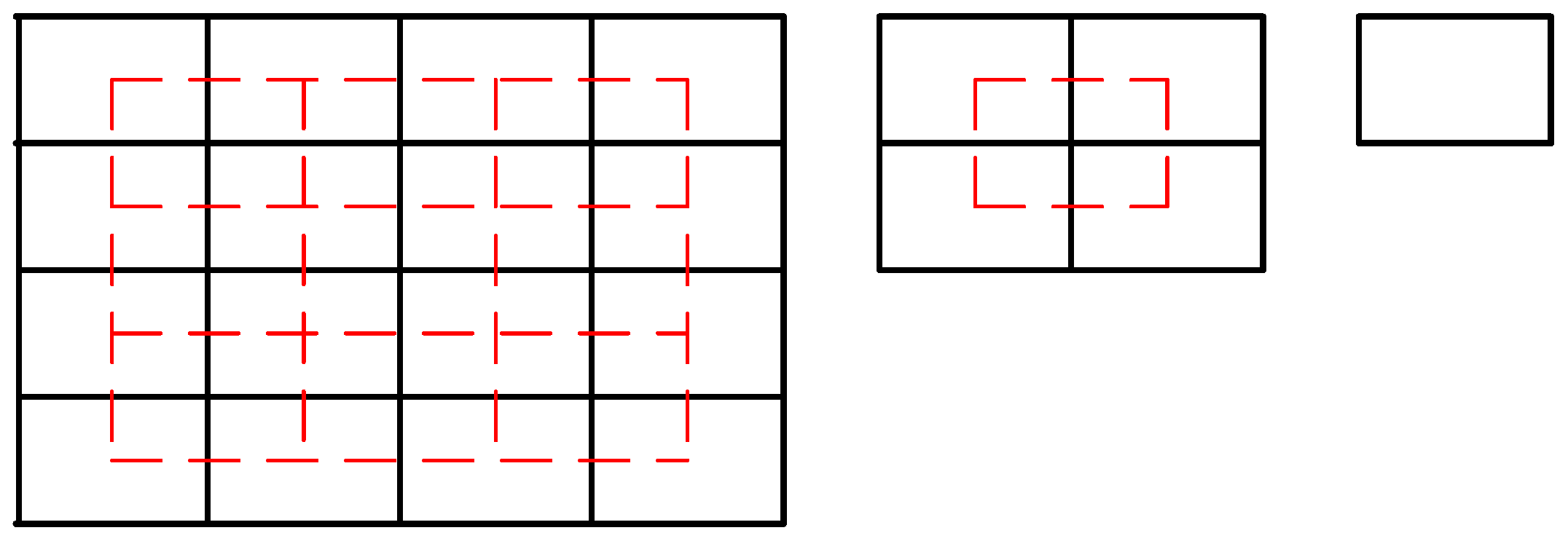
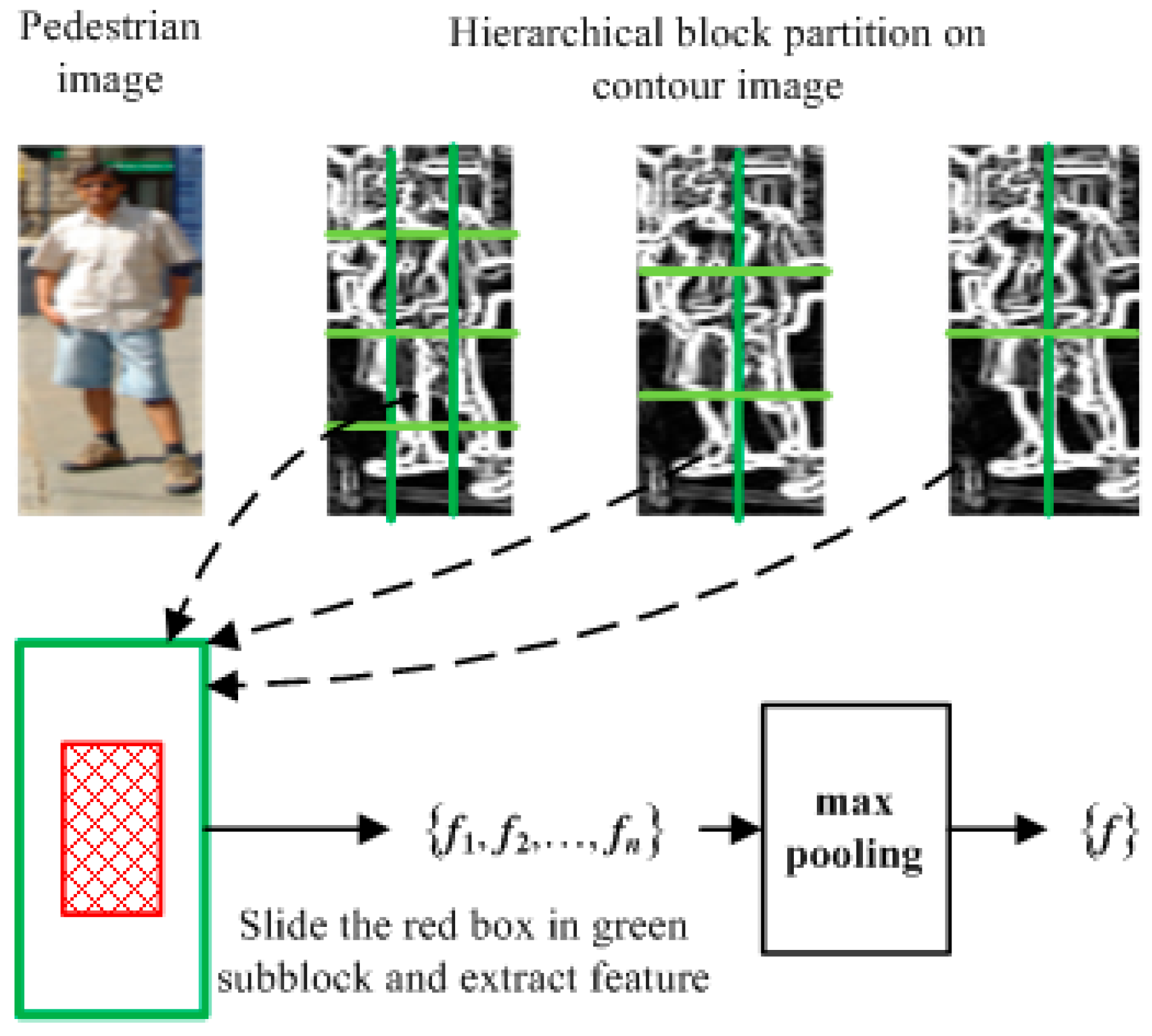
3.1. Hierarchical Features Extraction
3.2. Robust Kernel Sparse Representation
3.3. Occlusion Solution
3.4. Proposed Classification Algorithm
| Algorithm 1: Weighted Kernel Sparse Representation Classifier |
| 1. Hierarchical Features Extraction based on CENTRIST |
| 2. WKSR: Initialize the weight in each block as 1: While not converge, do (a) Compute weighted kernel sparse representation (b) Compute the reconstruction residual (c) Compute the weight value (d) Checking convergence condition where is a small positive scalar and is the weight value of ith block in the iteration t. |
| 3. Do classification where the sub-matrix of associated with the jth class, being the representation coefficient vector associated with the jth class. |
4. Experimental Results
4.1. Parameter Setting
4.2. Pedestrian Classification on INRIA Dataset
4.3. Pedestrian Classification on Daimler Dataset
4.4. Pedestrian Classification on Partial Occlusion Datasets
- (1)
- Pedestrian classification with random block occlusion. In the database of INRIA, we chose 100 non-occlusion images with normal-to-moderate lighting conditions for training, and 500 of the remaining images are randomly chosen for testing. Similar to the settings in [36], we simulate various levels of contiguous occlusion, from 0% to 50%, by replacing a randomly located square block of each testing image with an unrelated image, as illustrated in Figure 6, where (a) shows a pedestrian image with 20% block occlusion, (b) shows a pedestrian image with 30% block occlusion and (c) shows a pedestrian image with 40% block occlusion. Here the location of occlusion is randomly chosen for each image and is unknown to each algorithm, and the image size is normalized to 128 × 64.
- (2)
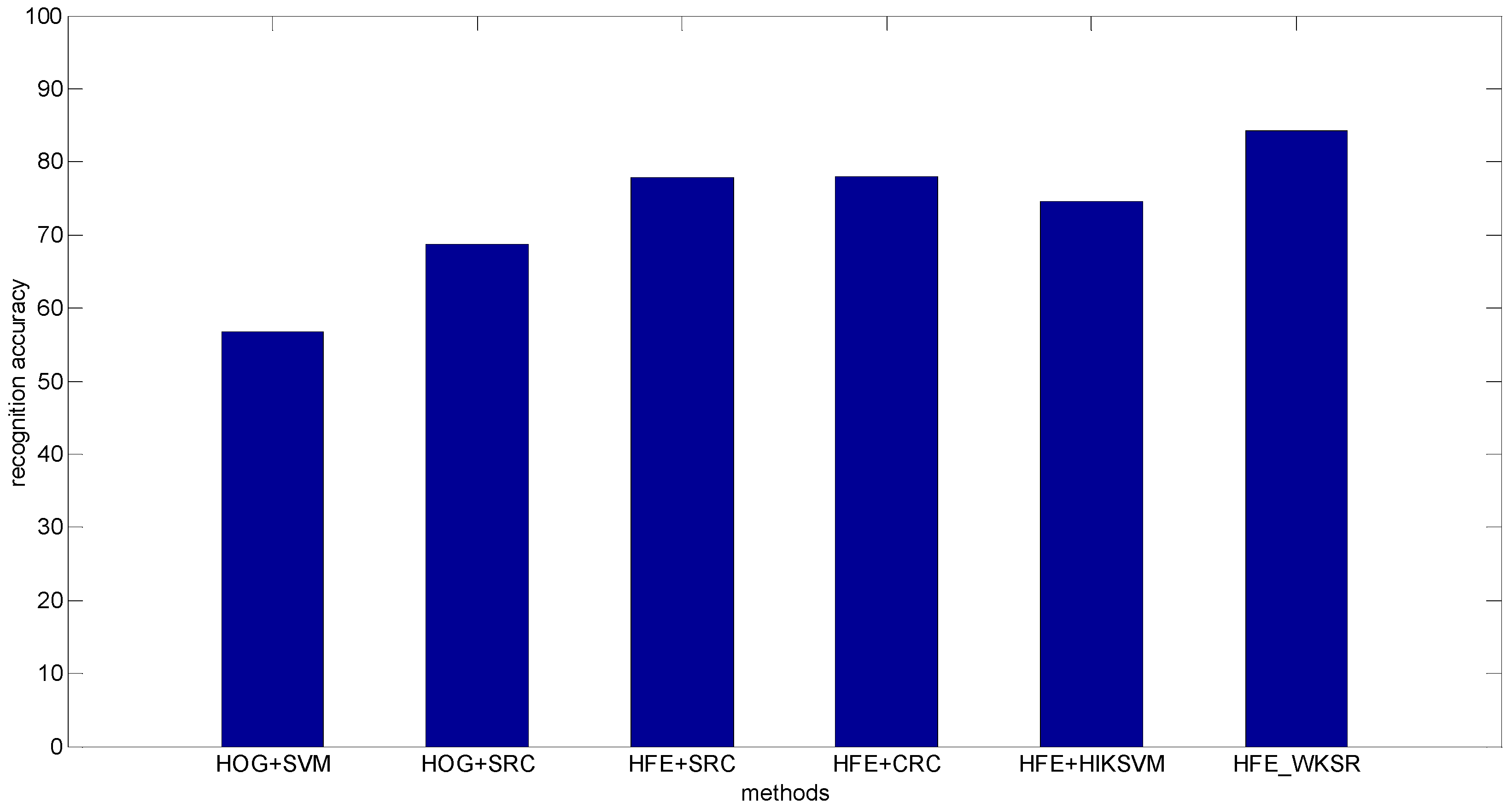
- Pedestrian classification real occlusion: The Daimler dataset is divided into partially occluded set and non-occluded test set. The partially occluded test set contains 11,160 pedestrians and 16,253 non-pedestrians. Example of images from the dataset are shown in Figure 7. Figure 8 shows the classification results. It can be seen that the proposed methods achieve 84.2% recognition accuracy, much higher than the state-of-the-art results, for example, 56.8% (HOG + SVM) and 68.7% (HOG + SRC), and 77.8% (HFE + SRC) and 78.0% (HFE + CRC), and 74.6%(HFE + HIKSVM). The improvement of HFE − WKSR over all the other methods is at least 6%, which clearly shows the superior classification ability of HFE − WKSR.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- David, G.; Antonio, M.L.; Angel, D.S. Survey of Pedestrian Detection for Advanced Driver Assistance Systems. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1239–1258. [Google Scholar]
- Dollar, P.; Wojek, C.; Schiele, B.; Perona, P. Pedestrian Detection: An Evaluation of the State of the Art. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 743–761. [Google Scholar] [CrossRef] [PubMed]
- Miron, A.; Rogozan, A.; Ainouz, S.; Bensrhair, A.; Broggi, A. An Evaluation of the Pedestrian Classification in a Multi-Domain Multi-Modality Setup. Sensors 2015, 15, 13851–13873. [Google Scholar] [CrossRef] [PubMed]
- Ess, A.; Leibe, B.; Gool, L.V. Depth and Appearance for Mobile Scene Analysis. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007.
- Wojek, C.; Walk, S.; Schiele, B. Multi-Cue Onboard Pedestrian Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 794–801.
- Enzweiler, M.; Gavrila, D.M. Monocular Pedestrian Detection: Survey and Experiments. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2179–2195. [Google Scholar] [CrossRef] [PubMed]
- Dalal, N.; Triggs, B. Histograms of Oriented Gradients for Human Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 886–893.
- Lee, Y.S.; Chan, Y.M.; Fu, L.C.; Hsiao, P.Y. Near-Infrared-Based nighttime pedestrian detection using grouped part models. IEEE Trans. Intell. Trans. Syst. 2015, 16, 1929–1940. [Google Scholar] [CrossRef]
- Hurbey, P.; Waldron, P.; Morgan, F.; Jones, E.; Glavin, M. Review of pedestrian detection techniques in automotive far-infrared video. IET Intell. Trans. Syst. 2015, 9, 824–832. [Google Scholar]
- Etinger, A.; Balal, N.; Litvak, B.; Einat, M.; Kapilevich, B.; Pinhasi, Y. Non-Imaging MM-Wave FMCW Sensor for Pedestrian Detection. IEEE Sens. J. 2014, 14, 1232–1237. [Google Scholar] [CrossRef]
- Kim, B.; Choi, B.; Park, S.; Kim, H. Pedestrian/Vehicle Detection Using a 2.5-D Multi-Layer Laser Scanner. IEEE Sens. J. 2016, 16, 400–408. [Google Scholar] [CrossRef]
- Gandhi, T.; Trivedi, M.M. Pedestrian Protection Systems: Issues, Surveys and Challenges. IEEE Trans. Intell. Trans. Syst. 2007, 8, 413–430. [Google Scholar] [CrossRef]
- Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; Henry Holt and Co., Inc.: New York, NY, USA, 1982. [Google Scholar]
- Viola, P.; Jones, M.; Snow, D. Detecting pedestrians using patterns of motion and appearance. Int. J. Comput. Vis. 2005, 63, 153–161. [Google Scholar] [CrossRef]
- Serre, T.; Wolf, L.; Bileschi, S.; Riesenhuber, M.; Poggio, T. Object recognition with cortex-like mechanisms. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 411–426. [Google Scholar] [CrossRef] [PubMed]
- Tuzel, O.; Porikli, F.; Meer, P. Pedestrian detection via classification on Riemannian manifolds. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1713–1727. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Han, T.X.; Yan, S. An HOG-LBP human detector with partial occlusion handling. In Proceedings of the IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009; pp. 32–39.
- Wu, B.; Nevatia, R. Detection of multiple, partially occluded humans in a single image by Bayesian combination of edgelet part detectors. In Proceedings of the IEEE International Conference on Computer Vision, Beijing, China, 17–20 October 2005; pp. 90–97.
- Sabzmeydani, P.; Mori, G. Detecting pedestrians by learning shapelet features. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007.
- Wu, J.X.; Liu, N.; Geyer, C.; Rehg, J.M. C4: A Real-time Object Detection Framework. IEEE Trans. Image Proc. 2013, 22, 4096–4107. [Google Scholar]
- Ye, Q.; Jiao, J.; Zhang, B. Fast Pedestrian detection with multi-scale orientation features and two-stage classifiers. In Proceedings of the IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 881–884.
- Wojek, C.; Schiele, B. A Performance Evaluation of Single and Multi-Feature People Detection. In Proceedings of the 30th DAGM Symposium Munich, Munich, Germany, 10–13 June 2008; pp. 82–91.
- Walk, S.; Majer, N.; Schindler, K.; Schiele, B. New Features and Insights for Pedestrian Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1030–1037.
- Wu, B.; Nevatia, R. Optimizing Discrimination-Efficiency Tradeoff in Integrating Heterogeneous Local Features for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008.
- Dollar, P.; Tu, Z.; Perona, P.; Belongie, S. Integral Channel Features. In Proceedings of the British Machine Vision Conference, London, UK, 7–10 September 2009.
- Enzweiler, M.; Eigenstetter, A.; Schiele, B.; Gavrila, D.M. Multi-cue pedestrian classification with partial occlusion handling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 990–997.
- Maji, S.; Berg, A.; Malik, J. Efficient classification for Additive Kernel SVMs. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 66–77. [Google Scholar] [CrossRef] [PubMed]
- Gavrila, D.M.; Munder, S. Multi-cue pedestrian detection and tracking from a moving vehicle. Int. J. Comput. Vis. 2007, 73, 41–59. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C.; Zisserman, A. Human detection based on a probabilistic assembly of robust part detectors. In Proceedings of the 8th European Conference on Computer Vision, Prague, Czech, 11–14 May 2004; pp. 69–81.
- Munder, S.; Gavrila, D.M. An experimental study on pedestrian classification. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1863–1868. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.W.; Cao, X.B.; Qiao, H. An efficient tree classifier ensemble-based approach for pedestrian detection. IEEE Trans. Syst. Man Cybern. Part B: Cybern. 2011, 41, 107–117. [Google Scholar]
- Felzenszwalb, P.; Girshick, R.; McAllester, D.; Ramanan, D. Object Detection with Discriminatively Trained Part Based Models. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1627–1645. [Google Scholar] [CrossRef] [PubMed]
- Enzweiler, M.; Gavrila, D.M. A multilevel mixture-of-experts framework for pedestrian classification. IEEE Trans. Image Proc. 2011, 20, 2967–2979. [Google Scholar] [CrossRef] [PubMed]
- Aly, S.; Hassan, L.; Sagheer, A.; Murase, H. Partially Occluded Pedestrian Classification using Part-Based Classifiers and Restricted Boltzmann Machine Model. In Proceedings of the 16th IEEE Conference on Intelligent Transportation Systems, Hague, The Netherlands, 6–9 October 2013; pp. 1065–1070.
- Benenson, R.; Omran, M.; Hosang, J.; Schiele, B. Ten years of pedestrian detection, what have we learned? In Proceedings of the 13th European Conference on Computer Vision, ECCV 2014, Zurich, Switzerland, 6–12 September 2014; pp. 613–627.
- Wright, J.; Yang, A.; Ganesh, A.; Sastry, S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [PubMed]
- Timo, A.; Abdenour, H.; Matti, P. Face recognition with local binary patterns. In Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 469–481.
- Liu, Y.G.; Ge, S.Z.; Li, C.G.; You, Z.S. K-NS: A classifier by the distance to the nearest subspace. IEEE Trans. Neural Netw. 2011, 22, 1256–1268. [Google Scholar] [PubMed]
- Zhang, L.; Yang, M.; Feng, X.C. Sparse representation or collaborative representation which helps face recognition? In Proceedings of the International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 471–478.
- Wu, J.; Rehg, J.M. CENTRIST: A visual descriptor for scene categorization. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1489–1501. [Google Scholar] [PubMed]
- Lazebnik, S.; Schmid, C.; Ponce, J. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; pp. 2169–2178.
- Piotr, D.; Ron, A.; Serge, B.; Perona, P. Fast Feature Pyramids for Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1532–1545. [Google Scholar]
- Yang, J.C.; Yu, K.; Gong, Y.; Huang, T. Linear spatial pyramid matching using sparse coding for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1794–1801.
- Han, H.; Han, Q.; Li, X. Hierarchical spatial pyramid max pooling based on SIFT features and sparse coding for image classification. Int. J. Comput. Vis. 2013, 79, 144–150. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.D.; Chang, P.C.; Liu, J.; Yan, Z.; Wang, T.; Li, F.Z. Kernel sparse representation-based classifier. IEEE Trans. Signal Process. 2012, 60, 1684–1695. [Google Scholar] [CrossRef]
- Lee, H.; Battle, A.; Raina, R.; Ng, A.Y. Efficient sparse coding algorithm. In Proceedings of the 20th Annual Conference on Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 4–7 December 2006; pp. 801–808.





| Method | INRIA | Daimler with Occlusion |
|---|---|---|
| HOG + SVM | 0.1806 | 0.0682 |
| HFE + SRC | 0.1239 | 0.0403 |
| HFE − WKSR | 0.1372 | 0.0463 |
| Procedure | Parameters | |
|---|---|---|
| Feature extraction | Hierarchical partition | P0 = 4, Q0 = 4 when S = 0 P0 = 4, Q0 = 4; P1 = 3, Q1 = 2; P2 = 2, Q2 = 2 when S = 2 |
| Histogram bin number | 16 | |
| WKSR | Kernel function | Histogram intersection kernel |
| Weight | for non-occlusion for occlusion | |
| convergence | ||
| Lagrange multiplier |
| N | 20 | 50 | 100 |
|---|---|---|---|
| HOG + SVM | 45.2 | 53.6 | 62.5 |
| HOG + SRC | 72.8 | 77.1 | 82.9 |
| HFE + SRC | 84.2 | 88.9 | 91.3 |
| HFE + CRC | 85.3 | 87.9 | 90.8 |
| HFE + HIKSVM | 62.7 | 68.2 | 77.9 |
| HFE − WKSR | 90.3 | 94.4 | 97.5 |
| Group | Illumination | Background | Appearance |
|---|---|---|---|
| HOG + SVM | 58.7 | 55.2 | 46.3 |
| HOG + SRC | 75.4 | 86.6 | 73.5 |
| HFE + SRC | 84.5 | 86.4 | 83.2 |
| HFE + CRC | 85.4 | 85.5 | 81.2 |
| HFE + HIKSVM | 73.5 | 76.3 | 68.3 |
| HFE − WKSR | 94.6 | 92.5 | 90.3 |
| HFE − WKSR (without MP) | 88.3 | 87.1 | 84.5 |
| Occlusion | 10% | 20% | 30% | 40% | 50% |
|---|---|---|---|---|---|
| HOG + SVM | 57.2 | 53.6 | 42.9 | 38.3 | 32.4 |
| HOG + SRC | 72.3 | 68.2 | 55.4 | 48.2 | 47.9 |
| HFE + SRC | 83.2 | 80.8 | 76.3 | 72.5 | 68.1 |
| HFE + CRC | 81.3 | 76.5 | 73.2 | 71.6 | 67.2 |
| HFE + HIKSVM | 75.2 | 71.3 | 68.2 | 63.3 | 61.4 |
| HFE − WKSR | 93.2 | 91.5 | 88.2 | 82.3 | 75.4 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, R.; Zhang, G.; Yan, X.; Gao, J. Robust Pedestrian Classification Based on Hierarchical Kernel Sparse Representation. Sensors 2016, 16, 1296. https://doi.org/10.3390/s16081296
Sun R, Zhang G, Yan X, Gao J. Robust Pedestrian Classification Based on Hierarchical Kernel Sparse Representation. Sensors. 2016; 16(8):1296. https://doi.org/10.3390/s16081296
Chicago/Turabian StyleSun, Rui, Guanghai Zhang, Xiaoxing Yan, and Jun Gao. 2016. "Robust Pedestrian Classification Based on Hierarchical Kernel Sparse Representation" Sensors 16, no. 8: 1296. https://doi.org/10.3390/s16081296
APA StyleSun, R., Zhang, G., Yan, X., & Gao, J. (2016). Robust Pedestrian Classification Based on Hierarchical Kernel Sparse Representation. Sensors, 16(8), 1296. https://doi.org/10.3390/s16081296