High Accuracy Passive Magnetic Field-Based Localization for Feedback Control Using Principal Component Analysis
Abstract
:1. Introduction
- A method using concurrent field measurements of a moving permanent magnet (PM) to infer its precise position in real-time is presented. This method employs a sensor array to provide bijective relationships between measurements of magnetic flux density (MFD) and position as well as spatially extending the sensing range. Instead of directly mapping sensor outputs to position, PCA is used to determine an optimized set of transformed measurements for ANN mapping.
- Through numerical simulations, the effects of geometric parameters (including the PM dimensions and sensor spacing and location) on sensing accuracy is examined. Simulated measurements are corrupted with artificial Gaussian noise to explore practical implementation issues of the system.
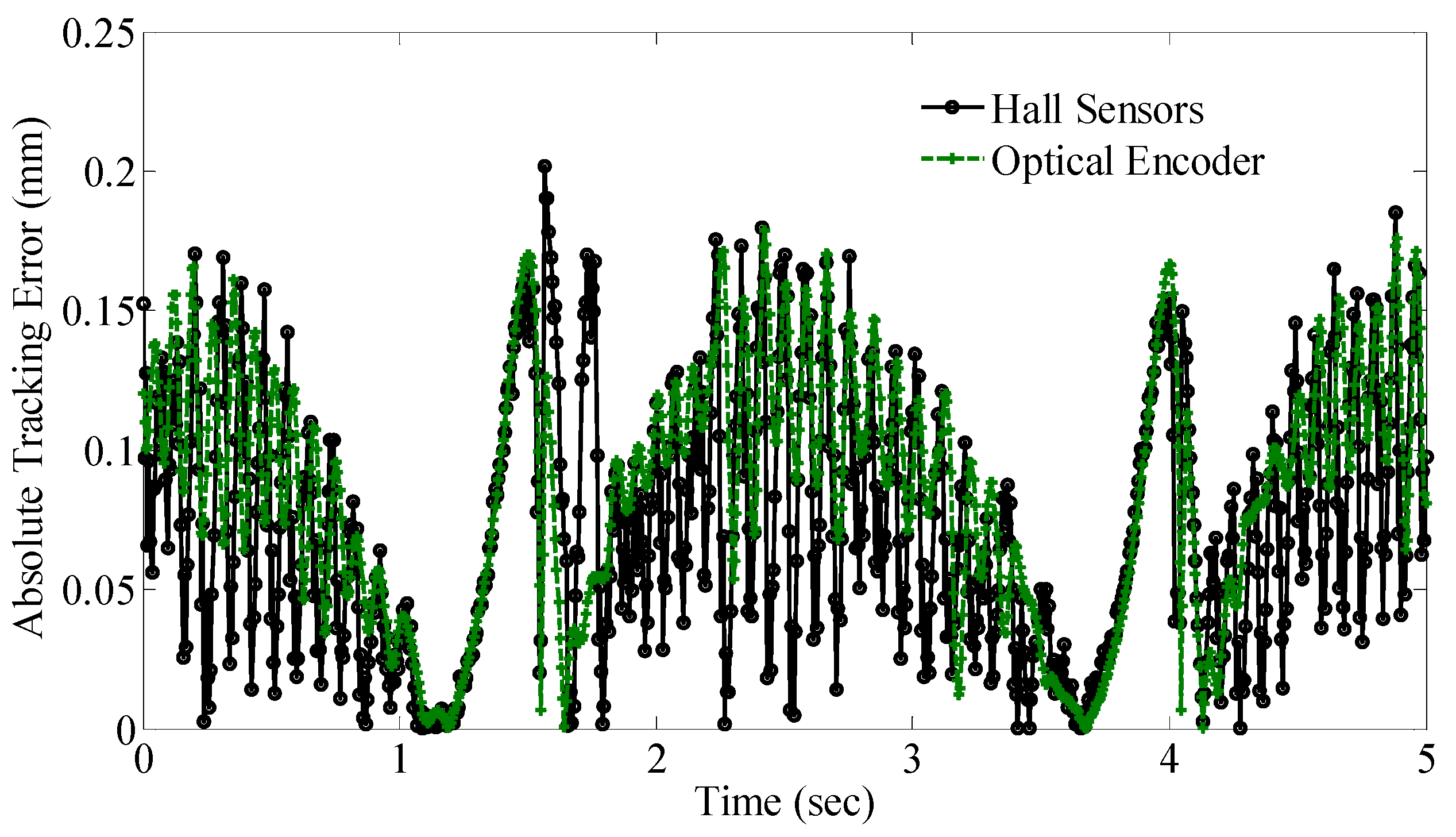
- Using an ironless brushless linear motor as a platform for analysis, the experimental performance of a 9-sensor field-based system using PCA optimized ANN mapping is investigated. The tracking error resulting from the closed-loop control of the system using the field-based system is compared with an optical encoder. The tracking performance using the field-based system gives a similar response of that obtained using the optical encoder with 1 µm resolution.
2. Materials and Methods
- A distributed spatial network of sensors to uniquely relate position of a magnetic source to its measured field from the sensors, and
- An approach using ANNs and PCA to optimally relate multiple concurrent field measurements to position coordinates and minimize time-consuming computation.
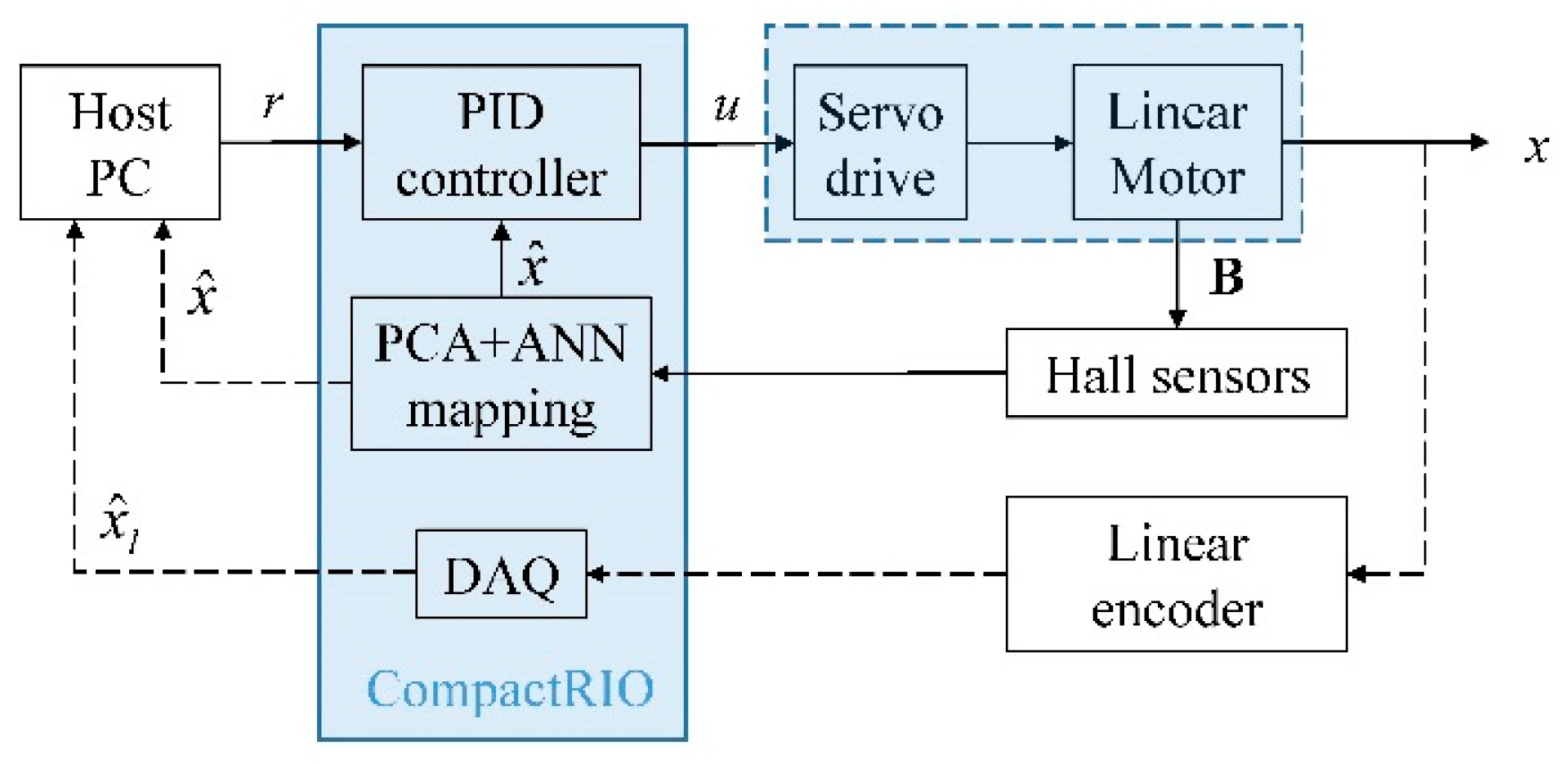
2.1. Inducing Bijectivity with a Spatial Network
2.2. PCA Optimized ANN Mapping
3. Results
3.1. Numerical Simulation
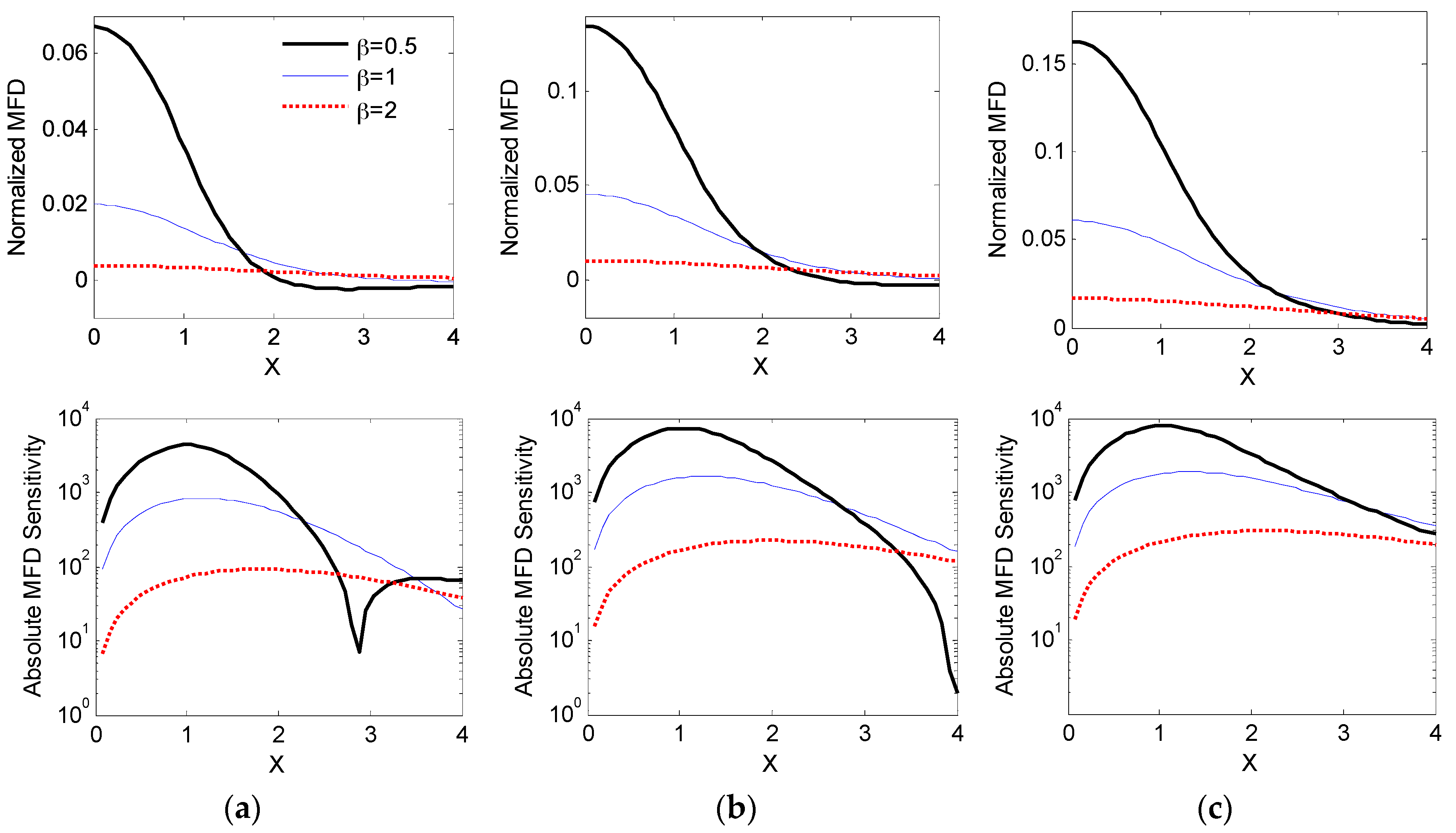
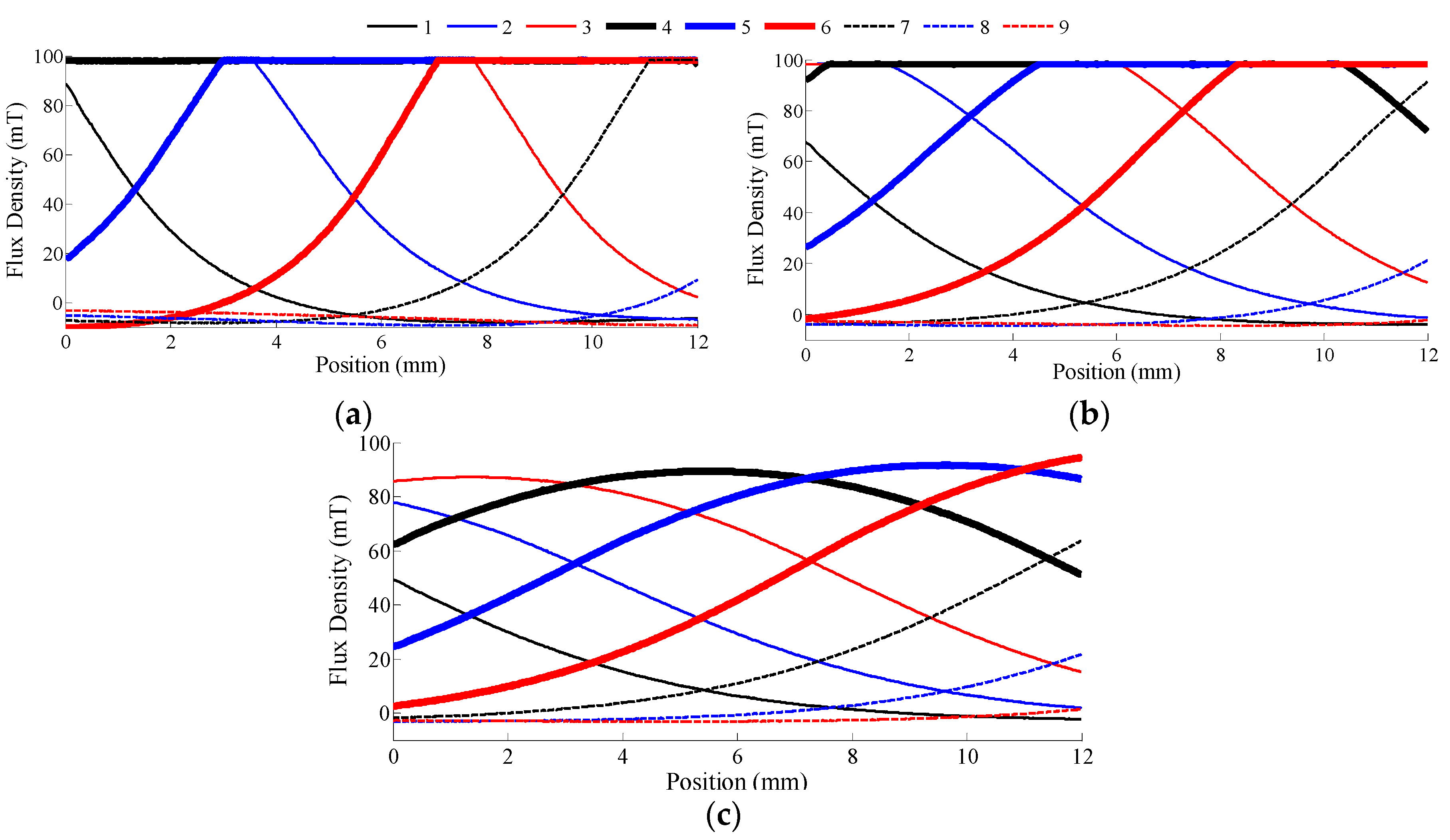
3.1.1. Singular Sensor Geometrical Considerations
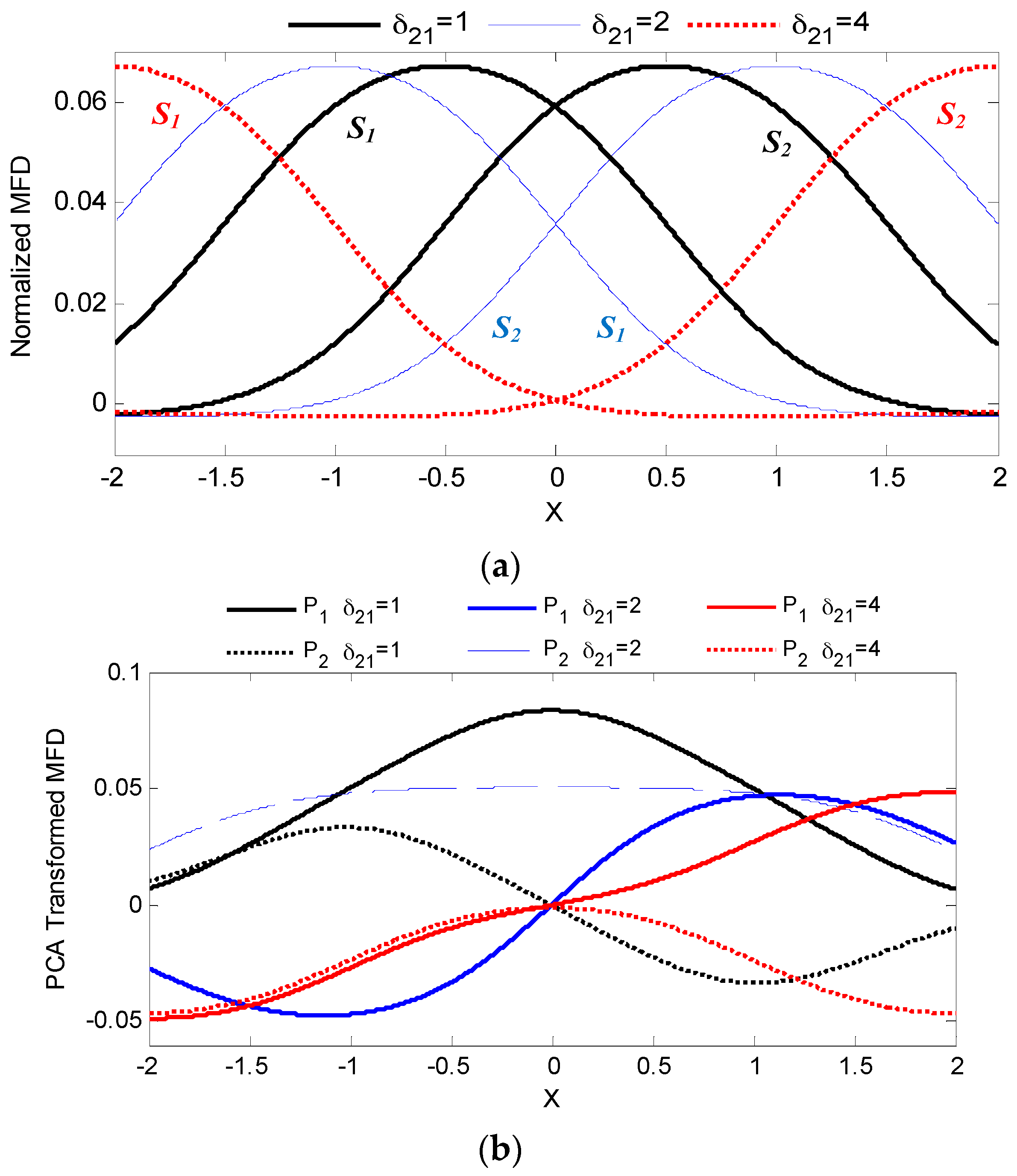
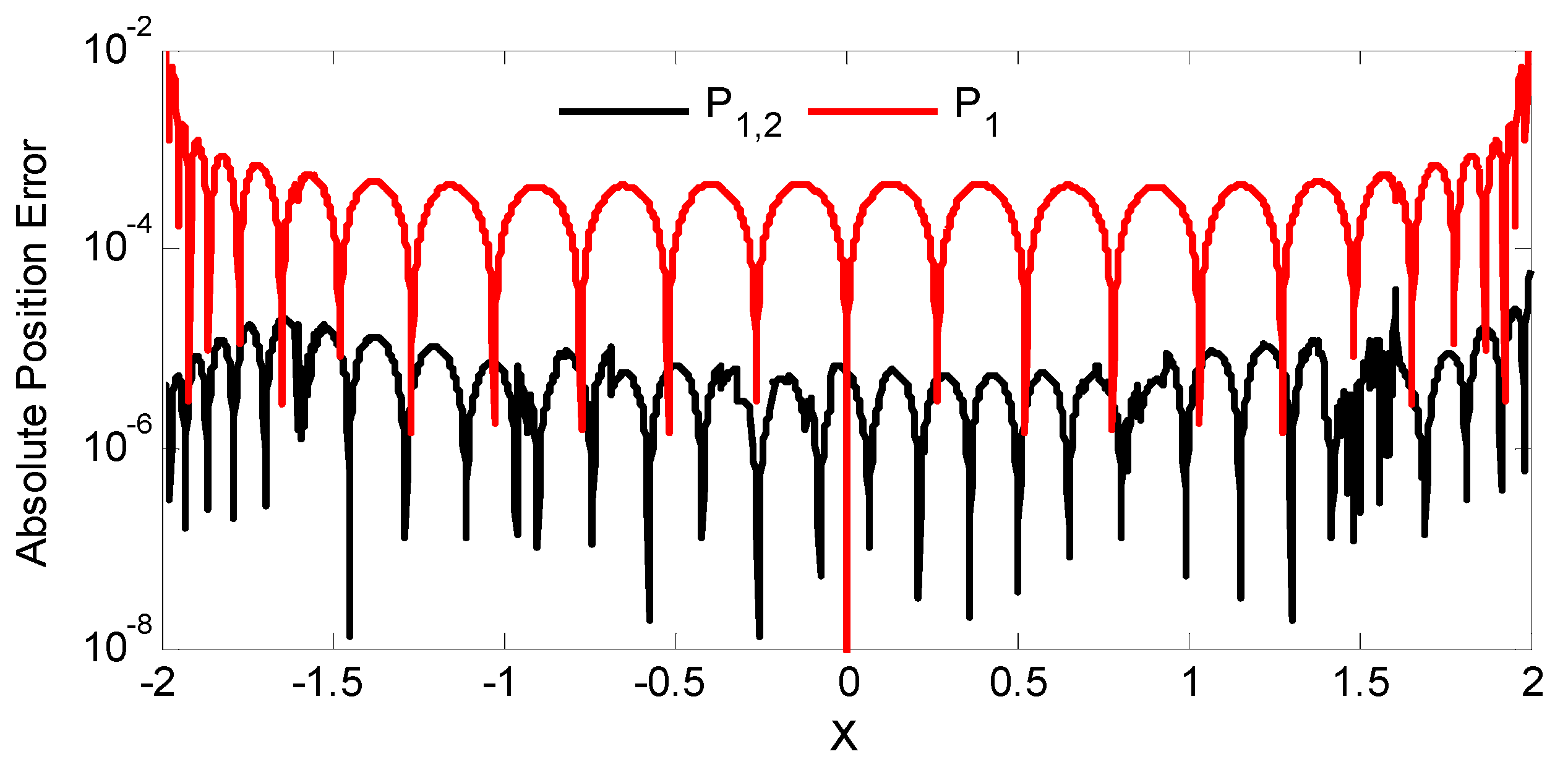
3.1.2. Dual-Sensor PCA ANN Mapping Analysis
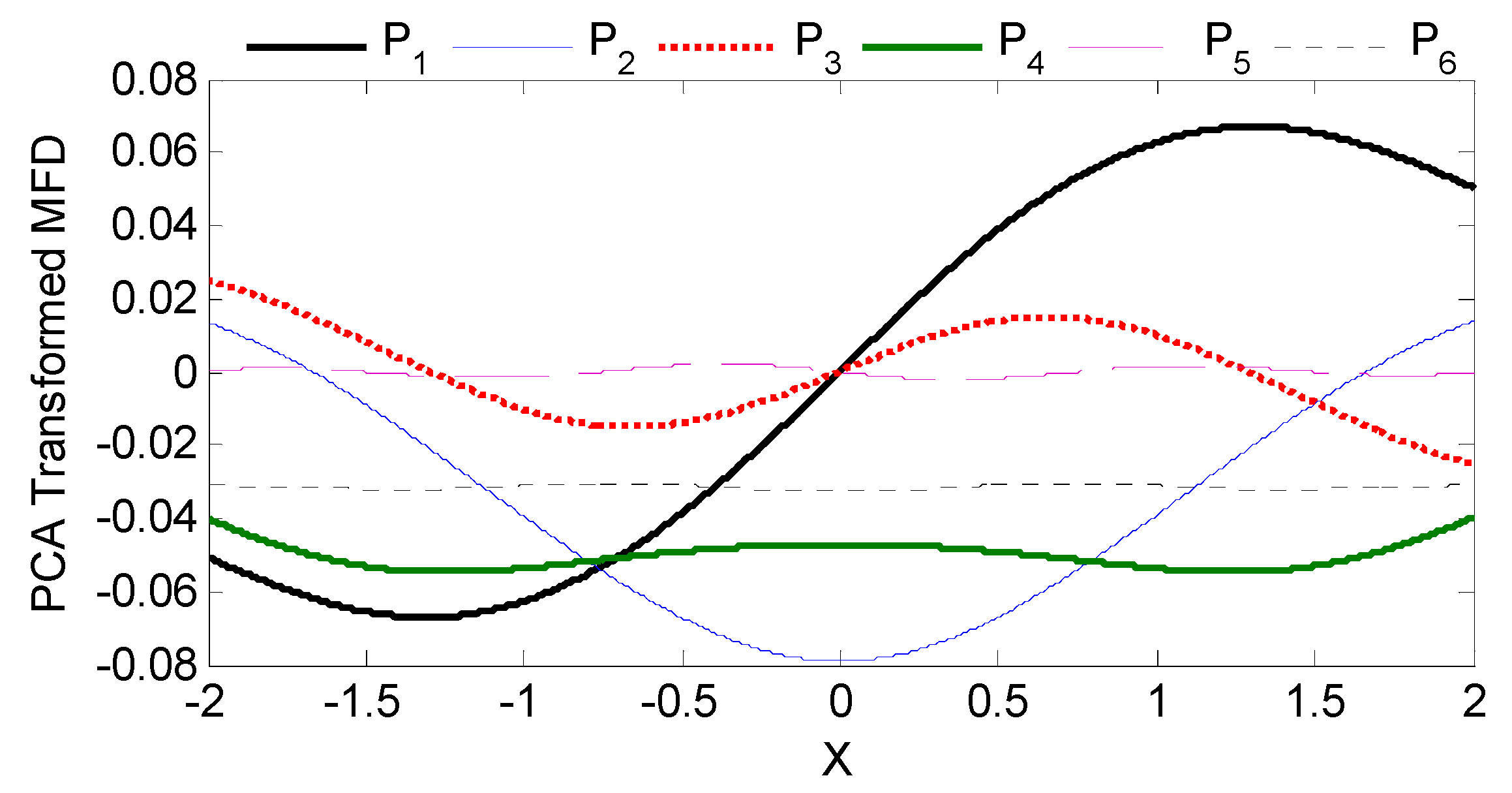
3.1.3. Multi-Sensor PCA ANN Mapping Analysis
3.2. Experimental Investigation
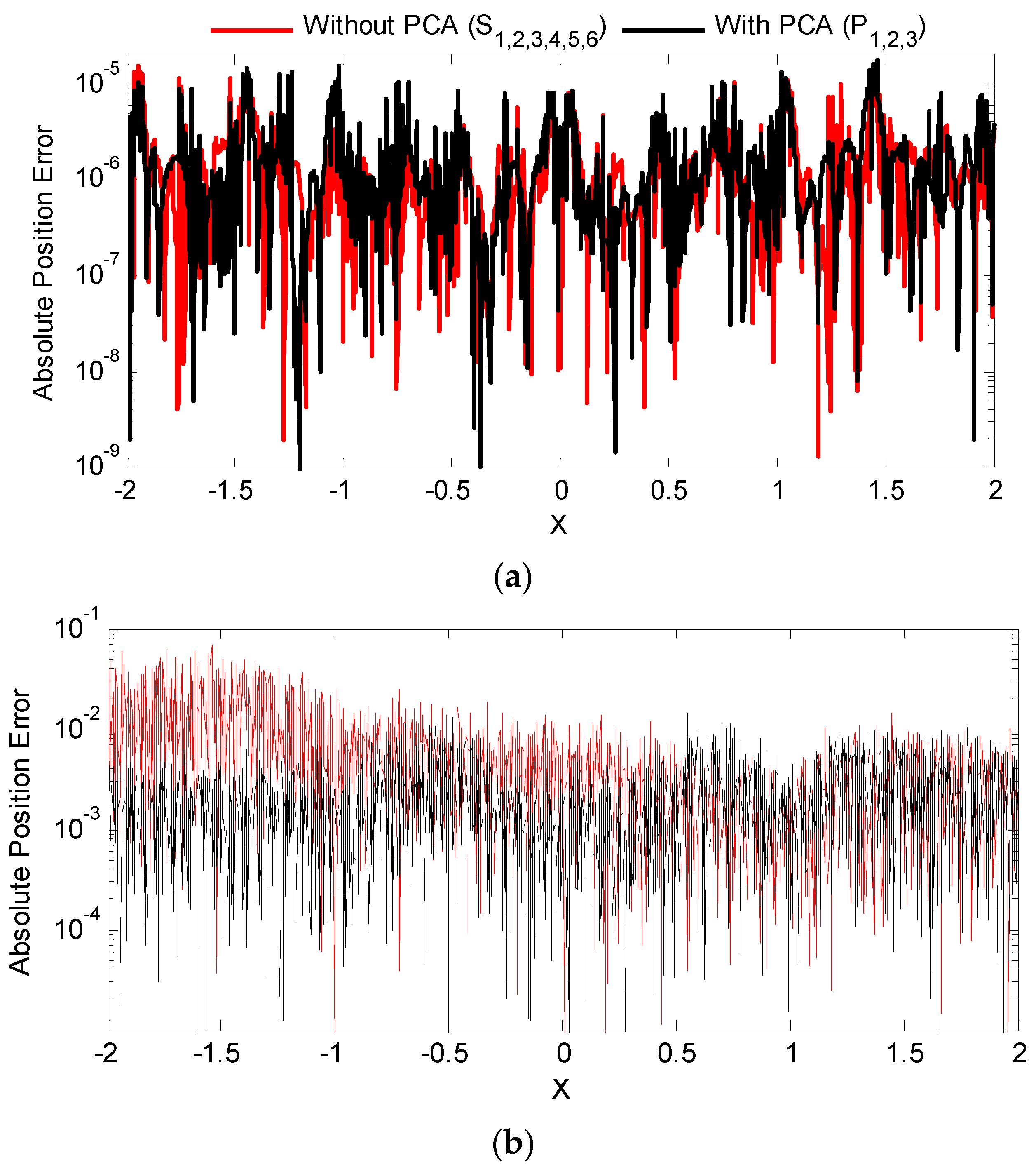
3.2.1. PCA-ANN Field-Based Localization
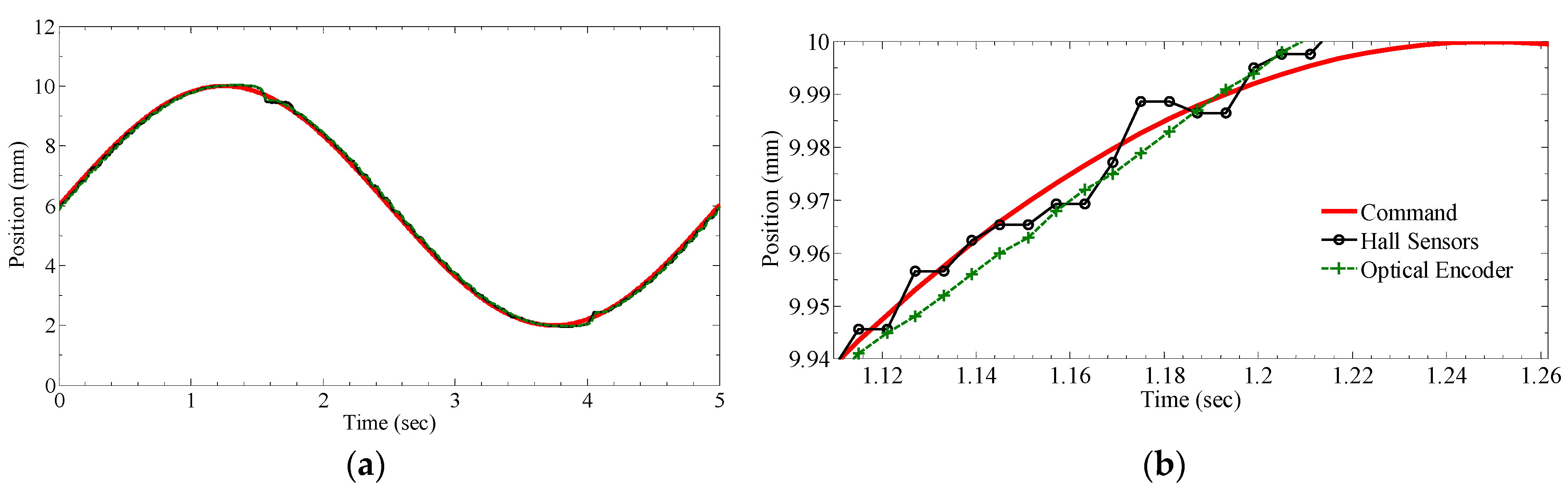
3.2.2. Closed-Loop Tracking Performance
4. Discussion
4.1. Numerical Results from Singular Sensor Geometrical Considerations
4.2. Numerical Results from Dual & Multi-Sensor PCA ANN Mapping Analysis
4.3. Experimental Results from PCA ANN Field-Based Localization
4.4. Experimental Results from Closed-Loop Tracking Performance
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Raab, F.H.; Blood, E.B.; Steiner, T.O.; Jones, H.R. Magnetic Position and Orientation Tracking System. IEEE Trans. Aerosp. Electron. Syst. 1979, AES-15, 709–718. [Google Scholar] [CrossRef]
- Lee, K.-M.; Zhou, D. A real-time optical sensor for simultaneous measurement of three-DOF motions. IEEE/ASME Trans. Mechatron. 2004, 9, 499–507. [Google Scholar] [CrossRef]
- Garner, H.; Klement, M.; Lee, K.-M. Design and analysis of an absolute non-contact orientation sensor for wrist motion control. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Como, Italy, 8–12 July 2001; Volume 1, pp. 69–74.
- Lenz, J.; Edelstein, S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Caruso, M.; Bratland, T.; Smith, C.; Schneider, R. A new perspective on magnetic field sensing. Sens. Magn. 1998, 15, 34–45. [Google Scholar]
- Marechal, L.; Foong, S.; Ding, S.; Wood, K.L.; Patil, V.; Gupta, R. Design Optimization of a Magnetic Field-Based Localization Device for Enhanced Ventriculostomy. J. Med. Devices 2016, 10. [Google Scholar] [CrossRef]
- Sun, Z.; Foong, S.; Marechal, L.; Tan, UX.; Teo, T.H.; Shabbir, A. A Non-invasive Real-time Localization System for Enhanced Efficacy in Nasogastric Intubation. Ann. Biomed. Eng. 2015, 43. [Google Scholar] [CrossRef] [PubMed]
- García-Diego, F.-J.; Sánchez-Quinche, A.; Merello, P.; Beltrán, P.; Peris, C. Array of Hall Effect Sensors for Linear Positioning of a Magnet Independently of Its Strength Variation. A Case Study: Monitoring Milk Yield during Milking in Goats. Sensors 2013, 13, 8000–8012. [Google Scholar] [CrossRef] [PubMed]
- Grandi, G.; Landini, M. Magnetic-field transducer based on closed-loop operation of magnetic sensors. IEEE Trans. Ind. Electron. 2006, 53, 880–885. [Google Scholar] [CrossRef]
- Paul, S.; Chang, J. A New Approach to Detect Mover Position in Linear Motors Using Magnetic Sensors. Sensors 2015, 15, 26694–26708. [Google Scholar] [CrossRef] [PubMed]
- McCall, W.D.; Rohan, E.J. A Linear Position Transducer Using a Magnet and Hall Effect Devices. IEEE Trans. Instrum. Meas. 1977, 26, 133–136. [Google Scholar] [CrossRef]
- Schlageter, V.; Drljaca, P.; Popovic, R.S.; Kucera, P. A Magnetic Tracking System based on Highly Sensitive Integrated Hall Sensors. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2002, 45, 967–973. [Google Scholar] [CrossRef]
- Hu, C.; Meng, M.Q.H.; Mandal; Wang, X. 3-Axis Magnetic Sensor Array System for Tracking Magnet’s Position and Orientation. In Proceedings of the 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 5304–5308.
- Sherman, J.T.; Lubkert, J.K.; Popovic, R.S.; DiSilvestro, M.R. Characterization of a Novel Magnetic Tracking System. IEEE Trans. Magn. 2007, 43, 2725–2727. [Google Scholar] [CrossRef]
- Akutagawa, M.; Kinouchi, Y.; Nagashino, H. Application of neural networks to a magnetic measurement system for mandibular movement. In Proceedings of the 20th IEEE International Conference of Engineering in Medicine and Biology Society, Hong Kong, China, 29 October–1 November 1998; pp. 1932–1935.
- Foong, S.; Lee, K.-M.; Bai, K. Harnessing Magnetic Fields for Angular Sensing with Nano-degree Accuracy. IEEE/ASME Trans. Mechatron. 2012, 17, 687–696. [Google Scholar] [CrossRef]
- Li, Z. Robust Control of PM Spherical Stepper Motor Based on Neural Networks. IEEE Trans. Ind. Electron. 2009, 56, 2945–2954. [Google Scholar]
- Karanayil, B.; Rahman, M.F.; Grantham, C. Online Stator and Rotor Resistance Estimation Scheme Using Artificial Neural Networks for Vector Controlled Speed Sensorless Induction Motor Drive. IEEE Trans. Ind. Electron. 2007, 54, 167–176. [Google Scholar] [CrossRef]
- Marino, P.; Milano, M.; Vasca, F. Linear quadratic state feedback and robust neural network estimator for field-oriented-controlled induction motors. IEEE Trans. Ind. Electron. 1999, 46, 150–161. [Google Scholar] [CrossRef]
- Chang, C.-Y.; Maciejewski, A.A.; Balakrishnan, V. Fast eigenspace decomposition of correlated images. IEEE Trans. Image Process. 2000, 9, 1937–1949. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.-M.; Li, Q.; Dalye, W. Effects of Classification Methods on Color-Based Feature Detection with Food Processing Applications. IEEE Trans. Autom. Sci. Eng. 2007, 4, 40–51. [Google Scholar] [CrossRef]
- Lee, K.-M.; Bai, K.; Lim, J. Dipole Models for Forward/Inverse Torque Computation of a Spherical Motor. IEEE/ASME Trans. Mechatron. 2009, 14, 1–46. [Google Scholar] [CrossRef]
- Cheng, D.K. Field and Wave Electromagnetics; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Lee, K.-M.; Son, H. Distributed Multipole Model for Design of Permanent-Magnet-Based Actuators. IEEE Trans. Magn. 2007, 43, 3904–3913. [Google Scholar] [CrossRef]
- Son, H.; Lee, K.-M. Distributed Multipole Models for Design and Control of PM Actuators and Sensors. IEEE/ASME Trans. Mechatron. 2008, 13, 228–238. [Google Scholar] [CrossRef]
- Wu, F.; Foong, S.; Sun, Z. A Hybrid Field Model for Enhanced Magnetic Localization and Position Control. IEEE/ASME Trans. Mechatron. 2015, 20, 1278–1287. [Google Scholar] [CrossRef]
- Xu, M.; Ida, N. Solution Of Magnetic Inverse Problems Using Artificial Neural Networks. In Proceedings of the 6th International Conference on Optimization of Electrical and Electronic Equipments, 14–15 May 1998; pp. 67–70.
- Nenonen, J.T. Solving the inverse problem in magnetocardiography. IEEE Eng. Med. Biol. Mag. 1994, 13, 487–496. [Google Scholar] [CrossRef]
- Lee, K.-M.; Li, Q.; Son, H. Effects of numerical formulation on magnetic field computation using meshless methods. IEEE Trans. Magn. 2006, 42, 2164–2171. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis; Springer-Verlag New York, Inc.: New York, NY, USA, 2002. [Google Scholar]

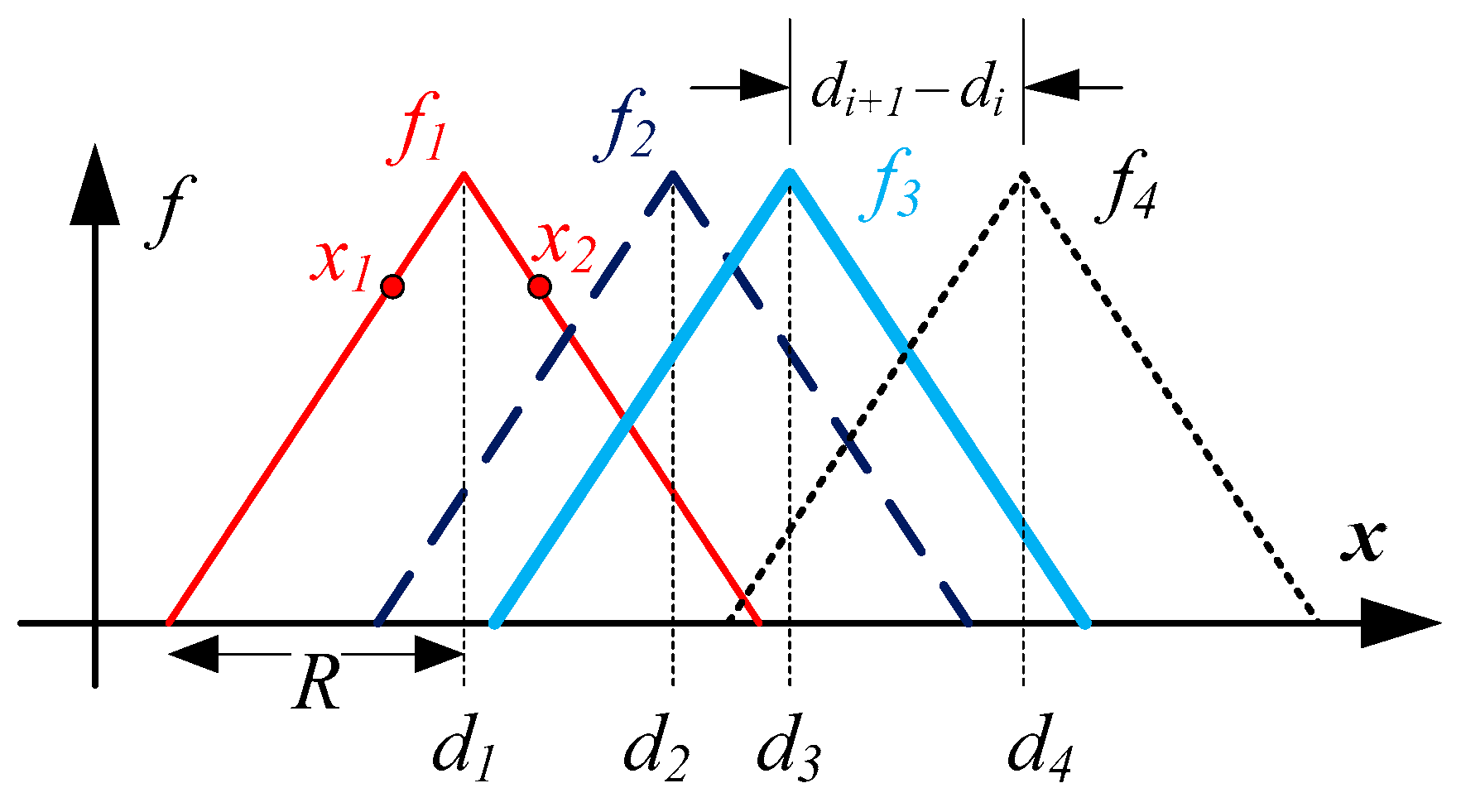
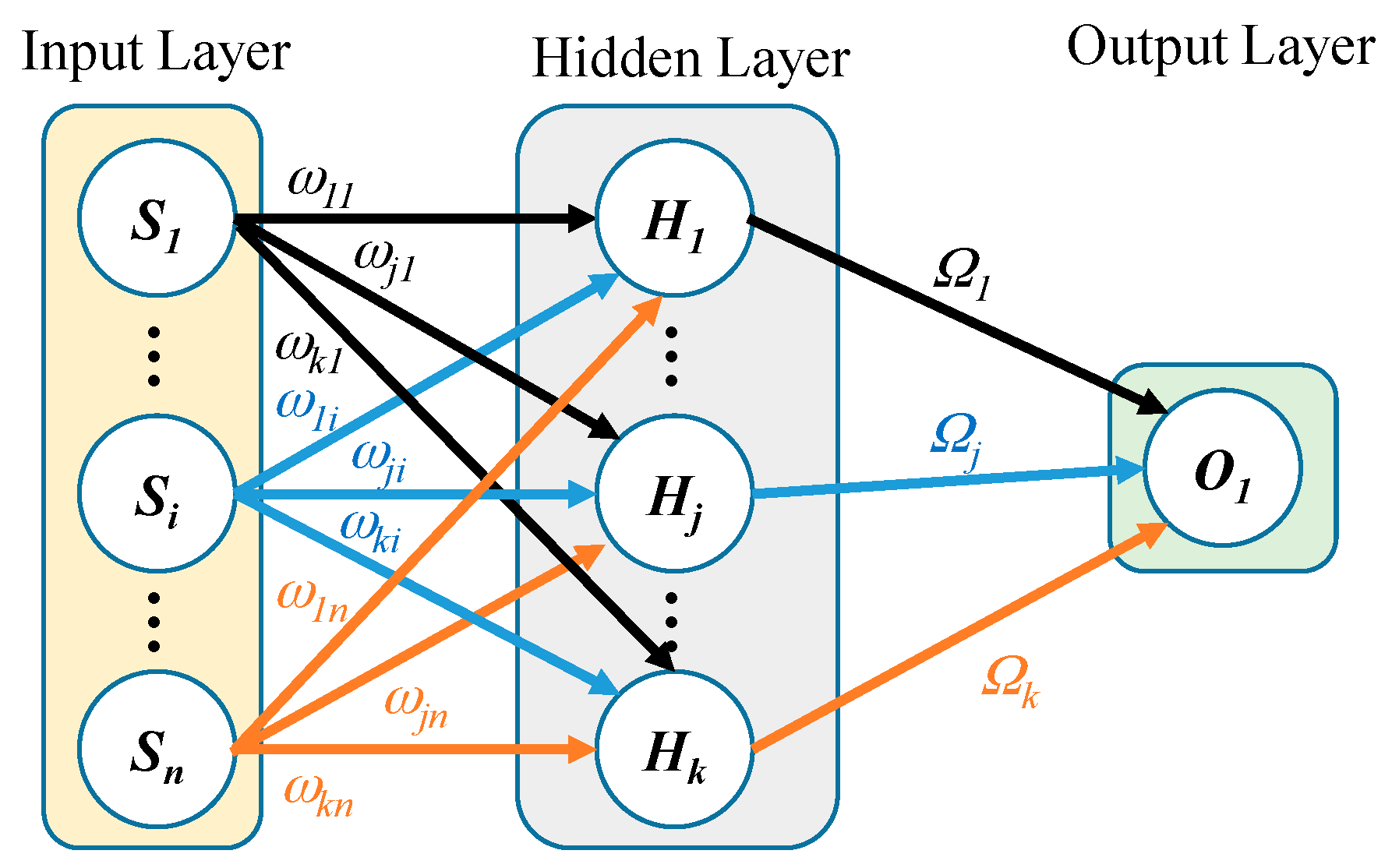
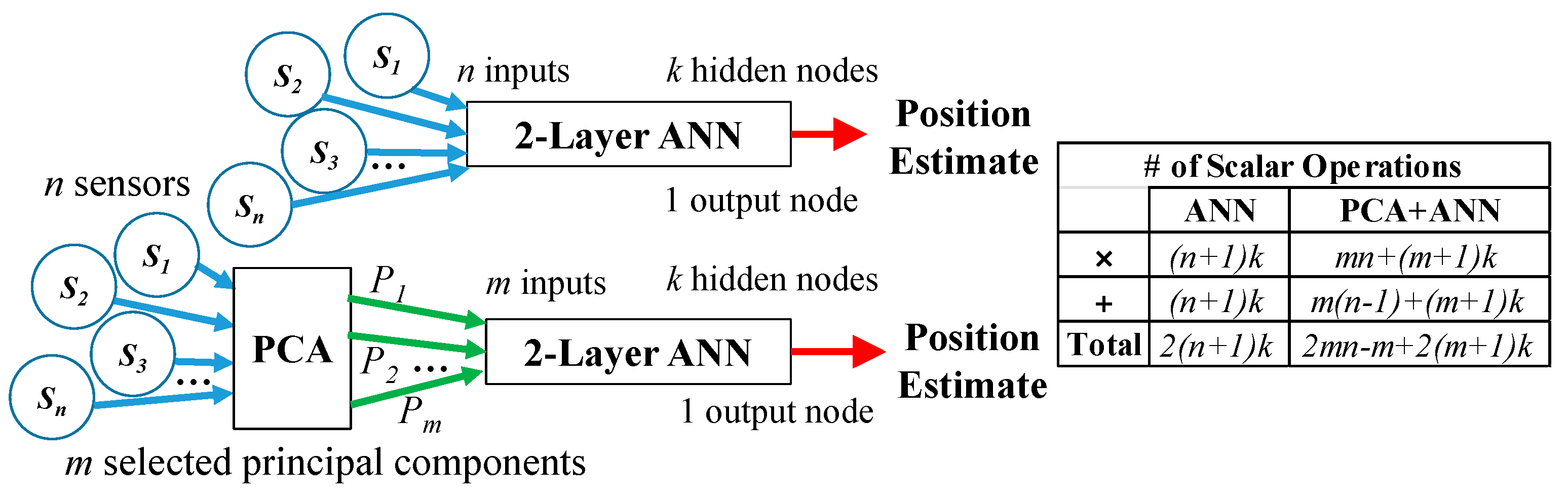
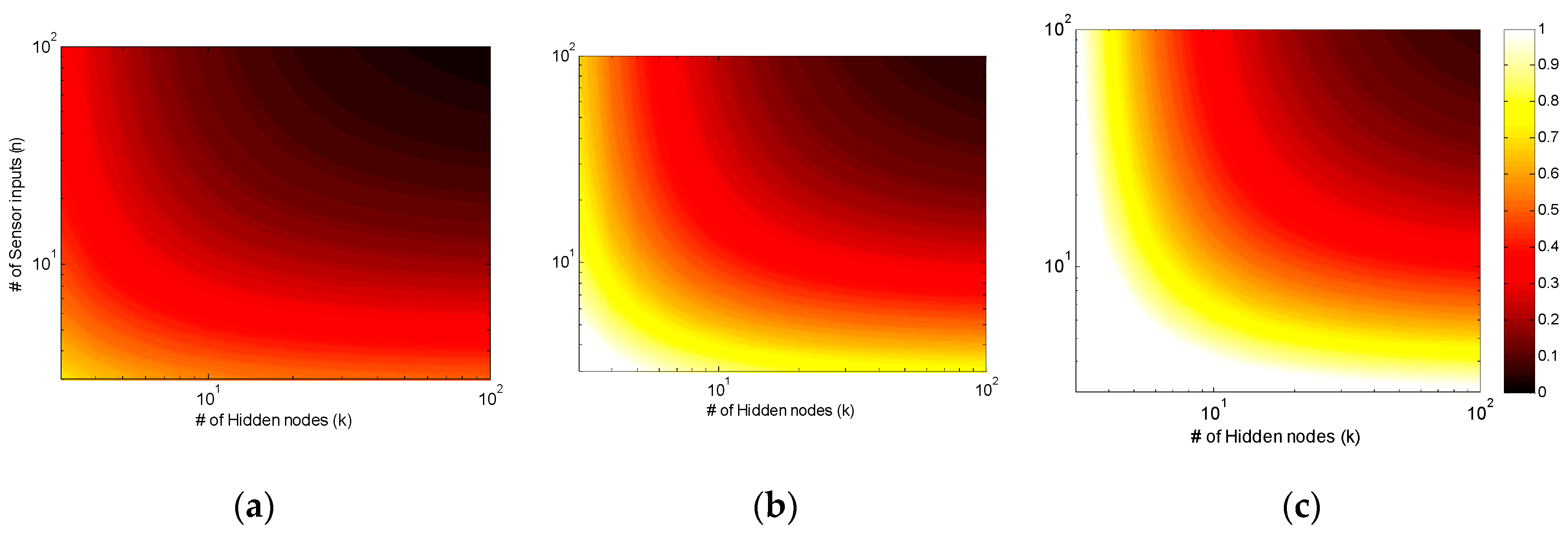




| Sensor Spacing | PCA | ANN RMSE (Normalized) | |||||
|---|---|---|---|---|---|---|---|
| % Variability | Coefficients | ||||||
| δ21 | P1 | P2 | C11 | C12 | C21 | C22 | |
| 1 | 52.2 | 47.8 | 1/√2 | −1/√2 | 1/√2 | 1/√2 | 1.60 × 10−5 (P1,P2) |
| 2 | 96.0 | 4.0 | 1/√2 | 1/√2 | −1/√2 | 1/√2 | 9.00 × 10−6 (P1,P2) |
| 4 | 78.5 | 21.5 | 1/√2 | −1/√2 | −1/√2 | −1/√2 | 7.53 × 10−6 (P1,P2) |
| 1.13 × 10−3 (P1 only) | |||||||
| PCA % Variability | ANN Position Mapping | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | Noise | Inputs | ANN RMSE (Normalized) | |
| 71.6 | 24.0 | 4.1 | 0.31 | 0.040 | 0.011 | 0% | P123 | 2.85 × 10−6 | |
| PCA Coefficient Matrix | S1–6 | 2.40 × 10−6 | |||||||
| Cij | i = 1 | 2 | 3 | 4 | 5 | 6 | 1% | P123 | 1.09 × 10−2 |
| j = 1 | 0.309 | −0.577 | 0.332 | −0.002 | 0.541 | −0.408 | S1–6 | 3.13 × 10−3 | |
| 2 | −0.309 | −0.577 | −0.332 | −0.002 | −0.541 | −0.408 | 10% | P123 | 1.05 × 10−1 |
| 3 | 0.499 | −0.160 | 0.246 | −0.649 | −0.436 | 0.230 | S1–6 | 3.32 × 10−2 | |
| 4 | −0.499 | −0.160 | −0.246 | −0.649 | 0.436 | 0.230 | |||
| 5 | 0.394 | 0.376 | −0.573 | −0.280 | 0.127 | −0.529 | |||
| 6 | −0.394 | 0.376 | 0.573 | −0.280 | −0.127 | −0.529 | |||
| Field Sensor Network | PM (Grade N42) | |||||
|---|---|---|---|---|---|---|
| n | d1 (mm) | di+1 − di (mm) | 2w (mm) | l (mm) | c (mm) | Mo (A/m) |
| 9 | −7.27 | 4.09 | 12.7 | 6.35 | 4.76 | 4.67 × 105 |
| h (mm) | SNR (dB) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | |
| 1.905 | 54.1 | 59.1 | 56.5 | 7.0 | 53.4 | 59.4 | 57.2 | 37.3 | 32.0 |
| 3.81 | 52.1 | 57.6 | 55.6 | 40.3 | 53.1 | 58.0 | 55.1 | 42.2 | 21.6 |
| 5.715 | 49.6 | 54.0 | 53.9 | 46.4 | 52.9 | 55.9 | 51.9 | 42.6 | 27.0 |
| h (mm) | % Variability, (SNR, dB) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | |
| 1.905 | 79.55 | 14.54 | 5.49 | 0.22 | 0.12 | 0.04 | 0.018 | ~0 | ~0 |
| (64.0) | (56.6) | (52.4) | (38.4) | (35.9) | (31.8) | (27.6) | (5.9) | (4.8) | |
| 3.81 | 86.81 | 10.67 | 1.98 | 0.37 | 0.11 | 0.04 | 0.004 | ~0 | ~0 |
| (63.0) | (53.9) | (46.6) | (39.3) | (34.1) | (29.9) | (19.1) | (10.7) | (−0.5) | |
| 5.715 | 91.50 | 8.20 | 0.27 | 0.03 | 0.001 | 0.0002 | 0.0001 | ~0 | ~0 |
| (61.0) | (50.6) | (35.8) | (26.3) | (12.8) | (4.4) | (1.2) | (−0.2) | (−1.4) | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foong, S.; Sun, Z. High Accuracy Passive Magnetic Field-Based Localization for Feedback Control Using Principal Component Analysis. Sensors 2016, 16, 1280. https://doi.org/10.3390/s16081280
Foong S, Sun Z. High Accuracy Passive Magnetic Field-Based Localization for Feedback Control Using Principal Component Analysis. Sensors. 2016; 16(8):1280. https://doi.org/10.3390/s16081280
Chicago/Turabian StyleFoong, Shaohui, and Zhenglong Sun. 2016. "High Accuracy Passive Magnetic Field-Based Localization for Feedback Control Using Principal Component Analysis" Sensors 16, no. 8: 1280. https://doi.org/10.3390/s16081280
APA StyleFoong, S., & Sun, Z. (2016). High Accuracy Passive Magnetic Field-Based Localization for Feedback Control Using Principal Component Analysis. Sensors, 16(8), 1280. https://doi.org/10.3390/s16081280







