Research on a Defects Detection Method in the Ferrite Phase Shifter Cementing Process Based on a Multi-Sensor Prognostic and Health Management (PHM) System
Abstract
:1. Introduction
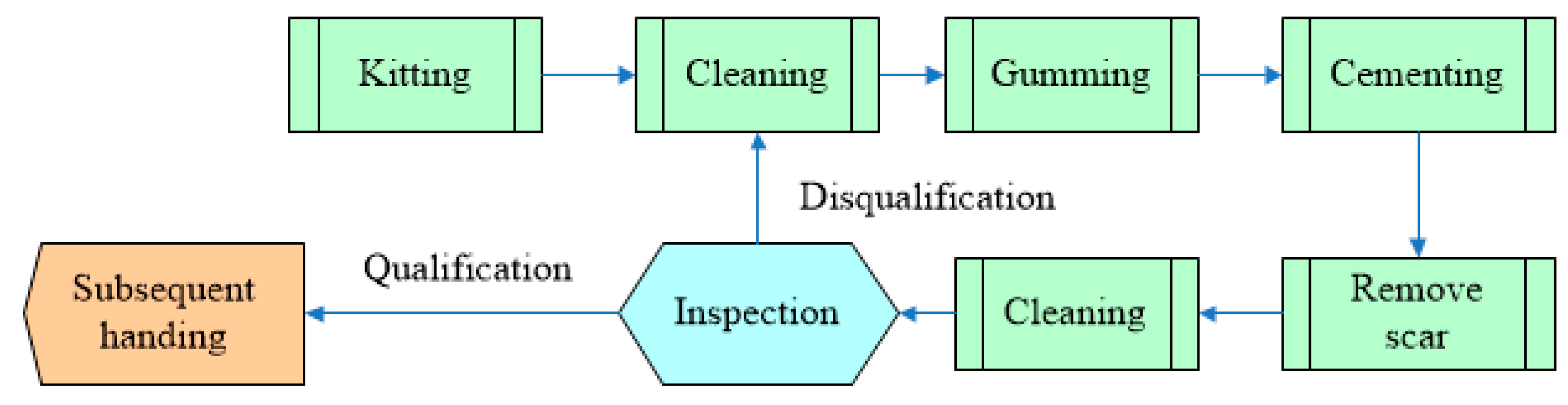
2. Cause Analysis of Cementing Process Defects
- (1)
- Cementing materials: different adhesives present different properties. The main factor that has an impact on cementing strength is the chemical groups in the adhesive.
- (2)
- Thickness of cementing coating: the relationship curve of thickness and strength has a single-peak. Over-thick or over-thin cementing coatings will individually lead to a decline of strength.
- (3)
- Treatment for joint surface: adhesive bonding is formed by mechanical, chemical, and adsorption factors. After surface treatment, variations of structure, morphology, chemical constituents and form of organization will occur on the joint surface. All changes of surface condition will have a great influence on the cementing properties.
- (4)
- Curing time and temperature: curing time and temperature are related to cementing materials. If the curing temperature is too low, the molecular chain of adhesive move difficultly. This results in low crosslinking density and incomplete curing reactions, and then influences the cementing strength. The curing time must be prolonged in order to have a complete curing reaction. On the contrary, there is an adhesive loss when the temperature is high. It also causes a decline of cementing strength.
- (5)
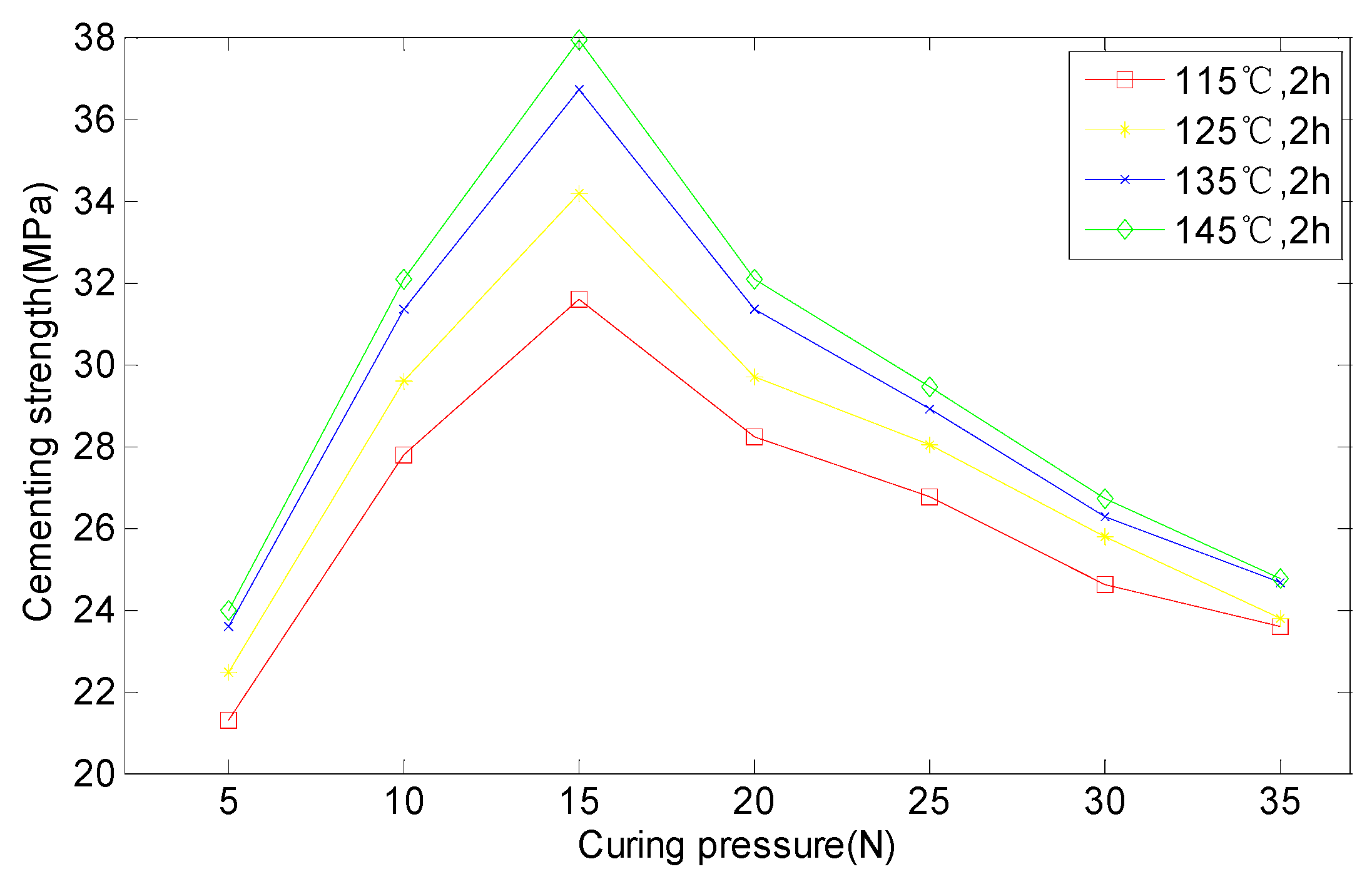
- Curing pressure: the role of curing pressure is to ensure that there is a close contact between adhesive and adherends. It is beneficial to expel gas and this makes the cementing layer uniform and compact. Bonding strength increases with the rise of curing pressure within a certain range, but a greater pressure leads to an increase of excessive glue, which may cause incomplete cementing coating and poor strength.
- (6)
3. Relation Model of Cementing Process Parameters
3.1. The Avrami Formula
- (1)
- Role of process parameters
- (a)
- Curing temperature: it mainly affects the curing temperature of the adhesive material, that is the curing rate of the thermosetting resin. On the one hand, a low temperature will slow down the curing process. The bonding performance will be affected if the curing time of the specification is still adopted. On the other hand, a high temperature will make the solvent of the adhesive volatilize earlier, influencing its viscosity. Meanwhile, it will also result in aging of the cured resin.
- (b)
- Curing time: it mainly affects the degree of curing of thermosetting resin. Curing time and temperature depend on each other within a certain range. Increasing the temperature (that is speed of the curing rate), can shorten the curing time.
- (c)
- Curing pressure: the effect of curing pressure is expelling bubbles in the adhesive and volatile solvent, as while as controlling the thickness of the cementing coating. Over-stress can cause a serious lack of glue. Inversely, insufficient pressure may make the cementing layer loose, thick, uneven and have large quantities of bubbles.
- (2)
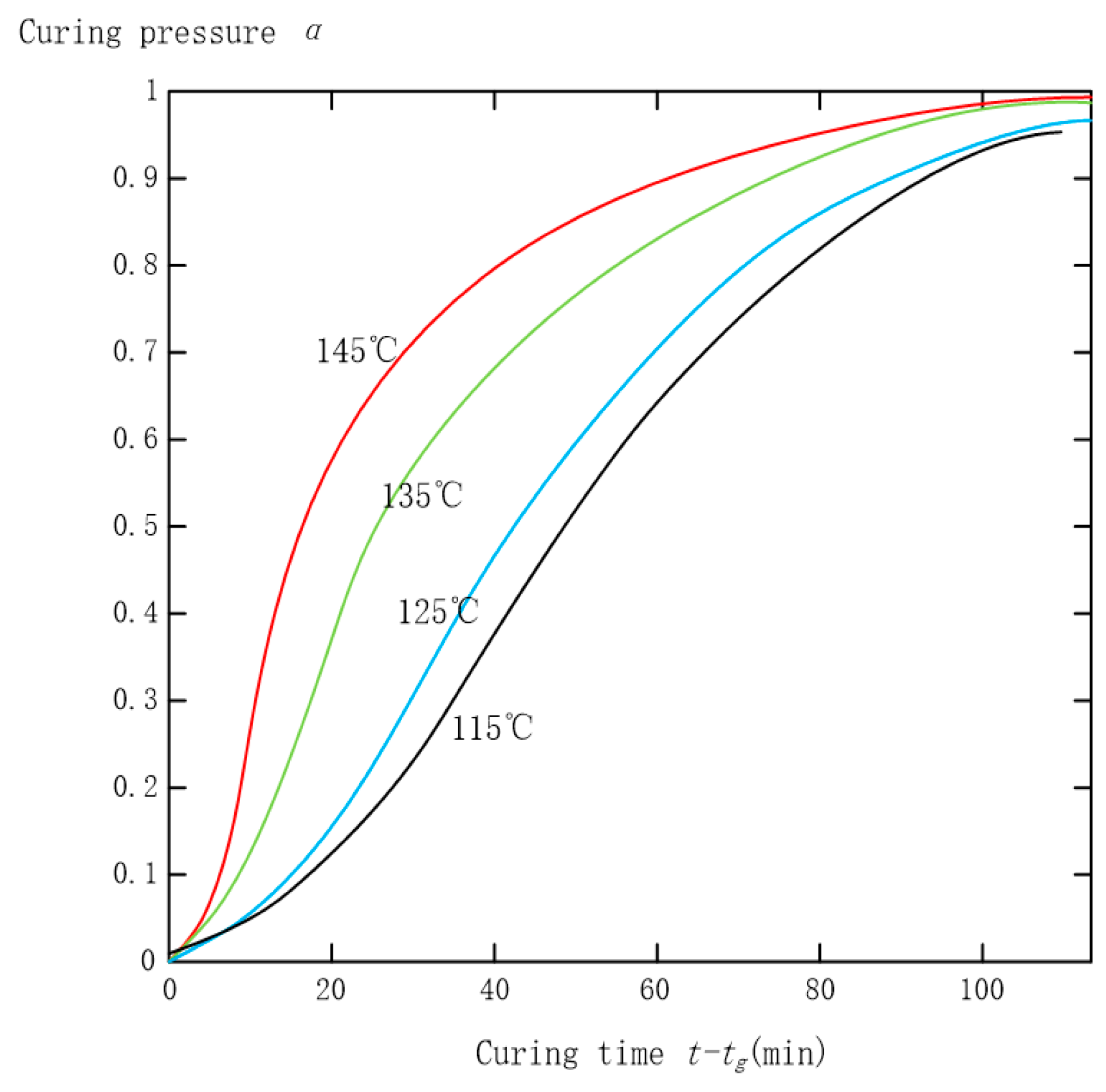
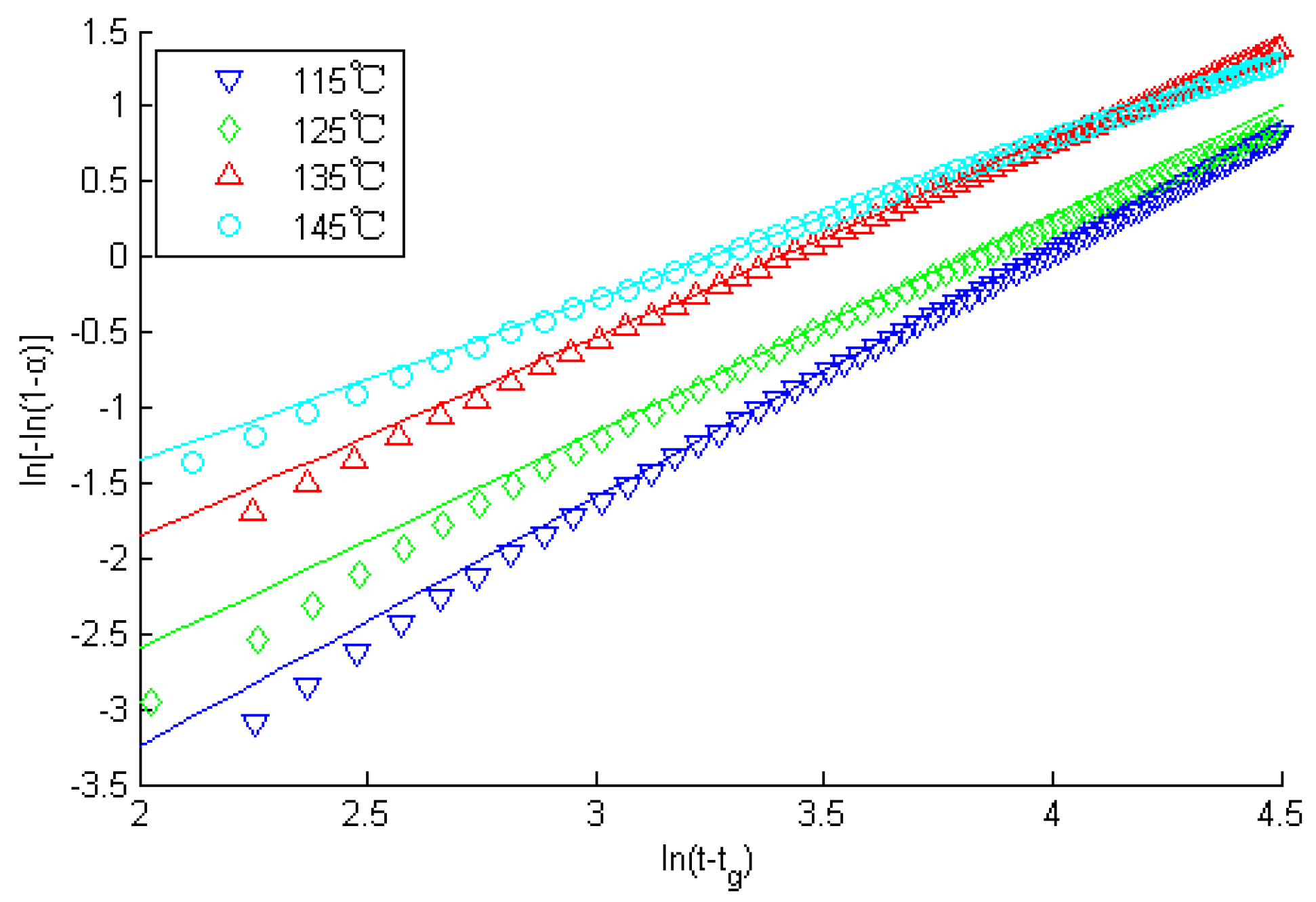
- The Avrami formula of the thermosetting resin’s curing process
3.2. DSC and Process Test of Adhesive Curing Process
- (1)
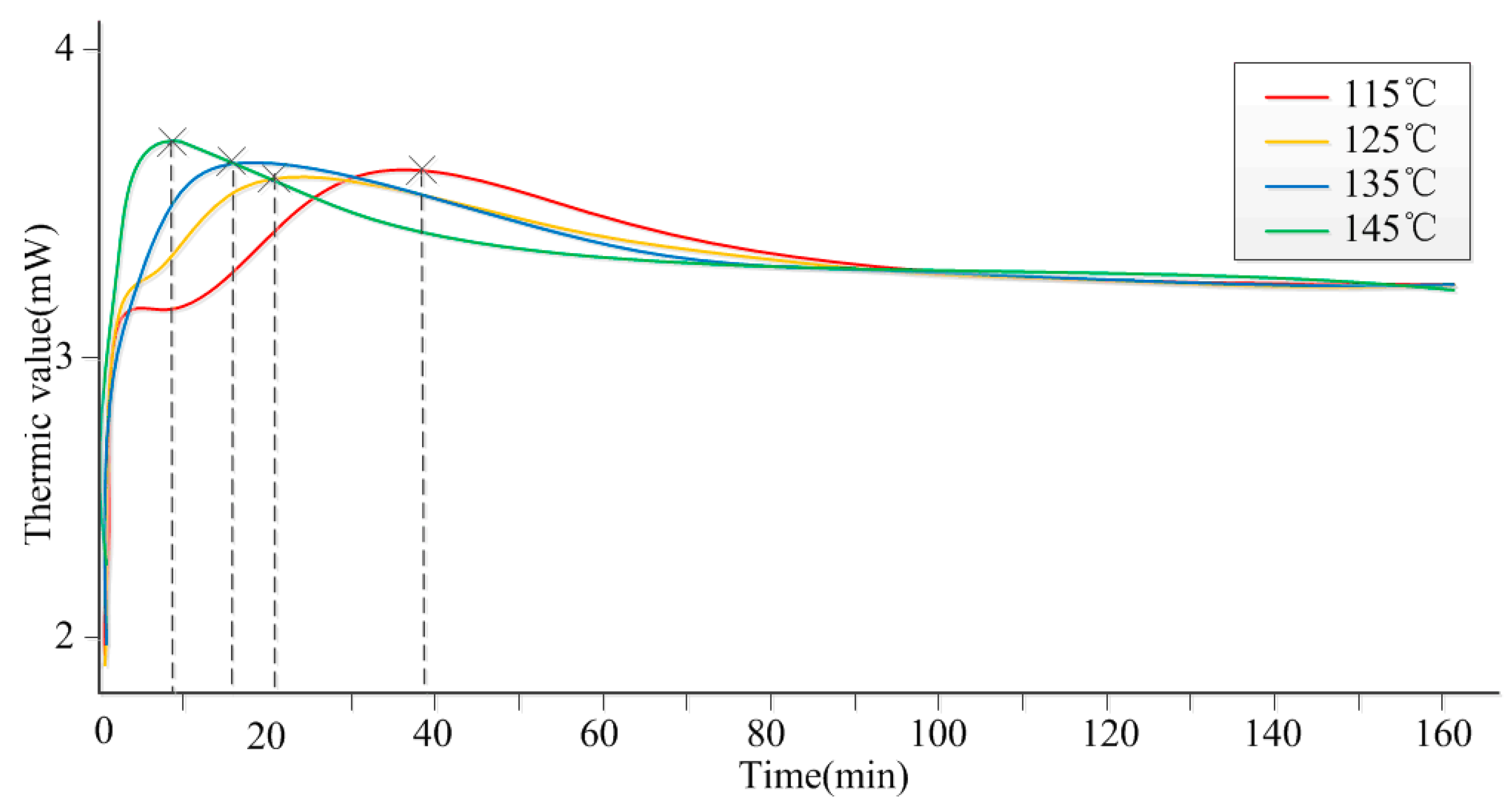
- DSC test for adhesive curing process
- (2)
- Process test for cementing process
3.3. The Establishment of Cementing Process Parameters’ Relation Model
- (1)
- Adhesive curing process kinetic parameters
- (2)
- Relationship of curing degree and bonding strength
- (3)
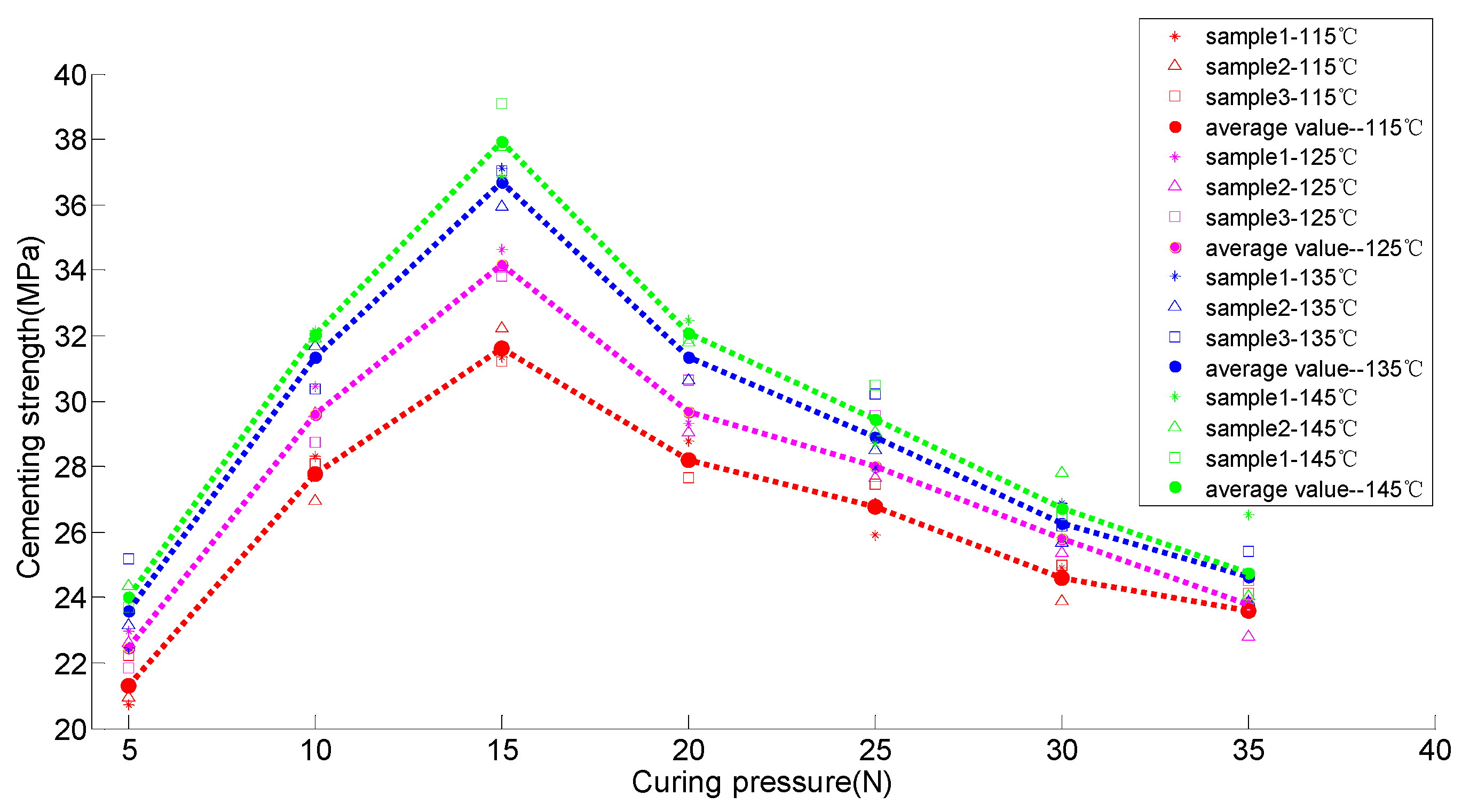
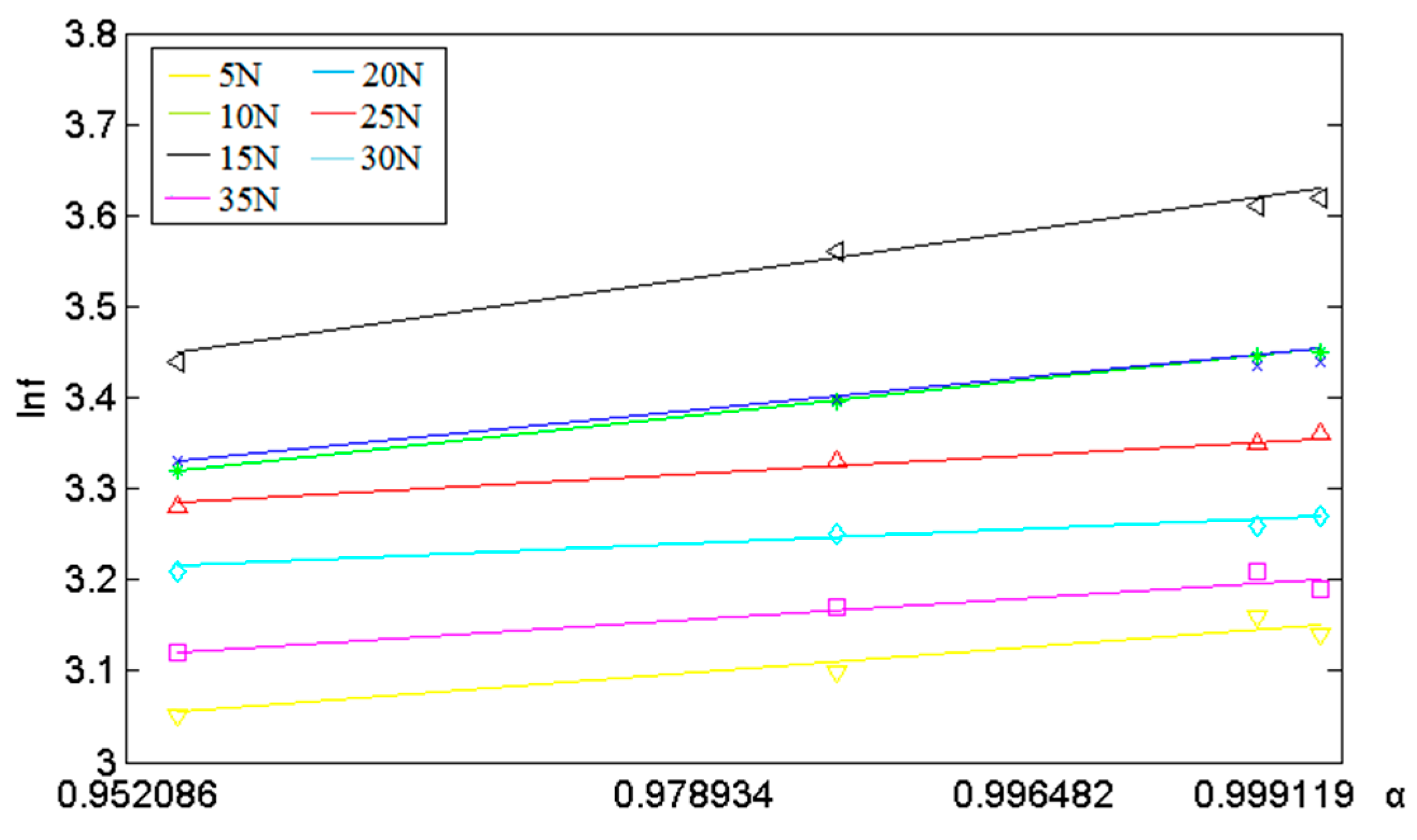
- Relationship of curing pressure and bonding strength
- (4)
- Relation model of cementing process parameters
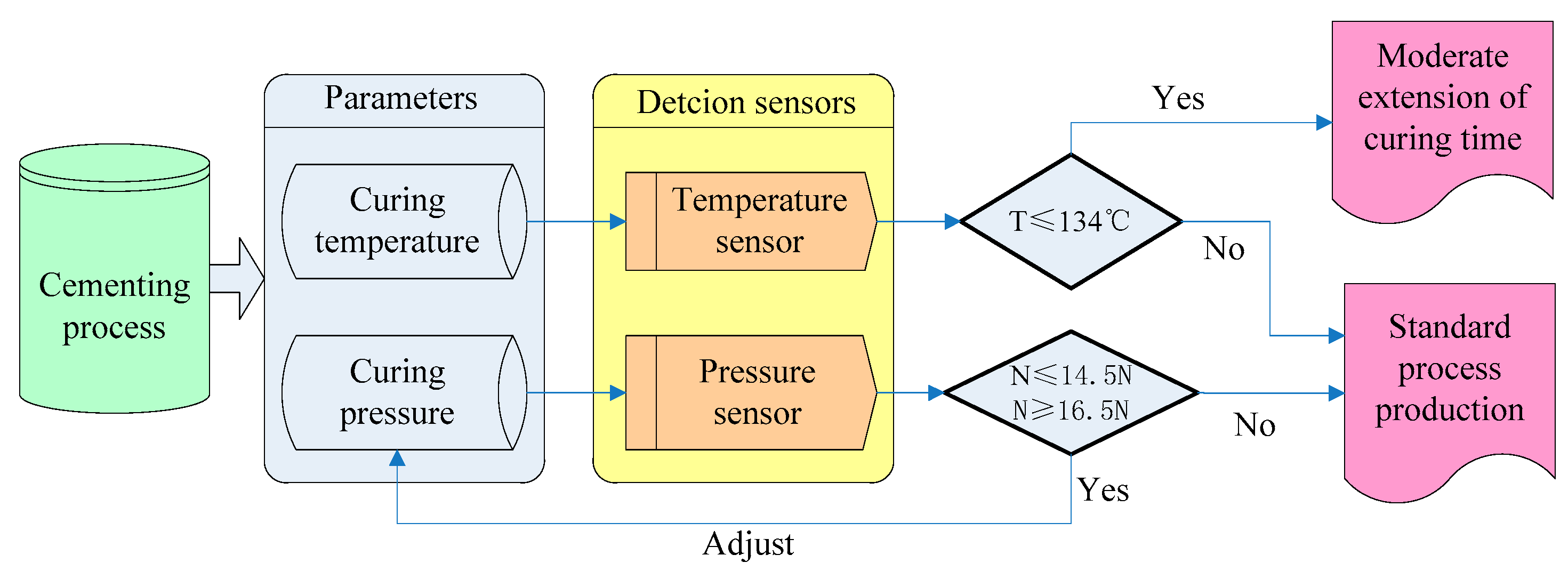
4. The Decision Criterion of Cementing Process Defect Detection Parameters
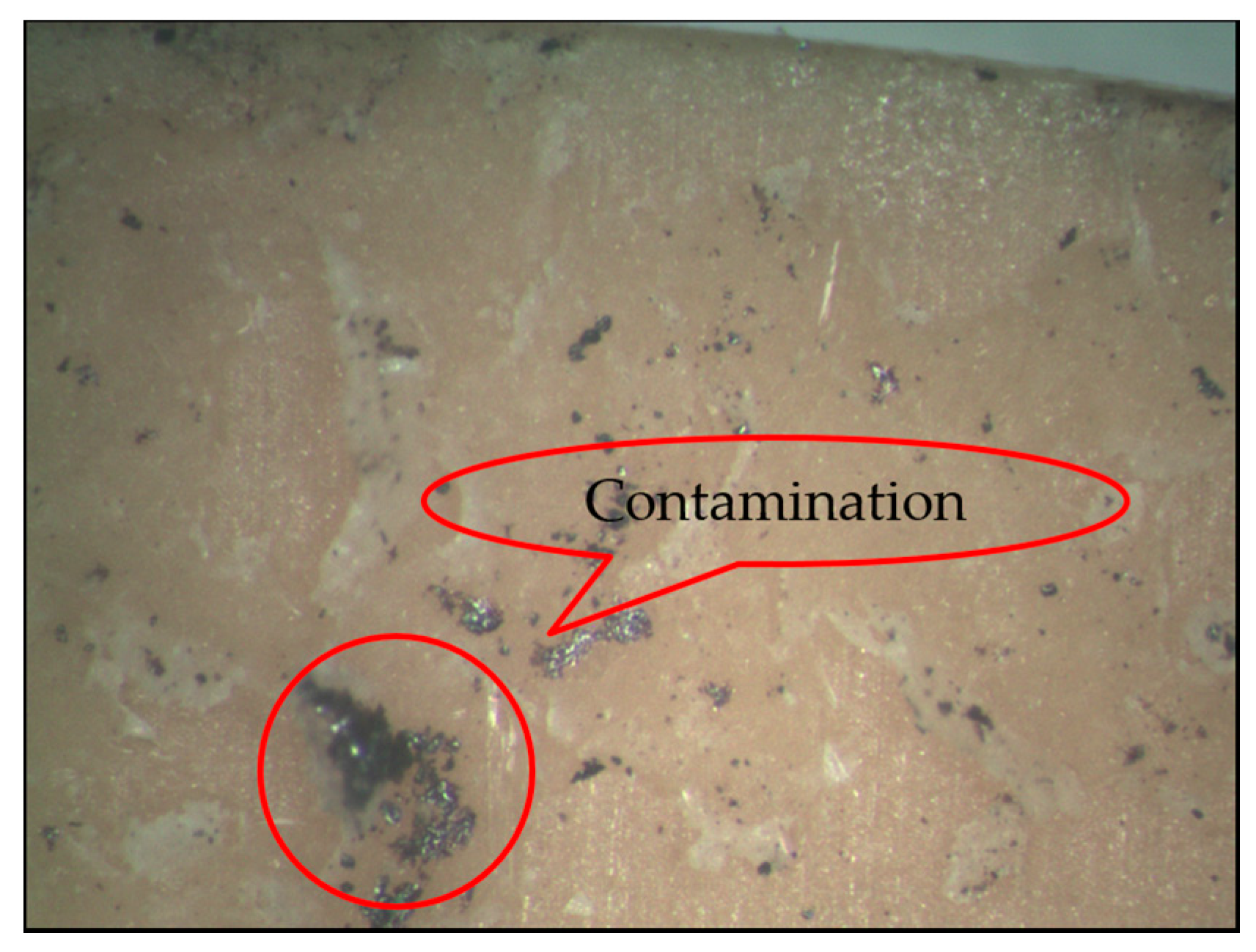
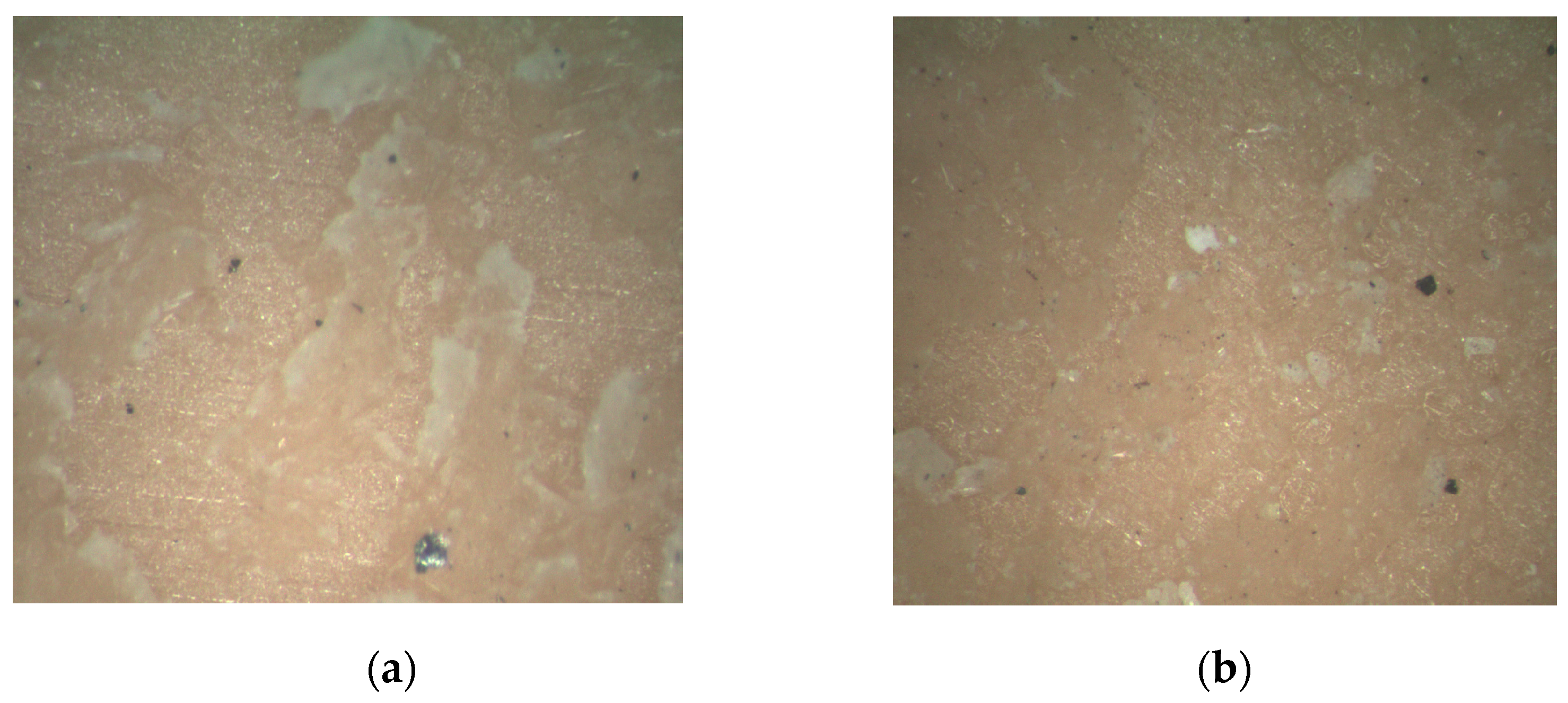
5. Case of Cementing Process Defect Detection and Accessment
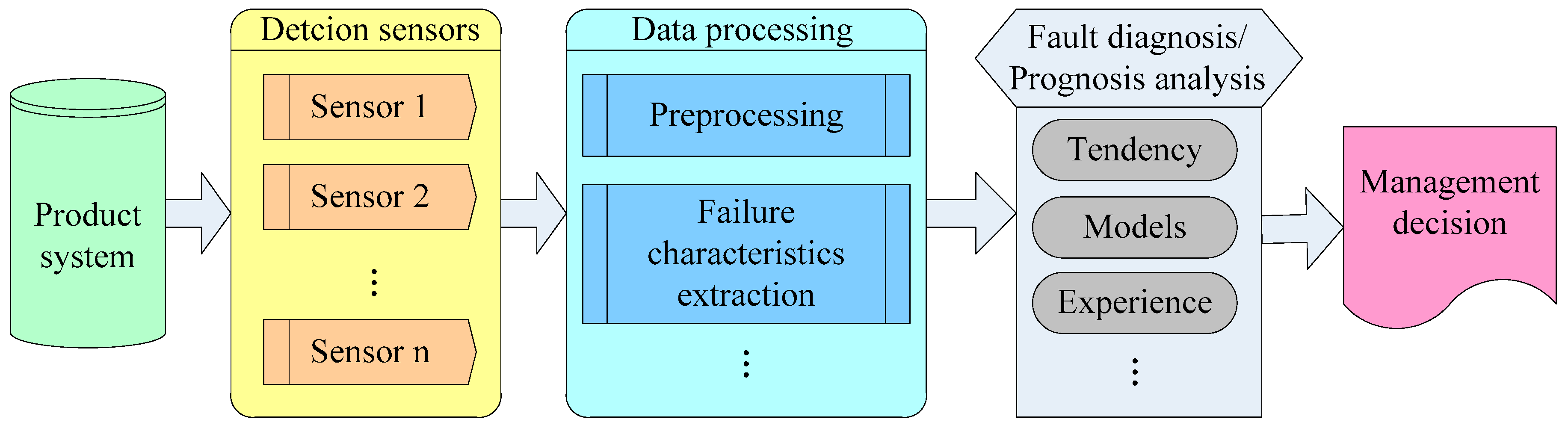
5.1. The Establishment of the Multi-Sensor PHM System Detection Scheme
5.2. Accessment
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gu, H.; Fu, G. Failure analysis of the adhesive joint of microwave ferrite phase shifter. Eng. Fail. Anal. 2013, 33, 367–380. [Google Scholar] [CrossRef]
- Haddad, H.; Al Kobaisi, M. Influence of moisture content on the thermal and mechanical properties and curing behavior of polymeric matrix and polymer concrete composite. Mater. Des. 2013, 49, 850–856. [Google Scholar] [CrossRef]
- Harris, V.G. Modern microwave ferrites. IEEE Trans. Magn. 2012, 48, 1075–1104. [Google Scholar] [CrossRef]
- Hull, D. Fractography: Observing, Measuring and Interpreting Fracture Surface Topography; Cambridge University Press: Cambridge, UK, 1999; pp. 71–72. [Google Scholar]
- Zielecki, W.; Pawlus, P.; Perłowski, R.; Dzierwa, A. Surface topography effect on strength of lap adhesive joints after mechanical pre-treatment. Arch. Civ. Mech. Eng. 2013, 13, 175–185. [Google Scholar] [CrossRef]
- Tang, Y.; Ye, L.; Deng, S.; Yang, C.; Yuan, W. Influences of processing methods and chemical treatments on fracture toughness of halloysite-epoxy composites. Mater. Des. 2012, 42, 471–477. [Google Scholar] [CrossRef]
- Smith, G.; Schroeder, J.B.; Navarro, S.; Haldeman, D. Development of a prognostics and health management capability for the Joint Strike Fighter. In Proceedings of the 1997 IEEE Autotestcon Proceedings Autotestcon, Anaheim, CA, USA, 22–25 September 1997; pp. 676–682.
- Ferrell, B.L. JSF prognostics and health management. In Proceedings of the 1999 IEEE Proceedings Aerospace Conference, Aspen Snowmass, CO, USA, 6–13 March 1999. [CrossRef]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Liu, H.; Yu, J.; Zhang, P.; Li, X. A review on fault prognostics in integrated health management. In Proceedings of the 9th International Conference Electronic on Measurement & Instruments (ICEMI), Beijing, China, 16–19 August 2009. [CrossRef]
- Deng, S.; Lv, G. On-line Detection Technology; China Machine Press: Beijing, China, 1996. [Google Scholar]
- Zhuang, L.; Yang, Y. Sensor technology application and development trend of the future. China Sci. Technol. Inf. 2011, 17, 120–126. [Google Scholar]
- Li, Y. Nondestructive testing standard status in abroad. Nondestruct. Test. 2007, 2, 31–36. [Google Scholar]
- Mahajan, P.M.; Kolhe, S.R.; Patil, P.M. A review of automatic fabric defect detection techniques. Adv. Comput. Res. 2009, 2, 18–29. [Google Scholar]
- Xie, X. A review of recent advances in surface defect detection using texture analysis techniques. Electron. Lett. Comput. Vis. Image Anal. 2008, 7, 1–22. [Google Scholar]
- Paladini, E.P. Intelligent processes for defect identification. Int. J. Math. Models Methods Appl. Sci. 2007, 1, 81–88. [Google Scholar]
- Elbehiery, H.; Hefnawy, A.; Elewa, M. Surface defects detection for ceramic tiles using image processing and morphological techniques. Trans. Eng. Comput. Technol. 2005, 5, 158–162. [Google Scholar]
- Kercel, S.W.; Kisner, R.A.; Klein, M.B.; Bacher, G.D.; Pouet, B.F. In-process detection of weld defects using laser-based ultrasound. Sens. Strust. Health Monit. 1999, 3852. [Google Scholar] [CrossRef]
- Park, M.P.; Jesse, S.; Jin, J.S.J.; Sherlock, L.; Au, S.L.A.; Luo, S.; Cui, Y. Automated defect inspection systems by pattern recognition. Int. J. Signal Process. Image Process. Pattern Recognit. 2009, 2, 31–42. [Google Scholar]
- Giordano, M.; Laudati, A.; Russo, M.; Nasserbet, J.; Persianoc, G.V.; Cusanoc, A. Advanced cure monitoring by optoelectronic multifunction sensing system. Thin Solid Films 2004, 450, 191–194. [Google Scholar] [CrossRef]
- Zheng, X. The Strength of Adhesive Joint and the Environmental Degradation of Ultrasonic Nondestructive Character. Ph.D. Thesis, Beijing University of Technology, Beijing, China, 2003. [Google Scholar]
- Heller, K.; Jacobs, L.J.; Qu, J. Characterization of adhesive bond properties using Lamb waves. NDT&E Int. 2000, 33, 555–563. [Google Scholar]
- Armstrong, K.B. Long-term durability in water of aluminium alloy adhesive joints bonded with epoxy adhesives. Int. J. Adhes. Adhes. 1997, 17, 89–105. [Google Scholar] [CrossRef]
- Wang, K.; Tian, J.; Pecht, M.; Xu, A. A prognostics and health management based method for refurbishment decision making for electromechanical systems. IFAC Pap. OnLine 2015, 48, 454–459. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Y.; Xu, L. PHM-oriented integrated fusion prognostics for aircraft engines based on sensor data. IEEE Sens. J. 2014, 14, 1124–1132. [Google Scholar] [CrossRef]
- Chen, Z.S.; Yang, Y.M.; Hu, Z. A technical framework and roadmap of embedded diagnostics and prognostics for complex mechanical systems in prognostics and health management systems. IEEE Trans. Reliab. 2012, 61, 314–322. [Google Scholar] [CrossRef]
- Martha, A.Z.; Rishi, R.; Andrew, R.M.; Harrison, R.F. Prognostics of gas turbine engine: An integrated approach, expert systems with applications. Exp. Syst. Appl. 2015, 42, 8472–8483. [Google Scholar]
- Liu, L.; Wang, S.; Liu, D.; Zhang, Y.; Peng, Y. Entropy-based sensor selection for condition monitoring and prognostics of aircraft engine. Microelectron. Reliab. 2015, 55, 2092–2096. [Google Scholar] [CrossRef]
- Elghazel, W.; Bahi, J.; Guyeux, C.; Hakem, M.; Medjaher, K.; Zerhouni, N. Dependability of wireless sensor networks for industrial prognostics and health management. Comput. Ind. 2015, 68, 1–15. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. I general theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. II transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Avrami, M. Granulation, phase change, and microstructure kinetics of phase change. III. J. Chem. Phys. 1941, 9, 177–184. [Google Scholar] [CrossRef]
- Avramov, I. Kinetics of distribution of infections in networks. Phys. A Stat. Mech. Appl. 2007, 379, 615–620. [Google Scholar] [CrossRef]
- Nazari, A.; Sanjayan, J.G. Johnson–Mehl–Avrami–Kolmogorov equation for prediction of compressive strength evolution of geopolymer. Ceram. Int. 2015, 41, 3301–3304. [Google Scholar] [CrossRef]





| Process Factors | Curing Temperature (°C) | Curing Time (h) | Curing Pressure (N) | Cementing Strength (MPa) | ||||
|---|---|---|---|---|---|---|---|---|
| Groups | Sample 1 | Sample 2 | Sample 3 | Average Value | ||||
| 1 | 115 | 2 | 5 | 20.7 | 20.96 | 22.24 | 21.3 | |
| 2 | 10 | 28.31 | 26.96 | 28.1 | 27.79 | |||
| 3 | 15 | 31.32 | 32.24 | 31.24 | 31.6 | |||
| 4 | 20 | 28.78 | 28.18 | 27.64 | 28.2 | |||
| 5 | 25 | 25.92 | 26.86 | 27.47 | 26.75 | |||
| 6 | 30 | 24.91 | 23.9 | 25.0 | 24.6 | |||
| 7 | 35 | 23.8 | 22.8 | 24.14 | 23.58 | |||
| 8 | 125 | 2 | 5 | 22.97 | 22.6 | 21.84 | 22.47 | |
| 9 | 10 | 30.43 | 29.63 | 28.74 | 29.6 | |||
| 10 | 15 | 34.63 | 34.05 | 33.83 | 34.17. | |||
| 11 | 20 | 29.31 | 29.05 | 30.64 | 29.67 | |||
| 12 | 25 | 26.89 | 27.64 | 29.54 | 28.02 | |||
| 13 | 30 | 26.18 | 25.37 | — | 25.78 | |||
| 14 | 35 | 23.94 | 22.8 | 24.53 | 23.76 | |||
| 15 | 135 | 2 | 5 | 22.46 | 23.15 | 25.18 | 23.6 | |
| 16 | 10 | 32.03 | 31.67 | 30.36 | 31.35 | |||
| 17 | 15 | 37.1 | 35.96 | 37.04 | 36.7 | |||
| 18 | 20 | 32.03 | 30.64 | — | 31.34 | |||
| 19 | 25 | 27.97 | 28.52 | 30.2 | 28.9 | |||
| 20 | 30 | 26.89 | 25.67 | 26.18 | 26.25 | |||
| 21 | 35 | 24.66 | 23.86 | 25.4 | 24.64 | |||
| 22 | 145 | 2 | 5 | 23.94 | 24.37 | 23.7 | 24.0 | |
| 23 | 10 | 32.17 | 31.92 | — | 32.05 | |||
| 24 | 15 | 36.86 | 37.78 | 39.08 | 37.91 | |||
| 25 | 20 | 32.46 | 31.8 | 31.92 | 32.06 | |||
| 26 | 25 | 28.72 | 29.06 | 30.48 | 29.42 | |||
| 27 | 30 | 25.84 | 27.8 | 26.55 | 26.73 | |||
| 28 | 35 | 26.53 | 24.05 | 23.67 | 24.75 | |||
| Curing Temperature | Gelation Time tg (min) | Avrami Index n | Avrami Rate Constant k | System’s Activation Energy Ea (kJ∙mol) | Antecedent Factor A | |
|---|---|---|---|---|---|---|
| (°C) | (K) | |||||
| 115 | 388 | 12.66 | 1.665 | 0.001417 | 34.17 | 746.2 |
| 125 | 398 | 4.38 | 1.46 | 0.003966 | ||
| 135 | 408 | 2.85 | 1.258 | 0.01287 | ||
| 145 | 418 | 1.63 | 1.104 | 0.02919 | ||
| Curing Temperature (K) | Gelation Time tg (min) | Avrami Index n | Avrami Rate Constant k | Activation Energy of Curing Reaction Ea (kJ·mol) | Adjusted Factor | |||
|---|---|---|---|---|---|---|---|---|
| A | B (MPa/N) | b | c (1/N) | |||||
| 388 | 12.66 | 1.665 | 0.001417 | 34.17 | 746.2 | 0.6018 | 2.3195 | 0.0635 |
| 398 | 4.38 | 1.46 | 0.003966 | |||||
| 408 | 2.85 | 1.258 | 0.01287 | |||||
| 418 | 1.63 | 1.104 | 0.02919 | |||||
| Process Condition | Process Parameter Sensitivity to the Cementing Strength | ||
|---|---|---|---|
| Curing Pressure | Curing Time | Curing Temperature | |
| (MPa/N) | (MPa/min) | (MPa/K) | |
| 135 °C, 2 h, 15 N | 0.1112 | 0.02582 | 0.0742 |
| 135 °C, 2 h, 16 N | −0.0352 | 0.02585 | 0.0743 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, B.; Fu, G.; Li, Y.; Zhao, Y. Research on a Defects Detection Method in the Ferrite Phase Shifter Cementing Process Based on a Multi-Sensor Prognostic and Health Management (PHM) System. Sensors 2016, 16, 1263. https://doi.org/10.3390/s16081263
Wan B, Fu G, Li Y, Zhao Y. Research on a Defects Detection Method in the Ferrite Phase Shifter Cementing Process Based on a Multi-Sensor Prognostic and Health Management (PHM) System. Sensors. 2016; 16(8):1263. https://doi.org/10.3390/s16081263
Chicago/Turabian StyleWan, Bo, Guicui Fu, Yanruoyue Li, and Youhu Zhao. 2016. "Research on a Defects Detection Method in the Ferrite Phase Shifter Cementing Process Based on a Multi-Sensor Prognostic and Health Management (PHM) System" Sensors 16, no. 8: 1263. https://doi.org/10.3390/s16081263
APA StyleWan, B., Fu, G., Li, Y., & Zhao, Y. (2016). Research on a Defects Detection Method in the Ferrite Phase Shifter Cementing Process Based on a Multi-Sensor Prognostic and Health Management (PHM) System. Sensors, 16(8), 1263. https://doi.org/10.3390/s16081263





