1. Introduction
Modern products are developed to have good quality and high reliability. For some safety-critical components and systems, they are even designed to last for an extremely long time to avoid the catastrophic consequences of potential failures. It is a big challenge to obtain sufficient amount of time-to-failure data by testing such products under the normal operating environments and sometimes even under harsher conditions [
1]. Obviously, the traditional failure-time data analysis and testing methods are unsuitable for reliability analysis of such highly reliable products.
In engineering applications, many failure mechanisms can be traced to underlying degradation processes (e.g., cumulative wear, crack growth, corrosion, fatigue, material aging, etc.) [
2]. As a result, the degradation analysis method has been introduced to handle reliability modeling problems based on the products’ degradation information obtained from historical data or degradation tests [
3]. Especially, accelerated degradation testing (ADT) has been used to collect the degradation data by exposing the test specimens to severer-than-normal conditions. In the last two decades, ADT has been intensively studied as an effective tool for reliability verification and lifetime evaluation of modern products. Successful applications of ADT include the reliability analyses of batteries [
4], super luminescent diode (SLD) [
5], smart electricity meter [
6], metal oxide semiconductor field effect transistors (MOSFETs) [
7], etc.
The essence of ADT-based decision-making is to find a suitable mathematical model, namely degradation model, which is capable of describing the degradation paths of samples tested at different stress levels. The existing degradation models can be categorized into two broad classes, i.e., stochastic process models and general path models [
1]. The stochastic process models have attracted more attention because of their properties of time-dependent structures. The typical models include the Wiener process (i.e., Brownian motion), Gamma process and Inverse Gaussian (IG) process. The Gamma and IG processes are suitable for modeling a degradation process which is always positive and strictly increasing. On the other hand, the Wiener process with a linear drift has become the most popular stochastic degradation model [
1,
8]. Its related work and variants for the cases involving covariates, random effects and measurement errors have been extensively reviewed by Ye and Xie [
1]. Nonetheless, the linear drift Wiener process cannot be directly used to describe a nonlinear degradation process. In many engineering applications, however, nonlinearity is quite natural due to the complex structures and failure mechanisms of the products. To overcome this obstacle, some transformation methods for degradation data have been used, e.g., time-scale transformation [
9,
10,
11] and log-transformation [
12,
13,
14]. However, not all nonlinear degradation processes can be properly transformed [
15]. To characterize the dynamics and nonlinearity of the degradation process, Si et al. [
15] developed a Wiener process model with a nonlinear drift coefficient, and presented analytical approximations to the probability distribution functions of the first hitting time under a mild assumption. Further, Wang et al. [
16,
17] presented a general Wiener process model for residual life estimation which jointly takes into account the nonlinearity, temporal uncertainty, and unit-to-unit variability. In this paper, we will first introduce the general Wiener process and then extend this model for analyzing nonlinear ADT data.
It is also worth pointing out that the aforementioned studies only consider the cases involving a single degradation measure. Indeed, modern engineering systems are often composed of multiple components with different functions [
18]. As a result, a product may have multiple degradation measures and any of them may be a cause of product failure [
19]. Such degradation measures may include not only the functional and/or performance parameters of the product, but also some indirect degradation features extracted from raw sensory signals [
20], such as vibration, force and acoustic signals, temperature and voltage. Usually, degradation measures are not independent of each other, and some failures may be attributed to the interaction of multiple degradation processes. In practice, it is often difficult to determine the importance of each source of degradation information. To avoid possible one-sidedness, it would be more appropriate and accurate to perform reliability estimation through suitable fusion of information from different degradation measures. When modeling ADT data, such efforts become more challenging as the data are collected under different stress levels.
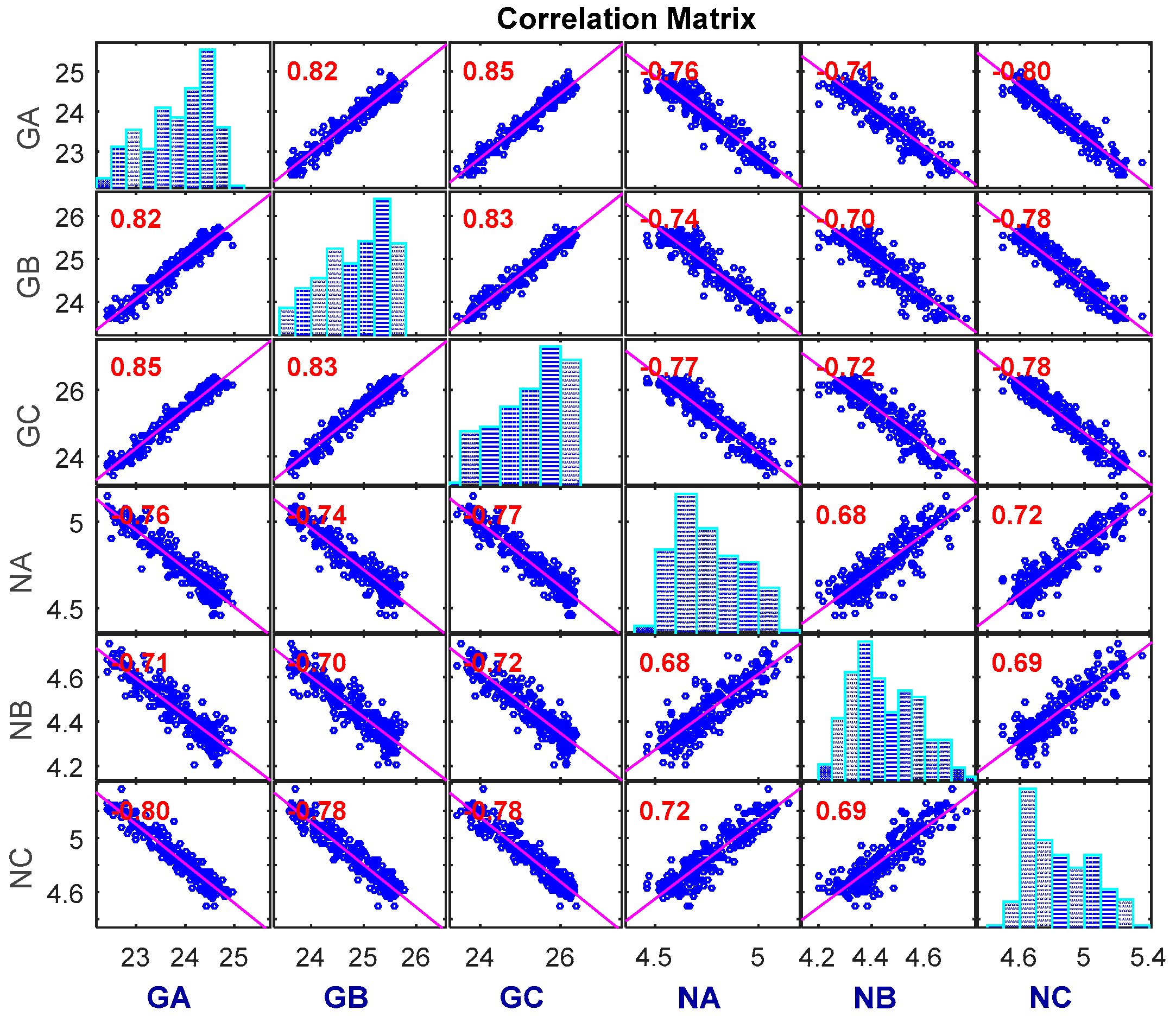
In the last decade, some progress has been made on multivariate degradation modeling. Huang and Askin [
21] discussed competing modes of catastrophic failure and degradation failure by assuming the independence of multiple degradation processes. Crowder [
22] suggested that such an independence assumption can only be made if a failure mechanism has absolutely no direct or indirect impact on the likelihood of other failure mechanisms in the system. He also pointed out that some shared factors (e.g., same environmental/operational stresses, usage history, materials quality, and maintenance of the system) may increase the possibility of dependence of different failure mechanisms in the system. Therefore, it is safer to consider the dependency between performance parameters in a multivariate degradation model.
In the literature, two popular methods have been utilized to capture the dependence between performance parameters, namely, the use of multivariate joint distributions [
23,
24,
25] and the copulas method [
18,
19,
26,
27,
28,
29,
30,
31,
32,
33]. In practice, assuming a multivariate joint distribution may not be suitable for all conditions [
34], and sometimes it is difficult, if not impossible, to find an appropriate joint distribution in many cases. As a useful alternative, the use copulas enables estimating a multivariate joint distribution by combining the marginal distributions using a joint dependence structure [
35]. Moreover, copulas do not impose constraints on the univariate marginal distributions [
36]. Due to these advantages, the copulas method has attracted much attention in reliability engineering. Sari et al. [
26] introduced a copula function to describe the correlation between two performance parameters, and combined it with a generalized linear model for bivariate constant-stress degradation data. Pan et al. [
27,
28] discussed the bivariate degradation modeling approaches based on Wiener processes and Copulas, respectively, under the normal operating stress and constant-stress accelerating conditions as well. Similarly, Peng et al. [
18], Liu et al. [
29] and Hao et al. [
30,
31] also adopted copulas to characterize the dependency between two performance parameters, and developed their own bivariate degradation models. Wang and Pham [
19] applied time-varying copulas for handling the
s-dependent relationship among competing degradation processes, and provided a numerical example with two degradation processes. Hong et al. [
32] used copulas to investigate the influence of degradation dependency of multiple components on the optimal maintenance decisions. Xi et al. [
33] developed a copula-based sampling method for data-driven prognostics. However, most of the previous work focuses on degradation processes under normal operating conditions, and scarce studies have been conducted on the dependency of multiple degradation processes under accelerated conditions.
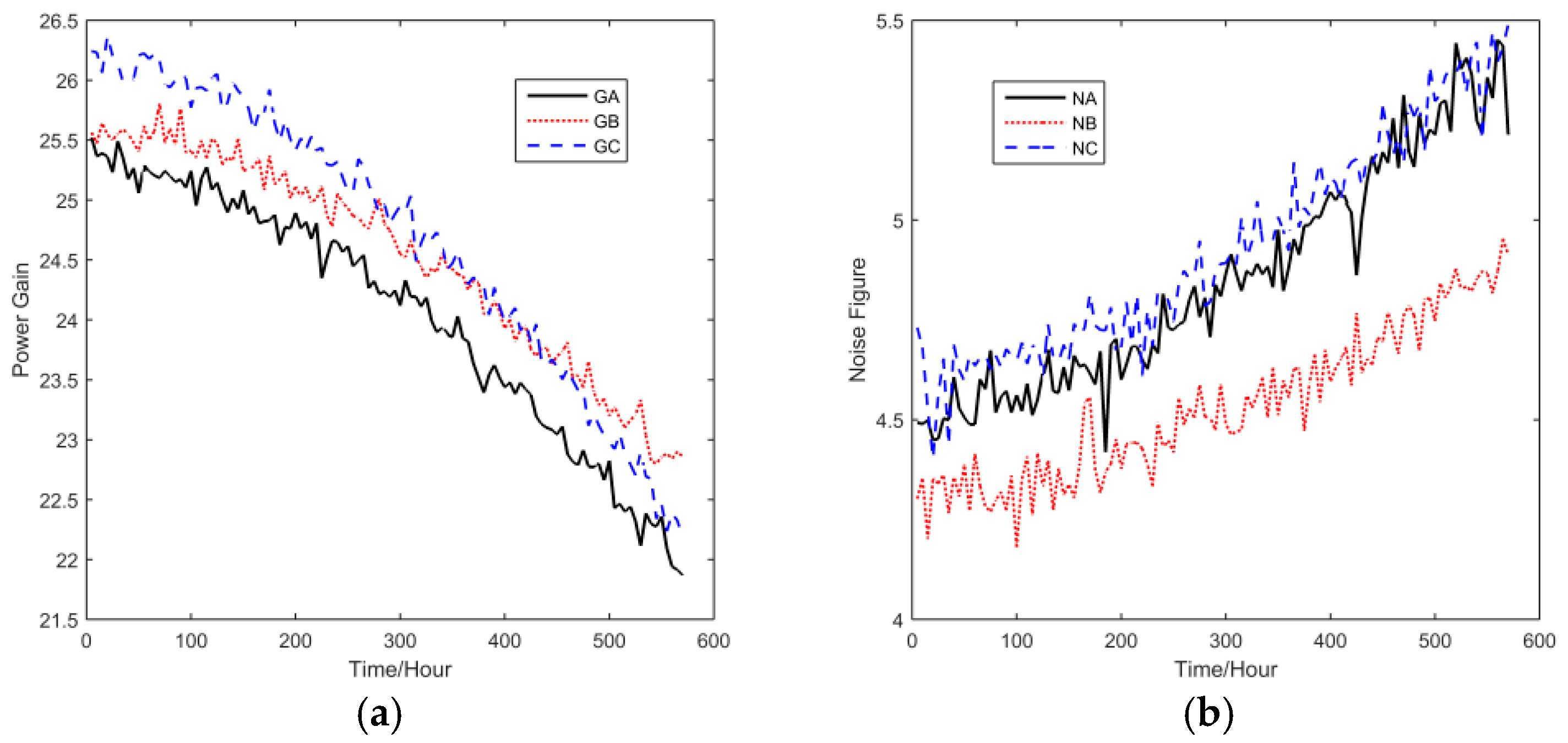
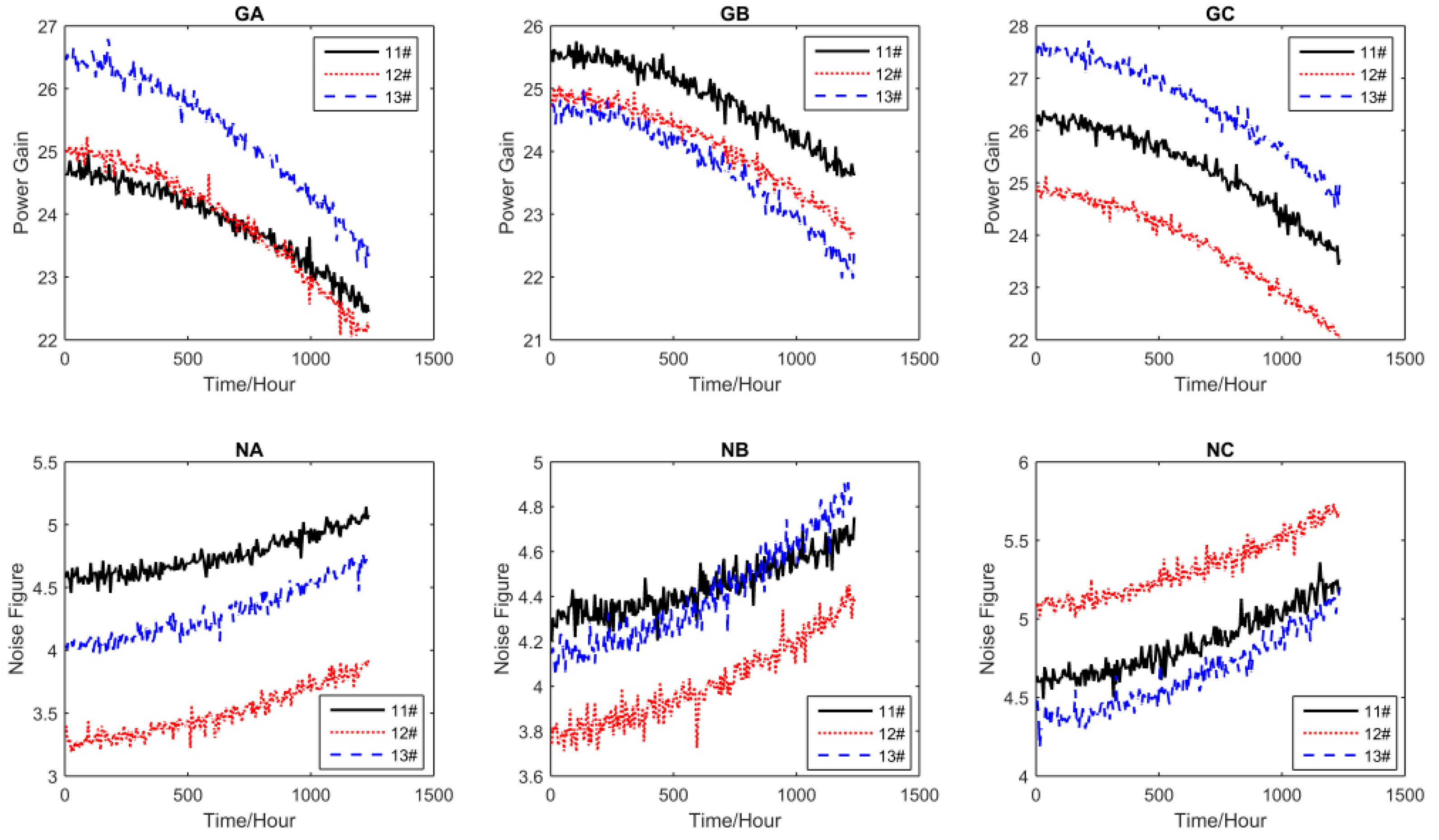
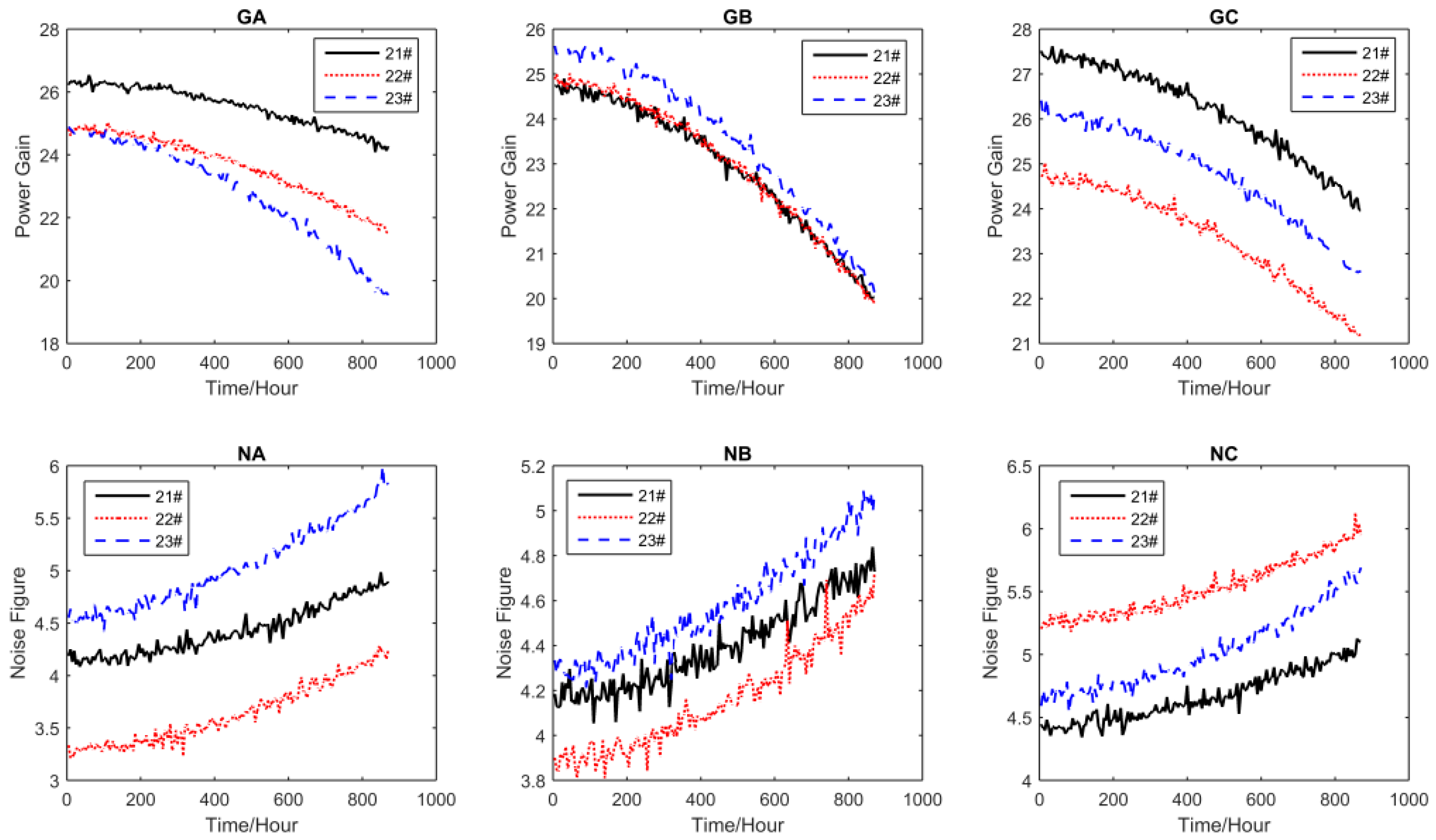
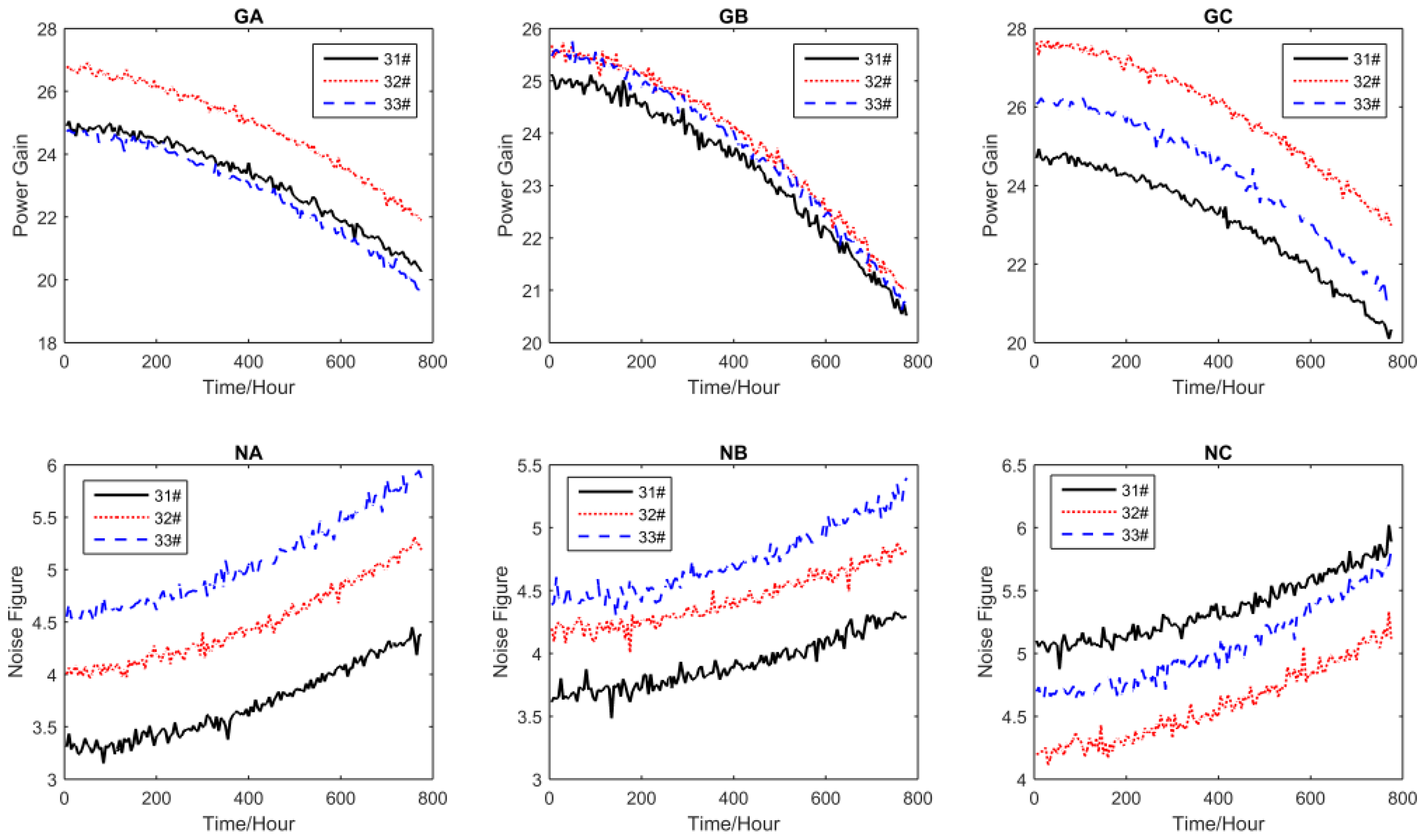
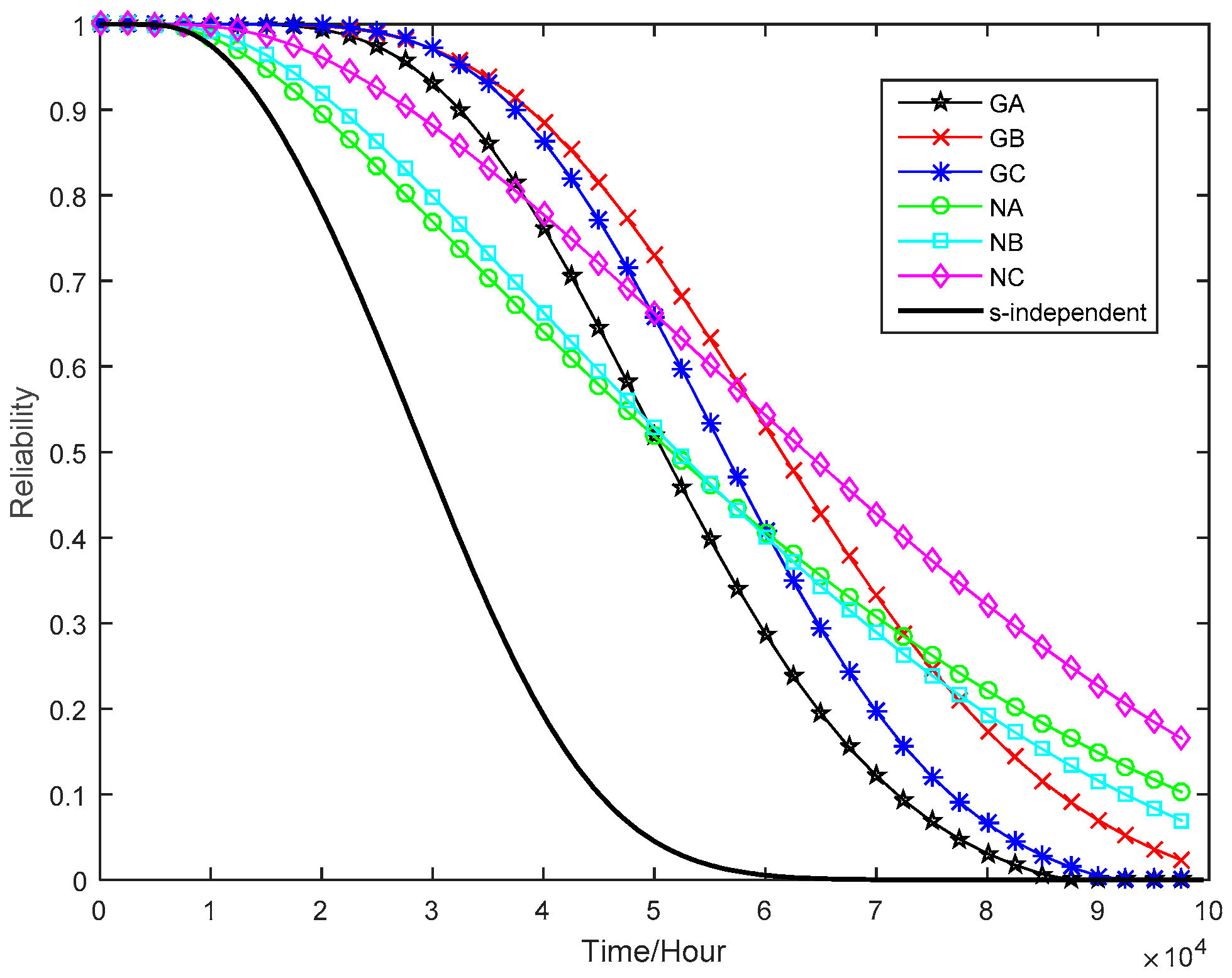
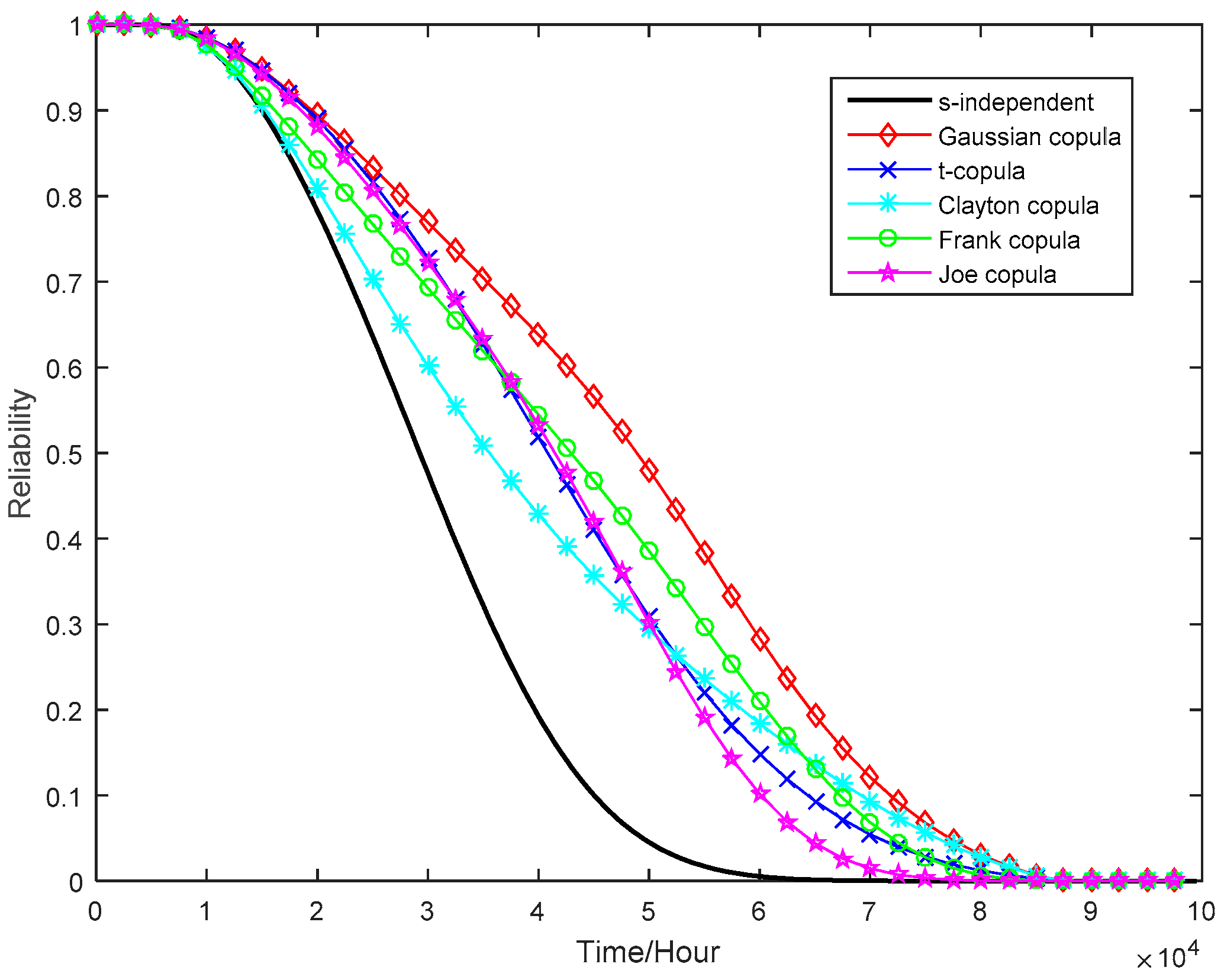
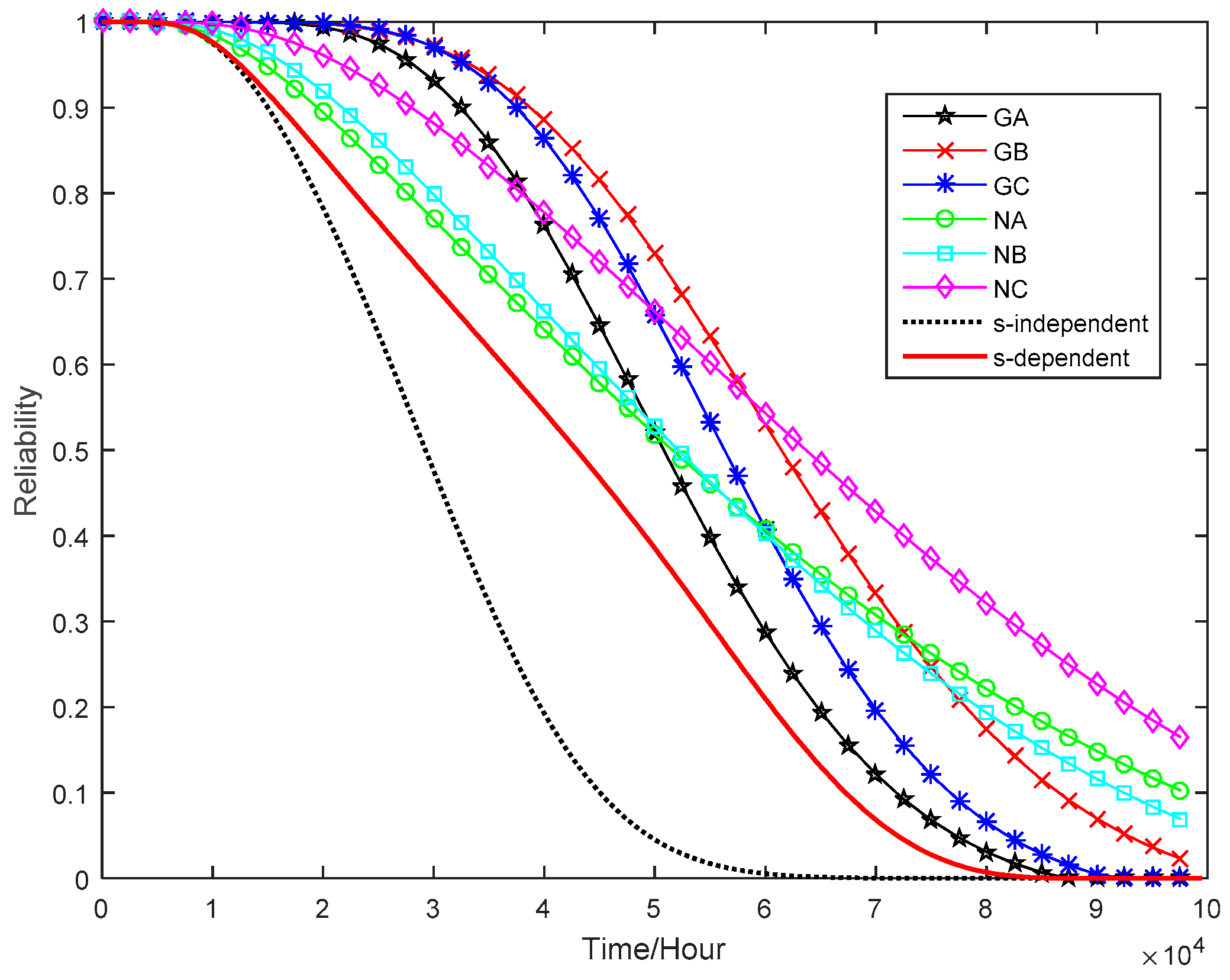
This paper is aimed at making an early attempt to model s-dependent multivariate ADT data using general Wiener process and copulas. First, the general Wiener process is used to model nonlinear univariate accelerated degradation processes. Then, the copula method is adopted to find the joint probability distribution of multiple degradation processes. Next, parameter estimation of the proposed model is performed using the Inference Functions for Margins (IFM) method, and the Akaike Information Criterion (AIC) is employed to compare the goodness-of-fit of candidate models. Finally, a real-world case study on the tuner’s CSADT data is utilized to demonstrate the usefulness of the proposed method.
The remainder of this paper is organized as follows:
Section 2 presents the univariate ADT model based on the general Wiener process and its parameter estimation method.
Section 3 elaborates on the copula-based multivariate ADT modeling method, including introduction to copulas, multivariate dependent accelerated degradation model, and statistical inference.
Section 4 provides the case study, and
Section 5 concludes the paper.