1. Introduction
Most of the developed countries are facing the problems of the aging of the human population and labor shortage. Then, intelligent mobile service robots have been developed with the main purpose of solving these problems. Consequently, one of the tasks that needs to be accomplished on an urgent basis is highly accurate and robust self-localization of robots. Many types of research have been conducted on the self-localization of indoor mobile robots. Several of the systems developed for this purpose employ vision sensors [
1,
2], lasers [
3], ultrasonic sensors [
4], infrared sensors [
5], radar [
6] and ultrasonic technology [
7]. However, these conventional approaches are not robust or accurate enough to localize an indoor mobile robot, given the presence of several kinds of disturbances. Vision sensors suffer from the change of illumination and environment conditions. Laser range finders (LRFs) cannot locate a robot accurately if the robot is surrounded by many unknown moving obstacles or when transparent walls are widely used in the environment, because LRF fails to detect them. Further, the performance of ultrasonic sensors is easily affected by obstacles around the robot.
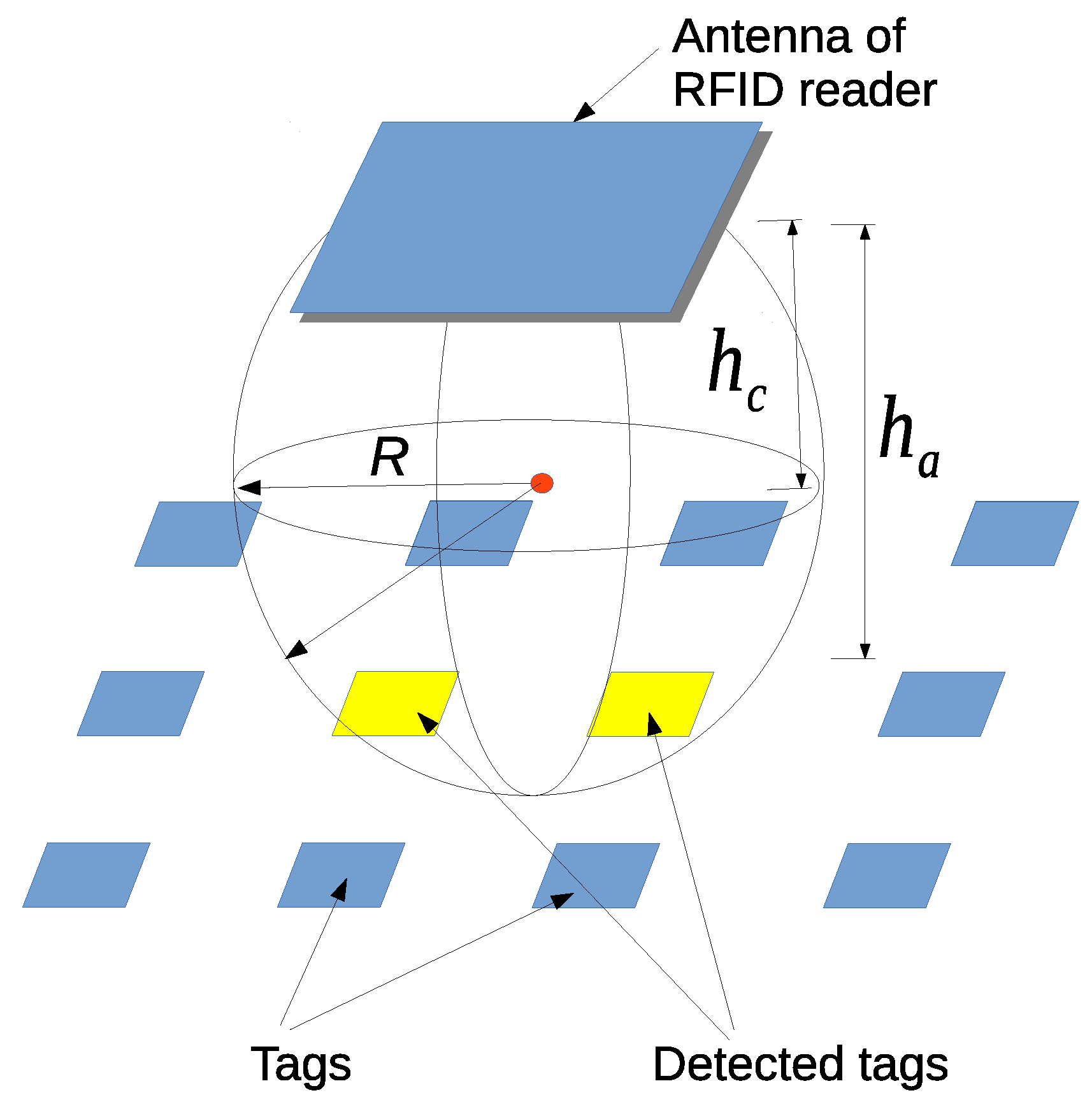
A radio frequency identification (RFID) system has recently attracted attention as one of the alternative sensing devices. RFID technology employs electromagnetic fields to transfer data between an RFID tag and an RFID reader. Each RFID tag has its own unique ID information, and RFID tags are inexpensive enough to be distributed in large densities among objects and environments. RFID systems are widely used for applications, such as identification, transpiration tracking and inventory control. These systems help to realize relatively robust wireless communication to exchange data between a tag and a reader. Researchers in the field of robotics have investigated the use of an RFID system for self-localization of a mobile robot. This can be achieved by two approaches. One is to use the RFID system to compensate for another self-localization system based on a vision sensor, LRF or GPS for instability or a huge exploration space [
8,
9,
10]. However, the disadvantages of the base self-localization system remain in this approach. The other approach is to use only an RFID system for self-localization [
11,
12,
13,
14,
15,
16]. Various methods for making use of an RFID system for self-localization have been proposed. One method is to use only kinematic constraints [
13,
14,
15]. However, the accuracy of self-localization depends on the density of tags; therefore, a high density of tags is required for accurate self-localization. Another method is based on a machine learning approach [
11]; however, the RFID system is adversely affected by obstacles surrounding the reader and tags. Yet another method entails the adaptation of probabilistic approaches [
12,
16]. In particular, the Monte-Carlo localization (MCL) method [
17] enables self-localization with relative accuracy. A previous study [
12] employed relatively large-tags and small readers. However, the large size of tags resulted in a large localization error. Another study [
16] employed small tags and a large number of readers with small antennas.
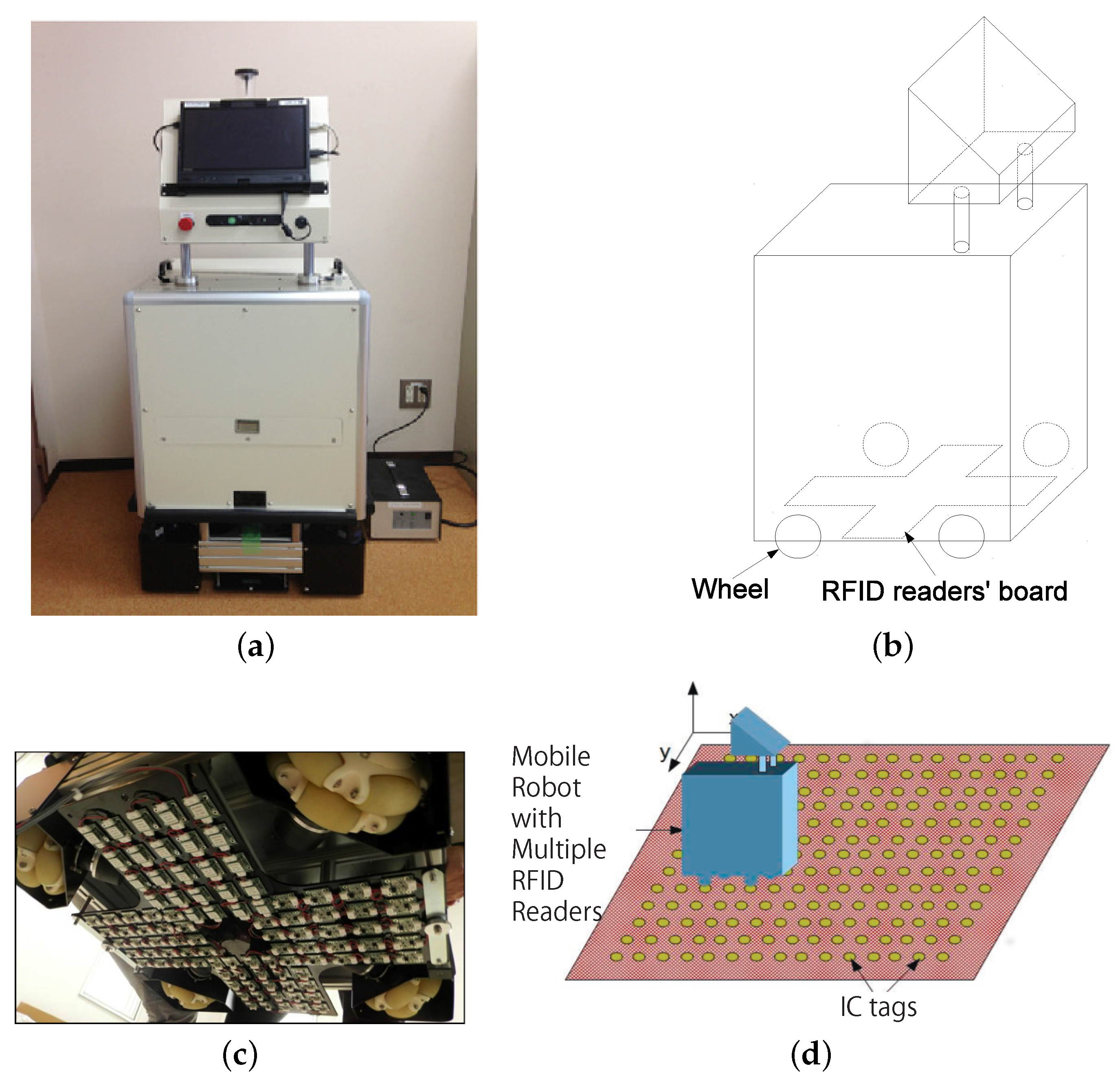
Figure 1 shows an omni-directional vehicle equipped with an HF-band RFID system, as employed in the previous study [
16]. In this RFID system, 96 RFID readers are installed at the bottom of the robot. A high density of RFID tags is embedded in carpets on the floor. The RFID self-localization system with 96 readers is quite robust, and it works flawlessly even in the case of stains or marker tapes on the carpet. However, the production cost of this RFID system with 96 RFID readers is relatively high. This drawback prevents widespread utilization of an RFID-based self-localization system in service robots employed in public facilities, such as those serving in hospitals. There is a high demand for a low-cost RFID system. Furthermore, although MCL enables robust self-localization, the estimated initial position and posture are crucial for rapid recovery after the robot has lost its position and posture.
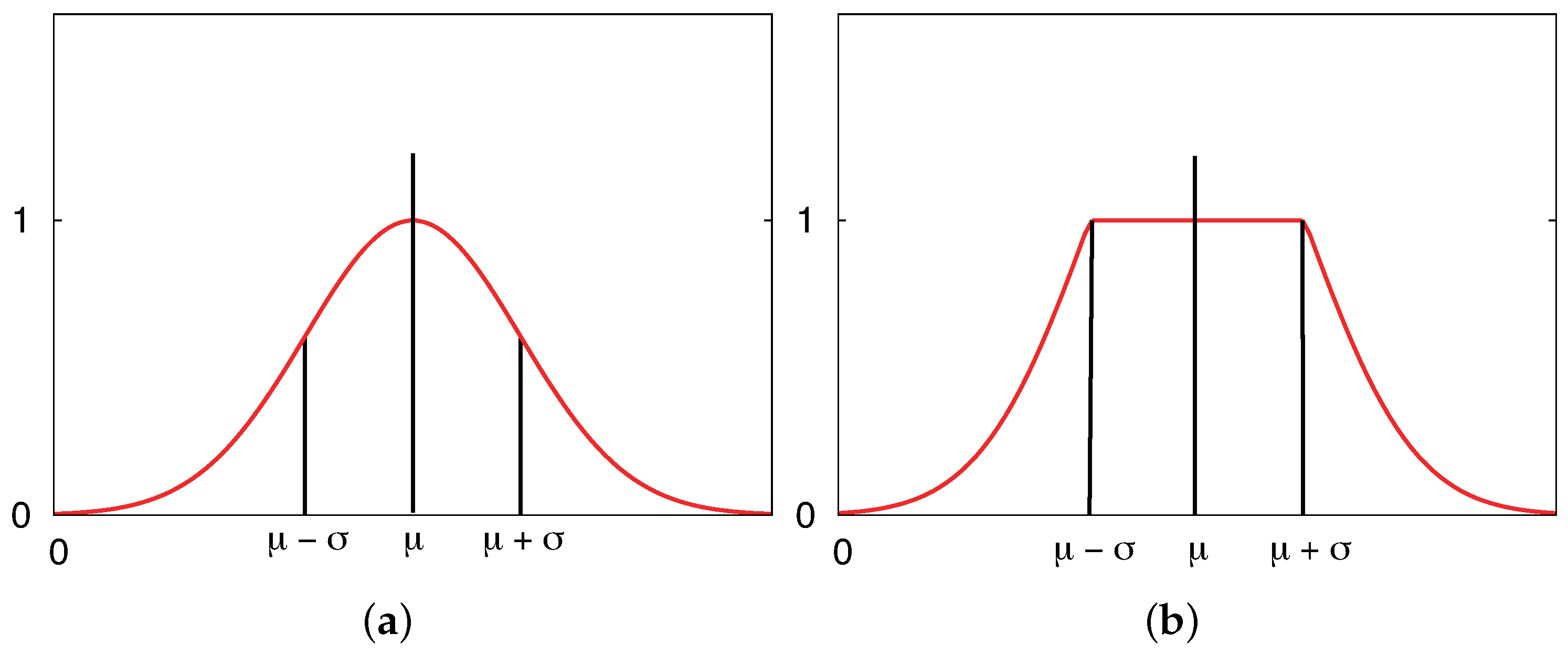
This paper proposes a novel configuration of a high frequency (HF)-band RFID system that employs fewer RFID readers, has a low density of passive tags and a low production cost and that maintains the self-localization accuracy. We find through experiments with real robots that the measurement model of the RFID system cannot be modeled by using a Gaussian distribution if the antenna is enlarged in size. We show that a likelihood function that considers the antenna size contributes to the accuracy of the self-localization. The key contributions of this study are as follows.
A novel particle reinitialization method based on MCL is proposed to enable rapid self-localization.
A likelihood function that considers the antenna size is proposed for accurate self-localization.
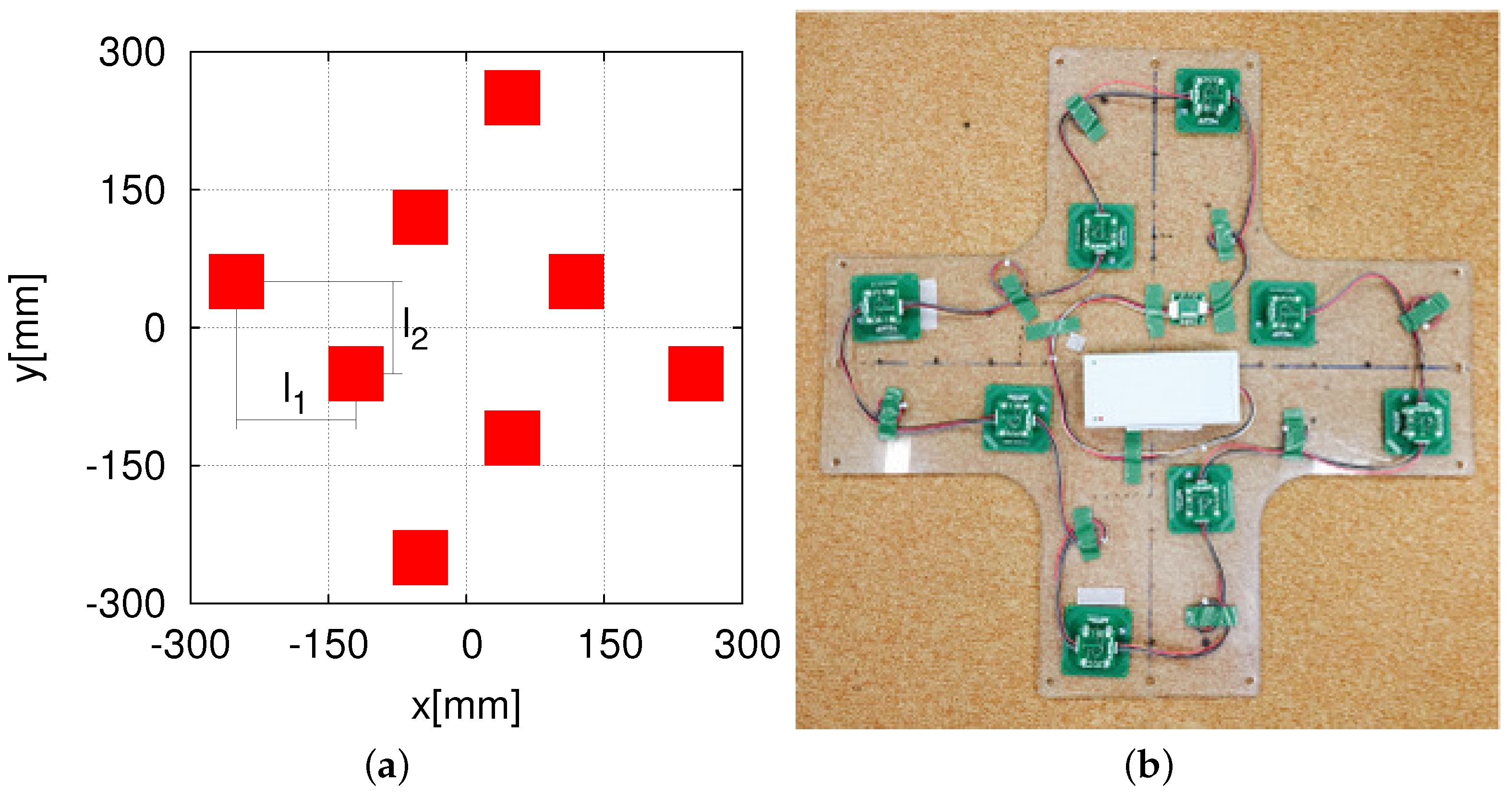
An HF-band RFID system with eight RFID readers placed in a new arrangement is developed by increasing the antenna size of the RFID reader.
Eventually, the proposed RFID system provides highly robust self-localization of an indoor mobile robot at low production cost.
2. Related Works
A basic RFID system consists of three components, a transceiver (commonly known as the RFID reader), a transponder (commonly known as the RFID tag) and an antenna. Depending on the communication method, RFID systems can be divided into two types. One type uses radio waves, and the other uses electromagnetic induction for communication between the transceiver and the transponder. Ultra-high-frequency (UHF)-band and super-high-frequency (SHF)-band RFID systems are based on the use of radio waves, which can realize long distance communication. HF-bandand low-frequency (LF)-band RFID systems use electromagnetic induction. The communication distance of HF-band and LF-band RFID systems is shorter than that of a UHF-band or SHF-band RFID system; however, an HF-band or LF-band RFID system is much more stable and accurate for tag detection and more robust against obstacles in the environment and environmental changes. LF-band, HF-band or UHF-band RFID systems have already been utilized for mobile robot self-localization. Details of related works on robot self-localization works are listed in
Table 1.
Miguel Pinto et al. [
18] used an omnidirectional camera and LRF sensors to realize robot self-localization. Their self-localization system performed well, and the average self-localization was less than 80 mm. However, in general, vision sensors suffer from the problem of illumination changes, and LRF sensors are unable to accurately locate the robot when numerous transparent walls are present in the robot’s environment.
Dirk Hahnel et al. [
8] proposed a combination system composed of a UHF-band RFID reader and an LRF. They used a probabilistic measurement model for RFID readers to locate RFID tags. In their system, two RFID reader antennas were installed on the robot, and tags were attached to walls, furniture, etc. The RFID system was used only to compensate for the global positioning of the localization based on the LRF. Then, the accuracy of their system was dependent on the LRF-based self-localization system, which is sensitive to the condition of unexpected obstacles in the robot’s environment. It is preferable to construct a single RFID system without any other sensors, which can be used in a dark environment or in an environment containing several transparent walls, such as in hospitals and other public facilities.
Lei Yang et al. [
19] proposed a hybrid particle filter method for object tracking using a UHF-band RFID system. This method is more computationally efficient than the particle filter while providing the same accuracy. The limitation of their system is that it can locate only the position of the robot and cannot estimate its orientation. However, for autonomous navigation of indoor mobile robots, high accuracy localization of the position and orientation of the robot is necessary. The UHF-band RFID system of Lei Yang [
19] realized self-localization with an error of about 186 mm, in contrast to the much higher accuracy of localization of the position and orientation achieved in our previous work, where we propose the use of a novel particle reinitialization method based on MCL to enable rapid self-localization. Instead of using the conventional Gaussian function (i.e., Gaussian model) as the likelihood model, we newly design a likelihood model that is a combination of the Gaussian distribution and the step function, which can improve the self-localization accuracy.
Both Park et al. [
13] and Han et al. [
14] proposed HF-band RFID systems for self-localization. Park et al. [
13] used only one RFID reader antenna in their system. However, it is difficult to estimate the orientation of the robot with only one reader antenna. Han et al. [
14] proposed a new triangular pattern for arranging the RFID tags on the floor, instead of the conventional square pattern, and they achieved accurate localization with an localization error of about 16 mm. However, their system suffers from the same problem as that of Park et al. [
13] because it also uses only one RFID reader. A common approach to solving this problem is to combine these systems with other sensors [
20,
21]. They developed a new localization method that uses trigonometric functions to estimate the position and orientation with only one RFID reader. Unfortunately, the system they developed cannot ensure the reliability of localization, especially when the robot moves quickly or when no tags are detected. HF-band RFID systems have also been utilized for object pose estimation [
22] or communication robots [
23]; however, the objectives of these works were different from those of our study.
Yang et al. [
24] used one HF-band RFID reader with a large antenna size of 660 × 300 mm
. They derived an exponential-based function to reflect the relationship between RFID tag distribution and localization precision. They proposed an approach of using sparsely-distributed passive RFID tags. They used a simple and efficient localization algorithm proposed by Han et al. [
14]. The RFID system with sparse RFID button tag distribution patterns realized better localization with precisions of about 36 mm and 38 mm in the
x direction and
y direction, respectively. However, this system was unable to realize real-time localization. The robot stayed for 40 s at each point for localization. In addition, the system could not estimate the orientation of the robot. Furthermore, installation of their sparse RFID tag distribution patterns in an indoor environment was difficult. Yang and Wu [
25] proposed a particle filter algorithm using a position-information-based straight observation model and a 2D Gaussian-based motion model to locate the robot. They used a dense tag distribution. Other experimental conditions in their study were the same as those in Yang et al. [
24]. They set the localization accuracy as 100 mm and the localization precisions of about 27 mm and 46 mm in the
x direction and
y direction, respectively. However, their system suffers from the same problems as did that of Yang et al. [
24]. In the present research, we designed a novel HF-band RFID system with eight RFID readers having an appropriately-sized antenna to eliminate uncertainties and to realize real-time position and orientation localization.
Mohd Yazed Ahmad et al. [
26] proposed a novel triangular-bridge-loop reader antenna for positioning and presented a method for the improvement of HF-RFID-based positioning. They used an HF-band RFID reader with a large-sized antenna having dimensions of 320 × 230 mm
, which was designed with a novel triangular-bridge-loop. In their system, passive RFID tags were sparsely distributed at a distance of about 1300 mm. Their system performed quite well and achieved an average positioning error of 40.5 mm, in contrast to the average positioning error of 124.1 mm in the case of a system employing a conventional reader antenna. However, their system has a limitation in that the speed of the robot is set to be consistent to ensure successful reading of the tags by the reader. If the robot moves faster, a faster reader and tag are required. If the robot moves slower or if an emergent circumstance occurs where the speed is required to be reduced, the system may not detect tags for a long time, as the distance between two tags is 1300 mm. Under this condition, only encoder data can be used for localization, which could make the localization difficult. In our proposed RFID system, there is no such speed limitation. We validate our proposed RFID system at various speeds and, thus, demonstrate its overall efficiency.
An LF-band RFID system for indoor mobile robot self-localization has been proposed in some studies [
12,
27]. For example, Kodaka et al. [
12] used a vehicle equipped with two RFID readers. In their study, RFID tags were installed on the floor, and the size of one tag was 260 × 260 mm
. The distance between adjacent tags was 300 mm. The MCL method was used for robot self-localization, and the localization error was less than 100 mm and 0.1 rad on average. Unfortunately, despite developing an active self-localization method [
28], the researchers faced difficulty in increasing the localization accuracy given the dependence on the size of a tag. The communication range of RFID readers also affects the accuracy of self-localization.
Takahashi et al. [
15] proposed an RFID-based self-localization system having eight RFID reader antennas at the bottom of the robot. In this system, the RFID tags were arranged in a lattice pattern, and a simple kinematics was used to localize the robot. The accuracy of self-localization was highly dependent on the density of the RFID tags. With eight RFID reader antennas and small-sized high-density RFID tags (100 tags/m
), the localization error was less than 17 mm and 0.12 rad on average. However, if the reader failed to read the tag, the error became relatively large, and the system faced a problem of latency in scanning the tags given that scanning needs to be performed by one antenna after another. Therefore, the system became unstable at high speeds. Takahashi and Hashiguchi [
16] developed a new mobile robot self-localization system using MCL based on the HF-band RFID system. This system included 96 RFID readers, and the density of the RFID tags was 100 tags/m
. They compared the performances of self-localization with an RFID system only and with an RFID system equipped with LRFs and found that in the absence of obstacles, both RFID systems were able to locate the robot accurately. However, in the presence of obstacles around the robot, the system using LRFs could not locate the robot accurately and stably, which demonstrated the efficiency of the RFID system used alone.
The limitation of their system is its high production cost. It is then necessary to redesign the system, reduce the number of RFID readers, use a low density of RFID tags and establish an efficient configuration of the system to cut down its production cost.
3. Self-Localization of an Indoor Mobile Robot by Using an RFID System with MCL
MCL, one of the probabilistic approaches [
17], has been shown to be a good method for real-time self-localization of robots. Takahashi and Hashiguchi [
16] applied MCL to their RFID-system-based self-localization. It is assumed that an RFID tag has a unique ID and that the tag ID map is maintained with the position of each tag. RFID readers work independently and asynchronously of each other. We briefly introduce the MCL using the RFID system [
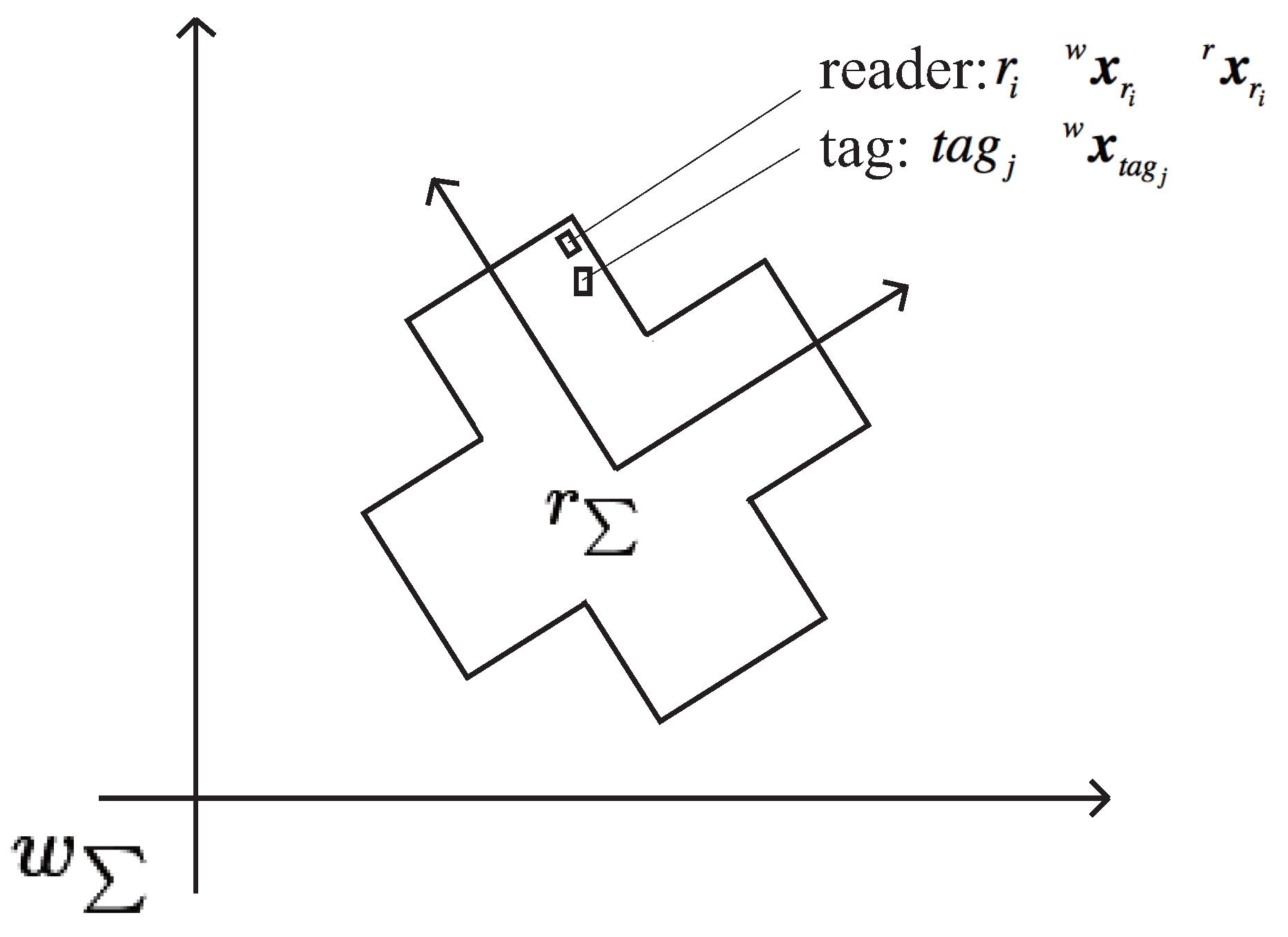
16] here. We define the world coordinate system
and the robot coordinate system
as shown in
Figure 2. The robot position and orientation is defined in the world coordinate system at time
t as
.
is the measurement output at time
t, and
is the tag detected with the RFID reader
. A motion model
is defined to estimate the next robot position and orientation of the robot,
from
. A measurement model
is also defined to calculate the posterior probability to receive the measurement output
if the robot position and orientation are
. A set of particles is defined as a set of hypotheses of the robot position and orientation denoted at time
t as
, where
M is the number of particles. The algorithm of MCL is given in Algorithm 1. The self-localization system updates the particles with a fixed sampling time
. If no RFID reader detects a tag within the sampling time, the procedure of belief calculation (Step 4 in Algorithm 1) is skipped.
The motion model of an omnidirectional vehicle is given by Equation (
1):
where
,
and
denote the velocity of the robot, sampling time and Gaussian distribution with the standard deviation
, respectively.
The position of
detected by RFID reader antenna
in world coordinates is
. The position of RFID reader
at time
t in world coordinates
is estimated by Equation (
2):
where
is the position of the RFID reader antenna
in the robot coordinate system and it is known in advance. We assume
and
to be constant.
| Algorithm 1 Monte Carlo localization. |
| 1: | Initialize particles |
| 2: | for to M do |
| 3: | Update particles with the motion model: |
| 4: | Calculate the belief of each particle with the measurement model: |
| 5: | |
| 6: | end for |
| 7: | for to M do |
| 8: | draw from with probability ∝ |
| 9: | add to |
| 10: | end for |
| 11: | for to M do |
| 12: | if (a constant), re-initialize |
| 13: | end for |
| 14: | return |
Then, the weight of each particle,
, is calculated using the measurement model
.
is a likelihood function defined in
Section 5. After the weights
are calculated, the algorithm estimates the position of the robot as the weighted mean of the particles.
As shown in Steps 7–10 of Algorithm 1, particles are updated with a probability proportional to the weight .
Particle Reinitialization
In conventional studies, in scenarios where the initial position of the robot was unknown or the weights of all particles became too small during the transportation because of an unexpected disturbance in the robot’s movement, the particles were distributed uniformly randomly in the possible exploration space. However, it is obviously undesirable to distribute the particles uniformly if the possible exploration space is too large. Once the robot detects one of the tags, it can narrow down its own possible position immediately according to the position of the detected tag and the reader that detects it.
Figure 3 shows examples of the possible poses of the robot when it detects a tag if its own position is unknown.
We propose a novel particle reinitialization method that is specific to the RFID system and that is aimed at the realization of highly efficient and accurate self-localization. The particle reinitialization process is performed from Step 11 onward in Algorithm 1. Once
becomes too small for the robot’s self-localization, particles
will be reinitialized as given in Equation (
4):
where
is generated using a uniform random function from
to
π. The re-sampling indicates that the robot is at a position where the RFID reader
is just above the detected tag
. The proposed re-sampling leads the self-localization system to localize the robot itself quickly and stably because it can eliminate unnecessary particles distributed over the possible exploration space. In our research, the number of particles is set as 500.
6. Experiments in a Real Environment
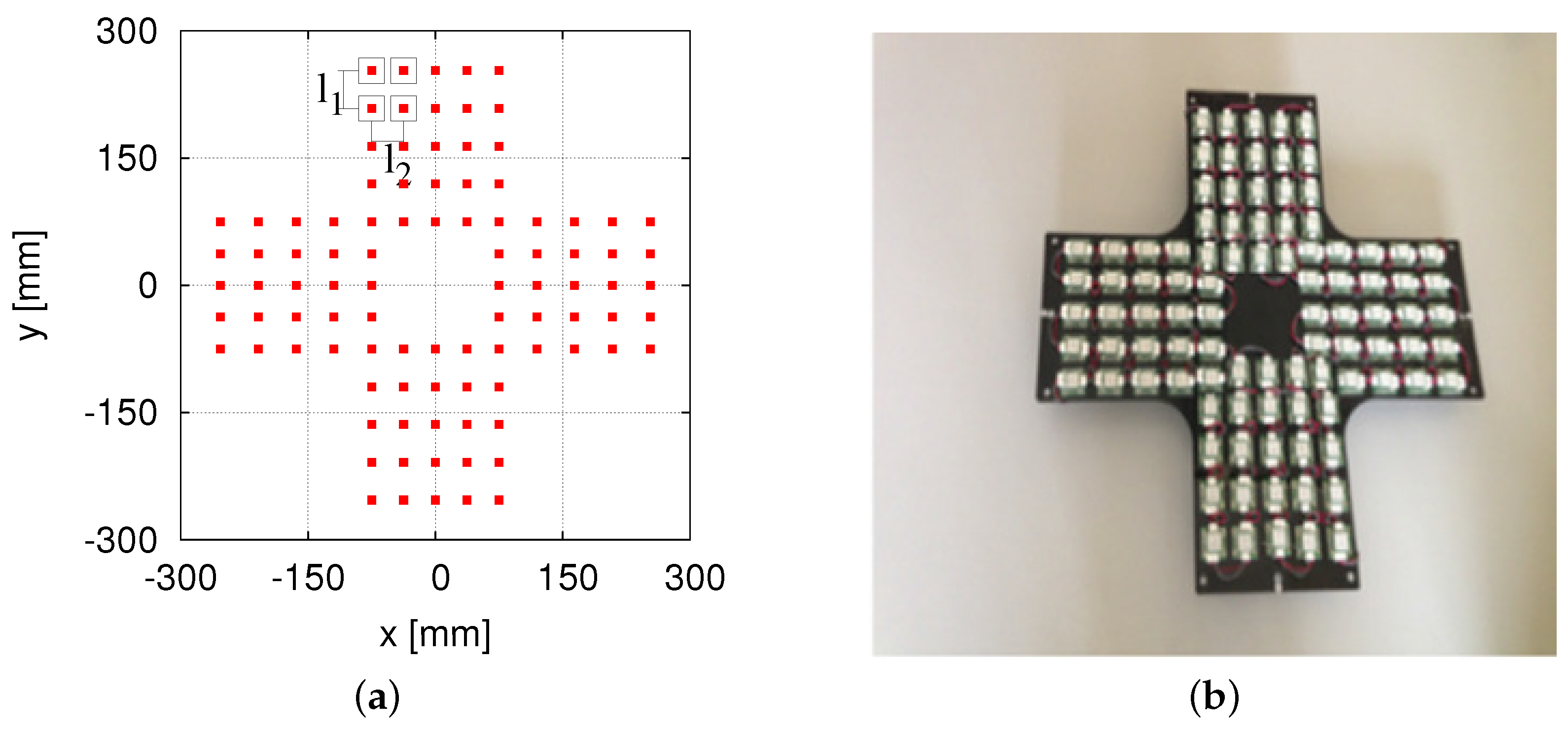
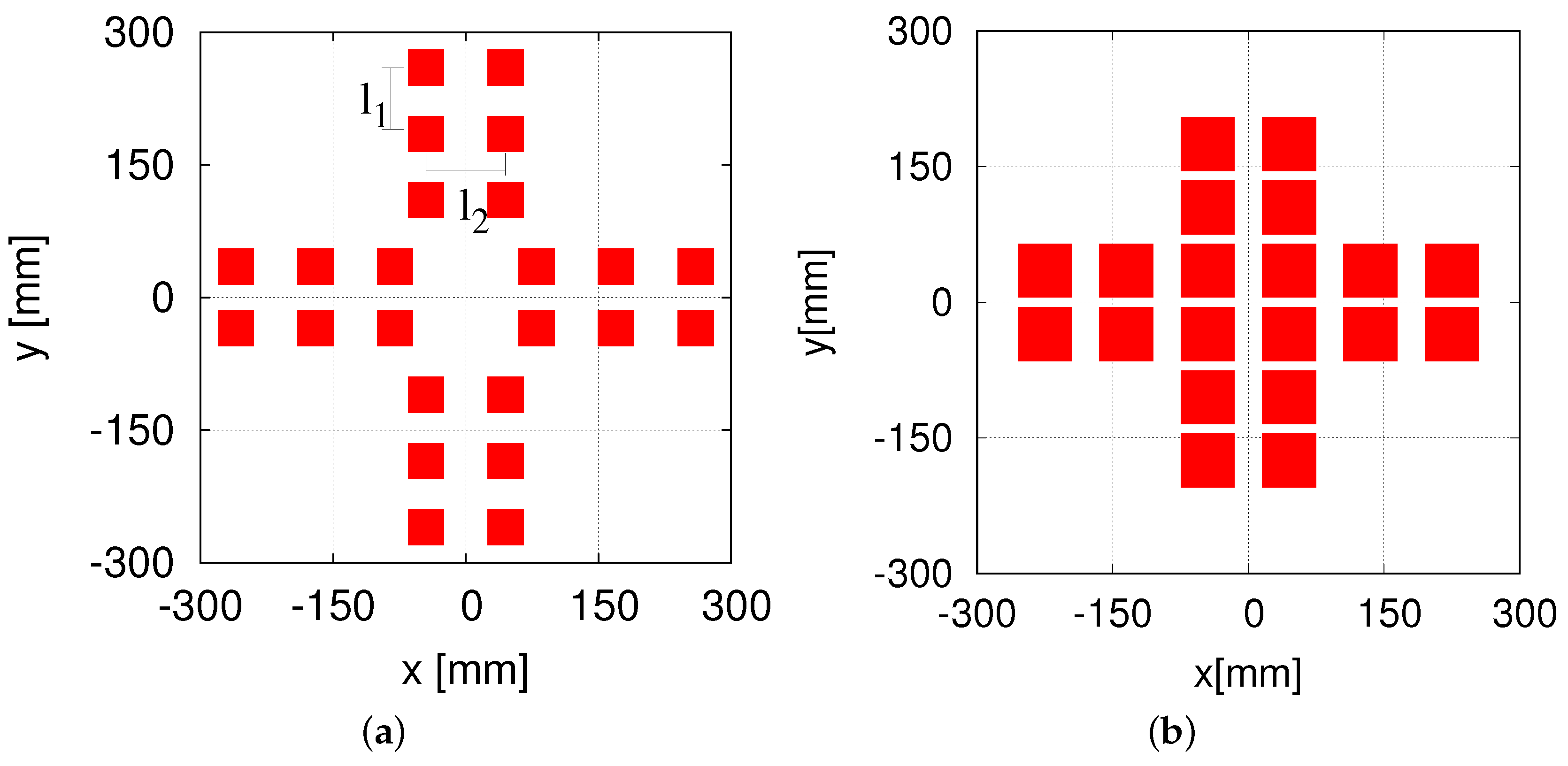
The eight RFID reader system (
Figure 6) was attached at the bottom of our omnidirectional vehicle, as shown in
Figure 12. As mentioned earlier,
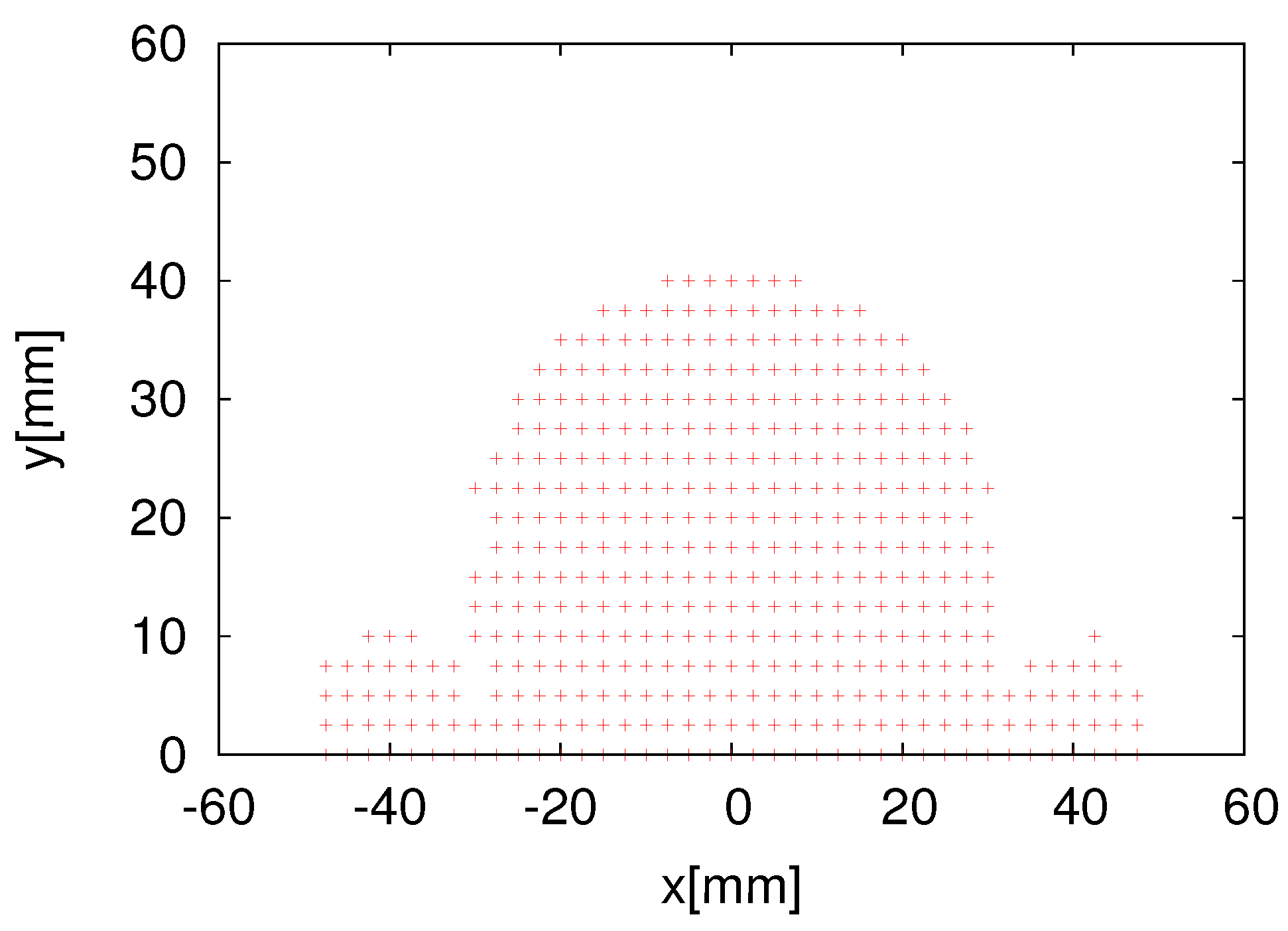
Figure 9 shows the tag detection area of one RFID reader antenna of the eight HF-band RFID reader system, and
Figure 10 shows the cross-sectional view of the tag detection area and the success rate at heights of 15 mm and 20 mm.
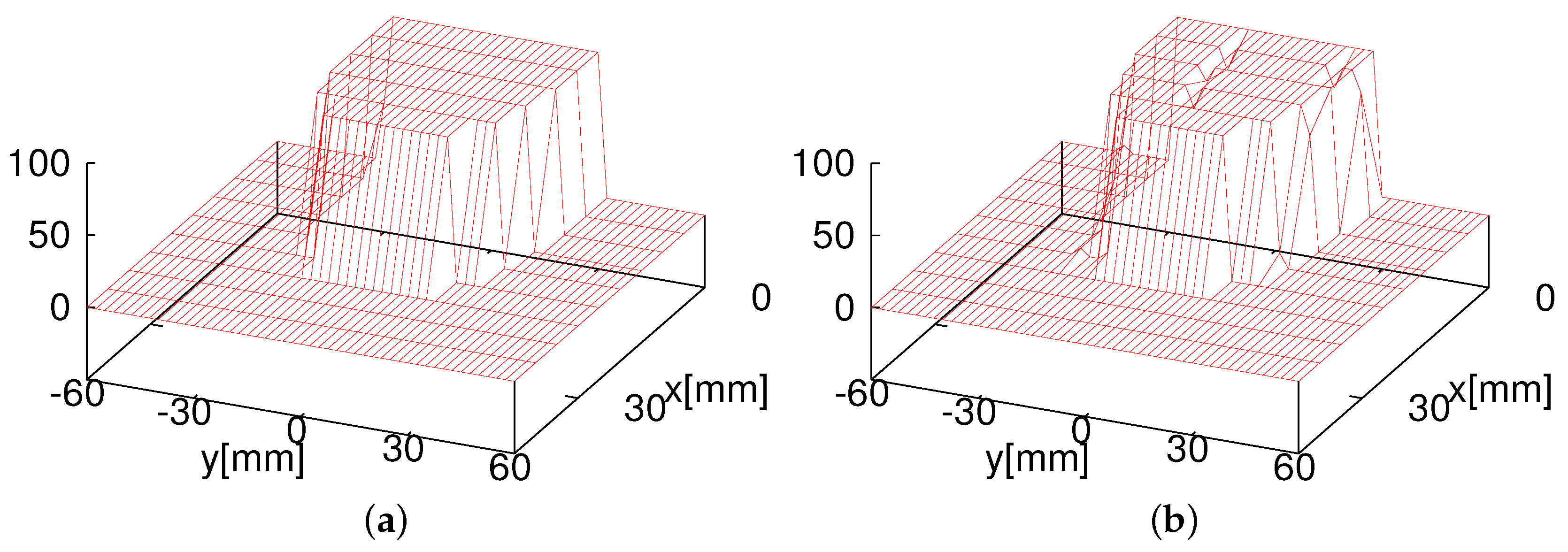
Figure 10 demonstrates that the combination likelihood model is more suitable than the Gaussian likelihood model at the heights of 15 mm and 20 mm. This also proves our hypothesis in simulations that the combination model performs better than the Gaussian model. Next, we verified whether or not the combination model performs better than the Gaussian model in a real environment.
As shown in
Figure 13a, we verified the eight HF-band RFID reader system using the two different likelihood models in the real environment. The height of the readers was set as 15 mm because the reader antenna has a better tag detection success rate.
The speed of the robot was set as 100 mm/s. The eight RFID readers and the 96 RFID readers detected ID tags every 50 ms. The frequency of the eight RFID readers and 96 RFID readers was the same, i.e., 13.56 MHz. ID tags were embedded in the carpet on the floor with densities of 100 tags/m
and 16 tags/m
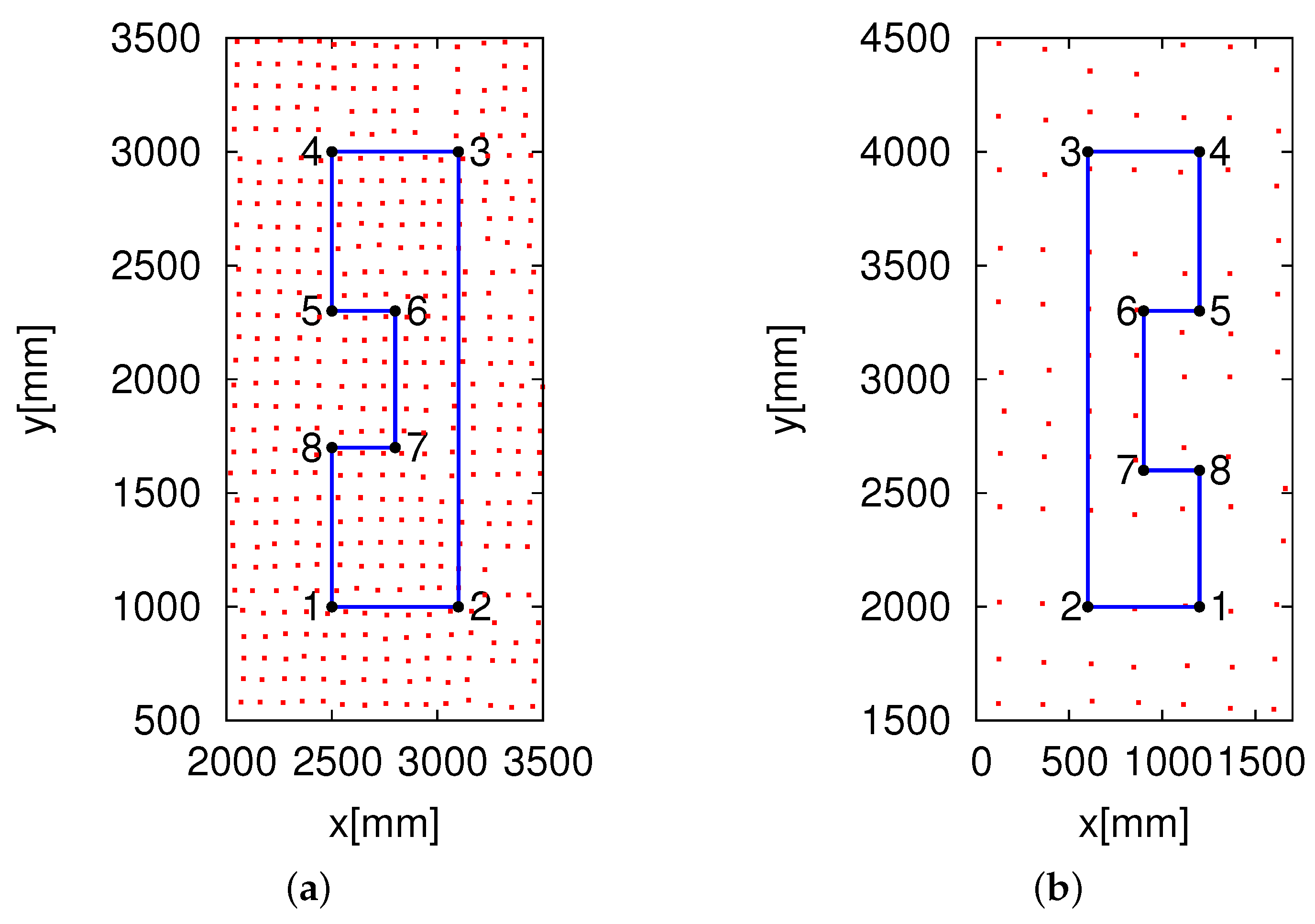
in the lattice pattern. We made the robot run the path shown in
Figure 13, from Point 1 to Point 8. It was difficult to determine the localization error for every position along which the robot moved. To calculate the localization errors, we marked eight points at which the positions were already known, as shown in
Figure 13. The robot stayed for 20 s at each of the eight points to perform self-localization, so that it could collect enough data to calculate the self-localization errors. We first verified our new eight HF-band RFID reader system. We also performed a comparison experiment with the 96 HF-band RFID reader system. To analyze the self-localization errors, we acquired a large amount of data through calculations at the eight points shown in
Figure 13.
The experimental results for the 96 HF-band RFID reader system are presented in
Table 5. At the density of 100 tags/m
, the average self-localization errors are smaller than 15 mm in the
x direction and smaller than 25 mm in the
y direction for both likelihood function models. The comparison of these two likelihood models reveals that in the
x direction, the average self-localization error when using the combination model is 8.2 mm, which is smaller than that when using the Gaussian model. In the
y direction, both the likelihood models perform self-localization with almost the same accuracy, with errors of 22.3 mm and 23.8 mm for the Gaussian and combination models, respectively. At the density of 16 tags/m
, the combination model performs better than the Gaussian model, where, as shown in
Table 5, the average self-localization errors are 26.2 mm in the
x direction and 18.0 mm in the
y direction for the Gaussian model and 17.7 mm in the
x direction and 13.5 mm in the
y direction for the combination model. From these average self-localization errors, it can be said that the self-localization at the density of 16 tags/m
is accurate enough: in the
x direction, the errors at this density are only slightly larger than those at 100 tags/m
, and in the
y direction, the errors at this density are smaller than those at 100 tags/m
. However, the self-localization at this density was not stable, as the maximum errors and variance were very large, as seen in
Table 5. This is because the system could not detect tags at some places when the density of the ID tags became as low as 16 tags/m
. The detection area of one RFID reader is narrow so that the size of the 96 RFID reader antenna is small. Eventually, the self-localization errors increase correspondingly. With the configuration of 96 small RFID readers and the ID tag density of 16 tags/m
, the system is unable to locate the robot stably.
Table 6 presents the results of self-localization errors in the case of the eight HF-band RFID reader system. The results show that the eight HF-band RFID reader system with large antennas performs highly accurate self-localization. As is seen from the table, the average self-localization errors in the case of both of the likelihood models at the density of 100 tags/m
are almost the same. However, as can be seen from the table, even though both of the likelihood models perform well at the density of 16 tags/m
, the combination model performs better than the Gaussian model. The maximum errors and variance at the density of 16 tags/m
are much larger than those at 100 tags/m
; however, the system still maintains stable localization.
From
Table 5 and
Table 6, it can be seen that at the density of 100 tags/m
, the average errors in the
x direction are much smaller than those in the
y direction. At the density of 16 tags/m
, the average errors in the
x direction are larger than those in the
y direction. As the arrangement of the RFID reader antennas is the same in both the
x and
y directions, we consider that these differences in average errors were caused by the ID tag installation. Because it is difficult to ensure the installation of every two adjacent tags at the same interval, the installation errors cannot be prevented.
From a comparison of the two RFID systems, we found that both systems performed highly accurate self-localization at the density of 100 tags/m and that there was only a slight difference in the average self-localization errors when the combination model was used. The eight HF-band RFID reader system performed slightly better than the 96 HF-band RFID reader system. The difference between the two RFID systems was that the eight HF-band RFID reader system could locate the robot accurately and stably under the condition of using a low density of ID tags, 16 tags/m, whereas the system with the 96 small RFID readers could not. This is because the eight RFID readers are equipped with enlarged antennas in order to widen the tag detection range of a single RFID reader. The efficient RFID readers of the two RFID systems that detect ID tags are almost the same. Moreover, we used MCL for self-localization, which could enable the robot to be located precisely even if only one or two tags were detected. The experimental results demonstrate the efficiency of our newly-developed eight HF-band RFID reader system with large antennas. This system performs robot self-localization stably and accurately, which proves that eight RFID readers with large antennas, instead of 96 RFID readers, can provide sufficient self-localization accuracy for robot localization. Moreover, because we use eight RFID readers, the production cost of the system can be reduced significantly in comparison to that of the 96 HF-band RFID reader system.
Trajectory of Real-Time Self-Localization
To verify the real-time self-localization performance of the developed eight HF-band RFID reader system, we obtained the statistics of the real-time localization of the robot.
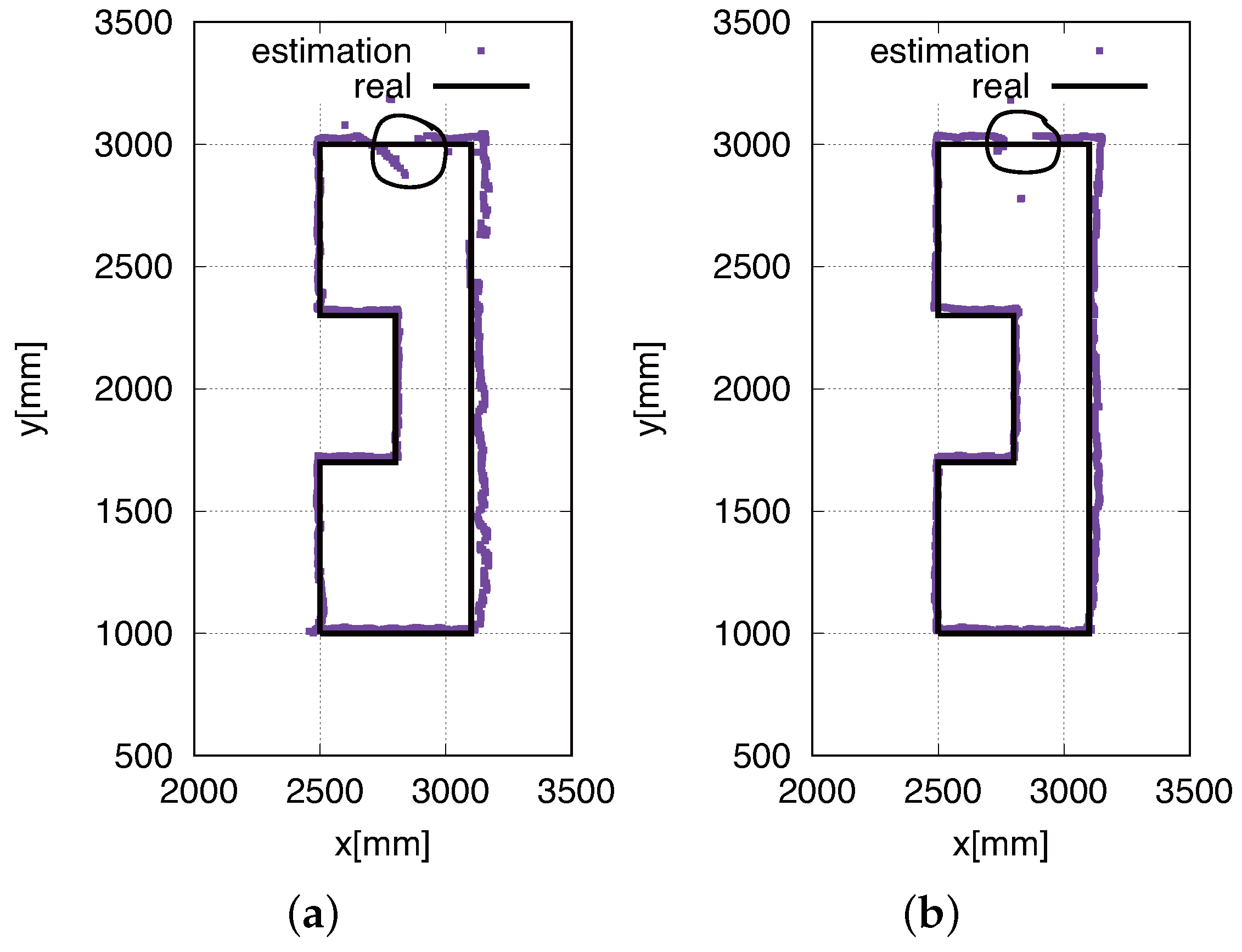
Figure 14 shows the trajectories of our proposed eight HF-band RFID reader system.
Figure 14a shows the real-time self-localization trajectory obtained using the conventional Gaussian model, whereas
Figure 14b shows that obtained using our proposed likelihood model. The comparison of
Figure 14a,b reveals that the proposed likelihood model works better than the conventional method employing the Gaussian model. As seen in both figures,
Figure 14a,b, the robot could not perform high-accuracy localization in the area indicated by the circle. This is because the system could not detect ID tags, since they had an installation error. On the other side, our eight RFID reader antenna is small; once tags are distributed in the gap of the detection area, the system could not detect tags. The reader detection area is shown in
Figure 9, and the installed RFID tags are shown in
Figure 13.
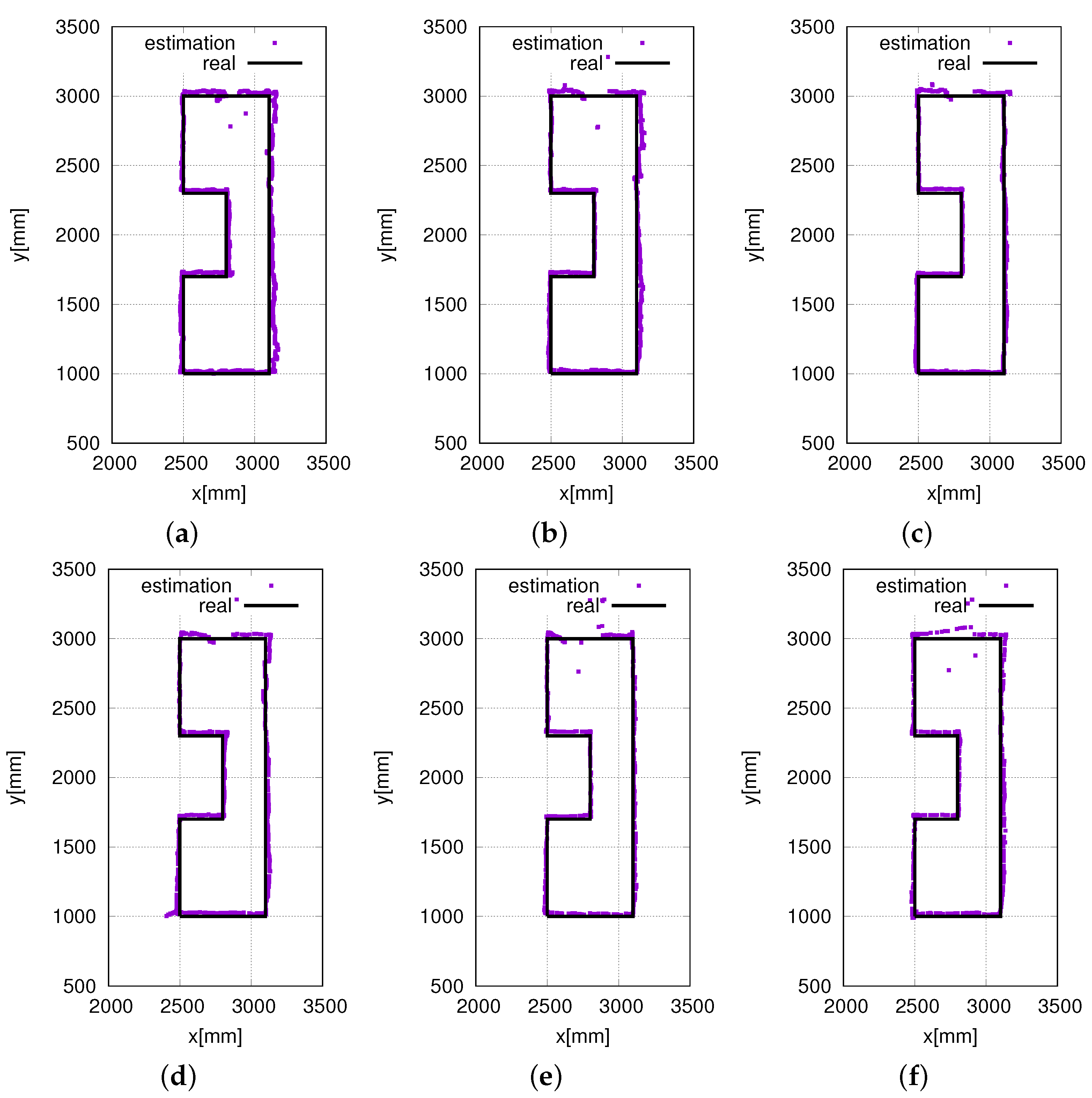
In our experiments, we also validated the performance of the proposed eight HF-band RFID reader system at different speeds.
Figure 14b shows the real-time localization at a speed of 100 mm/s.
Figure 15 shows the real-time localization at speeds in the range of 50 mm/s to 350 mm/s at intervals of 50 mm/s. From
Figure 15a to
Figure 15f, it is clear that the localization accuracy does not decrease with an increase in the speed. Furthermore, as shown in
Figure 15, to a certain extent, the system even performs better at high speeds. This is because when the robot moves at low speeds, the noise of the motors has a much greater effect on the system performance. In contrast, when the robot moves at high speeds, the noise of the motors has less time to have an effect on the system performance. Above all, the proposed RFID system was able to realize highly accurate and stable localization at various speeds. This proves the efficiency and stability of the proposed RFID system.