Wideband Fully-Programmable Dual-Mode CMOS Analogue Front-End for Electrical Impedance Spectroscopy
Abstract
:1. Introduction
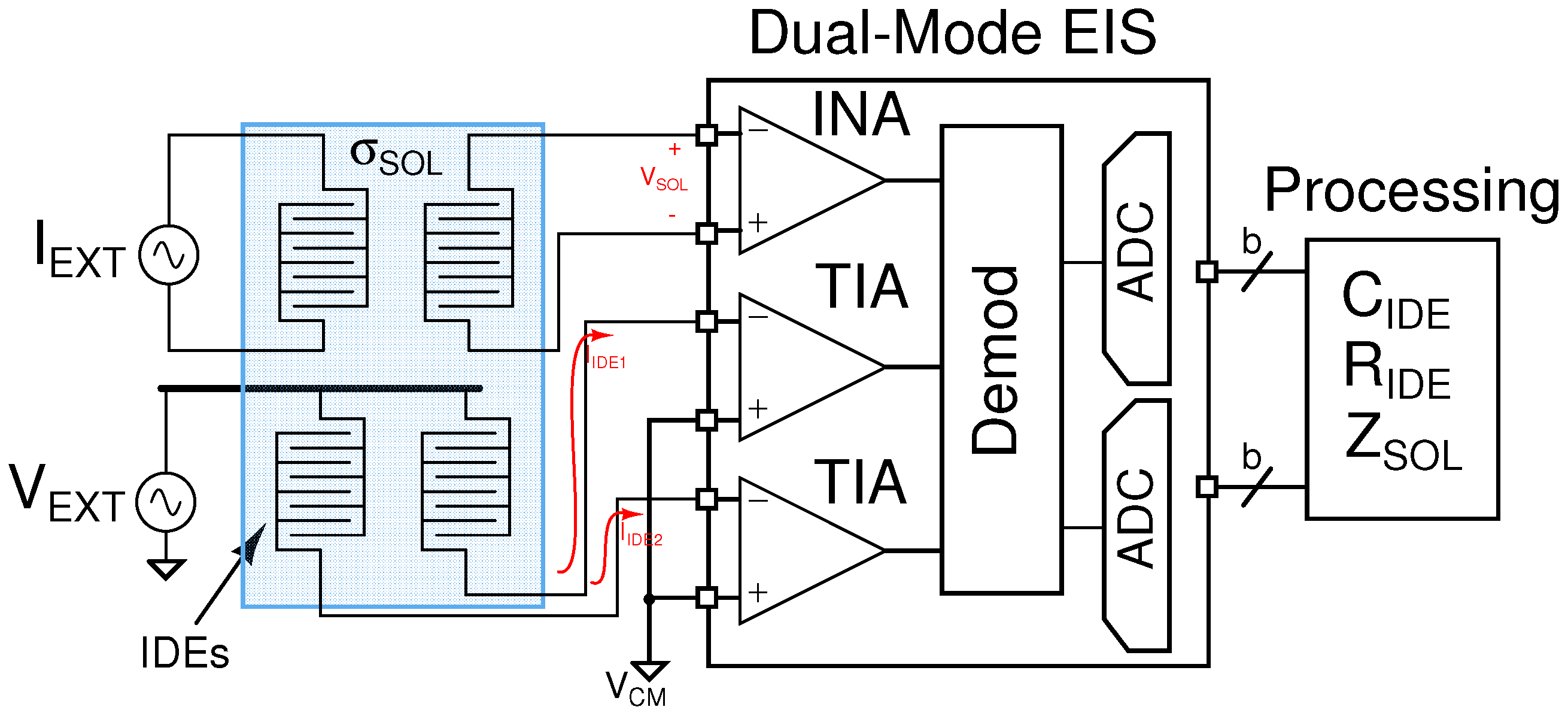
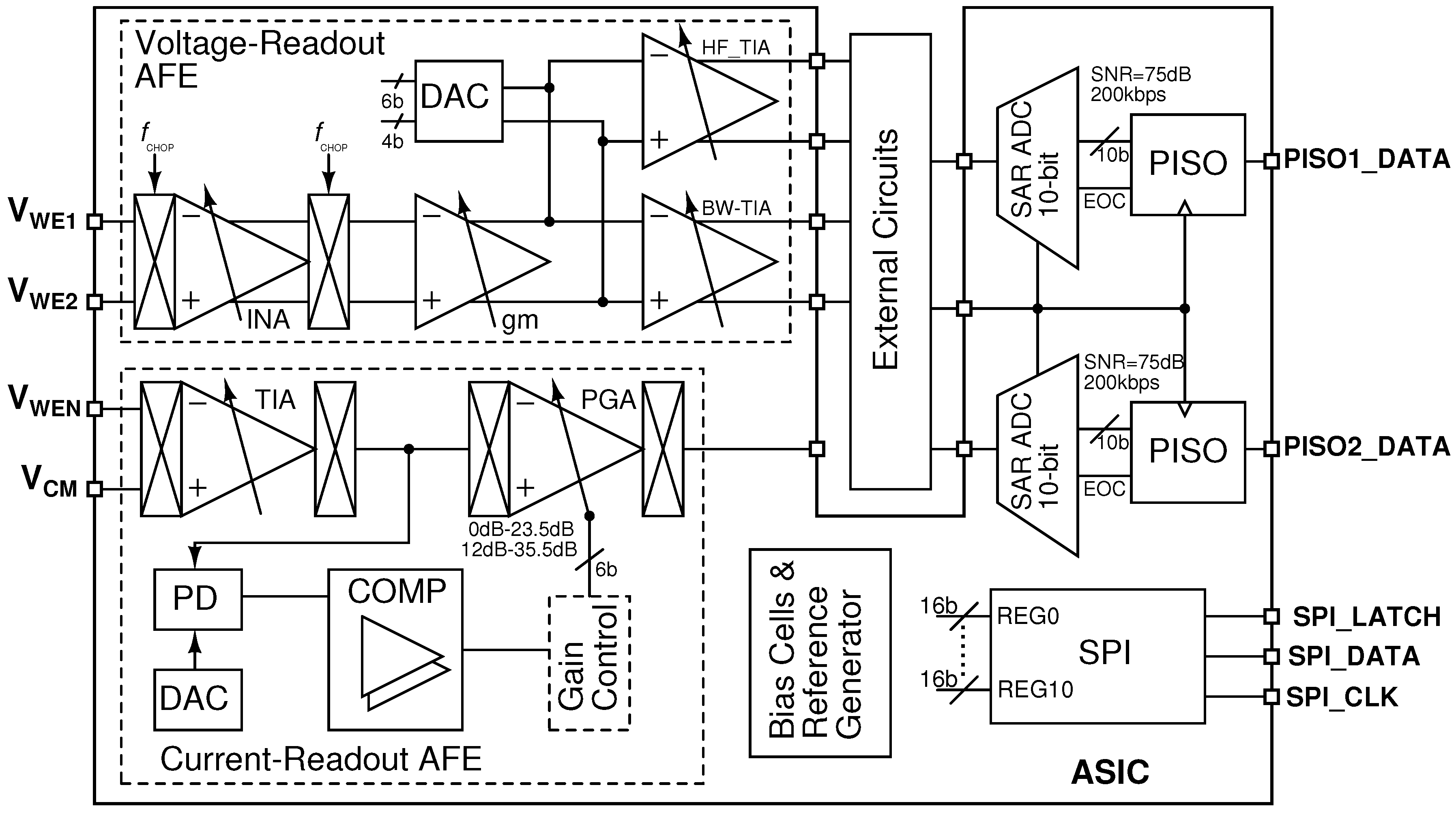
2. Analogue Front-End Chip
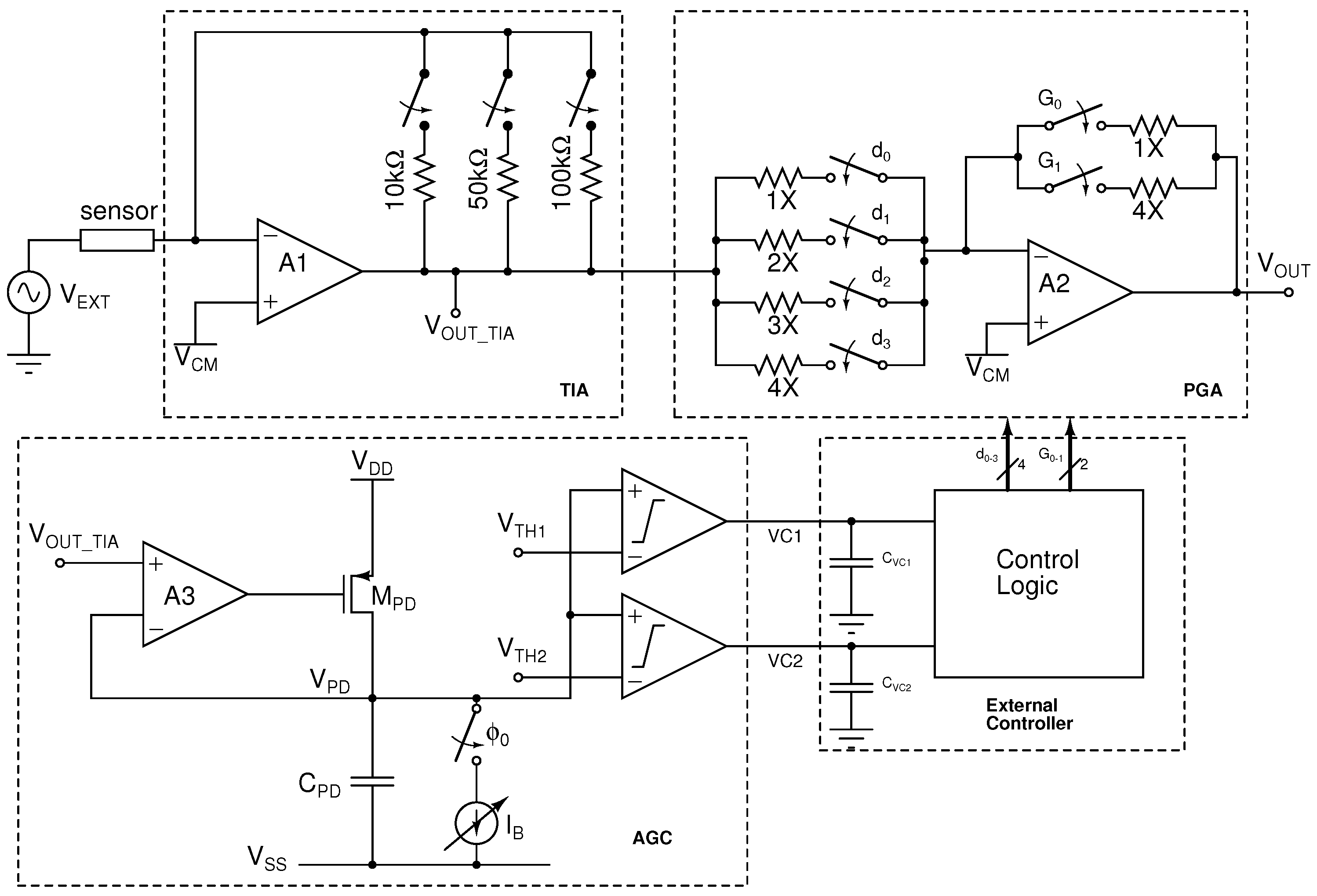
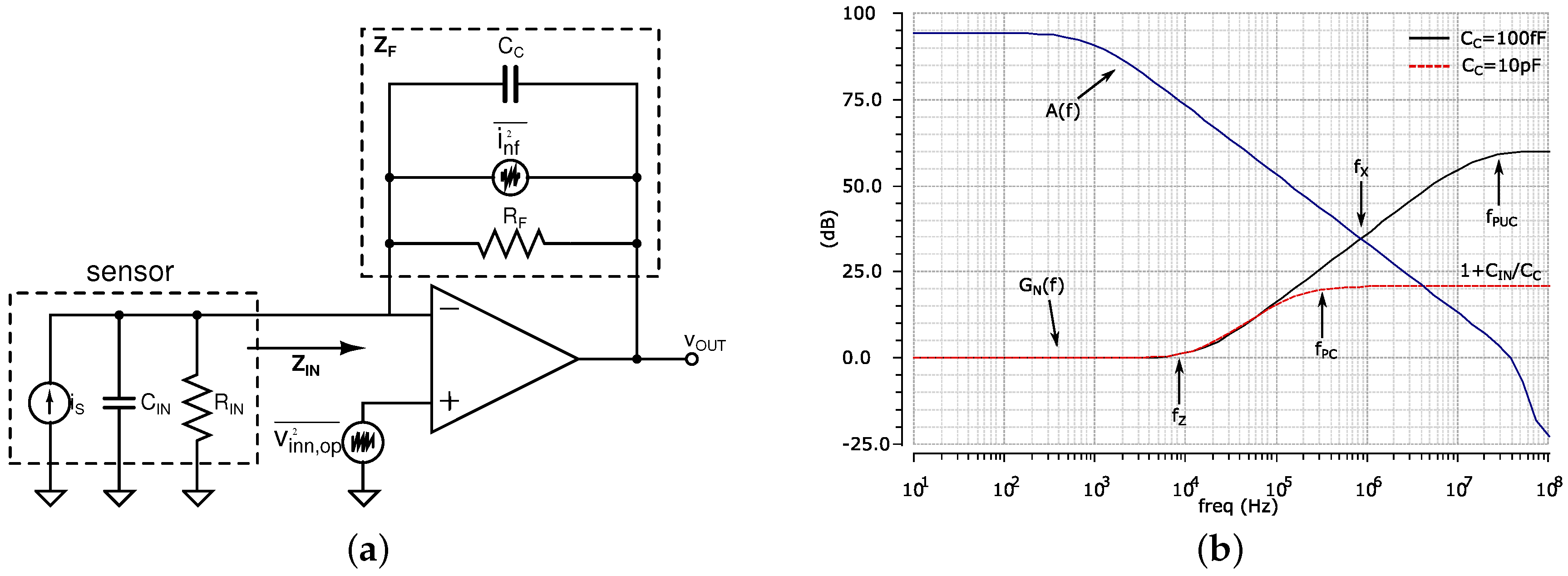
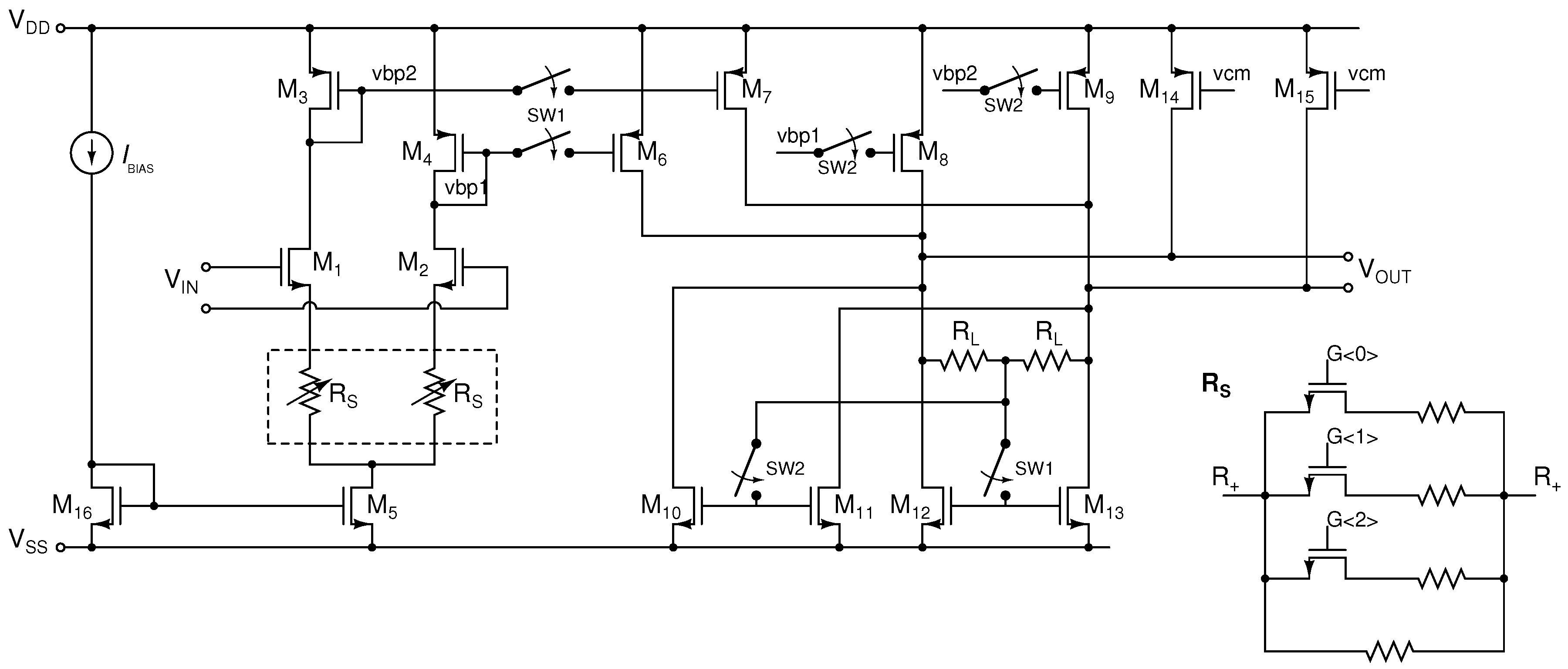
2.1. Current-Readout AFE
2.1.1. TIA Stability
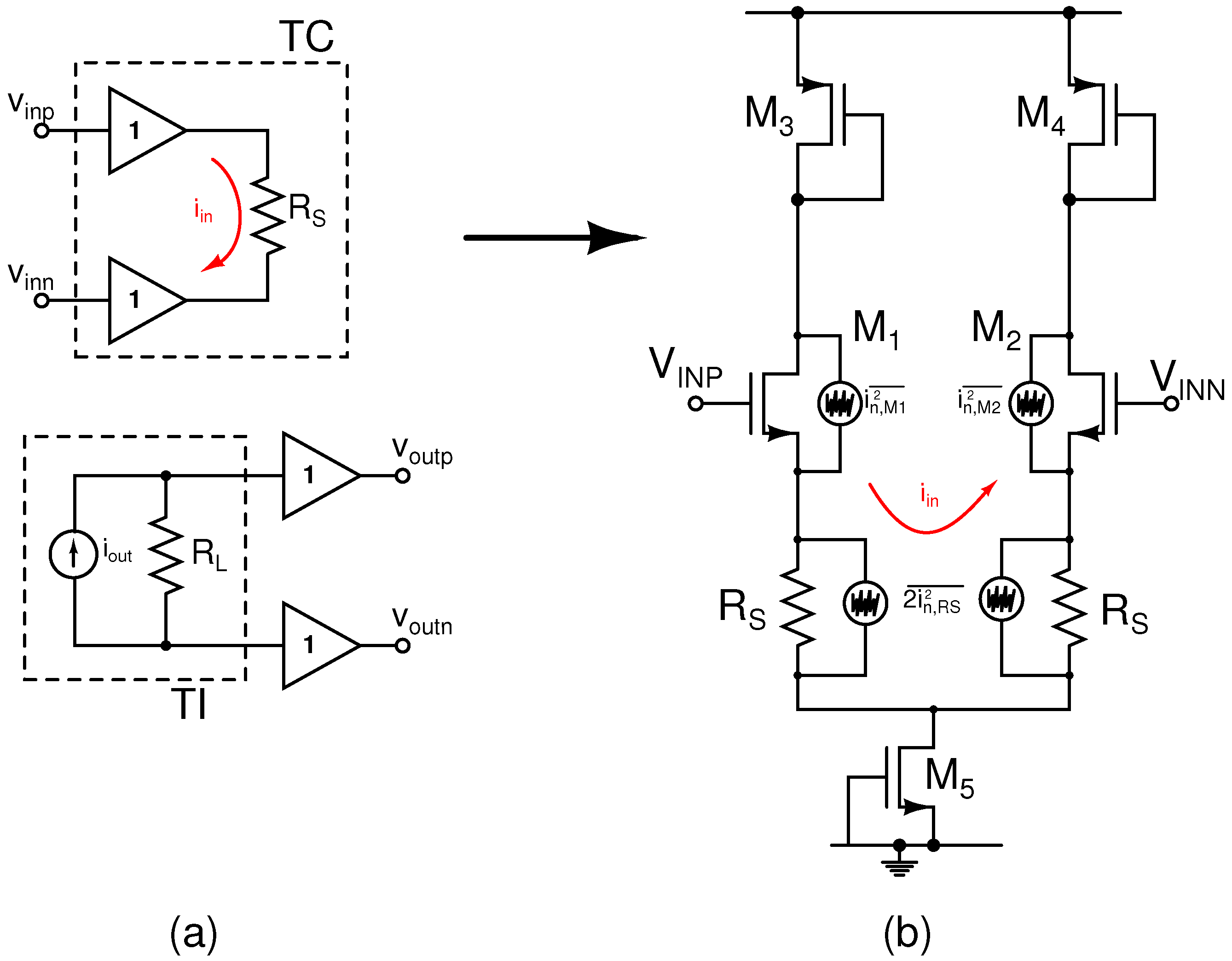
2.1.2. TIA Noise
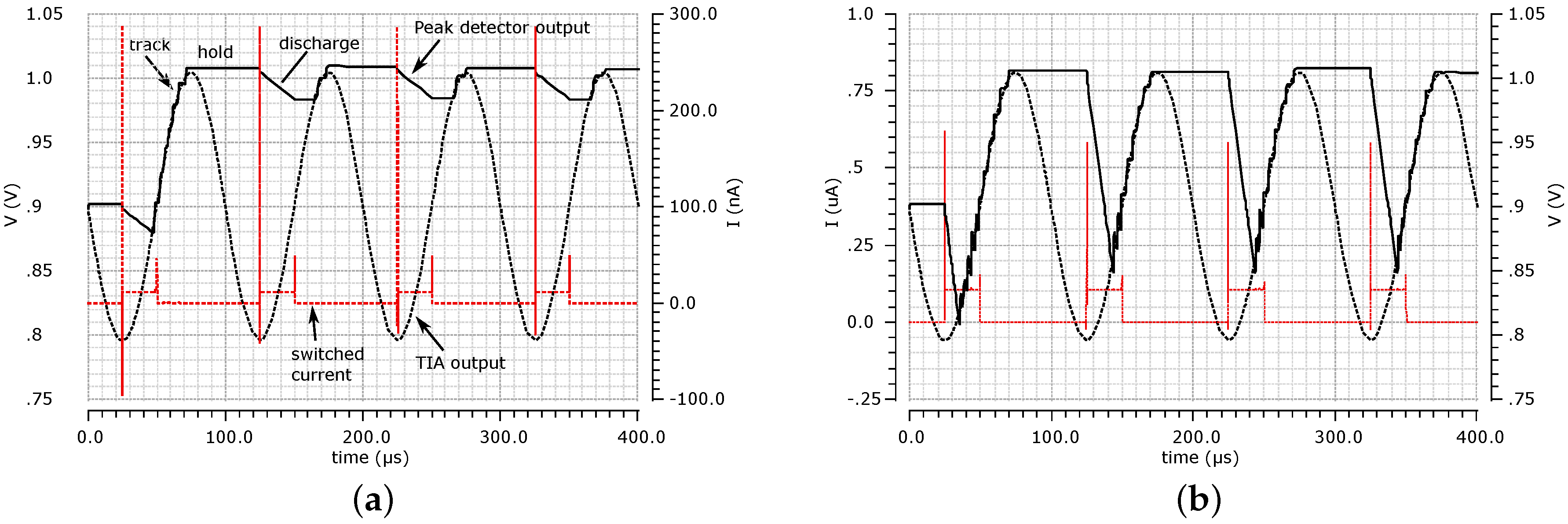
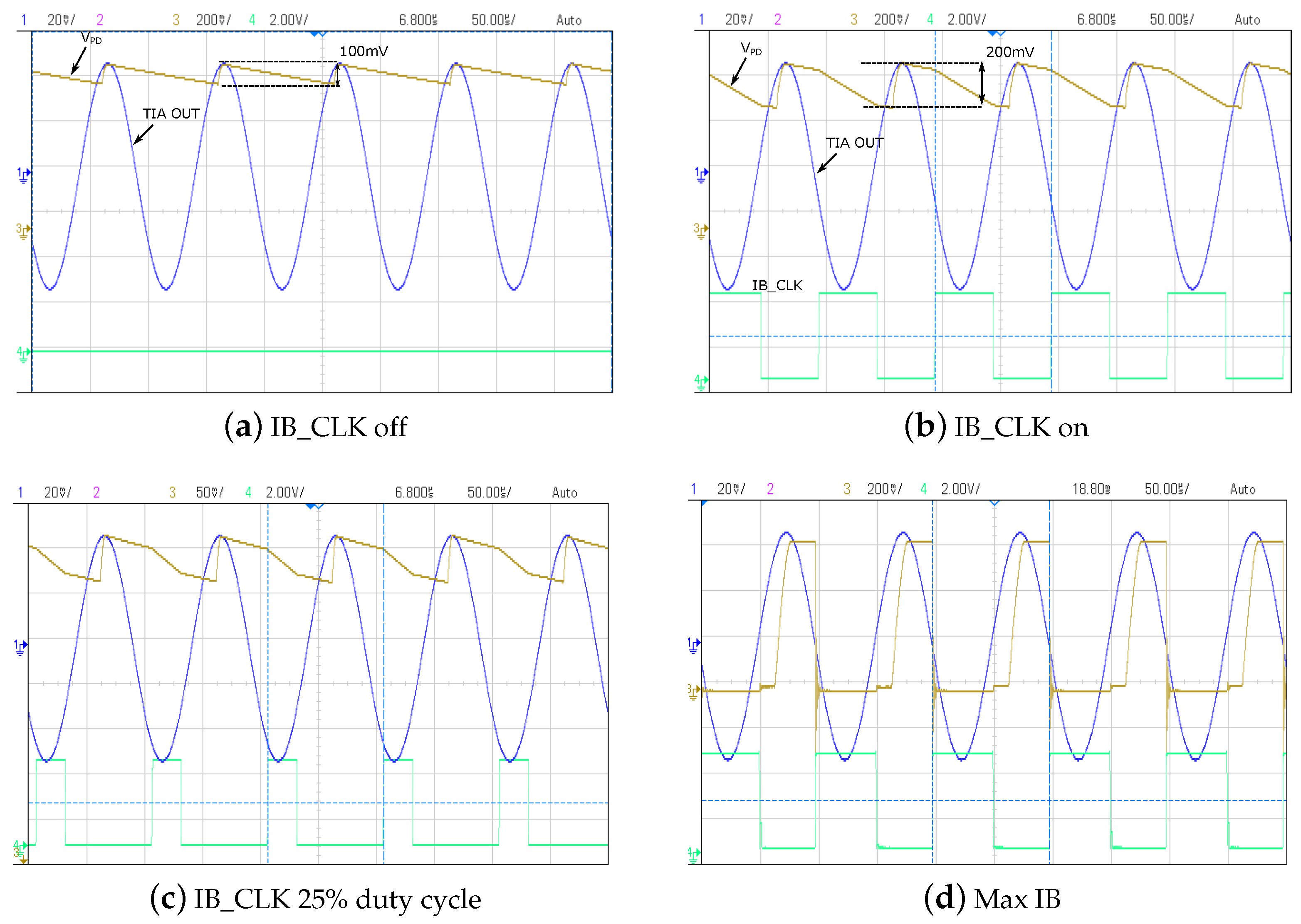
2.1.3. Automatic Gain Control
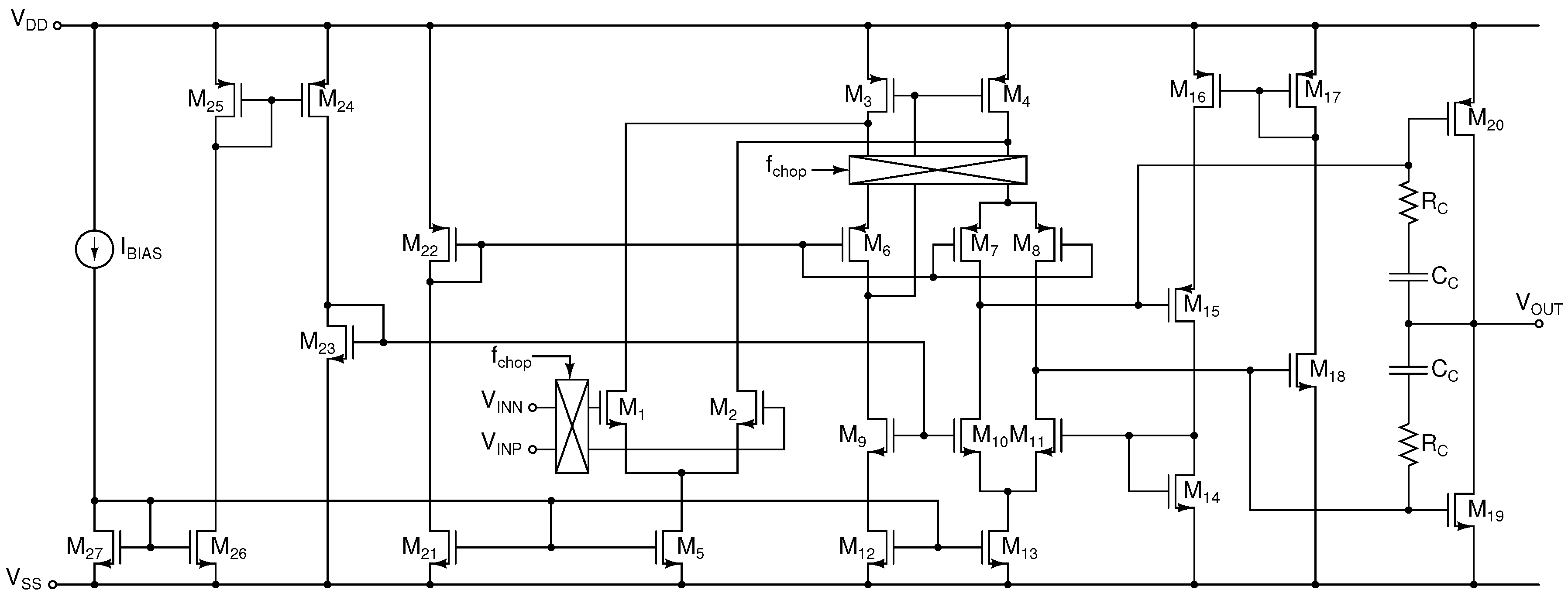
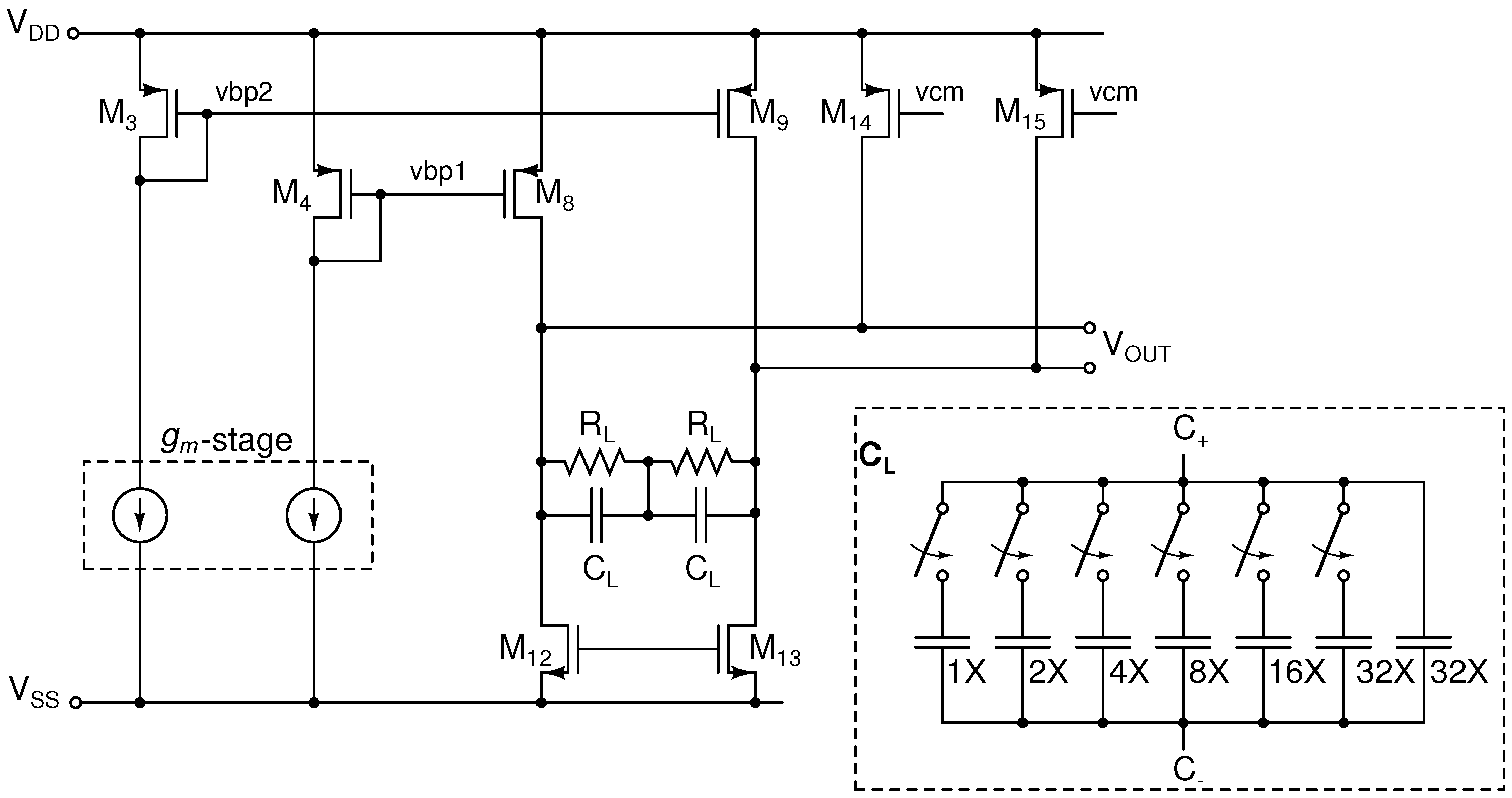
2.2. Voltage-Readout AFE
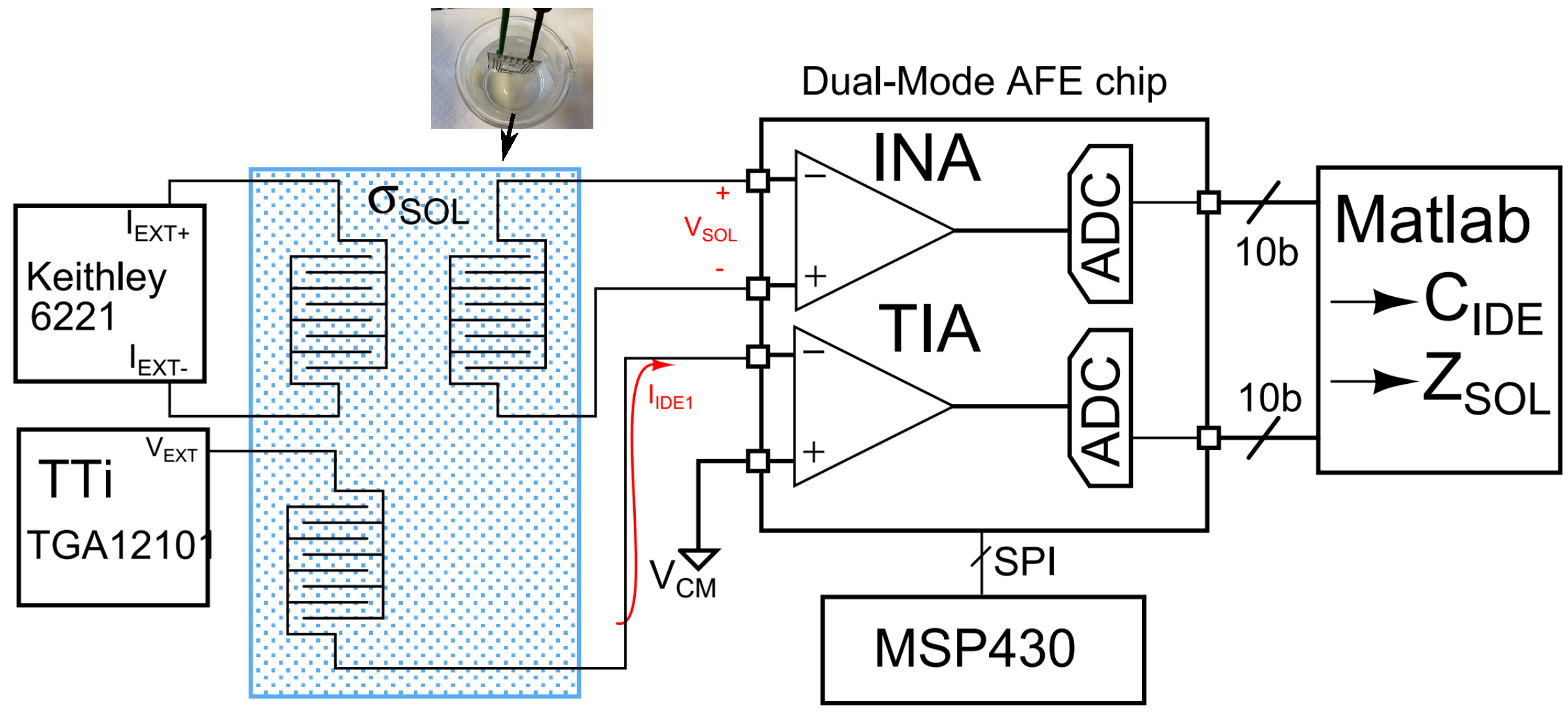
3. Measurements
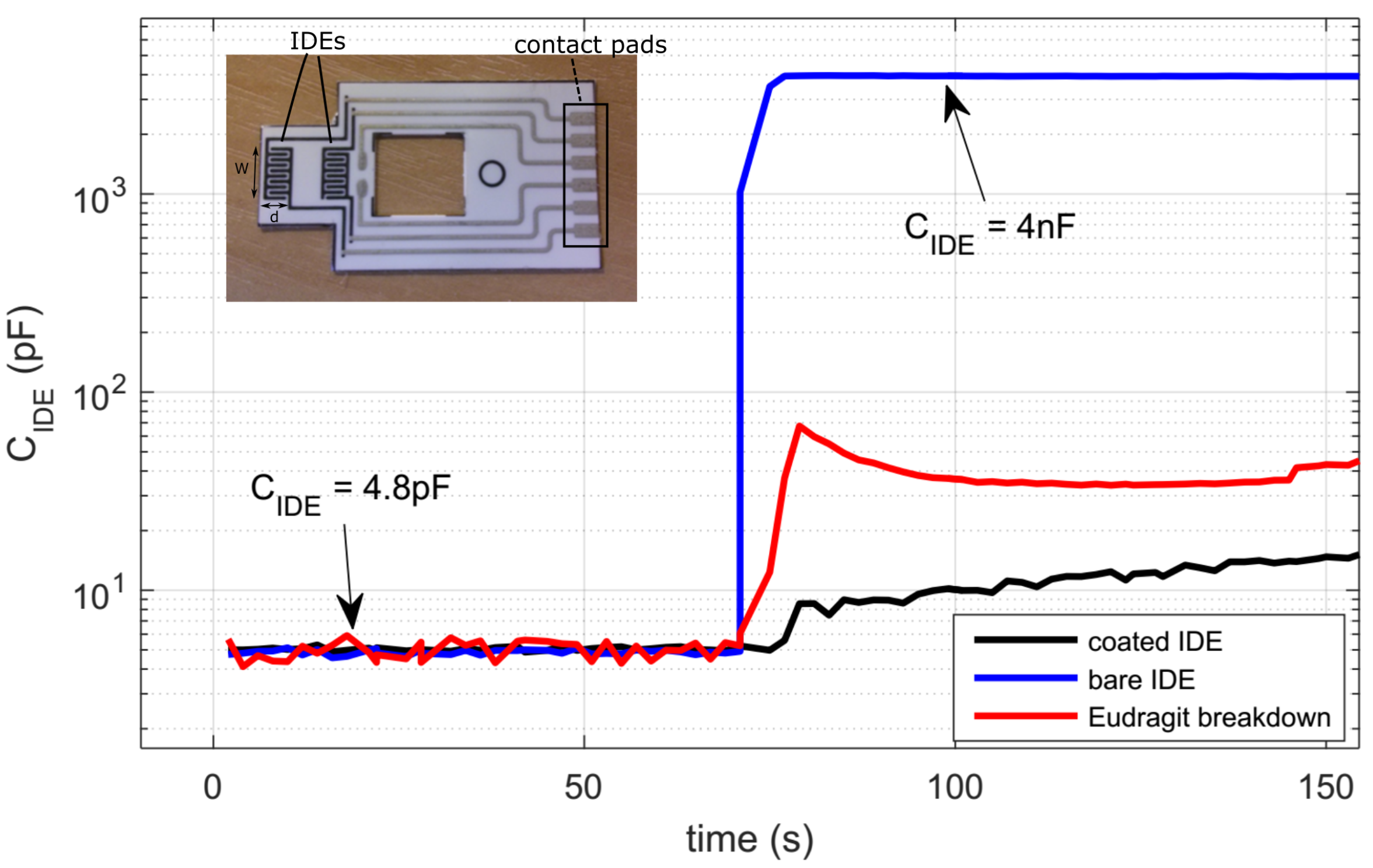
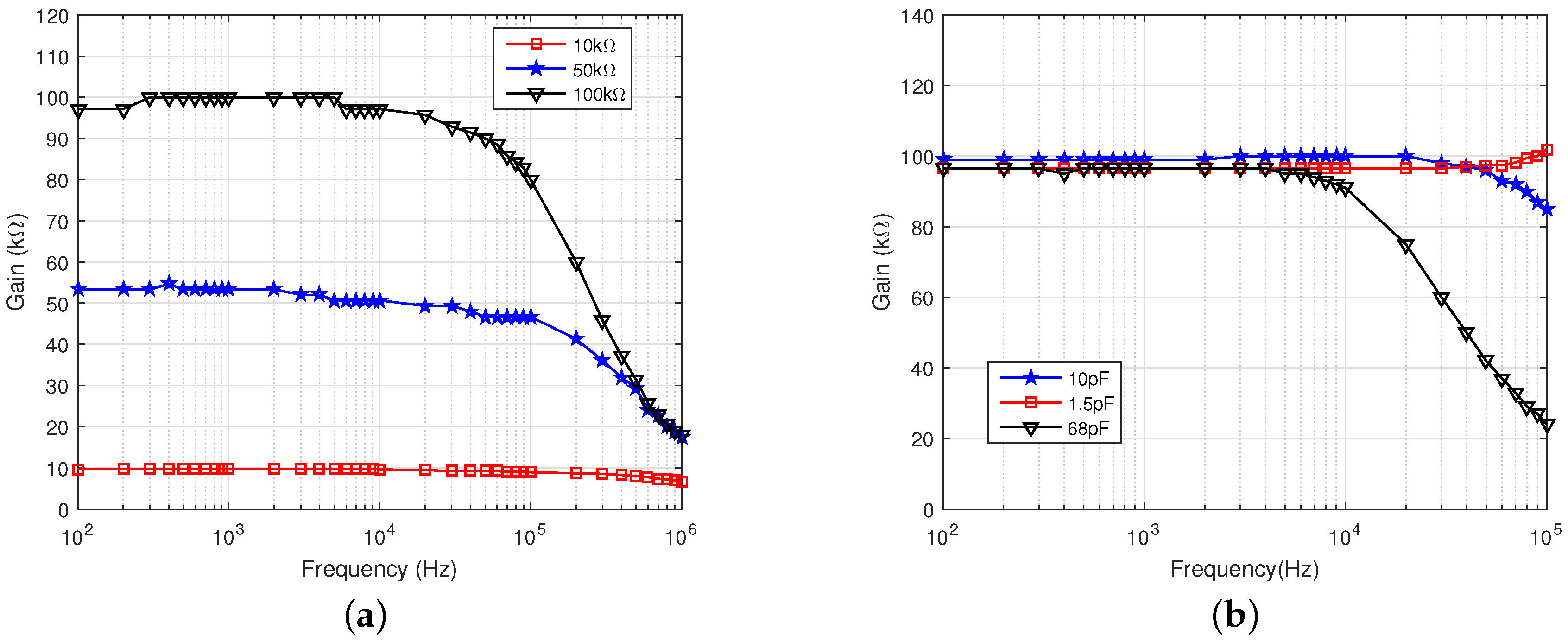
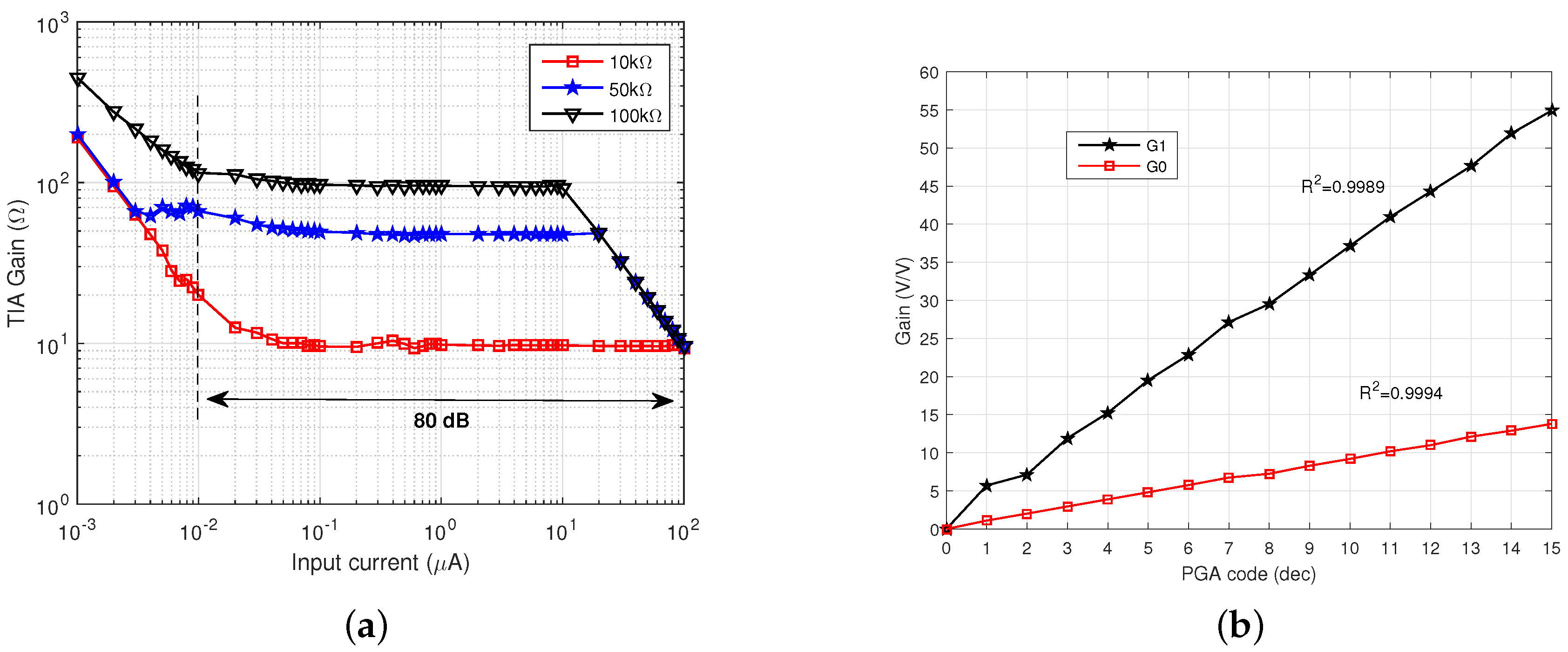
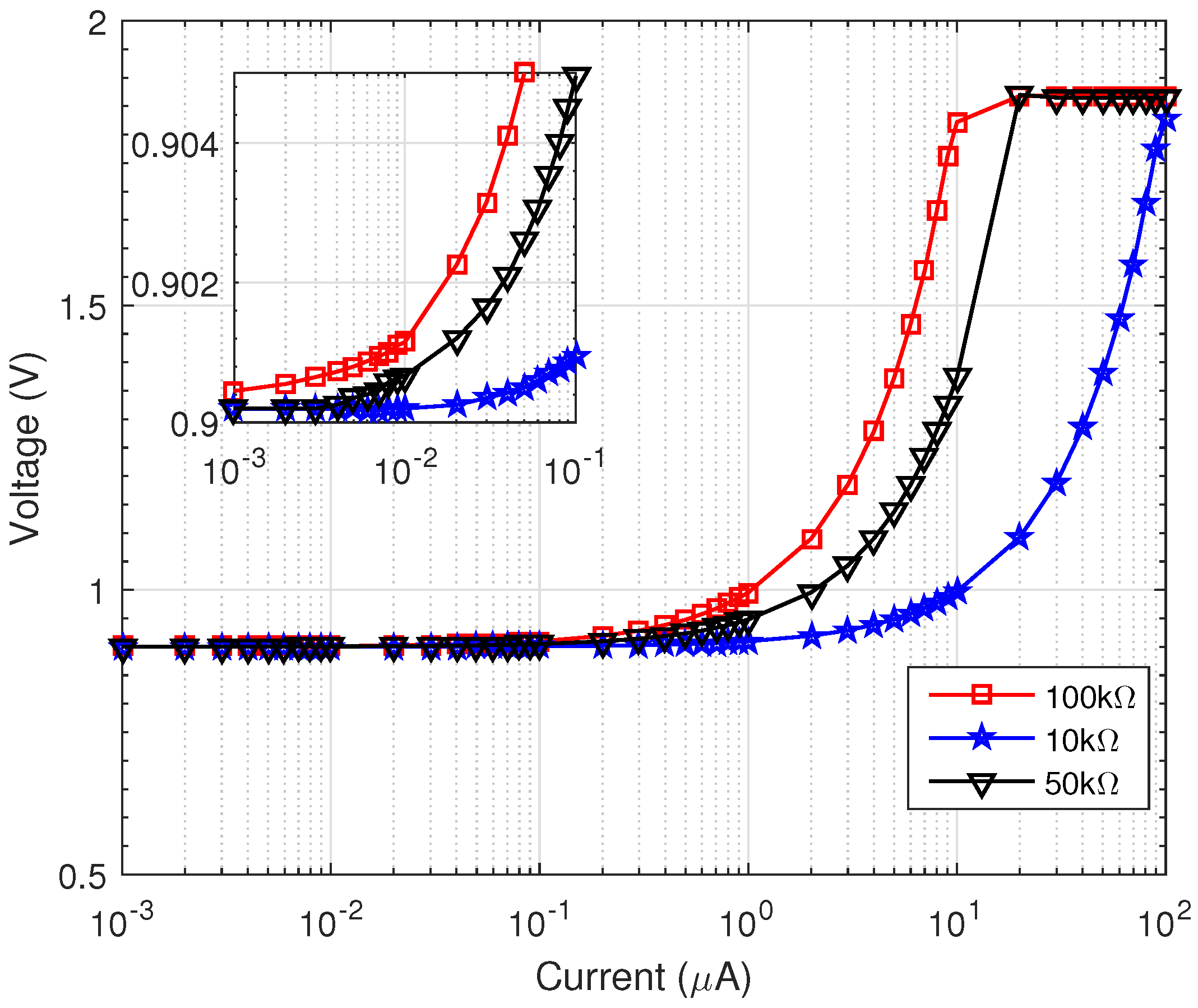
3.1. CR AFE
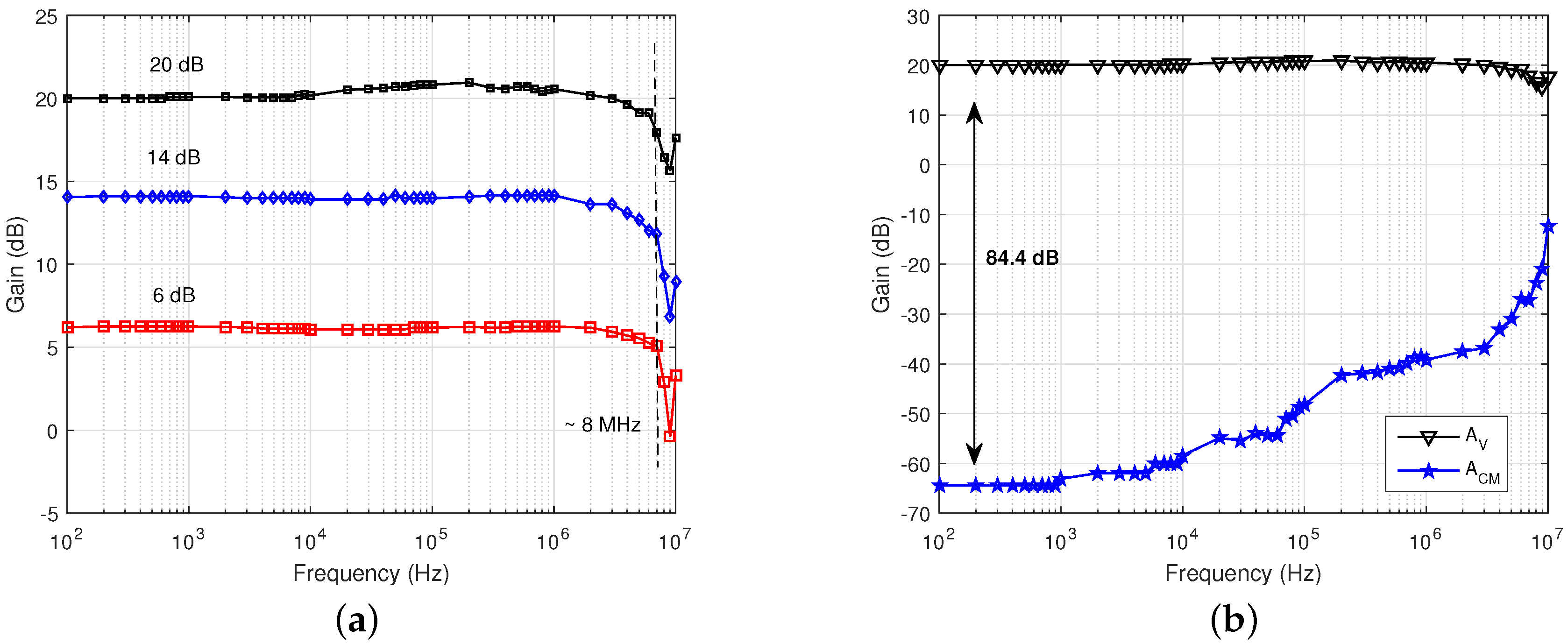
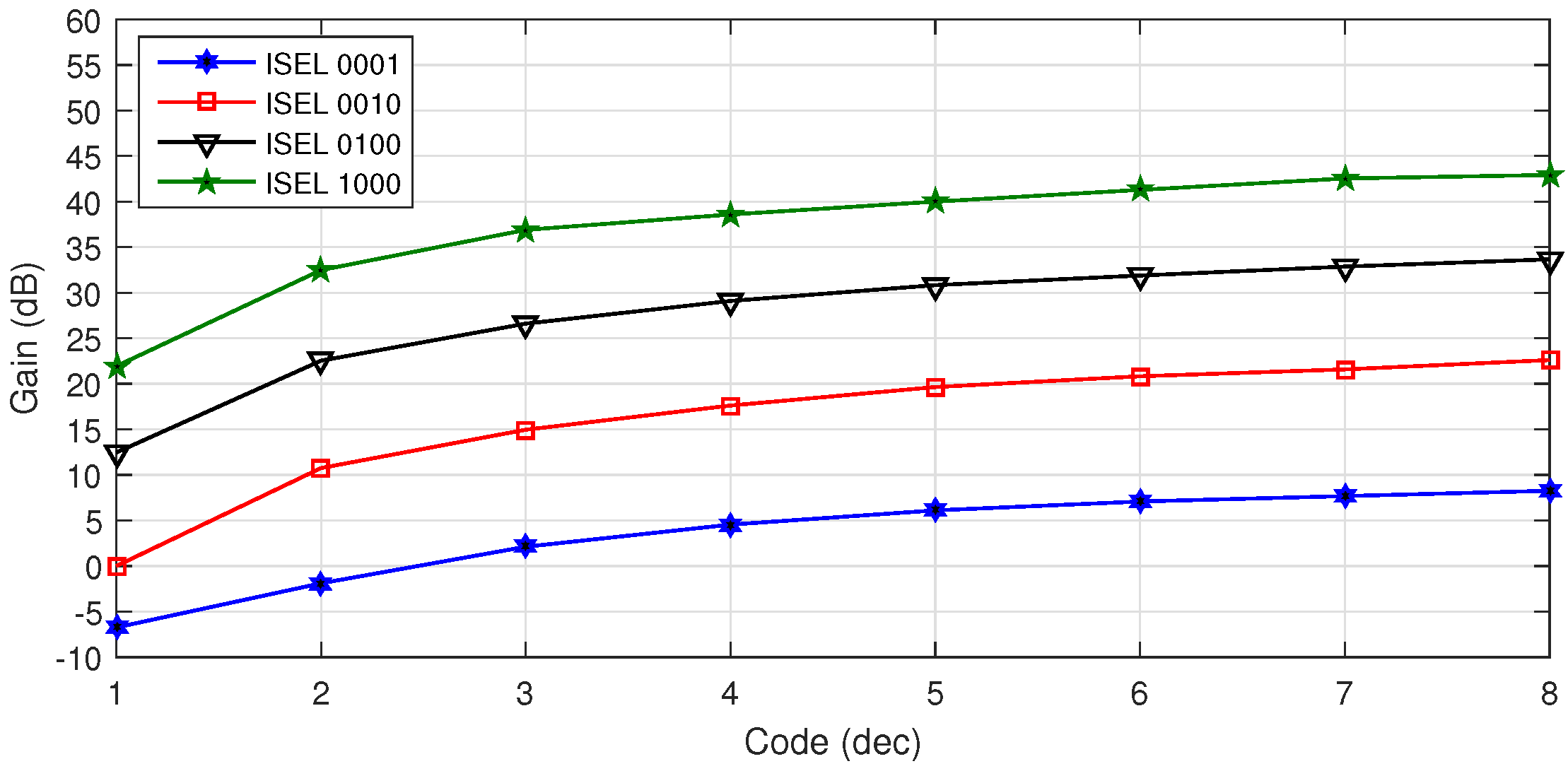
3.2. VR AFE
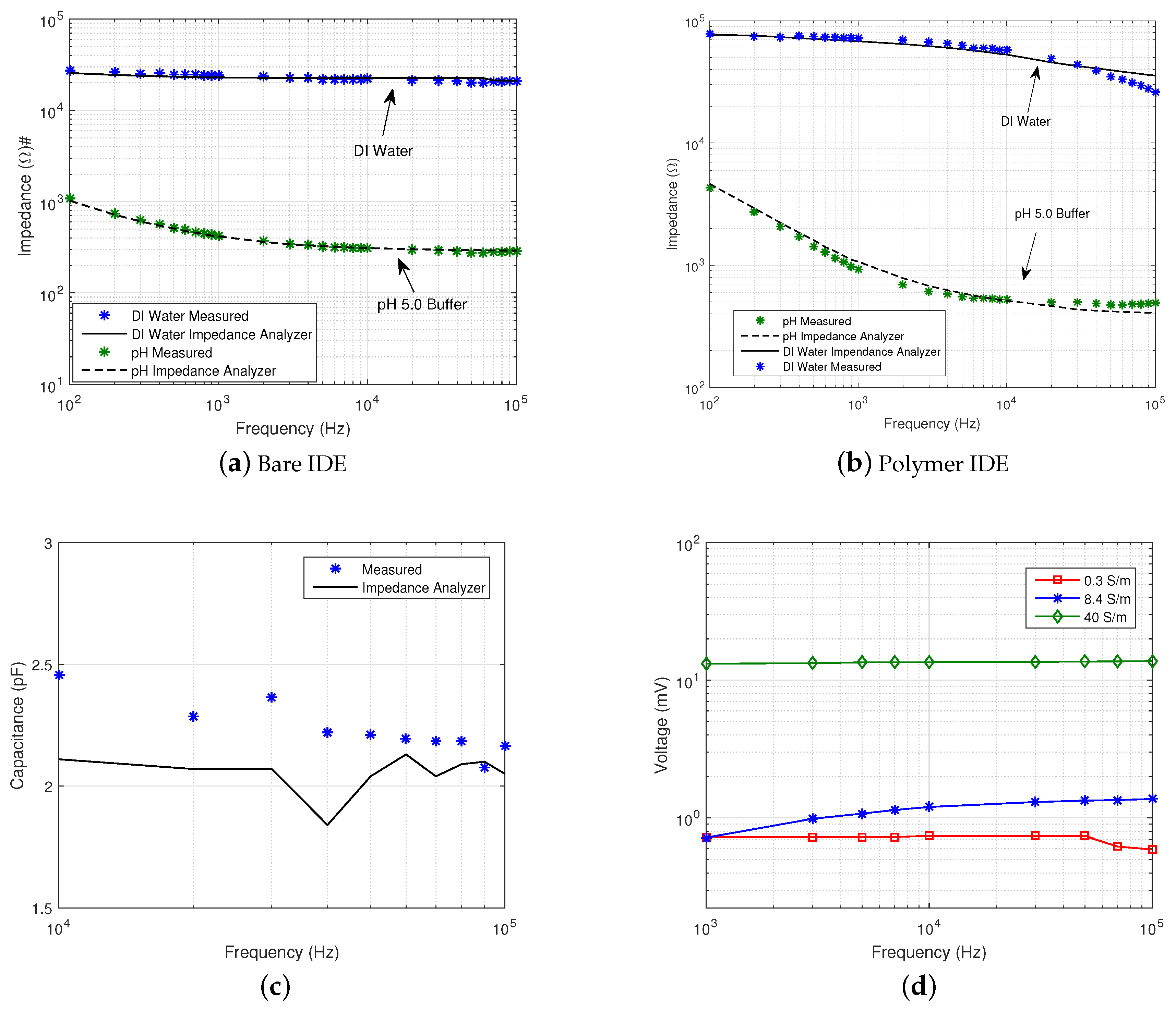
3.3. Impedance Measurements
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| IDEs | Interdigitated electrodes |
| EIS | Electrical impedance spectroscopy |
| AFE | Analogue front-end |
| VR | Voltage readout |
| CR | Current readout |
| TIA | Transimpedance amplifier |
| INA | Instrumentation amplifier |
| AGC | Automatic gain control |
| PD | Peak detector |
| SPI | Serial-to-peripheral interface |
| PISO | Parallel-in-serial-out |
| HF | High frequency |
| BW | Bandwidth limited |
| CMFB | Common-mode feedback |
| CMRR | Common-mode rejection ratio |
References
- Yufera, A.; Rueda, A.; Munoz, J.; Doldan, R.; Leger, G.; Rodriguez-Villegas, E.O. A tissue impedance measurement chip for myocardial ischemia detection. IEEE Trans. Circuits Syst. I Regul. Pap. 2005, 52, 2620–2628. [Google Scholar] [CrossRef]
- Halter, R.J.; Hartov, A.; Heaney, J.A.; Paulsen, K.D.; Schned, A.R. Electrical impedance spectroscopy of the human prostate. IEEE Trans. Biomed. Eng. 2007, 54, 1321–1327. [Google Scholar] [CrossRef] [PubMed]
- Constantinou, L.; Bayford, R.; Demosthenous, A. A wideband low-distortion CMOS current driver for tissue impedance analysis. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 154–158. [Google Scholar] [CrossRef]
- Hong, S.; Lee, K.; Ha, U.; Kim, H.; Lee, Y.; Kim, Y.; Yoo, H.-J. A 4.9 mΩ-sensitivity mobile electrical impedance tomography IC for early breast-cancer Detection System. IEEE J. Solid State Circuits 2015, 50, 245–257. [Google Scholar] [CrossRef]
- Cho, Y.C.Y.; Kim, H.S.K.H.S.; Frazier, A.B.; Chen, Z.G.; Shin, D.M.S.D.M.; Han, A. Whole-cell impedance analysis for highly and poorly metastatic cancer cells. J. Microelectromech. Syst. 2009, 18, 808–817. [Google Scholar]
- Qiao, G.; Wang, W.; Duan, W.; Zheng, F.; Sinclair, A.J.; Chatwin, C.R. Bioimpedance analysis for the characterization of breast cancer cells in suspension. IEEE Trans. Biomed. Eng. 2012, 59, 2321–2329. [Google Scholar] [CrossRef] [PubMed]
- Wi, H.; Sohal, H.; McEwan, A.L.; Woo, E.J.; Oh, T.I. Multi-frequency electrical impedance tomography system with automatic self-calibration for long-term monitoring. IEEE Trans. Biomed. Circuits Syst. 2014, 8, 119–128. [Google Scholar] [PubMed]
- Jafari, H.; Soleymani, L.; Genov, R. 16-channel CMOS impedance spectroscopy DNA analyser with dual-slope multiplying ADCs. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 468–478. [Google Scholar] [CrossRef] [PubMed]
- Park, J.-Y.; Park, S.-M. DNA hybridization sensors based on electrochemical impedance spectroscopy as a detection tool. Sensors 2009, 9, 9513–9532. [Google Scholar] [CrossRef] [PubMed]
- Manickam, A.; Johnson, C.A.; Kavusi, S.; Hassibi, A. Interface design for CMOS-integrated electrochemical impedance spectroscopy (EIS) biosensors. Sensors 2012, 12, 14467–14488. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Bashir, R. Electrical/electrochemical impedance for rapid detection of foodborne pathogenic bacteria. Biotechnol. Adv. 2008, 26, 135–150. [Google Scholar] [CrossRef] [PubMed]
- Munoz-Berbel, X.; Vigues, N.; Jenkins, A.T.A.; Mas, J.; Munoz, F.J. Impedimetric approach for quantifying low bacteria concentrations based on the changes produced in the electrode-solution interface during the pre-attachment stage. Biosens. Bioelectron. 2008, 23, 1540–1546. [Google Scholar] [CrossRef] [PubMed]
- Guimera, A.; Gabriel, G.; Prats-Alfonso, E.; Abramova, N.; Bratov, A.; Villa, R. Effect of surface conductivity on the sensitivity of interdigitated impedimetric sensors and their design considerations. Sens. Actuators B Chem. 2015, 207, 1010–1018. [Google Scholar] [CrossRef]
- Mallen-Alberdi, M.; Vigues, N.; Mas, J.; Fernandez-Sanchez, C.; Baldi, A. Impedance spectral fingerprint of E. coli cells on interdigitated electrodes: A new approach for label free and selective detection. Sens. Bio-Sens. Res. 2016, 7, 100–106. [Google Scholar] [CrossRef]
- Felice, C.J.; Valentinuzzi, M.E. Medium and interface components in impedance microbiology. IEEE Trans. Biomed. Eng. 1999, 46, 1483–1487. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Sanchez, C.; McNeil, C.J.; Rawson, K.; Nilsson, O. Disposable noncompetitive immunosensor for free and total prostate-specific antigen based on capacitance measurement. Anal. Chem. 2004, 76, 5649–5656. [Google Scholar] [CrossRef] [PubMed]
- Ha, S.; Kim, C.; Chi, Y.M.; Akinin, A.; Maier, C.; Ueno, A.; Cauwenberghs, G. Integrated circuits and electrode interfaces for noninvasive physiological monitoring. IEEE Trans. Biomed. Eng. 2014, 61, 1522–1537. [Google Scholar] [PubMed]
- Ma, H.; Su, Y.; Nathan, A. Cell constant studies of bipolar and tetrapolar electrode systems for impedance measurement. Sens. Actuators B Chem. 2015, 221, 1264–1270. [Google Scholar] [CrossRef]
- Felice, C.J.; Valentinuzzi, M.E.; Vercellone, M.I.; Madrid, R.E. Impedance bacteriometry: Medium and interface contributions during bacterial growth. IEEE Trans. Biomed. Eng. 1992, 39, 1310–1313. [Google Scholar] [CrossRef] [PubMed]
- Segura-Quijano, F.; Sacristan-Riquelme, J.; Garciaa-Cantonn, J.; Oses, M.T.; Baldi, A. Towards fully integrated wireless impedimetric sensors. Sensors 2010, 10, 4071–4082. [Google Scholar] [CrossRef] [PubMed]
- Song, K.; Ha, U.; Park, S.; Bae, J.; Yoo, H.-J. An impedance and multi-wavelength near-infrared spectroscopy IC for non-invasive blood glucose estimation. IEEE J. Solid State Circuits 2015, 50, 1025–1037. [Google Scholar] [CrossRef]
- Manickam, A.; Chevalier, A.; McDermott, M.; Ellington, A.D.; Hassibi, A. A CMOS electrochemical impedance spectroscopy (EIS) biosensor array. IEEE Trans. Biomed. Circuits Syst. 2010, 4, 379–390. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Wallbank, R.W.R.; Chaji, R.; Li, J.; Suzuki, Y.; Jiggins, C.; Nathan, A. An impedance-based integrated biosensor for suspended DNA characterization. Sci. Rep. 2013, 3, 2730–2736. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.; Jiang, H.; Venkatesh, A.G.; Hall, D.A. A hybrid semi-digital transimpedance amplifier with noise cancellation technique for nanopore-based DNA sequencing. IEEE Trans. Biomed. Circuits Syst. 2015, 9, 652–661. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Emaminejad, S.; Nyein, H.Y.Y.; Challa, S.; Chen, K.; Peck, A.; Javey, A. Fully integrated wearable sensor arrays for multiplexed in situ perspiration analysis. Nature 2016, 529, 509–514. [Google Scholar] [CrossRef] [PubMed]
- Hartov, A.; Mazzarese, R.A.; Reiss, F.R.; Kerner, T.E.; Osterman, K.S.; Williams, D.B.; Paulsen, K.D. A multichannel continuously selectable multifrequency electrical impedance spectroscopy measurement system. IEEE Trans. Bio Med. Eng. 2000, 47, 49–58. [Google Scholar] [CrossRef] [PubMed]
- Song, K.; Ha, U.; Lee, J.; Bong, K.; Yoo, H.J. An 87-mA · min iontophoresis controller IC with dual-mode impedance sensor for patch-type transdermal drug delivery system. IEEE J. Solid State Circuits 2014, 49, 167–178. [Google Scholar] [CrossRef]
- Chi, T.; Park, J.S.; Butts, J.C.; Hookway, T.A.; Su, A.; Zhu, C.; Styczynski, M.P.; McDevitt, T.C.; Wang, H. A Multi-Modality CMOS sensor array for cell-based assay and drug screening. IEEE Trans. Biomed. Circuits Syst. 2015, 9, 801–814. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Morgan, H. Single-cell microfluidic Impedance cytometry: A review. Microfluid. Nanofluid. 2010, 8, 423–443. [Google Scholar] [CrossRef]
- Heidari, H.; Bonizzoni, E.; Gatti, U.; Maloberti, F. A CMOS current-mode magnetic hall sensor with integrated front-end. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 1270–1278. [Google Scholar] [CrossRef]
- Goldstein, B.; Kim, D.; Xu, J.; Vanderlick, T.K.; Culurciello, E. CMOS low current measurement system for biomedical applications. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 111–119. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Goldstein, B.; Tang, W.; Sigworth, F.J.; Culurciello, E. Noise analysis and performance comparison of low current measurement systems for biomedical applications. IEEE Trans. Biomed. Circuits Syst. 2013, 7, 52–62. [Google Scholar]
- Bennati, M.; Thei, F.; Rossi, M.; Crescentini, M.; D’Avino, G.; Baschirotto, A.; Tartagni, M. 20.5 A Sub-pA ΔΣ Current amplifier for single-molecule nanosensors. In Proceedings of the 2009 IEEE International Solid-State Circuits Conference—Digest of Technical Papers, San Francisco, CA, USA, 8–12 February 2009; pp. 348–349.
- Zhao, Y.; Zhao, J.; Wang, X.; Xia, G.M.; Qiu, A.P.; Su, Y.; Xu, Y.P. A sub-μg bias-instability MEMS oscillating accelerometer with an ultra-low-noise read-out circuit in CMOS. IEEE J. Solid-State Circuits 2015, 50, 2113–2126. [Google Scholar] [CrossRef]
- Ferrari, G.; Gozzini, F.; Molari, A.; Sampietro, M. Transimpedance amplifier for high sensitivity current measurements on nanodevices. IEEE J. Solid State Circuits 2009, 44, 1609–1616. [Google Scholar] [CrossRef]
- Crescentini, M.; Bennati, M.; Carminati, M.; Tartagni, M. Noise limits of CMOS current interfaces for biosensors: A Review. IEEE Trans. Biomed. Circuits Syst. 2014, 8, 278–292. [Google Scholar] [CrossRef] [PubMed]
- De Langen, K.J.; Huijsing, J.H. Compact low-voltage power-efficient operational amplifier cells for VLSI. IEEE J. Solid State Circuits 1998, 33, 1482–1496. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Wu, J.T. A highly linear 125-MHz CMOS switched-resistor programmable-gain amplifier. IEEE J. Solid State Circuits 2003, 38, 1663–1670. [Google Scholar]
- Chai, K.T.C.; Davies, J.H.; Cumming, D.R.S. Electrical impedance tomography for sensing with integrated microelectrodes on a CMOS microchip. Sens. Actuators B Chem. 2007, 127, 97–101. [Google Scholar] [CrossRef]
- Valente, V.; Jiang, D.; Demosthenous, A. Design of a wideband CMOS impedance spectroscopy ASIC analog front-end for multichannel biosensor interfaces. In Proceedings of the IEEE 2015 Engineering in Medicine and Biology Conference (EMBC), Milan, Italy, 25–29 August 2015.
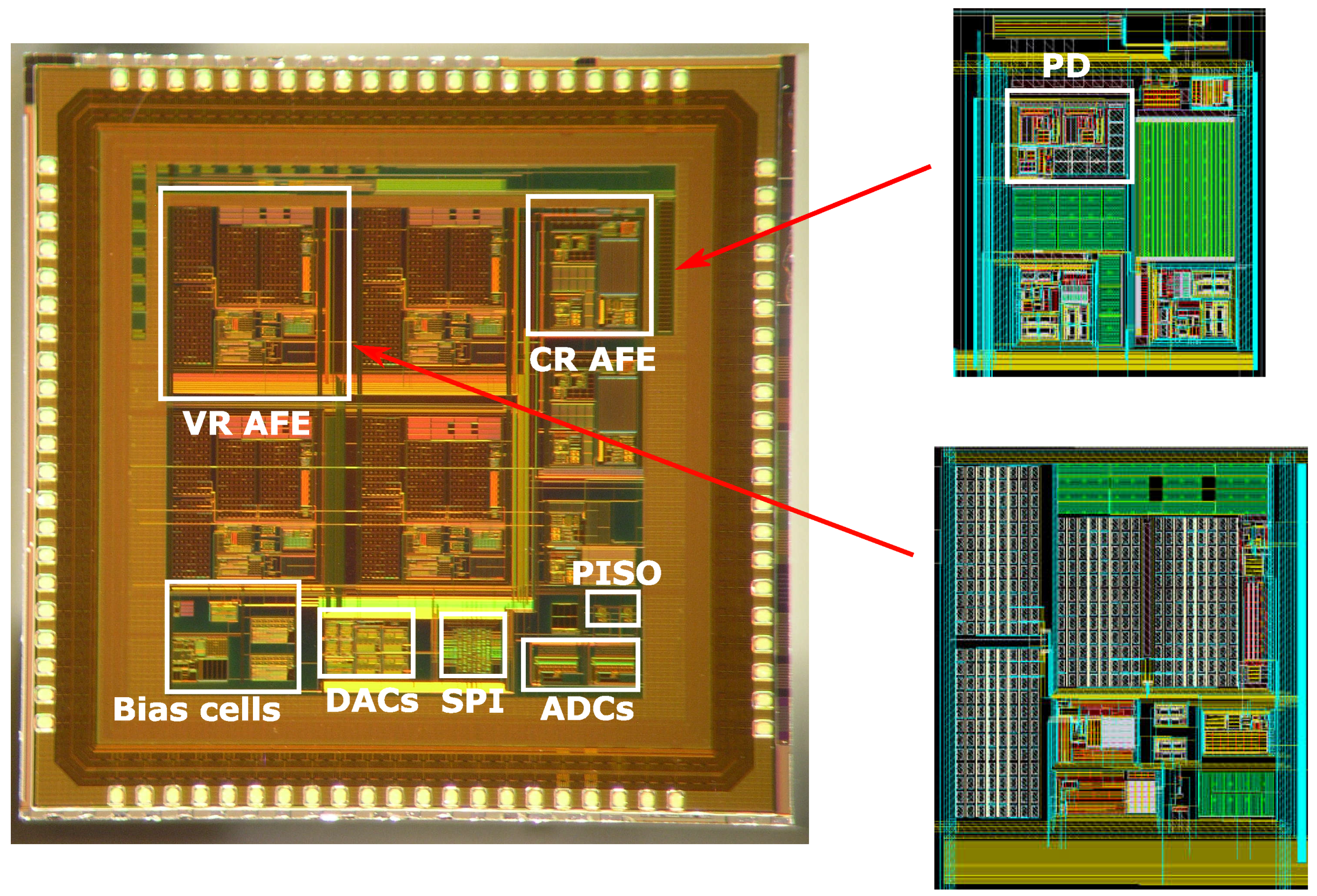
| PARAMETER | UNITS | VALUE |
|---|---|---|
| Technology | - | 0.18 m CMOS |
| Number of pads | - | 84 |
| Chip active area | mm | 4.2 |
| Supply voltage | V | 1.8 |
| VR AFE | ||
| Gain range | dB | −6 to 42 |
| BW LF | kHz | 30 to 80 |
| BW HF | MHz | 8 |
| CMRR | dB | 84.4 |
| Max current consumption | A | 690 |
| CR AFE | ||
| TIA gain | kΩ | 10, 50, 100 |
| TIA dynamic range | dB | 80 |
| PGA gain | V/V | 1 to 55 |
| Max current consumption | A | 530 |
| PARAMETER | CH | This Work | [35] | [33] | [21] | [4] |
|---|---|---|---|---|---|---|
| Technology | 0.18 m CMOS | 0.35 m CMOS | 0.35 m CMOS | 0.18 m CMOS | 0.18 m CMOS | |
| Supply voltage (V) | 1.8 | 3.3 | 3.3 | 5 | 1.8 | |
| Readout modality | Dual-mode | Current | Current | Voltage | Voltage | |
| Gain (kO) | CR | 10, 50, 100 | 60,000 | - | - | - |
| VR | −6 dB–42 dB | - | - | 15 dB–32 dB | 18 dB–60 dB | |
| Bandwidth (Hz) | CR | 100 k–1.59 M | 4 M | 4k | - | - |
| VR | 8 M | - | - | 76 k | 100 k | |
| Resolution (bits) | 10 | - | - | 10 | 14 | |
| Power/channel (mW) | CR | 1.24 | 55 | 23 | - | |
| VR | 0.95 | - | - | 6 | 53.4 | |
| (fA/) | CR | 450 | 4 | 5 | - | - |
| (nV/) | VR | 10 | - | - | - | 36 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valente, V.; Demosthenous, A. Wideband Fully-Programmable Dual-Mode CMOS Analogue Front-End for Electrical Impedance Spectroscopy. Sensors 2016, 16, 1159. https://doi.org/10.3390/s16081159
Valente V, Demosthenous A. Wideband Fully-Programmable Dual-Mode CMOS Analogue Front-End for Electrical Impedance Spectroscopy. Sensors. 2016; 16(8):1159. https://doi.org/10.3390/s16081159
Chicago/Turabian StyleValente, Virgilio, and Andreas Demosthenous. 2016. "Wideband Fully-Programmable Dual-Mode CMOS Analogue Front-End for Electrical Impedance Spectroscopy" Sensors 16, no. 8: 1159. https://doi.org/10.3390/s16081159
APA StyleValente, V., & Demosthenous, A. (2016). Wideband Fully-Programmable Dual-Mode CMOS Analogue Front-End for Electrical Impedance Spectroscopy. Sensors, 16(8), 1159. https://doi.org/10.3390/s16081159





