Model Study of the Influence of Ambient Temperature and Installation Types on Surface Temperature Measurement by Using a Fiber Bragg Grating Sensor
Abstract
:1. Introduction
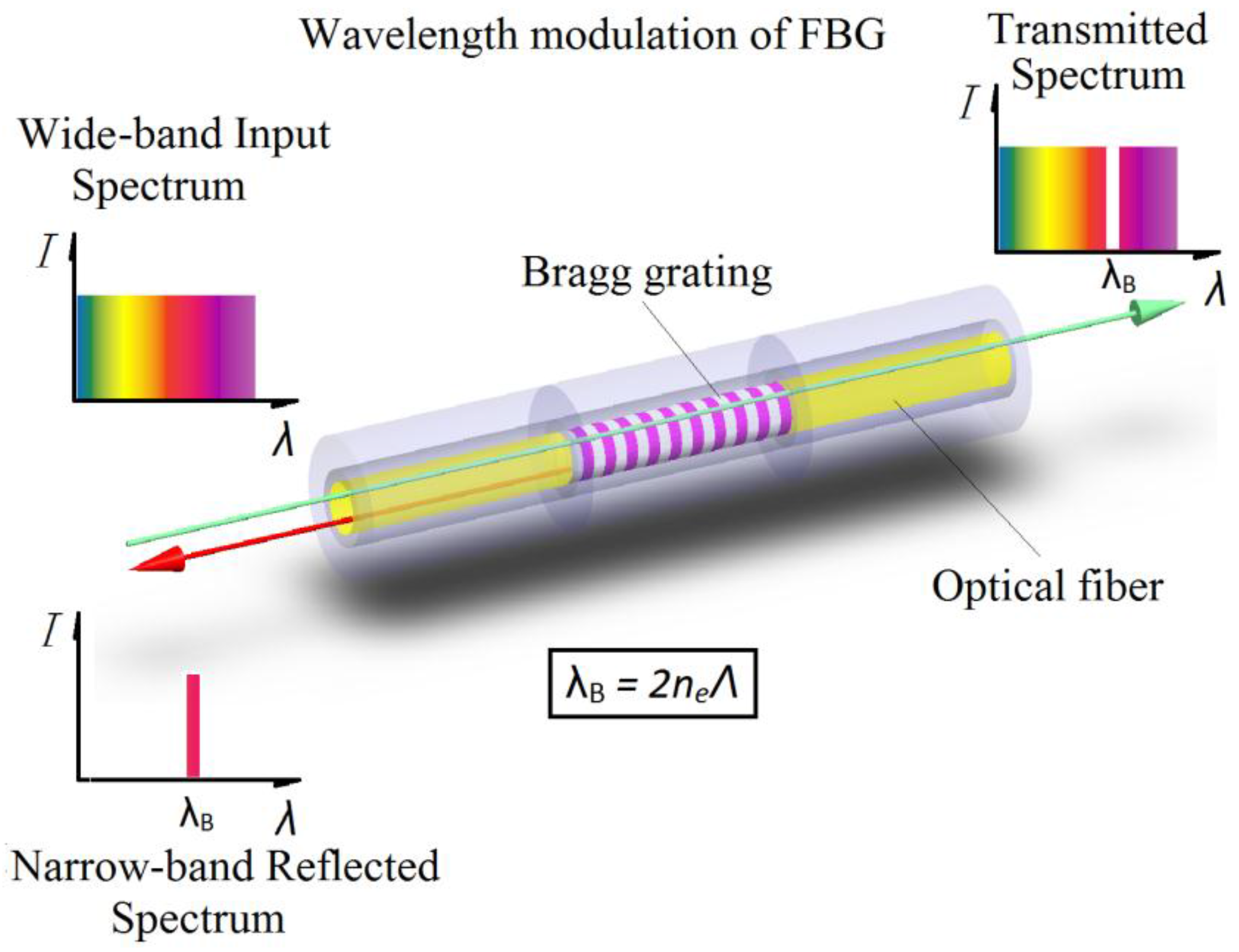
2. Surface Temperature Measurement Principle of FBG Sensor
2.1. Principle of FBG Sensor
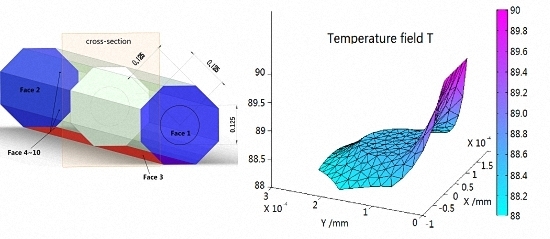
2.2. Temperature Field Model of FBG
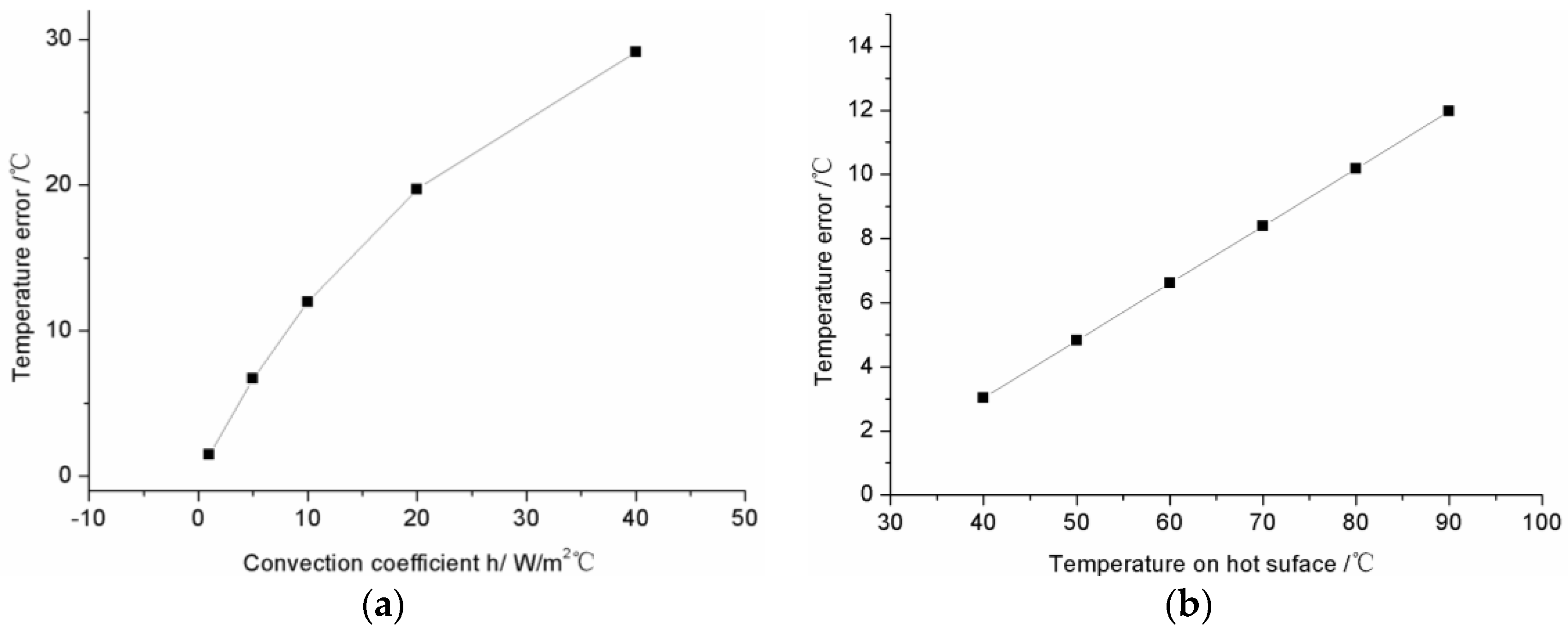
2.3. Numerical Analysises of Measurement Error of FBG Sensors
3. Measurement Errors of the FBG Sensor in Different Installation Types
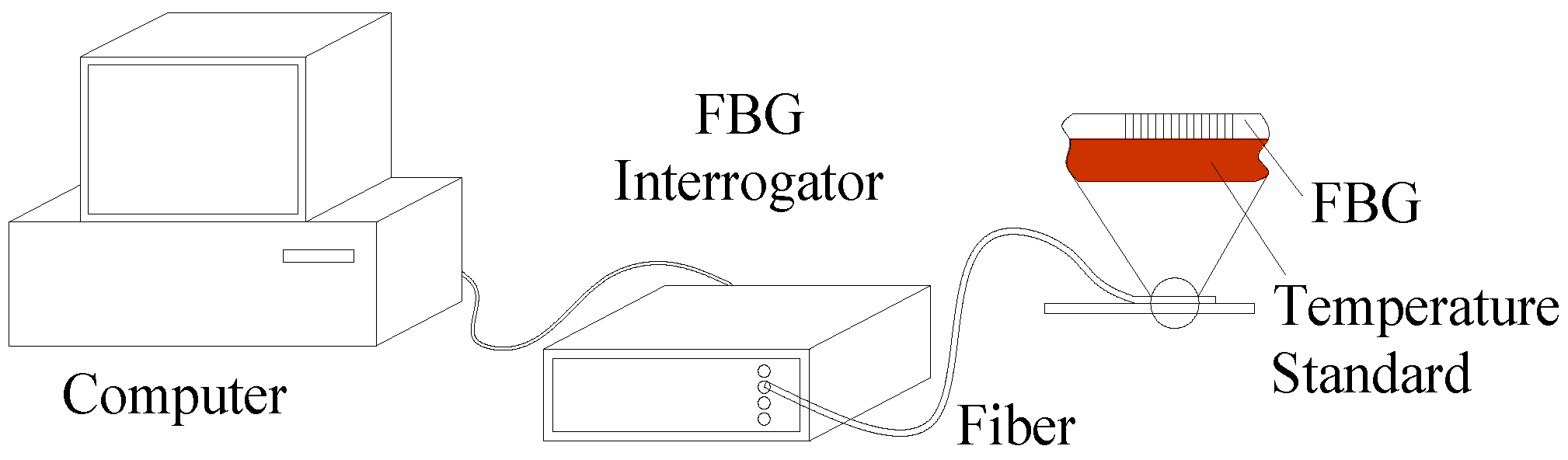
3.1. Experimental Principle and Method
3.2. Surface-Typed Temperature Standard Setup
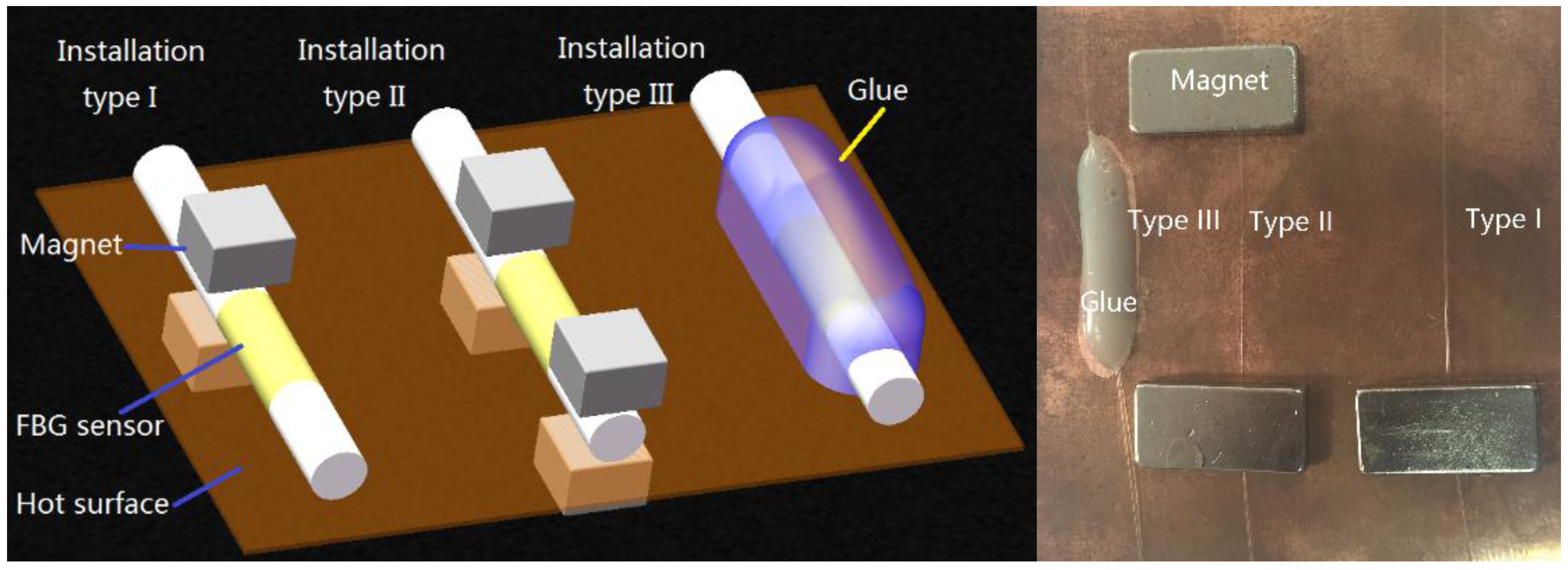
3.3. Experimental Sensor and Installation Types
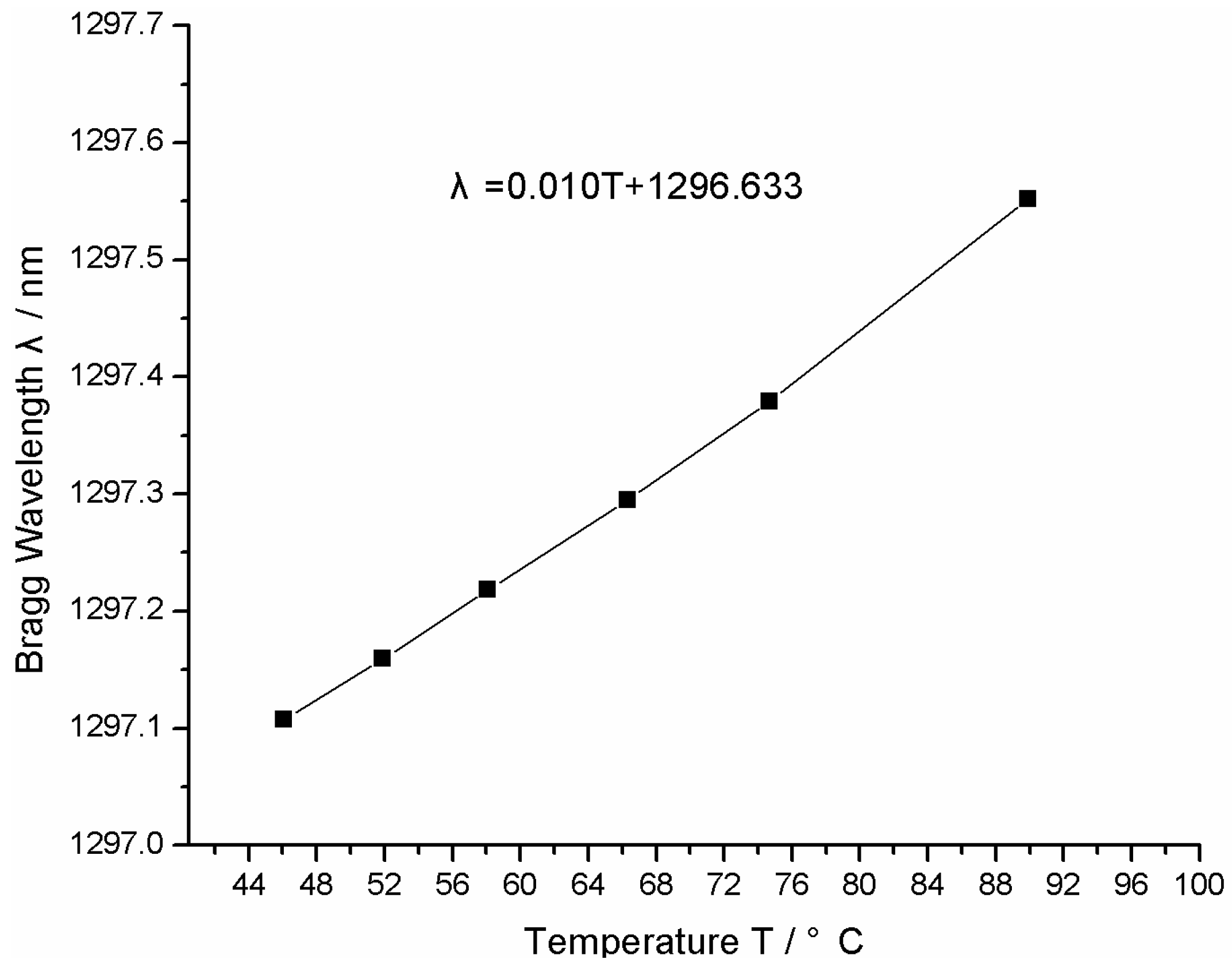
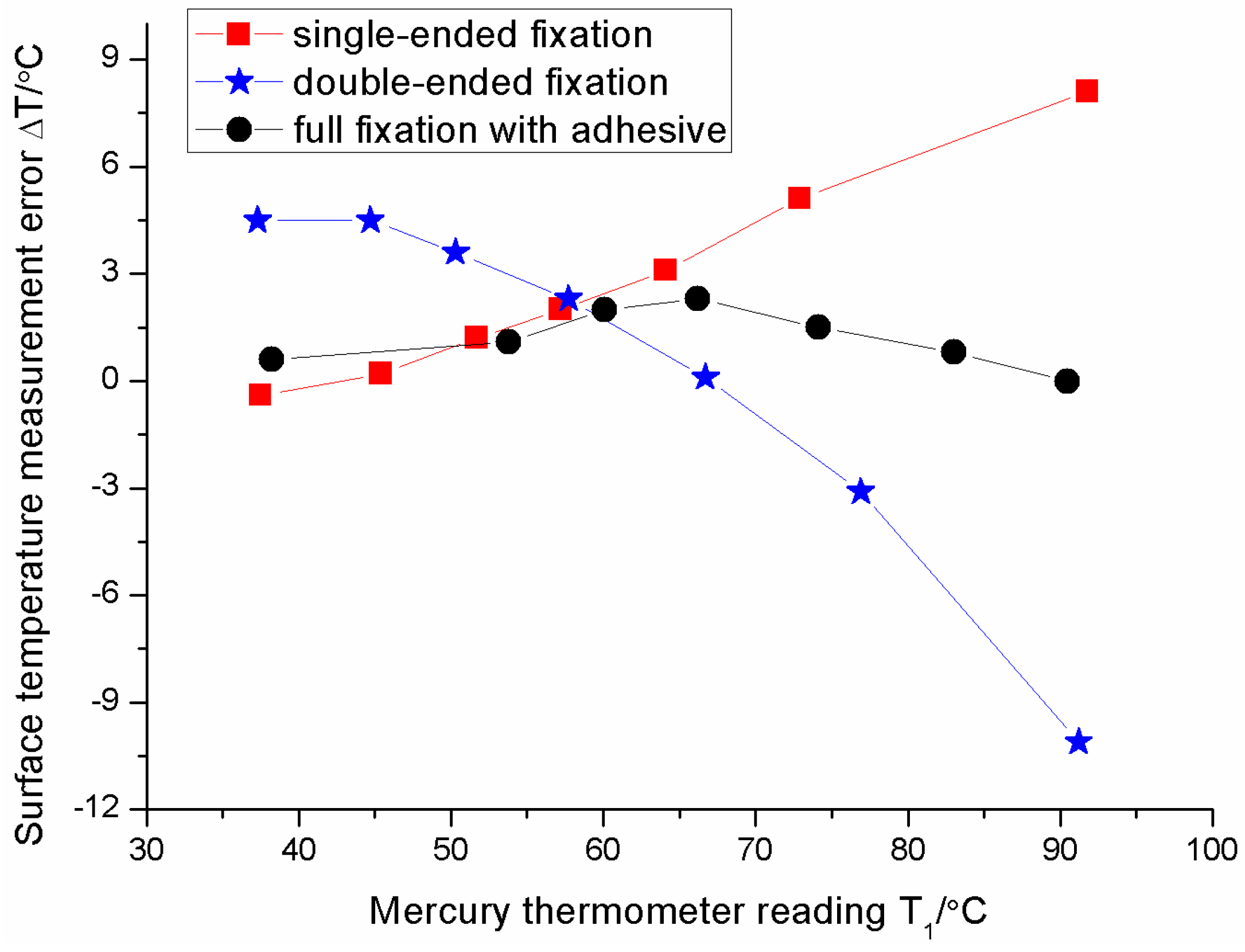
4. Results and Discussions
4.1. Measurement Errors of Sensor under Three Different Types of Installation
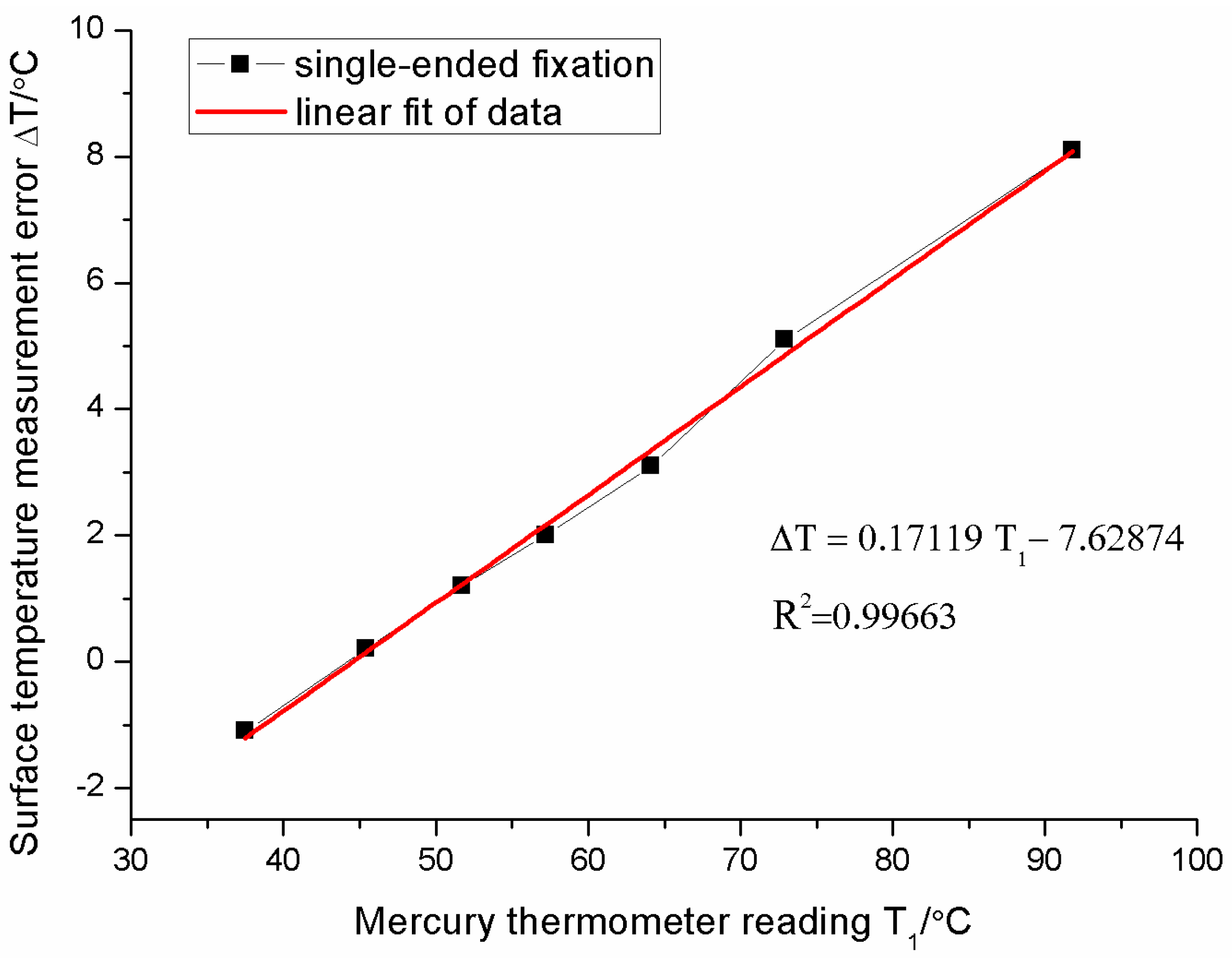
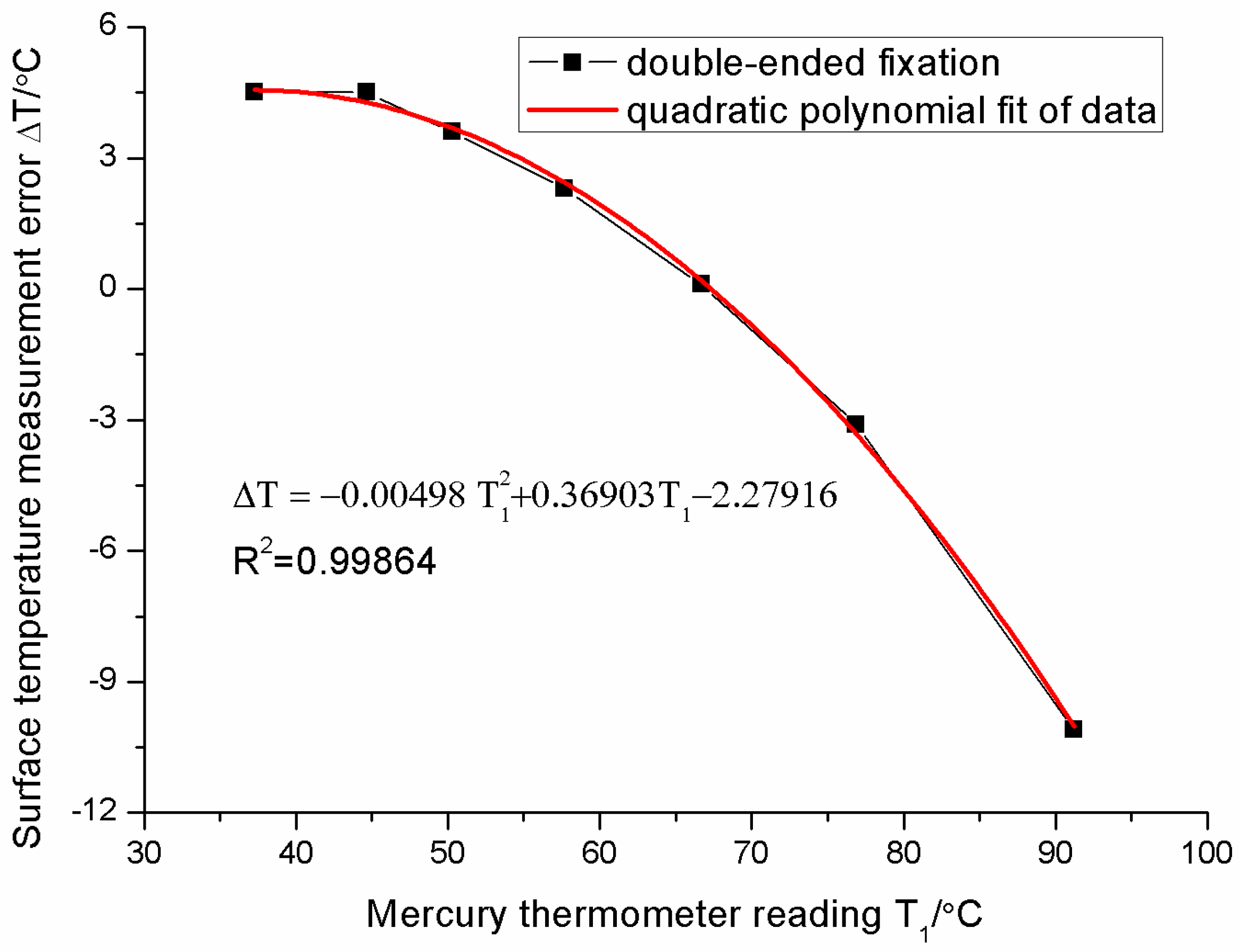
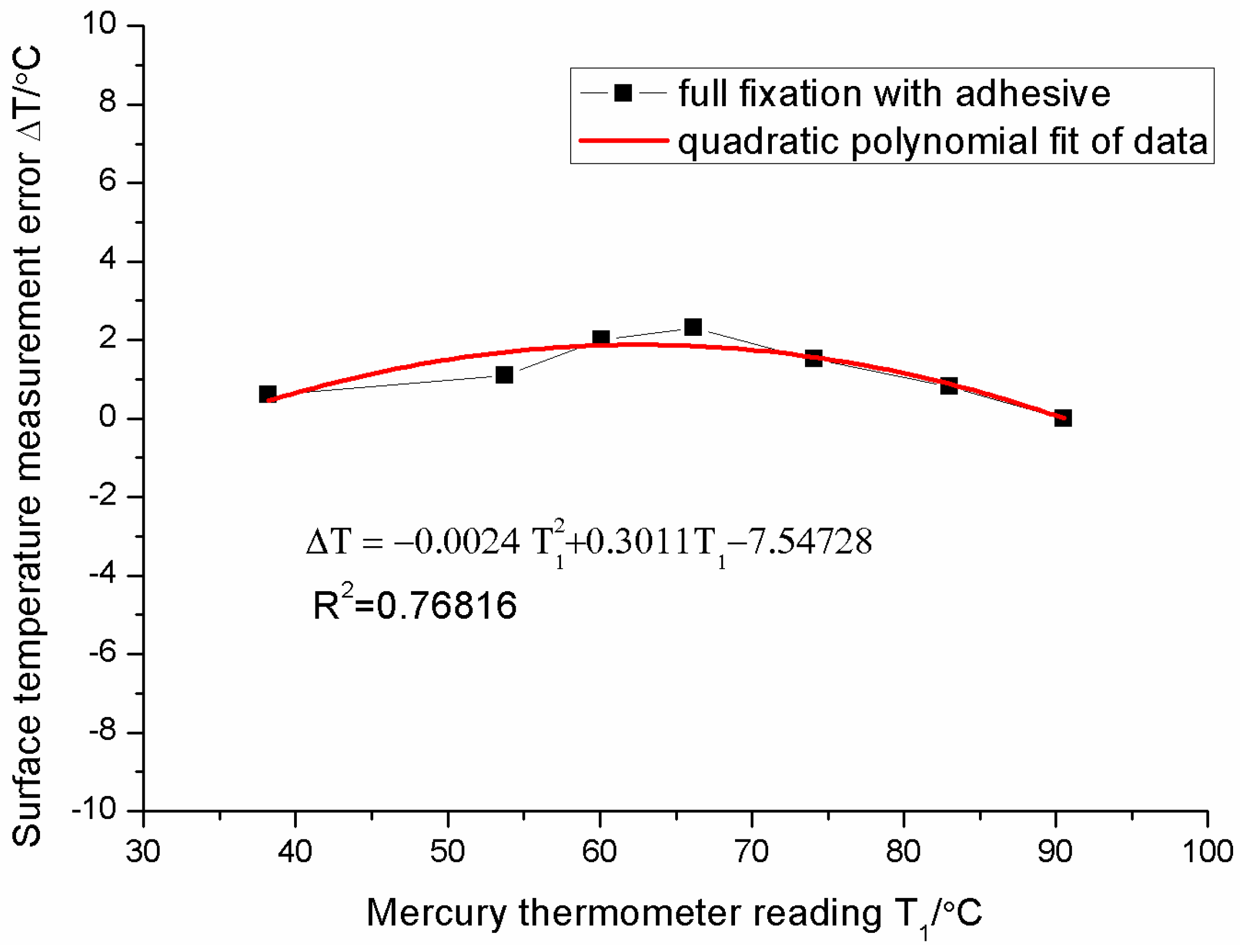
4.2. Influence of Installation Type of FBG on Measurement Error
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Psikuta, A.; Niedermann, R.; Rossi, R.M. Effect of ambient temperature and attachment method on surface temperature measurements. Int. J. Biometeorol. 2014, 58, 877–885. [Google Scholar] [CrossRef] [PubMed]
- Tarawneh, C.M.; Cole, K.D.; Wilson, B.M.; Alnaimat, F. Experiments and models for the thermal response of railroad tapered-roller bearings. Int. J. Heat Mass Transf. 2008, 51, 5794–5803. [Google Scholar] [CrossRef]
- Kuncha, S.P.; Chakravarthy, B.; Ramachandran, H.; Srinivasan, B. Distributed High Temperature Sensing Using Fiber Bragg Gratings. Int. J. Optomechatronics 2008, 2, 4–15. [Google Scholar] [CrossRef]
- Li, T.; Tan, Y.; Wei, L.; Zhou, Z.; Zheng, K.; Guo, Y. A non-contact fiber Bragg grating vibration sensor. Rev. Sci. Instrum. 2014, 85, 015002. [Google Scholar] [CrossRef] [PubMed]
- Ecke, W.; Latka, I.; Willsch, R.; Reutlinger, A.; Graue, R. Fibre optic sensor network for spacecraft health monitoring. Meas. Sci. Technol. 2001, 12, 974–980. [Google Scholar]
- Liu, Y.; Zhou, Z.; Zhang, E.; Zhang, J.; Tan, Y.; Liu, M. Measurement error of surface-mounted fiber Bragg grating temperature sensor. Rev. Sci. Instrum. 2014, 85. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.P.; Song, H.; Zhang, G. Characteristics of an Optical Fiber Hydrogen Gas Sensor Based on a Palladium and Yttrium Alloy Thin Film. IEEE Sens. J. 2013, 13, 2699–2704. [Google Scholar] [CrossRef]
- Komanduri, R.; Hou, Z.B. A review of experimental techniques for the measurement of heat and temperatures generated in some manufacturing processes and tribology. Tribol. Int. 2001, 34, 653–682. [Google Scholar] [CrossRef]
- Hennecke, D.K.; Sparrow, E.M. Local Heat Sink on a Convectively Cooled Surface-Application to Temperature Measurement Error. Int. J. Heat Mass Transf. 1970, 13, 287–304. [Google Scholar] [CrossRef]
- Zvizdic, D. Modelling of surface temperature measurement errors in vertical natural convection cooled channels. Measurement 1995, 16, 247–255. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Mukhammadeev, K.M. Numerical Estimation of Errors of Temperature Measurements by Thermocouples Using Special Glues and Pastes. J. Eng. Thermophys. 2010, 19, 17–22. [Google Scholar] [CrossRef]
- Mandal, S.; Mishra, V.; Tiwari, U.; Hanumaiah, N.; Sarepaka, R.G. Fiber Bragg Grating Sensor for Temperature Measurement in Micro Turning of Optical Surfaces with High Surface Integrity. Int. J. Optomechatronics 2013, 7, 244–252. [Google Scholar] [CrossRef]
- Powers, D.L. Powers Boundary Value Problems and Partial Differential Equations, 6th ed.; Elsevier Academic Press: Burlington, MA, USA, 2009. [Google Scholar]
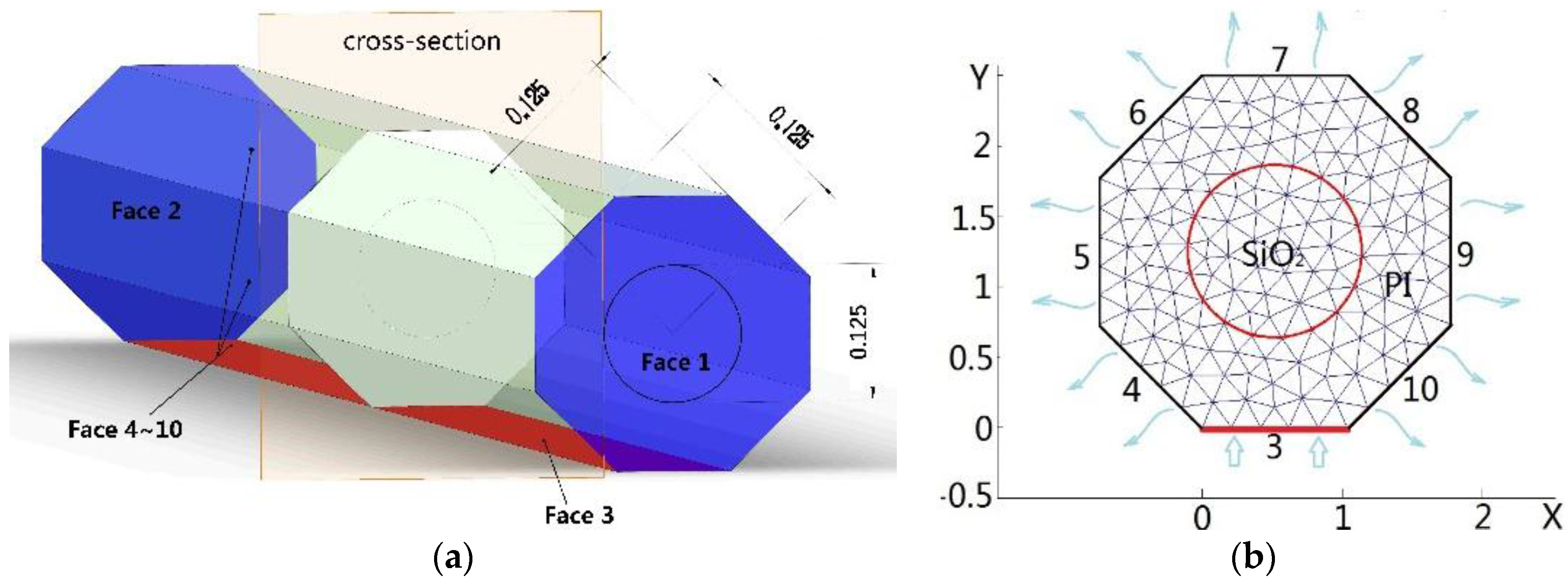
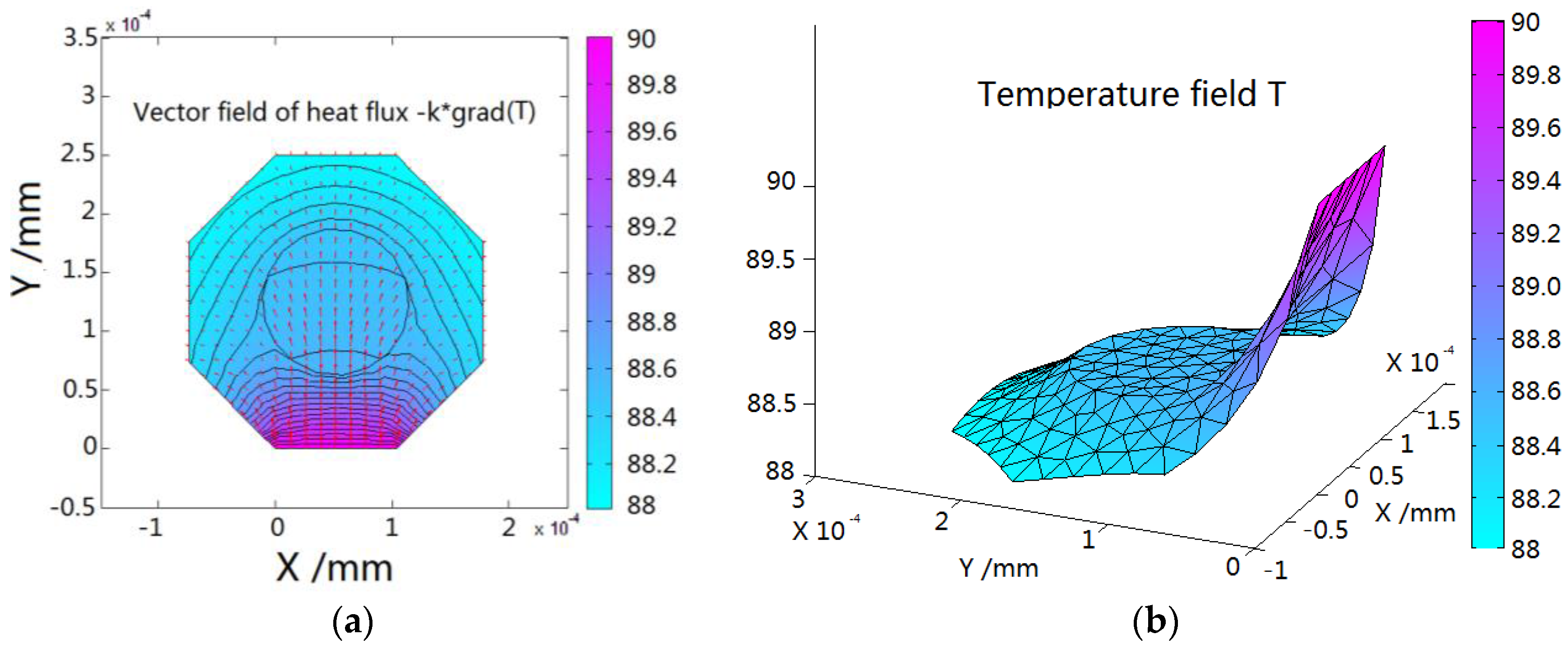

| Parameters | Values |
|---|---|
| Conductivity of Fiber Core Kf, W/(m·°C) | 1.4 (SiO2) |
| Conductivity of coating layer Kc, W/(m·°C) | 2 (Polyimide) |
| Convection coefficient of Coating h, W/(m2·°C) | 1 (laboratory condition) |
| Radii of coating rp (μm) | 125 |
| Surrounding Temperature , °C | 23 |
| Temperature on hot surface , °C | 90 |
| Radii of optical fiber rf, μm | 62.5 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, J. Model Study of the Influence of Ambient Temperature and Installation Types on Surface Temperature Measurement by Using a Fiber Bragg Grating Sensor. Sensors 2016, 16, 975. https://doi.org/10.3390/s16070975
Liu Y, Zhang J. Model Study of the Influence of Ambient Temperature and Installation Types on Surface Temperature Measurement by Using a Fiber Bragg Grating Sensor. Sensors. 2016; 16(7):975. https://doi.org/10.3390/s16070975
Chicago/Turabian StyleLiu, Yi, and Jun Zhang. 2016. "Model Study of the Influence of Ambient Temperature and Installation Types on Surface Temperature Measurement by Using a Fiber Bragg Grating Sensor" Sensors 16, no. 7: 975. https://doi.org/10.3390/s16070975
APA StyleLiu, Y., & Zhang, J. (2016). Model Study of the Influence of Ambient Temperature and Installation Types on Surface Temperature Measurement by Using a Fiber Bragg Grating Sensor. Sensors, 16(7), 975. https://doi.org/10.3390/s16070975