Localisation of Sensor Nodes with Hybrid Measurements in Wireless Sensor Networks †
Abstract
:1. Introduction
Related work
- A new unbiased observation model for localisation of static nodes is developed based on hybrid measurements, namely angle-of-arrival and received-signal-strength data.
- A WLLS framework based on the noise covariance of the signal is presented.
- The mathematical derivation of unbiasness and unbias constant is given.
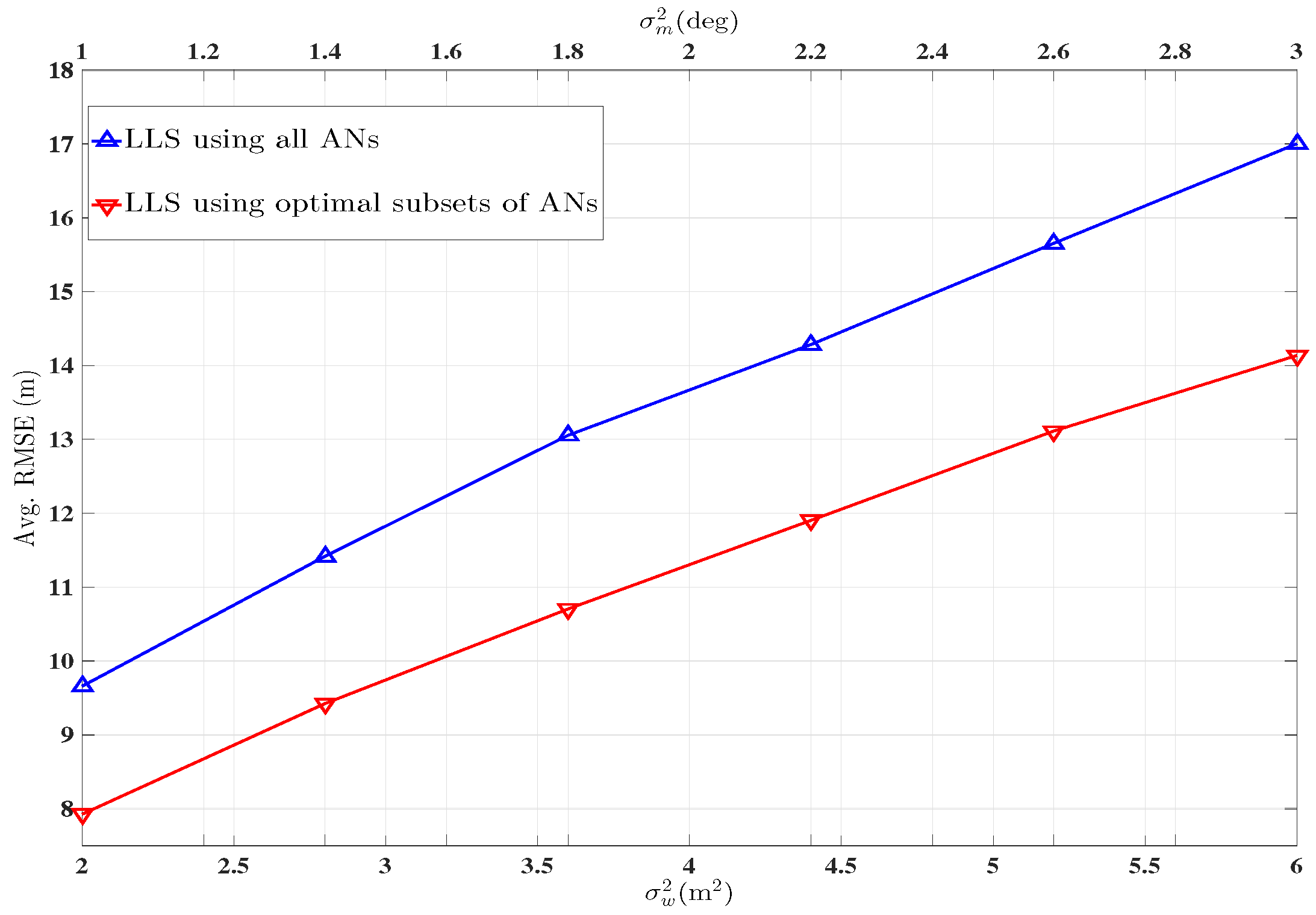
- A two step AN selection technique is presented which further improves the performance.
- Theoretical results for the mean square error (MSE) are derived.
- Joint PLE and sensor node coordinates estimation is proposed via generalised pattern search (A dynamic version was presented in [22] for mobile nodes).
- The linear Cramer-Rao bound (LCRB) is derived for the WLLS algorithm.
- A more practical scenario for simulation is considered where the TNs are situated inside as well as outside the convex hull defined by ANs.
2. System Model
3. Weighted Linear Least Squares Algorithm
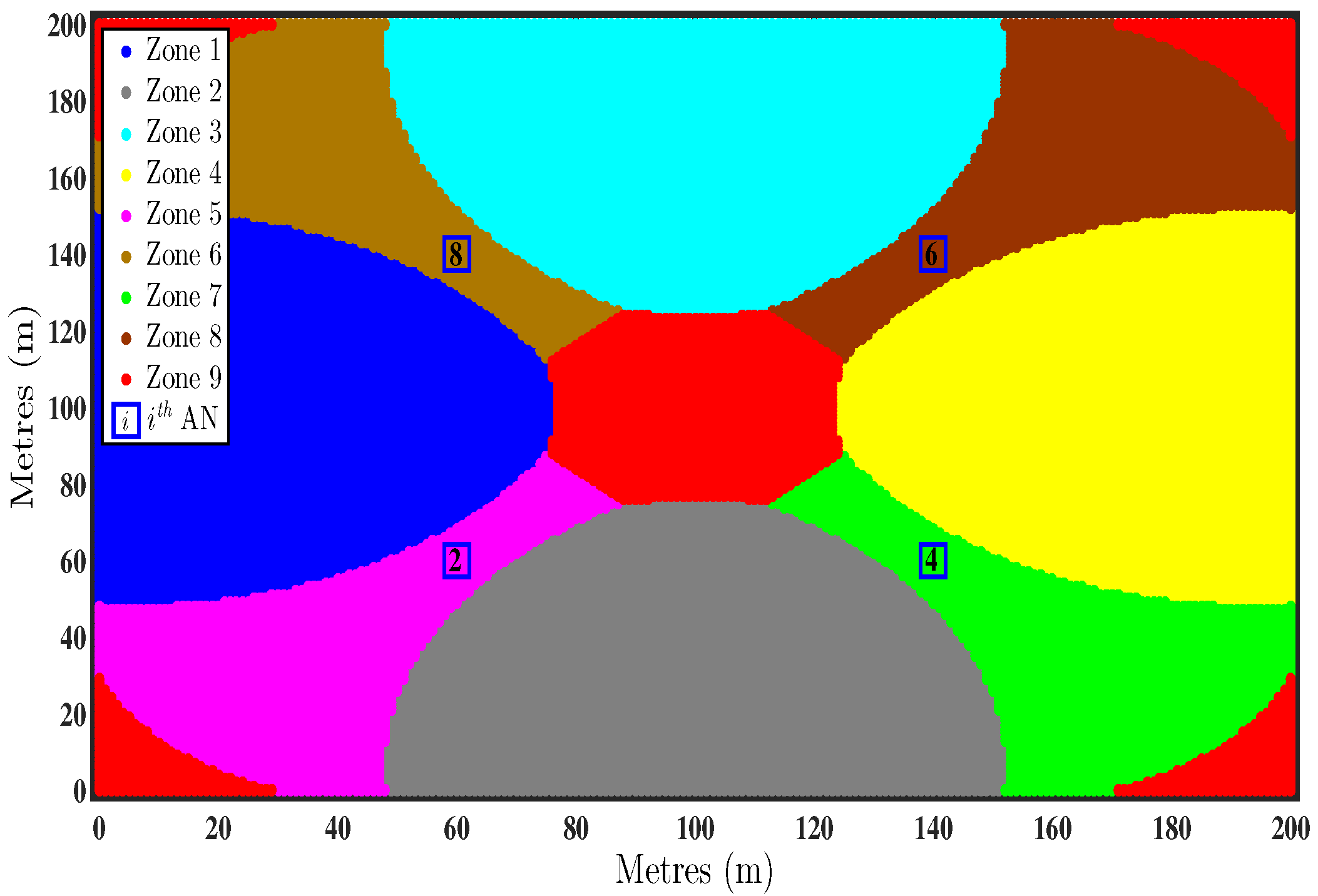
4. Two Step Optimal AN Selection
5. Estimation of Unknown PLE
Generalised Pattern Search
| Algorithm 1: Generalised Pattern Search |
| for |
| i. Initialize , |
| ii. Evaluate with all poll points from poll set . |
| iii-a. If improved poll point is found, accept set . |
| iii-b. If improved poll point cannot be found, set , set . |
| Repeat until . |
| end |
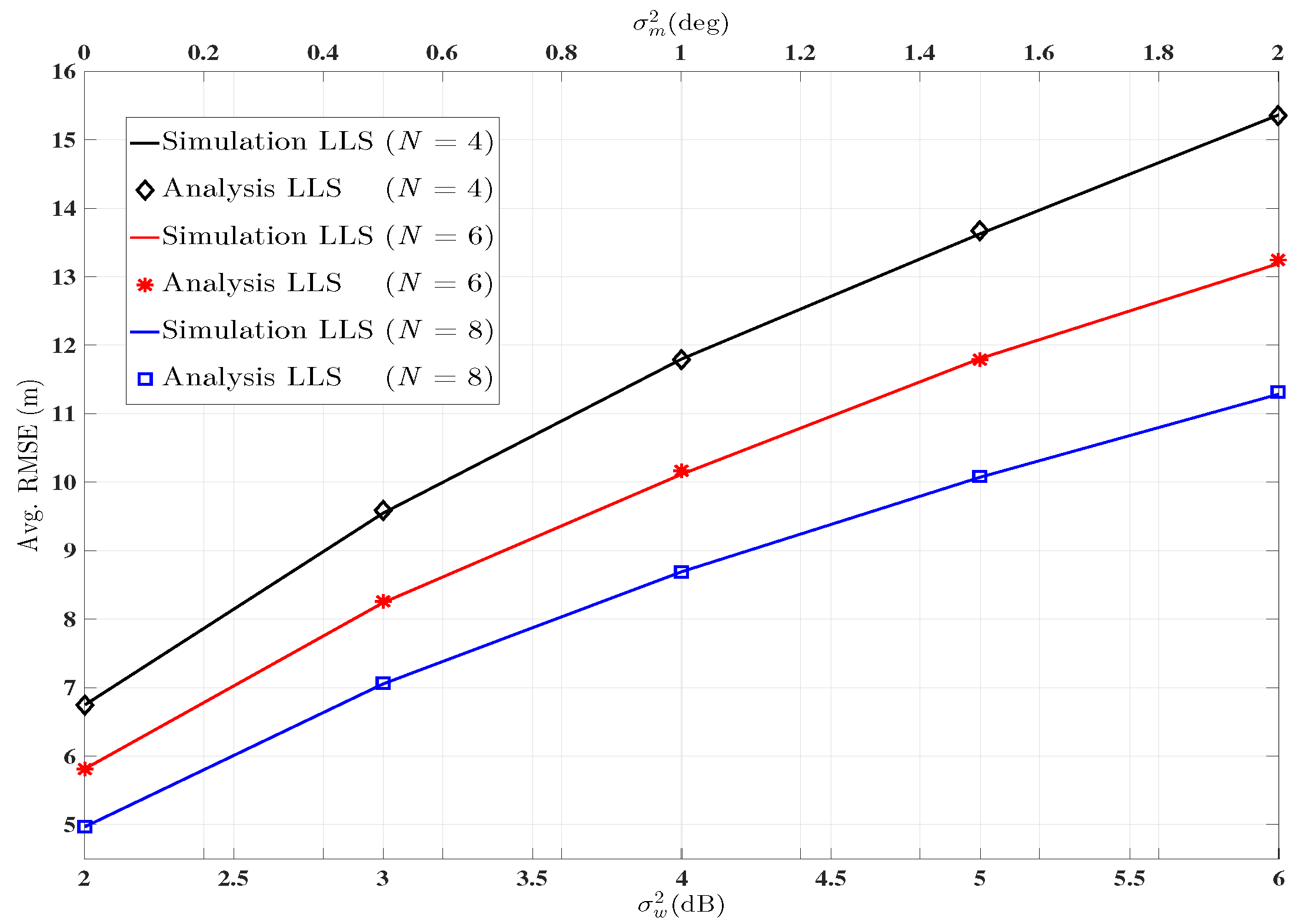
6. Linear Cramer-Rao Bound
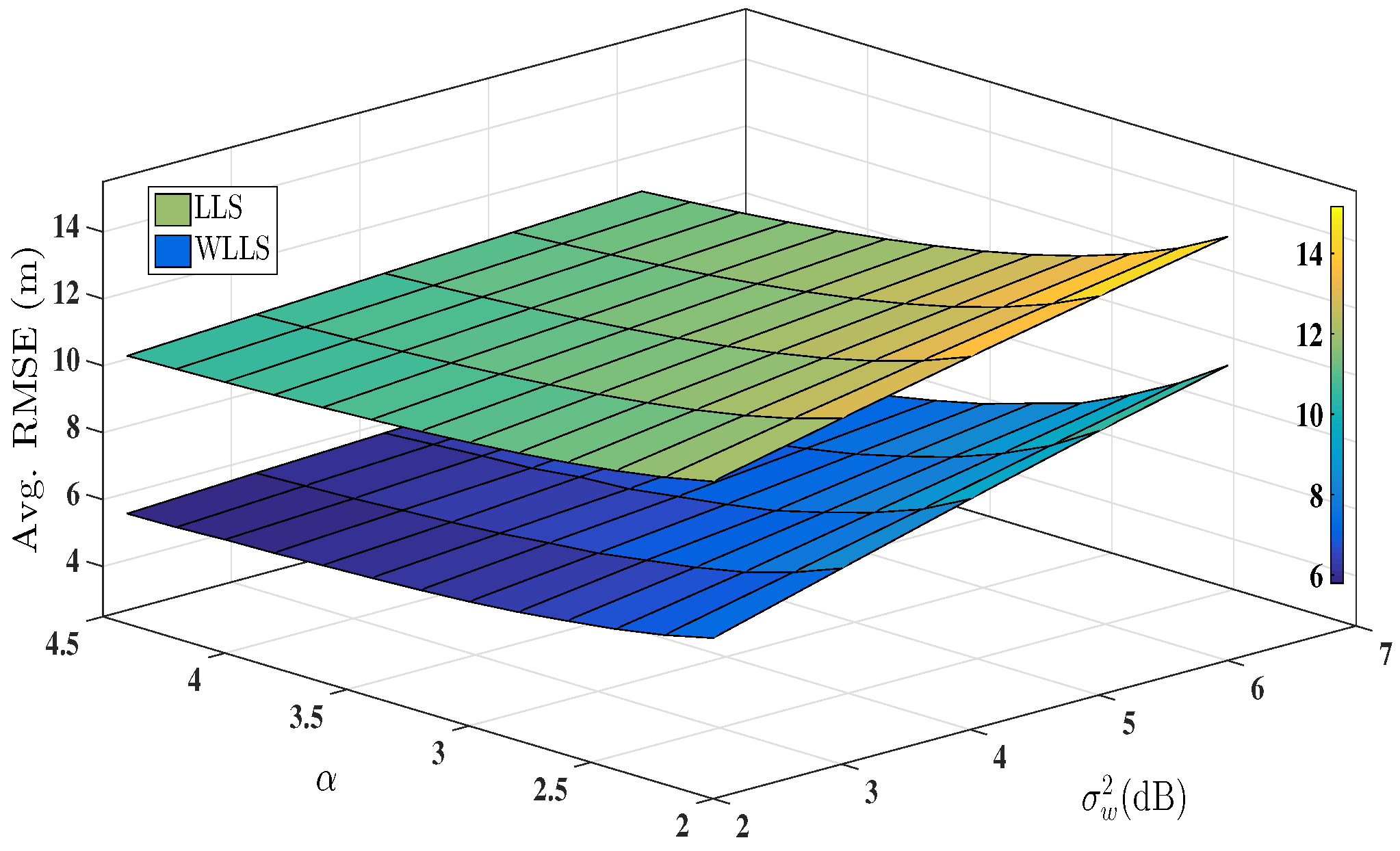
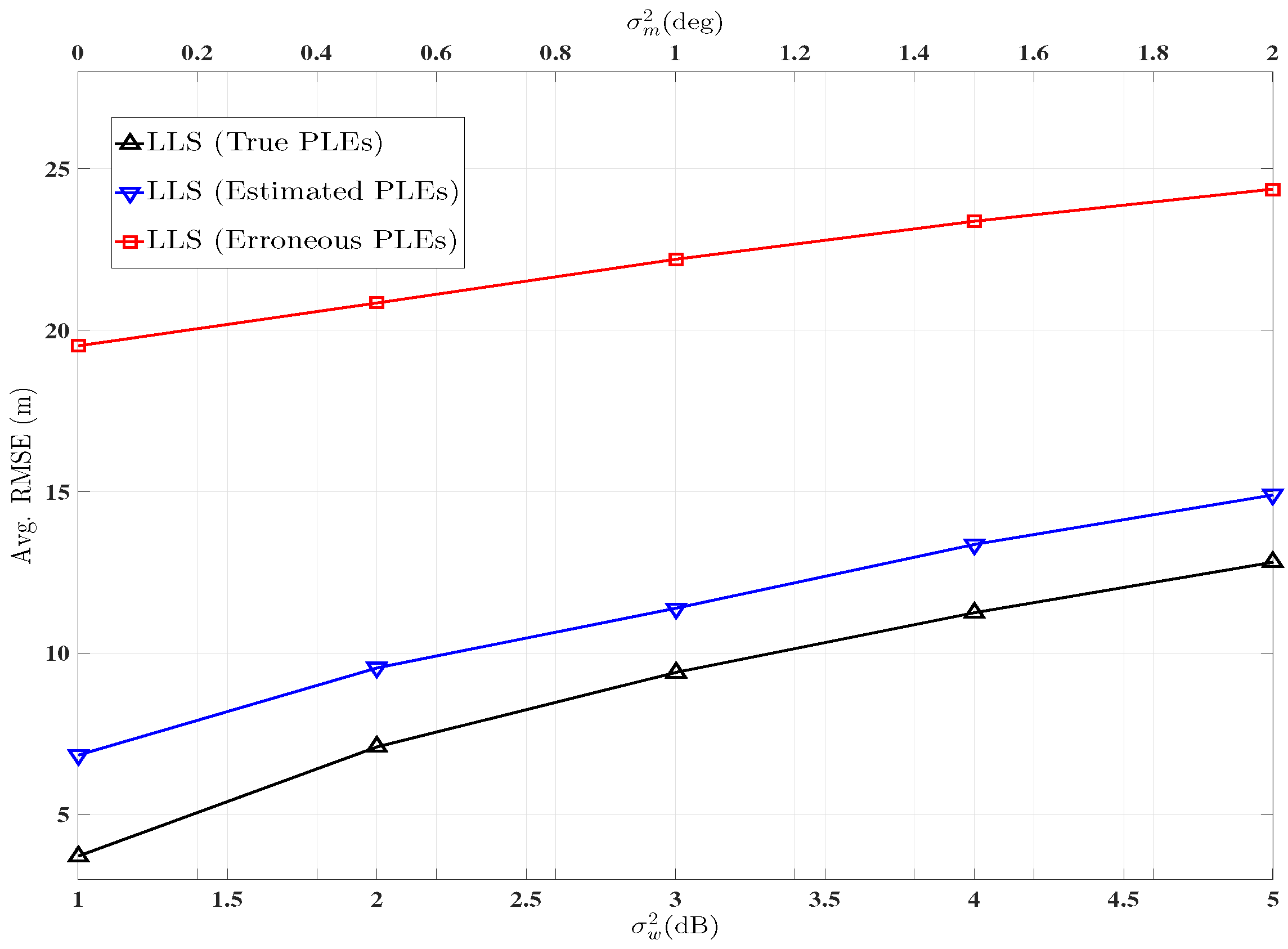
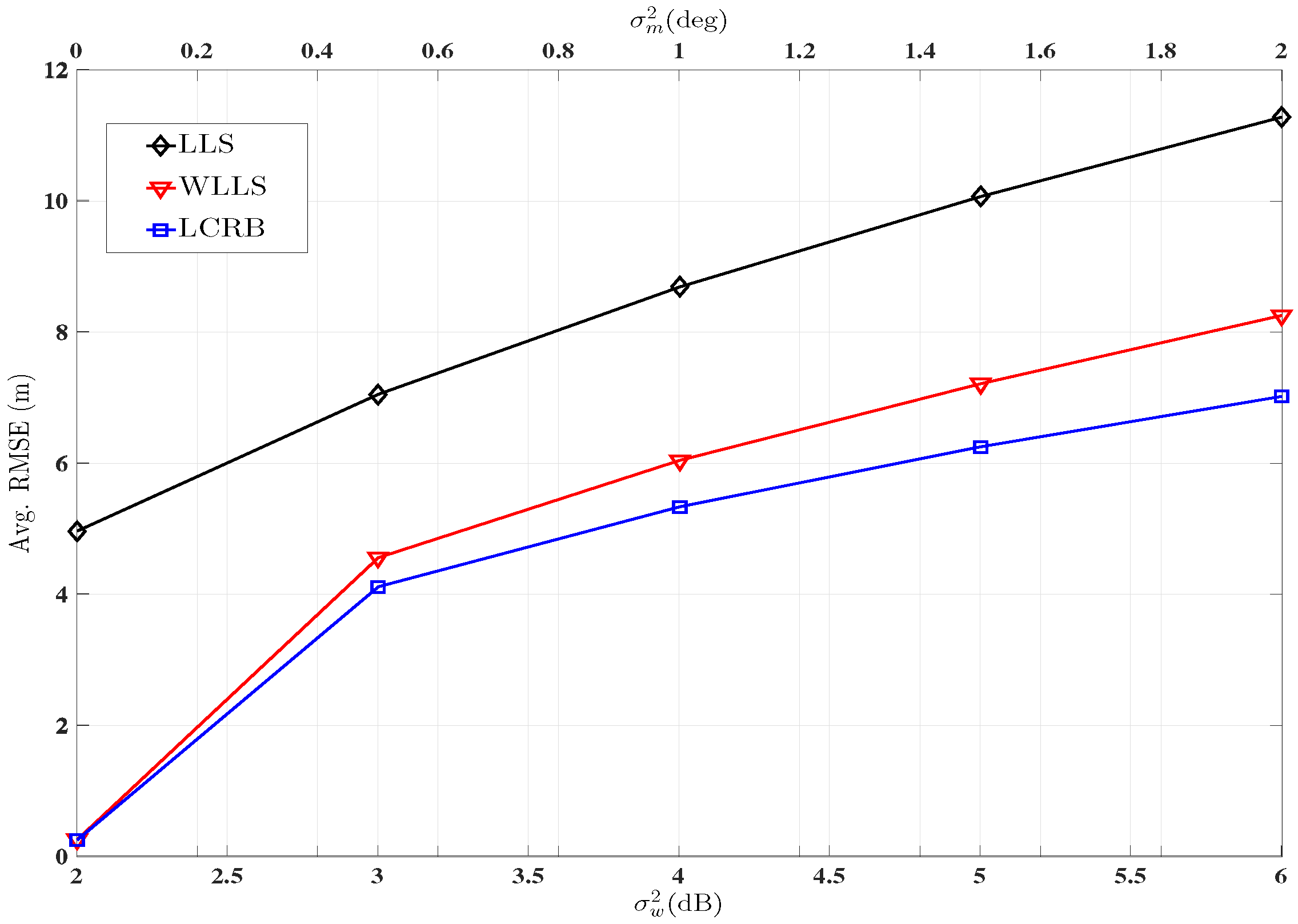
7. Simulation Results
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AN | Anchor node |
| TN | Target Node |
| AoA | Angle of Arrival |
| RSS | Received Signal Strength |
| ToA | Time of Arrival |
| MSE | Mean Squares Error |
| Avg. RMSE | Average Root Mean Squares Error |
| LLS | Linear Least Squares |
| WLLS | Weighted Linear Least Squares |
| PLE | Path-loss Exponent |
| LCRB | Linear Cramer-Rao Bound |
| FIM | Fisher Information Matrix |
Appendix A. Derivation of Unbiasing Constant
Appendix B. Derivation of FIM
References
- Patwari, N.; Ash, J.; Kyperountas, S.; Hero, A.; Moses, R.; Correal, N. Locating the nodes: Cooperative localization in wireless sensor networks. IEEE Signal Process. Mag. 2005, 22, 54–69. [Google Scholar] [CrossRef]
- Guvenc, I.; Chong, C.C. A Survey on TOA Based Wireless Localization and NLOS Mitigation Techniques. IEEE Commun. Surv. Tutor. 2009, 11, 107–124. [Google Scholar] [CrossRef]
- Salman, N.; Ghogho, M.; Kemp, A.H. Optimized Low Complexity Sensor Node Positioning in Wireless Sensor Networks. IEEE Sens. J. 2014, 14, 39–46. [Google Scholar] [CrossRef]
- Patwari, N.; Hero, A.; Perkins, M.; Correal, N.; O’Dea, R. Relative location estimation in wireless sensor networks. IEEE Trans. Signal Process. 2003, 51, 2137–2148. [Google Scholar] [CrossRef]
- Caffery, J.J. A new approach to the geometry of TOA location. In Proceedings of the 52nd Vehicular Technology Conference, Boston, MA, USA, 24–28 September 2000; Volume 4, pp. 1943–1949.
- Guvenc, I.; Gezici, S.; Sahinoglu, Z. Fundamental limits and improved algorithms for linear least-squares wireless position estimation. Wirel. Commun. Mob. Comput. 2012, 12, 1037–1052. [Google Scholar] [CrossRef]
- Chen, H.C.; Lin, T.H.; Kung, H.; Lin, C.K.; Gwon, Y. Determining RF angle of arrival using COTS antenna arrays: A field evaluation. In Proceedings of the IEEE Military Communications Conference, Orlando, FL, USA, 29 October–1 November 2012; pp. 1–6.
- Nasipuri, A.; Li, K. A Directionality Based Location Discovery Scheme for Wireless Sensor Networks. In Proceedings of the 1st ACM International Workshop on Wireless Sensor Networks and Applications, Atlanta, GA, USA, 28 September 2002; ACM: New York, NY, USA, 2002; pp. 105–111. [Google Scholar]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-Estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Yu, K. 3-D localization error analysis in wireless networks. IEEE Trans. Wirel. Commun. 2007, 6, 3472–3481. [Google Scholar]
- Khan, M.; Salman, N.; Kemp, A.H. Enhanced hybrid positioning in wireless networks I: AoA-ToA. In Proceedings of the IEEE International Conference on Telecommunications and Multimedia (TEMU), Heraklion, Greece, 28–30 July 2014; pp. 86–91.
- Jiang, J.R.; Lin, C.M.; Lin, F.Y.; Huang, S.T. ALRD: AoA localization with RSSI differences of directional antennas for wireless sensor networks. In Proceedings of the International Conference on Information Society (i-Society), London, UK, 25–28 June 2012; pp. 304–309.
- Bishop, A.N.; Fidan, B.; Doğançay, K.; Anderson, B.D.O.; Pathirana, P.N. Exploiting Geometry for Improved Hybrid AOA/TDOA-based Localization. Signal Process. 2008, 88, 1775–1791. [Google Scholar] [CrossRef]
- Wang, Y.; Wiemeler, M.; Zheng, F.; Xiong, W.; Kaiser, T. Two-step hybrid self-localization using unsynchronized low-complexity anchors. In Proceedings of the International Conference on Localization and GNSS (ICL-GNSS), Turin, Italy, 25–27 June 2013; pp. 1–5.
- Khan, M.; Salman, N.; Kemp, A.H. Cooperative positioning using angle of arrival and time of arrival. In Proceedings of the Sensor Signal Processing for Defence (SSPD), Edinburgh, UK, 8–9 September 2014; pp. 1–5.
- Horiba, M.; Okamoto, E.; Shinohara, T.; Matsumura, K. An improved NLOS detection scheme for hybrid-TOA/AOA-based localization in indoor environments. In Proceedings of the IEEE International Conference on Ultra-Wideband (ICUWB), Sydney, Australia, 15–18 September 2013; pp. 37–42.
- Lategahn, J.; Muller, M.; Rohrig, C. TDoA and RSS Based Extended Kalman Filter for Indoor Person Localization. In Proceedings of the 78th IEEE Vehicular Technology Conference (VTC Fall), Las Vegas, NV, USA, 2–5 September 2013; pp. 1–5.
- Tennina, S.; Di Renzo, M.; Kartsakli, E.; Graziosi, F.; Lalos, A.S.; Antonopoulos, A.; Mekikis, P.V.; Alonso, L. WSN4QoL: A WSN-Oriented Healthcare System Architecture. Int. J. Distrib. Sens. Netw. 2014, 2014, 503417. [Google Scholar] [CrossRef]
- Salman, N.; Kemp, A.H.; Ghogho, M. Low Complexity Joint Estimation of Location and Path-Loss Exponent. IEEE Wirel. Commun. Lett. 2012, 1, 364–367. [Google Scholar] [CrossRef]
- Li, X. RSS-Based Location Estimation with Unknown Pathloss Model. IEEE Trans. Wirel. Commun. 2006, 5, 3626–3633. [Google Scholar] [CrossRef]
- Khan, M.W.; Kemp, A.H.; Salman, N.; Mihaylova, L.S. Tracking of wireless mobile nodes in the presence of unknown path-loss characteristics. In Proceedings of the 18th International Conference on Information Fusion (Fusion), Washington, DC, USA, 6–9 July 2015; pp. 104–111.
- Yu, K.; Guo, Y. Statistical NLOS Identification Based on AOA, TOA, and Signal Strength. IEEE Trans. Veh. Technol. 2009, 58, 274–286. [Google Scholar] [CrossRef]
- Guvenc, I.; Chong, C.C.; Watanabe, F. NLOS Identification and Mitigation for UWB Localization Systems. In Proceedings of the IEEE Wireless Communications and Networking Conference, Hong Kong, China, 11–15 March 2007; pp. 1571–1576.
- Salman, N.; Khan, M.W.; Kemp, A.H. Enhanced hybrid positioning in wireless networks II: AoA-RSS. In Proceedings of the IEEE International Conference on Telecommunications and Multimedia (TEMU), Heraklion, Greece, 28–30 July 2014; pp. 92–97.
- Tang, H.; Park, Y.; Qiu, T. A TOA-AOA-based NLOS Error Mitigation Method for Location Estimation. EURASIP J. Adv. Signal Process. 2008, 2008, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.; Brown, A.K.; Malik, W.Q.; Edwards, D.J. High Resolution 3-D Angle of Arrival Determination for Indoor UWB Multipath Propagation. IEEE Trans. Wirel. Commun. 2008, 7, 3047–3055. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, S.-X. Azimuth and elevation estimation for multipath signals exploiting cyclostationarity and temporal smoothing technology. In Proceedings of the IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Beijing, China, 8–12 August 2005; Volume 2, pp. 1066–1070.
- Salman, N.; Ghogho, M.; Kemp, A.H. On the Joint Estimation of the RSS-Based Location and Path-loss Exponent. IEEE Wirel. Commun. Lett. 2012, 1, 34–37. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice Hall, Inc.: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Rappaport, T. Wireless Communications: Principles and Practice; Prentice-Hal: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Audet, C.; Dennis, J.E. Analysis of Generalized Pattern Searches. SIAM J. Optim. 2000, 13, 889–903. [Google Scholar] [CrossRef]

| S.No | Symbol | Description |
|---|---|---|
| 1 | Angle noise variance | |
| 2 | Shadowing noise variance | |
| 3 | PLE associated with ith link | |
| 4 | Initial PLE assumption (for initialising GenPS) | |
| 5 | Standard deviation of erroneous PLE | |
| 6 | Initial step size in GenPS | |
| 7 | Step size at kth iteration | |
| 8 | ξ | Step size indicator in GenPS |
| 9 | τ | Stopping criteria for GenPS |
| 10 | ℓ | Number of iterations |
| Zones | Optimal AN Combination |
|---|---|
| Zone 1 | |
| Zone 2 | |
| Zone 3 | |
| Zone 4 | |
| Zone 5 | |
| Zone 6 | |
| Zone 7 | |
| Zone 8 | |
| Zone 9 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.W.; Salman, N.; Kemp, A.H.; Mihaylova, L. Localisation of Sensor Nodes with Hybrid Measurements in Wireless Sensor Networks . Sensors 2016, 16, 1143. https://doi.org/10.3390/s16071143
Khan MW, Salman N, Kemp AH, Mihaylova L. Localisation of Sensor Nodes with Hybrid Measurements in Wireless Sensor Networks . Sensors. 2016; 16(7):1143. https://doi.org/10.3390/s16071143
Chicago/Turabian StyleKhan, Muhammad W., Naveed Salman, Andrew H. Kemp, and Lyudmila Mihaylova. 2016. "Localisation of Sensor Nodes with Hybrid Measurements in Wireless Sensor Networks " Sensors 16, no. 7: 1143. https://doi.org/10.3390/s16071143
APA StyleKhan, M. W., Salman, N., Kemp, A. H., & Mihaylova, L. (2016). Localisation of Sensor Nodes with Hybrid Measurements in Wireless Sensor Networks . Sensors, 16(7), 1143. https://doi.org/10.3390/s16071143







