Incentives for Delay-Constrained Data Query and Feedback in Mobile Opportunistic Crowdsensing
Abstract
:1. Introduction
1.1. Incentives and Selfishness
1.2. Contribution of this Work
2. Related Work
3. Proposed Incentive Scheme for Delay-Constrained Data Query and Feedback
3.1. Preliminaries
3.1.1. Deliveries
3.1.2. Appraisal
3.1.3. Delay-Constrained Category Contact Probability
3.2. Reward
3.3. Utility Function
3.4. Overview of the Proposed Scheme
- When User i meets User j, he or she first updates his or her , and , respectively. User i creates his or her candidate query, reply and feedback lists, i.e., , and . , and are sorted in a decreasing order of the reward of data packets. Note that they are the queries, replies and feedbacks at User j, but not at User i.
- User i checks if he or she is a data provider for any query in . If he or she is, User i requests those queries from User j. For each received query, e.g., Query q, User i replies to it, gives it back and authorizes User j to deliver it to the query issuer. Upon receiving the reply, User j decreases the deliveries of Query q by one, i.e., .
- User i checks if it is a query issuer of any reply in . If it is, User i pays User j a number of credits, which are equal to the appraisal of the reply, and User j removes the reply from .
- User i checks if he or she is a receiver for any feedback in . If he or she is, User i pays User j a number of credits, which are equal to the appraisal of the feedback, and User j removes the feedback from . At the same time, User j examines if he or she is a data provider for queries, a query issuer for replies or a receiver for feedbacks similarly.
- Users i and j bargain about which queries, replies and feedbacks should be traded. The bargaining process is formulated as a two-person cooperative game, and the Nash theorem is applied to reach the optimal solution. Users i and j exchange queries, replies and feedbacks pair by pair according to the Nash bargaining solution.
| Algorithm 1: Incentive algorithm for delay-constrained data query and feedback. |
|
3.5. Game Theory Model
4. Distributed Online Auction Algorithm
4.1. Analysis
4.2. Protocol Design
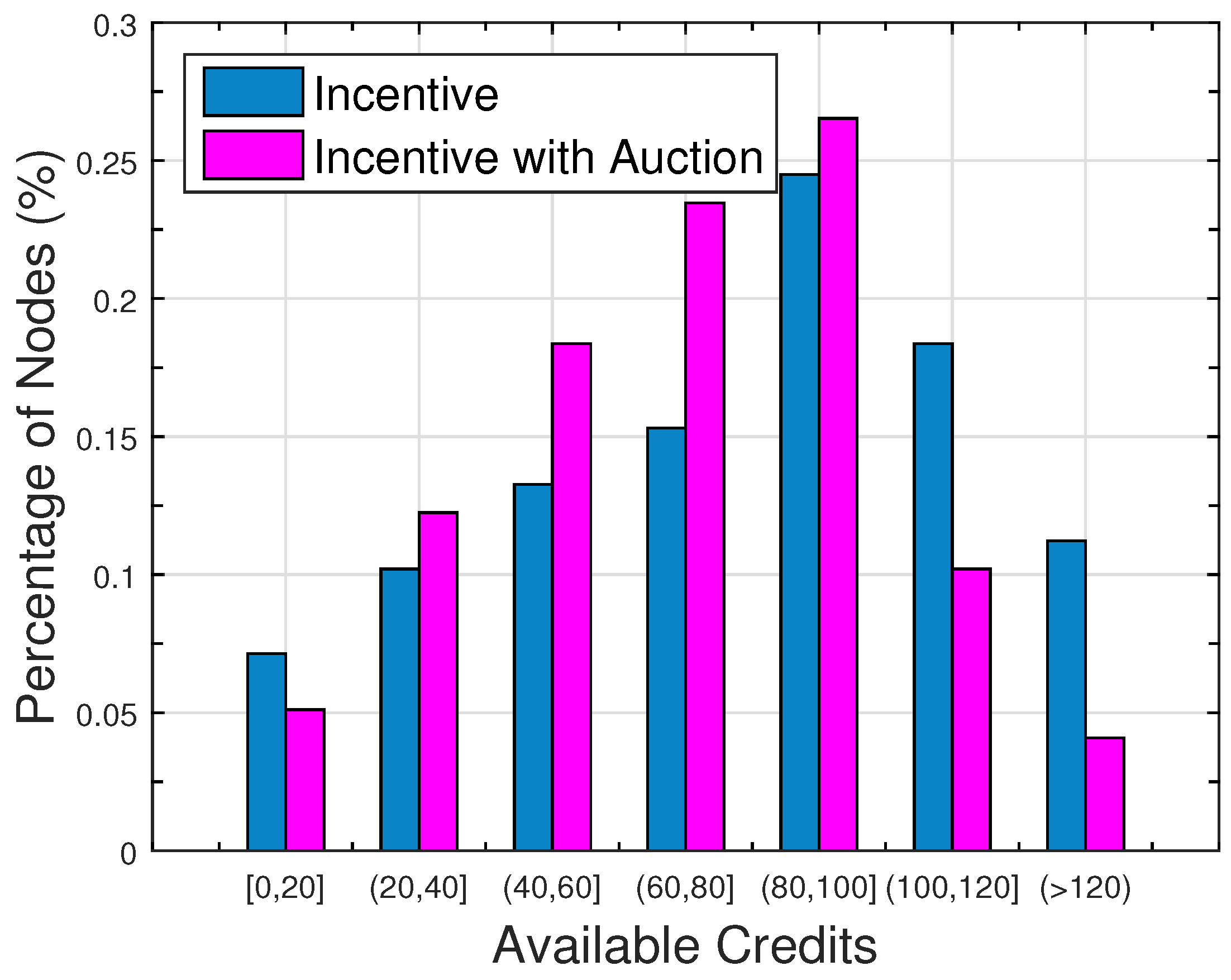
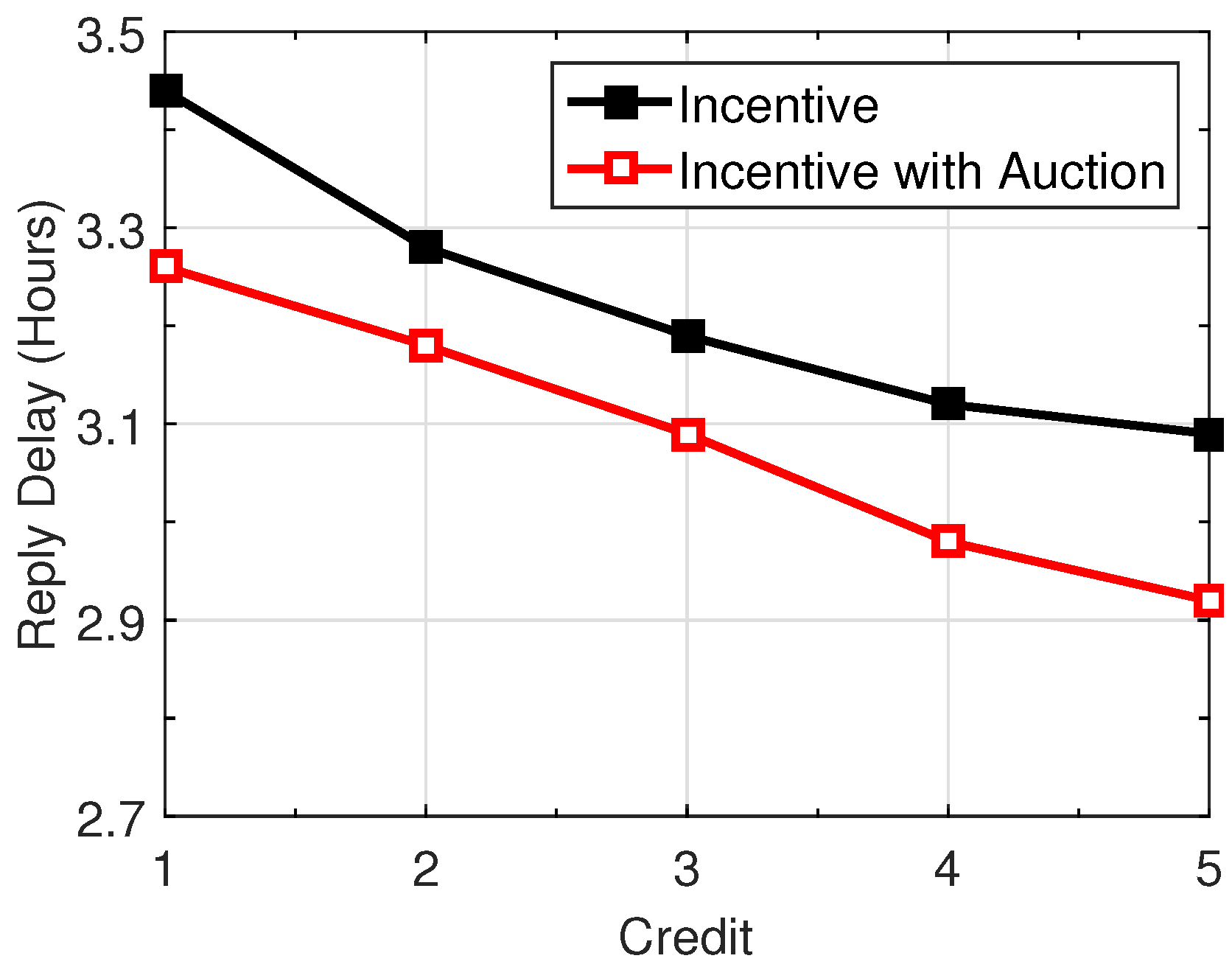
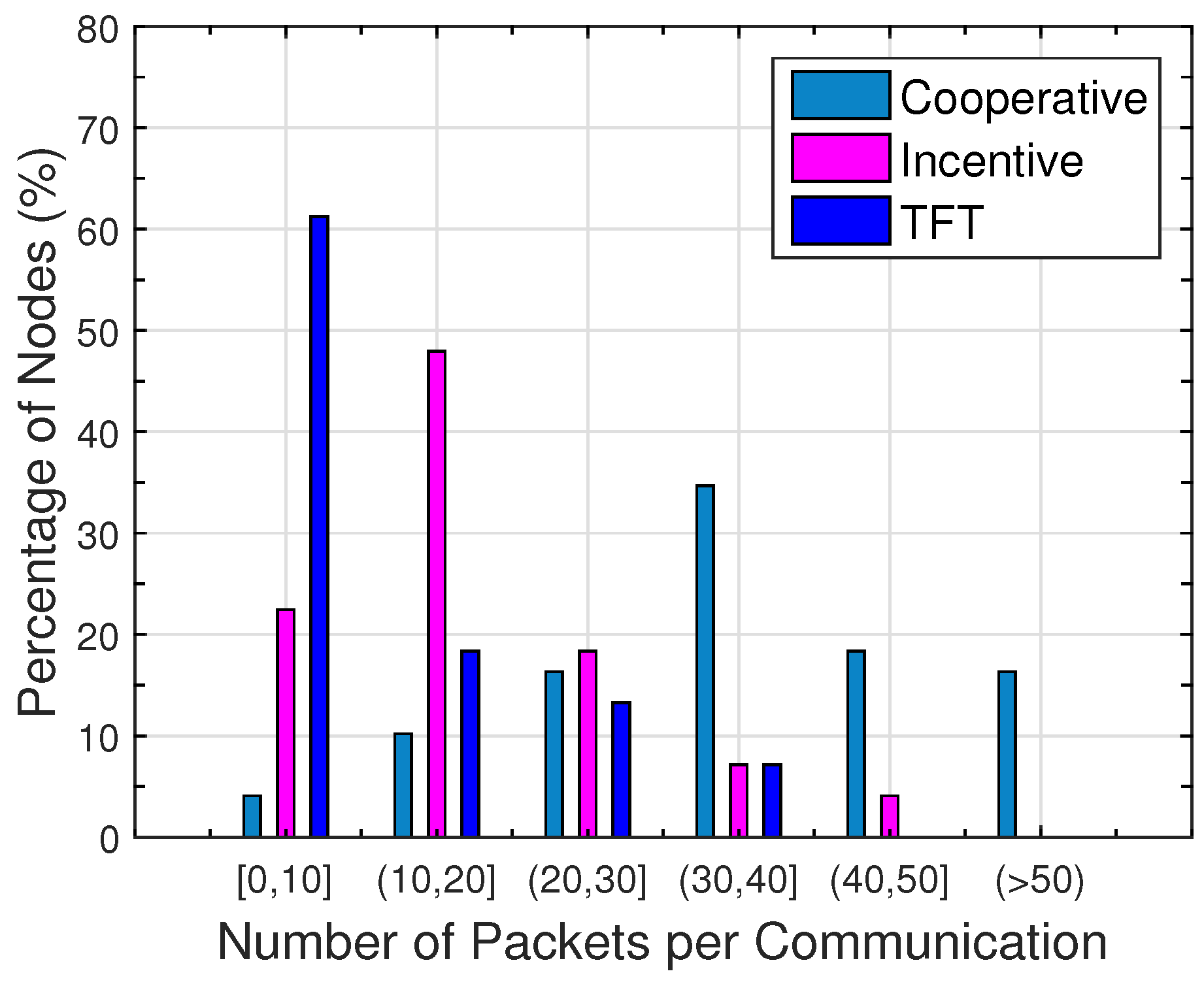
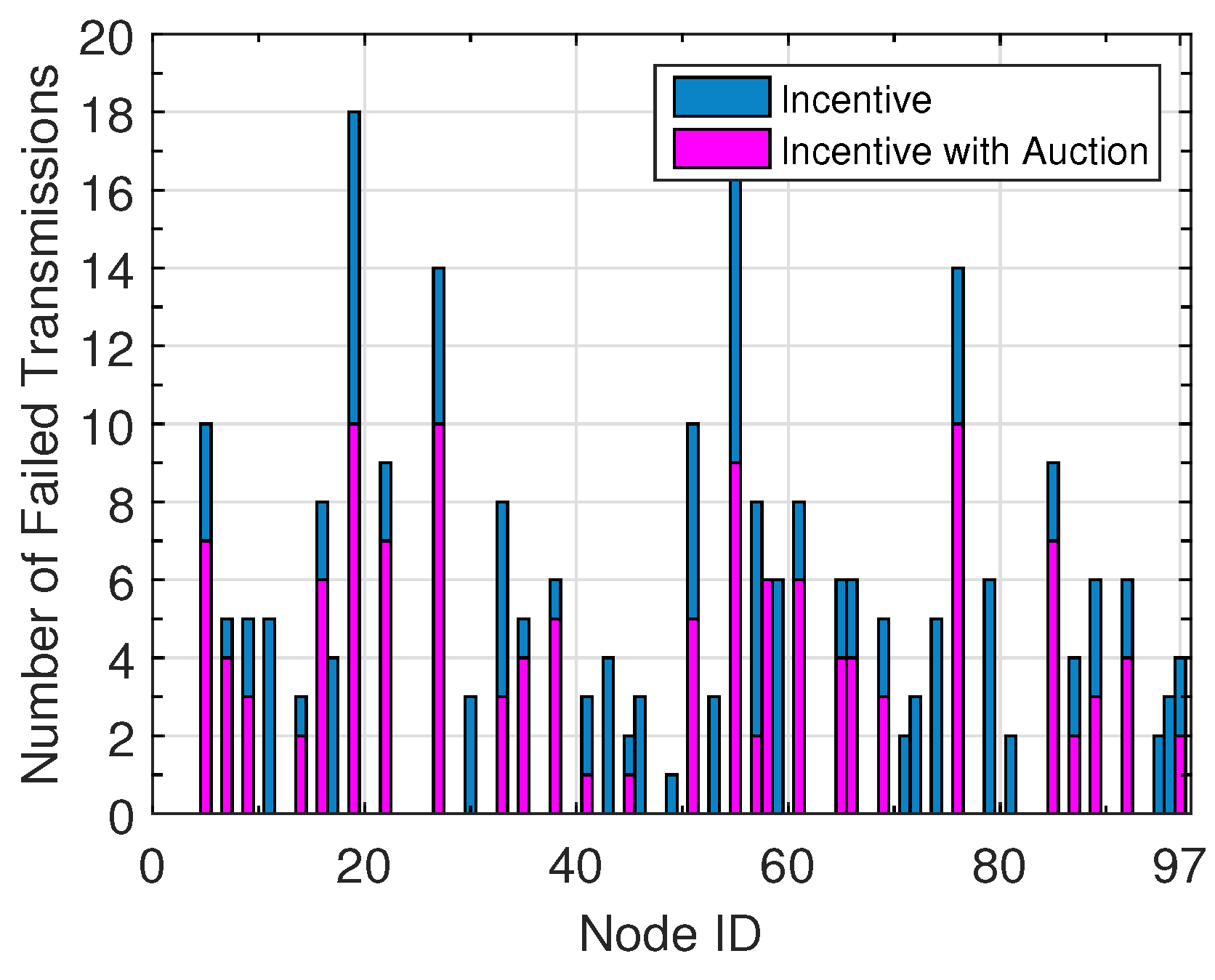
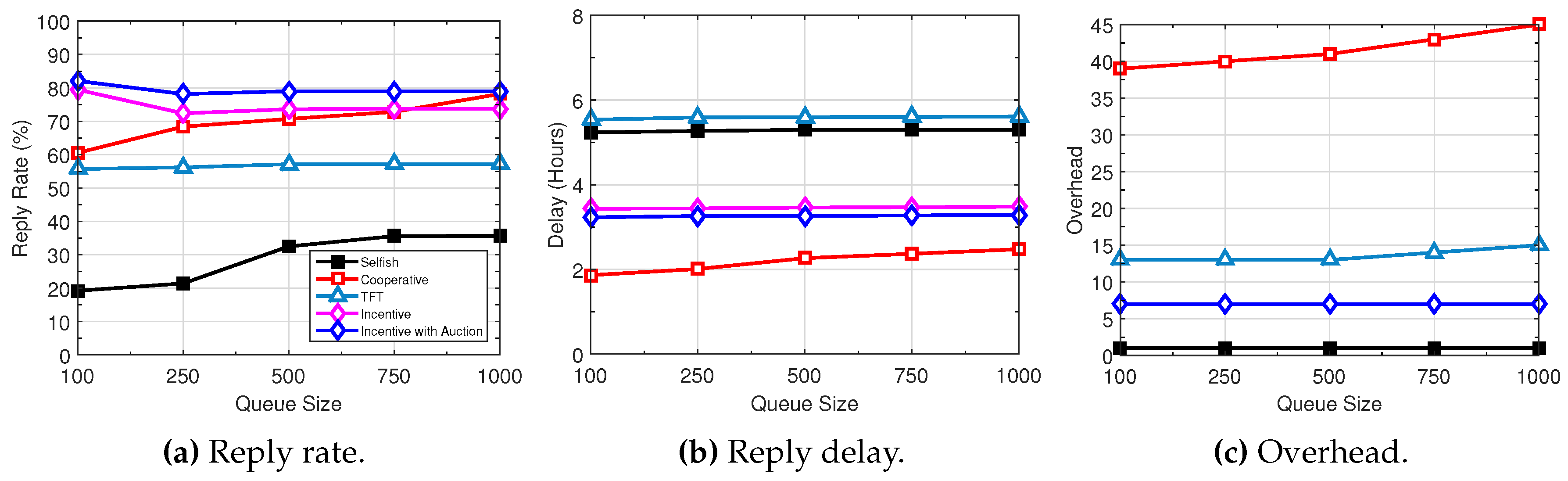
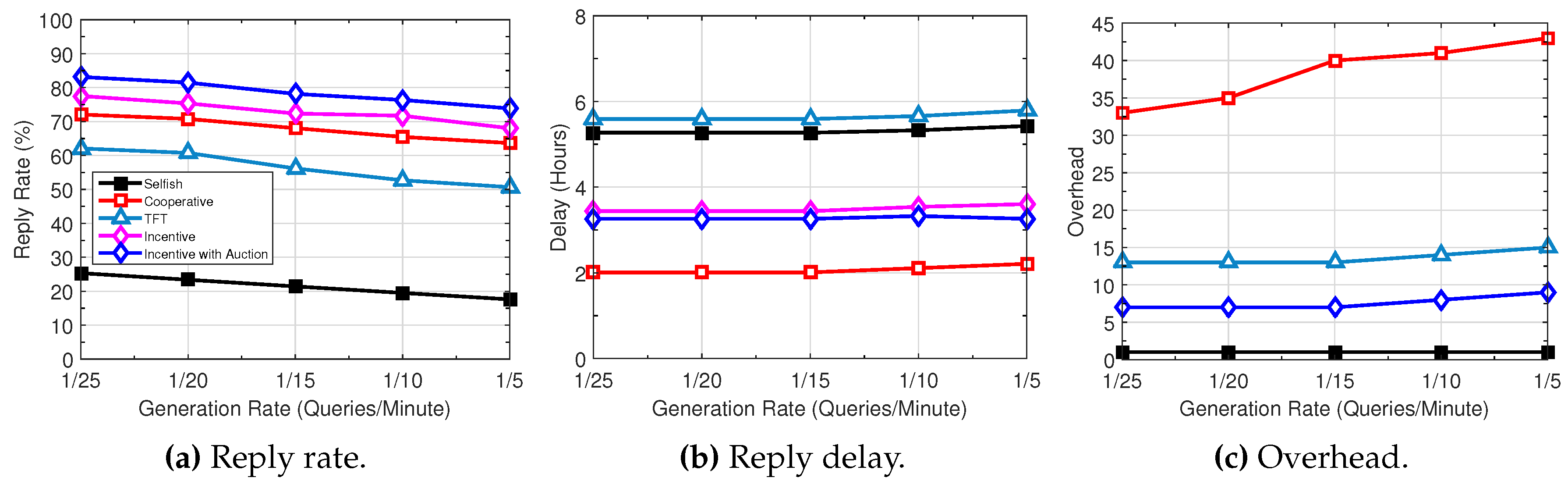
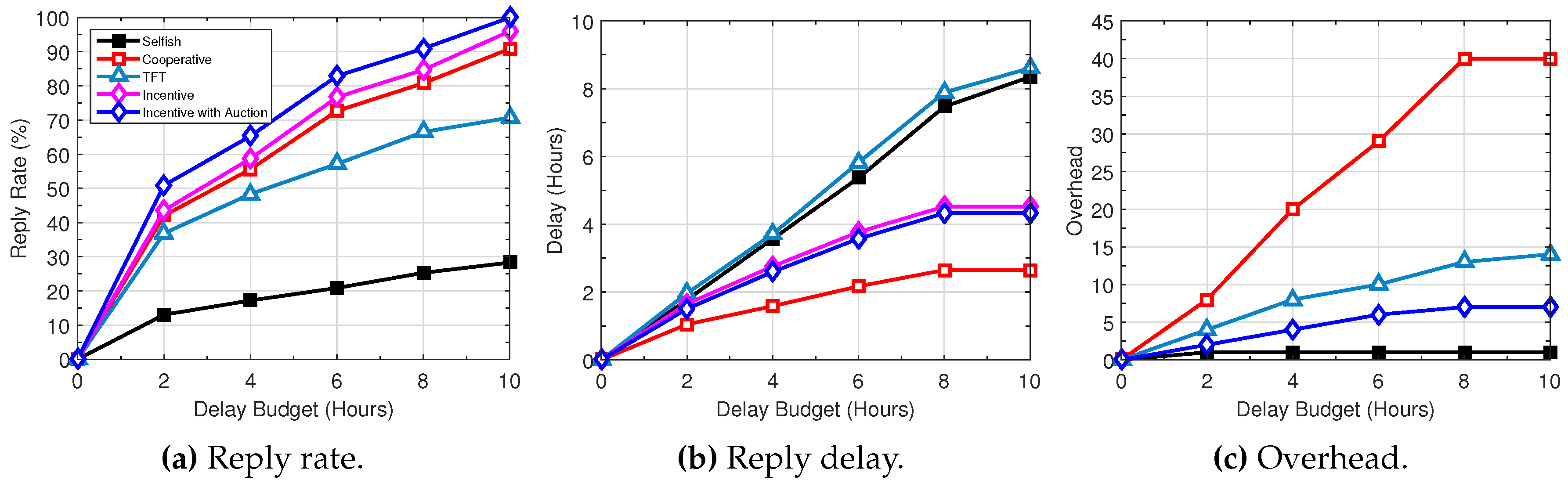
5. Performance Evaluation
5.1. Simulation Setup
5.2. Performance Comparison
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guo, B.; Wang, Z.; Yu, Z.; Wang, Y.; Yen, N.Y.; Huang, R.; Zhou, X. Mobile Crowd Sensing and Computing: The Review of an Emerging Human-Powered Sensing Paradigm. ACM Comput. Surv. 2015, 48, 7:1–7:31. [Google Scholar] [CrossRef]
- Wu, Z.; Li, J.; Yu, J.; Zhu, Y.; Xue, G.; Li, M. Poster: L3: Sensing Driving Conditions for Vehicle Lane-Level Localization on Highways. In Proceedings of the 13th ACM Conference on Embedded Networked Sensor Systems, Seoul, Korea, 2–5 November 2015; pp. 391–392.
- Zhu, Y.; Li, J.; Liu, L.; Tham, C.K. iCal: Intervention-free Calibration for Measuring Noise with Smartphones. In Proceedings of the 21st IEEE International Conference on Parallel and Distributed Systems, Melbourne, Australia, 14–18 December 2015; pp. 85–91.
- Tobe, Y.; Usami, I.; Kobana, Y.; Takahashi, J.; Lopez, G.; Thepvilojanapong, N. vCity Map: Crowdsensing towards Visible Cities. In Proceedings of the IEEE SENSORS 2014, Valencia, Spain, 2–5 November 2014; pp. 17–20.
- Pouryazdan, M.; Kantarci, B.; Soyata, T.; Song, H. Anchor-Assisted and Vote-Based Trustworthiness Assurance in Smart City Crowdsensing. IEEE Access 2016, 4, 529–541. [Google Scholar] [CrossRef]
- Hasenfratz, D.; Saukh, O.; Sturzenegger, S.; Thiele, L. Participatory Air Pollution Monitoring Using Smartphones. In Proceedings of the 2nd International Workshop on Mobile Sensing, Beijing, China, 16–20 April 2012.
- Wu, C.; Yang, Z.; Liu, Y. Smartphones Based Crowdsourcing for Indoor Localization. IEEE Trans. Mob. Comput. 2015, 14, 444–457. [Google Scholar] [CrossRef]
- Farshad, A.; Marina, M.K.; Garcia, F. Urban WiFi Characterization via Mobile Crowdsensing. In Proceedings of the 2014 IEEE Network Operations and Management Symposium (NOMS), Krakow, Poland, 5–9 May 2014; pp. 1–9.
- Fall, K. Delay-Tolerant Network Architecture for Challenged Internets. In Proceedings of the 2003 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, Karlsruhe, Germany, 25–29 August 2003; pp. 27–34.
- Liu, Y.; Yang, Z.; Ning, T.; Wu, H. Efficient Quality-of-Service (QoS) Support in Mobile Opportunistic Networks. IEEE Trans. Veh. Technol. 2014, 63, 4574–4584. [Google Scholar] [CrossRef]
- Spyropoulos, T.; Rais, R.N.; Turletti, T.; Obraczka, K.; Vasilakos, A. Routing for Disruption Tolerant Networks: Taxonomy and Design. Wirel. Netw. 2010, 16, 2349–2370. [Google Scholar] [CrossRef]
- Li, Z.; Li, M.; Wang, J.; Cao, Z. Ubiquitous Data Collection for Mobile Users in Wireless Sensor Networks. In Proceedings of the International Conference on Computer Communications 2011, Shanghai, China, 10–15 April 2011; pp. 2246–2254.
- Banerjee, N.; Corner, M.D.; Towsley, D.; Levine, B.N. Relays, Base Stations, and Meshes: Enhancing Mobile Networks with Infrastructure. In Proceedings of the 14th ACM International Conference on Mobile Computing and Networking, San Francisco, CA, USA, 14–19 September 2008; pp. 81–91.
- Liu, Y.; Bashar, A.M.A.E.; Li, F.; Wang, Y.; Liu, K. Multi-Copy Data Dissemination with Probabilistic Delay Constraint in Mobile Opportunistic Device-to-Device Networks. In Proceedings of the 27th IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks, Coimbra, Protugal, 21–24 June 2016.
- Wang, C.; Li, X.Y.; Jiang, C.; Yan, H. The Impact of Rate Adaptation on Capacity-Delay Tradeoffs in Mobile Ad Hoc Networks. IEEE Trans. Mob. Comput. 2014, 13, 2661–2674. [Google Scholar] [CrossRef]
- Liu, Y.; Han, Y.; Yang, Z.; Wu, H. Efficient Data Query in Intermittently-Connected Mobile Ad Hoc Social Networks. IEEE Trans. Parallel Distrib. Syst. 2015, 26, 1301–1312. [Google Scholar] [CrossRef]
- Osseiran, A.; Boccardi, F.; Braun, V.; Kusume, K.; Marsch, P.; Maternia, M.; Queseth, O.; Schellmann, M.; Schotten, H.; Taoka, H.; et al. Scenarios for 5G Mobile and Wireless Communications: The Vision of the METIS Project. IEEE Commun. Mag. 2014, 52, 26–35. [Google Scholar] [CrossRef]
- Hossain, E.; Rasti, M.; Tabassum, H.; Abdelnasser, A. Evolution Toward 5G Multi-tier Cellular Wireless Networks: An Interference Management Perspective. IEEE Wirel. Commun. 2014, 21, 118–127. [Google Scholar] [CrossRef]
- Andrews, J.; Buzzi, S.; Choi, W.; Hanly, S.; Lozano, A.; Soong, A.; Zhang, J. What Will 5G Be? IEEE J. Sel. Areas Commun. 2014, 32, 1065–1082. [Google Scholar] [CrossRef]
- Ning, T.; Yang, Z.; Xie, X.; Wu, H. Incentive-Aware Data Dissemination in Delay-Tolerant Mobile Networks. In Proceedings of the 2011 8th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, Salt Lake City, UT, USA, 27–30 June 2011; pp. 539–547.
- Xie, X.; Chen, H.; Wu, H. Bargain-based Stimulation Mechanism for Selfish Mobile Nodes in Participatory Sensing Network. In Proceedings of the 2009 6th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, Rome, Italy, 22–26 June 2009; pp. 72–80.
- Ning, T.; Yang, Z.; Wu, H.; Han, Z. Self-Interest-Driven Incentives for Ad Dissemination in Autonomous Mobile Social Networks. In Proceedings of the 2013 IEEE International Conference on Computer Communications, Turin, Italy, 14–19 April 2013; pp. 2358–2366.
- Marti, S.; Giuli, T.J.; Lai, K.; Baker, M. Mitigating Routing Misbehavior in Mobile Ad Hoc Networks. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking, Boston, MA, USA, 6–11 August 2000; pp. 255–265.
- Buttyan, L.; Hubaux, J.P. Enforcing Service Availability in Mobile Ad-hoc WANs. In Proceedings of the 1st ACM International Symposium on Mobile Ad Hoc Networking and Computing, Long Beach, CA, USA, 4–5 October 2001; pp. 87–96.
- Zhong, S.; Chen, J.; Yang, Y.R. Sprite, a Simple, Cheat-proof, Credit-based System for Mobile Ad-hoc Networks. In Proceedings of the 2003 22nd Annual Joint Conference of the IEEE Computer and Communications, San Francisco, USA, 30 March–3 April 2003; pp. 1987–1997.
- Jakobsson, M.; Hubaux, J.P.; Buttyan, L. A Micropayment Scheme Encouraging Collaboration in Multi-hop Cellular Networks. In Proceedings of the 7th International Conference on Financial Cryptography, Guadeloupe, French West Indies, 27–30 January 2003; pp. 15–33.
- Yang, D.; Xue, G.; Fang, X.; Tang, J. Crowdsourcing to Smartphones: Incentive Mechanism Design for Mobile Phone Sensing. In Proceedings of the 18th Annual International Conference on Mobile Computing and Networking, Istanbul, Turkey, 22–26 August 2012; pp. 173–184.
- Zhang, X.; Yang, Z.; Zhou, Z.; Cai, H.; Chen, L.; Li, X.Y. Free Market of Crowdsourcing: Incentive Mechanism Design for Mobile Sensing. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 3190–3200. [Google Scholar] [CrossRef]
- Wei, Y.; Zhu, Y.; Zhu, H.; Zhang, Q.; Xue, G. Truthful Online Double Auctions for Dynamic Mobile Crowdsourcing. In Proceedings of the 2015 IEEE Conference on Computer Communications (INFOCOM), HongKong, China, 26 April–1 May 2015; pp. 2074–2082.
- Hui, P.; Leguay, J.; Crowcroft, J.; Scott, J.; Friedmani, T.; Conan, V. Osmosis in Pocket Switched Networks. In Proceedings of the 2006 First International Conference on Communications and Networking, Beijing, China, 25–27 October 2006; pp. 1–6.
- Fan, J.; Chen, J.; Du, Y.; Wang, P.; Sun, Y. DelQue: A Socially Aware Delegation Query Scheme in Delay-Tolerant Networks. IEEE Trans. Veh. Technol. 2011, 60, 2181–2193. [Google Scholar] [CrossRef]
- Ning, T.; Yang, Z.; Wu, H. Counting in Delay-Tolerant Mobile Networks. In Proceedings of 2010 IEEE International Conference on Communications (ICC), Cape Town, South Africa, 23–27 May 2010; pp. 1–5.
- Jelasity, M.; Montresor, A.; Babaoglu, O. Gossip-based Aggregation in Large Dynamic Networks. ACM Trans. Comput. Syst. 2005, 23, 219–252. [Google Scholar] [CrossRef]
- Aslanyan, H.; Leone, P.; Rolim, J. Data Propagation with Guaranteed Delivery for Mobile Networks. In Proceedings of the 9th International Symposium, SEA 2010, Ischia Island, Naples, Italy, 20–22 May 2010; pp. 386–397.
- Gunawardena, D.; Karagiannis, T.; Proutiere, A. Scoop: Decentralized and Opportunistic Multicasting of Information Streams. In Proceedings of the 17th Annual International Conference on Mobile Computing and Networking, Las Vegas, NV, USA, 19–23 September 2011; pp. 169–180.
- Nash, J.F. Two-Person Cooperative Games. Econometrica 1953, 21, 128–140. [Google Scholar] [CrossRef]
- Shevade, U.; Song, H.H.; Qiu, L.; Zhang, Y. Incentive-Aware Routing in DTNs. In Proceedings of the IEEE International Conference on Network Protocols, Orlando, FL, USA, 19–22 October 2008; pp. 238–247.

| Definition | Description |
|---|---|
| The deliveries of Query q | |
| The deliveries of Feedback f | |
| The appraisal of Query q | |
| The appraisal of Feedback f | |
| The delay-constrained category contact probability () | |
| The direct delay-constrained contact probability of User i with data providers in Category c with remaining Delay Budget δ | |
| The indirect delay-constrained contact probability of User i with data providers in Category c with remaining Delay Budget δ | |
| The reward if User i trades Query q in Category c with Delay Budget δ | |
| The reward if User i trades Reply in Category c with Delay Budget δ | |
| The delay-constrained reply contact probability () | |
| The reward if User i trades Feedback f in Category c within Delay Budget δ | |
| The delay-constrained feedback contact probability () |
| Reply Rate | Reply Delay | Overhead | |
|---|---|---|---|
| Selfish | h | 1 | |
| Cooperative | h | 40 | |
| TFT | h | 13 | |
| Incentive | h | 7 | |
| Incentive with Auction | h | 7 |
| Reply Rate | Reply Delay | Overhead | |
|---|---|---|---|
| Selfish | h | 1 | |
| Cooperative | h | 42 | |
| TFT | h | 16 | |
| Incentive | h | 9 | |
| Incentive with Auction | h | 9 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, F.; Wang, Y. Incentives for Delay-Constrained Data Query and Feedback in Mobile Opportunistic Crowdsensing. Sensors 2016, 16, 1138. https://doi.org/10.3390/s16071138
Liu Y, Li F, Wang Y. Incentives for Delay-Constrained Data Query and Feedback in Mobile Opportunistic Crowdsensing. Sensors. 2016; 16(7):1138. https://doi.org/10.3390/s16071138
Chicago/Turabian StyleLiu, Yang, Fan Li, and Yu Wang. 2016. "Incentives for Delay-Constrained Data Query and Feedback in Mobile Opportunistic Crowdsensing" Sensors 16, no. 7: 1138. https://doi.org/10.3390/s16071138
APA StyleLiu, Y., Li, F., & Wang, Y. (2016). Incentives for Delay-Constrained Data Query and Feedback in Mobile Opportunistic Crowdsensing. Sensors, 16(7), 1138. https://doi.org/10.3390/s16071138






