On Inertial Body Tracking in the Presence of Model Calibration Errors
Abstract
:1. Introduction
1.1. Sensor Fusion Methods
1.2. Calibration Methods
1.3. Contributions
- The development of two EKF-based methods with different state-space models, which use the free-segments representation, inspired by [17]. These are subsequently denoted Quattracker IMU and Quattracker segment. Here, rotations are represented through unit quaternions.
- The development of an online capable version of the optimization-based method in [19], based on sliding window optimization. The method is subsequently denoted Optitracker.
- A performance comparison of the new/adapted methods with an existing EKF-based method that uses the kinematic chain representation and DH coordinates to represent joint angles [16]. Performance is measured in terms of angular error statistics on complex (i.e., simultaneous variations in all joint DoFs) moderate and fast human motion (real and simulated) and on artificially simulated complex motion from a case study. In particular, the influence of the selected model calibration errors, i.e., I2S calibration and segment length errors, on the performances of the different methods and their dependence on magnetometer usage are assessed.
2. Materials and Methods
2.1. Notation
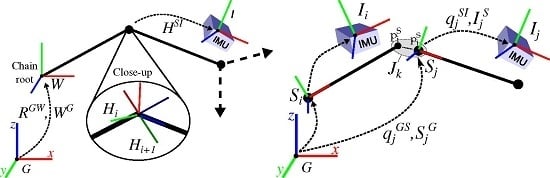
2.2. Biomechanical Model Representations
2.3. EKF-Based Methods
2.3.1. Measurement Models
2.3.2. State Spaces
2.3.3. Dynamic Models
2.3.4. Constraints
2.3.5. Initialization
2.4. Sliding Window Optimization
2.4.1. Biomechanical Constraints
2.4.2. Initialization
2.5. Summary and Overview
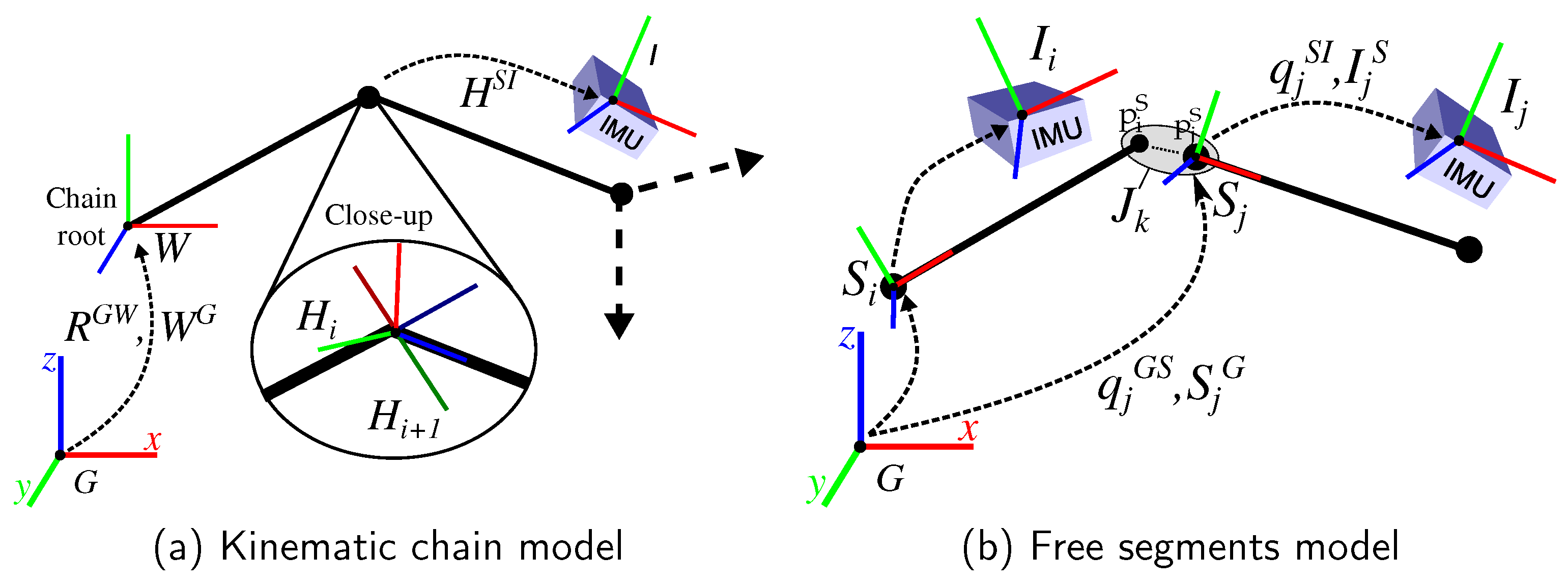
2.6. Evaluation Setup
2.6.1. Real Data Scenario
2.6.2. Real Data Scenario: Discussion of Major Error Sources
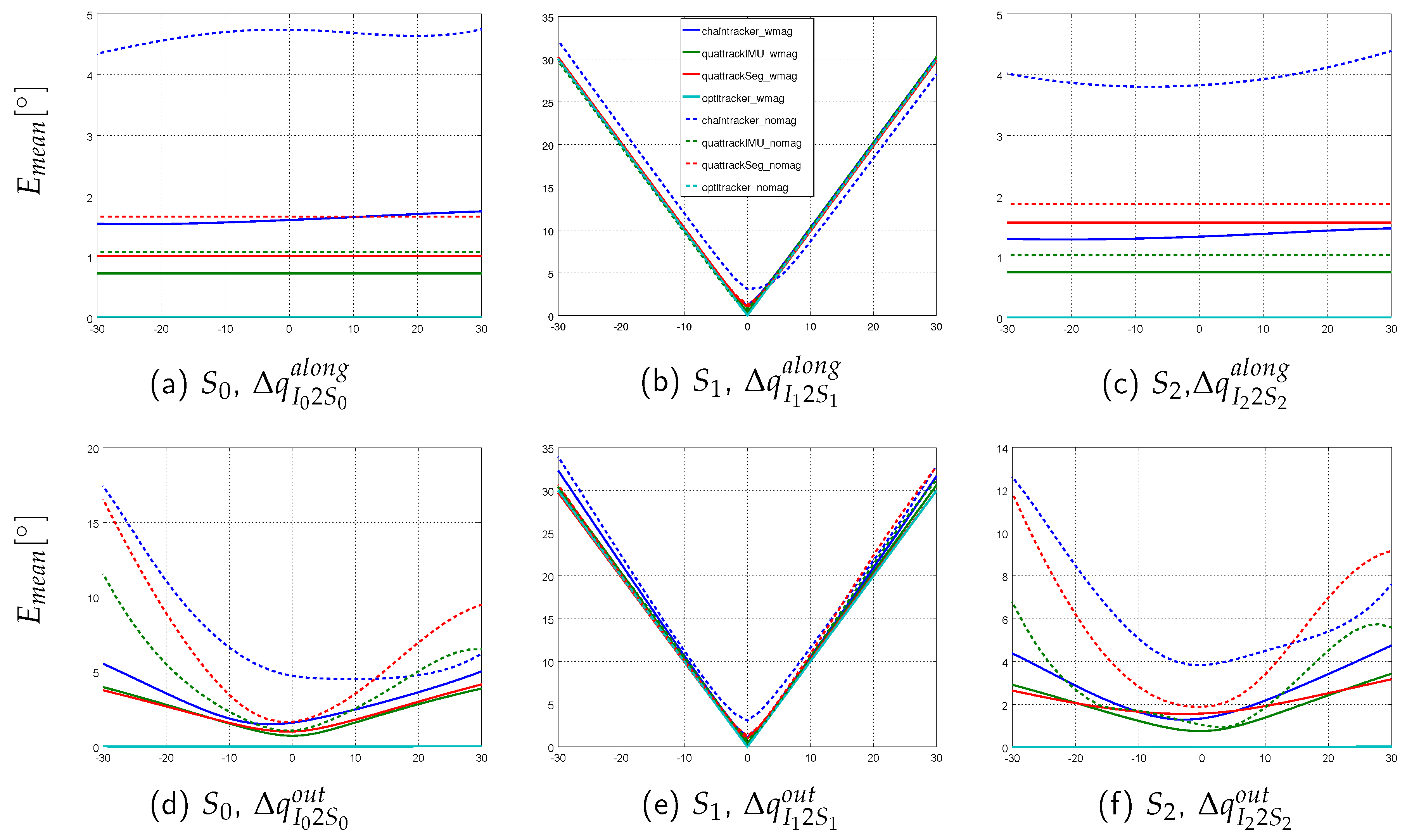
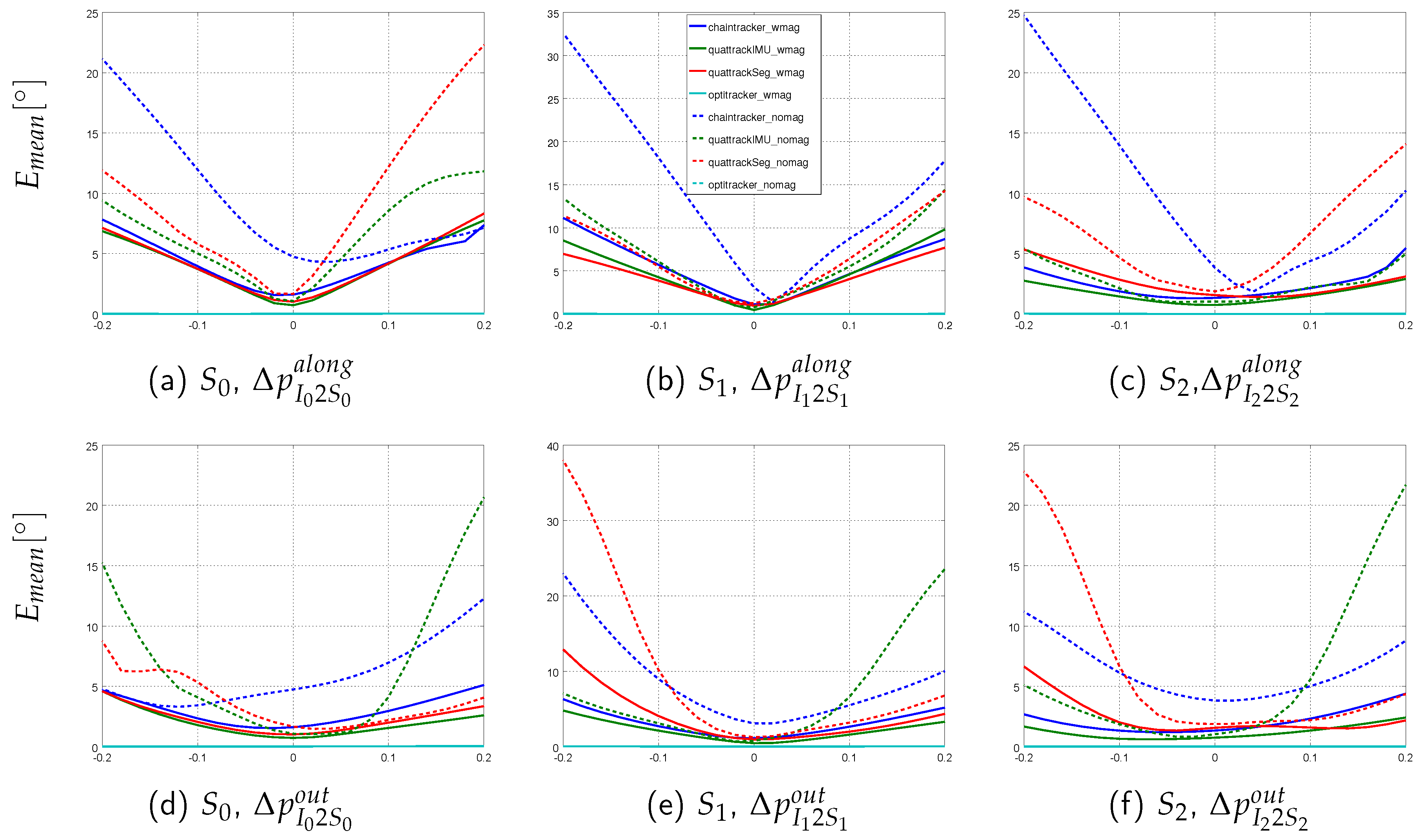
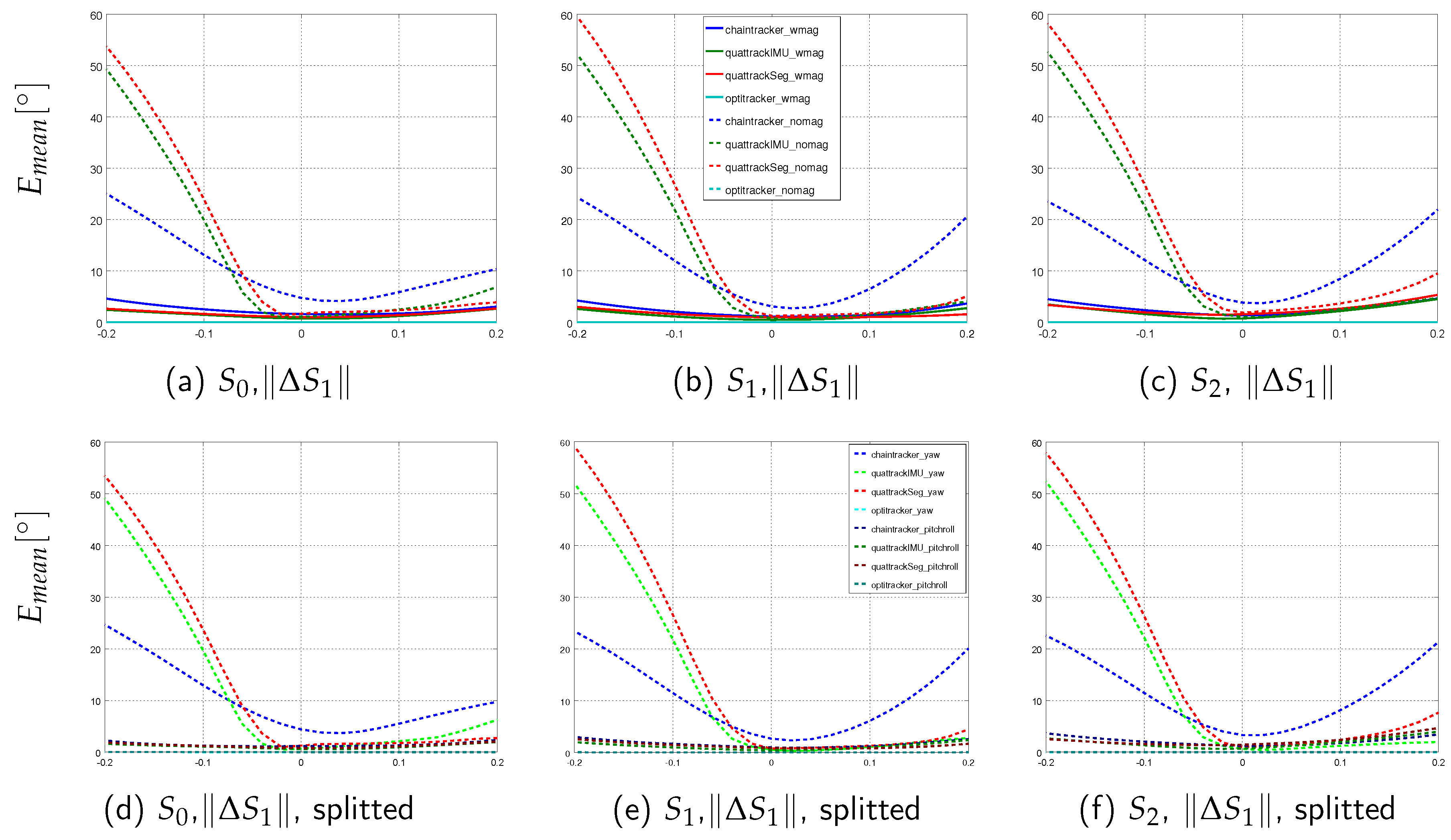
2.6.3. Simulation Scenario with Systematically Introduced Model Calibration Errors
- I2S position errors: , i.e., position changes along the segment axis.
- I2S position errors: , i.e., position changes perpendicular to the segment axis.
- Segment length variations: .
- I2S orientation errors: along the bone, i.e., rotations around the segment axis associated to the IMU.
- I2S orientation errors: out of bone, i.e., rotations around the IMU axis perpendicular to the surface of the associated segment.
2.6.4. Error Measures
3. Results
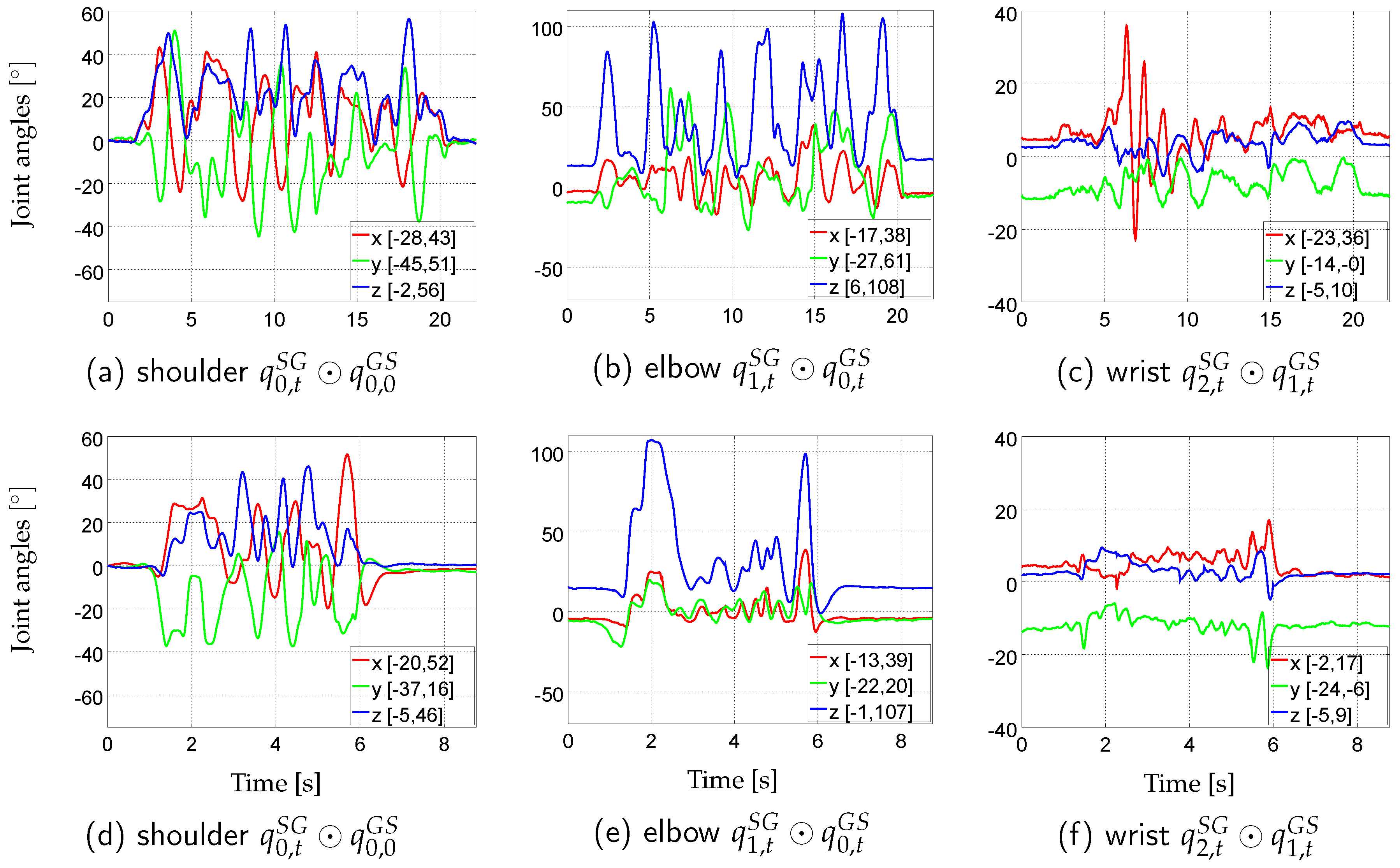
3.1. Tracking Performances on Real Data
3.2. Tracking Performances on Simulated Data with Model Calibration Errors
3.3. Tracking Performances on Simulated Data without Calibration Errors
4. Discussion and Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DH | Denavit Hartenberg |
| DoF(s) | Degree(s) of Freedom |
| EKF | Extended Kalman Filter |
| UKF | Unscented Kalman Filter |
| IMU | Inertial Measurement Unit |
| I2S | IMU-to-Segment |
| WLS | Weighted Least Squares |
Appendix A
Appendix B
Appendix C
Appendix D
| Chaintracker | Quattracker segment|IMU | Optitracker | |||
|---|---|---|---|---|---|
References
- Fong, D.T.P.; Chan, Y.Y. The use of wearable inertial motion sensors in human lower limb biomechanics studies: A systematic review. Sensors 2010, 10, 11556–11565. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.; Park, H.; Bonato, P.; Chan, L.; Rodgers, M. A review of wearable sensors and systems with application in rehabilitation. J. NeuroEng. Rehabil. 2012, 9, 21. [Google Scholar] [CrossRef] [PubMed]
- Hadjidj, A.; Souil, M.; Bouabdallah, A.; Challal, Y.; Owen, H. Wireless sensor networks for rehabilitation applications: Challenges and opportunities. J. Netw. Comput. Appl. 2013, 36, 1–15. [Google Scholar] [CrossRef]
- Zheng, Y.L.; Ding, X.R.; Poon, C.C.Y.; Lo, B.P.L.; Zhang, H.; Zhou, X.L.; Yang, G.Z.; Zhao, N.; Zhang, Y.T. Unobtrusive sensing and wearable devices for health informatics. IEEE Trans. Biomed. Eng. 2014, 61, 1538–1554. [Google Scholar] [CrossRef] [PubMed]
- Sabatini, A. Quaternion-based extended Kalman filter for determining orientation by inertial and magnetic sensing. IEEE Trans. Biomed. Eng. 2006, 53, 1346–1356. [Google Scholar] [CrossRef] [PubMed]
- Harada, T.; Mori, T.; Sato, T. Development of a tiny orientation estimation device to operate under motion and magnetic disturbance. Int. J. Robot. Res. 2007, 26, 547–559. [Google Scholar] [CrossRef]
- Young, A.D.; Ling, M.J.; Arvind, D.K. Orient-2: A realtime wireless posture tracking system using local orientation estimation. In Proceedings of the 4th Workshop on Embedded Networked Sensors (EmNets’07), Sydney, Australia, 25–26 June 2007; pp. 53–57.
- Bergamini, E.; Ligorio, G.; Summa, A.; Vannozzi, G.; Cappozzo, A.; Sabatini, A.M. Estimating orientation using magnetic and inertial sensors and different sensor fusion approaches: accuracy assessment in manual and locomotion tasks. Sensors 2014, 14, 18625–18649. [Google Scholar] [CrossRef] [PubMed]
- Ligorio, G.; Bergamini, E.; Pasciuto, I.; Vannozzi, G.; Cappozzo, A.; Sabatini, A.M. Assessing the Performance of Sensor Fusion Methods: Application to Magnetic-Inertial-Based Human Body Tracking. Sensors 2016, 16, 153. [Google Scholar] [CrossRef] [PubMed]
- Ligorio, G.; Sabatini, A.M. Dealing with Magnetic Disturbances in Human Motion Capture: A Survey of Techniques. Micromachines 2016, 7, 43. [Google Scholar] [CrossRef]
- Ligorio, G.; Sabatini, A. A Novel Kalman Filter for Human Motion Tracking with an Inertial-based Dynamic Inclinometer. IEEE Trans. Biomed. Eng. 2015, 62, 2033–2043. [Google Scholar] [CrossRef] [PubMed]
- Vignais, N.; Miezal, M.; Bleser, G.; Mura, K.; Gorecky, D.; Marin, F. Innovative system for real-time ergonomic feedback in industrial manufacturing. Appl. Ergon. 2013, 44, 566–574. [Google Scholar] [CrossRef] [PubMed]
- Bleser, G.; Damen, D.; Behera, A.; Hendeby, G.; Mura, K.; Miezal, M.; Gee, A.; Petersen, N.; Maçães, G.; Domingues, H.; et al. Cognitive learning, monitoring and assistance of industrial workflows using egocentric sensor networks. PLoS ONE 2015, 10, e0127769. [Google Scholar] [CrossRef] [PubMed]
- Bleser, G.; Steffen, D.; Reiss, A.; Weber, M.; Hendeby, G.; Fradet, L. Personalized Physical Activity Monitoring Using Wearable Sensors. In Smart Health; Springer International Publishing: Cham, Switzerland, 2015; pp. 99–124. [Google Scholar]
- Young, A.D. Use of Body Model Constraints to Improve Accuracy of Inertial Motion Capture. In Proceedings of the 2010 International Conference on Body Sensor Networks (BSN’10), Singapore, 7–9 June 2010; pp. 180–186.
- Miezal, M.; Bleser, G.; Schmitz, N.; Stricker, D. A generic approach to inertial tracking of arbitrary kinematic chains. In Proceedings of the 8th International Conference on Body Area Networks, Boston, MA, USA, 30 September–2 October 2013.
- Roetenberg, D.; Luinge, H.; Slycke, P. Xsens MVN: Full 6DOF Human Motion Tracking Using Miniature Inertial Sensors; Technical Report; Xsens Technologies: Enschede, The Netherlands, 2014. [Google Scholar]
- Seel, T.; Schauer, T.; Raisch, J. IMU-Based Joint Angle Measurement for Gait Analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef] [PubMed]
- Kok, M.; Hol, J.; Schön, T. An optimization-based approach to human body motion capture using inertial sensors. In Proceedings of the 19th World Congress of the International Federation of Automatic Control (IFAC), Cape Town, South Africa, 24–29 August 2014; pp. 79–85.
- El-Gohary, M.; McNames, J. Human Joint Angle Estimation with Inertial Sensors and Validation with a Robot Arm. IEEE Trans. Biomed. Eng. 2015, 62, 1759–1767. [Google Scholar] [CrossRef] [PubMed]
- Wagner, J. Adapting the principle of integrated navigation systems to measuring the motion of rigid multibody systems. Multibody Syst. Dyn. 2004, 11, 87–110. [Google Scholar] [CrossRef]
- Bouvier, B.; Duprey, S.; Claudon, L.; Dumas, R.; Savescu, A. Upper Limb Kinematics Using Inertial and Magnetic Sensors: Comparison of Sensor-to-Segment Calibrations. Sensors 2015, 15, 18813–18833. [Google Scholar] [CrossRef] [PubMed]
- Cutti, A.G.; Giovanardi, A.; Rocchi, L.; Davalli, A.; Sacchetti, R. Ambulatory measurement of shoulder and elbow kinematics through inertial and magnetic sensors. Med. Biol. Eng. Comput. 2008, 46, 169–178. [Google Scholar] [CrossRef] [PubMed]
- Leardini, A.; Chiari, L.; Della Croce, U.; Cappozzo, A. Human movement analysis using stereophotogrammetry: Part 3. Soft tissue artifact assessment and compensation. Gait Posture 2005, 21, 212–225. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Brantley, J.; Kim, T.; Ridenour, S.; Lach, J. Characterizing and Minimizing Sources of Error in Inertial Body Sensor Networks. Int. J. Autonom. Adapt. Commun. Syst. 2013, 6, 253. [Google Scholar] [CrossRef]
- Shuster, M.D. A survey of attitude representations. J. Astronaut. Sci. 1993, 41, 439–517. [Google Scholar]
- Wenk, F.; Frese, U. Posture from motion. In Proceedings of the International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 280–285.
- Zhang, Z.Q.; Wu, J.K. A Novel Hierarchical Information Fusion Method for Three-Dimensional Upper Limb Motion Estimation. IEEE Trans. Instrum. Meas. 2011, 60, 3709–3719. [Google Scholar] [CrossRef]
- Jazwinski, A.H. Stochastic Processes and Filtering Theory; Dover Publications, Inc.: Mineola, NY, USA, 2007. [Google Scholar]
- Uhlmann, J.; Julier, S.; Durrant-Whyte, H. A new method for the non linear transformation of means and covariances in filters and estimations. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar]
- Gustafsson, F.; Hendeby, G. Some relations between extended and unscented Kalman filters. IEEE Trans. Signal Proc. 2012, 60, 545–555. [Google Scholar] [CrossRef]
- Kok, M.; Pakazad, S.K.; Schön, T.B.; Hansson, A.; Hol, J.D. A Scalable and Distributed Solution to the Inertial Motion Capture Problem. In Proceedings of the 19th International Conference on Information Fusion, Heidelberg, Germany, 5–8 July 2016.
- Skoglund, M.A.; Hendeby, G.; Axehill, D. Extended Kalman filter modifications based on an optimization view point. In Proceedings of the 18th International Conference on Information Fusion, Washington, DC, USA, 6–9 July 2015; pp. 1856–1861.
- Palermo, E.; Rossi, S.; Marini, F.; Patané, F.; Cappa, P. Experimental evaluation of accuracy and repeatability of a novel body-to-sensor calibration procedure for inertial sensor-based gait analysis. Measurement 2014, 52, 145–155. [Google Scholar] [CrossRef]
- De Vries, W.; Veeger, H.; Cutti, A.; Baten, C.; van der Helm, F. Functionally interpretable local coordinate systems for the upper extremity using inertial & magnetic measurement systems. J. Biomech. 2010, 43, 1983–1988. [Google Scholar] [PubMed]
- Favre, J.; Aissaoui, R.; Jolles, B.; de Guise, J.; Aminian, K. Functional calibration procedure for 3D knee joint angle description using inertial sensors. J. Biomech. 2009, 42, 2330–2335. [Google Scholar] [CrossRef] [PubMed]
- Seel, T.; Schauer, T.; Raisch, J. Joint axis and position estimation from inertial measurement data by exploiting kinematic constraints. In Proceedings of the International Conference on Control Applications (CCA), Dubrovnik, Croatia, 3–5 October 2012; pp. 45–49.
- Bleser, G.; Hendeby, G.; Miezal, M. Using Egocentric Vision to Achieve Robust Inertial Body Tracking under Magnetic Disturbances. In Proceedings of the 10th International Symposium on Mixed and Augmented Reality (ISMAR-2011), Basel, Switzerland, 26–29 October 2011.
- Zatsiorsky, V.M. Kinematics of Human Motion; Human Kinetics: Champaign, IL, USA, 1998. [Google Scholar]
- Taetz, B.; Bleser, G.; Miezal, M. Towards Self-Calibrating Inertial Body Motion Capture. In Proceedings of the 19th International Conference on Information Fusion, Heidelberg, Germany, 5–8 July 2016.
- Palermo, E.; Rossi, S.; Patanè, F.; Cappa, P. Experimental evaluation of indoor magnetic distortion effects on gait analysis performed with wearable inertial sensors. Physiol. Meas. 2014, 35, 399–415. [Google Scholar] [CrossRef] [PubMed]
- Denavit, J.; Hartenberg, R.S. A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices. J. Appl. Mech. 1965, 22, 215–221. [Google Scholar]
- Bleser, G.; Stricker, D. Advanced tracking through efficient image processing and visual–inertial sensor fusion. Comput. Graph. 2009, 33, 59–72. [Google Scholar] [CrossRef]
- Ungarala, S.; Dolence, E.; Li, K. Constrained extended Kalman filter for nonlinear state estimation. In Proceedings of the 8th International Symposium on Dynamics and Control of Process Systems, Cancun, Mexico, 6–8 June 2007; Volume 2, pp. 63–68.
- Miezal, M.; Taetz, B.; Schmitz, N.; Bleser, G. Ambulatory inertial spinal tracking using constraints. In Proceedings of the 9th International Conference on Body Area Networks, London, UK, 29 September–1 October 2014.
- Black, H.D. A passive system for determining the attitude of a satellite. AIAA J. 1964, 2, 1350–1351. [Google Scholar] [CrossRef]
- Björck, A. Numerical Methods for Least Squares Problems; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Non-Linear Problems in Least Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics (Intelligent Robotics and Autonomous Agents); The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Optitrack. Available online: http://www.optitrack.com/ (accessed 29 April 2016).
- Xsens. Available online: https://www.xsens.com/ (accessed 29 April 2016).
- Nyqvist, H.E.; Skoglund, M.A.; Hendeby, G.; Gustafsson, F. Pose estimation using monocular vision and inertial sensors aided with ultra wide band. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 1–10.
- Ligorio, G.; Sabatini, A.M. A Simulation Environment for Benchmarking Sensor Fusion-Based Pose Estimators. Sensors 2015, 15, 32031–32044. [Google Scholar] [CrossRef] [PubMed]
- Tsai, R.; Lenz, R. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration. IEEE Trans. Robot. Autom. 1989, 5, 345–358. [Google Scholar] [CrossRef]
- National Metrology Institute of Germany. Available online: http://www.ptb.de/en (accessed 29 April 2016).
- De Vries, W.; Veeger, H.; Baten, C.; Van Der Helm, F. Magnetic distortion in motion labs, implications for validating inertial magnetic sensors. Gait Posture 2009, 29, 535–541. [Google Scholar] [CrossRef] [PubMed]
- Angermann, M.; Frassl, M.; Doniec, M.; Julian, B.J.; Robertson, P. Characterization of the indoor magnetic field for applications in localization and mapping. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sydney, Australia, 13–15 November 2012; pp. 1–9.
- Butterworth, S. On the Theory of Filter Amplifiers. Wirel. Eng. 1930, 7, 536–541. [Google Scholar]
- Faber, G.S.; Chang, C.C.; Rizun, P.; Dennerlein, J.T. A novel method for assessing the 3-D orientation accuracy of inertial/magnetic sensors. J. Biomech. 2013, 46, 2745–2751. [Google Scholar] [CrossRef] [PubMed]
- Bleser, G. Towards Visual-Inertial SLAM for Mobile Augmented Reality. Ph.D. Thesis, University of Kaiserslautern, München, Germany, 2009. [Google Scholar]
| Chaintracker (cf. [ 16]) | Quattracker segment | Quattracker IMU | Optitracker | |
|---|---|---|---|---|
| Estimation method | EKF | EKF | EKF | WLS |
| State | ||||
| Dimensions (state s, meas. vector k) | , , | , , | , , | , |
| Motion model | 1D const angular acc | 3D const angular & linear acc | 3D const angular vel; 3D const linear accel | IMU control input |
| Tuning parameters | , , , , , | |||
| Complexity | [49] | (Gauss Newton method) | ||
| Biomech. model | chain | free segments | free segments | free segments |
| State coordinate system | segment centered | segment centered | IMU centered | IMU and segment centered |
| Mode | Sequence → | Slow | Fast | ||
|---|---|---|---|---|---|
| Sensor → | Acc(m/s) | Gyr () | Acc (m/s) | Gyr () | |
| Real | |||||
| Re-simulated | |||||
| IMU | Residual Error |
|---|---|
| real-slow | |||
| real-fast | |||
| Segment () | d | a | IMU | Image | ||
|---|---|---|---|---|---|---|
| 0 | 0 | None |  | |||
| 0 | 0 | None | ||||
| 0 | 0 | 0 | None | |||
| 0 | 0 | 0 | ||||
| 0 | 0 | None | ||||
| 0 | 0 | None | ||||
| 0 | 0 | 0 | None | |||
| 0 | 0 | 0 | ||||
| 0 | 0 | None | ||||
| 0 | 0 | None | ||||
| 0 | 0 | 0 | None | |||
| 0 | 0 | 0 |
| Sequence → | sim-fast-artificial | |
|---|---|---|
| Sensor → | Acc (m/s) | Gyr () |
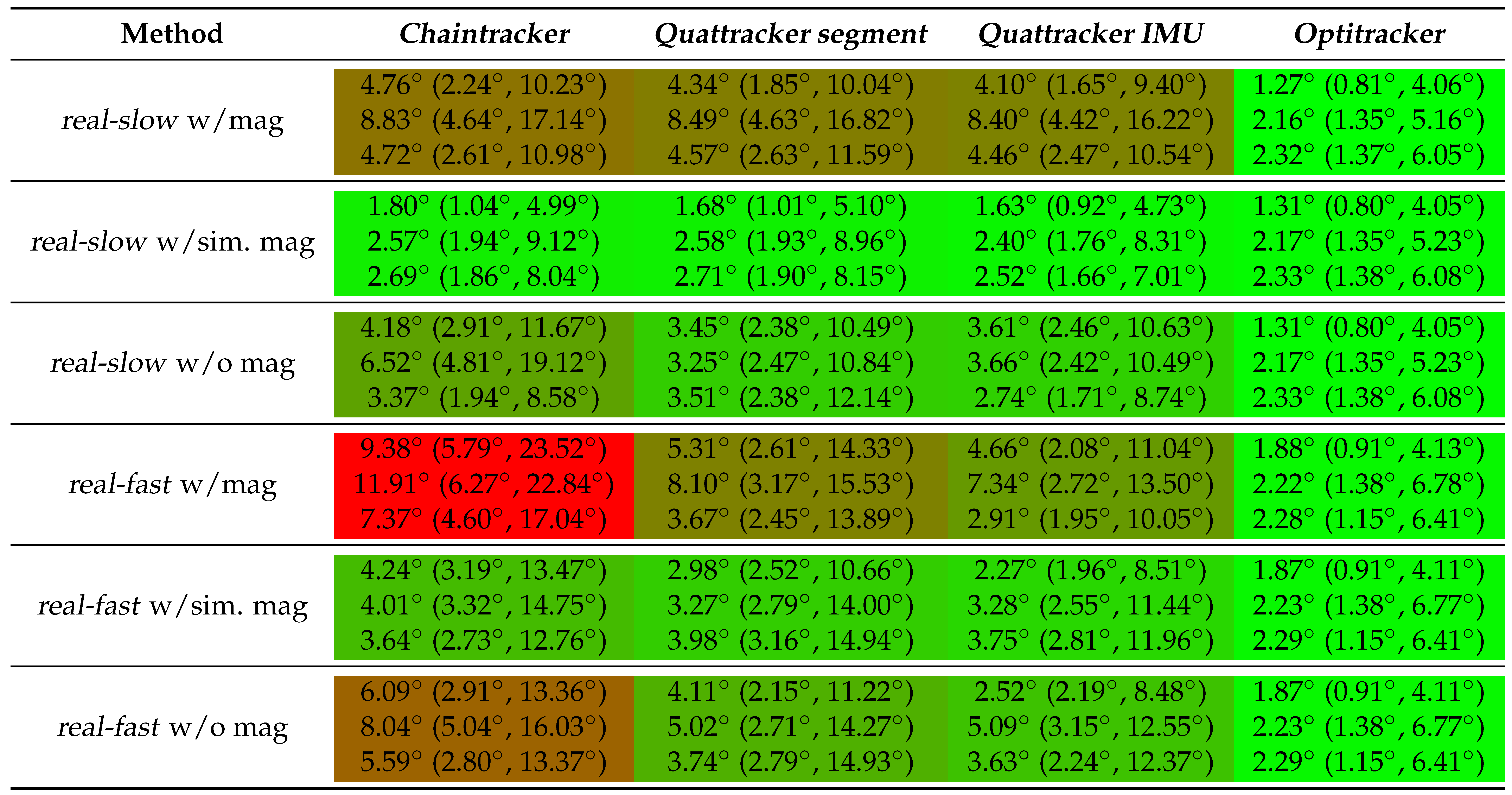
| Method | Chaintracker | Quattracker segment | Quattracker IMU | Optitracker |
|---|---|---|---|---|
| Noise-free w/mag | 1.42 (1.40; 8.04) | 1.19 (1.23; 6.83) | 0.66 (0.64; 3.30) | 0.01 (0.01; 0.06) |
| Noise-free w/o mag | 3.50 (2.57; 9.45) | 1.57 (1.45; 7.52) | 0.97 (0.65; 3.36) | 0.01 (0.01; 0.06) |
| Noise w/mag | 1.46 (1.39; 8.09) | 1.22 (1.21; 6.83) | 0.69 (0.62; 3.28) | 0.40 (0.05; 0.49) |
| Noise, w/o mag | 3.73 (2.68; 9.76) | 1.55 (1.40; 7.42) | 0.95 (0.65; 3.31) | 0.40 (0.05; 0.49) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miezal, M.; Taetz, B.; Bleser, G. On Inertial Body Tracking in the Presence of Model Calibration Errors. Sensors 2016, 16, 1132. https://doi.org/10.3390/s16071132
Miezal M, Taetz B, Bleser G. On Inertial Body Tracking in the Presence of Model Calibration Errors. Sensors. 2016; 16(7):1132. https://doi.org/10.3390/s16071132
Chicago/Turabian StyleMiezal, Markus, Bertram Taetz, and Gabriele Bleser. 2016. "On Inertial Body Tracking in the Presence of Model Calibration Errors" Sensors 16, no. 7: 1132. https://doi.org/10.3390/s16071132
APA StyleMiezal, M., Taetz, B., & Bleser, G. (2016). On Inertial Body Tracking in the Presence of Model Calibration Errors. Sensors, 16(7), 1132. https://doi.org/10.3390/s16071132