Towards Stochastic Optimization-Based Electric Vehicle Penetration in a Novel Archipelago Microgrid
Abstract
:1. Introduction
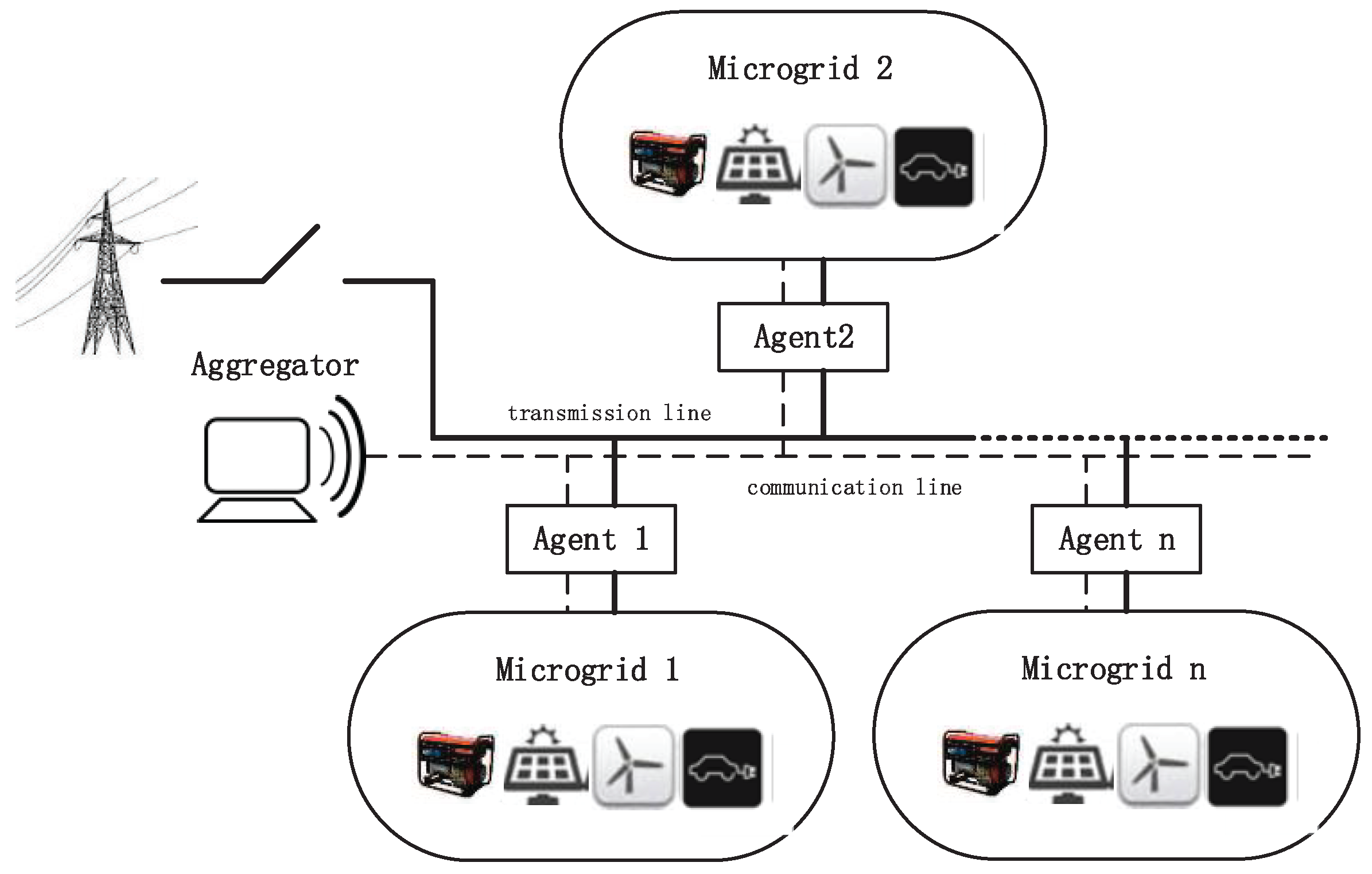
- To improve the energy efficiency and ensure the stability of IMG, we propose a novel multi-microgrid system concept named “archipelago microgrid”. In our proposed system, the required power will be fully provided by the distributed power generation in local MGs. Through the energy transmission controlled by a MicroGrid Center Controller (MGCC, aggregator) among the MGs, the emission and operation cost created by local units can be mitigated. The proposed system is helpful in reducing operation cost and enhancing the stability of the grid.
- We propose a Stochastic Optimal Penetration (SOP) model, aiming to minimize the cost of the proposed “archipelago microgrid” system. To address the uncertainties from RESs and electricity prices, the optimization problem is formalized as a two-stage stochastic programming problem. In the formalized problem, the uncertain parameters such as wind, solar generation capacity are captured by the Monte Carlo-based method [8]. For the sake of comparison, the Deterministic Optimal Penetration (DOP) model based on our prior work [9] is introduced as a baseline scheme. In the optimization problem, the emission cost created by CVs and local units, the operation cost of startup/shutdown expense of units, tariff compensation, battery capacity degradation, and power losses are considered in the optimization model. The proposed stochastic model offers a desired flexibility between the environmental and economic benefits by seeking the optimal number of EVs with the considerations of the RESs and units generation limits.
- To achieve the minimization of emission and operation cost, we propose the following two schemes to schedule the optimized scale of EVs: (i) Unlimited Coordinated Scheme (UCS); and (ii) Limited Coordinated Scheme (LCS). In UCS, we consider that all the surplus energy is utilized to charge as many EVs as possible. In this ideal scenario, the mutual transmission among MGs is also allowed to avoid energy wasted. Nonetheless, peak load limits and residence preference of energy usage should be considered in practice. To this end, we propose the LCS to achieve a more realistic number of penetrated EVs to minimize the total cost.
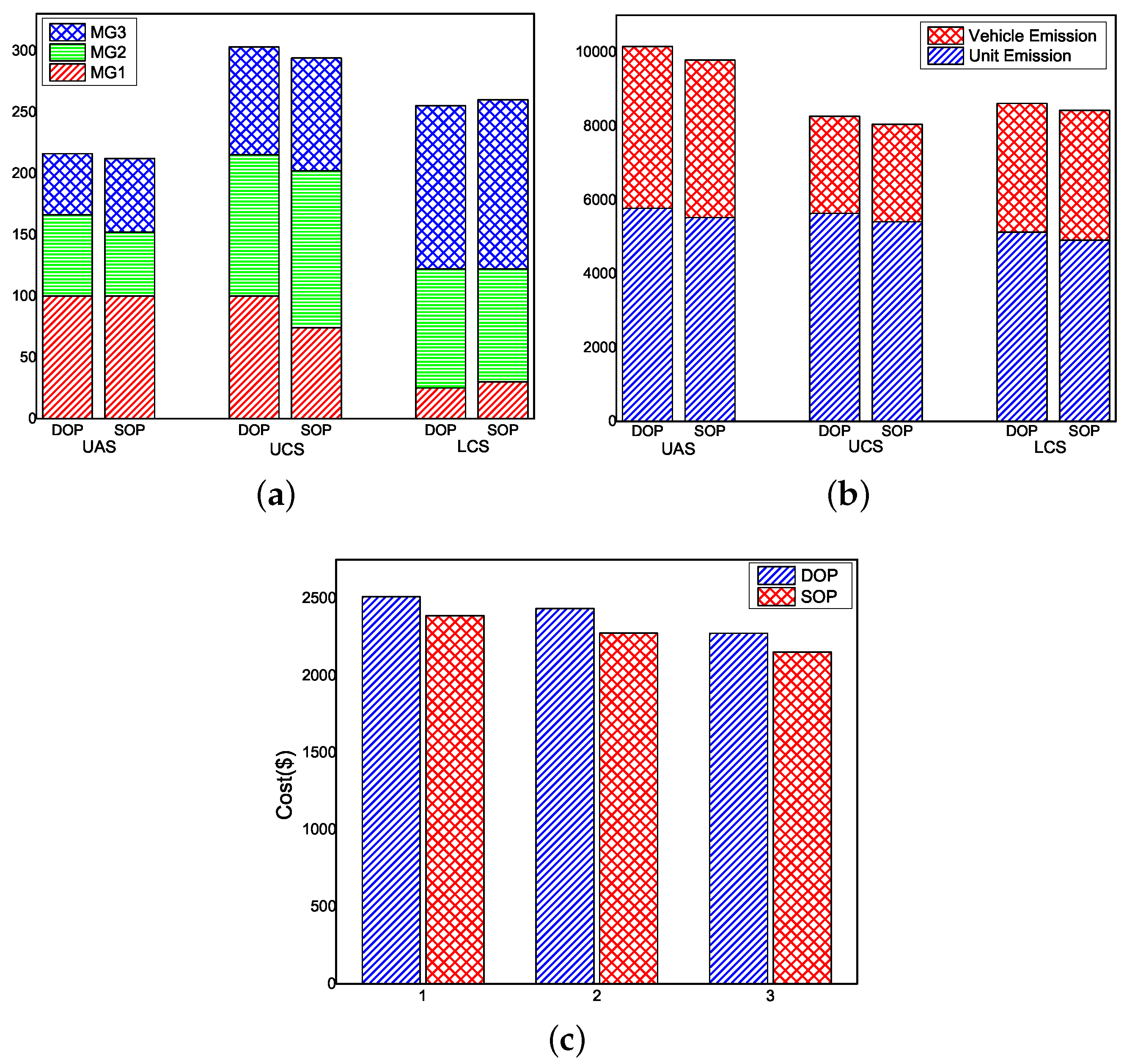
- We carry out an extensive simulation study on a modified IEEE 9-bus system to demonstrate the effectiveness of the proposed SOP model using the two scheduling schemes. The simulation results shows that, after addressing uncertainties, the emissions and operation cost are reduced in comparison with the deterministic-based optimization model. In addition, with respect to the two schedule schemes in SOP, the LCS has been proven to be more effective on arranging the scale of EVs and realizing the emission and operation cost reduction than the UCS. Our experimental data shows that, in comparison with a baseline non-coordinated average scheme, 15.2% of emissions can be reduced and 11.2% cost can be saved in the LCS, we conduct sensitivity analysis to validate the impact of different parameters on the optimal solution.
2. System Models
2.1. Archipelago Microgrid Model
2.2. Market Model and Aggregator
3. Our Approach
3.1. Basic Idea
3.2. Problem Formulation
3.2.1. Stochastic Optimal Penetration (SOP) Model
3.2.2. Deterministic Optimal Penetration (DOP) Model
3.3. Proposed Scheduling Schemes
3.3.1. Uncoordinated Average Scheme (UAS)
3.3.2. Unlimited Coordinated Scheme (UCS)
3.3.3. Limited Coordinated Scheme (LCS)
| Algorithm 1 Decentralized Algorithm | |
| Require: is the number of EVs charged at time slot t in MG i | |
| Ensure: , , , | |
| 1: | ; |
| 2: | Initialization: the scheduling period , the estimated vehicles number in MG i. Denote two new constraints (11) and (12) as empty; |
| 3: | Divide the optimization problem in Equation (1) into subproblems by scheduling intervals and queue the subproblems according to electricity prices ascending. |
| 4: | Set =Group of valid subproblems; |
| 5: | for |
| 6: | if then |
| 7: | The subproblem t is valid and add it into ; |
| 8: | end if |
| 9: | Compute the number of elements , in set of ; |
| 10: | for |
| 11: | Solve the optimization problem defined in Equation (1), subject to constraints defined in Equations (2)–(10), |
| 12: | if then |
| 13: | Add a new constraint: as constraint (11); |
| 14: | Recompute the optimization problem defined in Equation (1), subject to constraints (2–11); |
| 15: | Delete the constraints defined in Equation (11); |
| 16: | if then |
| 17: | Add new constraints: as constraint (12); |
| 18: | if then |
| 19: | break |
| 20: | end if |
| 21: | end if |
| 22: | end if return The optimized number of EVs . |
4. Performance Evaluation
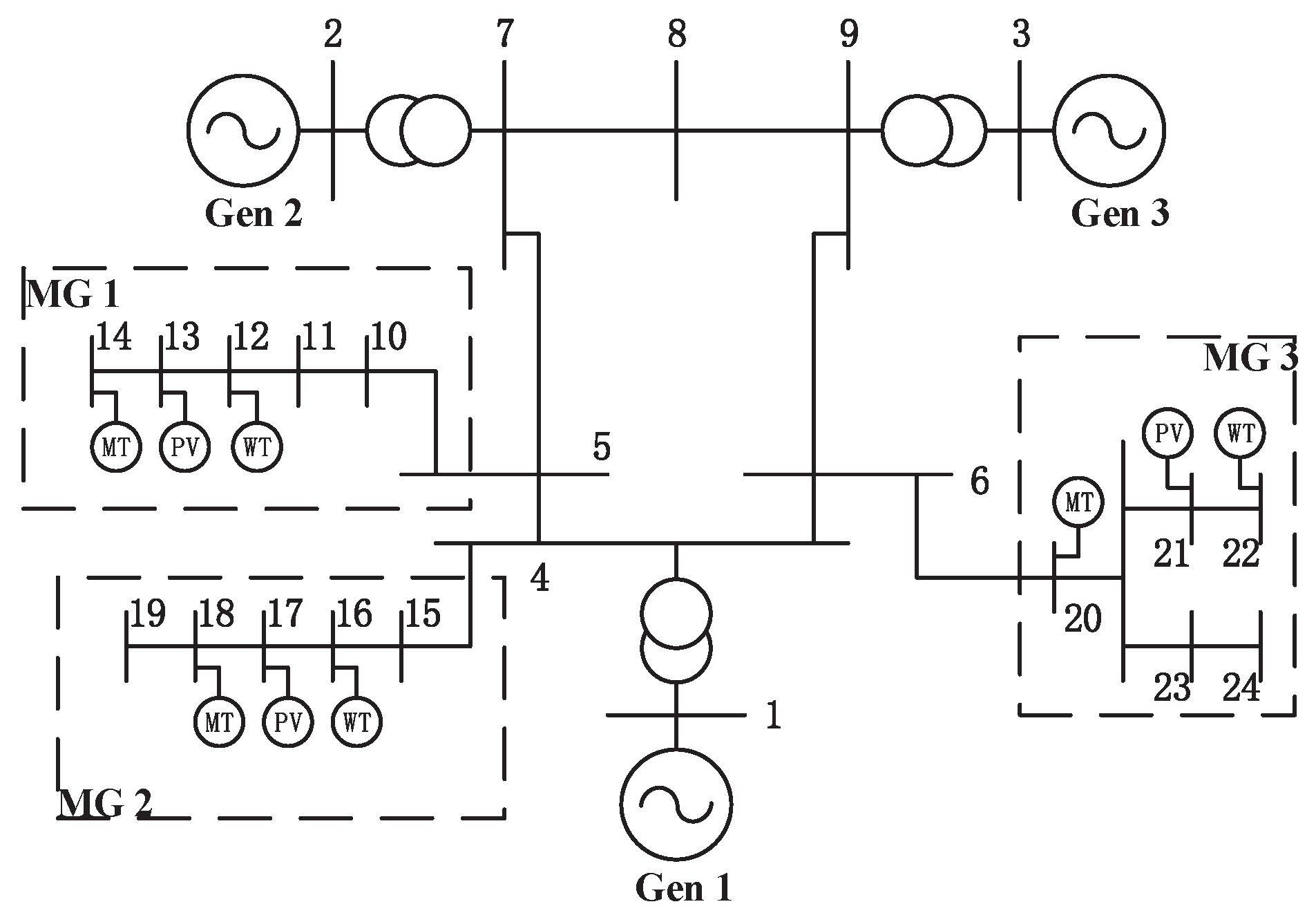
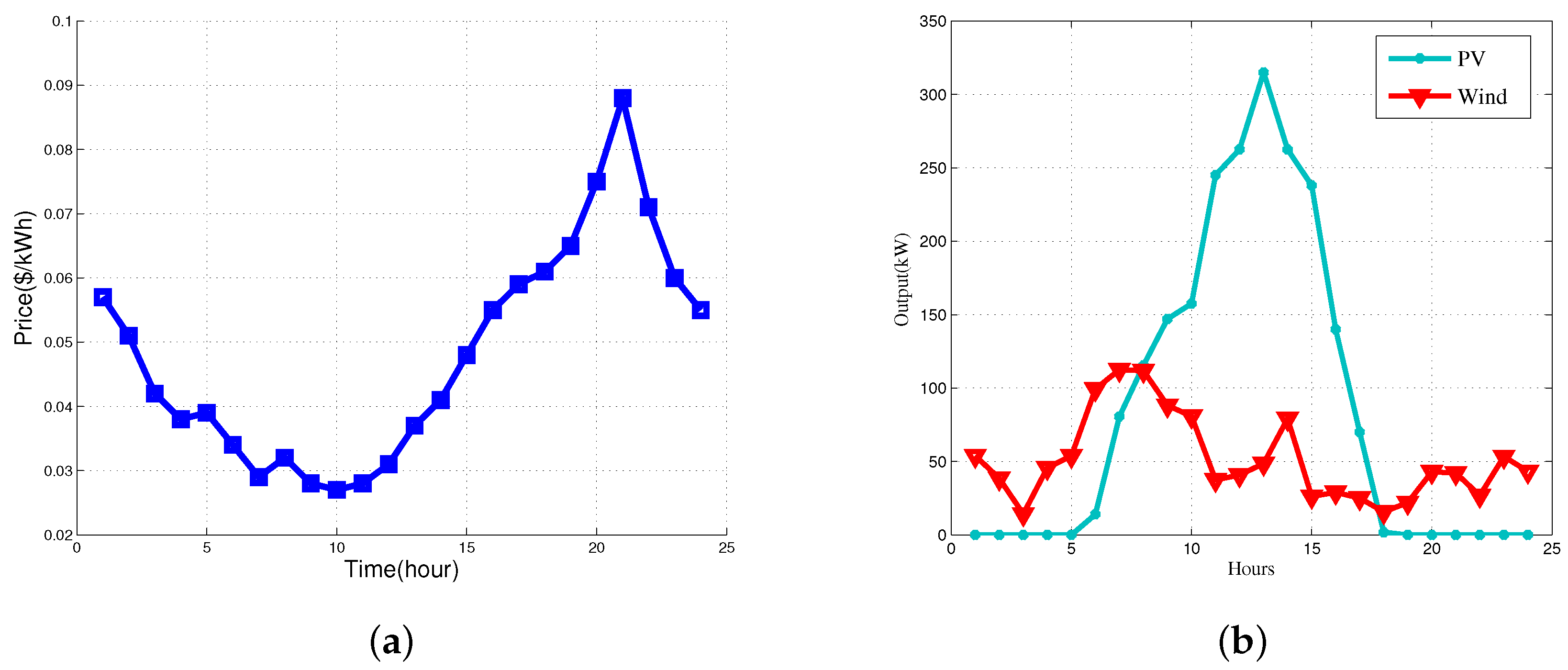
4.1. Evaluation Methodology
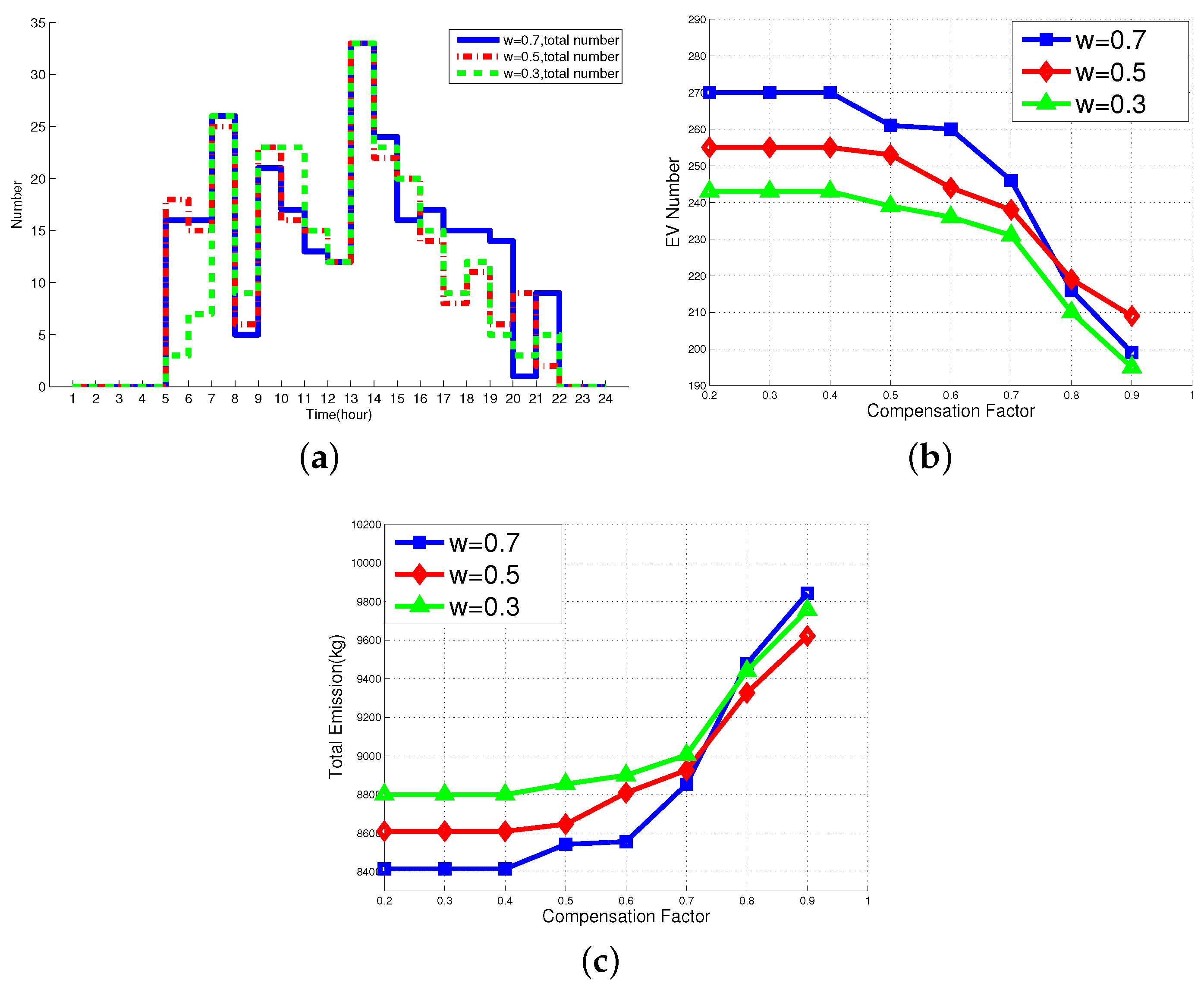
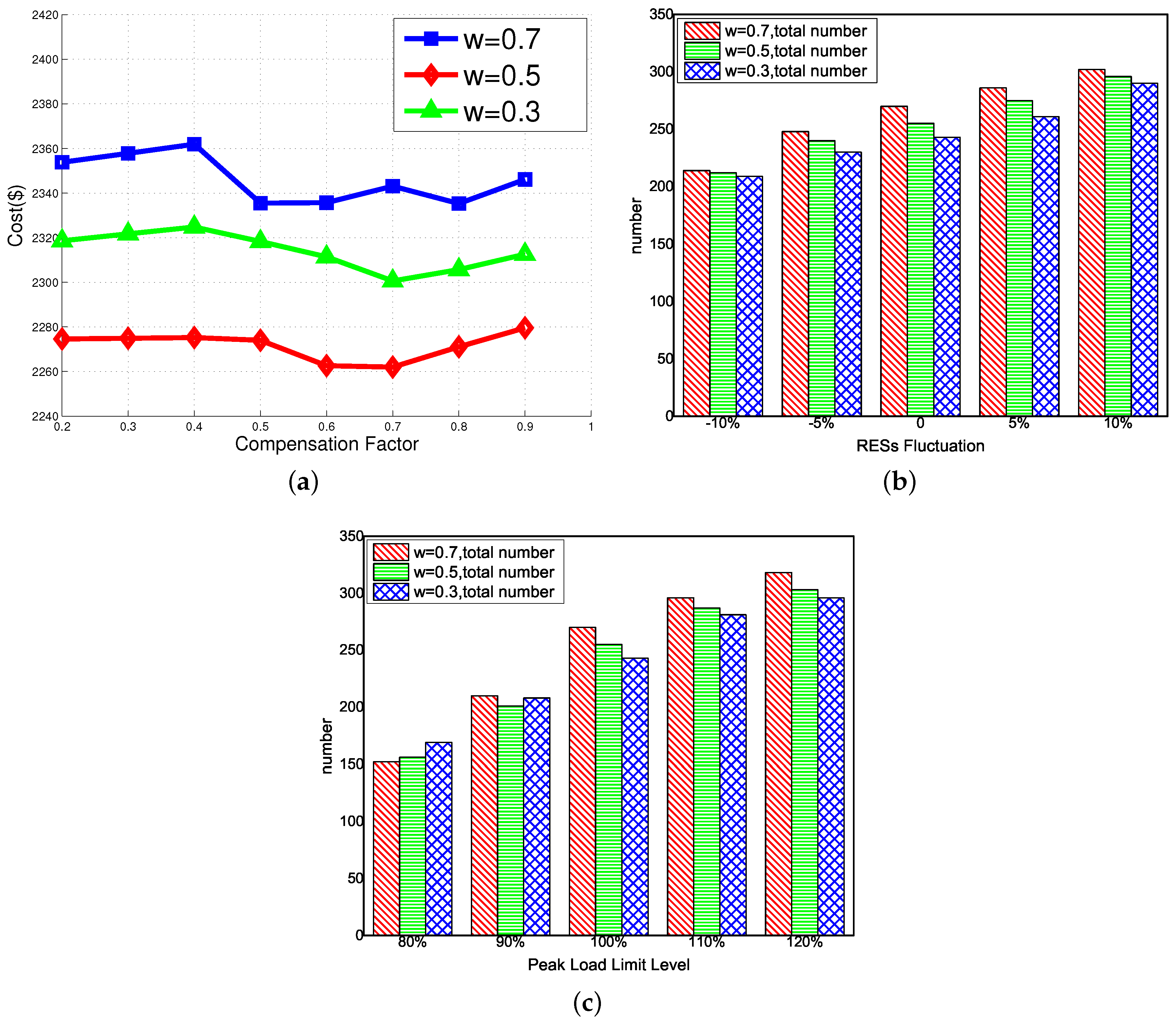
4.2. Evaluation Results
4.2.1. Results of SOP and DOP
4.2.2. Sensitivity Analysis
5. Related Works
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Baheti, R.; Gill, H. Cyber-physical systems. Impact Control Technol. 2011, 12, 161–166. [Google Scholar]
- Rani, S.; Talwar, R.; Malhotra, J.; Ahmed, S.H.; Sarkar, M.; Song, H. A novel scheme for an energy efficient Internet of Things based on wireless sensor networks. Sensors 2015, 15, 28603–28626. [Google Scholar] [CrossRef] [PubMed]
- Abdelaziz, M.M.; Shaaban, M.F.; Farag, H.E.; El-Saadany, E.F. A multistage centralized control scheme for islanded microgrids with PEVs. IEEE Trans. Sustain. Energy 2014, 5, 927–937. [Google Scholar] [CrossRef]
- Khodaei, A. Provisional microgrids. IEEE Trans. Smart Grid 2015, 6, 1107–1115. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, J. The energy management and optimized operation of electric vehicles based on microgrid. IEEE Trans. Power Deliv. 2014, 29, 1427–1435. [Google Scholar]
- Saber, A.Y.; Venayagamoorthy, G.K. Plug-in vehicles and renewable energy sources for cost and emission reductions. IEEE Trans. Ind. Electron. 2011, 58, 1229–1238. [Google Scholar] [CrossRef]
- Luis, H.; Baladrón, C.; Aguiar, J.M.; Calavia, L.; Carro, B.; Sánchez-Esguevillas, A.; Cook, D.J.; Chinarro, D.; Gómez, J. A study of the relationship between weather variables and electric power demand inside a smart grid/smart world framework. Sensors 2012, 12, 11571–11591. [Google Scholar]
- Moon, H.H.; Lee, J.J.; Choi, S.Y.; Cha, J.S.; Kang, J.M.; Kim, J.T.; Shin, M.C. A study using a Monte Carlo method of the optimal configuration of a distribution network in terms of power loss sensing. Sensors 2011, 11, 7823–7834. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Tan, Z.; An, D.; Yu, W.; Yang, X. On optimal electric vehicles penetration in a Novel Archipelago Microgrids. In Proceedings of the IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Shanghai, China, 30 May–1 June 2016.
- Wei, C.; Md Fadlullah, Z.; Kato, N.; Stojmenovic, I. A novel distributed algorithm for power loss minimizing in Smart Grid. In Proceedings of the 2014 IEEE International Conference on Smart Grid Communications (SmartGridComm), Venice, Italy, 3–6 November 2014.
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Yu, W.; An, D.; Griffith, D.; Yang, Q.; Xu, G. Towards statistical modeling and machine learning based energy usage forecasting in smart grid. ACM SIGAPP Appl. Comput. Rev. 2015, 15, 6–16. [Google Scholar] [CrossRef]
- Saad, W.; Han, Z.; Poor, H.V. Coalitional game theory for cooperative micro-grid distribution networks. In Proceedings of the 2011 IEEE International Conference on Communications Workshops (ICC), Kyoto, Japan, 5–9 June 2011.
- Colson, C.M.; Nehrir, M.H. Comprehensive real-time microgrid power management and control with distributed agents. IEEE Trans. Smart Grid 2013, 4, 617–627. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Le, L.B. Optimal bidding strategy for microgrids considering renewable energy and building thermal dynamics. IEEE Trans. Smart Grid 2014, 5, 1608–1620. [Google Scholar] [CrossRef]
- Roe, C.; Meliopoulos, A.; Meisel, J.; Overbye, T. Power system level impacts of plug-in hybrid electric vehicles using simulation data. In Proceedings of the IEEE Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008.
- Pourmousavi, S.A.; Nehrir, M.H.; Sharma, R.K. Multi-timescale power management for islanded microgrids including storage and demand response. IEEE Trans. Smart Grid 2015, 6, 1185–1195. [Google Scholar] [CrossRef]
- Tol, R.S. The marginal damage costs of carbon dioxide emissions: An assessment of the uncertainties. Energy Policy 2005, 33, 2064–2074. [Google Scholar] [CrossRef]
- Yang, Q.; An, D.; Cai, Y. A novel evolution Kalman Filter algorithm for short-term climate prediction. Asian J. Control 2014, 18, 400–405. [Google Scholar] [CrossRef]
- Robert, C.; Casella, G. Monte Carlo Statistical Methods; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Dvorkin, Y.; Wang, Y.; Pandzic, H.; Kirschen, D. Comparison of scenario reduction techniques for the stochastic unit commitment. In Proceedings of the 2014 IEEE PES General Meeting, Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014.
- Aghamohammadi, M.R.; Abdolahinia, H. A new approach for optimal sizing of battery energy storage system for primary frequency control of islanded microgrid. Int. J. Electr. Power Energy Syst. 2014, 54, 325–333. [Google Scholar] [CrossRef]
- Litchy, A.J.; Nehrir, M.H. Real-time energy management of an islanded microgrid using multi-objective Particle Swarm Optimization. In Proceedings of the 2014 IEEE PES General Meeting, Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014.
- Rua, D.; Lopes, J.P.; Ruela, J. Communications uncertainties in isolated multi-microgrid control systems. In Proceedings of the Power Systems Computation Conference (PSCC), Wroclaw, Poland, 18–22 August 2014.
- Kahrobaeian, A.; Mohamed, I.; Abdel-Rady, Y. Networked-based hybrid distributed power sharing and control for islanded microgrid systems. IEEE Trans. Power Electron. 2015, 30, 603–617. [Google Scholar] [CrossRef]
- Ahn, S.J.; Nam, S.R.; Choi, J.H.; Moon, S.I. Power scheduling of distributed generators for economic and stable operation of a microgrid. IEEE Trans. Smart Grid 2013, 4, 398–405. [Google Scholar] [CrossRef]
- Alipour, M.; Mohammadi-Ivatloo, B.; Zare, K. Stochastic scheduling of renewable and CHP based microgrids. IEEE Trans. Ind. Inform. 2015, 11, 1049–1058. [Google Scholar] [CrossRef]
- Rua, D.; Pereira, L.M.; Gil, N.; Lopes, J. Impact of multi-Microgrid Communication systems in islanded operation. In Proceedings of the 2011 2nd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies (ISGT Europe), Manchester, UK, 5–7 December 2011.
- Zhao, B.; Zhang, X.; Li, P.; Wang, K.; Xue, M.; Wang, C. Optimal sizing, operating strategy and operational experience of a stand-alone microgrid on Dongfushan Island. Appl. Energy 2014, 113, 1656–1666. [Google Scholar] [CrossRef]
- Zhao, B.; Dong, X.; Bornemann, J. Service restoration for a renewable-powered microgrid in unscheduled island mode. IEEE Trans. Smart Grid 2015, 6, 1128–1136. [Google Scholar] [CrossRef]
- Yang, Q.; An, D.; Yu, W.; Yang, X.; Fu, X. On stochastic optimal bidding strategy for microgrids. In Proceedigns of the 2015 IEEE International Conference on Performance Computing and Communications Conference (IPCCC), Nanjing, China, 14–16 December 2015.
- Kim, H.M.; Kinoshita, T.; Lim, Y.; Kim, T.H. A bankruptcy problem approach to load-shedding in multiagent-based microgrid operation. Sensors 2010, 10, 8888–8898. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.Y.; Jeon, J.H.; Kim, S.K.; Cho, C.; Park, J.H.; Kim, H.M.; Nam, K.Y. Cooperative control strategy of energy storage system and microsources for stabilizing the microgrid during islanded operation. IEEE Trans. Power Electron. 2010, 25, 3037–3048. [Google Scholar]
- Tushar, M.H.; Assi, C.; Maier, M.; Uddin, M.F. Smart microgrids: Optimal joint scheduling for electric vehicles and home appliances. IEEE Trans. Smart Grid 2014, 5, 239–250. [Google Scholar] [CrossRef]
- Tushar, M.H.; Assi, C.; Maier, M. Distributed real-time electricity allocation mechanism for large residential microgrid. IEEE Trans. Smart Grid 2015, 6, 1353–1363. [Google Scholar] [CrossRef]
- Gan, L.; Topcu, U.; Low, S.H. Optimal decentralized protocol for electric vehicle charging. IEEE Trans. Power Syst. 2013, 28, 940–951. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, N.; Li, Z.; Shahidehpour, M. Modeling and impact analysis of large scale V2G electric vehicles on the power grid. In Proceedings of the 2012 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Tianjin, China, 21–24 May 2012.
- Honarmand, M.; Zakariazadeh, A.; Jadid, S. Integrated scheduling of renewable generation and electric vehicles parking lot in a smart microgrid. Energy Convers. Manag. 2014, 86, 745–755. [Google Scholar] [CrossRef]
- Van Roy, J.; Leemput, N.; Geth, F.; Buscher, J.; Salenbien, R.; Driesen, J. Electric vehicle charging in an office building microgrid with distributed energy resources. IEEE Trans. Sustain. Energy 2014, 5, 1389–1396. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Jadid, S.; Siano, P. Multi-objective scheduling of electric vehicles in smart distribution system. Energy Convers. Manag. 2014, 79, 43–53. [Google Scholar] [CrossRef]
- Jian, L.; Xue, H.; Xu, G.; Zhu, X.; Zhao, D.; Shao, Z. Regulated charging of plug-in hybrid electric vehicles for minimizing load variance in household smart microgrid. IEEE Trans. Ind. Electron. 2013, 60, 3218–3226. [Google Scholar] [CrossRef]
- Mao, M.; Sun, S.; Su, J. Economic analysis of a microgrid with wind/photovoltaic/storages and electric vehicles. Autom. Electr. Power Syst. 2011, 35, 30–35. [Google Scholar]
| : | The number of local units, MGs, time slots, and scenarios |
| : | The minimum battery energy stored for handling EV’s normal driving activities |
| ω: | Weighting factor |
| μ: | Compensation factor of price gaps |
| : | Penalty factor of battery capacity degradation and power losses |
| : | Charging/discharging efficiency of storage battery |
| : | Fuel consumption coefficients of DG j in MG i |
| : | The operation cost coefficients of DG j in MG i |
| : | Cost of unit r to compensate RES prediction errors in MG i at time t |
| : | The number of EVs charged/discharged at time t in MG i |
| : | Minimum and real-time electricity price during the day ($/kWh) |
| : | Line resistance between MG i and l (Ω) |
| V: | Transmission voltage among MGs (kV) |
| : | Transported power between MG i and l (kW) |
| : | The number of EVs, CVs and total vehicles in MG i |
| : | The power losses during power transmission (kW) |
| : | Power generation of local unit j (kW) |
| : | Non-EV load in MG i at time t (kW) |
| : | Power generation of PV and wind (kW) |
| : | Startup and shutdown cost of unit j ($) |
| : | Ramp-up/down limit of unit j (kW) |
| : | Charging/discharging power of the EV (kWh) |
| : | Minimum/maximum power generation of unit j (kW) in MG i |
| : | The maximum and minimum capacity of EV’s battery (kWh) |
| : | Charging/discharging status of , where 0 indicates charging and 1 indicates discharging, respectively |
| : | Operation status of unit j, where 0 means the unit’s stop status and 1 indicates its operation status, respectively |
| : | Startup and shutdown status of unit j, where 0 and 1 means startup and shutdown, respectively |
| SC, IC: | Slope Coefficient and Intercept Coefficient of fuel consumption per unit generation |
| Rated Power (RP) (kW) | SC (a,L/h) | IC (b,L/h) |
|---|---|---|
| 30–100 kW | 0.273 | 0.033 |
| 100–300 kW | 0.253 | 0.028 |
| >300 kW | 0.244 | 0.014 |
| MG | Type | α ($) | β ($/kWh) | (kW) | (kW) |
| 1 | DG | 15 | 0.13 | 20 | 200 |
| 2 | DG | 25 | 0.35 | 20 | 400 |
| 3 | DG | 40 | 0.50 | 20 | 500 |
| MG | Type | ($) | ($) | (kW) | (kW) |
| 1 | DG | 50 | 5 | 30 | 10 |
| 2 | DG | 30 | 3 | 40 | 20 |
| 3 | DG | 20 | 2 | 50 | 30 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; An, D.; Yu, W.; Tan, Z.; Yang, X. Towards Stochastic Optimization-Based Electric Vehicle Penetration in a Novel Archipelago Microgrid. Sensors 2016, 16, 907. https://doi.org/10.3390/s16060907
Yang Q, An D, Yu W, Tan Z, Yang X. Towards Stochastic Optimization-Based Electric Vehicle Penetration in a Novel Archipelago Microgrid. Sensors. 2016; 16(6):907. https://doi.org/10.3390/s16060907
Chicago/Turabian StyleYang, Qingyu, Dou An, Wei Yu, Zhengan Tan, and Xinyu Yang. 2016. "Towards Stochastic Optimization-Based Electric Vehicle Penetration in a Novel Archipelago Microgrid" Sensors 16, no. 6: 907. https://doi.org/10.3390/s16060907
APA StyleYang, Q., An, D., Yu, W., Tan, Z., & Yang, X. (2016). Towards Stochastic Optimization-Based Electric Vehicle Penetration in a Novel Archipelago Microgrid. Sensors, 16(6), 907. https://doi.org/10.3390/s16060907





