Multi-Target State Extraction for the SMC-PHD Filter
Abstract
:1. Introduction
2. Problem Formulation
2.1. The PHD Filter
2.2. Review of the SMC-PHD Filter
- Step 1 Prediction:
- For , sample from a proposal density for persistent targets and compute the predicted weights:where .
- For , sample from a proposal density for newborn targets and compute the corresponding weights:where is the number of particles for newborn targets.
- Step 2 Update:
- For each , compute:where and is the likelihood of a measurement resulting from a particle .
- For , update weights:
- Step 3 Resampling:
- Compute the total mass and then resample to get .
- Rescale the weights by to obtain .
- Step 4 Multi-Target Parameter Estimation:
- Estimate the number of targets (by rounding ).
- Extract the target state set from the particles that represent the posterior intensity, where denote the estimated multi-target state.
3. The Proposed Multi-Target State Extraction Method
3.1. Particles and Measurements Classification
3.2. Multi-Target State Extraction
| Algorithm 1. Multi-target state extraction for detected targets. |
Given: The estimated target number , and .
|
| Algorithm 2. Methods for state estimation of undetected targets. |
| Given: and |
| 1. Set , |
| 2. for do |
| 3. |
| 4. |
| 5. end for |
| 6. . |
| 7. Compute according to (19) |
| 8. if |
| 9. State extraction using clustering method |
| 10. end |
3.3. Notes on Implementation
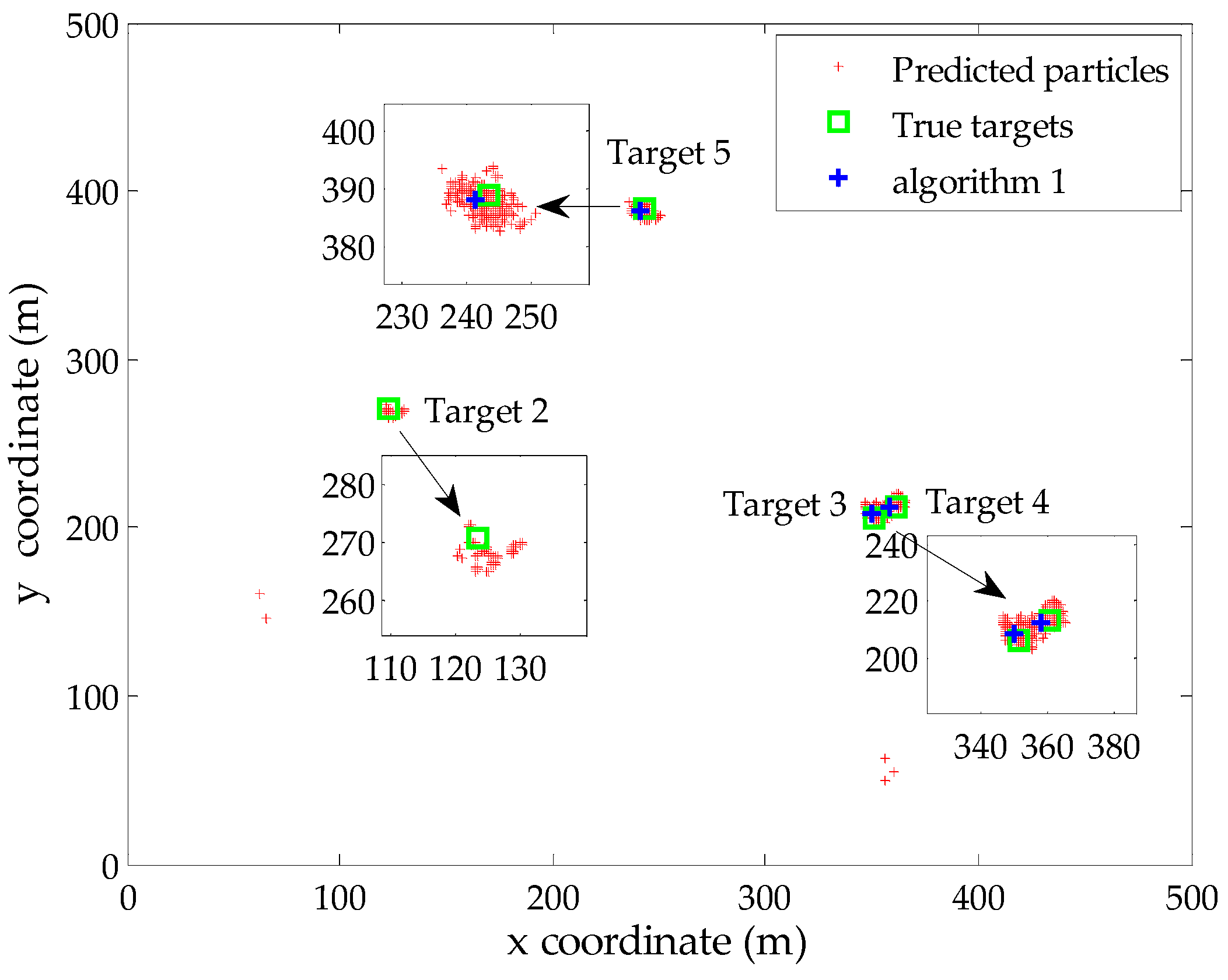
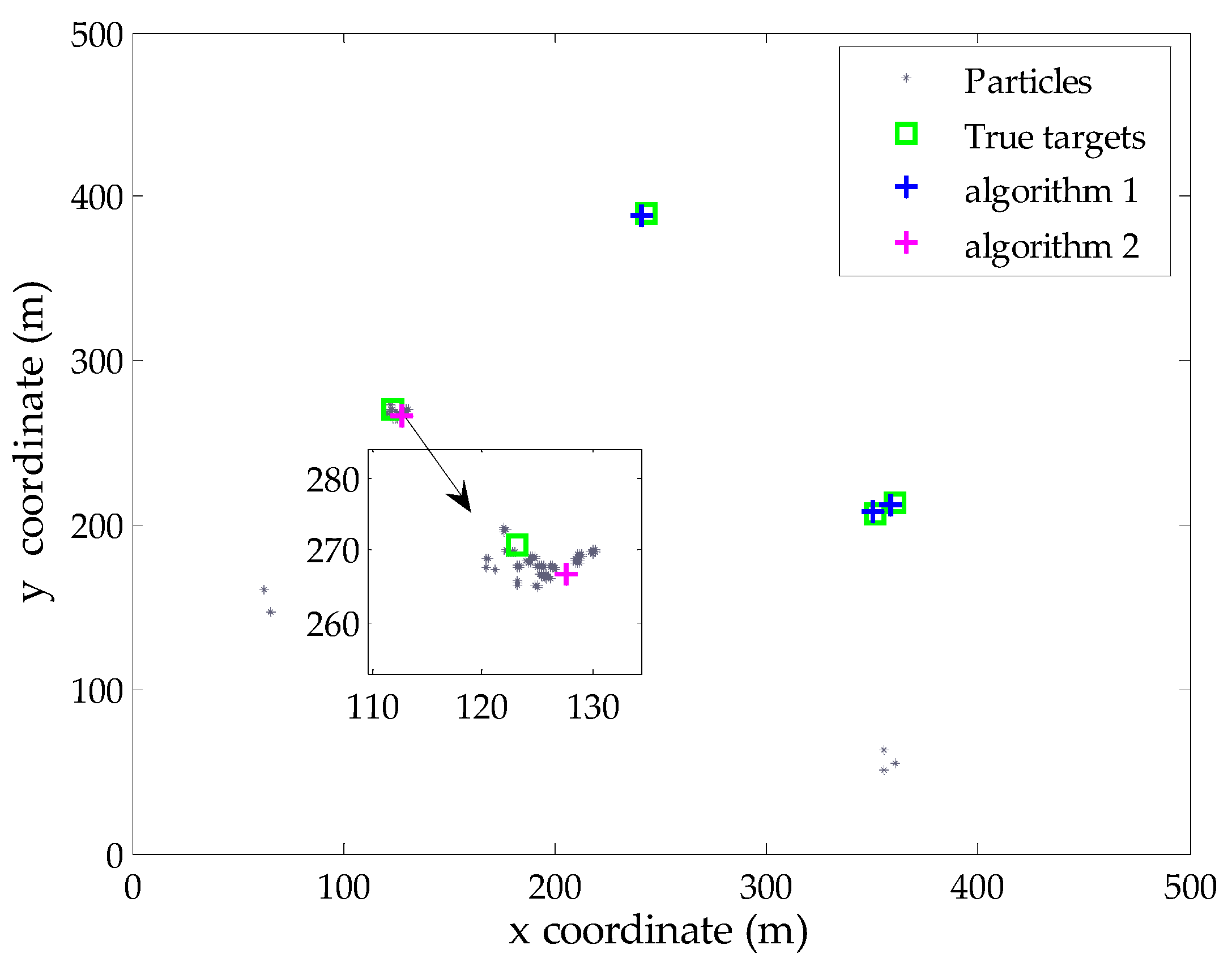
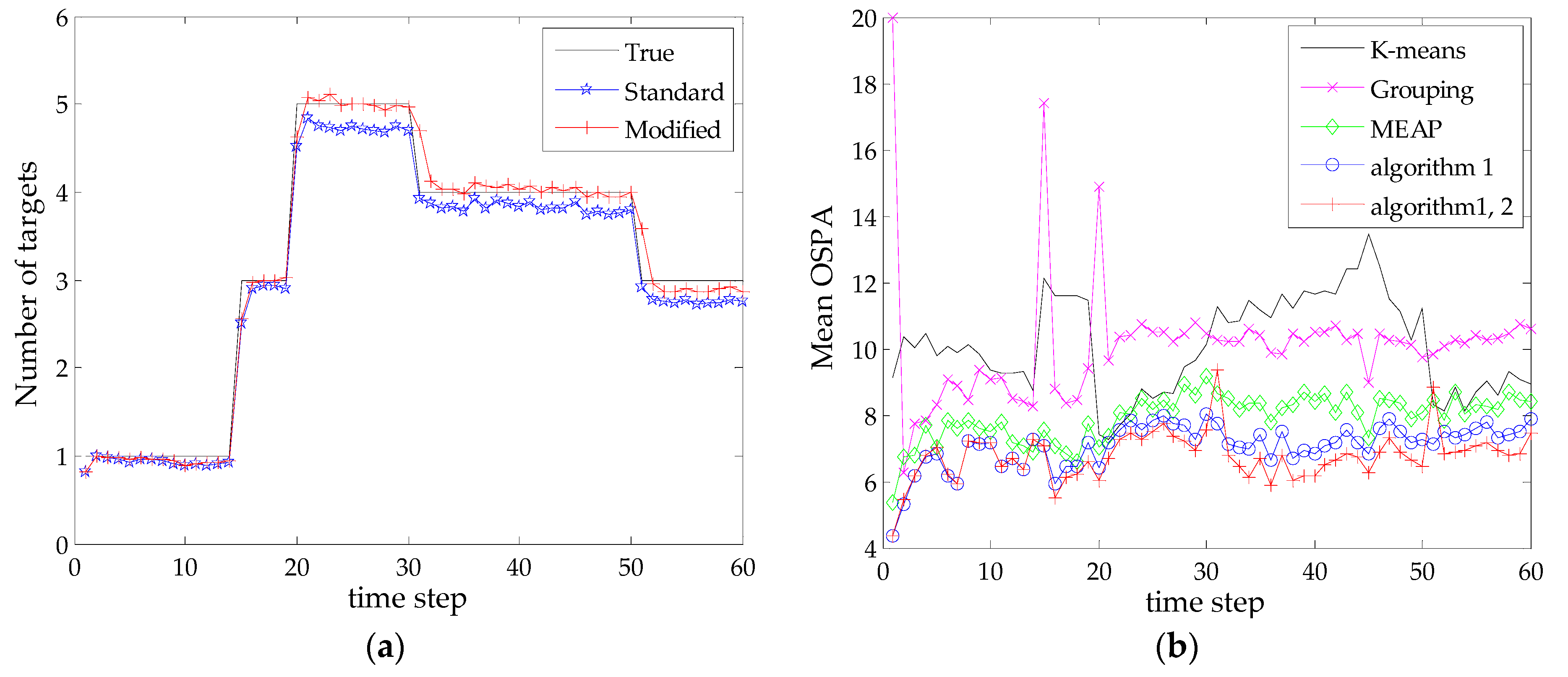
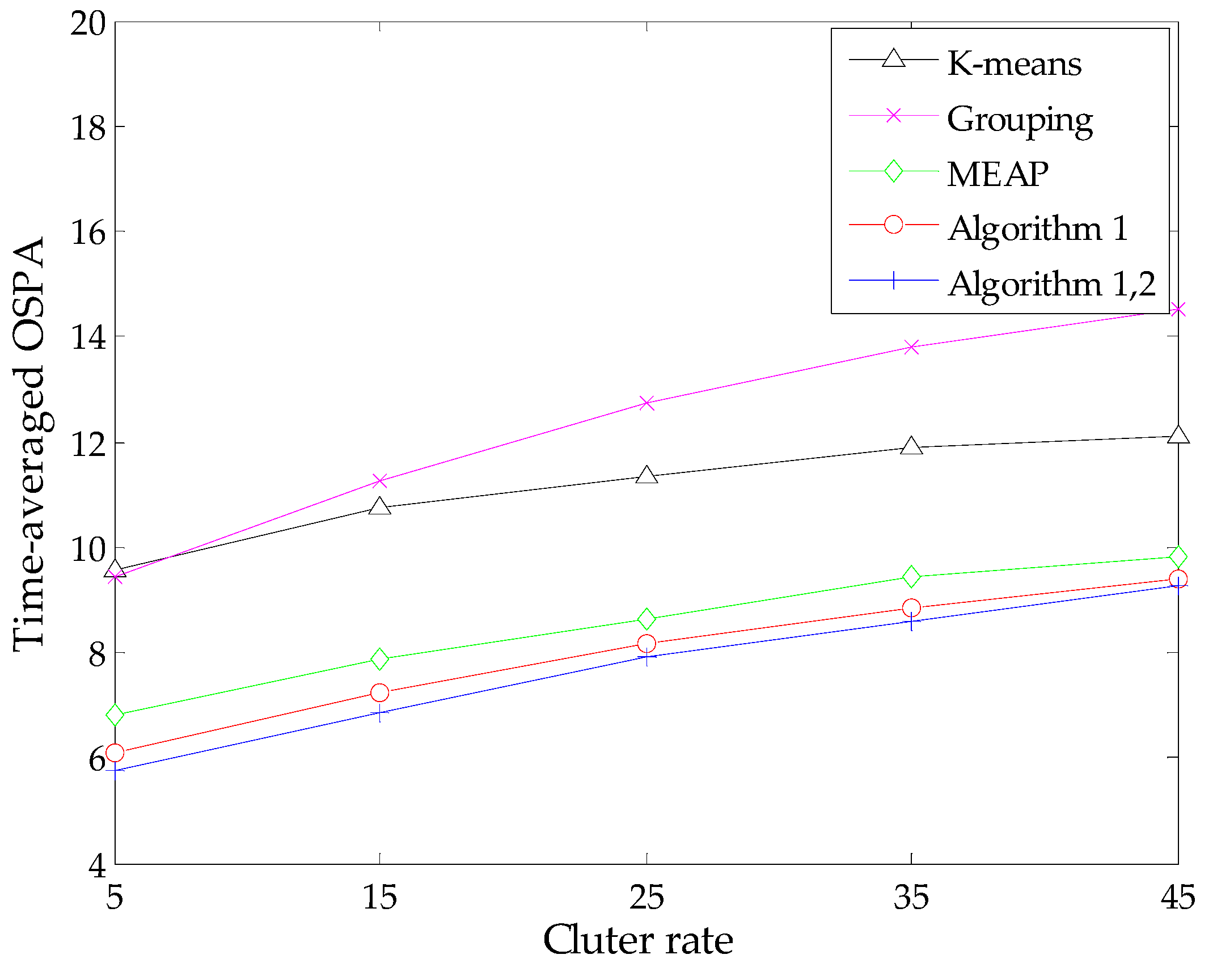
4. Simulation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FMM | Finite mixture models |
| JPDA | Joint probabilistic data association |
| MEAP | Multi-expected a posterior |
| MHT | Multiple hypothesis tracking |
| MTT | Multi-target tracking |
| OSPA | Optimal Sub-pattern Assignment |
| PHD | Probability hypothesis density |
| RFS | Random finite sets |
| SMC | Sequential Monte Carlo |
References
- Shalom, Y.B.; Daum, F.; Huang, J. The probabilistic data association filter estimation in the presence of measurement uncertainty. IEEE Control Syst. Mag. 2009, 6, 82–100. [Google Scholar] [CrossRef]
- Blackman, S.S. Multiple hypothesis tracking for multiple target tracking. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 5–18. [Google Scholar] [CrossRef]
- Habtemariam, B.; Tharmarasa, R.; Thayaparan, T.; Mallick, M.; Kirubarajan, T. A multiple-detection joint probabilistic data association filter. IEEE J. Sel. Top. Signal Process. 2013, 7, 461–471. [Google Scholar] [CrossRef]
- Mahler, R. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Phung, D. Labeled random finite sets and the Bayes multi-target tracking filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef]
- Vo, B.N.; Singh, S.; Doucet, A. Sequential Monte Carlo methods for multi-target filtering with random finite sets. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1224–1245. [Google Scholar]
- Whiteley, N.; Singh, S.; Godsill, S. Auxiliary particle implementation of probability hypothesis density filter. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1437–1454. [Google Scholar] [CrossRef]
- Vo, B.N.; Ma, W.K. The Gaussian mixture probability hypothesis density filter. IEEE Trans. Signal Process. 2006, 54, 4091–4104. [Google Scholar] [CrossRef]
- Yoon, J.H.; Kim, D.Y.; Yoon, K.J. Efficient importance sampling function design for sequential Monte Carlo PHD filter. Signal Process. 2012, 92, 2315–2321. [Google Scholar] [CrossRef]
- Zhang, F.H.; Buckl, C.; Knoll, A. Multiple Vehicle Cooperative Localization with Spatial Registration Based on a Probability Hypothesis Density Filter. Sensors 2014, 14, 995–1009. [Google Scholar] [CrossRef] [PubMed]
- Ristic, B.; Clark, D.; Vo, B.N.; Vo, B.T. Adaptive target birth intensity in PHD and CPHD filters. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 1656–1668. [Google Scholar] [CrossRef]
- Battistelli, G.; Chisci, L.; Morrocchi, S.; Papi, F.; Farina, A.; Graziano, A. Robust multisensor multitarget tracker with application to passive multistatic radar tracking. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3450–3472. [Google Scholar] [CrossRef]
- Ristic, B. Efficient update of persistent particles in the SMC-PHD filter. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing, Brisbane, Australia, 19–24 April 2015; pp. 4120–4124.
- Clark, D.E.; Bell, J. Multi-target state estimation and track continuity for the particle PHD filter. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1441–1452. [Google Scholar] [CrossRef]
- Dunne, D.; Tharmarasa, R.; Lang, T.; Kirubarajan, T. SMC-PHD-based multi-target tracking with reduced peak extraction. In Proceedings of the SPIE 7445, Signal and Data Processing of Small Targets, San Diego, CA, USA, 4–6 August 2009.
- Liu, W.F.; Han, C.Z.; Lian, F.; Zhu, H.Y. Multitarget state extraction for the PHD filter using MCMC approach. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 864–883. [Google Scholar] [CrossRef]
- Tobias, M.; Lanterman, A.D. Techniques for birth-particle placement in the probability hypothesis density particle filter applied to passive radar. IET Radar Sonar Navig. 2008, 2, 351–365. [Google Scholar] [CrossRef]
- Tang, X.; Wei, P. Multi-target state extraction for the particle probability hypothesis density filter. IET Radar Sonar Navig. 2011, 5, 877–883. [Google Scholar] [CrossRef]
- Ristic, B.; Clark, D.; Vo, B.N. Improved SMC implementation of the PHD filter. In Proceedings of the 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010; pp. 1–8.
- Lin, L.K.; Xu, H.; Sheng, W.D.; Wei, A. Multi-target state-estimation technique for the particle probability hypothesis density filter. Sci. China Inform. Sci. 2012, 55, 2318–2328. [Google Scholar] [CrossRef]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]
- Baum, M.; Willett, P.; Hanebeck, U.D. MMOSPA-based track extraction in the PHD filter-a justification for k-means clustering. In Proceedings of the 53th IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 1816–1821.
- Li, T.C.; Sun, S.D.; Bolić, M.; Corchado, J.M. Algorithm design for parallel implementation of the SMC-PHD filter. Signal Process. 2016, 119, 115–127. [Google Scholar] [CrossRef]
- Pierre, D.M.; Houssineau, J. Particle Association Measures and Multiple Target Tracking. In Theoretical Aspects of Spatial-Temporal Modeling; Peters, G.W., Matsui, T., Eds.; Springer: Tokyo, Japan, 2015; pp. 1–30. [Google Scholar]
- Erdinc, O.; Willett, P.; Bar-Shalom, Y. The bin-occupancy filter and its connection to the PHD filters. IEEE Trans. Signal Process. 2009, 57, 4232–4246. [Google Scholar] [CrossRef]
- Blackrnan, S.; House, A. Design and Analysis of Modern Tracking Systems; Artech House: Boston, MA, USA, 1999; pp. 336–337. [Google Scholar]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Si, W.; Wang, L.; Qu, Z. Multi-Target State Extraction for the SMC-PHD Filter. Sensors 2016, 16, 901. https://doi.org/10.3390/s16060901
Si W, Wang L, Qu Z. Multi-Target State Extraction for the SMC-PHD Filter. Sensors. 2016; 16(6):901. https://doi.org/10.3390/s16060901
Chicago/Turabian StyleSi, Weijian, Liwei Wang, and Zhiyu Qu. 2016. "Multi-Target State Extraction for the SMC-PHD Filter" Sensors 16, no. 6: 901. https://doi.org/10.3390/s16060901
APA StyleSi, W., Wang, L., & Qu, Z. (2016). Multi-Target State Extraction for the SMC-PHD Filter. Sensors, 16(6), 901. https://doi.org/10.3390/s16060901




