Gyro Drift Correction for An Indirect Kalman Filter Based Sensor Fusion Driver
Abstract
:1. Introduction
- We have proposed a new software architecture for sensor fusion driver utilizing the quaternion based indirect Kalman filter in conjunction with additional feedback components for gyro drift correction. These components do not only handle the external feedback loop issue between the device driver and applications, but also cancel the non-gyro signal in the measured state vector.
- The developed sensor fusion driver abstracts underlying sensor hardware to provide an unified framework for mobile applications. The multi-sensing information is facilitated without any requirement of re-programming or modification in the existing applications. It supports backward compatibility for the legacy applications as well.
- The implementation in the device driver layer provides greater performance up to 10 times from 538 to 5,347 samples per second, and lower latency in calculation time from 1.8579 ns to 0.18702 ns. The duplication of sensor fusion process among applications is completely addressed.
2. Related Work
2.1. Systematical Designs
2.2. Theoretical Approaches
3. Preliminaries
3.1. Problem Statement
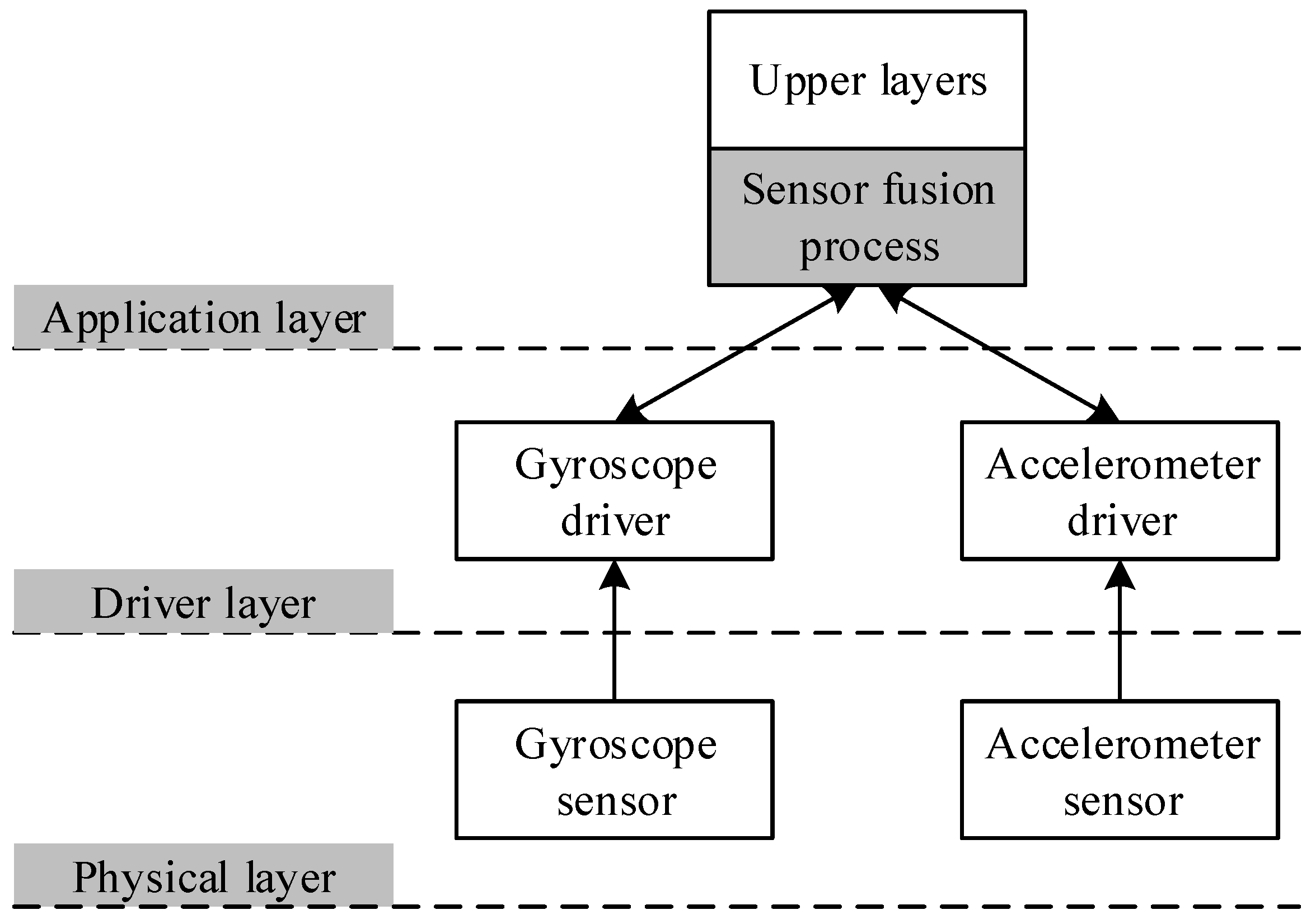
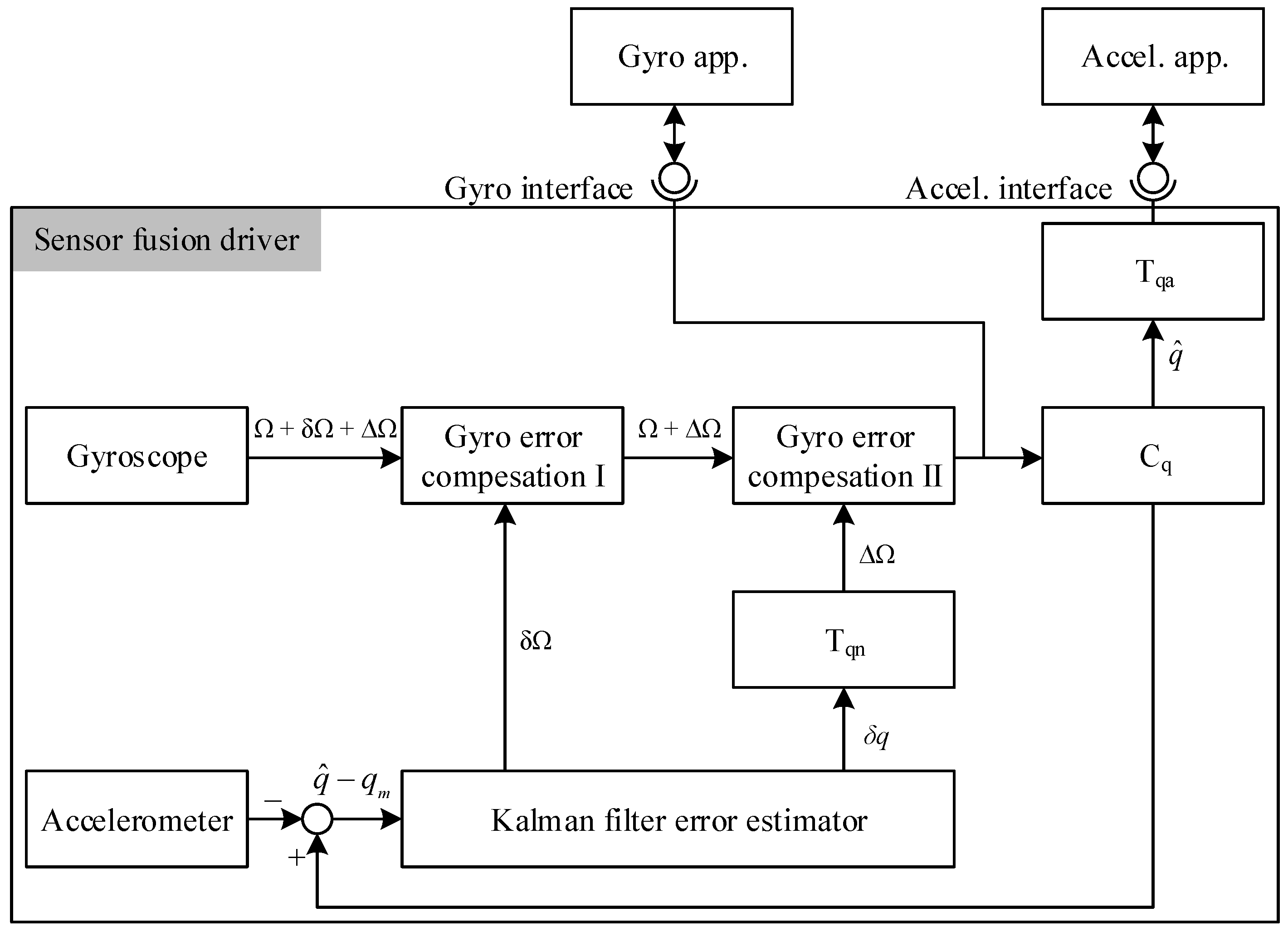
- External feedback loop: There is a feedback loop between the modules of the filter. If the indirect Kalman filter were directly applied, it would result in a feedback loop signal between the applications and the device driver, which is not a desirable configuration. When the Kalman filter is implemented in the device driver level, it would use Euler angle kinematics in calculation, which is not linear. The orientation value is transformed to gyro value before coming out of the Kalman filter, then it has to be converted to orientation value again inside the applications. The repeated transformations may cause error accumulations because Euler angle kinematics is not linear. Note that the feedback loop is outside of the Kalman filter.
- Non-gyro signal in the measured state vector: Within the original indirect Kalman filter, a non-gyro signal always appears in the state vector after measurement. It is not hard to resolve this problem in the desired applications, but it wastes more time.
3.2. Our Approach
4. Proposed Solution
4.1. Sensor Fusion Driver Architecture
4.2. Gyro Drift Correction
5. Experimental Results and Discussions
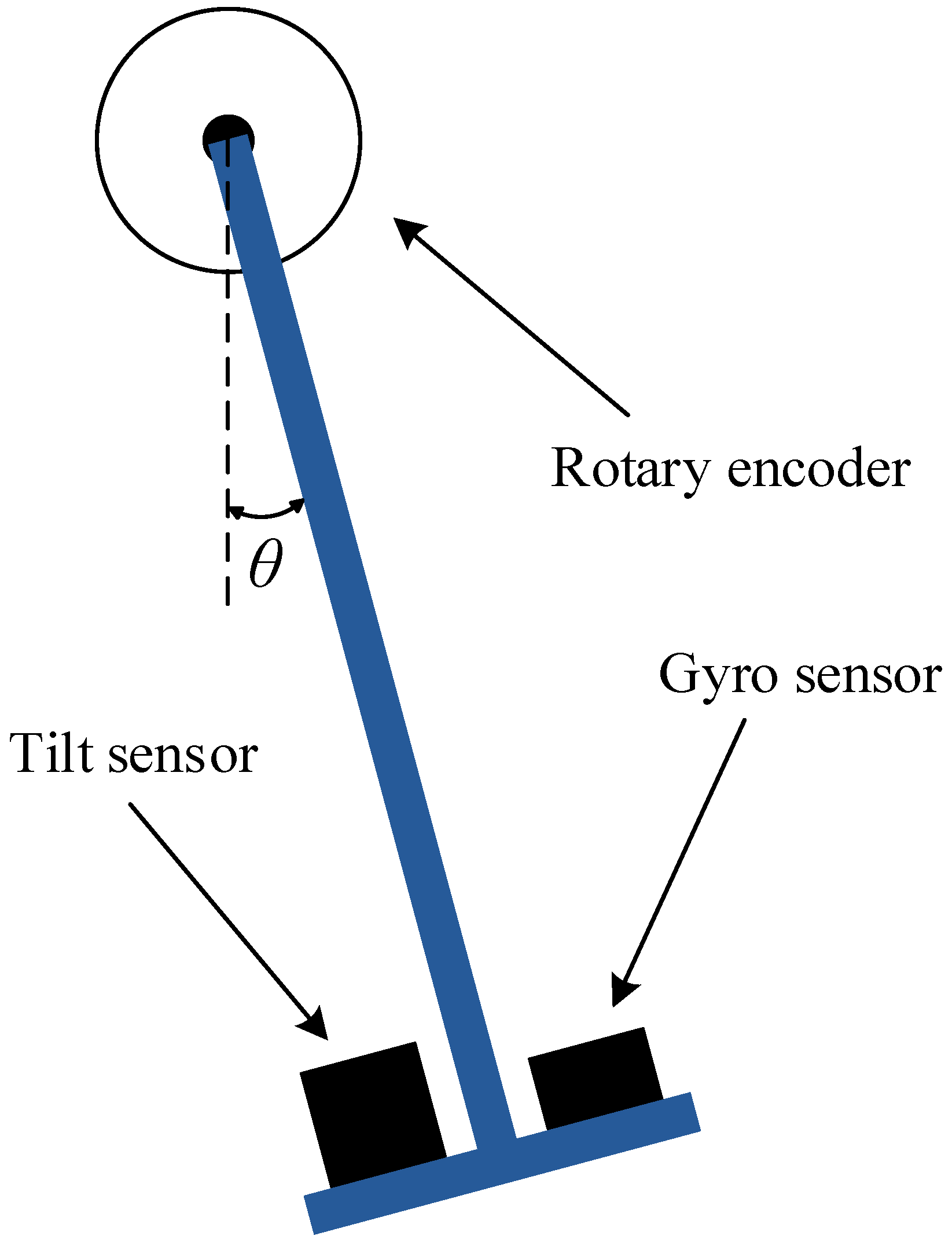
5.1. Preparation
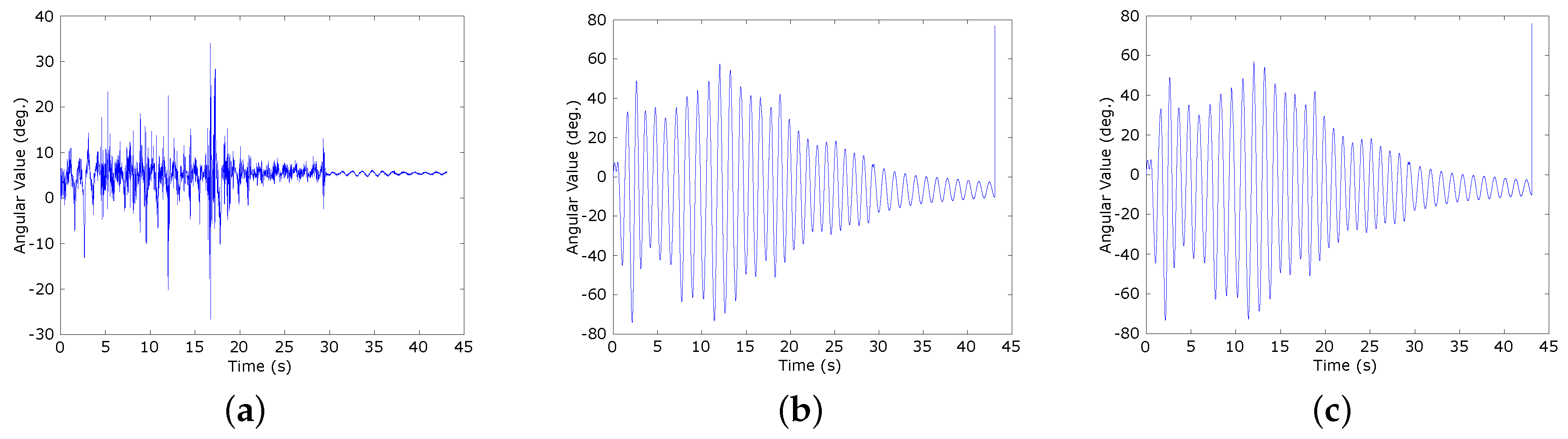
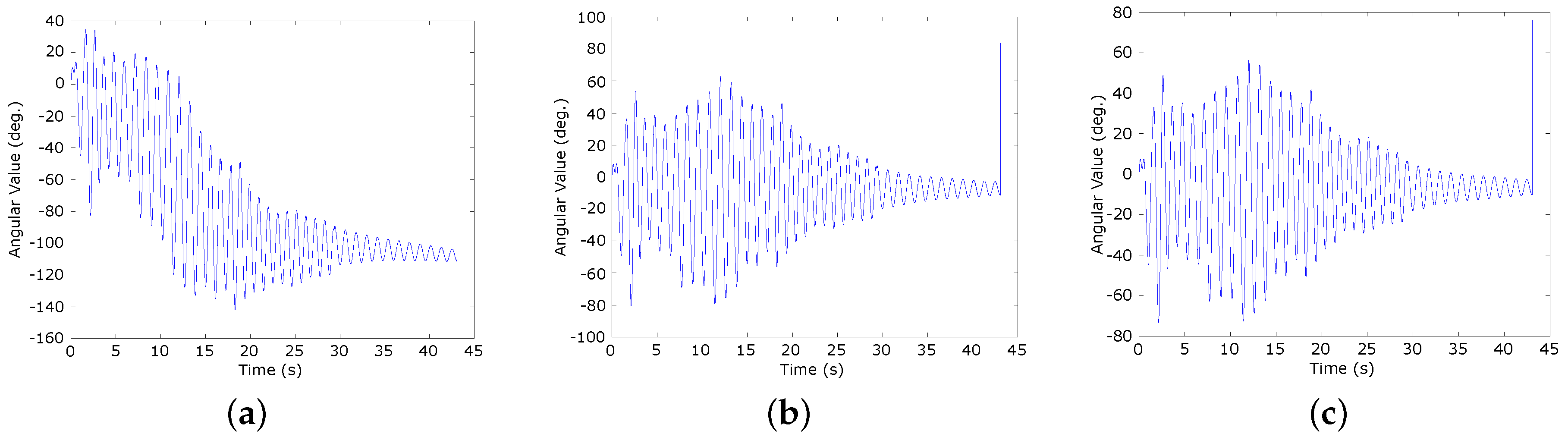
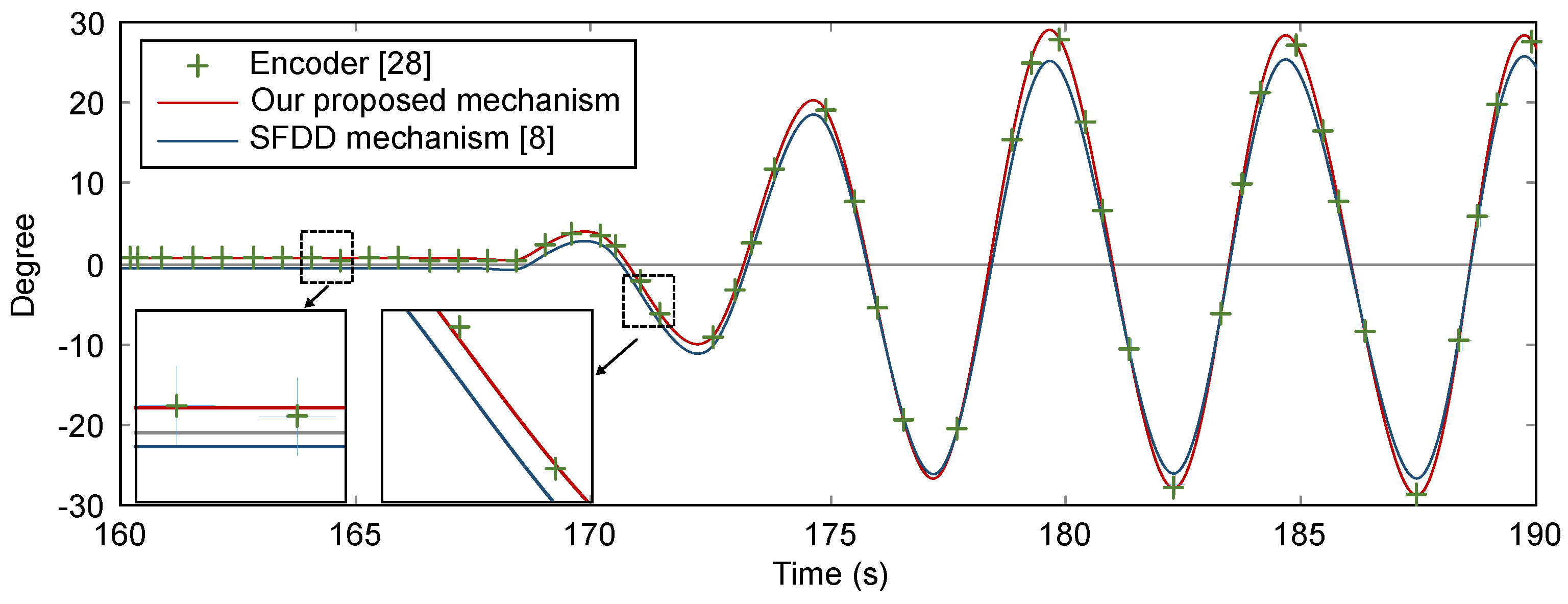
5.2. Accuracy Evaluation
5.3. Performance Evaluation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kalns, E.T.; Freitag, D.B.; Mark, W.S.; Ayan, N.F.; Wolverton, M.J.; Lee, T.J. Rapid Development of Virtual Personal Assistant Applications. U.S. Patent 9,081,411, 7 July 2015. [Google Scholar]
- Ranjan, R.; Wang, M.; Perera, C.; Jayaraman, P.P.; Zhang, M.; Strazdins, P.; Shyamsundar, R.K. City Data Fusion: Sensor Data Fusion in the Internet of Things. Int. J. Distrib. Syst. Technol. 2016, 7, 15–36. [Google Scholar]
- Pires, I.M.; Garcia, N.M.; Pombo, N.; Flórez-Revuelta, F. From Data Acquisition to Data Fusion: A Comprehensive Review and a Roadmap for the Identification of Activities of Daily Living Using Mobile Devices. Sensors 2016, 16. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.; Gu, Y. Data fusion in the Internet of Things. Proced. Eng. 2011, 15, 3023–3026. [Google Scholar] [CrossRef]
- Shivaprasad Yadav, S.G.; Chitra, A.; Lakshmi Deepika, C. Reviewing the process of data fusion in wireless sensor network: a brief survey. Int. J. Wirel. Mob. Comput. 2015, 8, 130–140. [Google Scholar] [CrossRef]
- Khaleghi, B.; Khamis, A.; Karray, F.O.; Razavi, S.N. Multisensor data fusion: A review of the state-of-the-art. Inf. Fusion 2013, 14, 8–44. [Google Scholar] [CrossRef]
- Ganti, R.K.; Srinivasan, S.; Gacic, A. Multisensor Fusion in Smartphones for Lifestyle Monitoring. In Proceedings of the 2010 International Conference on Body Sensor Networks, Singapore, 7–9 June 2010.
- Gim, D.H.; Min, S.H.; Lee, C.G. A Novel Technique for Composing Device Drivers for Sensors on Smart Devices. In IT Convergence and Services; Springer Lecture Notes in Electrical Engineering; Springer: Gwangju, Korea, 2011; Volume 107, pp. 671–677. [Google Scholar]
- Alamri, A.; Ansari, W.S.; Hassan, M.M.; Hossain, M.S.; Alelaiwi, A.; Hossain, M.A. A survey on sensor-cloud: Architecture, applications, and approaches. Int. J. Distrib. Sens. Netw. 2013, 2013, 1–18. [Google Scholar] [CrossRef]
- La, H.M.; Sheng, W. Distributed sensor fusion for scalar field mapping using mobile sensor networks. IEEE Trans. Cybern. 2013, 43, 766–778. [Google Scholar] [PubMed]
- Rawat, P.; Singh, K.D.; Chaouchi, H.; Bonnin, J.M. Wireless sensor networks: a survey on recent developments and potential synergies. J. Supercomput. 2014, 68, 1–48. [Google Scholar] [CrossRef]
- Mishra, S.; Thakkar, H. Features of WSN and data aggregation techiques in WSN: A survey. Int. J. Eng. Innov. Technol. 2012, 1, 264–273. [Google Scholar]
- Tripathi, A.; Gupta, S.; Chourasiya, B. Survey on data aggregation techniques for wireless sensor networks. Int. J. Adv. Res. Comput. Commun. Eng. 2014, 3, 7366–7371. [Google Scholar]
- Novak, D.; Riener, R. A survey of sensor fusion methods in wearable robotics. Robot. Auton. Syst. 2015, 73, 155–170. [Google Scholar] [CrossRef]
- Van der Merwe, R.; Wan, E.A.; Julier, S. Sigma-point Kalman filters for nonlinear estimation and sensor-fusion: Applications to integrated navigation. In Proceedings of the AIAA Guidance, Navigation & Control Conference, Providence, RI, USA, 16–19 August 2004; pp. 16–19.
- Sun, S.L.; Deng, Z.L. Multi-sensor optimal information fusion Kalman filter. Automatica 2004, 40, 1017–1023. [Google Scholar] [CrossRef]
- Chen, S.Y. Kalman filter for robot vision: A survey. IEEE Trans. Ind. Electron. 2012, 59, 4409–4420. [Google Scholar] [CrossRef]
- Enders, R.H.; Brodzik, A.K.; Pellegrini, M.R. Algebra of Dempster-Shafer evidence accumulation. In Proceedings of the SPIE 6968, Signal Processing, Sensor Fusion, and Target Recognition XVII, 696810, Orlando, FL, USA, 16 March 2008.
- Jenkins, M.P.; Gross, G.A.; Bisantz, A.M.; Nagi, R. Towards context aware data fusion: Modeling and integration of situationally qualified human observations to manage uncertainty in a hard + soft fusion process. Inf. Fusion 2015, 21, 130–144. [Google Scholar] [CrossRef]
- Chen, S.; Deng, Y.; Wu, J. Fuzzy sensor fusion based on evidence theory and its application. Appl. Artif. Intell. Int. J. 2013, 27, 235–248. [Google Scholar] [CrossRef]
- Izadi, D.; Abawajy, J.H.; Ghanavati, S.; Herawan, T. A data fusion method in wireless sensor networks. Sensors 2015, 15, 2964–2979. [Google Scholar] [CrossRef] [PubMed]
- Maren, A.J.; Craig, H.T.; Robert, P.M. Handbook of Neural Computing Applications; Academic Press: San Diego, CA, USA, 2014. [Google Scholar]
- Paul, P.S.; Varadarajan, A.S. A multi-sensor fusion model based on artificial neural network to predict tool wear during hard turning. J. Eng. Manuf. 2012, 226, 853–860. [Google Scholar] [CrossRef]
- Pinto, A.R.; Montez, C.; Araujo, G.; Vasques, F.; Portugal, P. An approach to implement data fusion techniques in wireless sensor networks using genetic machine learning algorithms. Inf. Fusion 2014, 15, 90–101. [Google Scholar] [CrossRef]
- Diebel, J. Representing Attitude: Euler Angles, Unit Quaternions, and Rotation Vectors; Technical report; Stanford University: Stanford, CA, USA, 2006. [Google Scholar]
- Chonkroun, D.; Bar-Itzhack, I.Y.; Oshman, Y. Novel quaternion Kalman filter. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 174–190. [Google Scholar] [CrossRef]
- Trawny, N.; Roumeliotis, S. Indirect Kalman Filter for 3D Attitude Estimation; University of Minnesota: Minneapolis, MN, USA, TR 2005-002, Rev. 57; March 2005. [Google Scholar]
- Lee, H.J.; Jung, S. Gyro sensor drift compensation by Kalman filter to control a mobile inverted pendulum robot system. In Proceedings of the IEEE International Conference on Industrial Technology, Gippsland, Australia, 10–13 February 2009; pp. 1–6.
| Specification | Value |
|---|---|
| CPU | S5PV210 ARM-CORTEX A8 [1 GHz] |
| Memory | 512M DDR SDRAM |
| Kernel | Linux kernel 2.6.32 (Android OS) |
| Accelerometer sensor | 3-axis accelerometer sensor |
| Gyroscope sensor | 2-axis gyroscope sensor |
| Sampling frequency | 100 Hz |
| Angle range |
| Method | Sensor | |||
|---|---|---|---|---|
| Separate sensor | Accelerometer | 22.3546 | 21.9589 | 35.5267 |
| Gyroscope | 70.9580 | 72.6149 | 307.1894 | |
| Our proposed methods | Accelerometer | 0.04875 | 0.0537 | 0.2537 |
| Gyroscope | 1.8702 | 1.9309 | 8.6471 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-G.; Dao, N.-N.; Jang, S.; Kim, D.; Kim, Y.; Cho, S. Gyro Drift Correction for An Indirect Kalman Filter Based Sensor Fusion Driver. Sensors 2016, 16, 864. https://doi.org/10.3390/s16060864
Lee C-G, Dao N-N, Jang S, Kim D, Kim Y, Cho S. Gyro Drift Correction for An Indirect Kalman Filter Based Sensor Fusion Driver. Sensors. 2016; 16(6):864. https://doi.org/10.3390/s16060864
Chicago/Turabian StyleLee, Chan-Gun, Nhu-Ngoc Dao, Seonmin Jang, Deokhwan Kim, Yonghun Kim, and Sungrae Cho. 2016. "Gyro Drift Correction for An Indirect Kalman Filter Based Sensor Fusion Driver" Sensors 16, no. 6: 864. https://doi.org/10.3390/s16060864
APA StyleLee, C.-G., Dao, N.-N., Jang, S., Kim, D., Kim, Y., & Cho, S. (2016). Gyro Drift Correction for An Indirect Kalman Filter Based Sensor Fusion Driver. Sensors, 16(6), 864. https://doi.org/10.3390/s16060864






