A Core-Offset Mach Zehnder Interferometer Based on A Non-Zero Dispersion-Shifted Fiber and Its Torsion Sensing Application
Abstract
:1. Introduction
2. MZI Fabrication Process and Operation Principle
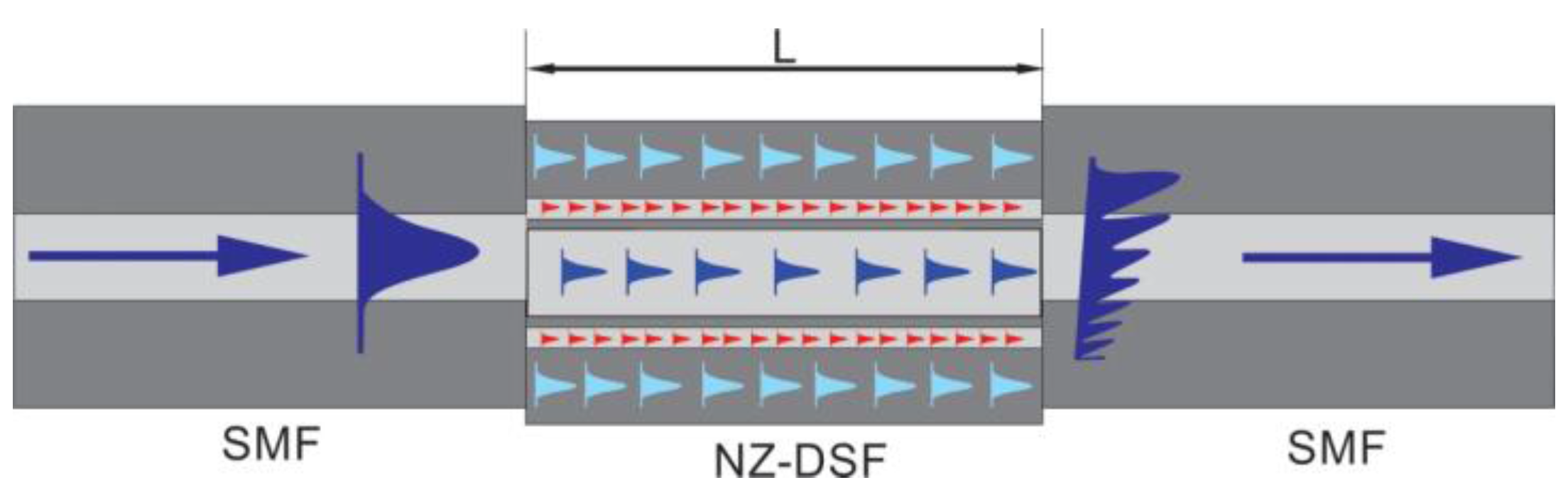
2.1. The Core-Offset Fusion Splicing of a NZ-DSF and SMF
2.2. Priciple of Operation
3. Characterization of MZIs with a NZ-DSF
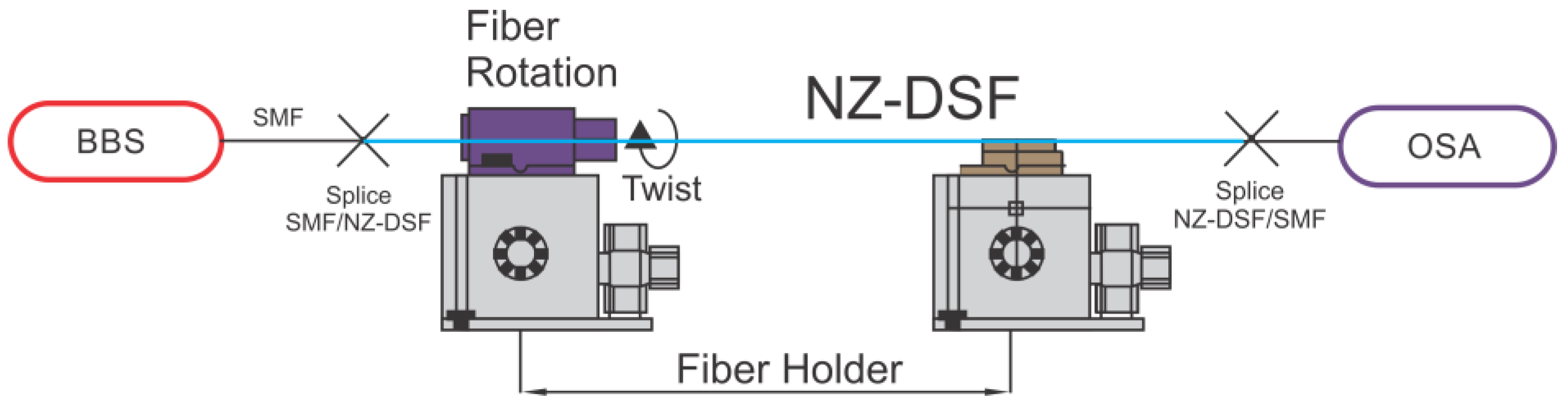
3.1. Experimental Setup
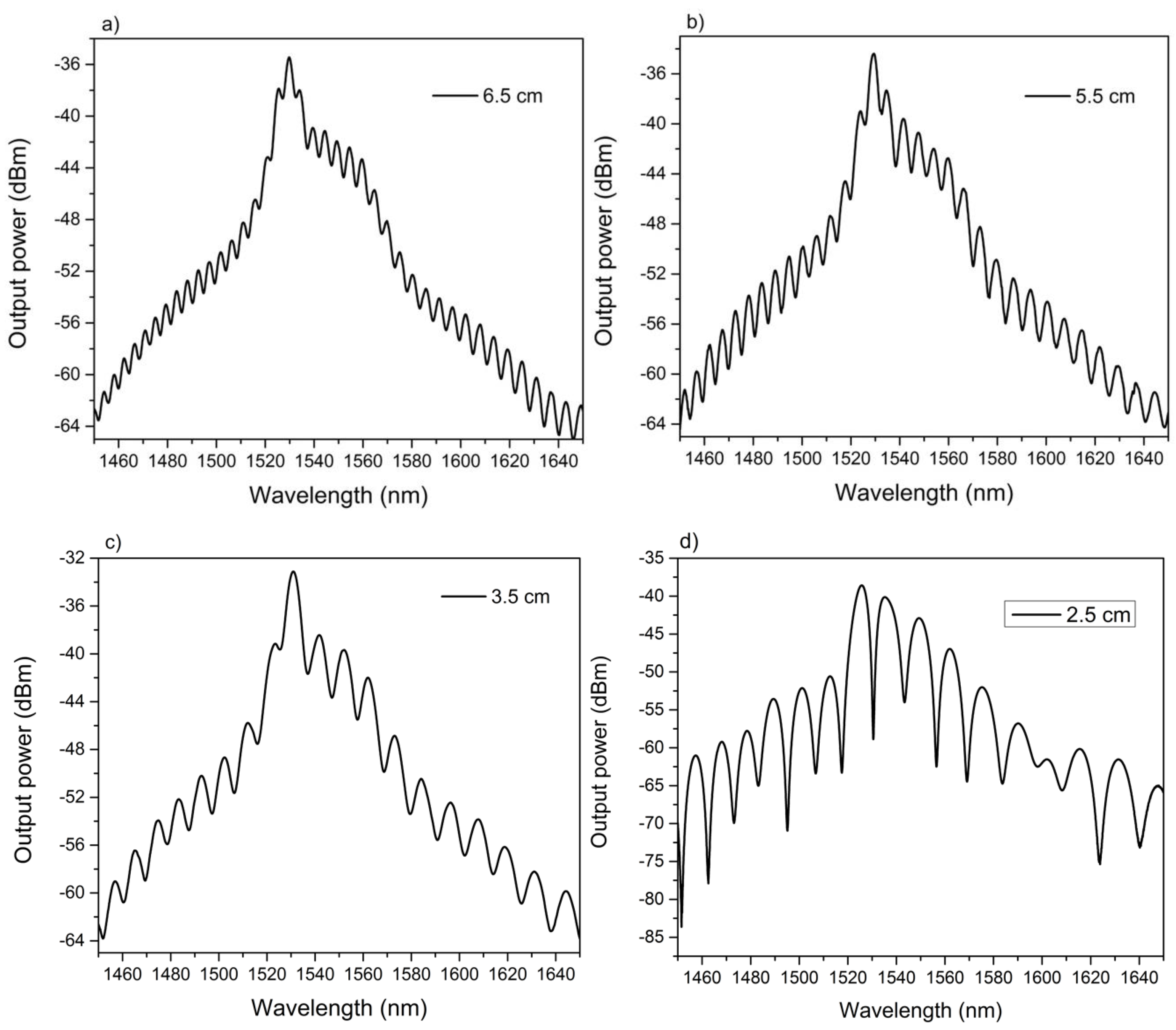
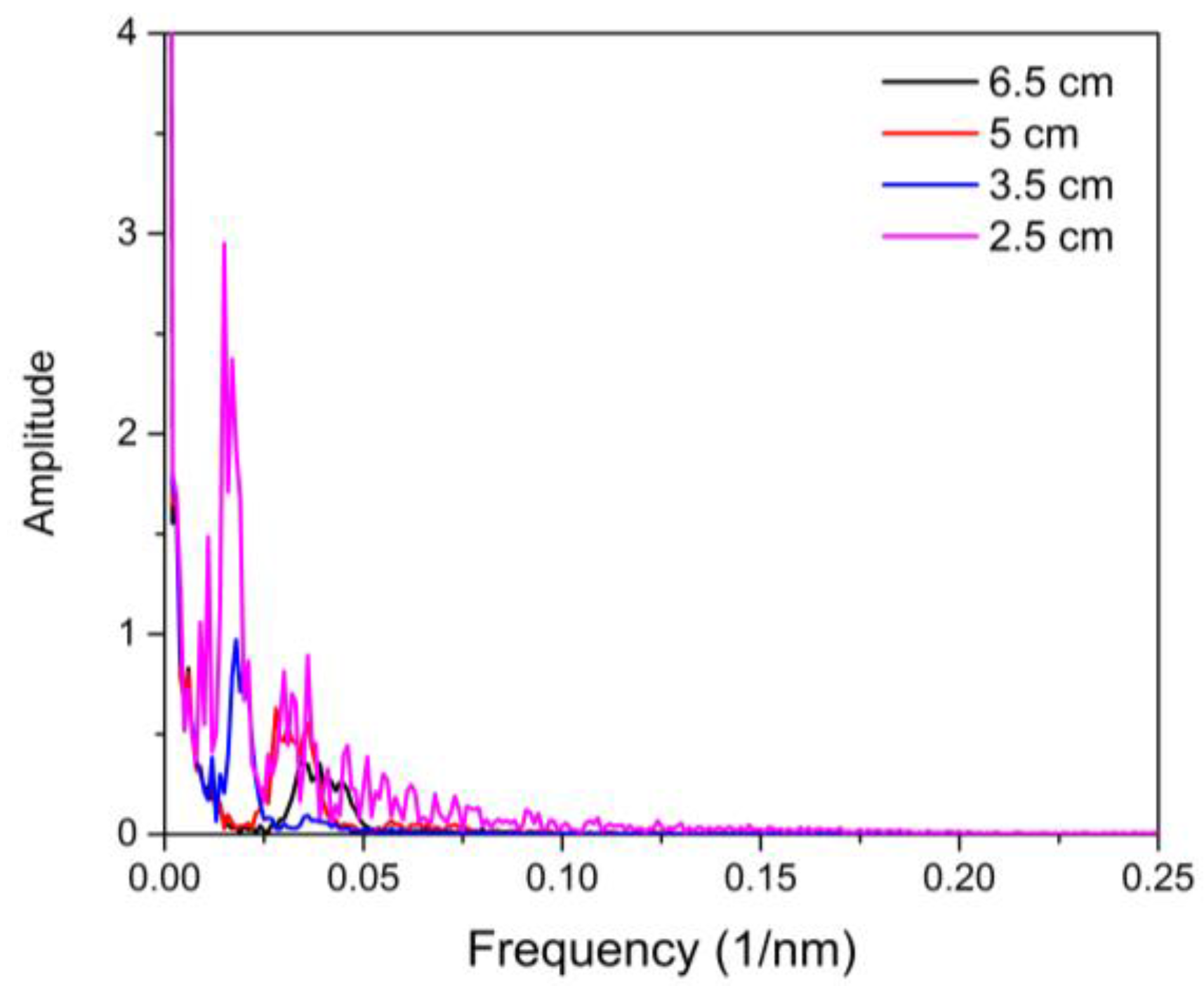
3.2. Characterization of the MZI with Different Lengths of NZ-DSF
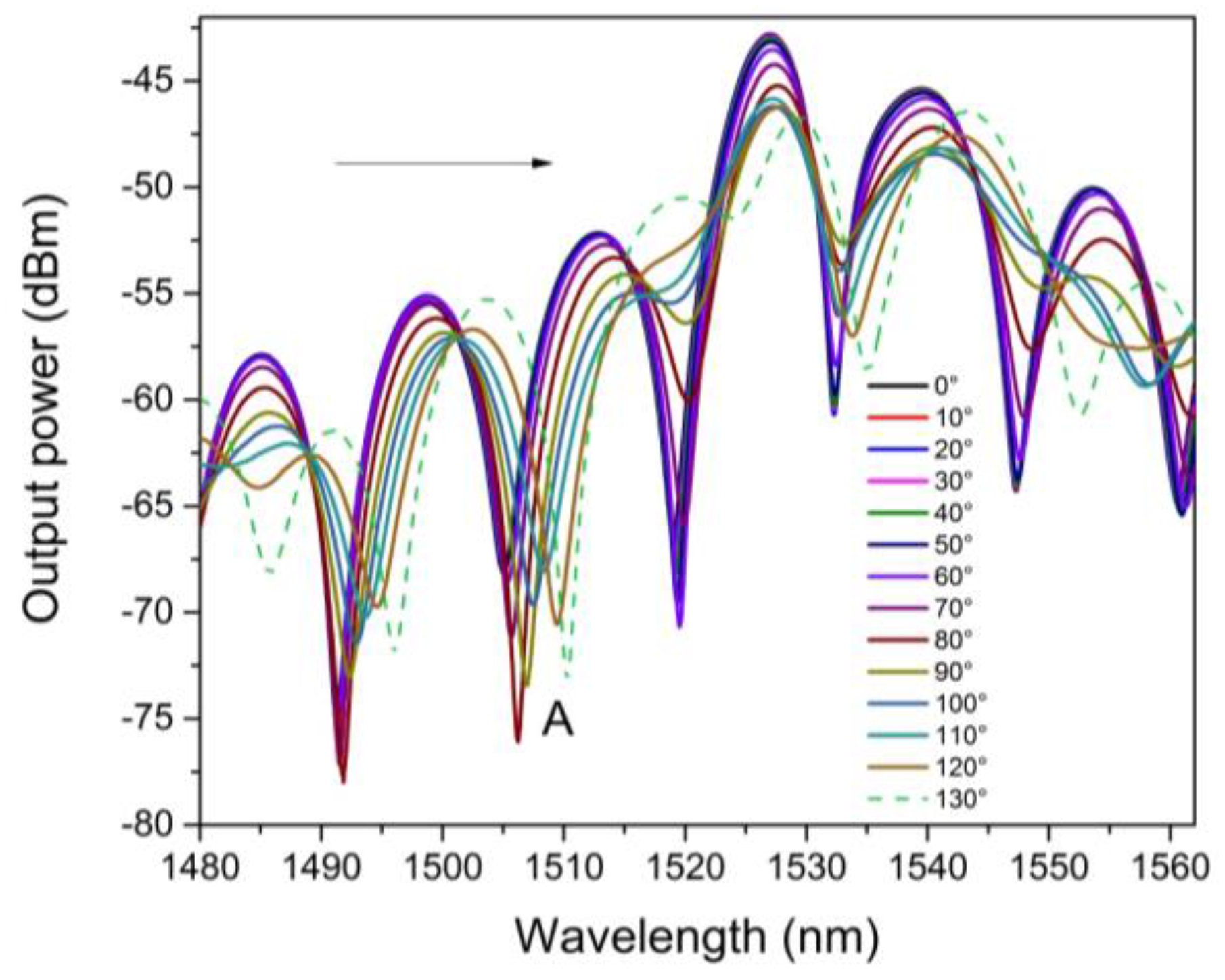
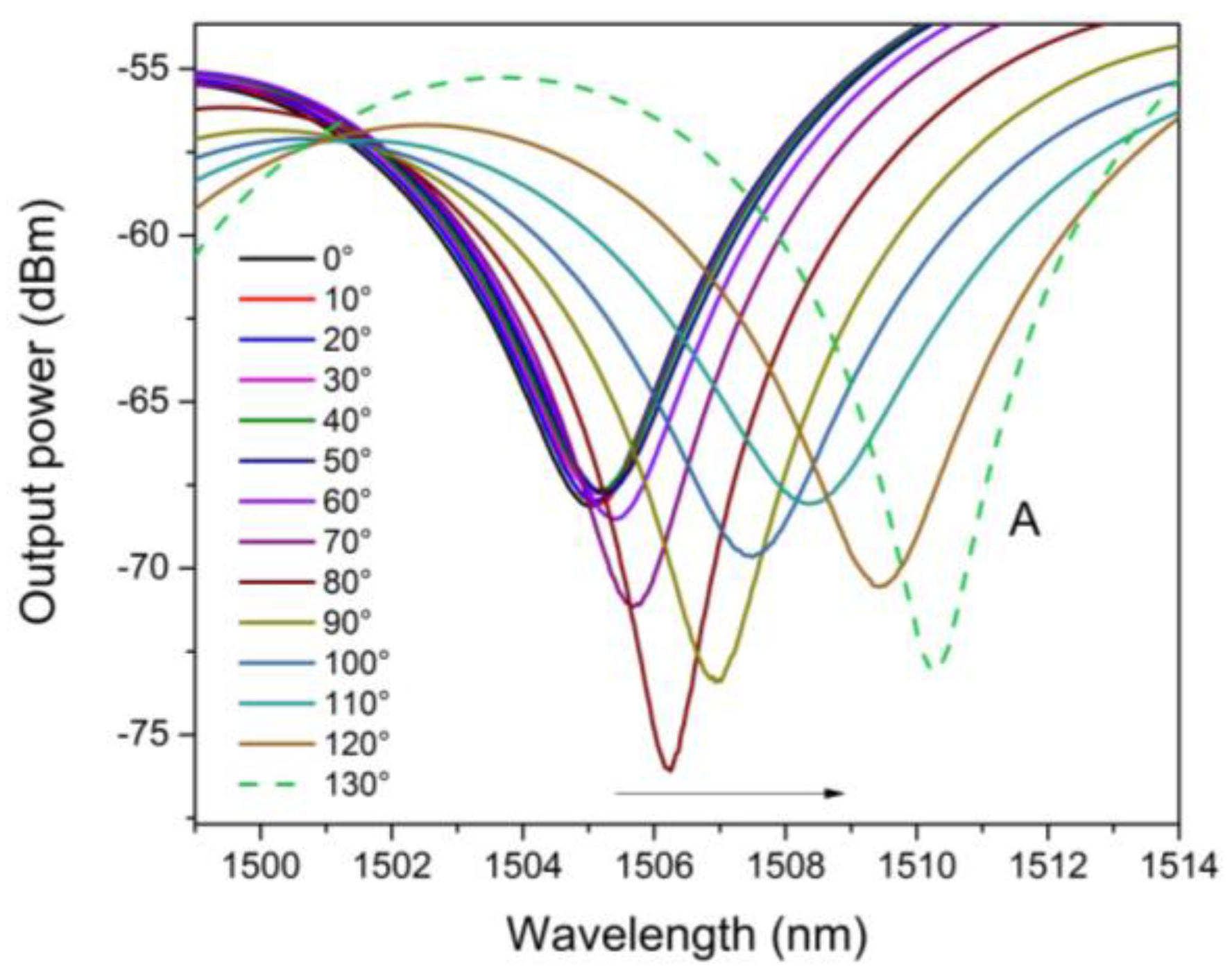
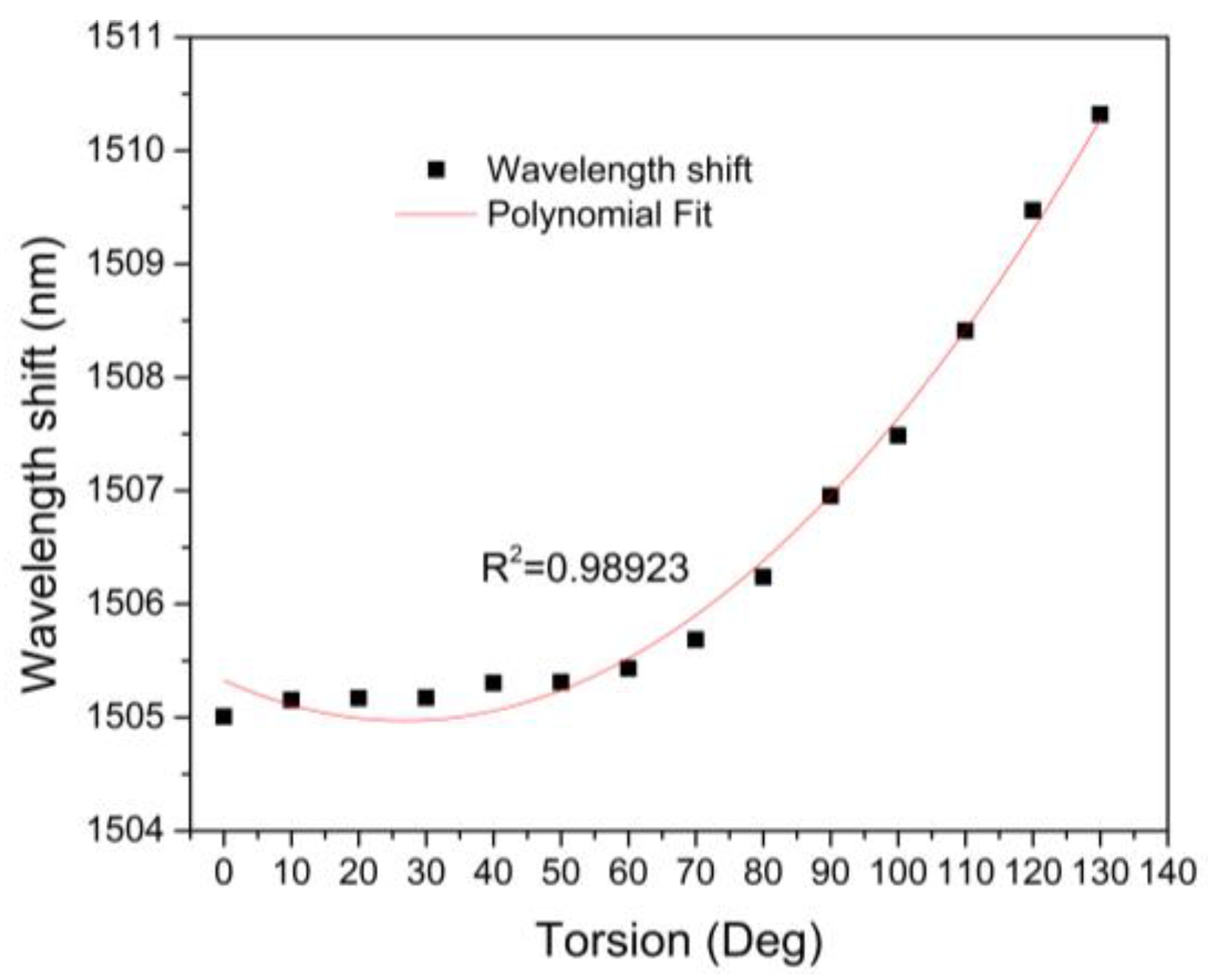
4. Experimental Results and Discussions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Villatoro, J.; Van Newkirk, A.; Antonio-Lopez, E.; Zubia, J.; Schulzen, A.; Amezcua-Correa, R. Ultrasensitive vector bending sensor based on multicore optical fiber. Opt. Lett. 2016, 41, 832–835. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Xie, H.; Zeng, X.; Fu, G.; Bi, W. Refractive index insensitive temperature sensor based on specialty triple-clad fiber. Opt. Express 2015, 23, 2320–2327. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-M.; Kim, T.-H.; BongKyun, K.; Youngjoo, C. Temperature-insensitive torsion sensor with enhanced sensitivity by using of highly birefringence photonic crystal fiber. IEEE Photon. Technol. Lett. 2010, 22, 579–583. [Google Scholar] [CrossRef]
- Bock, W.; Chen, J.; Mikulic, P.; Eftimov, Y.; Korwin-Pawlowski, M. Pressure sensing using a periodically tapered long-period grating written in photonic crystal fiber. Meas. Sci. Technol. 2007, 18, 3098. [Google Scholar] [CrossRef]
- Nalawade, S.M.; Harnol, S.S.; Thakur, V. Temperature and strain independent modal interferometric torsion sensor using photonic crystal fiber. IEEE Sens. J. 2012, 12, 2614–2615. [Google Scholar] [CrossRef]
- Lu, P.; Men, L.; Sooley, K.; Chen, Q. Tapered fiber Mach-Zehnder interferometer for simultaneous measurement of refractive index and temperature. Appl. Phys. Lett. 2009, 94, 131110. [Google Scholar] [CrossRef]
- Li, B.; Jiang, L.; Wang, S.; Zhou, L.; Xiao, H.; Tsai, H.-L. Ultra-abrupt tapered Mach-Zehnder interferometer sensor. Sensors 2011, 11, 5729–5739. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Li, X.; Xie, Z.; Liao, Z.; Tu, F.; Liu, D. Simultaneous measurement of refractive index and temperature using thinned fiber based Mach-Zehnder interferometer. Opt. Commun. 2012, 285, 3945–3949. [Google Scholar] [CrossRef]
- Allsop, T.; Reeves, R.; Webb, D.J.; Bennion, I. A high sensitivity refractometer based upon a long period grating Mach-Zehnder interferometer. Rev. Sci. Instrum. 2002, 73, 1702–1705. [Google Scholar] [CrossRef]
- Mata-Chavez, R.I.; Martines-Rios, A.; Torres-Gomez, I.; Selvas-Aguilar, R.; Estudillo-Ayala, J.M. Mach-Zehnder all Interferometer using two in-serie fattened gratings. Opt. Rev. 2008, 15, 230–235. [Google Scholar] [CrossRef]
- Villatoro, J.; Finazzi, V.; Minkovich, V.P.; Pruneri, V.; Badenes, G.A. Temperature insensitive photonic crystal fiber interferometer for absolute strain sensing. Appl. Phys. Lett. 2007, 91, 091109. [Google Scholar] [CrossRef]
- Wang, J.-N.; Tang, J.-L. Photonic crystal fiber Mach-Zehnder all Interferometer for refractive index sensing. Sensors 2012, 12, 2983–2995. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.M.; Chan, C.C.; Dong, X.Y.; Wang, Y.P.; Zu, P.; Wong, W.C.; Qian, W.W.; Li, T. Photonic crystal fiber strain sensor based on modified Mach-Zehnder interferometer. IEEE Photon. J. 2012, 4, 114–118. [Google Scholar] [CrossRef]
- Zhong, C.; Shen, C.; You, Y.; Chu, J.; Zou, X.; Dong, X.; Jin, Y.; Wang, J. Temperature-insensitive optical fiber two-dimensional micrometric displacement sensor based on an in-line Mach-Zehnder interferometer. J. Opt. Soc. Am. B 2012, 29, 1136–1140. [Google Scholar] [CrossRef]
- Tian, Z.; Yam, S.S.-C.; Loock, H.-P. Single-mode refractive index sensor based on core offset attenuators. IEEE Photon. Technol. Lett. 2008, 20, 1387–1389. [Google Scholar] [CrossRef]
- Yin, G.; Lou, S.; Zou, H. Refractive index sensor with asymmetrical fiber Mach-Zehnder interferometer based on a concatenating single-mode abrupt taper and core offset section. Opt. Laser Technol. 2013, 223, 119–124. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.-G.; Cai, L. High sensitive Mach-Zehnder interferometric refractive index sensor based on core-offset single mode fiber. Sens. Actuators A 2015, 223, 119–124. [Google Scholar] [CrossRef]
- Shen, C.; Zhong, C.; You, Y.; Chu, J.; Zou, J.; Dong, X.; Jin, Y.; Wang, J.; Gong, H. Polarization-dependent curvature sensor based on an in-fiber Mach-Zehnder interferometer with a difference arithmetic demodulation method. Opt. Express 2012, 20, 15406–15417. [Google Scholar] [CrossRef] [PubMed]
- Yao, Q.; Meng, H.; Wang, W.; Xue, H.; Huang, B.; Tan, H.; Huang, X. Simultaneous measurement of refractive index and temperature based on a core-offset Mach-Zehnder interferometer combined with a fiber Bragg grating. Sens. Actuators A 2014, 209, 73–79. [Google Scholar] [CrossRef]
- Mao, L.; Lu, P.; Lao, Z.; Liu, D.; Zhang, J. Highly sensitive curvature sensor based on single-mode fiber using core-offset splicing. Opt. Laser Technol. 2014, 54, 39–43. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Cai, L.; Yang, Y. Refractive index sensing based on photonic crystal fiber interferometer structure with up-tapered joint. Sens. Actuators B 2015, 221, 406–410. [Google Scholar] [CrossRef]
- Huang, Q.; Yu, Y.; Li, X.; Chen, X.; Zhang, Y.; Zhou, W.; Du, C. Micro-bending vector sensor based on six-air-hole grape fruit microstructure fiber using lateral offset splicing. Opt. Express 2015, 23, 3010–3019. [Google Scholar] [CrossRef] [PubMed]
- Sierra-Hernandez, J.M.; Castillo-Guzman, A.; Selvas-Aguilar, R.; Vargas-Rodriguez, E.; Gallegos-Arellano, E.; Guzman-Chavez, A.D.; Estudillo-Ayala, J.M.; Jauregui-Vazquez, D.; Rojas-Laguna, R. Torsion sensing setup based on three beam path Mach-Zehnder interferometer. Microw. Opt. Technol. Lett. 2015, 57, 1857–1860. [Google Scholar] [CrossRef]
- Lesnick, D.; Donlagic, D. In-line, fiber optic polarimetric twist/torsion sensor. Opt. Lett. 2013, 38, 1494–1496. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, L.A.; Grenier, J.R.; Stewart Aitchison, J.; Herman, P.R. Fiber optic stress-independent helical torsion sensor. Opt. Lett. 2015, 40, 657–660. [Google Scholar] [CrossRef] [PubMed]
- Sierra-Hernandez, J.M.; Rojas-Laguna, R.; Vargas-Rodriguez, E.; Estudillo-Ayala, J.M.; Jauregui-Vazquez, D.; Guzman-Chavez, A.D.; Zaca-Moran, P. A tunable multi-wavelength erbium doped fiber laser based on a Mach-Zehnder interferometer and photonic crystal fiber. Laser Phys. 2013, 23, 125103. [Google Scholar] [CrossRef]
- Chen, W.G.; Lou, S.Q.; Feng, S.C.; Wang, L.W.; Li, H.L.; Guo, T.Y.; Jian, S.S. Switchable multi-wavelength fiber ring laser based on compact in-fiber Mach-Zehnder interferometer with photonic crystal fiber. Laser Phys. 2009, 19, 2115–2119. [Google Scholar] [CrossRef]
- Cardenas-Sevilla, G.; Favero, F.; Villatoro, J. High-visibility photonic crystal fiber interferometer as multifunctional sensor. Sensors 2013, 13, 2339–2358. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.-Y.; Zhang, Q.; Qian, X.-S.; Lin, X.-W.; Xu, F.; Hu, W.; Lu, Y.-Q. A three-beam path photonic crystal fiber modal interferometer and its sensing applications. J. Appl. Phys. 2010, 108, 023107. [Google Scholar] [CrossRef]
- Li, S.-S.; Huang, Z.-D.; Song, X.-S.; Zhang, S.-Y.; Zhong, Q.; Xu, F.; Lu, Y.-Q. Photonic crystal fibre based high temperature sensor with three-beam path interference. Electron. Lett. 2010, 46, 1394–1396. [Google Scholar] [CrossRef]
- Song, X.-S.; Xu, F.; Lu, Y.-Q. Photonic crystal fibre based modal interferometer with four-beam path interference. Electron. Lett. 2011, 47, 719–720. [Google Scholar]
- Zhao, Z.; Tang, M.; Fu, S.; Liu, S.; Wei, H.; Cheng, Y.; Tong, W.; Pin-Shum, P.; Liu, D. All-solid multi-core fiber-based multipath Mach-Zehnder interferometer for temperature sensing. Appl. Phys. B 2013, 112, 491–497. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, T.; Fan, Y.; Chiang, K.S.; Rao, Y. Torsion sensing with a fiber ring laser incorporating a pair rotatory long-period fiber gratings. Opt. Commun. 2011, 284, 5299–5302. [Google Scholar] [CrossRef]
- Gong, H.P.; Chan, C.C.; Zu, P.; Chen, L.H.; Dong, X.P. Curvature measurement by using low-birefringence photonic crystal fiber based Sagnac loop. Opt. Commun. 2010, 283, 3142–3144. [Google Scholar] [CrossRef]
- Popov, E.P.; Nagarajan, S.; Lu, S. Mechanics of Materials, 2nd ed.; Prenticed-Hall, Inc.: Englewood Cliffs, NJ, USA, 1978; pp. 57–76. [Google Scholar]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huerta-Mascotte, E.; Sierra-Hernandez, J.M.; Mata-Chavez, R.I.; Jauregui-Vazquez, D.; Castillo-Guzman, A.; Estudillo-Ayala, J.M.; Guzman-Chavez, A.D.; Rojas-Laguna, R. A Core-Offset Mach Zehnder Interferometer Based on A Non-Zero Dispersion-Shifted Fiber and Its Torsion Sensing Application. Sensors 2016, 16, 856. https://doi.org/10.3390/s16060856
Huerta-Mascotte E, Sierra-Hernandez JM, Mata-Chavez RI, Jauregui-Vazquez D, Castillo-Guzman A, Estudillo-Ayala JM, Guzman-Chavez AD, Rojas-Laguna R. A Core-Offset Mach Zehnder Interferometer Based on A Non-Zero Dispersion-Shifted Fiber and Its Torsion Sensing Application. Sensors. 2016; 16(6):856. https://doi.org/10.3390/s16060856
Chicago/Turabian StyleHuerta-Mascotte, Eduardo, Juan M. Sierra-Hernandez, Ruth I. Mata-Chavez, Daniel Jauregui-Vazquez, Arturo Castillo-Guzman, Julian M. Estudillo-Ayala, Ana D. Guzman-Chavez, and Roberto Rojas-Laguna. 2016. "A Core-Offset Mach Zehnder Interferometer Based on A Non-Zero Dispersion-Shifted Fiber and Its Torsion Sensing Application" Sensors 16, no. 6: 856. https://doi.org/10.3390/s16060856
APA StyleHuerta-Mascotte, E., Sierra-Hernandez, J. M., Mata-Chavez, R. I., Jauregui-Vazquez, D., Castillo-Guzman, A., Estudillo-Ayala, J. M., Guzman-Chavez, A. D., & Rojas-Laguna, R. (2016). A Core-Offset Mach Zehnder Interferometer Based on A Non-Zero Dispersion-Shifted Fiber and Its Torsion Sensing Application. Sensors, 16(6), 856. https://doi.org/10.3390/s16060856







