Determination of Specific Losses in the Limbs of an Epstein Frame Using a Three Epstein Frame Methodology Applied to Grain Oriented Electrical Steels
Abstract
:1. Introduction
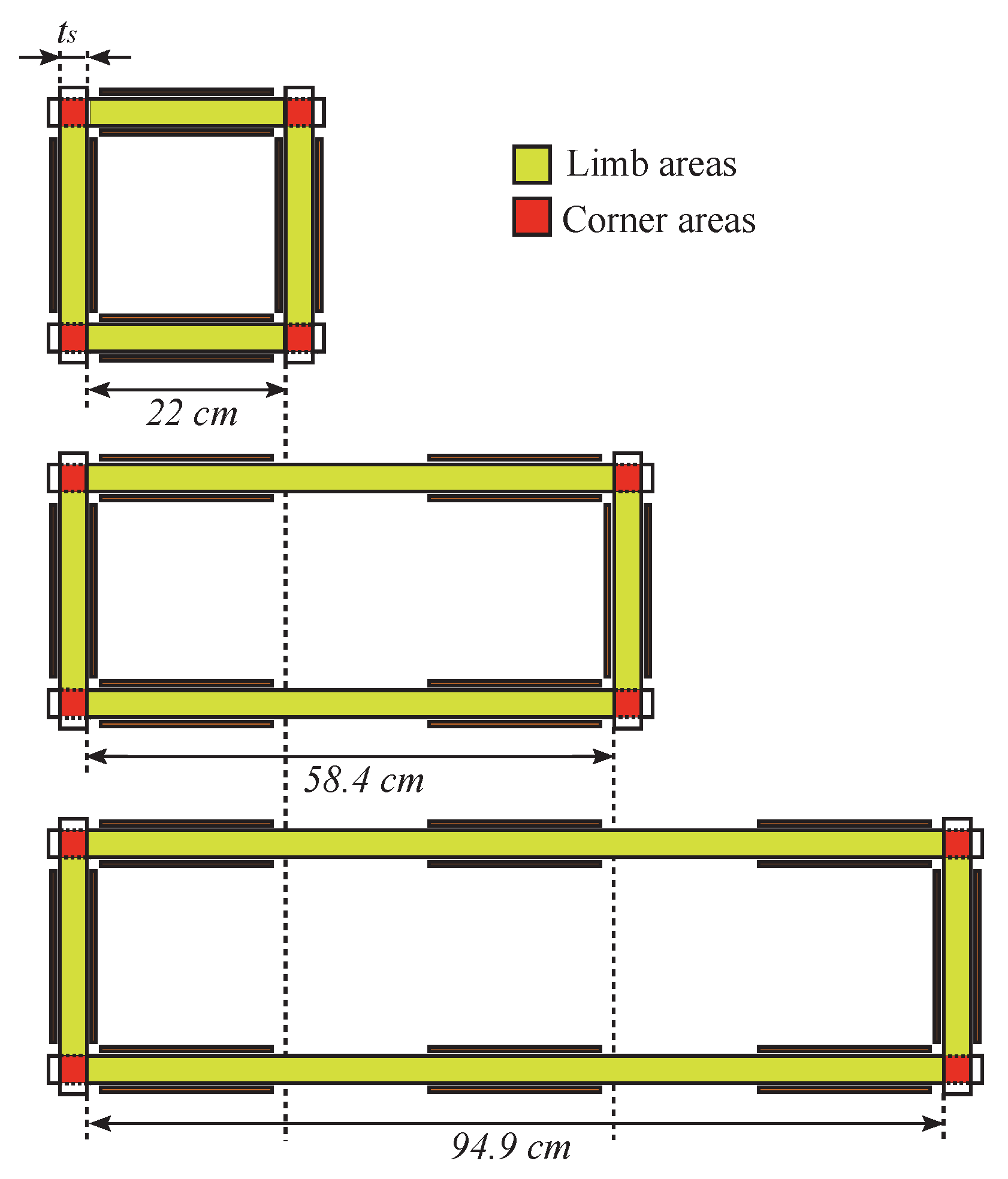
- the modified Epstein frames have longer limbs than the standard frame. That is a crucial point for the experimental approach because steel of high performance is analyzed and, in this case, grains have a like size. It is thus more convenient to extend the limb length instead of shorten it, as it has been done up to now,
- the use of three frames instead of two allows to draw more reliable characteristics concerning the influence of the frame size variations,
- only the length of a pair of parallel limbs has a varying value. The two others are kept constant. This feature is determinant to strengthen the hypothesis of the uniformity of the flux in the area close to the corners. It will make it possible to justify that differences on the losses measured in the different frames enable to find the real characteristics of the measured GOES grade.
2. The Reasons for Using Three Different Frame Sizes
2.1. Magnetic Circuit Structure
2.2. Experimental Method Description
2.3. First Experimental Results: Measurement and Magnetic Property Characterizations
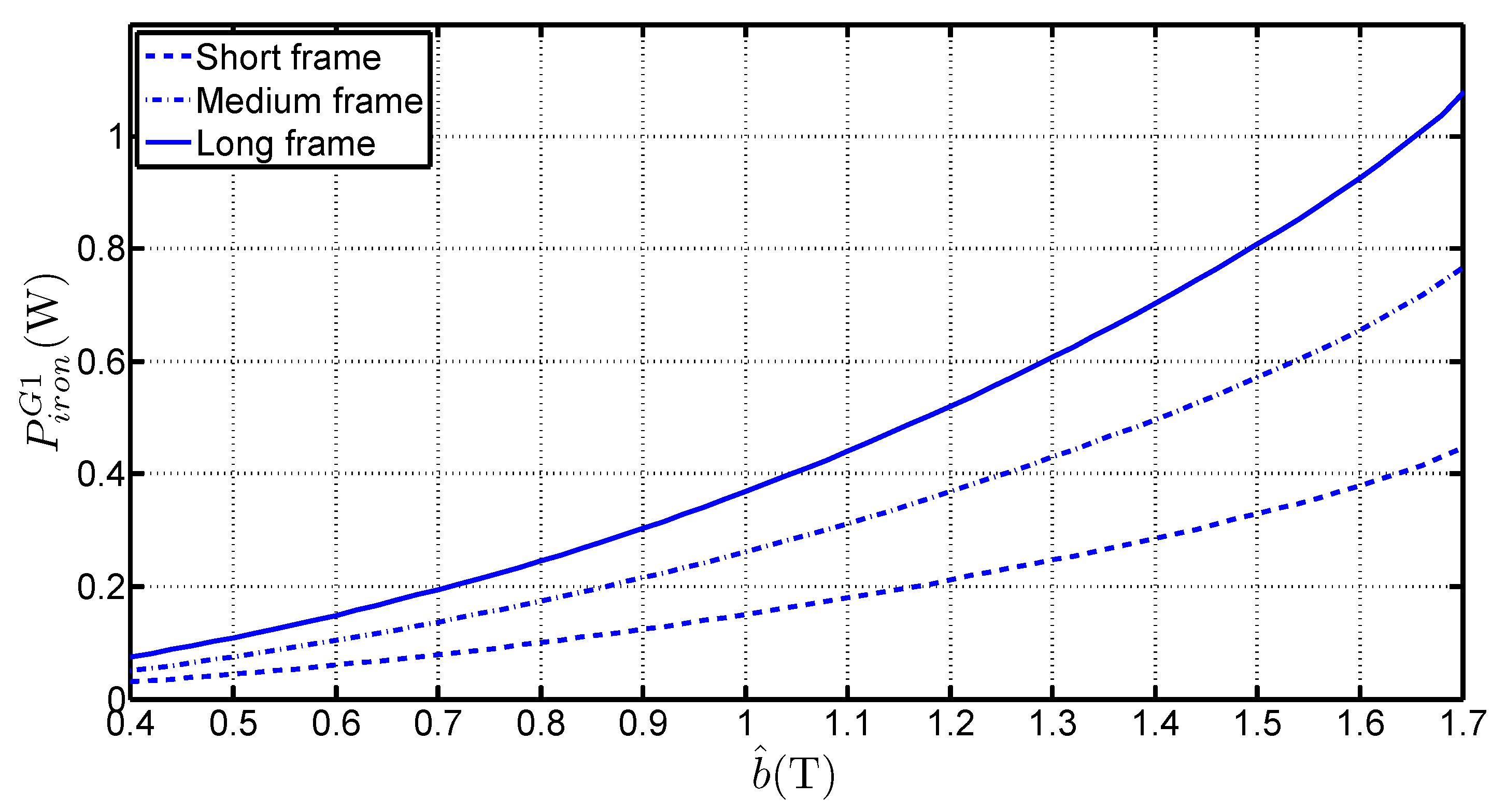
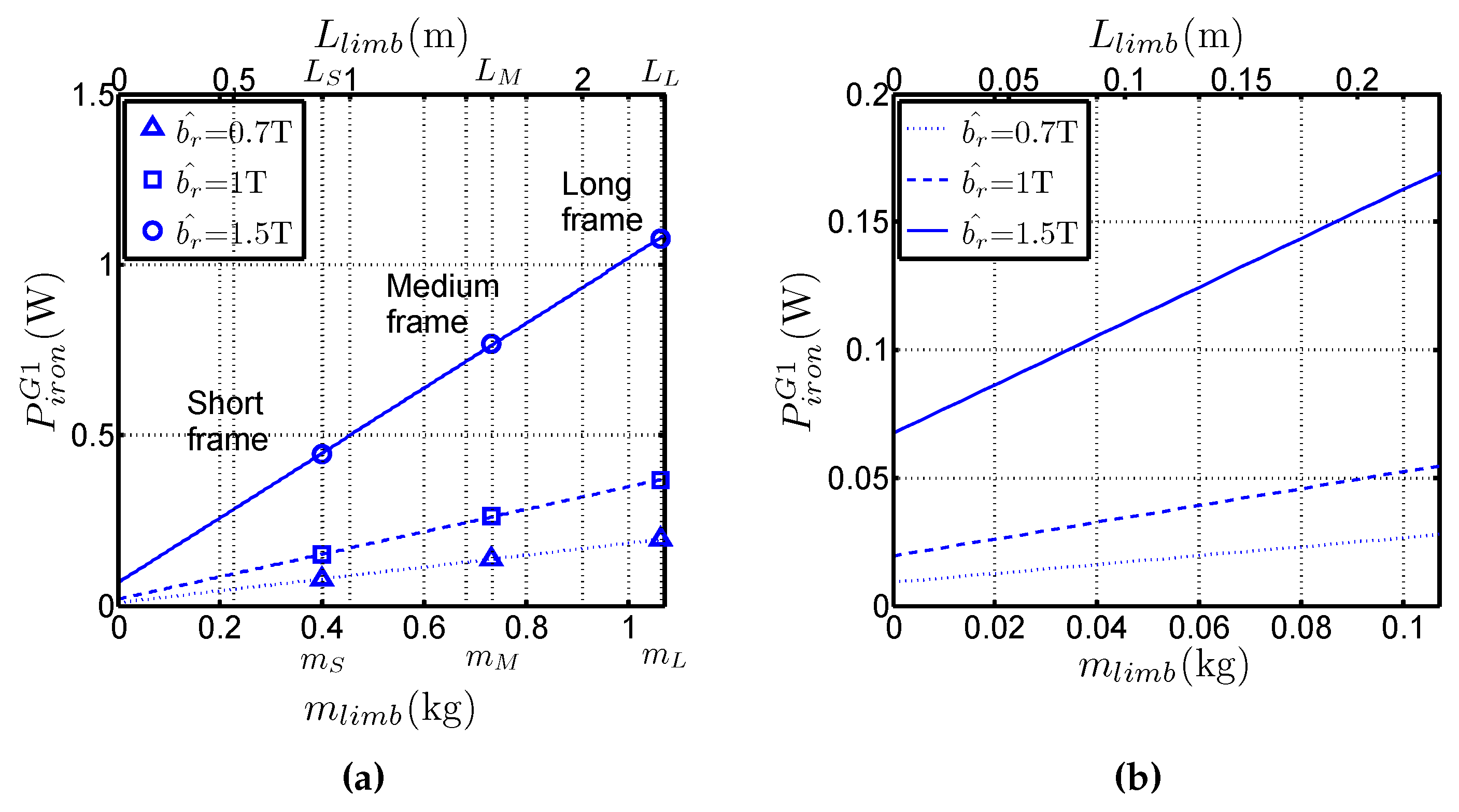
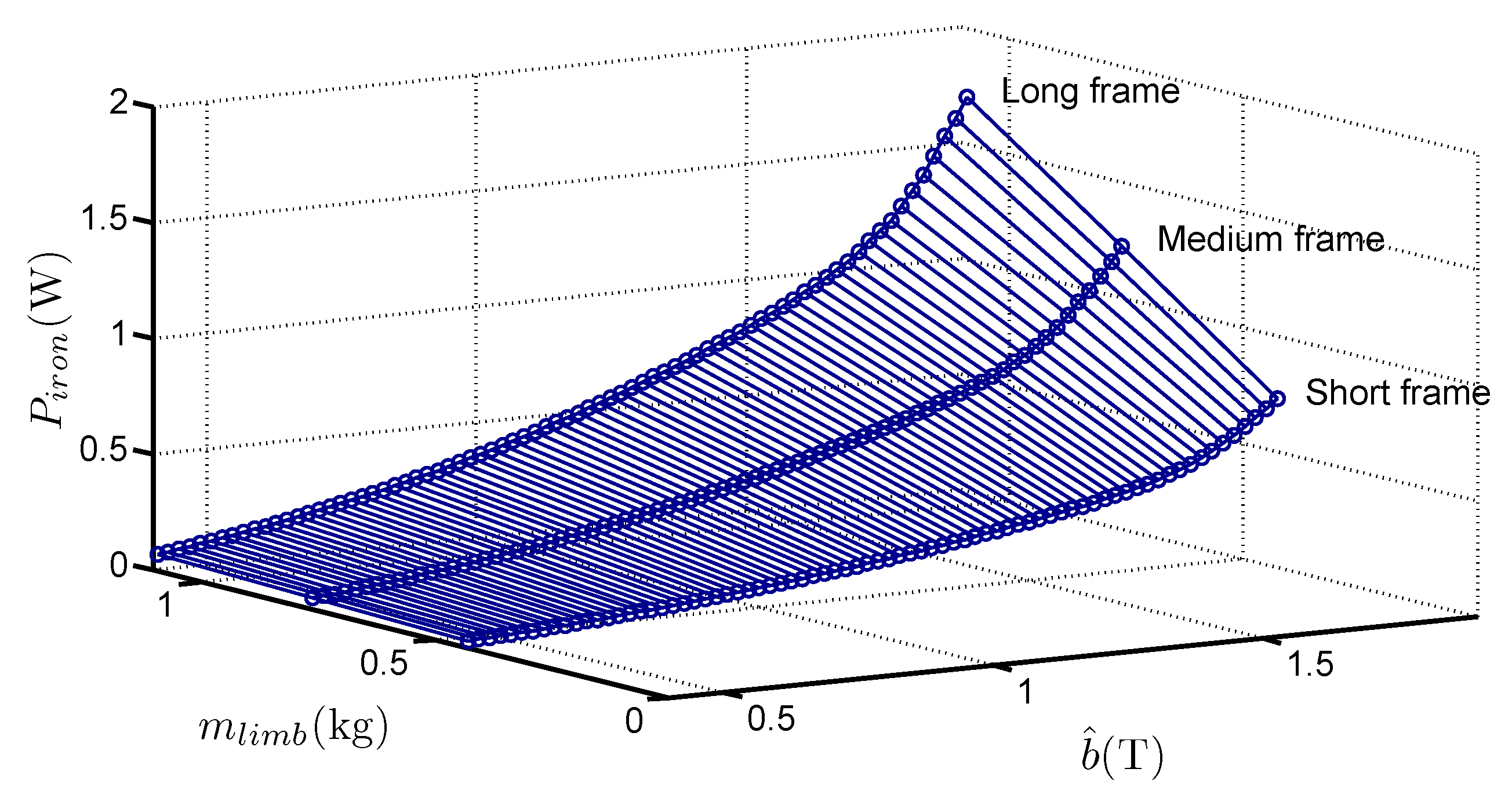
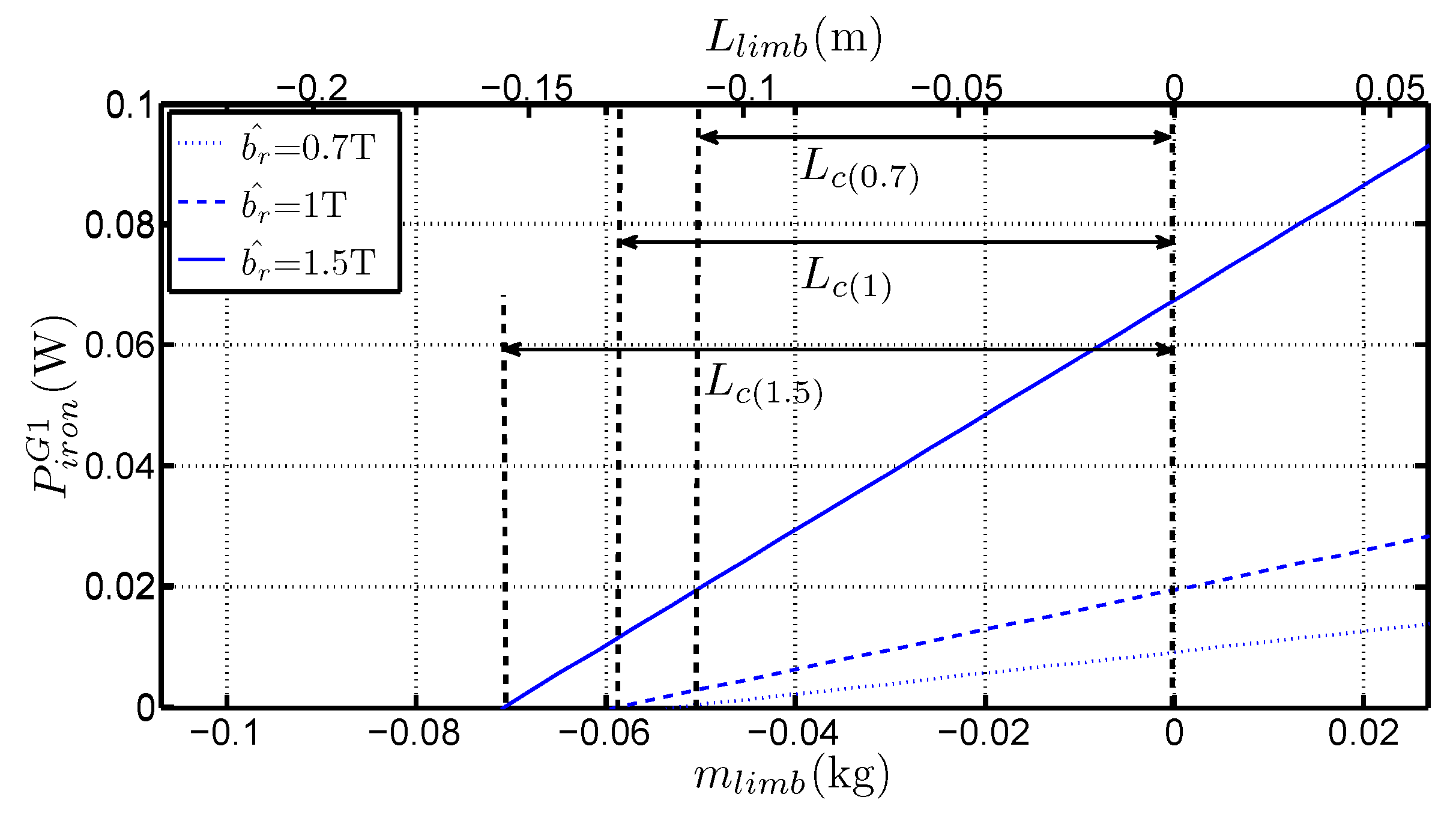
- the slopes of straight lines in Figure 4a give access to (which are the real specific losses of the material) without considering the mean path length in the frame, but only with the total limb mass (or with the length increase of the limbs). That constitutes a real advantage of the method,
- depends on the mean path length in the corners and it changes with the considered grade and flux density,
- the variations of are linear with , even though the medium and long frames are asymmetrical. It constitutes an original approach because it proves that the method is suitable for separating corner losses and limb losses. That confirms the basic hypothesis which considers that the flux distribution is the same near the corners, regardless the frame geometry for a sufficiently long limb. This hypothesis is valid because the short frame dimensions are much bigger than the corner size. Simulations of magnetic behaviour of the laminations [2,9,10] performed with Finite Element software shows that this hypothesis is consistent especially for the GOES because the magnetic polarisation tends to lay along the RD as far as possible in the corner before it changes direction towards adjacent lamination.
2.4. Influence of the Frame and Sample Structure
2.5. Discussion about the Measurement Uncertainty
3. Experimental Results for Different GO Steel Grades
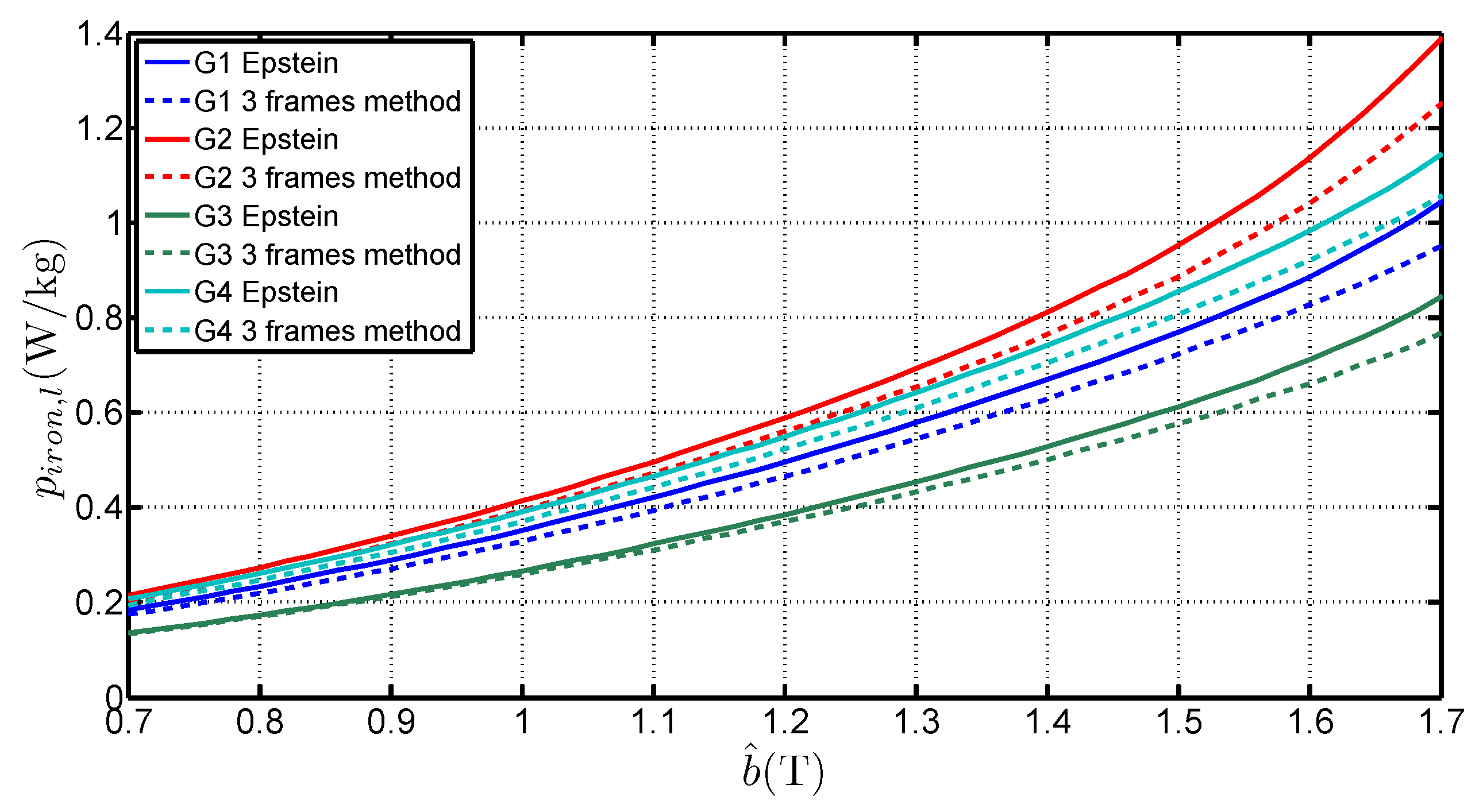
3.1. Specific Loss Determinaton—Comparison with the Epstein Frame
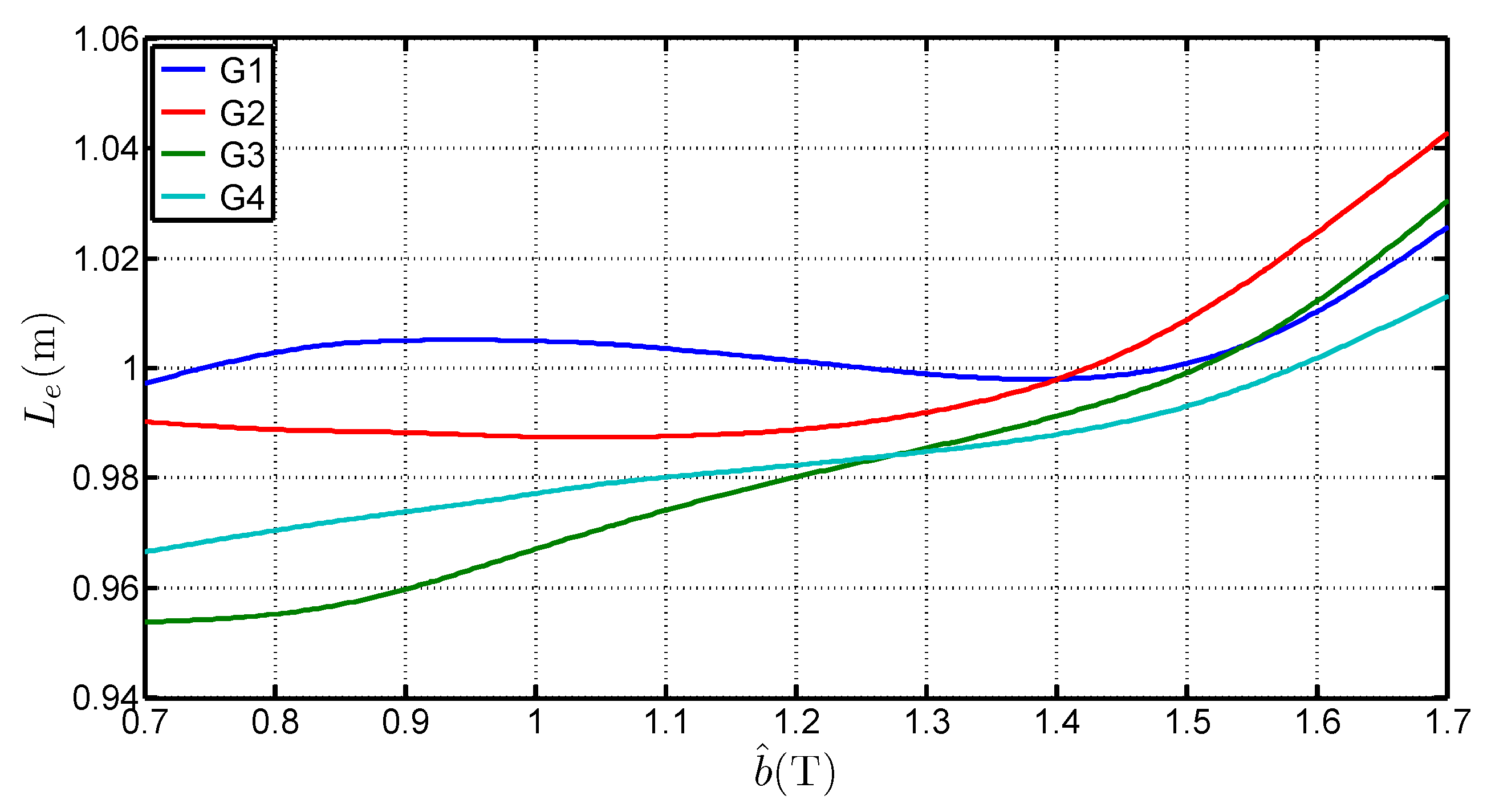
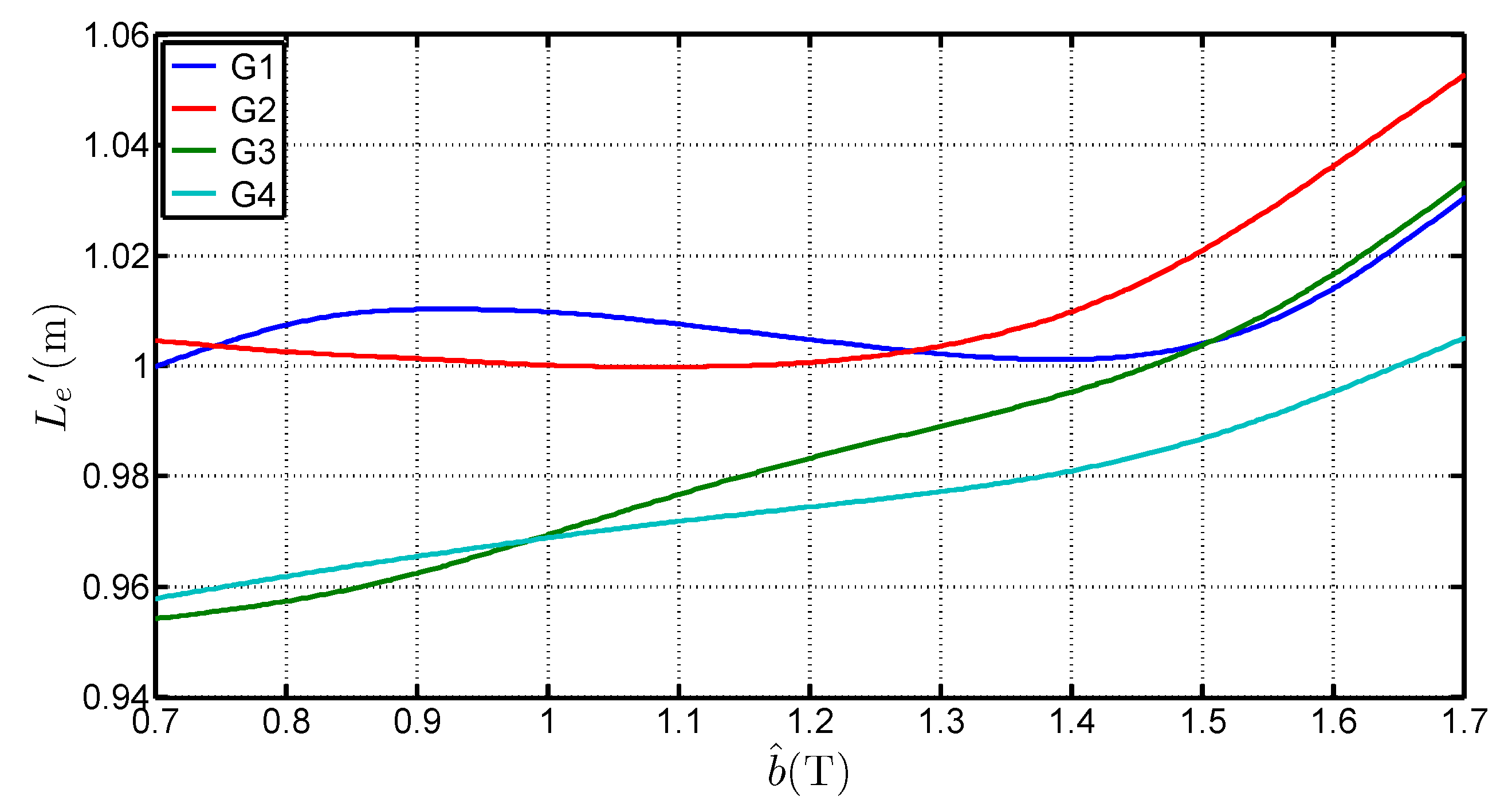
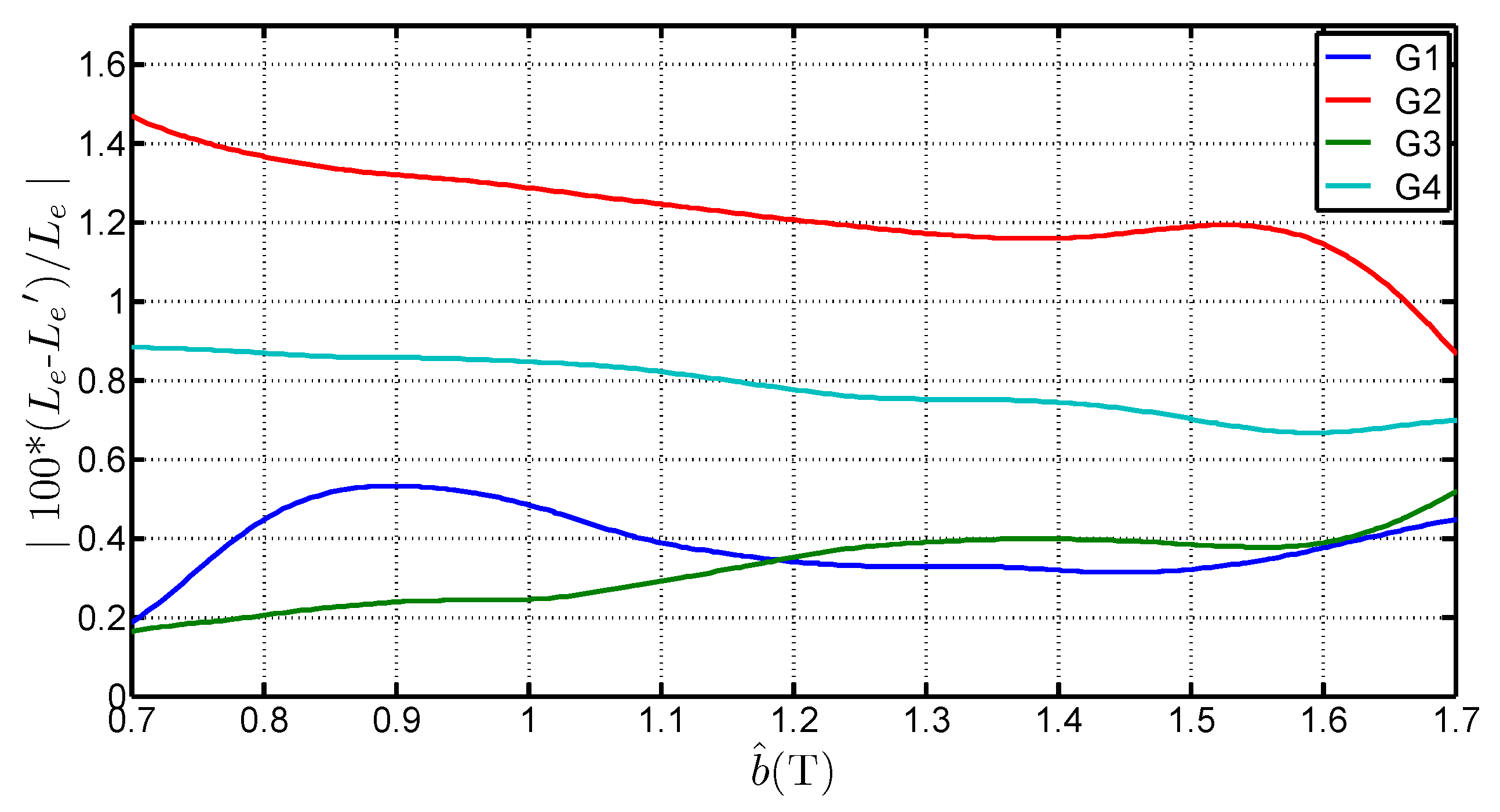
3.2. Recalculation of the Epstein Equivalent Mean Path Length
- is higher than the standardized length. It can even be superior to 1 which is the geometrical average length of the Epstein frame. The average of the determined values for each grades, considering a range of [0.7 ;1.7 ] is 1.0038 , 0.9983 , 0.9817 and 0.9842 for G1, G2, G3 and G4 respectively. That shows that the 0.94 length is too low and not representative of the iron losses,
- depends on the peak value of the flux density. The deviation to the standard value is over 6% between 0.7 and 1.7 . This expresses the fact that in the corner joints the flux establishes in twice the limb cross section. The local reluctance of the magnetic circuit is thus very different from the one in the limb and influences the overall estimation for the whole magnetic circuit. It also shows that, whatever the grade, this equivalent mean path length tends to increase with the flux density peak value. This variation is similar to the curves obtained by Marketos in [4] for a high performance GOES magnetized with an excitation frequency of 50 ,
- depends on several parameters. Indeed, is influenced by the peak flux density value, the steel grade but also the anisotropy ratio. The latter influences the flux distribution in the corners and may explain the differences on .
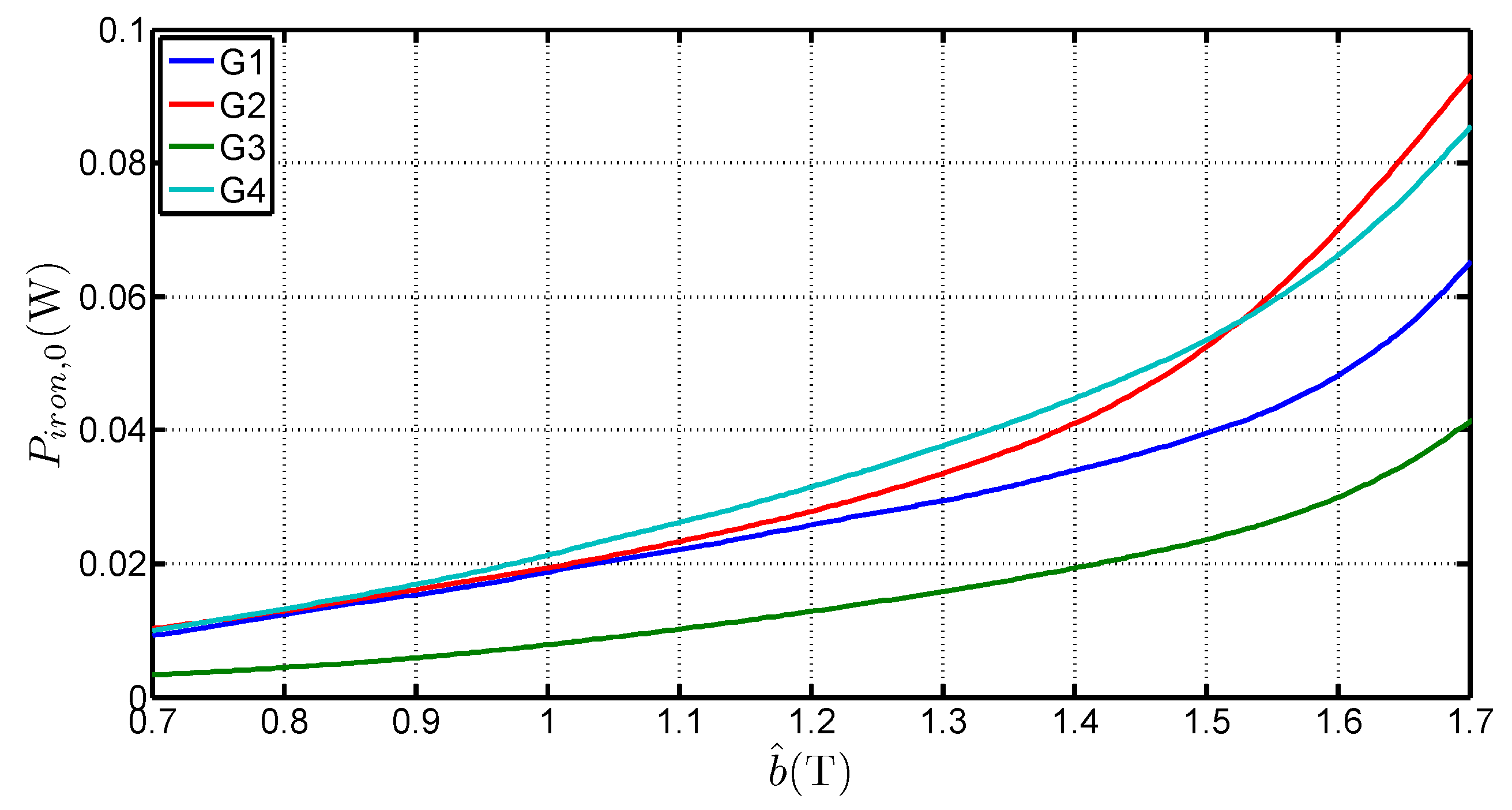
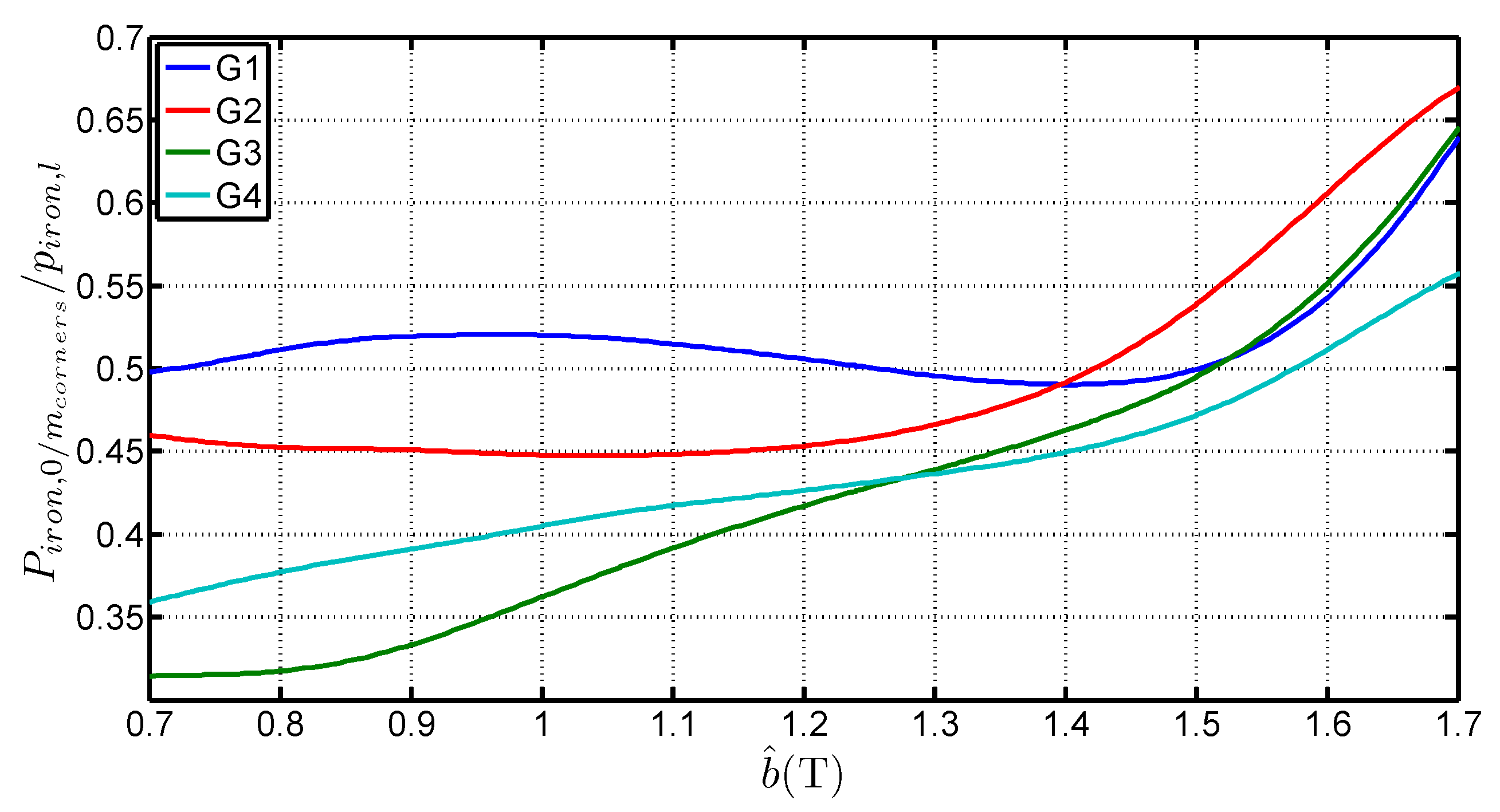
3.3. Losses at the Corner Joints
3.4. Equivalent Mean Path Length in the Corner Joints
4. Conclusions
- it gives access to the magnetic steel properties without considering the magnetic path length. That constitutes the main advantage because no supposition concerning the mean path length has to be done,
- it makes it possible to separate the corner iron losses and the leg iron losses,
- it shows that the mean path length of the magnetic flux depends on the steel grade and characteristics, but also on the flux density level.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- IEC 60404-2: Methods of Measurement of the Magnetic Properties of Electrical Steel Sheet and Strip by Means of an Epstein Frame, 3.1 ed. Available online: https://webstore.iec.ch/publication/2064 (accessed on 2 June 2016).
- Ossart, F.; Mekhiche, M.; Waeckerlé, T. Numerical simulation of an Epstein frame used for anisotropy measurements. In Proceedings of the Twelfth International Conference on Soft Magnetic Materials, Kraków, Poland, 12–14 September 1995.
- Marketos, P.; Zurek, S.; Moses, A. A method for defining the mean path length of the Epstein frame. IEEE Trans. Magn. 2007, 43, 2755–2757. [Google Scholar] [CrossRef]
- Marketos, P.; Zurek, S.; Moses, A.J. Calculation of the mean path length of the Epstein frame under non-sinusoidal excitations using the double Epstein method. J. Magn. Magn. Mater. 2008, 320, 2542–2545. [Google Scholar] [CrossRef]
- Pfützner, H.; Futschik, K.; Hamberger, P.M.A. Concept for more correct iron loss measurements considering path length dynamics. In Proceedings of the 12th International Workshop on 1 & 2 Dimensional Magnetic Measurement and Testing, Wien, Austria, 3–6 September 2012; pp. 24–25.
- Wang, Y.Q.; Wang, H.J.; Ma, C. Triple Epstein frame first-level weighted processing method for determining the effective path length of the Epstein frame. Adv. Mater. Res. 2014, 873, 121–127. [Google Scholar] [CrossRef]
- Dieterly, D. DC permeability testing of Epstein samples with double-lap joints. In Proceedings of the 51st Annual Meeting of the American Society for Testing Materials, Detroit, MI, USA, 21–25 June 1948; pp. 39–62.
- Lopez, S.; Cassoret, B.; Brudny, J.F.C.; Vincent, J.N. Magnetic characterization of grain oriented steel for variable anisotropic direction assemblies. In Proceedings of the 10th Symposium on Electromagnetic Phenomena in Nonlinear Circuits (EPNC), Lille, France, 2–4 July 2008; pp. 87–88.
- Hihat, N.; Napieralska-Juszczak, E.; Lecointe, J.P.; Sykulski, J.; Komeza, K. Equivalent Permeability of step-lap joints of transformer Cores: Computational and experimental considerations. IEEE Trans. Magn. 2011, 47, 244–251. [Google Scholar] [CrossRef]
- Parent, G.; Penin, R.; Lecointe, J.P.; Brudny, J.F.; Belgrand, T. Analysis of the magnetic flux distribution in a new shifted non-segmented Grain Oriented AC motor magnetic circuit. IEEE Trans. Magn. 2013, 49, 1977–1980. [Google Scholar] [CrossRef]
- Hamrit, O. Study of Magnetic Losses on Magntic Materials Destinated to Transport Applications at High Frequency and under Bidirectionnal Magnetic Field. Ph.D. Thesis, Université Paris-Saclay, Saint-Aubin, France, 2015. [Google Scholar]


| IEC Grade | Grade Name | Iron Losses at 1.5 T | Iron Losses at 1.7 T |
|---|---|---|---|
| (W kg) | (W kg) | ||
| M105-30P | G1 | 0.77 | 1.03 |
| M140-30S | G2 | 0.95 | 1.39 |
| M085-23P | G3 | 0.61 | 0.84 |
| M135-35P | G4 | 0.93 | 1.26 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parent, G.; Penin, R.; Lecointe, J.-P.; Brudny, J.-F.; Belgrand, T. Determination of Specific Losses in the Limbs of an Epstein Frame Using a Three Epstein Frame Methodology Applied to Grain Oriented Electrical Steels. Sensors 2016, 16, 826. https://doi.org/10.3390/s16060826
Parent G, Penin R, Lecointe J-P, Brudny J-F, Belgrand T. Determination of Specific Losses in the Limbs of an Epstein Frame Using a Three Epstein Frame Methodology Applied to Grain Oriented Electrical Steels. Sensors. 2016; 16(6):826. https://doi.org/10.3390/s16060826
Chicago/Turabian StyleParent, Guillaume, Rémi Penin, Jean-Philippe Lecointe, Jean-François Brudny, and Thierry Belgrand. 2016. "Determination of Specific Losses in the Limbs of an Epstein Frame Using a Three Epstein Frame Methodology Applied to Grain Oriented Electrical Steels" Sensors 16, no. 6: 826. https://doi.org/10.3390/s16060826
APA StyleParent, G., Penin, R., Lecointe, J.-P., Brudny, J.-F., & Belgrand, T. (2016). Determination of Specific Losses in the Limbs of an Epstein Frame Using a Three Epstein Frame Methodology Applied to Grain Oriented Electrical Steels. Sensors, 16(6), 826. https://doi.org/10.3390/s16060826






