Data-Driven Design of Intelligent Wireless Networks: An Overview and Tutorial
Abstract
:1. Introduction
1.1. What Is Data Science?
1.2. Motivation
- More and more data is generated by existing wireless deployments [22] and by the continuously growing network of everyday objects (the IoT).
1.3. Contributions and Organization of the Paper
- An overview of types of problems in wireless network research that can be addressed using data science methods together with state-of-the-art algorithms that can solve each problem type. In this way, we provide a guide for researchers to help them formulate their wireless networking problem as a data science problem.
- A brief survey on the on-going research in the area of data-driven wireless network research that illustrates the diversity of problems that can be solved using data science techniques including references to these research works.
- A generic framework as a guideline for researchers wanting to solve their wireless networking problem as a data science problem using best practices developed by the data science community.
- A comprehensive hands-on introduction for newcomers to data-driven wireless network research, which illustrates how each component of the generic framework can be instantiated for a specific wireless network problem. We demonstrate how to correctly apply the proposed methodology by solving a timely problem on fingerprinting wireless devices, that was originally introduced in [12]. Finally, we show benefits of using the proposed framework compared to taking a custom approach.
2. Introduction to Data Science in Wireless Networks
2.1. Types of Learning Paradigms
2.1.1. Data Mining vs. Machine Learning
2.1.2. Supervised vs. Unsupervised vs. Semi-Supervised Learning
Supervised Learning
Unsupervised Learning
Semi-Supervised Learning
2.1.3. Offline vs. Online vs. Active Learning
Offline Learning
Online Learning
Active Learning
2.2. Types of Data Science Problems in Wireless Networks
2.2.1. Regression
Linear Regression
Nonlinear Regression
2.2.2. Classification
Neural Networks
Deep Learning
Decision Trees
Logistic Regression
SVM
k-NN
2.2.3. Clustering
k-Means
2.2.4. Anomaly Detection
2.2.5. Summarization
2.3. Summary
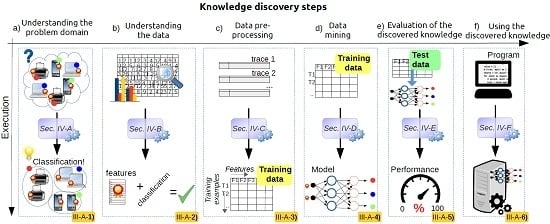
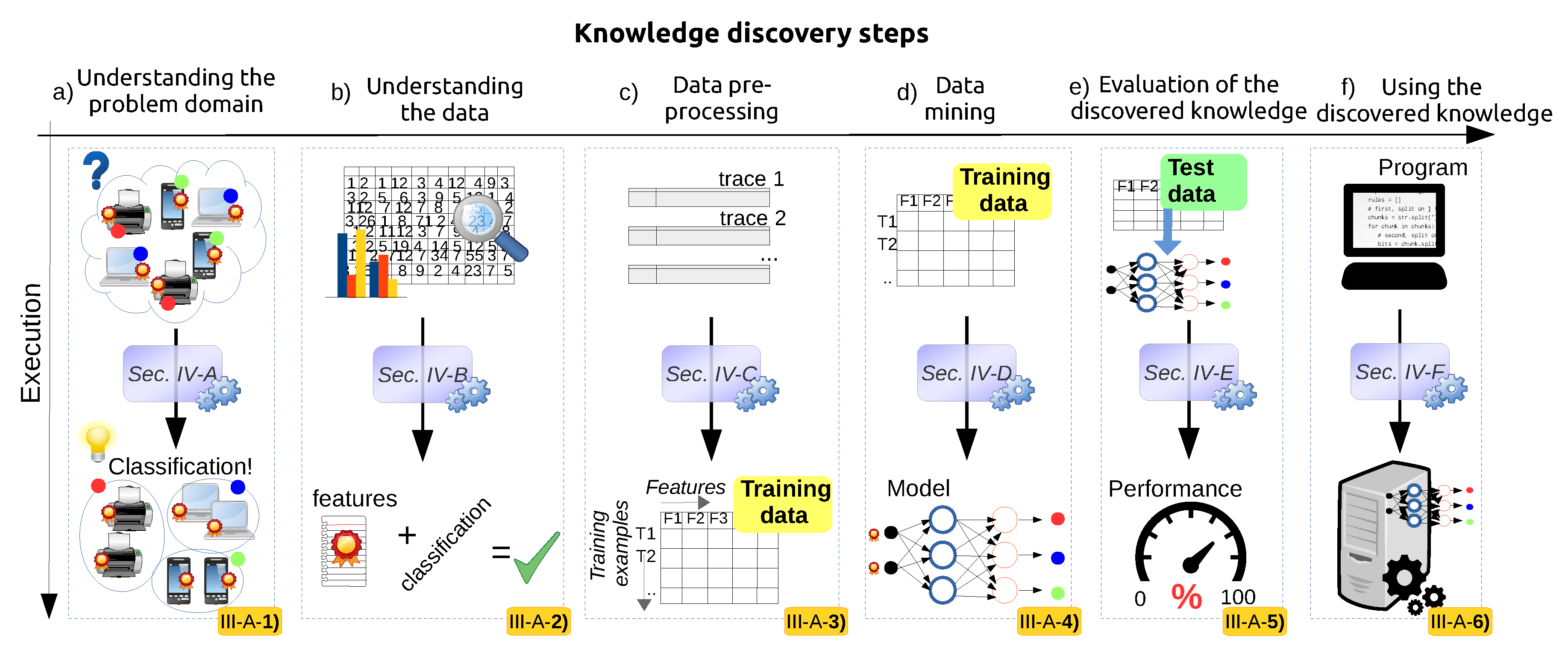
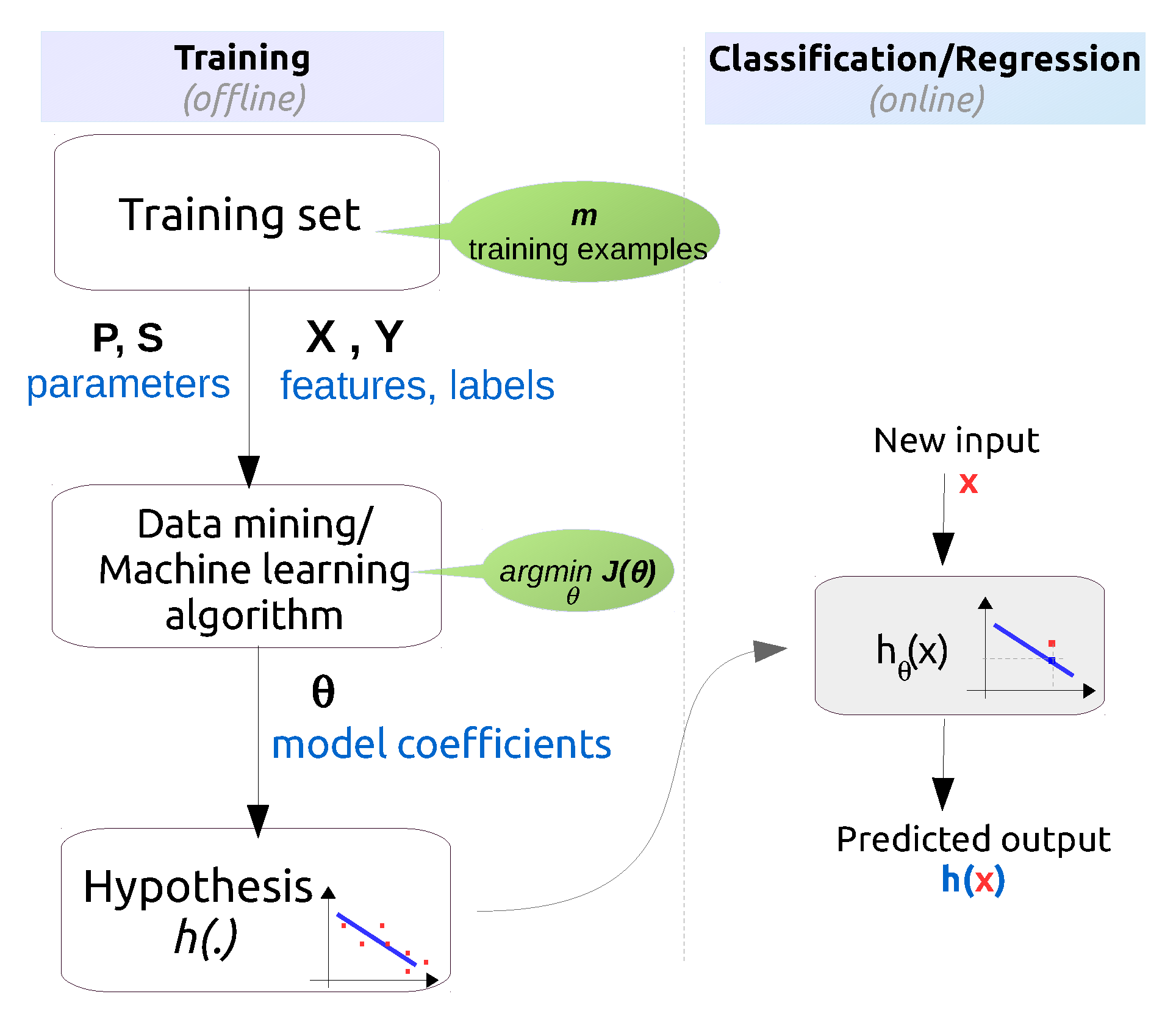
3. A Generic Framework for Applying Data Science in Wireless Networks
3.1. Understanding the Problem Domain
3.2. Understanding the Data
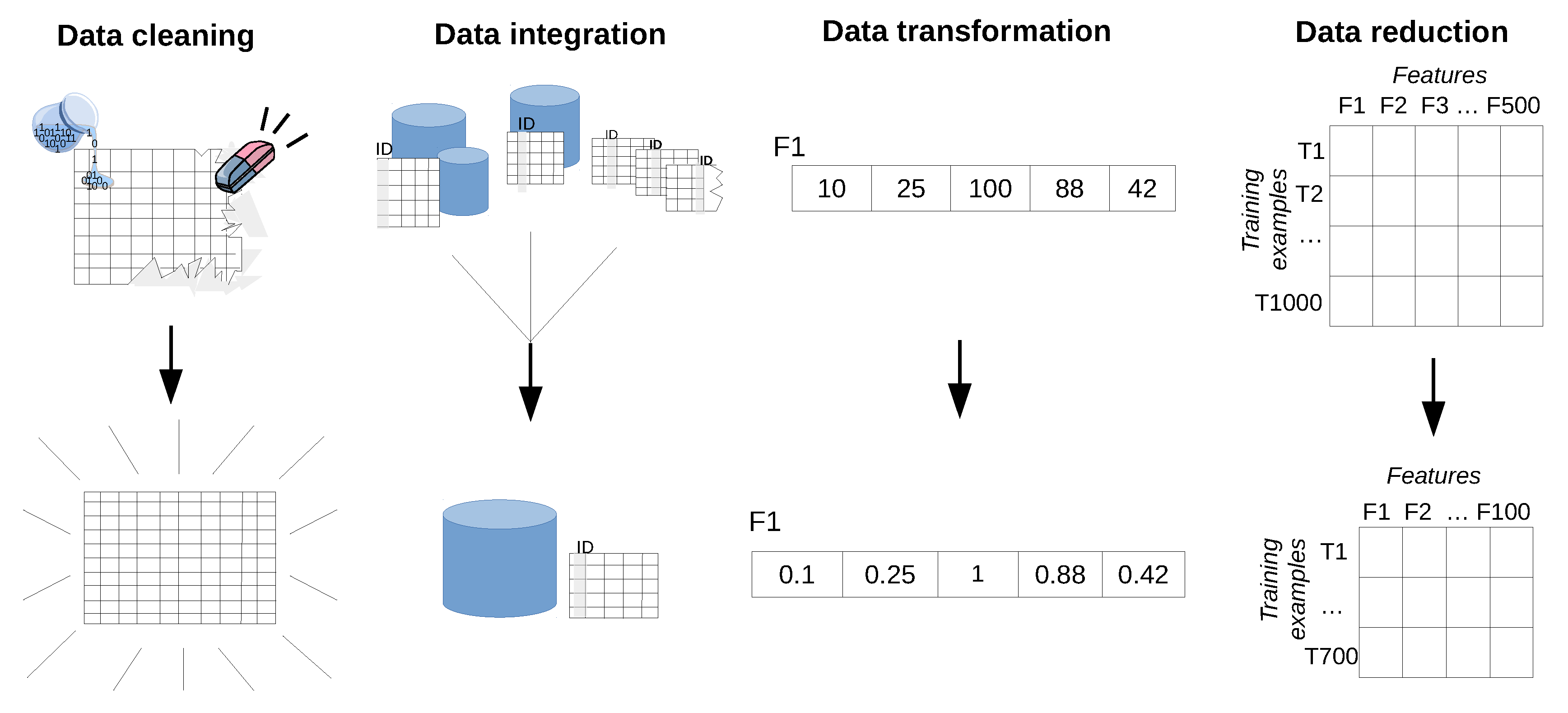
3.3. Data Pre-Processing
- raw data often contains values that do not reflect the real behavior of the target problem (e.g., faulty measurements);
- data is spread over multiple sources (e.g., across several databases);
- data does not have the most optimal form for efficient training (e.g., parameters with different scales);
- data contains irrelevant or insignificant measurements/parameters (e.g., a system parameter that is not likely to help solve the problem).
3.4. Data Mining
3.5. Evaluation of the Discovered Knowledge
3.6. Using the Discovered Knowledge
3.7. Examples of Using Data Science in Wireless Networks
Use Case 1: Link Quality Estimation
Use Case 2: Traffic Classification
Use Case 3: Device Fingerprinting
4. Case Study
4.1. Solving a Classification Problem in Wireless Networks
Wireless Device Fingerprinting: A Brief Overview
- PHY layer features: PHY features are derived from the RF waveform of the received signal. The most common PHY layer information for device fingerprinting are RSSI measures. However, the RSSI depends on the transmission power, propagation of the signal and attenuation imposed by the channel. More fine-grained features are channel state information at the receiver (CSIR) [126,127], channel frequency response (CFR) [128,129], channel impulse response (CIR) [126,130], carrier-frequency difference (CFD) [131], phase shift difference (PSD) [131], second-order cyclostationary feature (SOCF) [131], signal samples [132], etc.
- MAC layer features: The motivation behind utilizing MAC layer features for device identification is that some of the MAC layer implementation details are not specified in the standard and are left to the vendors. Therefore, MAC layer features are usually vendor specific. Some example works are: observing unique traffic patterns on the MAC layer to detect unauthorized users [133,134], observing the clock skew of an IEEE 802.11 access point from the Time Synchronization function (TSF) timestamps sent in the beacon/probe frames [135]; MAC features such as transmission rate, frame size, medium access time (e.g., backoff), transmission time and frame inter-arrival time [136].
- Network and upper layer features: Features at the network and upper layers typically look into user’s traffic patterns or inter-arrival times calculated at the network and application layer. For instance, in [137] Gao et al. and in [12] Radhakrishnan et al. use inter-arrival times from TCP and UDP packets as features. Ahmed et al. [138] uses traffic patterns of digital TV broadcasting to identify devices. On the other hand, in [139] Eckersley uses higher layer features by tracking the web browser behaviour by analyzing the browser’s requests/replies.
4.2. Understanding the Problem Domain
4.2.1. Understanding and Formulating the Device Fingerprinting Problem
- How much can data from one device (e.g., a Dell Netbook) tell about the data from other similar devices (e.g., other Dell Notebooks)?
- How much can a certain type of device (e.g., Dell Netbooks) tell about other device types (e.g., iPhones)?
4.2.2. Collecting the Data for Validating the Hypothesis
Practical Considerations for Understanding the Problem Domain
4.3. Understanding the Data
4.3.1. Generic EDA Techniques
- Computational techniques utilize statistical distributions, five-number summary, coefficient of determination, advanced multivariate exploratory techniques (e.g., cluster analysis, principal components and classification analysis, classification trees, self-organizing maps, etc.). In this tutorial, we use the five-number summary and the coefficient of determination to guide the reader through the process of understanding the data. More advanced techniques can be adopted from the domain specific literature [159].The five-number summary consists of five reference values that summarize the behavior of a dataset: —the minimum value, —first or lower quartile (the middle number between the minimum value and the median), —the “middle number” of the sorted dataset, —third or upper quartile (the middle number between the median and the maximum value), and —the maximum value.The coefficient of determination (denoted by ) is a simple statistic frequently used for determining relationships between system variables. It is defined as:where is the target value, is the value modeled (predicted) by a linear function f, while the denominator represents the total variation of the target variable’s instances.In general, describes how well some of the data can be approximated by a regression line constructed from some other data (i.e., one feature from the feature vector). High values of scores will indicate that there is a high linear dependency between a particular feature and the target value, while low values of may indicate the opposite.
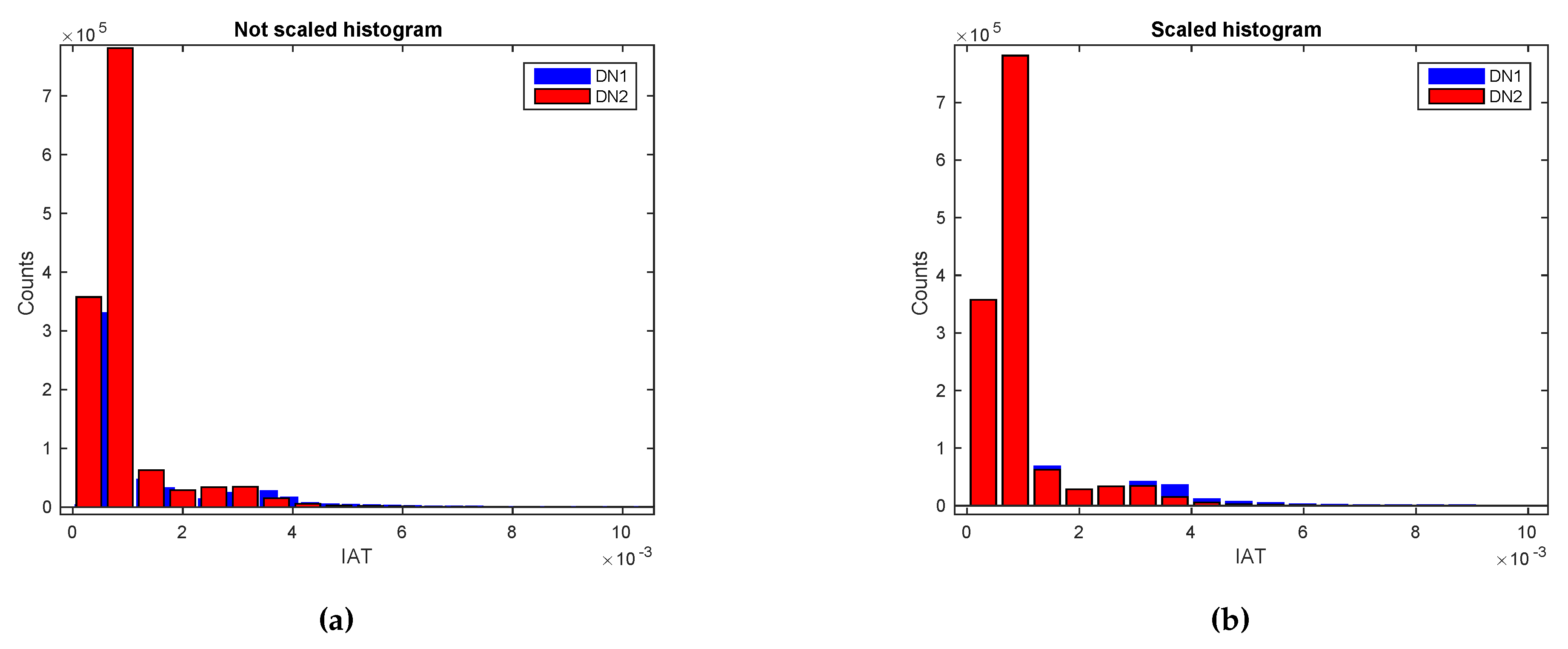
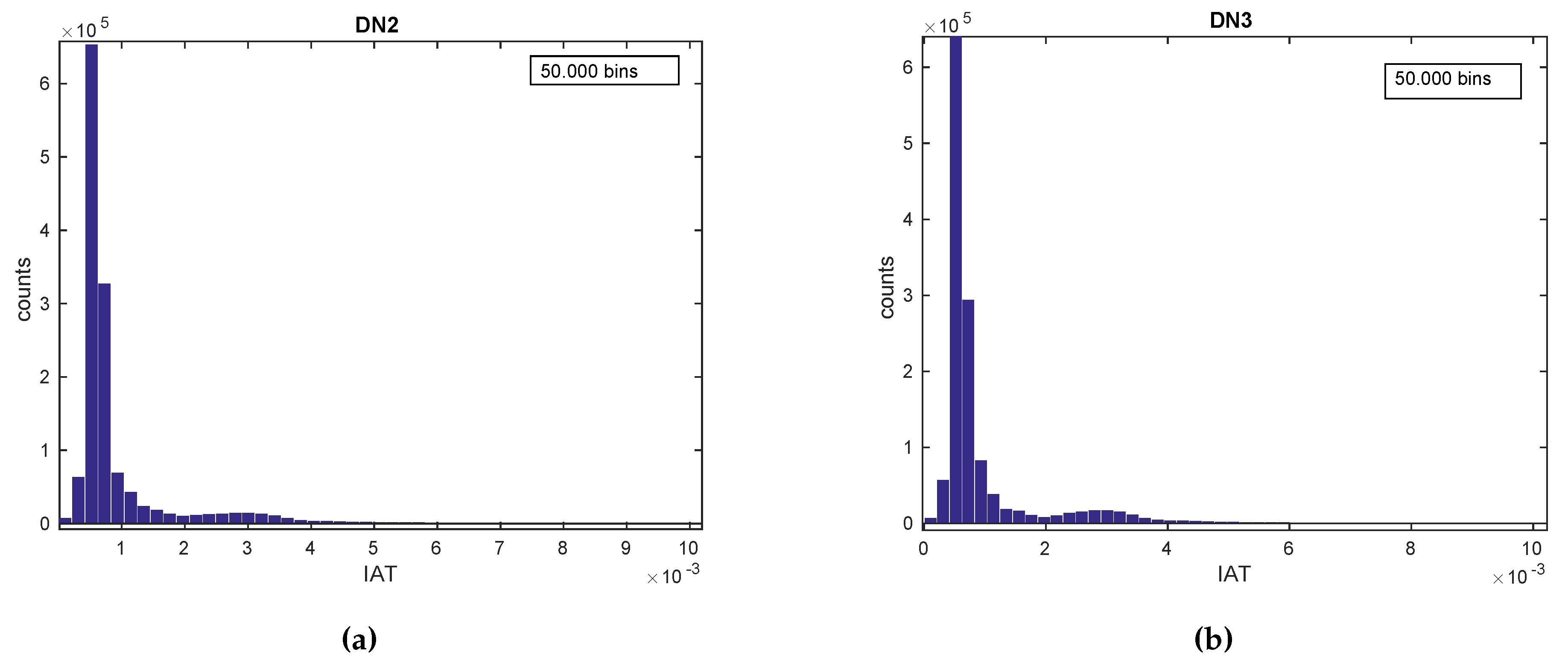
- Visual techniques utilize histograms, box plots, scatter plots, contour plots (for functions of two variables), matrix plots, etc [160]. Histograms, also used throughout the rest of the tutorial, reflect the frequency density of events over discrete time intervals. They help understand and graphically verify obtained results [161]. For instance, they display the distribution, the mean, skewness and range of the data. They are also a useful tool for identifying deviating points which should perhaps be removed from the dataset. A practical feature of histograms is their ability to readily summarize and display large datasets.
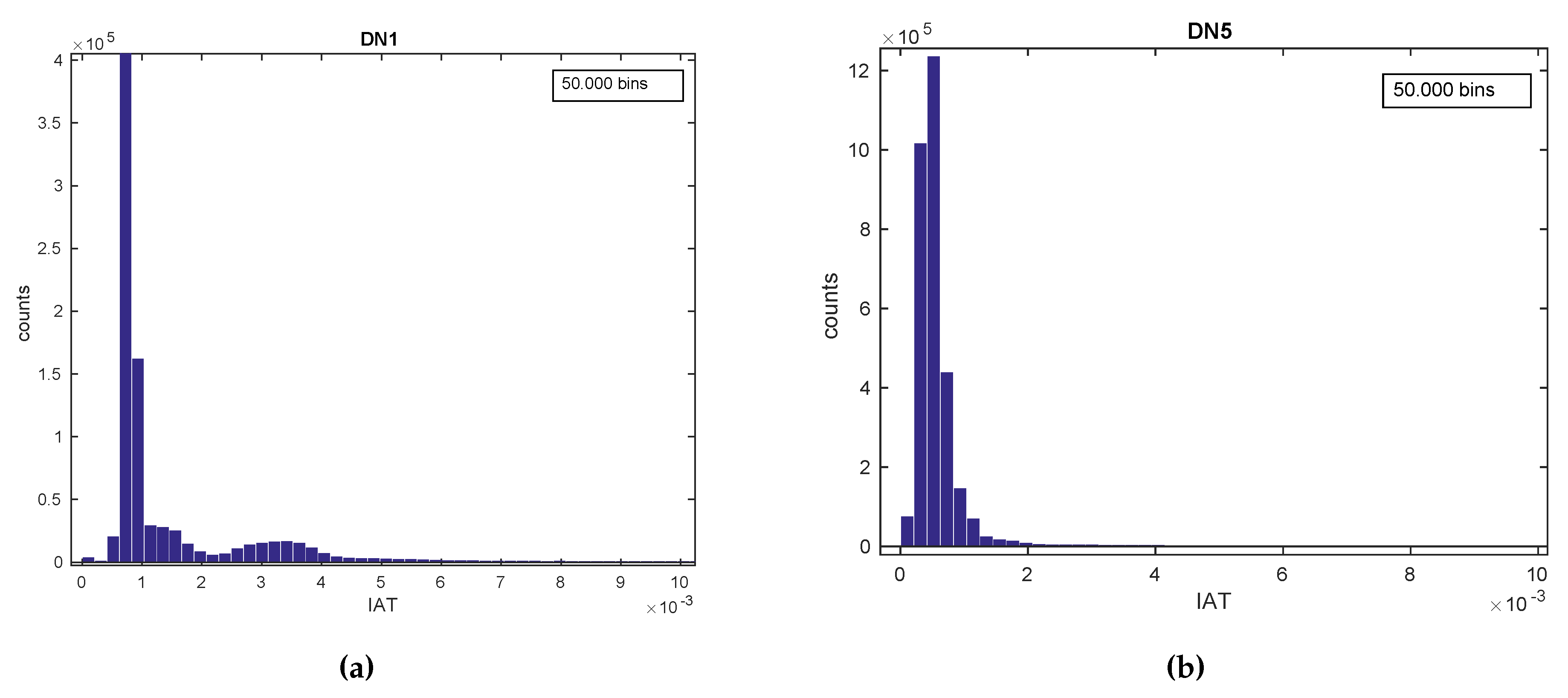
4.3.2. Applying EDA Techniques to the GaTech Data
Validating the Fingerprinting Data
Validating the Fingerprinting Hypothesis
Practical Considerations for Understanding the Data
4.4. Data Pre-Processing
4.4.1. Generic Data Pre-Processing Techniques
4.4.2. Pre-Processing the GaTech Dataset
Practical Considerations for Pre-Processing
4.5. Data Mining
4.5.1. Generic Data Mining Process
- Start with a simple algorithm which is easy to understand and easy to implement.
- Train the algorithm and evaluate its performance.
- If the algorithm performs poorly, try to understand why:
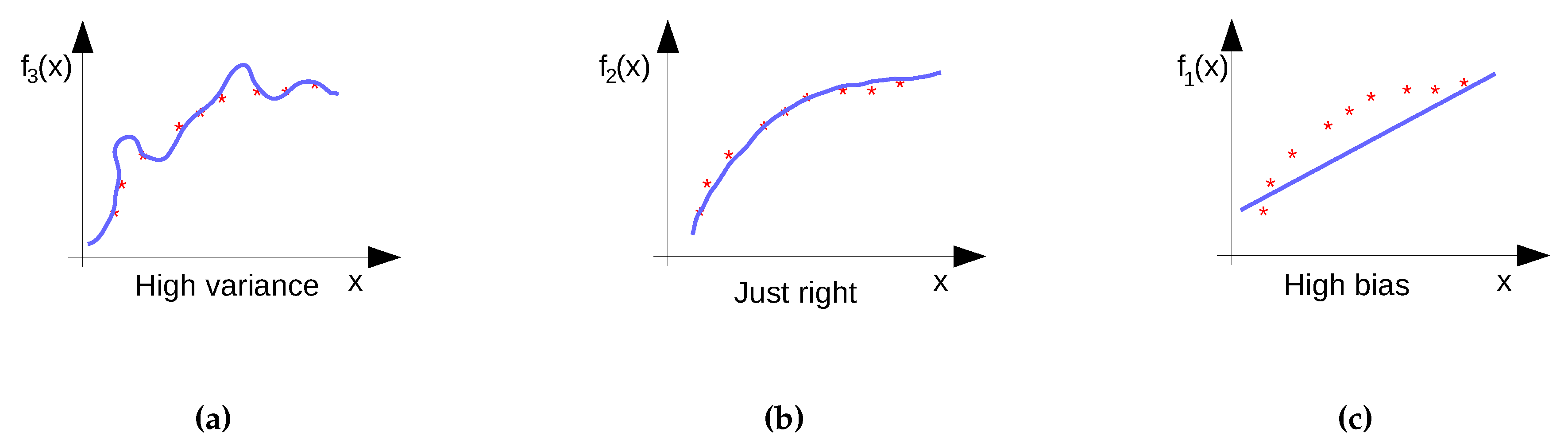
- Diagnose if the model is too complex or too simple, i.e., whether it suffers from under- or over-fitting.
- Depending on the diagnosis tune appropriate parameters (system parameters, model parameters, etc.).
- If necessary analyze manually where and why errors occur (i.e., error analysis). This helps to get an intuition whether the features are representative.
- If the algorithm still performs poor, select a new one and repeat all the steps.
4.5.2. Mining the Device Fingerprinting Problem
Practical Considerations for Data Mining
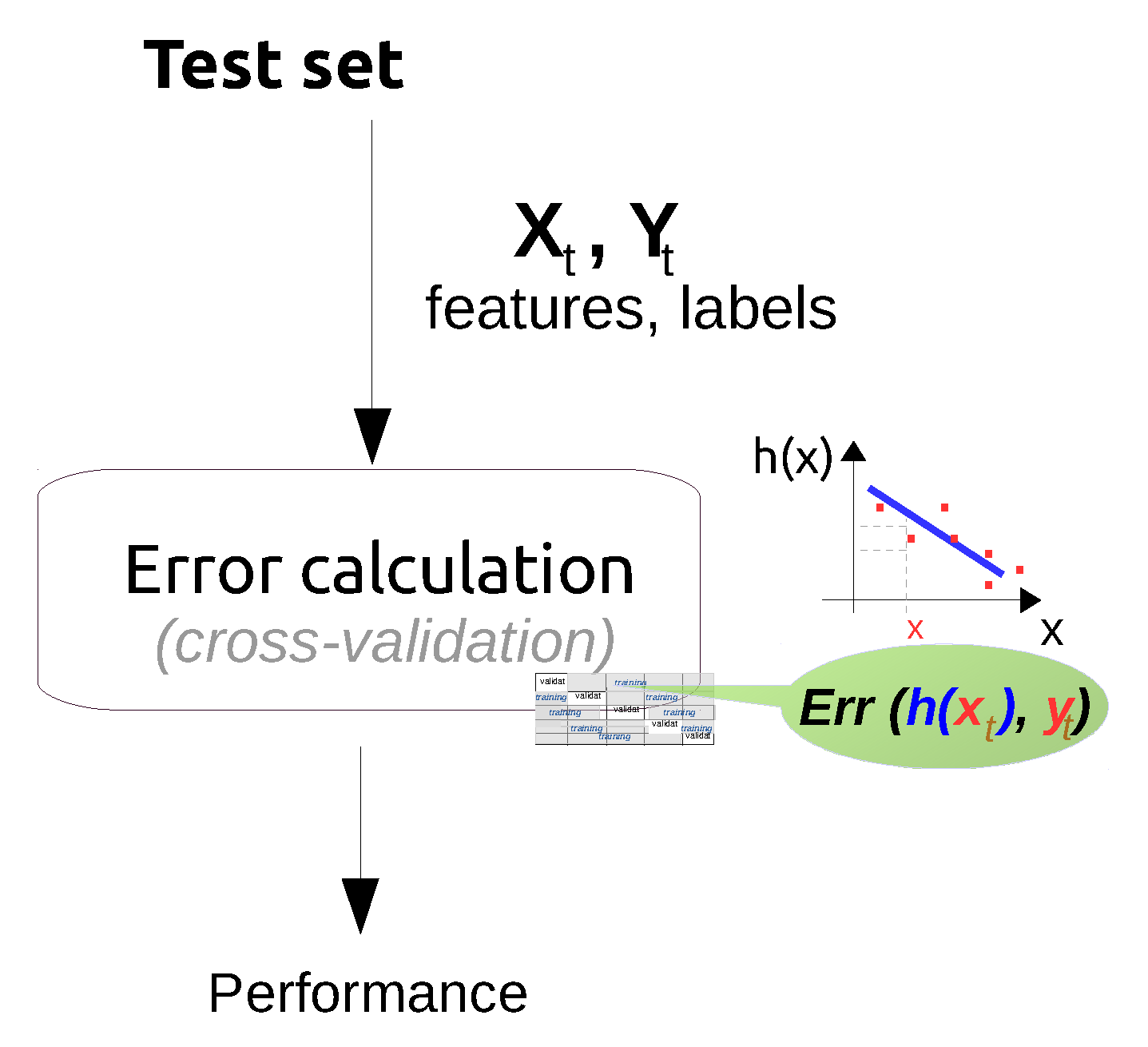
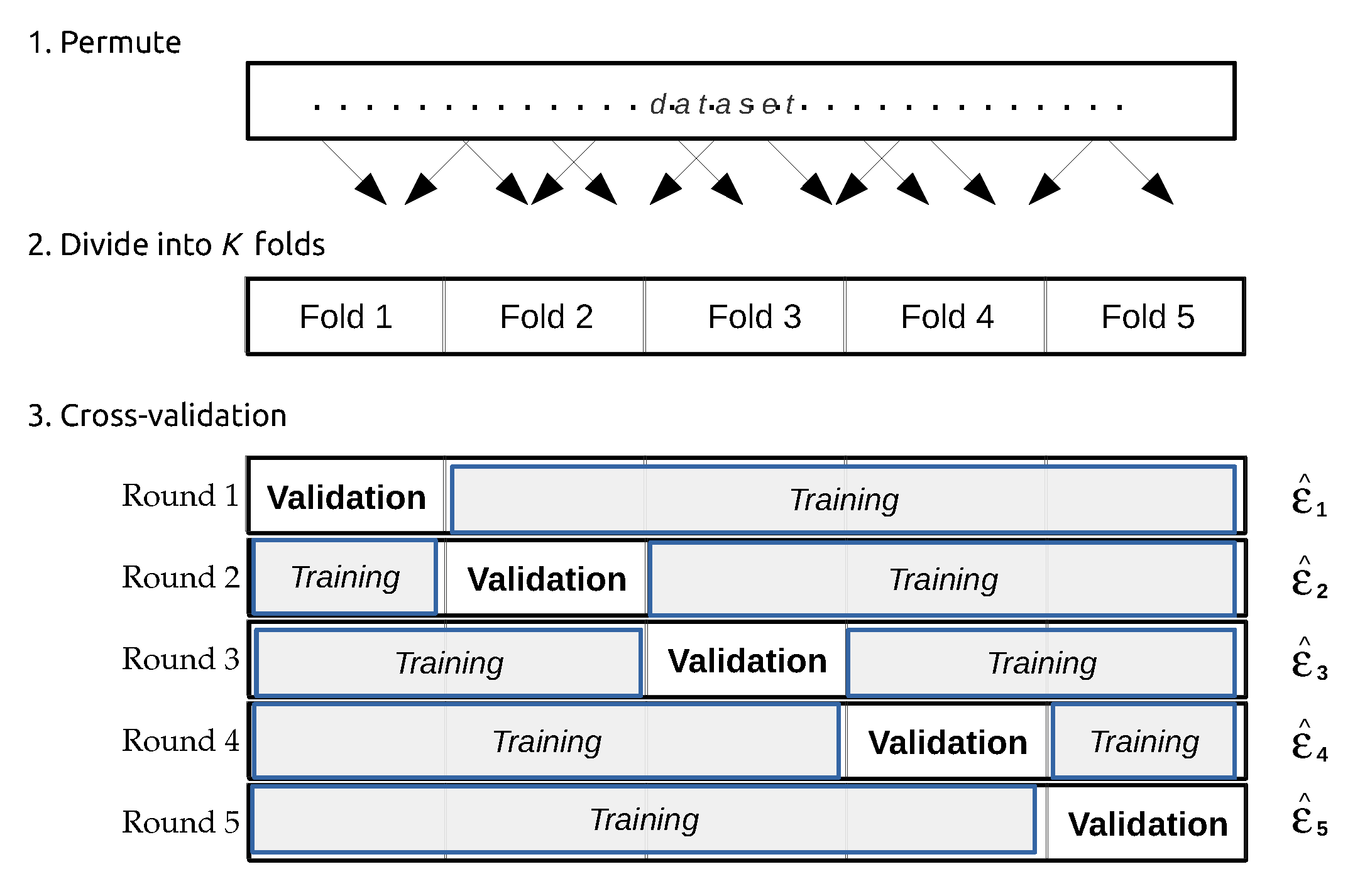
4.6. Performance Evaluation
4.6.1. Performance Evaluation Techniques
4.6.2. Performance Evaluation Metrics
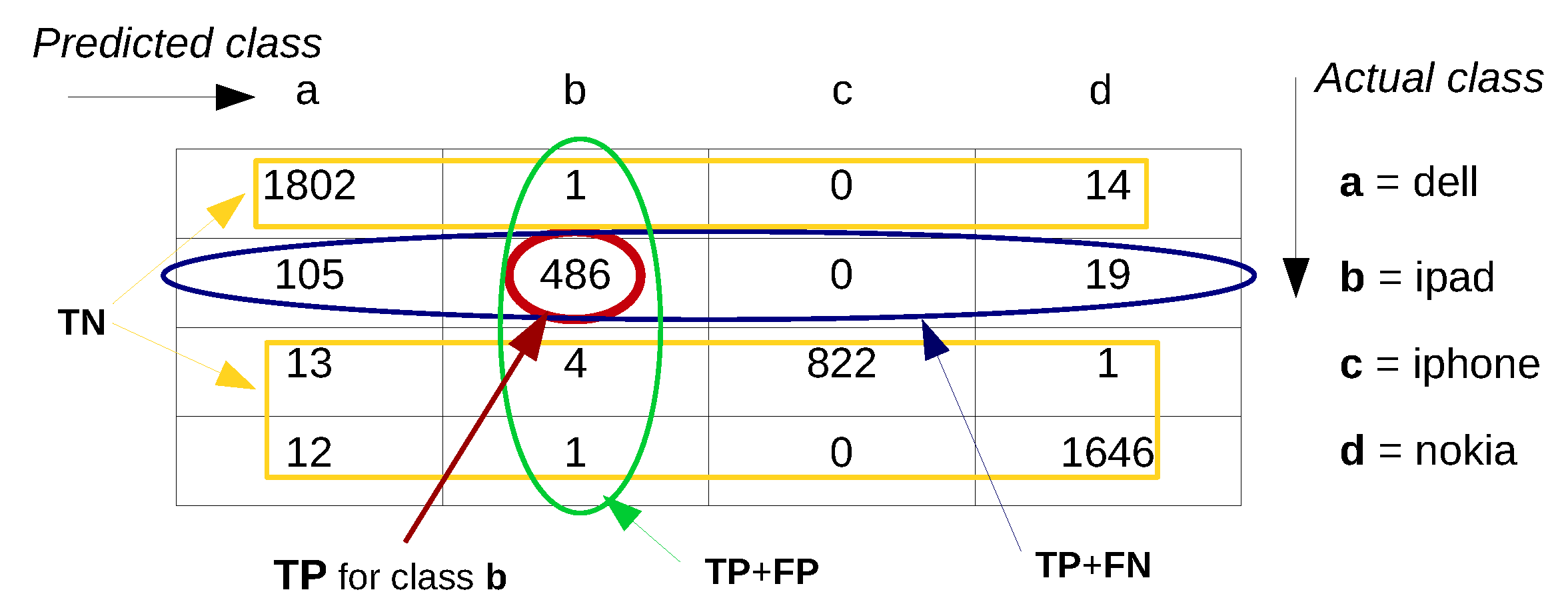
- The accuracy of a classification system is defined as , where TP, TN, FP and FN are respectively the: true positives— instances that are correctly classified as the actual class, true negatives—instances that are correctly classified as not being the actual class, false positives or Type I error—instances that are misclassified as the actual class, and false negatives or Type II error—instances from the actual class that are misclassified as another class [169]. In machine learning and data mining literature the accuracy is also referred to as the overall recognition rate of the classifier [169] and gives information about the percentage of correctly classified instances.
- Precision, defined as represents the fraction of correctly classified instances within all instances that were classified (correctly and incorrectly) as a particular class. In other words, it is the percentage of positive instances within all positive labeled instances. Hence, it can be thought as the exactness of the classifier.
- Recall, sensitivity or the true positive rate, defined as is the fraction of correctly classified instances of a particular class within all instances that belong to that class.
- An alternative way of using precision and recall is to combine them into F1 or F-score defined as the harmonic mean of precision and recall: .
4.6.3. Improving the Performance of a Learning Algorithm
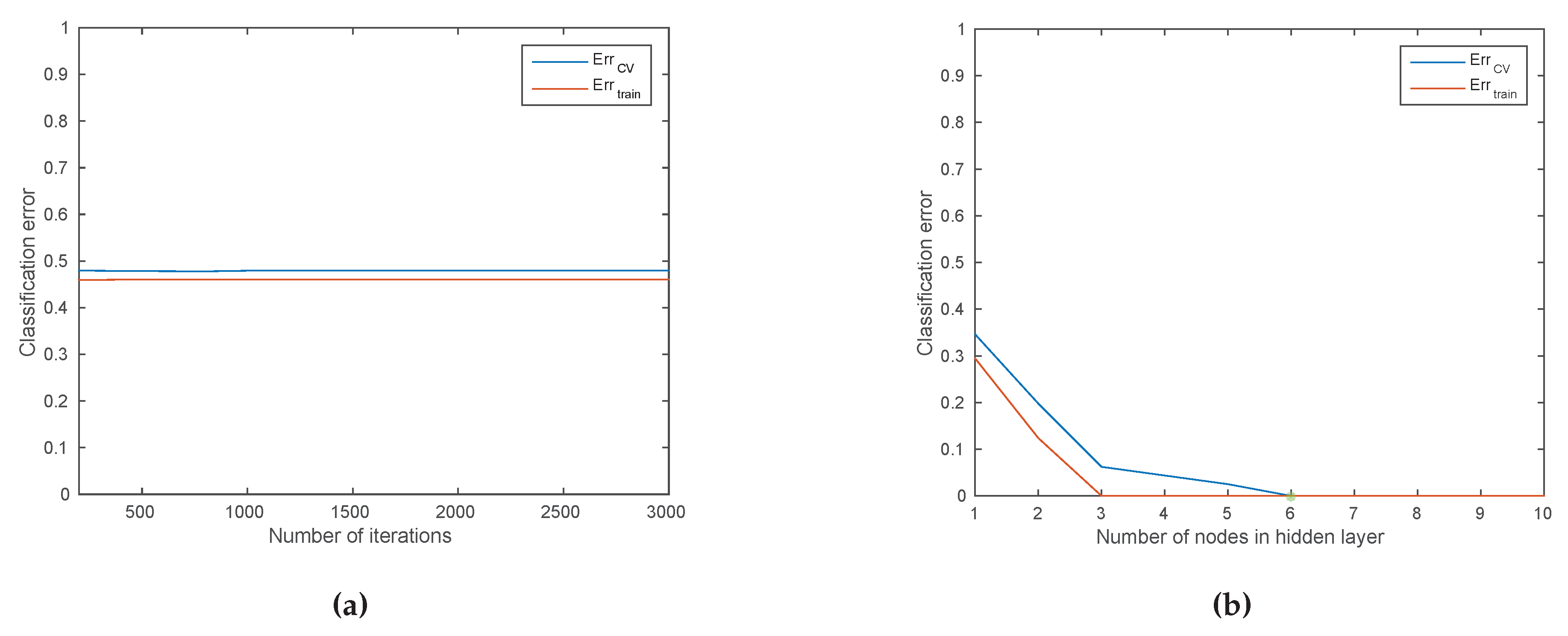
4.6.4. Performance Evaluation for the Fingerprinting Problem
Practical Considerations for Performance Evaluation
4.7. Using the Discovered Knowledge
Using the Discovered Knowledge for the Fingerprinting Problem
- Extract the model coefficients, i.e., the weights between each pair of neurons in the network, calculated by Weka. The trained neural networks model consists of three layers: the output, hidden and input layer. Each layer consists of a set of sigmoid nodes. The Weka GUI outputs: (i) the output layer sigmoid nodes (4 for device type classification or 14 nodes for device classification), which are the output connections to each class, and their weights towards each node in the hidden layer, (ii) the hidden layer sigmoid nodes (6 nodes) and their weights towards each node of the input layer. Those coefficients will act as parameters within a data mining library. Because the target system for wireless device fingerprinting can be a general purpose computer located in the corporate access network, Weka’s Java API may be a candidate for model implementation (the only prerequisite is the JVM installed).
- Define how to collect data in the online system. Packets can be captured using tcpdump [190], or any other traffic-capture mechanism and packet analyzer.
- Define how to extract the inter-arrival times (IAT), i.e., the difference between arrival times of two successive packets, produced by the same device or device type class and the same application running on top of that device. This may be achieved by processing the captured traffic flows, i.e., sequence of packets with same source and destination IP, source and destination UDP/TCP ports.
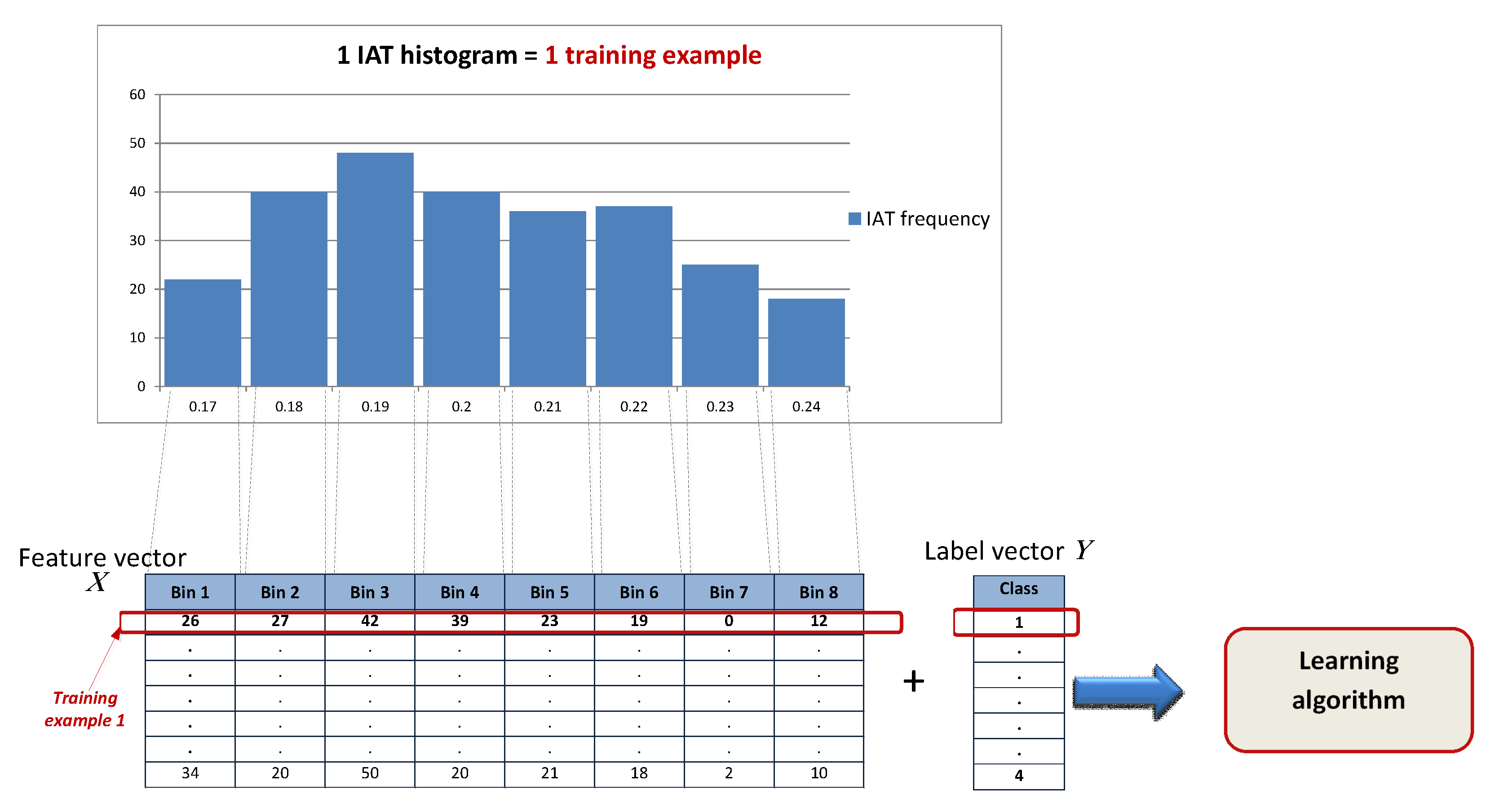
- Define how to pre-process the raw captured data. Histograms should be created similar to how the training and testing data was pre-processed in Section 4.4.2.
- Define how many packets (L) to collect to form the set of features needed to feed into the classification model and perform a prediction task. This is defined by the previously established system parameter ‘window size’ W used to train the model. W determines the length of the traffic flow, L, which is the number of packets that need to be collected to form the histogram with 500 bins (features) and feed as a new instance into the classifier. The relation between W and L is .
- Deploy and start the classification engine on the target system.
4.8. Final Considerations: Future Recommendations and Implementation Challenges
Understanding the domain
Understanding the Data
Data Pre-Processing
Data Mining
Performance Evaluation
Using the Discovered Knowledge
- Transmission power consumption: Compared to the local model where the main limitation factor for model implementation is the computing power consumption (i.e., power consumption due to heavy computations), in a global model deployment the processing tasks at the nodes need to be optimized to reduce the transmitting power consumption (i.e., power consumption due to extensive transmission of information to the central node).
- Network throughput consumption: A global model makes predictions based on data that is being sampled by local nodes and sent over the wireless network to the target central point having the global model deployed. Forwarding each particular data sample, also called raw data, may result in high bandwidth consumption as well as transmission power consumption on the local nodes. One way to prevent unnecessary communication overhead is to perform data pre-processing already at the nodes locally, and send only aggregate reports to the central point. Advanced deployments may consider also to distribute the processing load related to the data mining task over several wireless nodes. In this way, each local node will contains partial event patterns and transmit only reduced data amounts with partial mining results to the central point. One example can be found in an earlier introduced work [99].
- Large data volumes: Even after applying data aggregation and distributed data mining techniques to reduce data transmissions, large-scale wireless networks with thousands of nodes may produce large volumes of data due to continuous transmissions by heterogeneous devices. The performance for processing and mining the data samples is limited by the central point’s hardware resources, which are too expensive to be updated frequently. Several parallel programming models have been introduced to process large amounts of data in a fast and efficient way using distributed processing across clusters of computers. There is still open research in adapting some data mining algorithms for these parallel programming platforms (e.g., parallel k-means clustering).
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dhar, V. Data science and prediction. Commun. ACM 2013, 56, 64–73. [Google Scholar] [CrossRef]
- Liao, S.H.; Chu, P.H.; Hsiao, P.Y. Data mining techniques and applications—A decade review from 2000 to 2011. Expert Syst. Appl. 2012, 39, 11303–11311. [Google Scholar] [CrossRef]
- Palaniappan, S.; Awang, R. Intelligent heart disease prediction system using data mining techniques. In Proceedings of the 2008 IEEE/ACS International Conference on International Conference on Computer Systems and Applications, Doha, Qatar, 31 March–4 April 2008; pp. 108–115.
- Russell, M.A. Mining the Social Web: Data Mining Facebook, Twitter, LinkedIn, Google+, GitHub, and More; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2013. [Google Scholar]
- Adomavicius, G.; Tuzhilin, A. Using data mining methods to build customer profiles. Computer 2001, 34, 74–82. [Google Scholar] [CrossRef]
- Chen, H.; Turk, A.; Duri, S. S.; Isci, C.; Coskun, A.K. Automated system change discovery and management in the cloud. IBM J. Res. Dev. 2016, 60, 2:1–2:10. [Google Scholar] [CrossRef]
- Kartsakli, E.; Antonopoulos, A.; Alonso, L.; Verikoukis, C. A Cloud-Assisted Random Linear Network Coding Medium Access Control Protocol for Healthcare Applications. Sensors 2014, 4, 4806–4830. [Google Scholar] [CrossRef] [PubMed]
- Bastug, E.; Bennis, M.; Zeydan, E.; Kader, M.A.; Karatepe, A.; Er, A.S.; Debbah, M. Big data meets telcos: A proactive caching perspective. J. Commun. Netw. 2015, 17, 549–558. [Google Scholar] [CrossRef]
- Liu, T.; Cerpa, A.E. Foresee (4C): Wireless link prediction using link features. In Proceedings of the 2011 10th International Conference on Information Processing in Sensor Networks (IPSN), Chicago, IL, USA, 12–14 April 2011; pp. 294–305.
- Liu, T.; Cerpa, A.E. Temporal Adaptive Link Quality Prediction with Online Learning. ACM Trans. Sen. Netw. 2014, 10, 1–41. [Google Scholar] [CrossRef]
- Crotti, M.; Dusi, M.; Gringoli, F.; Salgarelli, L. Traffic classification through simple statistical fingerprinting. ACM SIGCOMM Comput. Commun. Rev. 2007, 37, 5–16. [Google Scholar] [CrossRef]
- Radhakrishnan, S.V.; Uluagac, A.S.; Beyah, R. GTID: A Technique for Physical Device and Device Type Fingerprinting. IEEE Trans. Depend. Secur. Comput. 2014, 12, 519–532. [Google Scholar] [CrossRef]
- Tsai, C.W.; Lai, C.F.; Chiang, M.C.; Yang, L.T. Data mining for internet of things: A survey. IEEE Commun. Surv. Tutor. 2014, 16, 77–97. [Google Scholar] [CrossRef]
- Mahmood, A.; Shi, K.; Khatoon, S.; Xiao, M. Data mining techniques for wireless sensor networks: A survey. Int. J. Distrib. Sens. Netw. 2013, 2013. [Google Scholar] [CrossRef]
- Chen, F.; Deng, P.; Wan, J.; Zhang, D.; Vasilakos, A.V.; Rong, X. Data mining for the internet of things: Literature review and challenges. Int. J. Distrib. Sens. Netw. 2015, 501. [Google Scholar] [CrossRef]
- Di, M.; Joo, E.M. A survey of machine learning in wireless sensor netoworks from networking and application perspectives. In Proceedings of the 2007 6th International Conference on IEEE Information, Communications & Signal Processing, Singapore, 10–13 December 2007; pp. 1–5.
- Abu Alsheikh, M.; Lin, S.; Niyato, D.; Tan, H.P. Machine learning in wireless sensor networks: Algorithms, strategies, and applications. IEEE Commun. Surv. Tutor. 2014, 16, 1996–2018. [Google Scholar] [CrossRef]
- Kulkarni, R.V.; Förster, A.; Venayagamoorthy, G.K. Computational intelligence in wireless sensor networks: A survey. IEEE Commun. Surv. Tutor. 2011, 13, 68–96. [Google Scholar] [CrossRef]
- Bkassiny, M.; Li, Y.; Jayaweera, S.K. A survey on machine-learning techniques in cognitive radios. IEEE Commun. Surv. Tutor. 2013, 15, 1136–1159. [Google Scholar] [CrossRef]
- Thilina, K.M.; Choi, K.W.; Saquib, N.; Hossain, E. Machine learning techniques for cooperative spectrum sensing in cognitive radio networks. IEEE J. Sel. Areas Commun. 2013, 31, 2209–2221. [Google Scholar] [CrossRef]
- Bulling, A.; Blanke, U.; Schiele, B. A tutorial on human activity recognition using body-worn inertial sensors. ACM Comput. Surv. (CSUR) 2014, 46, 33. [Google Scholar] [CrossRef]
- Gluhak, A.; Krco, S.; Nati, M.; Pfisterer, D.; Mitton, N.; Razafindralambo, T. A survey on facilities for experimental internet of things research. IEEE Commun. Mag. 2011, 49, 58–67. [Google Scholar] [CrossRef]
- Kulin, M.. An instance of the knowledge discovery framework for solving a wireless device fingerprinting problem. Available online: http://crawdad.org/gatech/fingerprinting/ (accessed on 25 May 2016).
- Uluagac, A.S. CRAWDAD Data Set Gatech/fingerprinting (v. 2014-06-09). Available online: http://crawdad.org/gatech/fingerprinting/ (accessed on 25 May 2016).
- Fayyad, U.; Piatetsky-Shapiro, G.; Smyth, P. The KDD process for extracting useful knowledge from volumes of data. Commun. ACM 1996, 39, 27–34. [Google Scholar] [CrossRef]
- Yau, K.L.A.; Komisarczuk, P.; Teal, P.D. Reinforcement learning for context awareness and intelligence in wireless networks: Review, new features and open issues. J. Netw. Comput. Appl. 2012, 35, 253–267. [Google Scholar] [CrossRef]
- Venayagamoorthy, G.K.K. A successful interdisciplinary course on coputational intelligence. IEEE Comput. Intell. Mag. 2009, 4, 14–23. [Google Scholar] [CrossRef]
- Khatib, E.J.; Barco, R.; Munoz, P.; Bandera, L.; De, I.; Serrano, I. Self-healing in mobile networks with big data. IEEE Commun. Mag. 2016, 54, 114–120. [Google Scholar] [CrossRef]
- Sha, M.; Dor, R.; Hackmann, G.; Lu, C.; Kim, T.S.; Park, T. Self-adapting mac layer for wireless sensor networks. In Proceedings of the 2013 IEEE 34th Real-Time Systems Symposium (RTSS), Vancouver, BC, Canada, 3–6 December 2013; pp. 192–201.
- Esteves, V.; Antonopoulos, A.; Kartsakli, E.; Puig-Vidal, M.; Miribel-Català, P.; Verikoukis, C. Cooperative energy harvesting-adaptive MAC protocol for WBANs. Sensors 2015, 15, 12635–12650. [Google Scholar] [CrossRef] [PubMed]
- Yoon, S.; Shahabi, C. The Clustered AGgregation (CAG) technique leveraging spatial and temporal correlations in wireless sensor networks. ACM Trans. Sens. Netw. (TOSN) 2007, 3. [Google Scholar] [CrossRef]
- Chen, X.; Xu, X.; Huang, J.Z.; Ye, Y. TW-k-means: Automated two-level variable weighting clustering algorithm for multiview data. IEEE Trans. Knowl. Data Eng. 2013, 25, 932–944. [Google Scholar] [CrossRef]
- Vanheel, F.; Verhaevert, J.; Laermans, E.; Moerman, I.; Demeester, P. Automated linear regression tools improve rssi wsn localization in multipath indoor environment. EURASIP J. Wirel. Commun. Netw. 2011, 2011, 1–27. [Google Scholar] [CrossRef]
- Tennina, S.; Di Renzo, M.; Kartsakli, E.; Graziosi, F.; Lalos, A.S.; Antonopoulos, A.; Mekikis, P.V.; Alonso, L. WSN4QoL: A WSN-oriented healthcare system architecture. Int. J. Distrib. Sens. Netw. 2014, 2014. [Google Scholar] [CrossRef]
- Blasco, P.; Gunduz, D.; Dohler, M. A learning theoretic approach to energy harvesting communication system optimization. IEEE Trans. Wirel. Commun. 2013, 12, 1872–1882. [Google Scholar] [CrossRef]
- Hu, H.; Song, J.; Wang, Y. Signal classification based on spectral correlation analysis and SVM in cognitive radio. In Proceedings of 22nd International Conference on the Advanced Information Networking and Applications (AINA 2008), Okinawa, Janpan, 25–28 March 2008; pp. 883–887.
- Huang, Y.; Jiang, H.; Hu, H.; Yao, Y. Design of learning engine based on support vector machine in cognitive radio. In Proceedings of the International Conference on IEEE Computational Intelligence and Software Engineering (CiSE 2009), Wuhan, China, 11–13 December 2009; pp. 1–4.
- Förster, A. Machine learning techniques applied to wireless ad-hoc networks: Guide and survey. In Proceedings of the 3rd International Conference on ISSNIP 2007 IEEE Intelligent Sensors, Sensor Networks and Information, Melbourne, Australia, 3–6 December 2007; pp. 365–370.
- Lara, O.D.; Labrador, M.A. A survey on human activity recognition using wearable sensors. IEEE Commun. Surv. Tutor. 2013, 15, 1192–1209. [Google Scholar] [CrossRef]
- Clancy, C.; Hecker, J.; Stuntebeck, E.; Shea, T.O. Applications of machine learning to cognitive radio networks. IEEE Wirel. Commun. 2007, 14, 47–52. [Google Scholar] [CrossRef]
- Anagnostopoulos, T.; Anagnostopoulos, C.; Hadjiefthymiades, S.; Kyriakakos, M.; Kalousis, A. Predicting the location of mobile users: A machine learning approach. In Proceedings of the 2009 International Conference on Pervasive Services, New York, NY, USA, 13 July 2009; pp. 65–72.
- Kulkarni, R.V.; Venayagamoorthy, G.K. Neural network based secure media access control protocol for wireless sensor networks. In Proceedings of the 2009 International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009; pp. 1680–1687.
- Kim, M.H.; Park, M.G. Bayesian statistical modeling of system energy saving effectiveness for MAC protocols of wireless sensor networks. In Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing; Springer: Heidelberg, Germany, 2009; pp. 233–245. [Google Scholar]
- Shen, Y.J.; Wang, M.S. Broadcast scheduling in wireless sensor networks using fuzzy Hopfield neural network. Expert Syst. Appl. 2008, 34, 900–907. [Google Scholar] [CrossRef]
- Barbancho, J.; León, C.; Molina, J.; Barbancho, A. Giving neurons to sensors. QoS management in wireless sensors networks. In Proceedings of the IEEE Conference on Emerging Technologies and Factory Automation (2006 ETFA’06), Prague, Czech Republic, 20–22 September 2006; pp. 594–597.
- Liu, T.; Cerpa, A.E. Data-driven link quality prediction using link features. ACM Trans. Sens. Netw. (TOSN) 2014, 10. [Google Scholar] [CrossRef]
- Wang, Y.; Martonosi, M.; Peh, L.S. Predicting link quality using supervised learning in wireless sensor networks. ACM SIGMOBILE Mobile Comput. Commun. Rev. 2007, 11, 71–83. [Google Scholar] [CrossRef]
- Ahmed, G.; Khan, N.M.; Khalid, Z.; Ramer, R. Cluster head selection using decision trees for wireless sensor networks. In Proceedings of the ISSNIP 2008 International Conference on Intelligent Sensors, Sensor Networks and Information Processing, Sydney, Australia, 15–18 December 2008; pp. 173–178.
- Shareef, A.; Zhu, Y.; Musavi, M. Localization using neural networks in wireless sensor networks. In Proceedings of the 1st International Conference on MOBILe Wireless MiddleWARE, Operating Systems, and Applications, ICST (Institute for Computer Sciences, Social-Informatics and Telecommunications Engineering), Brussels, Belgium, 13 February 2008.
- Chagas, S.H.; Martins, J.B.; De Oliveira, L.L. An approach to localization scheme of wireless sensor networks based on artificial neural networks and genetic algorithms. In Proceedings of the 2012 IEEE 10th International New Circuits and systems Conference (NEWCAS), Montreal, QC, Canada, 2012; pp. 137–140.
- Tran, D.A.; Nguyen, T. Localization in wireless sensor networks based on support vector machines. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 981–994. [Google Scholar] [CrossRef]
- Tumuluru, V.K.; Wang, P.; Niyato, D. A neural network based spectrum prediction scheme for cognitive radio. In Proceedings of the 2010 IEEE International Conference on IEEE Communications (ICC), Cape Town, South Africa, 23–27 May 2010; pp. 1–5.
- Baldo, N.; Zorzi, M. Learning and adaptation in cognitive radios using neural networks. In Proceedings of the 2008 5th IEEE Consumer Communications and Networking Conference, Las Vegas, NV, USA, 10–12 January 2008; pp. 998–1003.
- Tang, Y.J.; Zhang, Q.Y.; Lin, W. Artificial neural network based spectrum sensing method for cognitive radio. In Proceedings of the 2010 6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM), Chengdu, China, 23–25 September 2010; pp. 1–4.
- Xu, G.; Lu, Y. Channel and modulation selection based on support vector machines for cognitive radio. In Proceedings of the 2006 International Conference on Wireless Communications, Networking and Mobile Computing, Wuhan, China, 22–24 September 2006; pp. 1–4.
- Petrova, M.; Mähönen, P.; Osuna, A. Multi-class classification of analog and digital signals in cognitive radios using Support Vector Machines. In Proceedings of the 2010 7th International Symposium on Wireless Communication Systems (ISWCS), York, UK, 19–22 September 2010; pp. 986–990.
- Mannini, A.; Sabatini, A.M. Machine learning methods for classifying human physical activity from on-body accelerometers. Sensors 2010, 10, 1154–1175. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.H.; Kim, N.J.; Cha, E.J.; Lee, T.S. Classification technique of human motion context based on wireless sensor network. In Proceedings of the 27th Annual International Conference of the Engineering in Medicine and Biology Society (IEEE-EMBS 2005), Shanghai, China, 17–18 January 2006; pp. 5201–5202.
- Bao, L.; Intille, S.S. Activity Recognition from User-Annotated Acceleration Data. In Pervasive Computing; Springer: Heidelberg, Germany, 2004; pp. 1–17. [Google Scholar]
- Bulling, A.; Ward, J.A.; Gellersen, H. Multimodal recognition of reading activity in transit using body-worn sensors. ACM Trans. Appl. Percept. 2012, 9. [Google Scholar] [CrossRef]
- Yu, L.; Wang, N.; Meng, X. Real-time forest fire detection with wireless sensor networks. In Proceedings of the 2005 International Conference on Wireless Communications, Networking and Mobile Computing, Wuhan, China, 23–26 September 2005; pp. 1214–1217.
- Bahrepour, M.; Meratnia, N.; Havinga, P.J. Use of AI techniques for residential fire detection in wireless sensor networks. In Proceedings of the AIAI 2009 Workshop Proceedings, Thessaloniki, Greece, 23–25 April 2009; pp. 311–321.
- Bahrepour, M.; Meratnia, N.; Poel, M.; Taghikhaki, Z.; Havinga, P.J. Distributed event detection in wireless sensor networks for disaster management. In Proceedings of the 2010 2nd International Conference on Intelligent Networking and Collaborative Systems (INCOS), Thessaloniki, Greece, 24–26 November 2010; pp. 507–512.
- Zoha, A.; Imran, A.; Abu-Dayya, A.; Saeed, A. A Machine Learning Framework for Detection of Sleeping Cells in LTE Network. In Proceedings of the Machine Learning and Data Analysis Symposium, Doha, Qatar, 3–4 March 2014.
- Khanafer, R.M.; Solana, B.; Triola, J.; Barco, R.; Moltsen, L.; Altman, Z.; Lazaro, P. Automated diagnosis for UMTS networks using Bayesian network approach. IEEE Trans. Veh. Technol. 2008, 57, 2451–2461. [Google Scholar] [CrossRef]
- Ridi, A.; Gisler, C.; Hennebert, J. A survey on intrusive load monitoring for appliance recognition. In Proceedings of the 2014 22nd International Conference on Pattern Recognition (ICPR), Stockholm, Sweden, 24–28 August 2014; pp. 3702–3707.
- Chang, H.H.; Yang, H.T.; Lin, C.L. Load identification in neural networks for a non-intrusive monitoring of industrial electrical loads. In Computer Supported Cooperative Work in Design IV; Springer: Melbourne, Australia, 2007; pp. 664–674. [Google Scholar]
- Branch, J.W.; Giannella, C.; Szymanski, B.; Wolff, R.; Kargupta, H. In-network outlier detection in daa wireless sensor networks. Knowl. Inf. Syst. 2013, 34, 23–54. [Google Scholar] [CrossRef]
- Kaplantzis, S.; Shilton, A.; Mani, N.; Şekercioğlu, Y.A. Detecting selective forwarding attacks in wireless sensor networks using support vector machines. In Proceedings of the 2007 3rd International Conference on IEEEIntelligent Sensors, Sensor Networks and Information (2007 ISSNIP), Melbourne, Australia, 3–6 December 2007; pp. 335–340.
- Kulkarni, R.V.; Venayagamoorthy, G.K.; Thakur, A.V.; Madria, S.K. Generalized neuron based secure media access control protocol for wireless sensor networks. In Proceedings of IEEE Symposium on Computational Intelligence in Miulti-Criteria Decision-Making (MCDM’09), Nashville, TN, USA, 30 March–2 April 2009; pp. 16–22.
- He, H.; Zhu, Z.; Mäkinen, E. A neural network model to minimize the connected dominating set for self-configuration of wireless sensor networks. IEEE Trans. Neural Netw. 2009, 20, 973–982. [Google Scholar] [PubMed]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Liu, C.; Wu, K.; Pei, J. A dynamic clustering and scheduling approach to energy saving in data collection from wireless sensor networks. In Proceedings of the IEEE SECON, Santa Clara, CA, USA, 26–29 September 2005; pp. 374–385.
- Taherkordi, A.; Mohammadi, R.; Eliassen, F. A communication-efficient distributed clustering algorithm for sensor networks. In Proceedings of the 22nd International Conference on Advanced Information Networking and Applications-Workshops (AINAW 2008), Okinawa, Japan, 25–28 March 2008; pp. 634–638.
- Guo, L.; Ai, C.; Wang, X.; Cai, Z.; Li, Y. Real time clustering of sensory data in wireless sensor networks. In Proceedings of the 2009 IEEE 28th International Performance Computing and Communications Conference (IPCCC), Scottsdale, AZ, USA, 14–16 December 2009; pp. 33–40.
- Wang, K.; Ayyash, S.A.; Little, T.D.; Basu, P. Attribute-based clustering for information dissemination in wireless sensor networks. In Proceedings of the 2nd Annual IEEE Communications Society Conference on Sensor and ad hoc Communications and Networks (SECON’05), Santa Clara, CA, USA, 26–29 September 2005; pp. 498–509.
- Ma, Y.; Peng, M.; Xue, W.; Ji, X. A dynamic affinity propagation clustering algorithm for cell outage detection in self-healing networks. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 2266–2270.
- Clancy, T.C.; Khawar, A.; Newman, T.R. Robust signal classification using unsupervised learning. IEEE Trans. Wirel. Commun. 2011, 10, 1289–1299. [Google Scholar] [CrossRef]
- Shetty, N.; Pollin, S.; Pawełczak, P. Identifying spectrum usage by unknown systems using experiments in machine learning. In Proceedings of the 2009 IEEE Wireless Communications and Networking Conference, Budapest, Hungary, 5–8 April 2009; pp. 1–6.
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques, Second Edition (Morgan Kaufmann Series in Data Management Systems); Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2005. [Google Scholar]
- Guan, D.; Yuan, W.; Lee, Y.K.; Gavrilov, A.; Lee, S. Activity recognition based on semi-supervised learning. In Proceedings of the 13th IEEE International Conference on Embedded and Real-Time Computing Systems and Applications, Daegu, Korea, 21–24 August 2007; pp. 469–475.
- Stikic, M.; Larlus, D.; Ebert, S.; Schiele, B. Weakly supervised recognition of daily life activities with wearable sensors. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2521–2537. [Google Scholar] [CrossRef] [PubMed]
- Huỳnh, T.; Schiele, B. Towards less supervision in activity recognition from wearable sensors. In Proceedings of the 2006 10th IEEE International Symposium on Wearable Computers, Montreux, Switzerland, 11–14 October 2006; pp. 3–10.
- Pulkkinen, T.; Roos, T.; Myllymäki, P. Semi-supervised learning for wlan positioning. In Artificial Neural Networks and Machine Learning–ICANN 2011; Springer: Espoo, Finland, 2011; pp. 355–362. [Google Scholar]
- Erman, J.; Mahanti, A.; Arlitt, M.; Cohen, I.; Williamson, C. Offline/realtime traffic classification using semi-supervised learning. Perform. Eval. 2007, 64, 1194–1213. [Google Scholar] [CrossRef]
- bin Abdullah, M.F.A.; Negara, A.F.P.; Sayeed, M.S.; Choi, D.J.; Muthu, K.S. Classification algorithms in human activity recognition using smartphones. Int. J. Comput. Inf. Eng. 2012, 6, 77–84. [Google Scholar]
- Bosman, H.H.; Iacca, G.; Tejada, A.; Wörtche, H.J.; Liotta, A. Ensembles of incremental learners to detect anomalies in ad hoc sensor networks. Ad Hoc Netw. 2015, 35, 14–36. [Google Scholar] [CrossRef]
- Zhang, Y.; Meratnia, N.; Havinga, P. Adaptive and online one-class support vector machine-based outlier detection techniques for wireless sensor networks. In Proceedings of the International Conference on Advanced Information Networking and Applications Workshops (WAINA’09), Bradford, UK, 26–29 May 2009; pp. 990–995.
- Dasarathy, G.; Singh, A.; Balcan, M.F.; Park, J.H. Active Learning Algorithms for Graphical Model Selection. J. Mach. Learn. Res. 2016. [Google Scholar]
- Castro, R.M.; Nowak, R.D. Minimax bounds for active learning. IEEE Trans. Inf. Theory 2008, 54, 2339–2353. [Google Scholar] [CrossRef]
- Beygelzimer, A.; Langford, J.; Tong, Z.; Hsu, D.J. Agnostic active learning without constraints. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; pp. 199–207.
- Hanneke, S. Theory of disagreement-based active learning. In Foundations and Trends® in Machine Learning; Now Publishers Inc.: Hanover, MA, USA, 2014; pp. 131–309. [Google Scholar]
- Son, D.; Krishnamachari, B.; Heidemann, J. Experimental study of concurrent transmission in wireless sensor networks. In Proceedings of the 4th International Conference on Embedded Networked Sensor Systems; ACM: New York, NY, USA, 2006; pp. 237–250. [Google Scholar]
- Levis, K. RSSI is under appreciated. In Proceedings of the Third Workshop on Embedded Networked Sensors, Cambridge, MA, USA, 30–31 May 2006; pp. 239–242.
- Haykin, S.S.; Haykin, S.S.; Haykin, S.S.; Haykin, S.S. Neural Networks and Learning Machines; Pearson Education: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward Networks Are Universal Approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Baldo, N.; Tamma, B.R.; Manoj, B.; Rao, R.; Zorzi, M. A neural network based cognitive controller for dynamic channel selection. In Proceedings of the IEEE International Conference on Communications (ICC’09), Dresden, Germany, 14–18 June 2009; pp. 1–5.
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- Li, C.; Xie, X.; Huang, Y.; Wang, H.; Niu, C. Distributed data mining based on deep neural network for wireless sensor network. Int. J. Distrib. Sens. Netw. 2015, 2015. [Google Scholar] [CrossRef] [PubMed]
- Zorzi, M.; Zanella, A.; Testolin, A.; De Filippo De Grazia, M.; Zorzi, M. Cognition-Based Networks: A New Perspective on Network Optimization Using Learning and Distributed Intelligence. IEEE Access 2015, 3, 1512–1530. [Google Scholar] [CrossRef]
- Rokach, L.; Maimon, O. Data Mining with Decision Trees: Theory and Applications; World Scientific Publishing Company: Singapore, 2008. [Google Scholar]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1990, 21, 660–674. [Google Scholar] [CrossRef]
- Freedman, D.A. Statistical Models: Theory and Practice; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Alizai, M.H.; Landsiedel, O.; Link, J.Á.B.; Götz, S.; Wehrle, K. Bursty traffic over bursty links. In Proceedings of the 7th ACM Conf on Embedded Networked Sensor Systems, New York, NY, USA, 14–17 March 2009; pp. 71–84.
- Fonseca, R.; Gnawali, O.; Jamieson, K.; Levis, P. Four-Bit Wireless Link Estimation. In Peoceedings of the Sixth Workshop on Hot Topics in Networks (HotNets), Atlanta, GA, USA, 14–15 November 2007.
- Vapnik, V.N.; Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Ramon, M.M.; Atwood, T.; Barbin, S.; Christodoulou, C.G. Signal classification with an SVM-FFT approach for feature extraction in cognitive radio. In Proceedings of the 2009 SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC), Belem, Brazil, 3–6 November 2009; pp. 286–289.
- Larose, D.T. k-Nearest Neighbor Algorithm. In Discovering Knowledge in Data: An Introduction to Data Mining; John Wiley & Sons, Inc.: New York, NJ, USA, 2005; pp. 90–106. [Google Scholar]
- Jatoba, L.C.; Grossmann, U.; Kunze, C.; Ottenbacher, J.; Stork, W. Context-aware mobile health monitoring: Evaluation of different pattern recognition methods for classification of physical activity. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS 2008), Vancouver, BC, Canada, 20–25 August 2008; pp. 5250–5253.
- Abbasi, A.A.; Younis, M. A survey on clustering algorithms for wireless sensor networks. Comput. Commun. 2007, 30, 2826–2841. [Google Scholar] [CrossRef]
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Meratnia, N.; Havinga, P. Outlier detection techniques for wireless sensor networks: A survey. Tutor. IEEE Commun. Surv. 2010, 12, 159–170. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: a new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on IEEE Neural Networks, Budapest, Hungary, 25–29 July 2004; pp. 985–990.
- Duarte, M.F.; Eldar, Y.C. Structured compressed sensing: From theory to applications. IEEE Trans. Signal Process. 2011, 59, 4053–4085. [Google Scholar] [CrossRef]
- Masiero, R.; Quer, G.; Munaretto, D.; Rossi, M.; Widmer, J.; Zorzi, M. Data acquisition through joint compressive sensing and principal component analysis. In Proceedings of the Global Telecommunications Conference (GLOBECOM), Honolulu, HI, USA, 30 November–4 December 2009; pp. 1–6.
- Masiero, R.; Quer, G.; Rossi, M.; Zorzi, M. A Bayesian analysis of compressive sensing data recovery in wireless sensor networks. In Proceedings of the International Conference on Ultra Modern Telecommunications & Workshops (ICUMT), Padova, Italy, 12–14 October 2009; pp. 1–6.
- Lalos, A.S.; Antonopoulos, A.; Kartsakli, E.; Di Renzo, M.; Tennina, S.; Alonso, L.; Verikoukis, C. RLNC-Aided Cooperative Compressed Sensing for Energy Efficient Vital Signal Telemonitoring. IEEE Trans. Wirel. Commun. 2015, 14, 3685–3699. [Google Scholar] [CrossRef]
- Kimura, N.; Latifi, S. A survey on data compression in wireless sensor networks. In Proceedings of the International Conference on Information Technology: Coding and Computing, Las Vegas, NV, USA, 4–6 April 2005; pp. 8–13.
- Fayyad, U.; Fayyad, U.; Piatetsky-shapiro, G.; Piatetsky-shapiro, G.; Smyth, P.; Smyth, P. Knowledge Discovery and Data Mining: Towards a Unifying Framework; AAAI Press: Portland, Oregon, 1996. [Google Scholar]
- Klösgen, W.; Zytkow, J.M. The knowledge discovery process. In Handbook of Data Mining and Knowledge Discovery; Oxford University Press, Inc.: New York, NY, USA, 2002; pp. 10–21. [Google Scholar]
- Lewis, D.D. Naive (Bayes) at forty: The independence assumption in information retrieval. In Machine Learning: ECML-98; Springer: Chemnitz, Germany, 1998; pp. 4–15. [Google Scholar]
- Liu, H.; Motoda, H. Feature Extraction, Construction and Selection: A Data Mining Perspective; Springer Science & Business Media: Norwell, MA, USA, 1998. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Levis, P.; Madden, S.; Polastre, J.; Szewczyk, R.; Whitehouse, K.; Woo, A.; Gay, D.; Hill, J.; Welsh, M.; Brewer, E. Tinyos: An Operating System for Sensor Networks. In Ambient intelligence; Springer: Berlin/Heidelberg, Germany, 2005; pp. 115–148. [Google Scholar]
- Xu, Q.; Zheng, R.; Saad, W.; Han, Z. Device Fingerprinting in Wireless Networks: Challenges and Opportunities. In Proceedings of the IEEE Communications Surveys & Tutorials, New York, NY, USA, 27 January 2016; pp. 94–104.
- Tugnait, J.K.; Kim, H. A channel-based hypothesis testing approach to enhance user authentication in wireless networks. In Proceedings of the 2010 Second International Conference on Communication Systems and NETworks (COMSNETS), Bangalore, India, 5–9 January 2010; pp. 1–9.
- Yu, P.L.; Sadler, B.M. Mimo authentication via deliberate fingerprinting at the physical layer. IEEE Trans. Inf. Forensics Secur. 2011, 6, 606–615. [Google Scholar] [CrossRef]
- Xiao, L.; Greenstein, L.; Mandayam, N.; Trappe, W. Fingerprints in the ether: Using the physical layer for wireless authentication. In Proceedings of the International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 4646–4651.
- Xiao, L.; Greenstein, L.J.; Mandayam, N.B.; Trappe, W. Using the physical layer for wireless authentication in time-variant channels. IEEE Trans. Wirel. Commun. 2008, 7, 2571–2579. [Google Scholar] [CrossRef]
- Liu, F.J.; Wang, X.; Primak, S.L. A two dimensional quantization algorithm for cir-based physical layer authentication. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 4724–4728.
- Nguyen, N.T.; Zheng, G.; Han, Z.; Zheng, R. Device fingerprinting to enhance wireless security using nonparametric Bayesian method. In Proceedings of the IEEE INFOCOM, Shanghai, China, 10–15 April 2011; pp. 1404–1412.
- Brik, V.; Banerjee, S.; Gruteser, M.; Oh, S. Wireless device identification with radiometric signatures. In Proceedings of the 14th ACM International Conference on Mobile Computing and Networking, New York, NY, USA, 17 April 2008; pp. 116–127.
- Corbett, C.L.; Beyah, R.A.; Copeland, J.A. Using active scanning to identify wireless NICs. In Proceedings of the Information Assurance Workshop, New York, NY, USA, 21–23 June 2006; pp. 239–246.
- Corbett, C.L.; Beyah, R.A.; Copeland, J.A. Passive classification of wireless nics during rate switching. J. Wirel. Commun. Netw. 2007, 2008, 1–12. [Google Scholar] [CrossRef]
- Jana, S.; Kasera, S.K. On fast and accurate detection of unauthorized wireless access points using clock skews. IEEE Trans. Mob. Comput. 2010, 9, 449–462. [Google Scholar] [CrossRef]
- Neumann, C.; Heen, O.; Onno, S. An empirical study of passive 802.11 device fingerprinting. In Proceedings of the 32nd International Conference on Distributed Computing Systems Workshops (ICDCSW), Macau, China, 18–21 June 2012; pp. 593–602.
- Gao, K.; Corbett, C.; Beyah, R. A passive approach to wireless device fingerprinting. In Proceedings of the 2010 IEEE/IFIP International Conference on Dependable Systems&Networks (DSN), Chicago, IL, USA, 28 June–1 July 2010; pp. 383–392.
- Ahmed, M.E.; Song, J.B.; Han, Z.; Suh, D.Y. Sensing-transmission edifice using bayesian nonparametric traffic clustering in cognitive radio networks. IEEE Trans. Mob. Comput. 2014, 13, 2141–2155. [Google Scholar] [CrossRef]
- Eckersley, P. How unique is your web browser? In Privacy Enhancing Technologies; Springer: Berlin, Germany, 2010; pp. 1–18. [Google Scholar]
- Zhu, X.; Vondrick, C.; Ramanan, D.; Fowlkes, C. Do We Need More Training Data or Better Models for Object Detection? In Proceedings of the British Machine Vision Conference (BMVC), Surrey, England, 3–7 September 2012.
- Kotz, D.; Henderson, T. Crawdad: A community resource for archiving wireless data at dartmouth. IEEE Pervasive Comput. 2005, 4, 12–14. [Google Scholar] [CrossRef]
- CONAN Project. The CONAN (Congestion Analysis of Wireless Networks) Project. Available online: http://moment.cs.ucsb.edu/conan/ (accessed on 25 May 2016).
- UC San Diego Measurements Repository. The UC San Diego wireless measurements. Available online: http://sysnet.ucsd.edu/pawn/sigcomm-trace/ (accessed on 25 May 2016).
- University of Washington Measurements Repository. The University of Washington “Wireless Measurements Project”. Available online: http://research.cs.washington.edu/networking/wireless/ (accessed on 25 May 2016).
- Van Haute, T.; De Poorter, E.; Rossey, J.; Moerman, I.; Handziski, V.; Behboodi, A.; Lemic, F.; Wolisz, A.; Wiström, N.; Voigt, T. The evarilos benchmarking handbook: Evaluation of rf-based indoor localization solutions. In Proceedings of the 2e International Workshop on Measurement-based Experimental Research, Methodology and Tools (MERMAT), Dublin, Ireland, 7 May 2013; pp. 1–6.
- UMass Measurements Repository. The UMass Trace Repository. Available online: http://traces.cs.umass.edu/index.php/Network/Network (accessed on 25 May 2016).
- FIRE Project. The FIRE (Future Internet Research and Experimentation Initative) federations of European Experimental Facilities. Available online: http://cordis.europa.eu/fp7/ict/fire/ (accessed on 25 May 2016).
- Bouckaert, S.; Vandenberghe, W.; Jooris, B.; Moerman, I.; Demeester, P. The w-iLab. t testbed. In Testbeds and Research Infrastructures. Development of Networks and Communities; Springer: Berlin, Germany, 2011; pp. 145–154. [Google Scholar]
- Handziski, V.; Köpke, A.; Willig, A.; Wolisz, A. TWIST: A scalable and reconfigurable testbed for wireless indoor experiments with sensor networks. In Proceedings of the 2nd International Workshop on Multi-Hop ad hoc Networks: From Theory to Reality, Florence, Italy, 26 May 2006; pp. 63–70.
- Sutton, P.; Lotze, J.; Lahlou, H.; Fahmy, S.; Nolan, K.; Ozgul, B.; Rondeau, T.W.; Noguera, J.; Doyle, L.E. Iris: An architecture for cognitive radio networking testbeds. IEEE Commun. Mag. 2010, 48, 114–122. [Google Scholar] [CrossRef]
- Šolc, T.; Fortuna, C.; Mohorčič, M. Low-cost testbed development and its applications in cognitive radio prototyping. In Cognitive Radio and Networking for Heterogeneous Wireless Networks; Springer: Cham, Switzerland, 2015; pp. 361–405. [Google Scholar]
- Giatsios, D.; Apostolaras, A.; Korakis, T.; Tassiulas, L. Methodology and Tools for Measurements on Wireless Testbeds: The NITOS Approach. In Measurement Methodology and Tools; Springer: Berlin/Heidelberg, Germany, 2013; pp. 61–80. [Google Scholar]
- GENI Project. The GENI (Global Environment for Network Innovations) federations of Experimental Facilities in the United States. Available online: http://www.geni.net/ (accessed on 25 May 2016).
- Werner-Allen, G.; Swieskowski, P.; Welsh, M. Motelab: A wireless sensor network testbed. In Proceedings of the 4th International Symposium on Information Processing in Sensor Networks, Boise, ID, USA, 15 April 2005.
- Raychaudhuri, D.; Seskar, I.; Ott, M.; Ganu, S.; Ramachandran, K.; Kremo, H.; Siracusa, R.; Liu, H.; Singh, M. Overview of the ORBIT radio grid testbed for evaluation of next-generation wireless network protocols. In Proceedings of the Wireless Communications and Networking Conference, New Orleans, LA, USA, 13–17 March 2005; pp. 1664–1669.
- Kansei Testbed. The Kansei testbed at the Ohio State University. Available online: http://kansei.cse.ohio-state.edu/ (accessed on 25 May 2016).
- NetEye Testbed. The NetEye testbed at the State hall building at Wayne state University. Available online: http://neteye.cs.wayne.edu/neteye/home.php (accessed on 25 May 2016).
- Gorunescu, F. Data Mining: Concepts, Models and Techniques; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Tukey, J. Exploratory Data Analysis; Addison-Wesley series in behavioral science; Addison-Wesley Publishing Company: Boston, MA, USA, 1977. [Google Scholar]
- Tufte, E. Beautiful Evidence; Graphics Press: New York, NY, USA, 2006. [Google Scholar]
- Devore, J.; Peck, R. Statistics: The Exploration & Analysis of Data; Duxbury Press: Pacific Grove, CA, USA, 1997. [Google Scholar]
- Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kulin, M. R2 results for several device types and for different traffic cases (ICMP, SCP, TCP and UDP). Available online: https://github.com/merimak/DataDrivenDesignWirelessNetworks /tree/master/Results/R%20squared%20results/Results%20in%20KDP%20step%202 (accessed on 25 May 2016).
- Matloff, N. The art of R Programming: A Tour of Statistical Software Design; No Starch Press: San Francisco, CA, USA, 2011. [Google Scholar]
- MATLAB. Version 8.4.0.150421 (R2014b), The MathWorks Inc.: Natick, MA, USA, 2014.
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA Data Mining Software: An Update. SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Hofmann, M.; Klinkenberg, R. RapidMiner: Data Mining Use Cases and Business Analytics Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Williams, G. Data Mining with Rattle and R: The Art of Excavating Data for Knowledge Discovery; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Jiawei, H.; Kamber, M. Data Mining: Concepts and Techniques; Elsevier: Waltham, MA, USA, 2001. [Google Scholar]
- Acuna, E.; Rodriguez, C. The treatment of missing values and its effect on classifier accuracy. In Classification, Clustering, and Data Mining Applications; Springer: Heidelberg, Germany, 2004; pp. 639–647. [Google Scholar]
- Agresti, A.; Kateri, M. Categorical Data Analysis; Springer: Heidelberg, Germany, 2011. [Google Scholar]
- Sola, J.; Sevilla, J. Importance of input data normalization for the application of neural networks to complex industrial problems. IEEE Trans. Nucl. Sci. 1997, 44, 1464–1468. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Hall, M.A.; Smith, L.A. Feature Selection for Machine Learning: Comparing a Correlation-Based Filter Approach to the Wrapper. In Proceedings of the Twelfth International Florida Artificial Intelligence Research Society Conference, Orlando, FL, USA, 3 March 1999; pp. 235–239.
- Chakrabarti, S.; Cox, E.; Frank, E.; Güting, R.H.; Han, J.; Jiang, X.; Kamber, M.; Lightstone, S.S.; Nadeau, T.P.; Neapolitan, R.E.; et al. Data Mining: Know It All: Know It All; Morgan Kaufmann: Burlington, MA, USA, 2008. [Google Scholar]
- Gaber, M.M.; Zaslavsky, A.; Krishnaswamy, S. Mining Data Streams: A Review. ACM Sigmod Rec. 2005, 34, 18–26. [Google Scholar] [CrossRef]
- Kulin, M. R2 Results after Dataset Pre-Processing for Several Device Types and for Different Traffic Cases (ICMP, SCP, TCP and UDP). Available online: https://github.com/merimak/DataDrivenDesignWirelessNetworks/tree/master/Results/R%20squared%20results/Results%20in%20KDP%20step%203 (accessed on 25 May 2016).
- Achtert, E.; Kriegel, H.P.; Zimek, A. ELKI: A software system for evaluation of subspace clustering algorithms. In Scientific and Statistical Database Management; Springer: Heidelberg, Germany, 2008; pp. 580–585. [Google Scholar]
- Abu-Mostafa, Y.S.; Magdon-Ismail, M.; Lin, H.T. Learning From Data: A Short Course; AMLBook: New York, NY, USA, 2012. [Google Scholar]
- Mitchell, T.M. Machine Learning; McGraw-Hill Education: New York, NY, USA, 1997. [Google Scholar]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Philip, S.Y.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-validation. In Encyclopedia of Database Systems; Springer Science Business Media LLC: New York, NY, USA, 2009; pp. 532–538. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence (IJCAI’95); Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; pp. 1137–1145. [Google Scholar]
- Bouckaert, R.R. Choosing between two learning algorithms based on calibrated tests. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 51–58.
- Sammut, C.; Webb, G.I. Encyclopedia of machine learning; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Ng, A. Advice for Applying Machine Learning. Available online: http://cs229.stanford.edu/materials/ML-advice.pdf (accessed on 25 May 2016).
- Kulin, M. Performance Evaluation Results for Several Data Mining Algorithms for the Wireless Device Fingerprinting Problem. Available online: https://github.com/merimak/DataDrivenDesignWirelessNetworks/tree/master/Results/Performance%20results (accessed on 25 May 2016).
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 161–168.
- Jacobson, V.; Leres, C.; McCanne, S. TCPDUMP Public Repository. Available online: http://www.tcpdump.org (accessed on 25 May 2016).
- Mehari, M.T.; De Poorter, E.; Couckuyt, I.; Deschrijver, D.; Vanhie-Van Gerwen, J.; Pareit, D.; Dhaene, T.; Moerman, I. Efficient global optimization of multi-parameter network problems on wireless testbeds. Ad Hoc Netw. 2015, 29, 15–31. [Google Scholar] [CrossRef]
| Categorization Criteria | Learning Types | Comment | |
|---|---|---|---|
| Learning paradigms | Amount of feedback given to the learner | Supervised | The learner knows all inputs/outputs |
| Unsupervised | The learner knows only the inputs | ||
| Semi-supervised | The learner knows only a few input/output pairs | ||
| Amount of information given to the learner | Offline | The learner is trained on the entire dataset | |
| Online | The learner is trained sequentially as data becomes available | ||
| Active | The learner selects the most useful training data |
| Problem Type | Optimizing Wireless Network Performance | Information Processing for Wireless Network Applications | |||||
|---|---|---|---|---|---|---|---|
| MAC | Routing | Data Aggregation | Cognitive Radio | Activity Recognition | Security | Localization | |
| Regression | [94] | [33] | |||||
| Classification | [29] | [9,10] | [99] | [36,37,97,107] | [109] | ||
| Clustering | [74] | ||||||
| Anomaly Detection | [42,87] | ||||||
| Summarization | [31] | ||||||
| Device Type | Number of Devices | Traffic Type | Minimum | Maximum | Average | Standard Deviation |
|---|---|---|---|---|---|---|
| Dell Netbook | 5 | iPerf TCP (1 case × 5 traces) | 841,299 | 3,059,247 | 1,820,062 | 948,900 |
| iPerf UDP (3 cases × 5 traces) | 298,956 | 5,702,776 | 2,382,538 | 1,799,493 | ||
| Ping ICMP (2 cases × 3 traces) | 359,220 | 359,996 | 359,865 | 316 | ||
| SCP TCP (1 case × 5 traces) | 1,514,216 | 1,569,352 | 1,543,571 | 27,750 | ||
| iPad | 3 | iPerf TCP (1 case × 3 traces) | 1,305,673 | 1,780,640 | 1,527,179 | 239,090 |
| iPerf UDP (3 cases × 3 traces) | 297,957 | 2,181,618 | 1,305,483 | 769,987 | ||
| Ping ICMP (2 cases × 3 traces) | 301,966 | 322,124 | 309,749 | 7,991 | ||
| SCP TCP (1 case × 3 traces) | 1,598,030 | 1,847,037 | 1,749,059 | 132,710 | ||
| iPhone | 4 | iPerf TCP (1 case × 4 traces) | 440,623 | 4,162,438 | 2,357,540 | 2,072,695 |
| iPerf UDP (3 cases × 4 traces) | 306,413 | 4,094,728 | 1,791,755 | 1,378,019 | ||
| Ping ICMP (2 cases × 4 traces) | 314,176 | 673,590 | 494,099 | 190,049 | ||
| SCP TCP (1 case × 4 traces) | 599,460 | 1,599,098 | 1,348,888 | 499,619 | ||
| Nokia Phone | 2 | iPerf TCP (1 case × 2 traces) | 718,480 | 844,531 | 781,505 | 89,131 |
| iPerf UDP (3 cases × 2 traces) | 300,924 | 5,131,699 | 2,189,739 | 2,094,815 | ||
| Ping ICMP (2 cases × 2 traces) | 250,532 | 359,209 | 331,915 | 54,255 | ||
| SCP TCP (1 case × 2 traces) | 1,316,782 | 1,570,745 | 1,443,763 | 179,579 |
| Device Type | Device | min[][s] | Q1[][s] | median[][s] | Q3[][s] | max[s] |
|---|---|---|---|---|---|---|
| Dell Netbook | DN1 | 5.96 | 6.91 | 8.24 | 13 | 0.1872 |
| DN2 | 5.96 | 5.67 | 6.20 | 7.35 | 0.2845 | |
| DN3 | 5.96 | 5.72 | 6.18 | 7.70 | 0.1769 | |
| DN4 | 2.86 | 4.16 | 5.80 | 6.56 | 0.2017 | |
| DN5 | 2.86 | 3.82 | 4.72 | 6.22 | 0.6571 | |
| iPad | iPad1 | 1.91 | 5.46 | 6.20 | 12 | 5.2795 |
| iPad2 | 1.91 | 5.80 | 7.83 | 13 | 10.3603 | |
| iPad3 | 2.86 | 16 | 19 | 34 | 0.1102 | |
| iPhone 3G and 4G | iPhone3G1 | 2.86 | 6.84 | 9.82 | 21 | 2.95 |
| iPhone3G2 | 1.91 | 15 | 18 | 35 | 0.4726 | |
| iPhone4G1 | 3.81 | 9.55 | 13 | 25 | 0.1456 | |
| iPhone4G2 | 4.77 | 14 | 16 | 31 | 0.1487 | |
| Nokia Phone | NP1 | 1.91 | 5.39 | 6.43 | 11 | 0.1481 |
| NP2 | 1.91 | 5.50 | 6.49 | 11 | 0.1486 |
| DN1 | DN2 | DN3 | DN4 | DN5 | iPad1 | iPad2 | iPad3 | iPhone1 | iPhone2 | iPhone3 | iPhone4 | Nokia1 | Nokia2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DN1 | 1 | 0.2407 | 0.2213 | 0.1624 | 0.0968 | 0.1130 | 0.1326 | 0.0527 | 0.3364 | 0.0770 | 0.1858 | 0.0412 | 0.2390 | 0.1935 |
| DN2 | 0.2407 | 1 | 0.9981 | 0.8620 | 0.6961 | 0.9248 | 0.7738 | 0.0656 | 0.4497 | 0.1512 | 0.2688 | 0.0133 | 0.8659 | 0.8382 |
| DN3 | 0.2213 | 0.9981 | 1 | 0.8604 | 0.6950 | 0.9273 | 0.7702 | 0.0657 | 0.4633 | 0.1508 | 0.2694 | 0.0122 | 0.8656 | 0.8391 |
| DN4 | 0.1624 | 0.8620 | 0.8604 | 1 | 0.9581 | 0.8056 | 0.6613 | 0.0616 | 0.4238 | 0.1213 | 0.2278 | 0.0106 | 0.8212 | 0.7756 |
| DN5 | 0.0968 | 0.6961 | 0.6950 | 0.9581 | 1 | 0.6550 | 0.5230 | 0.0493 | 0.3408 | 0.0901 | 0.1667 | 0.0057 | 0.6870 | 0.6396 |
| iPad1 | 0.1130 | 0.9248 | 0.9273 | 0.8056 | 0.6550 | 1 | 0.9285 | 0.0818 | 0.3830 | 0.1646 | 0.3298 | 0.0626 | 0.8741 | 0.8724 |
| iPad2 | 0.1326 | 0.7738 | 0.7702 | 0.6613 | 0.5230 | 0.9285 | 1 | 0.1207 | 0.3734 | 0.2001 | 0.4456 | 0.1948 | 0.8286 | 0.8337 |
| iPad3 | 0.0527 | 0.0656 | 0.0657 | 0.0616 | 0.0493 | 0.0818 | 0.1207 | 1 | 0.1575 | 0.6292 | 0.2366 | 0.1978 | 0.1028 | 0.0986 |
| iPhone1 | 0.3364 | 0.4497 | 0.4633 | 0.4238 | 0.3408 | 0.3830 | 0.3734 | 0.1575 | 1 | 0.1709 | 0.3572 | 0.0592 | 0.5170 | 0.4687 |
| iPhone2 | 0.0770 | 0.1512 | 0.1508 | 0.1213 | 0.0901 | 0.1646 | 0.2001 | 0.6292 | 0.1709 | 1 | 0.2353 | 0.4011 | 0.1837 | 0.1778 |
| iPhone3 | 0.1858 | 0.2688 | 0.2694 | 0.2278 | 0.1667 | 0.3298 | 0.4456 | 0.2366 | 0.3572 | 0.2353 | 1 | 0.1486 | 0.5019 | 0.5197 |
| iPhone4 | 0.0412 | 0.0133 | 0.0122 | 0.0106 | 0.0057 | 0.0626 | 0.1948 | 0.1978 | 0.0592 | 0.4011 | 0.1486 | 1 | 0.0460 | 0.0411 |
| Nokia1 | 0.2398 | 0.8659 | 0.8656 | 0.8212 | 0.6870 | 0.8741 | 0.8286 | 0.1028 | 0.5170 | 0.1837 | 0.5019 | 0.0460 | 1 | 0.9922 |
| Nokia2 | 0.1935 | 0.8382 | 0.8391 | 0.7756 | 0.6396 | 0.8724 | 0.8337 | 0.0986 | 0.4687 | 0.1778 | 0.5197 | 0.0411 | 0.9922 | 1 |
| DN | iPad | iPhone | Nokia | |
|---|---|---|---|---|
| DN | 1 | 0.6254 | 0.4013 | 0.8235 |
| iPad | 0.6254 | 1 | 0.6562 | 0.7359 |
| iPhone | 0.4013 | 0.6562 | 1 | 0.5188 |
| Nokia | 0.8235 | 0.7359 | 0.5188 | 1 |
| Threshold → | 0.3 | 0.1 | 0.01 |
|---|---|---|---|
| Misclassification error | 5.3% | 3.4% | 0.8% |
| Average data loss | 0.0032% | 0.035% | 0.387% |
| DN1 | DN2 | DN3 | DN4 | DN5 | |
|---|---|---|---|---|---|
| DN1 | 1 | 0.5915 | 0.6084 | 0.3660 | 0.1787 |
| DN2 | 0.5915 | 1 | 0.9991 | 0.8546 | 0.6394 |
| DN3 | 0.6084 | 0.9990 | 1 | 0.8516 | 0.6350 |
| DN4 | 0.3660 | 0.8546 | 0.8516 | 1 | 0.9356 |
| DN5 | 0.1787 | 0.6394 | 0.6350 | 0.9356 | 1 |
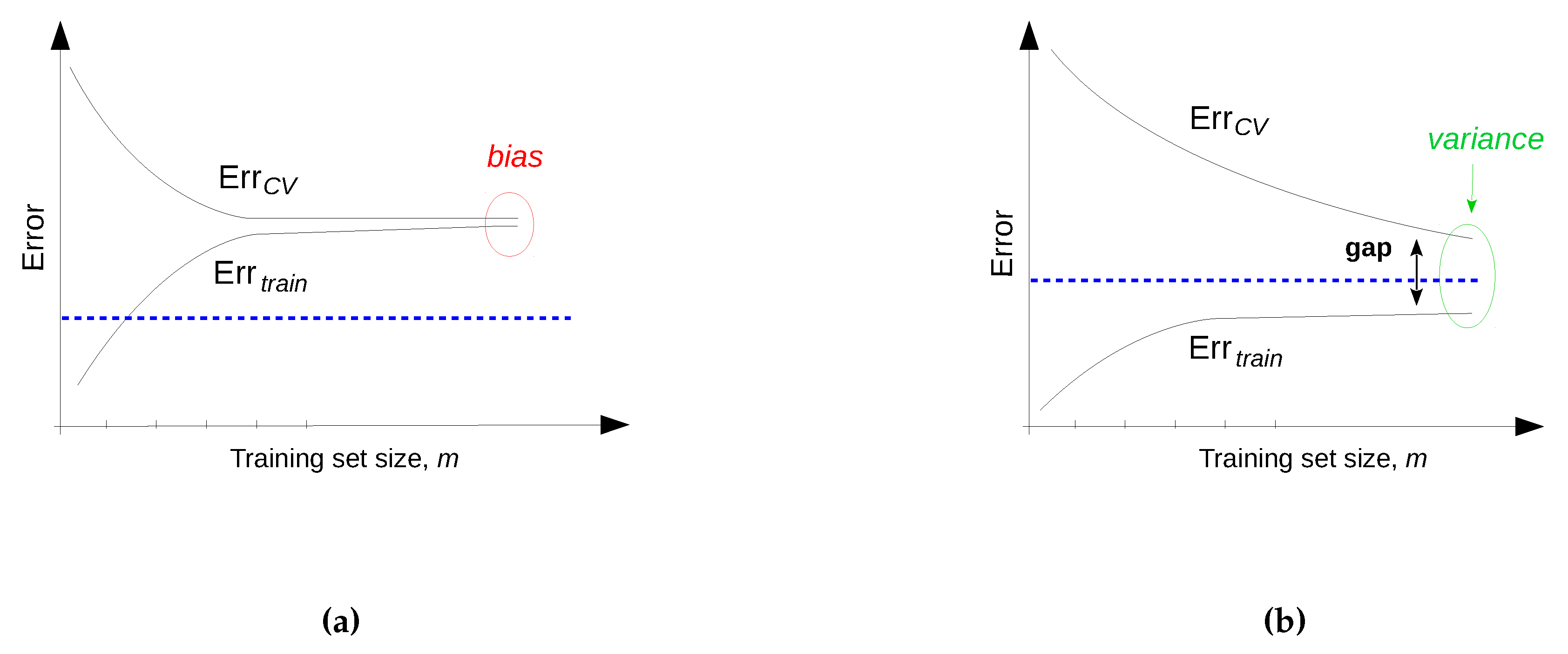
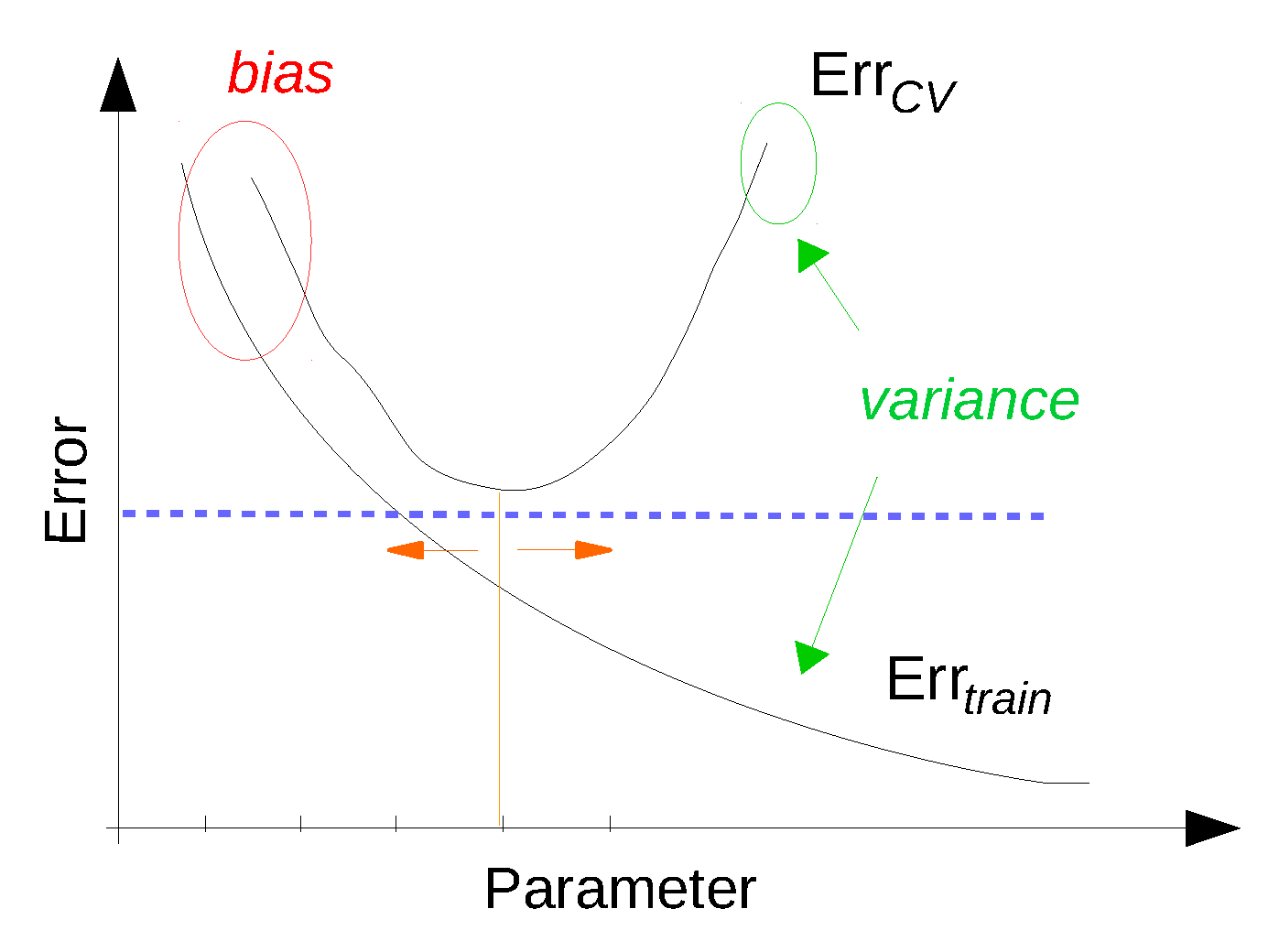
| Diagnosed Problem | Solution |
|---|---|
| The model is suffering from high variance | Utilize more training data |
| Try a smaller set of features | |
| Reduce the model complexity | |
| Increase regularization (* for parametric models) | |
| The model is suffering from high bias | Reduce the number of training instances (also increase speed) |
| Obtain additional features | |
| Increase the model complexity | |
| Decrease regularization (* for parametric models) | |
| Convergence problem | Use more training iterations |
| Reduce the learning rate (* for parametric models) |
| dell1 | dell2 | dell3 | dell4 | dell5 | ipad1 | ipad2 | ipad3 | iphone1 | iphone2 | iphone3 | iphone4 | nokia1 | nokia2 | ← predicted |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 164 | 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | dell1 |
| 0 | 190 | 61 | 7 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 5 | 1 | dell2 |
| 0 | 36 | 217 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | dell3 |
| 0 | 3 | 1 | 472 | 34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 2 | dell4 |
| 0 | 0 | 2 | 31 | 576 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | dell5 |
| 0 | 44 | 18 | 5 | 0 | 58 | 37 | 0 | 0 | 0 | 0 | 0 | 4 | 2 | ipad1 |
| 0 | 27 | 12 | 1 | 1 | 7 | 82 | 0 | 0 | 0 | 0 | 0 | 8 | 5 | ipad2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 299 | 0 | 0 | 0 | 0 | 0 | 0 | ipad3 |
| 3 | 3 | 2 | 2 | 0 | 1 | 0 | 0 | 342 | 0 | 0 | 0 | 2 | 0 | iphone1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 257 | 0 | 0 | 0 | 0 | iphone2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 137 | 0 | 0 | 0 | iphone3 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 86 | 0 | 0 | iphone4 |
| 0 | 3 | 0 | 7 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 536 | 284 | nokia1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 208 | 617 | nokia2 |
| Algorithm | Confusion Matrix | Precision | Recall | ||||
|---|---|---|---|---|---|---|---|
| Dell | Ipad | Iphone | Nokia | ← Predicted | |||
| k-NN | 1807 | 1 | 0 | 12 | dell | 0.935 | 0.993 |
| 111 | 479 | 0 | 21 | ipad | 0.98 | 0.784 | |
| 8 | 9 | 824 | 1 | iphone | 1 | 0.979 | |
| 7 | 0 | 0 | 1653 | nokia | 0.98 | 0.996 | |
| weighted average [%] → | 96.7 | 96.6 | |||||
| Decision trees | 1807 | 1 | 0 | 12 | dell | 0.99 | 1 |
| 111 | 479 | 0 | 21 | ipad | 0.995 | 0.992 | |
| 8 | 9 | 824 | 1 | iphone | 0.998 | 0.993 | |
| 7 | 0 | 0 | 1653 | nokia | 0.997 | 0.998 | |
| weighted average [%] → | 99.7 | 99.7 | |||||
| Logistic regression | 1807 | 1 | 0 | 12 | dell | 0.973 | 0.982 |
| 111 | 479 | 0 | 21 | ipad | 0.916 | 0.84 | |
| 8 | 9 | 824 | 1 | iphone | 0.966 | 0.884 | |
| 7 | 0 | 0 | 1653 | nokia | 0.939 | 0.999 | |
| weighted average [%] → | 95.3 | 95.3 | |||||
| Neural networks | 1807 | 1 | 0 | 12 | dell | 0.443 | 0.699 |
| 111 | 479 | 0 | 21 | ipad | 0.6 | 0.005 | |
| 8 | 9 | 824 | 1 | iphone | 0.627 | 0.6 | |
| 7 | 0 | 0 | 1653 | nokia | 0.398 | 0.3 | |
| weighted average [%] → | 47.9 | 46.2 | |||||
| dell | ipad | iphone | nokia | ← predicted |
|---|---|---|---|---|
| 1820 | 0 | 0 | 0 | dell |
| 0 | 611 | 0 | 0 | ipad |
| 0 | 0 | 842 | 0 | iphone |
| 0 | 0 | 0 | 1660 | nokia |
| I: Custom Approach [12] | II: Proposed Methodology Section 3 | Recommendations. | ||
|---|---|---|---|---|
| Understanding the problem domain | Problem formulation | Stated classification problem✓ | Stated classification problem✓ | Use guidelines in Section 2 |
| Data collection | Collected Experimental data✓ | Experimental data from Repository✓ | Use real data | |
| Understanding the data | Data validation | - | 5 number summary✓ | Use visual and |
| Hypothesis validation | Visual techniques✓ | Computational techniques✓ | computational techniques | |
| Data pre-processing | Data cleaning | - | Th-based cleaning✓ | Ensure reliability of data |
| Data reduction | Histograms | Histograms with optimized granularity✓ | Find optimal data representation | |
| Data transformation | - | min-max normalization✓ | Increase computational efficiency | |
| Data mining | NN✓ | NN, k-NN, LR, DT✓ | Select and evaluate the most suitable algorithms | |
| Performance evaluation | Metrics | Accuracy, Recall | Precision, Recall✓ | Exploit best |
| Model selection | Custom approach | Cross-validation✓ | practices from the | |
| Results representation | Partial results | Complete results—confusion matrix✓ | data science community (Section 4.6) | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulin, M.; Fortuna, C.; De Poorter, E.; Deschrijver, D.; Moerman, I. Data-Driven Design of Intelligent Wireless Networks: An Overview and Tutorial. Sensors 2016, 16, 790. https://doi.org/10.3390/s16060790
Kulin M, Fortuna C, De Poorter E, Deschrijver D, Moerman I. Data-Driven Design of Intelligent Wireless Networks: An Overview and Tutorial. Sensors. 2016; 16(6):790. https://doi.org/10.3390/s16060790
Chicago/Turabian StyleKulin, Merima, Carolina Fortuna, Eli De Poorter, Dirk Deschrijver, and Ingrid Moerman. 2016. "Data-Driven Design of Intelligent Wireless Networks: An Overview and Tutorial" Sensors 16, no. 6: 790. https://doi.org/10.3390/s16060790
APA StyleKulin, M., Fortuna, C., De Poorter, E., Deschrijver, D., & Moerman, I. (2016). Data-Driven Design of Intelligent Wireless Networks: An Overview and Tutorial. Sensors, 16(6), 790. https://doi.org/10.3390/s16060790