Improving Kinematic Accuracy of Soft Wearable Data Gloves by Optimizing Sensor Locations
Abstract
:1. Introduction
2. Kinematic Model of the Thumb
2.1. Anatomy and Kinematics of the CMC-Joint
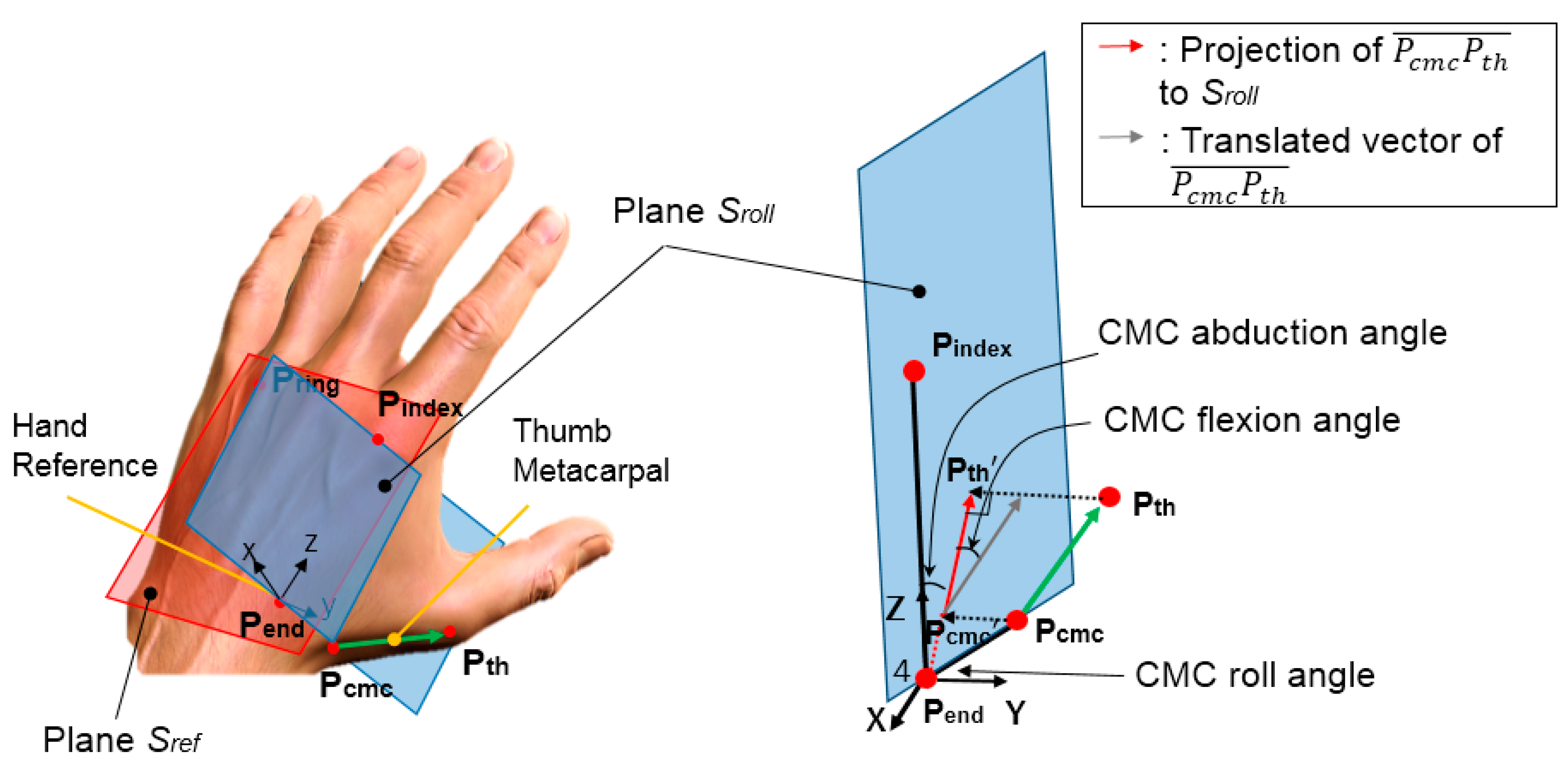
2.2. Proposed CMC-Joint Angle Definition
3. Optimal Bending Sensor Locations for CMC-Joint Angle Measurement
3.1. Sensor Selection and Characteriztion
3.2. Method Overview
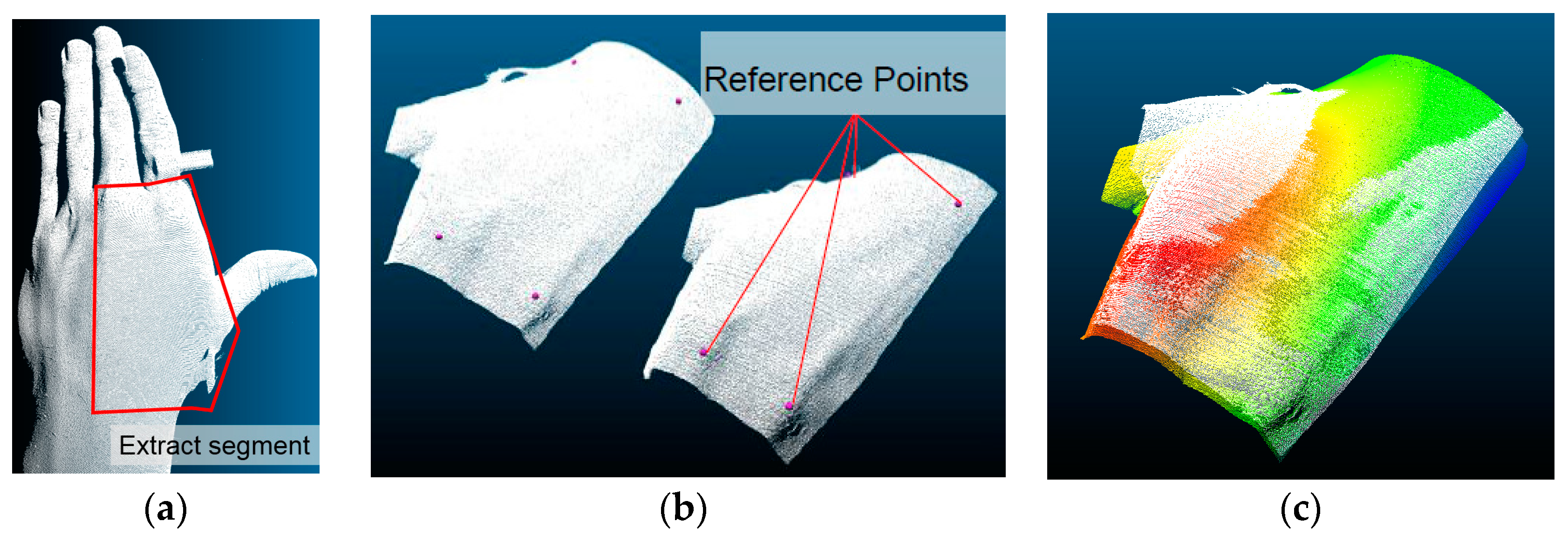
3.3. Experimental Design
3.4. Analysis
3.4.1. Data Conditioning
3.4.2. Estimation of Sensor Outputs
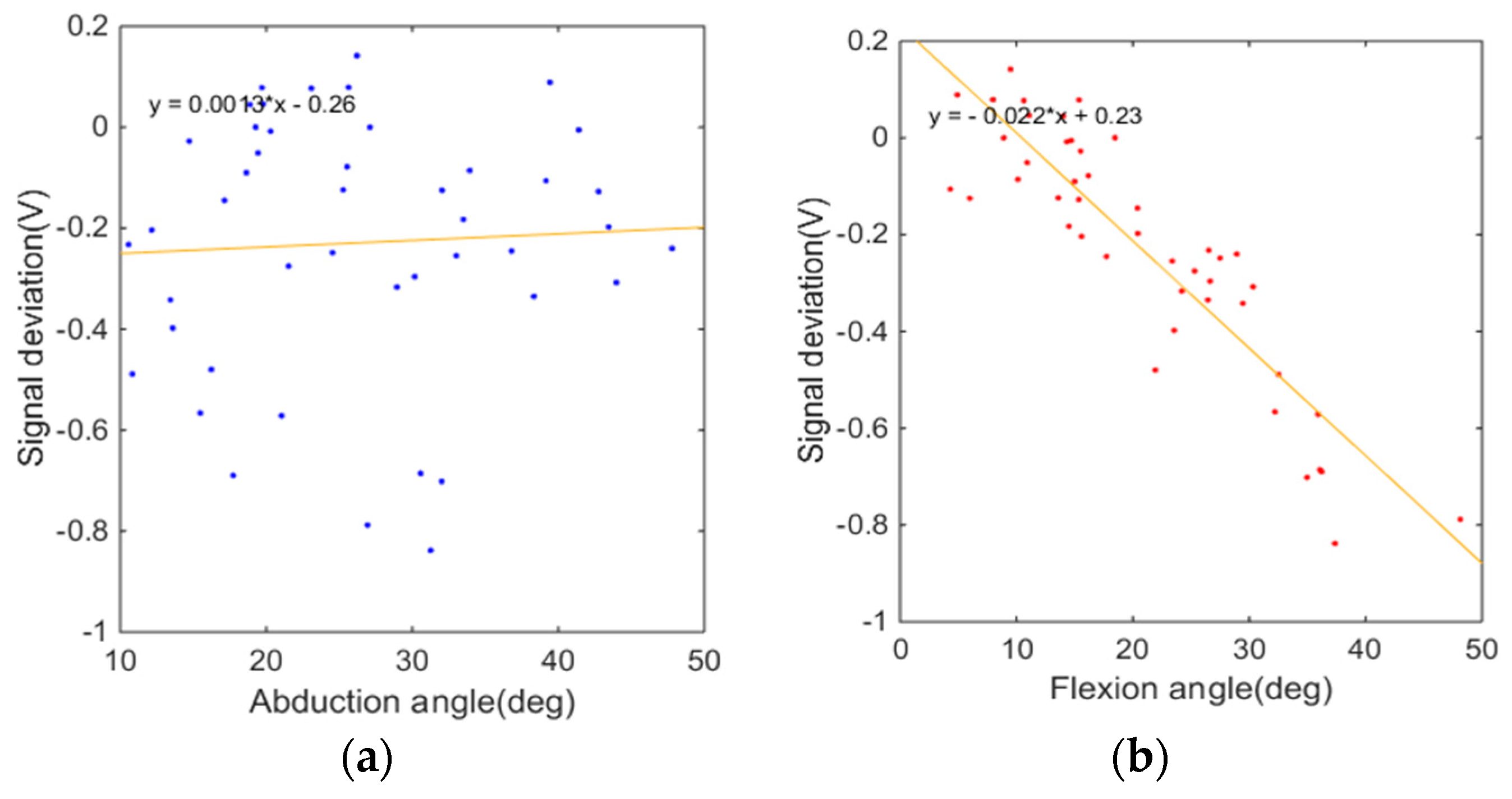
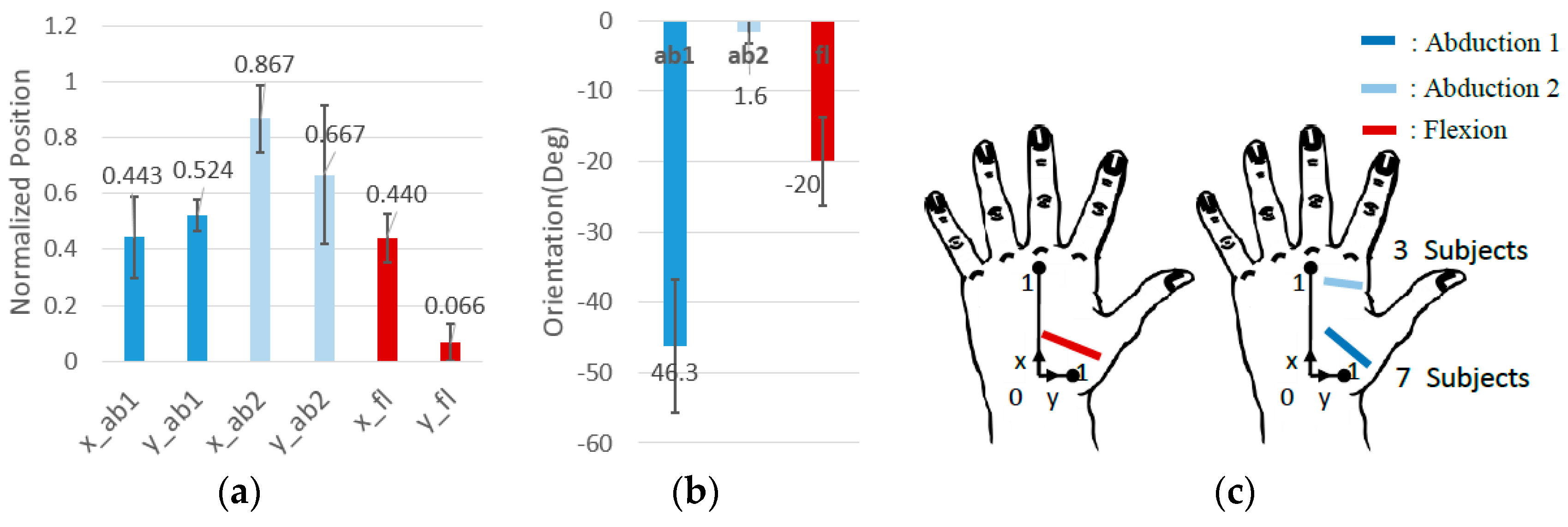
3.4.3. Optimizing Sensor Locations
3.4.4. Crosstalk Analysis for Optimally-Located Sensors
4. Experimental Evaluation
4.1. Experimental Protocol
4.2. Results
4.2.1. Crosstalk Magnitude
4.2.2. Accuracy of CMC-Joint Angle Estimation
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cook, J.R.; Baker, N.A.; Cham, R.; Hale, E.; Redfern, M.S. Measurements of wrist and finger postures: A comparison of goniometric and motion capture techniques. J. Appl. Biomech. 2007, 23, 70–78. [Google Scholar] [PubMed]
- Lorussi, F.; Scilingo, E.P.; Tesconi, M.; Tognetti, A.; Rossi, D.D. Strain sensing fabric for hand posture and gesture monitoring. IEEE Trans. Inf. Technol. Biomed. 2005, 9, 372–381. [Google Scholar] [CrossRef] [PubMed]
- Vanoglio, F.; Luisa, A.; Garofali, F.; Mora, C. Evaluation of the effectiveness of Gloreha (Hand Rehabilitation Glove) on hemiplegic patients. In Pilot Study; XIII Congress of Italian Society of Neurorehabilitation: Bari, Italy, 2013. [Google Scholar]
- Lee, S.W.; Landers, K.A.; Park, H.S. Development of a biomimetic hand exotendon device (BiomHED) for restoration of functional hand movement post-stroke. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 886–898. [Google Scholar] [PubMed]
- In, H.; Cho, K.J. Analysis of the forces on the finger joints by a joint-less wearable robotic hand, SNU Exo-Glove. In Converging Clinical and Engineering Research on Neurorehabilitation; Pons, L.J., Torricelli, D., Pajaro, M., Eds.; Springer: Berlin, Germany, 2013; pp. 93–97. [Google Scholar]
- Van Duinen, H.; Gandevia, S.C. Constraints for control of the human hand. J. Physiol. 2011, 589, 5583–5593. [Google Scholar] [CrossRef] [PubMed]
- Hollister, A.; Buford, W.L.; Myers, L.M.; Giurintano, D.J.; Novick, A. The axes of rotation of the thumb carpometacarpal joint. J. Orthop. Res. 1992, 10, 454–460. [Google Scholar] [CrossRef] [PubMed]
- Valero-Cuevas, F.J.; Johanson, M.E.; Towles, J.D. Towards a realistic biomechanical model of the thumb: The choice of kinematic description may be more critical than the solution method or the variability/uncertainty of musculoskeletal parameters. J. Biomech. 2003, 36, 1019–1030. [Google Scholar] [CrossRef]
- Crisco, J.J.; Halilaj, E.; Moore, D.C.; Patel, T.; Weiss, A.P.C.; Ladd, A.L. In vivo kinematics of the trapeziometacarpal joint during thumb extension-flexion and abduction-adduction. J. Hand Surg. Am. 2015, 40, 289–296. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.Y.; Pollard, N.S. Method for determining kinematic parameters of the in vivo thumb carpometacarpal joint. IEEE Trans. Biomed. Eng. 2008, 55, 1897–1906. [Google Scholar] [CrossRef] [PubMed]
- Griffin, W.B.; Findley, R.P.; Turner, M.L.; Cutkosky, M.R. Calibration and mapping of a human hand for dexterous telemanipulation. In Proceedings of the ASME IMECE 2000 Conference on Haptic Interfaces for Virtual Environments and Teleoperator Systems Symposium, Orlando, FL, USA, 5–10 November 2000; pp. 1–8.
- Lim, C.K.; Luo, Z.; Chen, I.M.; Yeo, S.H. A low cost wearable optical-based goniometer for human joint monitoring. Front. Mech. Eng. 2011, 6, 13–22. [Google Scholar] [CrossRef]
- Tognetti, A.; Lorussi, F.; Bartalesi, R.; Quaglini, S.; Tesconi, M.; Zupone, G.; de Rossi, D. Wearable kinesthetic system for capturing and classifying upper limb gesture in post-stroke rehabilitation. J. Neuroeng. Rehab. 2005, 2, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, B.S.; Lee, I.J.; Hsiao, P.C.; Yang, S.Y.; Chou, W. Data glove embedded with 6-DOF inertial sensors for hand rehabilitation. In Proceedings of the 2014 Tenth International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP), Kitakyushu, Japan, 27–29 August 2014; pp. 25–28.
- Quam, D.L.; Williams, G.B.; Agnew, J.R.; Browne, P.C. An experimental determination of human hand accuracy with a DataGlove. Proc. Hum. Factors Ergon. Soc. Ann. Meet. 1989, 33, 315–319. [Google Scholar] [CrossRef]
- Kessler, G.D.; Hodges, L.F.; Walker, N. Evaluation of the CyberGlove as a whole-hand input device. ACM Trans. Comput. Hum. Interact. 1995, 2, 263–283. [Google Scholar] [CrossRef]
- Gajdosik, R.L.; Bohannon, R.W. Clinical measurement of range of motion review of goniometry emphasizing reliability and validity. Phys. Ther. 1987, 67, 1867–1872. [Google Scholar] [PubMed]
- Simone, L.K.; Kamper, D.G. Design considerations for a wearable monitor to measure finger posture. J. Neuroeng. Rehabil. 2005, 2, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, D.H.; Park, H.S. Thumb joint angle estimation for soft wearable hand robotic devices. In Proceedings of the 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), Singapore, 11–14 August 2015; pp. 91–94.
- CloudCompare—Open Source project. Available online: http://www.cloudcompare.org (accessed on 20 February 2015).



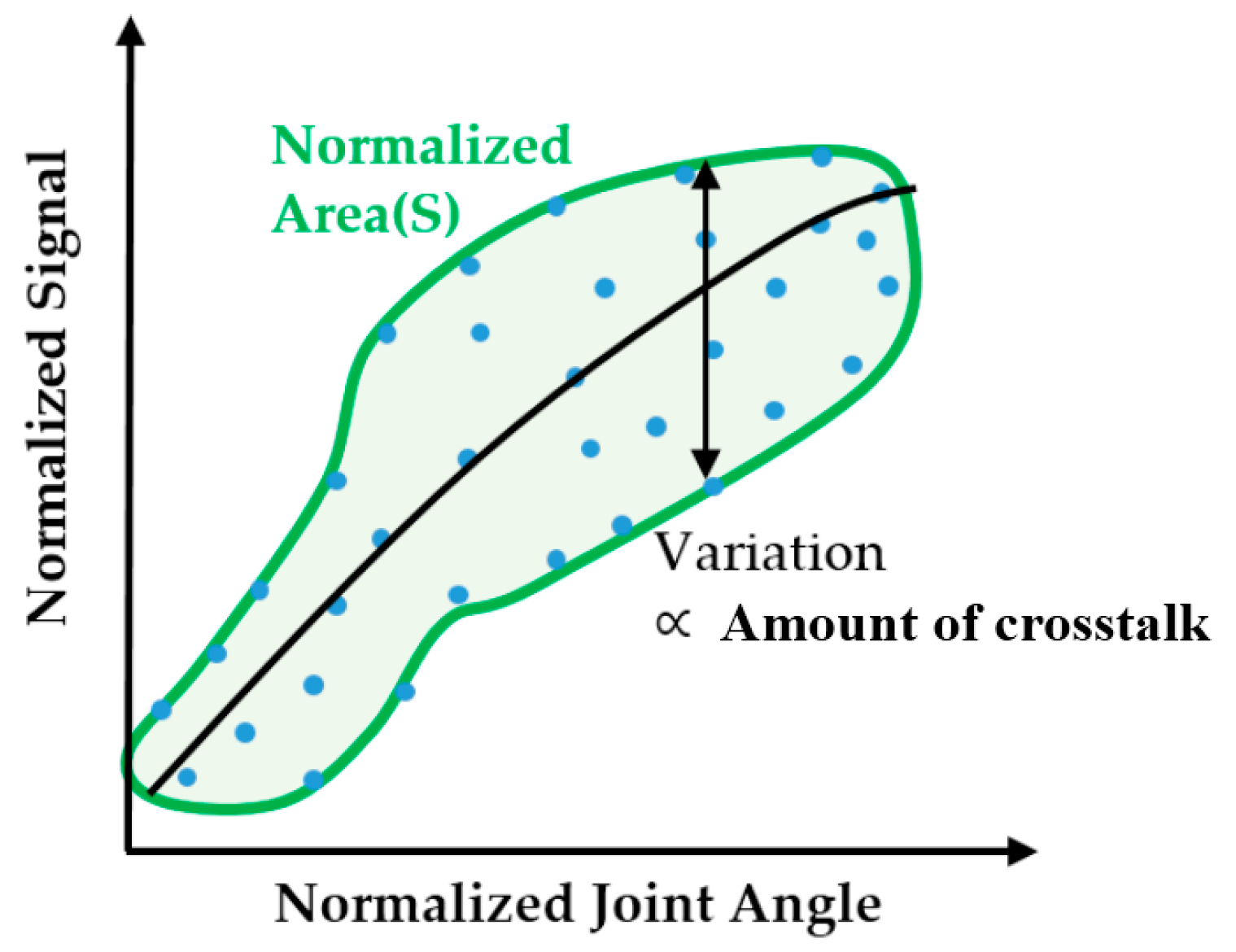


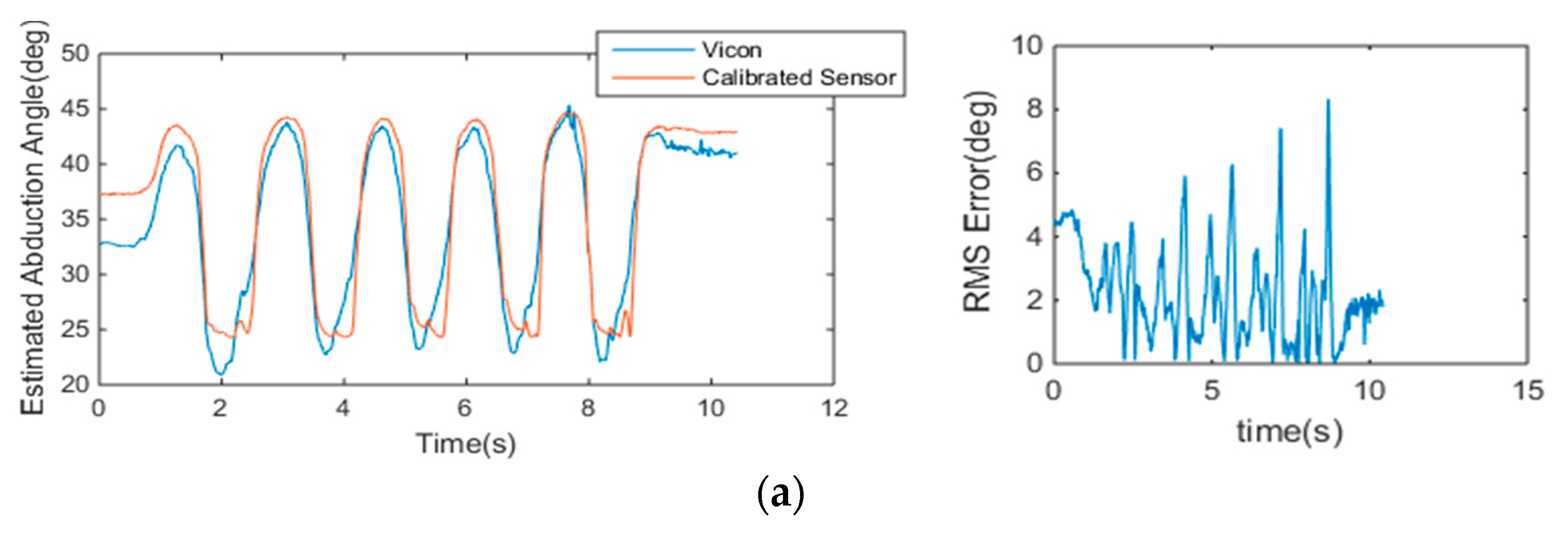

| Subject | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | Mean |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Normalized area (flexion sensor) | 0.384 | 0.234 | 0.190 | 0.349 | 0.154 | 0.316 | 0.307 | 0.315 | 0.176 | 0.324 | 0.275 |
| Normalized area (abduction sensor) | 0.255 | 0.275 | 0.239 | 0.367 | 0.372 | 0.308 | 0.341 | 0.353 | 0.203 | 0.298 | 0.298 |
| Subject | Normalized Area | ||
|---|---|---|---|
| Abduction Sensor 1 | Abduction Sensor 2 | Flexion Sensor | |
| S1 | 0.272 | 0.210 | 0.278 |
| S2 | 0.462 | 0.352 | 0.334 |
| S3 | 0.278 | 0.461 | 0.242 |
| S4 | 0.644 | 0.285 | 0.260 |
| Avg. | 0.281 ± 0.0581 | 0.279 ± 0.0399 | |
| Subject | RMSE (°) | |
|---|---|---|
| Abduction Sensor | Flexion Sensor | |
| S1 | 1.6 ± 1.1 | 1.6 ± 0.96 |
| S2 | 2.6 ± 1.1 | 4.6 ± 1.7 |
| S3 | 1.3 ± 0.94 | 3.1 ± 1.4 |
| S4 | 2.2 ± 1.2 | 2.0 ± 1.2 |
| Avg. | 1.9 ± 1.2 | 2.8 ± 1.9 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.H.; Lee, S.W.; Park, H.-S. Improving Kinematic Accuracy of Soft Wearable Data Gloves by Optimizing Sensor Locations. Sensors 2016, 16, 766. https://doi.org/10.3390/s16060766
Kim DH, Lee SW, Park H-S. Improving Kinematic Accuracy of Soft Wearable Data Gloves by Optimizing Sensor Locations. Sensors. 2016; 16(6):766. https://doi.org/10.3390/s16060766
Chicago/Turabian StyleKim, Dong Hyun, Sang Wook Lee, and Hyung-Soon Park. 2016. "Improving Kinematic Accuracy of Soft Wearable Data Gloves by Optimizing Sensor Locations" Sensors 16, no. 6: 766. https://doi.org/10.3390/s16060766
APA StyleKim, D. H., Lee, S. W., & Park, H.-S. (2016). Improving Kinematic Accuracy of Soft Wearable Data Gloves by Optimizing Sensor Locations. Sensors, 16(6), 766. https://doi.org/10.3390/s16060766





